Calculation of thermodynamic hydricities and the design of hydride donors for CO₂ reduction

Abstract

We have developed a correlation between experimental and density functional theory-derived results of the hydride-donating power, or “hydricity”, of various ruthenium, rhenium, and organic hydride donors. This approach utilizes the correlation between experimental hydricity values and their corresponding calculated free-energy differences between the hydride donors and their conjugate acceptors in acetonitrile, and leads to an extrapolated value of the absolute free energy of the hydride ion without the necessity to calculate it directly. We then use this correlation to predict, from density functional theory-calculated data, hydricity values of ruthenium and rhenium complexes that incorporate the pbnHH ligand—pbnHH = 1,5-dihydro-2-(2-pyridyl)-benzo[b]-1,5-naphthyridine—to model the function of NADPH. These visible light-generated, photocatalytic complexes produced by disproportionation of a protonated-photoreduced dimer of a metal-pbn complex may be valuable for use in reducing CO₂ to fuels such as methanol. The excited-state lifetime of photoexcited [Ru(bpy)₂(pbnHH)]²⁺ is found to be about 70 ns, and this excited state can be reductively quenched by triethylamine or 1,4-diazabicyclo[2.2.2]octane to produce the one-electron-reduced [Ru(bpy)₂(pbnHH)]⁺ species with half-life exceeding 50 μs, thus opening the door to new opportunities for hydride-transfer reactions leading to CO₂ reduction by producing a species with much increased hydricity.

Natural photosystems in plants convert CO₂ to carbohydrates using absorbed photons for energy and water as a reducing agent. The light energy is converted to chemical energy in the form of ATP and reduced NADH in a complex sequence in which a reduced hydrogen equivalent (i.e., hydride) is stored by the reduction of NAD⁺. The ATP and NADH are used to reduce CO₂ in light-independent processes through net hydride ion transfer reactions. In artificial photochemical CO₂ reduction, CO and formate have been successfully produced (1); however, it is very difficult to produce methanol and methane because of the involvement of more than two electrons and two protons. We previously obtained clear evidence of photochemical and radiolytic formation of the reduced form of a transition-metal complex having a NADH-like ligand (2), and this reduced form has been shown separately to catalyze the reduction of acetone to 2-propanol under acidic conditions (3) and to transfer a hydride ion to the trityl cation (4). These results opened a new door for photocatalytic hydride (or proton-coupled electron) transfer reactions originating from metal-to-ligand charge-transfer (MLCT) excited states of metal complexes. It has been shown that 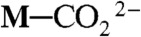can be converted to M─CO by acid-base reaction, and that NaBH₄ can reduce M─CO to M─CHO^-, M─CH₂OH^- (precursor of methanol), and 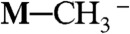(a precursor of methane), when M = Ru(bpy)₂(CO)²⁺ (5, 6). NaBH₄ can also reduce M─CO to M─CHO^-, M─CH₂OH^-, and 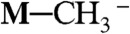, when M = Re(Cp)(NO)(CO)⁺ (7). Can we use photogenerated hydride donors as a replacement for NaBH₄? How strong is [Ru(bpy)₂(pbnHH)]²⁺ as a hydride donor?

In the present work we report the results of photoexcitation of and reductive quenching of this reduced form of the model complex and investigate the thermodynamic hydricities of the reduced 2-(2-pyridyl)-benzo[b]-1,5-naphthyridine (pbn) complexes through density functional theory (DFT)-based computations.

Koizumi and Tanaka (3) reported the electrocatalytic ability of [Ru(bpy)₂(pbn)]²⁺ (bpy = 2,2′-bipyridine; see Fig. 1) for the reduction of acetone to isopropanol, presumably with [Ru(bpy)₂(pbnHH)]²⁺—pbnHH = 1,5-dihydro-2-(2-pyridyl)-benzo[b]-1,5-naphthyridine—as the key intermediate. It has been proposed that this complex can act as a catalyst because it contains bulky bpy ligands that protect against the formation of the Ru dimer via coupling of the C-centered radicals. In collaboration with Tanaka and coworkers, we recently investigated the excited-state properties of [Ru(bpy)₂(pbn)]²⁺ and photochemical production of [Ru(bpy)₂(pbnHH)]²⁺ (2, 8). Flash photolysis experiments showed that the 532-nm excitation of the [Ru(bpy)₂(pbn)]²⁺ complex yields its metal-to-ligand charge-transfer (MLCT) excited state (d → π_pbn∗) with a lifetime of 140 ns in acetonitrile and 30 ns in water (pH above 5). The excited state can be readily quenched by amines, and the one-electron-reduced (OER) species is produced. The product obtained by continuous photolysis (> 400 nm) of a CH₃CN or dimethylformamide solution containing [Ru(bpy)₂(pbn)]²⁺ and an amine was identified as [Ru(bpy)₂(pbnHH)]²⁺ by comparing the spectroscopic and other properties (i.e, UV–visible, NMR, electrospray ionization MS, etc.) to those of [Ru(bpy)₂(pbnHH)]²⁺ prepared by a Na₂S₂O₄ reduction. Furthermore, both [Ru(bpy)₂(pbn)]²⁺ and [Ru(bpy)₂(pbnHH)]²⁺ were characterized by X-ray single-crystal diffraction.

Fig. 1.

Structures of various Ru complexes, where [Ru] indicates Ru(bpy)₂.

We further investigated the mechanistic pathways of formation of the [Ru(bpy)₂(pbnHH)]²⁺ species from [Ru(bpy)₂(pbn)]²⁺ in an aqueous medium using pulse radiolysis and ⁶⁰Co irradiation (8). Formation of the OER species as a result of reduction by a solvated electron (k = 3.0·10¹⁰ M^-1 s^-1) or (k = 4.6·10⁹ M^-1 s^-1) is followed by protonation of the reduced species to form [Ru(bpy)₂(pbnH^•)]²⁺ with pK_a = 11. Dimerization (k_d = 2.2·10⁸ M^-1 s^-1) of the singly reduced protonated species, [Ru(bpy)₂(pbnH^•)]²⁺, takes place at pH < 9, and this is followed by disproportionation of the dimer in parallel with the cross-reaction between the singly reduced protonated and nonprotonated species (k_cross = 1.2·10⁸ M ^-1 s^-1) at near pH 11 resulting in the formation of the final [Ru(bpy)₂(pbnHH)]²⁺ product together with an equal amount of the starting complex, [Ru(bpy)₂(pbn)]²⁺. At 0.2 °C, a dimeric intermediate, most likely a π-stacked dimer, was observed that decomposes thermally to an equimolar mixture of [Ru(bpy)₂(pbnHH)]²⁺ and [Ru(bpy)₂(pbn)]²⁺ (pH < 9). We provided further evidence for the π-stacked dimer mechanism by demonstrating stereospecific hydrogenation to give Λ-(S)- and Λ-(R)- [Ru(bpy)₂(pbnDD)]²⁺ {pbnDD = 5,10-dideutero-2-(2-pyridyl)benzo[b]-1,5-naphthyridine} upon visible-light irradiation in a D₂O/CH₃CN/triethylamine solution (9).

Recently, we have studied the reactivity of a Ru complex containing the iso-pbn ligand [iso - pbn = 3-(pyrid-2′-yl)-4-azaacridine], which is a structural isomer of the pbn moiety (4, 10). In [Ru(bpy)₂(iso─pbnHH)]²⁺ the hydride center is not sterically hindered compared to [Ru(bpy)₂(pbnHH)]²⁺, which affects the mechanism of its formation and reactivity toward hydride acceptors. Reduction of [Ru(bpy)₂(iso─pbn)]²⁺ proceeds through the formation of an unstable C─C─bonded dimer and results in a doubly reduced, doubly protonated species. The rate of hydride transfer to trityl cation was found to be approximately 25 times faster for [Ru(bpy)₂(iso─pbnHH)]²⁺ compared to [Ru(bpy)₂(pbnHH)]²⁺ (4). This difference was attributed to the more sterically hindered environment around hydride-donor center in [Ru(bpy)₂(pbnHH)]²⁺.

Model

DuBois and coworkers (11–14) investigated the thermodynamic hydride-donor abilities (i.e., hydricities) of transition-metal hydrides, formyl complexes, and NADPH-model complexes, such as 1-benzyl-1,4-dihydronicotinamide, in order to develop CO₂-reduction catalysts in CH₃CN. The thermodynamic hydricity of a species AH^- (or BH) is defined as the standard free energy change for the reaction:

[1A]

[1B]

in a specified solvent. We denote the hydricity of the reaction in Eq. 1A to be:

[2]

where is the thermodynamic hydricity and the various G^∗ values correspond to absolute free energies of the species indicated. In this work we denote the standard state of one mole per liter in solution with the asterisk symbol to distinguish it from one atmosphere of pressure in the gas phase, the quantum chemical standard state for all species, which we denote by the symbol “o”. The thermodynamic hydricity defined in Eq. 2 can be determined experimentally by means of a thermodynamic cycle, as shown in SI Appendix, Fig. S1, but the difficulty in calculating the absolute standard free energy of the solvated hydride ion precludes its direct theoretical estimation. Previous ab initio approaches to calculating the thermodynamic hydricity of hydride-donor molecules have circumvented this problem in one of two ways. One is by calculating the free-energy change of isodesmic reactions (Of the several definitions of an isodesmic reaction in use, here we use the term to refer to a chemical reaction in which the type of chemical bonds broken in the reactants is the same as the type of bonds formed in the reaction products.) with a reference hydride-donor molecule for which the thermodynamic hydricity has been experimentally determined (15, 16). The other is to employ a similar isodesmic reaction scheme to calculate values and then empirically fit the value of G^∗(H^-), the absolute free energy of the solvated hydride ion in a specified solvent (usually acetonitrile), to obtain the best overall agreement between calculated and experimental values of 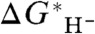. With this assumption, the value of G^∗(H^-) was found to be -400.7 and -404.7 kcal/mol (1 kcal = 4.18 kJ) in two recent studies (16, 17).

In the thermodynamic cycle in SI Appendix, Fig. S1, is the heterolysis standard free energy, the acid-dissociation standard free energy, and the hydricity of H₂, and is assigned a value of 76 kcal/mol in acetonitrile by DuBois and others (18, 19). This is a difficult quantity to calculate or to measure because it involves the solvation of both the gas-phase proton and the gas-phase hydride ion. Any hydricity scale based on the value of 76 kcal/mol would be internally consistent, but would be in error in the actual hydricities by any error in the value of 76 kcal/mol.

The key feature of the isodesmic reaction approach is that the standard free energy of reaction of a hydride donor (AH^-) with the hydride acceptor corresponding to a different hydride donor (BH^-) is the difference between the two thermodynamic hydricities,

[3A]

and

[3B]

This suggests defining, in analogy with redox couples, “hydricity half-reactions” (HHR) of the form AH^- → A (i.e., half of a hydride-transfer reaction as in Eq. 3A), with corresponding standard free-energy change:

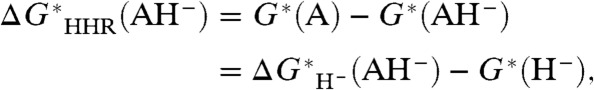[4A]

so that the standard free energy change of Eq. 3A is:

[4B]

The benefit of the half-reaction convention is that the values

[4C]

can be readily calculated because they do not involve G^∗(H^-). Given a reference reaction and at least one value of , we can evaluate G^∗(H^-) and construct a scale of theoretical thermodynamic hydricities based on the isodesmic reaction scheme expressed by Eq. 4B. The solvent (in the present case, acetonitrile) is defined as the reference hydride acceptor with a zero value of so that, from Eq. 4A, . 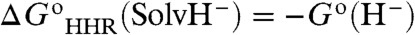Here, SolvH^- represents the hydride ion in the solvent, often written as or .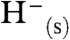

We mention in passing that, in the case of acetonitrile as the solvent, we determined that a useful picture for describing the structure of the solvated hydride ion is as a molecule of “hydrided acetonitrile,” CH₃CHN^-, that is, isoelectronic with and similar in structure to acetaldehyde, CH₃CHO. The computed value (-404.5 kcal/mol) of G^∗(H^-) ≈ G^∗([CH₃CHN^-·(CH₃CN)]_(S)) - 2G^∗(CH₃CN_(liq)), where the subscript “(S)” indicates that the CH₃CHN^- explicitly solvated by one acetonitrile molecule is immersed in a polarizable continuum model (PCM) of the surrounding bulk solvent, and the subscript “(liq)” refers to the standard state of the pure liquid solvent (20), is quite close to the previously fitted values, and reasonably close to the value of ΔG^∗(H^-) = -412.7 kcal/mol that we obtain in this work from extrapolation of experimental 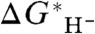values using our hydricity half-reaction procedure (see below). The straightforward calculation of the hydride ion in a PCM treatment (21–23) of the solvent with the methodology employed here gives -391.4 kcal/mol.

The hydricity of 1-benzyl-1,4-dihydronicotinamide (BNAH) is reported to be 59 ± 2 kcal mol^-1 (12). This species is about in the middle of the hydricity scale defined by DuBois, with Ph₃CH as the weakest hydride donor (99 kcal mol^-1) and [HRh(dppb)₂] as the strongest hydride donor [dppb = 1,2-bis(diphenylphosphinato)benzene, 34 ± 2 kcal mol^-1]. Metal hydrides such as [Ru(bpy)(tpy)H]⁺ (tpy = 2,2′:6′,2″-terpyridine) react with CO₂ to form the formato complex (24, 25); however, [Ru(bpy)₂(pbnHH)]²⁺ does not react with CO₂ (4). Although C─H hydrides such as [Ru(bpy)₂(pbnHH)]²⁺ can be photoregenerated, they are expected to be weak hydride donors. M─H hydrides can be stronger hydride donors, but their photogeneration may be difficult.

We have carried out calculations of the thermodynamic hydricity of [Ru(bpy)₂(pbnHH)]²⁺, [Ru(bpy)₂(iso-pbnHH)]²⁺, and the hydrided forms of possible hydride acceptor molecules for intermolecular H^- transfer reactions related to CO₂ reduction. Because we found that [Ru(bpy)₂(pbnHH)]²⁺ is not a sufficiently strong hydride donor for such reactions, we pursued the possibility of increasing the hydricity of [Ru(bpy)₂(pbnHH)]²⁺. Here, our theoretical calculations predict that a further reduced [Ru(bpy)₂(pbnHH)]⁺ species formed by another visible-light MLCT excitation/reductive-quenching step starting from the [Ru(bpy)₂(pbnHH)]²⁺ complex can create a species with a dramatically increased hydricity that, in principle, could donate its hydride to M─CO species to form M─CHO^-, the most difficult step in CO₂ reduction to methanol.

Computational Methods

All calculations quoted here were carried out using DFT as implemented in the Gaussian 03 program package (26). Unless otherwise specified, they correspond to the use of a hybrid functional and an all-electron double-zeta with polarization basis for each atom, except for transition metal atoms for which an effective core potential (ECP) and at least a double-zeta with polarization basis was employed. All structure optimizations and vibrational frequency calculations were carried out using a PCM incorporating the dielectric constant of the acetonitrile solvent. Further details of the calculations are provided in SI Appendix.

The approach described by Eq. 4A handles all cases considered here with one important exception: H₂. In the case of the gas-phase H₂ hydride donor, we employ the absolute free energy of the solvated proton in acetonitrile solution (-266.5 kcal/mol) recommended by Kelly et al. (20). This value is based on the gas-phase free energy of the proton (-6.3 kcal/mol) and its experimental solvation energy (-260.2 kcal/mol) at standard conditions. The use of the experimentally derived value is problematic for the case of H₂ because there is no solvation of the reactant molecule to compensate for any error in G^∗(H^-) arising from systematic errors in the implicit solvation model in the calculations from which its value was determined.

Results and Discussion

Calculation of Hydricities.

According to Eqs. 2 and 4C, we would expect the experimental thermodynamic hydricity, , to be a linear function of the experimental hydricity half-reaction, , with a slope of unity and an intercept of G^∗(H^-), the constant absolute free energy of the solvated hydride ion. Therefore, in the absence of any systematic error in the calculated value of the standard free energy of the hydricity half-reaction, 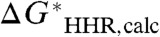, we would expect the least-squares linear fit to behave in the same way. However, it is more convenient to invert this relation, and plot the calculated 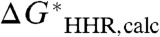, henceforth denoted simply as 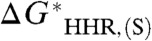, versus the experimental 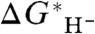, with intercept 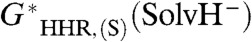. Because the hydricity of the hydride ion in the solvent is zero, this implies that the best-fit value of G^∗(H^-), denoted , is the negative of .

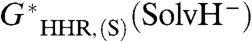Such a plot is shown in Fig. 2 for five hydride donors with “known” experimental hydricity. Although the hydricities of these species may depend on the hydricity of H₂, we do not include H₂ in this calibration because of the aforementioned difficulty in computing its hydricity half-reaction, and also because, as will be shown below, it is an “outlier” in a plot such as Fig. 2. We see that the linear correlation between 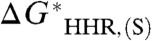and the experimental 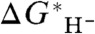is very good, with correlation coefficient r = 0.9979. However, the slope of the line is 0.9300 rather than unity, implying a small systematic dependence of on the value of , probably a differential solvation error in 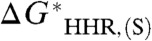arising from deficiencies in the solvation model. The intercept (i.e., zero of 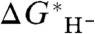) is 412.7 kcal/mol, giving a value of -412.7 kcal/mol for 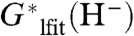, where the subscript “lfit” indicates a quantity with a value based on the linear fit shown in Fig. 2. We note that the donation of a hydride ion from type AH^-, AH, or AH⁺ hydride donors results in the HHR’s involving A and AH^-, A⁺ and AH, or A²⁺ and AH⁺, respectively. In all cases, one of the species of each pair will dominate the 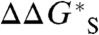of the HHR so that systematic error in the solvation free energy of the dominant species will not be canceled. There could also be residual systematic error in the computed arising from deficiencies in the electronic structure method and basis, and from the fact that the hydride donor and its conjugate acceptor differ by two electrons and a proton. It is therefore best to regard the specific correlation between the experimental 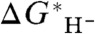and calculated 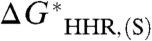in Fig. 2 as pertaining to the present treatment of the species considered here.

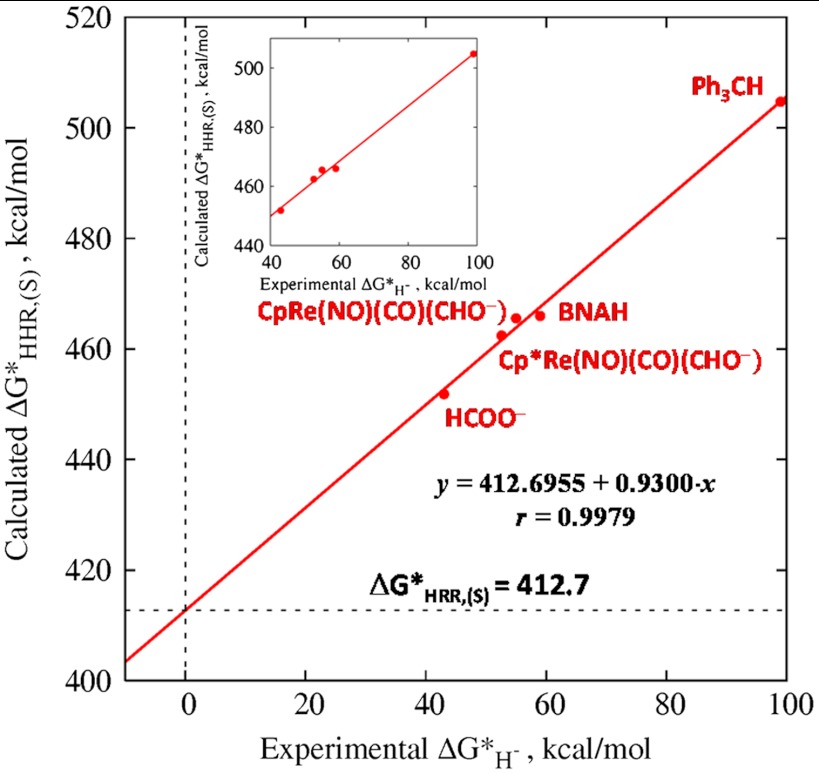
Fig. 2.

Correlation between the calculated value of 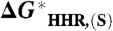and 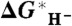based on five species with known experimental hydricity in acetonitrile (red points): formate anion, Cp^∗ Re(NO)(CO)₂(CHO^-), CpRe(NO)(CO)₂(CHO^-), BNAH, and Ph₃CH. The equation of the least-squares linear fit, the correlation coefficient, and the intercept are also indicated. (Inset) Blow-up of the fitted region.

To the extent that the slope of the line in Fig. 2 differs from unity, it reflects the degree of breakdown of any isodesmic scheme based on taking differences between 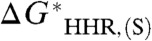values. Also, the straightforward estimation of experimental hydricities (denoted by the addition of a prime to the superscript) based on calculated values,

[5]

would similarly break down. We therefore seek to incorporate the empirically derived correction to the slope of the correlation in Fig. 2. We should point out that there should be no error arising from differential solvation for the case of because the hydride donor and hydride acceptor are the same (the solvent) on both sides of the isodesmic relation—i.e., the best-fit line should yield the correct value of .

The plot in Fig. 2 can be inverted to yield the predicted value of the experimental hydricity as a function of the calculated hydricity half-reaction as

[6]

where the linear correlation is used to obtain the “lfit” approximation to the hydricity of a given hydride donor from the calculated free-energy change of its hydricity half-reaction and the extrapolated value of the absolute free energy of the solvated hydride ion. This line is shown in a plot of Eq. 6 for the experimental calibration points corresponding to the five species in Fig. 2 as the red line and points, respectively, in Fig. 3.

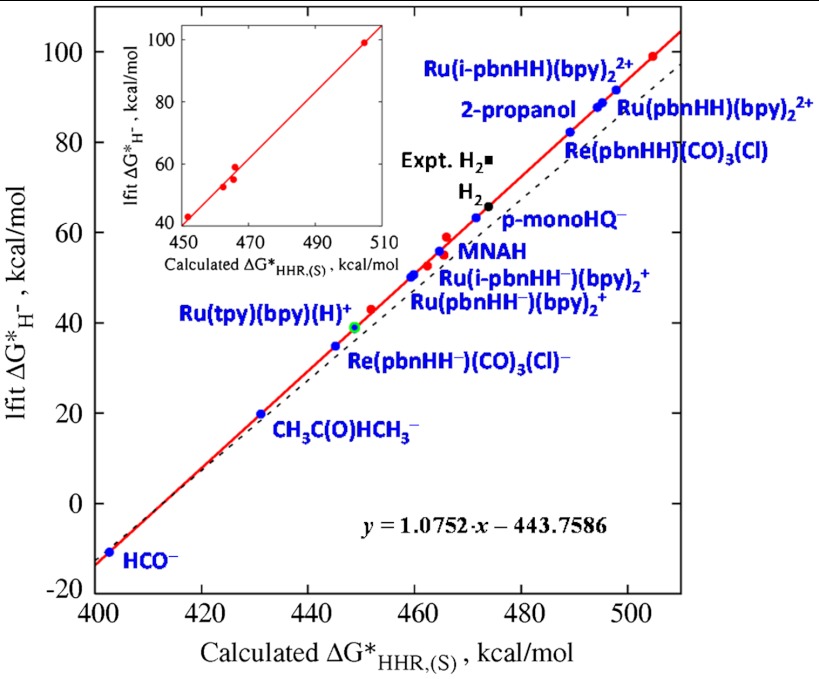
Fig. 3.

Predicted values of as a function of the computed for the five calibration species from Fig. 2 (red points), the least-squares fit to the five calibration points (red line), the predicted values of the additional hydride donors listed in Table 1 (blue points), and the straightforward ΔG^∗′(H^-) prediction based on Eq. 5 (dashed line). The equation of the least-squares linear fit and the “experimental” (black square) and predicted values (black point) of 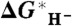(H₂) are also indicated. The experimental value of Ru(tpy)(bpy)(H)⁺ is indicated by the green open circle. (Inset) Blow-up of the fitted region.

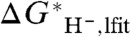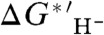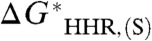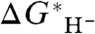The dashed line in Fig. 3 shows the values obtained by application of Eq. 5. This prediction is seen to deviate from the best-fit red line at high values of . Taking the difference between Eqs. 5 and 6, we find the correction term, denoted , between and values owing to the systematic dependence of on is:

[7]

The computed thermodynamic hydricities, , of various hydrides in acetonitrile are listed in Table 1, where they are compared to experimental values in the cases where they are available. For comparison, the value of in acetonitrile from Eq. 5 is also given. The values for all entries including the five calibration species (red points) are also plotted in Fig. 3 (blue points), and, of course, they all lie along the red line. The experimental and calculated values for H₂ are represented in Fig. 3 by the black square and the black point, respectively.

Table 1.

Calculated and experimental^* thermodynamic hydricities (kcal/mol) in CH₃CN solution

Hydride donor	Conjugate hydride acceptor	Expt.
CHO-	CO		−10.0	−10.8
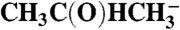	CH3COCH3		18.5	19.8
[Re(pbnHH•-)(CO)3(Cl)]-	[Re(pbnH•)(CO)3(Cl)]0		32.4	34.9
[RuII(bpy)(tpy)(H)]+	[RuII(bpy)(tpy)(NCMe)]2+	39†	36.0	38.7
HCOO-	CO2	43	39.1	42.1
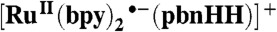	[RuII(bpy)2(pbnH•)]2+		46.6	50.1
	[RuII(bpy)2(iso-pbnH•)]2+		47.1	50.7
[Cp∗ ReI(NO)(CO)(CHO)]0	[Cp∗ ReI(NO)(CO)2]+	52.6	49.7	53.4
MNAH	MNA+		52.0	55.8
[CpReI(NO)(CO)(CHO)]0	[CpReI(NO)(CO)2]+	55	52.8	56.8
BNAH	BNA+	59	53.3	57.2
p - monohydroquinone-	p-benzoquinone		58.9	63.3
H2	H+	76	61.2	65.8
[Re(pbnHH)(CO)3(Cl)]0	[Re(pbnH+)(CO)3(Cl)]+		76.5	82.2
CH3C(OH)HCH3			81.6	87.7
[RuII(bpy)2(pbnHH)]2+	[RuII(bpy)2(pbnH+)]3+		82.6	88.7
[RuII(bpy)2(iso-pbnHH)]2+	[RuII(bpy)2(iso-pbnH+)]3+		85.2	91.5
Ph3CH	Ph3C+	99	92.0	98.9

^*Experimental data taken from refs. 12 and 14 unless otherwise indicated.

^†Value from our preliminary work.

The value of obtained by extrapolation in Fig. 2 of -412.7 kcal/mol is somewhat more negative that previous values (-400.7 and -404.7 kcal/mol) of G^∗(H^-) obtained as a fitting parameter in isodesmic schemes (16, 17). This can be understood by comparing the “Expt.” and “” columns in Table 1. If G^∗(H^-) were used as a fitting parameter to bring the average error in to zero, the resulting value of G^∗(H^-) would be -406.6 kcal/mol, in much better agreement with the previous estimates. This higher value of an isodesmic G^∗(H^-) compensates (on the average) for the correction term given by Eq. 7.

The most hydridic species have the smallest (most negative) hydricity values. One important feature of Table 1 is that, analogous to standard reduction potentials, any entry for a hydride donor in the table is predicted to have an exergonic reaction with the reverse hydricity half-reaction (i.e., the conjugate acceptor) of any entry in the table below it. For example, for the species with opposite direction 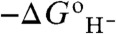of -56 kcal/mol, any hydride donor above it in the table should, in principle, be able to donate a hydride to it to form CpRe(NO)(CO)(CHO^-). These results are consistent with the experimental result of Koizumi and Tanaka (3), that the Ru─pbnHH complex can reduce acetone to isopropanol in acidic acetonitrile solution because the reaction is predicted to be essentially thermoneutral. We see that the Ru─pbnHH complex should be (within the expected error in the calculations) capable to transfer a hydride to protonated acetone, but not to acetone itself, indicating that the mechanism likely proceeds by protonation followed by hydride transfer.

It is noteworthy that the formyl anion is the strongest hydride donor listed in Table 1, indicating that it is extremely difficult to transfer a hydride ion to free CO. However, it is also apparent in the table that binding CO to a transition metal leads to a greatly reduced CHO^- hydricity in M─CHO^- complexes. Furthermore, the data in the table indicate that the addition of another electron to [Ru(bpy)₂(pbnHH)]²⁺ is predicted to be the key to opening the door to new opportunities for hydride-transfer reactions leading to CO₂ reduction by producing a species with much increased hydricity (see below). Finally, we see that the computed hydricity values are in fairly close agreement (i.e., within the expected combined error of the electronic structure method and solvation model used, with the exception of H₂ as mentioned above) with experimental values in the cases where they are known, including our preliminary value for the hydricity of [Ru(bpy)(tpy)(H)]⁺ (green open circle in Fig. 3).

Previously, we have determined that [Ru(bpy)₂(pbnHH)]²⁺ is formed by two [Ru(bpy)₂(pbnH^•)]²⁺ molecules undergoing bimolecular disproportionation (8). We can therefore think of [Ru(bpy)₂(pbnHH)]²⁺ as being a doubly reduced, doubly protonated species that “pools” the two electrons and two protons carried by the two [Ru(bpy)₂(pbnH^•)]²⁺ molecules. Our calculations predict that the triply reduced, doubly protonated species, 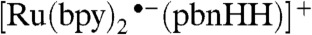, and other complexes containing the or pbnHH^•- ligands can be produced by an additional reduction. These highly reduced species can donate hydrides to become singly reduced, singly protonated complexes with the pbnH^• ligand. Calculations of the electronic spectra and spin density indicate that these are the same [Ru(bpy)₂(pbnH^•)]²⁺ species that disproportionate to form the corresponding pbnHH complexes (see below).

An Additional Reduction.

The [Ru(bpy)₂(pbnHH)]²⁺ complex exhibits a visible absorption peak between 400 and 450 nm in a region where the parent [Ru(bpy)₂(pbn)]²⁺ complex does not strongly absorb. Our TD-B3LYP/LANL2DZ calculations (SI Appendix, Fig. S2) show that this transition is primarily of the MLCT type. This may be followed by reductive quenching to produce a ligand anion radical in which the unpaired electron is delocalized over the π^∗ system of the two bpy ligands, as shown in SI Appendix, Fig. S3. Thus, it may be possible to generate a triply reduced, doubly protonated 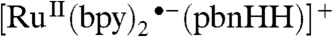species, as indicated in Eq. 8:

[8]

When the triply reduced, doubly protonated structure donates a hydride, it reforms Ru─pbnH^•. Our Mulliken atomic spin density results (SI Appendix, Fig. S4), are consistent with this; the unpaired electron is on the hydride carbon. Importantly, the exact location of the unpaired electron in 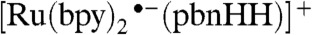does not matter, as it supplies the driving force for hydride transfer, and the [Ru(bpy)₂(pbnH^•)]²⁺ product following that hydride transfer is the species that can be “recycled” into [Ru(bpy)₂(pbnHH)]²⁺. With regard to that, our calculations (SI Appendix, Table S1) indicate that disproportionation of [Ru(bpy)₂(pbnH^•)]²⁺ is energetically favorable.

In the case of the iso-pbnHH complex, the reduction by a third electron and the “recycling” to iso-pbnH are similar to those for pbnHH [Eq. 9]. The excited state may be reductively quenched to produce an anion radical. TD-DFT analysis shows that transitions are in the minority.

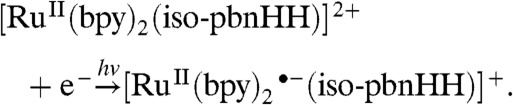[9]

Intermolecular Hydride Transfer.

It was mentioned above that metal hydride complexes such as [Ru(bpy)(tpy)(H)]⁺ are strong hydride donors, and this is corroborated by the position of [Ru(bpy)(tpy)(H)]⁺ near the top of Table 1, with a predicted hydricity in excellent agreement with the experimental value. Interestingly, we predict the hydricities of and to approach that of [Ru(bpy)(tpy)(H)]⁺, and even that of [Re(pbnHH^•-)(CO)₃(Cl)]^-, in which we calculated the unpaired third electron to be localized on the bpy part of the pbn ligand, which we predict to be an even stronger hydride donor.

Calculations (Table 1) indicate that the triply reduced, doubly protonated ruthenium complex is sufficiently hydridic to reduce a metal-bound carbonyl on CpRe(NO)(CO)₂, as indicated in Eq. 10:

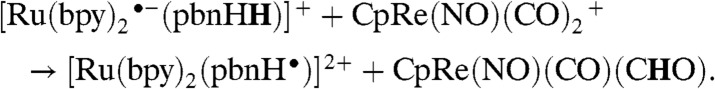[10]

The transition state (TS) for the complex (SI Appendix, Fig. S5) shows the hydride being transferred from the complex to the acceptor molecule. Both the and 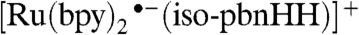species show promise for transferring a hydride ion to a metal-bound carbonyl group, because those reactions are exothermic with small enthalpic barriers but substantial free-energy barriers (SI Appendix, Table S2). Selected geometric parameters of the reactants and transition states are listed in SI Appendix, Table S3.

It is fortuitous that the two isomeric 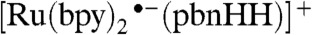complexes are both strong hydride donors and donate a hydride to form [Ru(bpy)₂(pbnH^•)]²⁺, which can disproportionate into [Ru(bpy)₂(pbnHH)]²⁺ and [Ru(bpy)₂(pbn)]²⁺. If the formation of 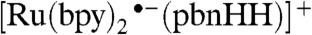could successfully be demonstrated, it would establish a second catalytic cycle that is interconnected with the one elucidated previously for the formation of the [Ru(bpy)₂(pbnHH)]²⁺ species (SI Appendix).

Chemical and Photochemical Reduction of [Ru(bpy)₂(pbnHH)]²⁺.

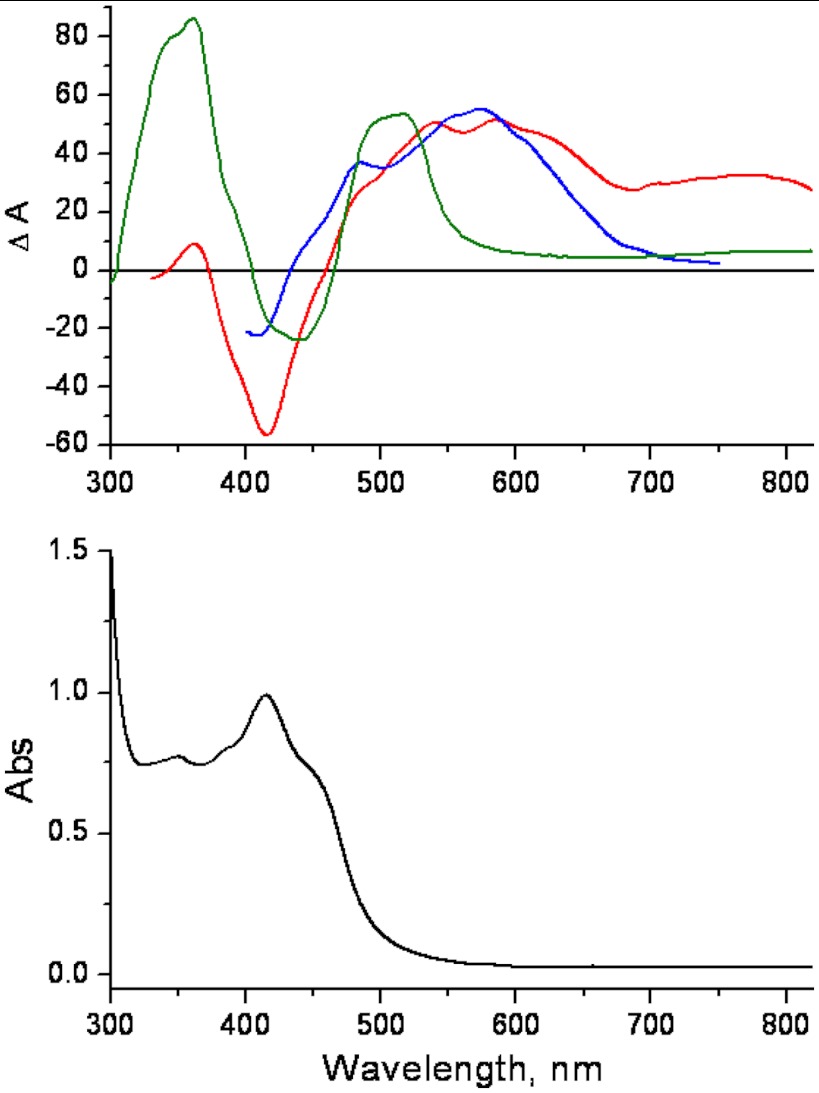
Photoexcitation into the MLCT transition of [Ru(bpy)₂(pbnHH)]²⁺ results in an excited state with a lifetime of about 70 ns (Fig. 4, Top: red difference spectrum) in acetonitrile. The excited state is readily quenched by an amine [0.1 M triethylamine (TEA) or 1,4-diazabicyclo[2.2.2]octane (DABCO)] producing a long-lived (half-life above 50 μs) one-electron-reduced species (Fig. 4, Top: blue difference spectrum). However, Na/Hg-amalgam reduction of [Ru(bpy)₂(pbnHH)]²⁺ yields the one-electron-reduced species (Fig. 4, Top: green difference spectrum) with the absorption band blue-shifted by about 50 nm. This blue shift can possibly be attributed to a corresponding red shift in the absorption of 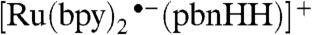arising from the interaction between the and an amine. The DABCO radical cation itself has no significant absorption above 520 nm (27). The one-electron-reduced species obtained by pulse radiolysis showed an identical spectrum to that obtained by Na/Hg reduction (4).

Fig. 4.

(Bottom) UV–visible spectrum of [Ru(bpy)₂(pbnHH)]²⁺ in acetonitrile; (Top) difference spectra of the excited state of [Ru(bpy)₂(pbnHH)]²⁺(red) measured after 355 nm excitation, from quenching of the excited state by DABCO (blue), and 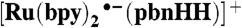from Na/Hg reduction of [Ru(bpy)₂(pbnHH)]²⁺ (green). The transient spectra of the excited state of [Ru(bpy)₂(pbnHH)]²⁺ were measured in dry deaerated acetonitrile after excitation by the third harmonic of a Nd³⁺YAG laser and probed by a Xe-pulsed lamp. The excited-state quenching experiments were conducted using similar conditions and using 100 mM of DABCO as a quencher (SI Appendix).

Irradiation of a solution containing [Ru(bpy)₂(pbn)]²⁺, TEA as a sacrificial electron donor, and [CpRe(NO)(CO)₂]⁺ did not produce [CpRe(NO)(CO)(CHO)]⁰. However, Na/Hg-amalgam reduction of [Ru(bpy)₂(pbnHH)]²⁺ produced [Ru(bpy)₂(pbnHH)]⁺ (experimental details in SI Appendix). The products of the reaction of [Ru(bpy)₂(pbnHH)]⁺ with [CpRe(NO)(CO)₂]⁺ in dry acetonitrile showed no NMR signal for Re ─CHO despite the fact that the reaction is predicted to have a ΔG^∗ of -6.7 kcal/mol. However, the products of electron- and hydride-transfer reactions, [Ru(bpy)₂(pbnHH)]²⁺ and [Ru(bpy)₂(pbn)]²⁺, were observed. Furthermore, CO and CH₄ (but no H₂) were reproducibly detected by GC, suggesting that the Re ─CHO species may have been further reduced to CH₄, accompanied by the release of CO from the 19e^- species [CpRe(NO)(CO)₂]⁰ produced by the electron-transfer reaction. The electron-transfer reaction is probably caused by the large driving force (ΔE_1/2 = 0.9 V), which causes it to compete with the kinetically impeded (ΔG^∗‡ = 12.6 kcal/mol) hydride transfer.

Conclusions

We have investigated through DFT calculations the hydride-donating power, or hydricity, of various catalysts that incorporate the pbnHH ligand to model the function of NADH. These visible light-generated, photocatalytic complexes show promise for use in reducing CO₂ and converting that pollutant molecule into fuels such as methanol. We examined potential catalysts based on the metals ruthenium and rhenium. The modification of the previously characterized [Ru(bpy)₂(pbnHH)]²⁺ that showed the most promise was the addition of a third electron to form the triply reduced, doubly protonated isomeric species. These species are predicted to donate hydrides to produce the pbnH^• intermediate, which has been shown to form the active species pbnHH through a disproportionation reaction. The calculations indicate that the reaction of the species with carbonyl ligands bound to transition-metal centers may provide a promising route to producing the formyl anion and beyond. Experimental evidence that the excited-state lifetime of photoexcited [Ru(bpy)₂(pbnHH)]²⁺ is about 70 ns, and that this excited state can be reductively quenched by TEA or DABCO to produce the one-electron-reduced [Ru(bpy)₂(pbnHH)]⁺ species with half-life exceeding 50 μs, is presented, thus opening the door to new opportunities for hydride-transfer reactions leading to CO₂ reduction by producing a species with much increased hydricity. A preliminary experimental exploration indicated that the reaction of the strong hydride donor [Ru(bpy)₂(pbnHH)]⁺ with [CpRe(NO)(CO)₂]⁺ may be complicated by the competition between electron- and hydride-transfer reactions.