Experimental results from a preclinical X-ray phase-contrast CT scanner

Abstract

To explore the future clinical potential of improved soft-tissue visibility with grating-based X-ray phase contrast (PC), we have developed a first preclinical computed tomography (CT) scanner featuring a rotating gantry. The main challenge in the transition from previous bench-top systems to a preclinical scanner are phase artifacts that are caused by minimal changes in the grating alignment during gantry rotation. In this paper, we present the first experimental results from the system together with an adaptive phase recovery method that corrects for these phase artifacts. Using this method, we show that the scanner can recover quantitatively accurate Hounsfield units in attenuation and phase. Moreover, we present a first tomography scan of biological tissue with complementary information in attenuation and phase contrast. The present study hence demonstrates the feasibility of grating-based phase contrast with a rotating gantry for the first time and paves the way for future in vivo studies on small animal disease models (in the mid-term future) and human diagnostics applications (in the long-term future).

One of the main shortcomings of existing biomedical X-ray imaging systems is their weak contrast in soft tissue. This limitation can be addressed by phase-sensitive imaging methods that rely on the phase shift that X-rays undergo when passing through matter (1). The resultant refraction angle can be utilized as contrast mechanism in a grating-based interferometer in radiographic (2, 3) and tomographic acquisition mode (4, 5). In a computed tomography scan, quantitative information about the sample’s composition can be extracted—i.e., the linear attenuation coefficient μ and decrement of the refractive index δ can be reconstructed (6–8). Because the grating-based phase-contrast imaging method is compatible with X-ray tube sources, when operated as Talbot–Lau interferometer (9), a translation to a clinical application scenario is currently discussed with great enthusiasm in the research community. Recent studies with laboratory X-ray sources have shown excellent imaging results with respect to soft-tissue contrast (10–14). In order to explore the envisioned clinical potential, we have developed a first preclinical phase-contrast CT scanner. This development represents an important milestone in the translation of phase-contrast imaging to clinical settings, as all grating-based phase-contrast setups, which are reported in the literature so far, use a rotating sample for tomographic scans. Because this mode of operation is obviously not preferable for intended in vivo animal studies, we have explored with this work the step from rotating sample to rotating gantry. The main challenge in this translation process was mechanical stability regarding the required precise alignment of the X-ray optical components (gratings). Even mechanical movements of either grating of only fractions of a micrometer during gantry rotation already cause a harmful artifact in the phase-contrast signal. Besides these mechanical stability aspects, the required compactness of the gantry itself imposes challenges in the mechanical design and construction of such a system. For the design of the compact gantry, one has to particularly consider shadowing effects of the X-ray absorbing bars in the gratings due to the diverging X-ray beam. Moreover, phase-contrast cone-beam reconstruction schemes have to be implemented in the reconstruction algorithms used with this prototype (15–17).

In this work we report on the mechanical challenges imposed by the translation to a compact rotating gantry system and present the first results of phase-contrast CT using an advanced phase recovery method that corrects for the occurring phase drifts. Using this method, we show in particular that the scanner performs quantitatively accurate with respect to phase and absorption Hounsfield units. Moreover, we show a first tomography scan of a biological specimen with complementary contrast in the attenuation and phase image.

Results

Design and Layout of the First Preclinical Phase-Contrast CT Scanner.

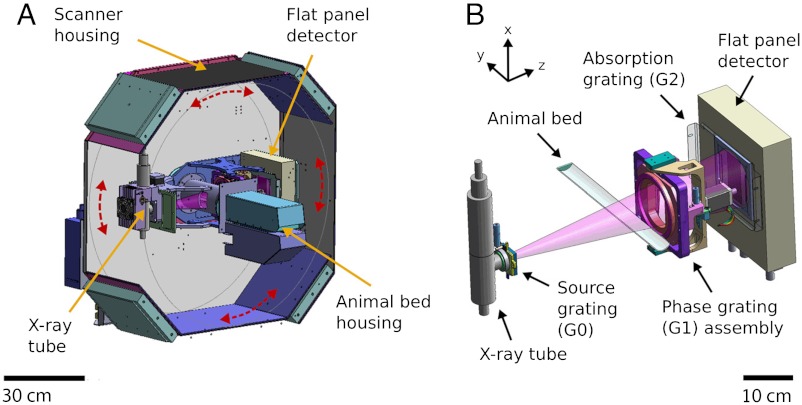
The prototype scanner consists of a standard rotating micro-CT gantry (with X-ray source, specimen opening, and a flat-panel detector) and comprises additionally a three-grating Talbot–Lau interferometer to extract multimodal X-ray projection images. This allows the system to deliver conventional transmission images (TI), differential phase-contrast images (PCI), and dark-field scattering images (DFI) (9, 18). In the first step of the development, the compact gantry was built and operated standalone in rotating sample mode. A previous and preparatory performance study was conducted, which showed that the gantry performs well and quantitatively accurately (8). In the final configuration presented here, the gantry is now implemented into a typical preclinical micro-CT scanner housing, featuring an animal bed, animal monitoring, and gas anaesthesia with enlarged field of view (FOV) and a flat-panel imaging detector. In order to manipulate the grating positions with high precision for alignment, several motors are installed to rotate, tilt, and shift the gratings. Fig. 1 shows a schematic 3D view of the scanner and schematic drawing of the grating interferometer. Further technical details about the scanner’s hardware and interferometer characteristics can be found in Materials and Methods.

Fig. 1.

Technical drawing of the first preclinical phase-contrast CT scanner. (A) Scanner housing with rotating gantry (gantry movement indicated by red arrows). The gantry contains the X-ray tube on one end and the flat-panel detector on the other end and is oriented horizontally in the displayed view. The overall scanner housing dimensions are approximately 95 cm in width, 100 cm in height, and 85 cm in depth. (B) Three-grating interferometer, which is contained within the gantry.

Stability.

The aforementioned artifacts in the phase signal are caused by minimal changes in the grating alignment. In the present setup of the scanner, there are two different causes of grating movements: (i) thermal expansion of the source grating’s mounting due to conducted heat of the X-ray target. This effect is especially relevant in this setup due to the required compactness of the system and associated proximity of source grating to X-ray source. (ii) Relative mechanical movement of either grating, due to gravitational and mechanical influences on the rotating gantry system. The consequence of both effects is a drift in the phase signal occurring after power on of the X-ray tube and during gantry rotation. To measure and quantify both drifts, the fringe phases in the PC images were monitored as a function of time after X-ray tube power up (φ_temp) and gantry rotation angle (φ_rot). To reduce noise, the average fringe phase value φ of a 10 × 10 pixel array in the center of the PC image without sample in the FOV was analyzed in the following way:

[1]

[2]

with i denoting subsequent exposures with stationary gantry, α denoting the gantry rotation angle, and φ_ref being the fringe phase value of the first image as reference. To eliminate temperature drift in Δφ_rot, that measurement was performed after the system had stabilized for several hours. Fig. 2 displays Δφ_temp and Δφ_rot expressed in units of multiples of π. Ideally both quantities should remain zero, and a deviation reflects a mechanical grating movement perpendicular to the bars of a grating on the order of the corresponding grating period per drift of 2π. For the temperature curve (A), one can see that the system stabilizes after approximately three hours and no further thermal expansion occurs. The shown exemplary measurement was performed with 50 kVp and 800 μA and stabilization time varies with the X-ray tube operating parameters. For Δφ_rot (B), three independent rotation stability measurements are shown in different colors. Each measurement shows a curve with approximately sinusoidal shape and change in sign of slope at approximately 90° and 270°, which corresponds to a horizontally oriented gantry. From this shape we conclude that the force of gravity and associated bending of support structures and play in the gears of the grating alignment motors are the main sources of mechanical movement. The few steeper sections of the curve are presumably caused by mechanical hitch in the gears of the grating alignment motors. However, the behavior of Δφ_rot is very reproducible and, most importantly, the shape of all curves is smooth, thus allowing for software correction of the drift.

Fig. 2.

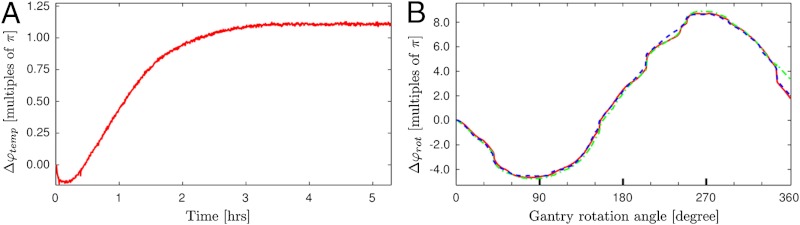
Temperature and rotation stability of the fringe phase in the phase-contrast images. (A) Temperature-induced fringe phase drift Δφ_temp as a function of time after power on of the X-ray tube. (B) Gravitationally induced fringe phase drift Δφ_rot of three independent measurements as a function of gantry rotation angle.

Adaptive Differential Phase Recovery (ADPR) Method.

Naturally, a drift in the differential phase-contrast signal, caused by gantry rotation (φ_rot), poses a problem in a tomographic scan. To circumvent this, one could straightforwardly acquire a reference image at each angular position, but this is time consuming and not feasible for in vivo studies. That is why we propose a software post-processing method, which is based on the observation that the result of the described temperature and rotation drifts are an offset (as shown in Fig. 2) and a ramp in the differential phase projection. More precisely, the fringe phase value φ does show a spatially dependent offset in the shape of an inclined plane, which is superimposed on the regular differential phase projection. To compensate this artifact, the ramp in the differential phase projection is determined and subsequently subtracted such that the original differential phase information is recovered. More technical details about this adaptive differential phase recovery (ADPR) procedure can be found in Materials and Methods. Fig. 3 shows two exemplary projection images to demonstrate how the ADPR method works. In A, a differential phase projection with strongly pronounced phase ramp and differential phase wrapping is shown. The existent phase ramp of that projection is determined by the ADPR method and is shown in B. The ADPR-corrected differential phase projection is shown in C. The bottom row of Fig. 3 shows the same procedure for a differential phase projection with only moderate phase ramp (D). Again, the differential phase ramp was determined (E), subsequently subtracted, and (F) shows the ADPR-corrected projection. The exemplary differential phase recovery of these two projection images illustrates that the phase ramp does vary for different projections, that the method can handle phase wrapping and that the original differential phase information can be recovered. The quantitativeness of this method in CT reconstructions is assessed in the next section.

Fig. 3.

Adaptive differential phase recovery (ADPR). In order to be able to appreciate the magnitude of the phase ramp, the shown images are displayed on a linear gray scale with the windowing range indicated in square brackets. Signal saturation in these differential phase projections corresponds to image values of ± π. (A) Uncorrected differential phase projection with a strongly pronounced differential phase ramp, which causes differential phase wrapping [-π,π]. (B) Subtracted differential phase plane [-1.45,0]. (C) ADPR-corrected differential phase projection using the described adaptive differential phase recovery method [-1.1,1.1]. (D) Uncorrected differential phase projection with a moderate differential phase ramp [-0.8,1.65]. (E) Subtracted differential phase plane [-1,0.8]. (F) ADPR-corrected differential phase projection [-1.1,1.1].

Quantitative Phase-Contrast CT of a Fluid Phantom and a Soft-Tissue Sample.

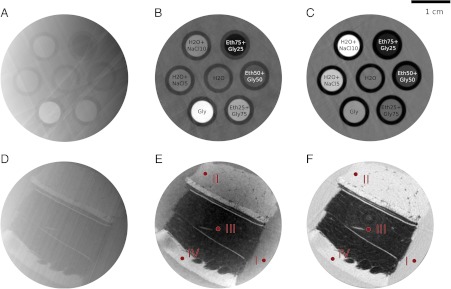
To asses how the preclinical scanner and adaptive differential phase recovery method perform in CT measurements, two samples were measured. The tomographic reconstructions in absorption and phase contrast were then evaluated in terms of image quality and reconstruction accuracy. The first sample was a well-defined fluid phantom, which was used for the quantitative reconstruction analysis. The second sample was formalin fixated porcine rind, which consists of several layers of soft tissue. This sample was used for the benchmarking of the soft-tissue-enhancement capabilities of the presented scanner. Fig. 4 shows the tomographic reconstruction of the two samples: A and D phase contrast without applying the ADPR method, B and E phase contrast using the aforementioned ADPR method, C and F attenuation contrast. From this figure the importance of accurate phase recovery is directly noticeable, and one can conclude that the method performs well in the sense that no artifacts remain in the corrected reconstructions (B and E).

Fig. 4.

Quantitative reconstructions of the fluid phantom (Top) and the porcine rind sample (Bottom). To reduce image noise, the reconstructions were averaged over 30 adjacent slices for the fluid phantom and over 5 slices for the porcine rind. (A and D) Phase contrast without adaptive differential phase recovery. (B and E) Phase contrast with adaptive differential phase recovery. (C and F) Attenuation contrast. Fluid phantom (Top row): Labels—H2O + NaCl10 (water and 10% NaCl solution), Eth25Gly75 (25% ethanol and 75% glycerol solution); other substances are named accordingly. Image windowing: (B) HU-P [-144,232], (C) HU-A [-335,400]. Porcine rind (Bottom row): Labels—(I) formalin background, (II) muscle, (III) two layers of subcutis (divided by connective tissue), (IV) dermis/epidermis. Image windowing: (E) HU-P [-249,91], (F) HU-A [-307,69].

In order to assess whether the tomographic reconstruction also yields quantitatively accurate results regarding the linear attenuation coefficient μ and decrement of the refractive index δ, the mentioned phantom study was evaluated quantitatively. A quantity derived from μ, which is commonly used in clinical CT scanners, is the Hounsfield unit. As suggested by Donath et al. (12), a corresponding quantity can be defined for phase images. To discriminate between these two Hounsfield units, the conventional attenuation Hounsfield units are referred to as HU-A and the phase Hounsfield units as HU-P. HU-P are defined as (12)

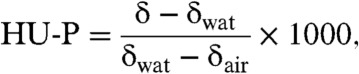[3]

where δ_wat and δ_air denote the refractive index decrement of water and air. The mentioned phantom comprised seven polyethylene tubes that were embedded in a water-filled plastic container of approximately 3 cm in diameter. The individual tubes were filled with chemically pure liquids and mixtures with salts to span a range of Hounsfield units in absorption and phase contrast. To evaluate the accuracy of the experimentally measured HU-A and HU-P, theoretical Hounsfield units were calculated for comparison. These theoretical values were determined for one effective photon energy that was identified independently for absorption (E_μ = 30 keV) and phase contrast (E_δ = 27 keV). For a detailed description of the experimental and theoretical procedure, the reader is referred to Materials and Methods and the studies of Herzen et al. (6) and Tapfer et al. (8). Table 1 contains the measured and calculated HU-A and HU-P for all substances in the phantom. From this table it is obvious that calculated and measured HU data agree well, the maximum deviation is 4 HU for phase and 11 HU for absorption. This means that the proposed ADPR method does allow for quantitatively accurate CT reconstruction of Hounsfield phase and attenuation units.

Table 1.

Quantitative analysis of the performed CT scans of the fluid phantom (Top) and porcine rind sample (Bottom)

Region of interest	HU-A(m)	HU-A(c)	HU-P(m)	HU-P(c)
Fluid Phantom
Ethanol (75%) + Glycerol (25%)	–251 ± 9	−260	–112 ± 6	−114
Ethanol (50%) + Glycerol (50%)	–157 ± 9	−161	–17 ± 6	−18
Ethanol (25%) + Glycerol (75%)	–41 ± 10	−39	99 ± 7	100
Glycerol	94 ± 12	105	236 ± 8	235
H2O + NaCl (5%)	230 ± 14	230	32 ± 7	29
H2O + NaCl (10%)	466 ± 15	463	61 ± 6	57
H2O	0 ± 14	0	0 ± 7	0

Porcine rind
Formalin background (I)	–9 ± 7	—	–37 ± 7	—
Muscle (II)	31 ± 7	—	12 ± 6	—
Subcutis (III)	–251 ± 11	—	–198 ± 7	—
Dermis/Epidermis (IV)	25 ± 9	—	57 ± 8	—

Measured (m) and calculated (c) attenuation (HU-A) and phase (HU-P) Hounsfield units are quoted for different region of interests (ROI). Fluid phantom (Top): The HU data was extracted from a ROI analysis covering the central 80% of the individual substance containers of 30 averaged adjacent transverse CT slices. The standard deviation is quoted as error. Porcine rind sample (Bottom): The measured Hounsfield units of a ROI analysis (region marked with red circle in Fig. 4) of the different tissue composites and formalin background are quoted. The standard deviation is quoted as error.

The potential of the phase-contrast scanner for biomedical imaging was examined by scanning a porcine rind sample because it contains different layers of soft tissue. For a quantitative comparison of both contrast modes, Hounsfield units for the different types of tissues were determined at the indicated positions in Fig. 4 (red colored circles, 20 pixel in diameter) and are also quoted in Table 1. In order to be able to compare both contrast modes visually in an objective manner, the gray value windowing was chosen such that the tissue with the highest (lowest) Hounsfield unit corresponds to 90% (15%) of the available gray value range. This results in an image windowing of [-307,69] for HU-A and [-249,91] for HU-P.

Whereas the subcutis (III) can be identified well in both the phase-contrast image (E) and absorption-contrast image (F), especially the muscle (II) and dermis/epidermis (IV) can be more clearly distinguished from the embedding medium formalin (I) and in particular from one another in phase contrast. This visual observation is also reflected in the quantitative HU data in Table 1. As very clearly visible for the fluid phantom study, also for biological tissues, absorption and phase contrast are complementary. When comparing attenuation and phase contrast, it should be noted that for conventional attenuation contrast no gratings and in particular no analyzer grating G2, which absorbs approximately half of the X-ray photons and hence decreases counting statistics, are needed. However, grating-based phase contrast on the other hand makes two perfectly registered and complementary images available in one CT scan.

Discussion

In order to take the next step toward a translation of X-ray phase contrast to clinical CT applications, we developed a first preclinical CT scanner. The main challenge in the transition from bench-top systems with rotating sample to a rotating gantry scanner were phase artifacts that are caused by minute changes in the grating alignment during gantry rotation. Using the proposed adaptive differential phase recovery method, these artifacts could be addressed. This correction procedure was applied to all differential phase projection images in the CT scan of the fluid phantom and a quantitatively accurate reconstruction of attenuation and phase Hounsfield units was demonstrated. This implies that phase artifacts, which were caused by gantry rotation in the differential phase projection images were accurately corrected and one can conclude that the presented procedure performs robust. Moreover, we have demonstrated clearly the general feasibility of phase contrast in a preclinical scanner. The now available complementary information in absorption and phase-contrast images does imply great potential for improved diagnosis and therapy response monitoring in preclinical imaging.

With respect to the goal of future in vivo animal studies, several technological improvements are still necessary. These improvements are mainly related to the reduction of X-ray dose to a tolerable level of several hundred mGy for repetitive animal studies. For the presented proof-of-principle grating-based CT scans, the dose was estimated to be several Gy. Dose in a grating-based CT scan in general is governed by the number of projections, detector exposure time, and the visibility of the implemented grating interferometer. For the described scanner there is great potential for both lowering the number of projections and exposure time, mainly by optimizing the interferometer hardware. From the fluid phantom study we discovered, for example, that the effective X-ray energy (E_μ = 30 keV, E_δ = 27 keV) does not match the interferometer design energy of 23 keV. So as to enhance sensitivity, the X-ray optical components (gratings) have to be optimized for the de facto higher effective energy. This can be realized by increasing the height of the absorbing grating bars. With the described optimizations, the visibility of the implemented interferometer will increase and we expect a significant improvement of the contrast-to-noise ratio. This in turn will allow for shorter detector exposure times. Moreover the silicon wafer grating support, which is currently 550 μm thick, can be considerably thinned, still providing sufficient mechanical support. As a result, this would decrease the exposure time and additionally lower the dose.

In summary, we have shown experimental stability and imaging results of a phase-contrast rotating gantry CT scanner, which—with a few technological improvements—is applicable for in vivo studies. We believe that this work represents a crucial milestone in translating X-ray phase-contrast imaging from proof-of-principle experiments to preclinical imaging applications on small-animal models (in the mid-term future) and finally to human phase-contrast CT applications (in the long-term future).

Materials and Methods

Technical Parameters of the Preclinical Phase-Contrast CT Scanner.

The preclinical phase-contrast scanner is based on a prototype gantry system, which was previously designed, characterized, and further developed to fit into a conventional micro-CT casing. A detailed description of the gantry can be found in Tapfer et al. (8). In short, the scanner features a tungsten X-ray source (RTW, MCBM 65B-50 W, focal spot size approximately 50 μm in diameter) and flat-panel detector (Hamamatsu, C9312SK-06, GOS scintillator, 50 μm pixel size, active area of 124.8 × 115.2 mm²). The source-to-sample and the sample-to-detector distances are approximately 272 mm and 201 mm, respectively, with a field of view of 3.5 × 2.5 cm² at the position of the sample. Conventional transmission, differential phase and dark-field contrast images are extracted by a three grating Talbot–Lau interferometer (9, 18): The source grating G0 (period 10 μm, gold height 35 μm) is positioned 3 cm from the emission point inside the X-ray source, the phase grating G1 (period 3.24 μm, nickel height 4.0 μm, phase shift π/2) is placed 55 mm behind the gantry axis, and the analyzer grating G2 (period 4.8 μm, gold height 25.0 μm) is positioned in contact with the flat-panel detector. All gratings were produced by the LIGA process, involving X-ray lithography and electroplating (19). For the required precise relative alignment of the gratings with micron precision, the following movements are motorized. G0: rotation (around z-axis); G1: rotation (around z-axis), tilt (along x- and y-axis), translation in z-direction. The interferometer is designed for 23 keV and operates in the first fractional Talbot distance as a compromise between a compact, but yet sensitive setup with sufficient transmission through a mouse. The visibility of the interferometer is approximately 15% for 40 kV X-ray tube voltage, as used in the presented CT scans. The cone-beam angle of the compact gantry is approximately 7.3° perpendicular to the tomography axis and 5.2° along the tomography axis. Reconstruction of the tomographic cone-beam data is performed using Feldkamp’s generalized filtered backprojection (FBP) algorithm (20). For attenuation images, a Ram–Lak filter with Hamming window and for phase-contrast images, a Hilbert filter is used (21). The cut-off frequency for both filters is chosen according to the Nyquist theorem.

Adaptive Differential Phase Recovery (ADPR) Method.

The adaptive differential phase recovery method corrects for phase artifacts in differential phase projection images that are caused by minute changes in the grating alignment during gantry rotation. Firstly, the phase ramp in the shape of an inclined plane is determined in the differential phase projection image. For this purpose, the complex exponential I^′(x,y) of all image values I(x,y) is taken: I^′(x,y) = e^i·I(x,y). In I^′(x,y), the image gradient in x and y direction is determined by averaging the x- and y-gradient of all pixels in I^′(x,y). Taking the complex exponential of the image values has the advantage that phase wrapping can be dealt with due to the periodic nature of the function itself. The extracted differential phase gradients in x- and y-direction are then used to define a mathematical plane (i.e., the phase ramp). This ramp is subtracted from the original differential phase image. The resultant flat differential phase projection image can still exhibit a constant offset value. As the fringe phase value outside the sample is known to be zero, this offset value is determined from a region that does not contain the sample. This constant offset value is subtracted from the differential phase image in the last step of the processing routine. Please note that the described correction routine only removes phase wrapping, which is caused by a phase ramp or phase offset. Phase wrapping that is caused by a strong phase shift of the sample itself is not addressed by the ADPR procedure but does also not deteriorate the correction procedure due to the mentioned periodicity of I’(x,y).

An accurate determination of the phase ramp requires an empty narrow strip on both sides of the projection images (in the direction perpendicular to the tomography axis) that is not covered by the sample. This effectively limits the size of the scanned object in that direction. The FOV in this direction is 3.5 cm, which allows for imaging of objects up to approximately 3 cm and in particular does allow mouse imaging as the sample size is not limited along the tomography axis.

Image Acquisition and Processing.

The X-ray tube was operated at 40 kV and 750 μA. For the two tomography scans, the following parameters were used for the fluid phantom (pork tissue) scan: 1,000 (1,500) projections over 360°, 8 (8) phase steps per projection, exposure time of 7 (5) s per phase step. The scanner was operated in step-an-shoot mode (i.e., at each projection angle one phase stepping procedure was performed) then the gantry was rotated to the next angular position and again phase stepping was performed, and so on. After every 15 acquisitions of this kind, 10 flat-field acquisitions were taken with static gantry. For these flat field acquisitions, the sample was moved out of the FOV. This results in a total exposure time of 26 (28) hours for the fluid phantom (pork tissue) CT scan. The X-ray tube was powered constantly throughout the acquisition sequence in order to preserve thermal equilibrium and avoid temperature-induced phase drift. The projection images of both scans CT scans were 2 × 2 binned before reconstruction, resulting in a reconstructed voxel size of 60 × 60 × 60 μm³. Ring artifact reduction in the reconstruction routine and projection-based filtering (2D symmetric normalized Gaussian function with a variance of 0.5 pixels) for smoothing were applied. Additionally, the fluid phantom reconstruction was post-processed to reduce the existing cupping artifact caused by beam hardening.

Quantitative Reconstruction of Attenuation and Phase Hounsfield Units (HU-A and HU-P).

In attenuation-based CT the linear attenuation coefficient μ can be reconstructed from transmission projections using a filtered backprojection algorithm (22). For compounds or mixtures, the total attenuation coefficient of a substance s with density ρ_s is given by μ_s = (μ/ρ)_s·ρ_s. The mass attenuation coefficient of a substance consisting of several chemical elements i is given by

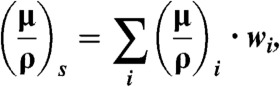[4]

where w_i is the weight fraction of the i-th element. Hounsfield units (23) are then derived from μ_s according to

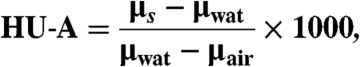[5]

with μ_wat and μ_air denoting the linear attenuation coefficient of water and air. To reconstruct the refractive index decrement δ from differential phase-contrast projections, an adjusted filter function (Hilbert) in the FBP reconstruction can be used (21). For substances of density ρ_s consisting of several elemental constituents i, the total refractive index decrement can be determined according to refs. 6, 8, and 24

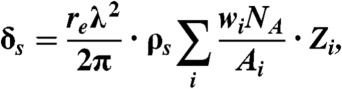[6]

with the elemental weight fraction w_i, classical electron radius r_e, x-ray wavelength λ, Avogadro’s Number N_A, atomic mass A_i and total number of electrons Z_i. Please note that X-ray energies are assumed to be considerably above absorption edges here as the real part of the atomic scattering factor is approximated by the total number of electrons in the atom. Phase Hounsfield units (HU-P) are then derived from δ_s according to Eq. 3. In the present compact cone-beam geometry setup, the sensitivity is reduced by a factor of r₁/l with r₁ being the source-to-sample and l the source-to-G1 distance (25, 26). To correct for this, the reconstructed δ data was renormalized by a factor of l/r₁ = 1.2.

The mass attenuation coefficients were obtained from the online program XCOM operated by the National Institute of Standards and Technology (27). The density of each fluid was determined using a high precision scale (Sartorius LA 230 S) by measuring the buoyancy of a gauged glass structure of 10 ml volume floating in the liquid. Because both μ and δ depend on energy, an effective photon energy of the polychromatic spectrum has to be determined. This effective energy can be different in both contrast modes, because the two image formation processes are inherently different. In addition to that, the interferometer efficiency is energy dependent, which leads to different weighting of the incoming energy spectrum. The effective energies were therefore determined for both contrast modes independently. Water was selected as reference substance for this purpose and the effective energies E_μ and E_δ were determined by matching the measured and theoretical μ and δ value for water. Table 2 lists the measured density of the fluids that were used for calculating the theoretical HU data. For the calculation of HU data of the porcine sample, the required water μ and δ value from the fluid phantom measurement were used as the same X-ray tube settings were applied in both CT scans.

Table 2.

Substances contained in the phantom and their measured density

Substance	Density [g/cm3]
Ethanol (75%) + Glycerol (25%)	0.877
Ethanol (50%) + Glycerol (50%)	0.982
Ethanol (25%) + Glycerol (75%)	1.110
Glycerol	1.260
H2O + NaCl (5%)	1.033
H2O + NaCl (10%)	1.069
H2O	0.997