Interplay of oxygen-evolution kinetics and photovoltaic power curves on the construction of artificial leaves

Abstract

An artificial leaf can perform direct solar-to-fuels conversion. The construction of an efficient artificial leaf or other photovoltaic (PV)-photoelectrochemical device requires that the power curve of the PV material and load curve of water splitting, composed of the catalyst Tafel behavior and cell resistances, be well-matched near the thermodynamic potential for water splitting. For such a condition, we show here that the current density-voltage characteristic of the catalyst is a key determinant of the solar-to-fuels efficiency (SFE). Oxidic Co and Ni borate (Co-B_i and Ni-B_i) thin films electrodeposited from solution yield oxygen-evolving catalysts with Tafel slopes of 52 mV/decade and 30 mV/decade, respectively. The consequence of the disparate Tafel behavior on the SFE is modeled using the idealized behavior of a triple-junction Si PV cell. For PV cells exhibiting similar solar power-conversion efficiencies, those displaying low open circuit voltages are better matched to catalysts with low Tafel slopes and high exchange current densities. In contrast, PV cells possessing high open circuit voltages are largely insensitive to the catalyst’s current density-voltage characteristics but sacrifice overall SFE because of less efficient utilization of the solar spectrum. The analysis presented herein highlights the importance of matching the electrochemical load of water-splitting to the onset of maximum current of the PV component, drawing a clear link between the kinetic profile of the water-splitting catalyst and the SFE efficiency of devices such as the artificial leaf.

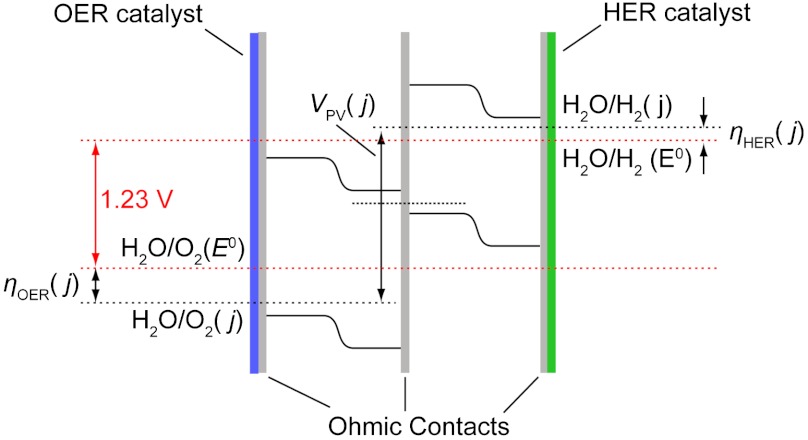
Water splitting is the central chemistry that underlies the storage of solar energy in the form of chemical fuels because it delivers hydrogen from a renewable source (1–3). Direct solar-to-fuels conversion can be achieved by interfacing suitable catalysts that carry out two separate half-reactions of water splitting—the four electron-four proton oxidation of water to O₂ and the two electron two-proton reduction of the produced protons to H₂—to a photovoltaic (PV) material. Numerous device configurations have been proposed for photoelectrochemical (PEC) water splitting (4–10), and they can be broadly categorized into those devices wherein the photovoltaic material makes a rectifying junction with solution as opposed to those in which the rectifying junctions are protected from solution or “buried.” Fig. 1 schematically depicts the latter with a double-junction configuration of absorber materials with progressively larger band gaps that are connected in series using thin-film ohmic contacts to generate open circuit voltages (V_oc) that are large enough to drive water splitting. Thin-film ohmic contacts at the termini of this stack serve both to protect the semiconductor from the chemistries occurring in solution and to enable efficient charge transfer to catalyst overlayers, which execute the oxygen-evolution reaction (OER) and hydrogen-evolution reaction (HER). Whereas water-splitting catalysis is combined with charge separation, current rectification, and photovoltage generation in a solution junction PEC device, in a buried junction device, catalysis is separated from the current rectification, charge separation, and photovoltage generation, which occur at the internal junction. The photovoltages produced at buried junctions are not fixed relative to a material-specific flatband potential (5). Unlike a solution junction, therefore, there is no requirement for the buried junction device that the flatband potentials of the semiconductors result in band edges that straddle the thermodynamic potentials of the OER and HER under the conditions of operation. This advantage of a buried junction dramatically expands the number of light-absorbing materials and catalysts that are available for constructing water-splitting devices. Additionally, as the buried junction device represents a photovoltaic power source in series with an electrochemical load, the OER and HER catalysts may be optimized independently such that maximum power transfer occurs to drive water splitting. We elaborate here on this latter issue and show that the kinetic profile of the catalyst is a key determinant of the overall solar-to-fuels efficiency (SFE).

Fig. 1.

Qualitative band diagram of a double-junction PV-PEC water-splitting cell depicting the thermodynamic potential separation of the OER and HER (dashed red lines), and the quasi-Fermi level (dashed black lines) and bend edge positions (solid black lines) throughout the cell under illumination with sustained water splitting at current density, j. The potential at each solution interface is given by the OER, η_OER, and HER, η_HER, overpotentials required to sustain the operating current density, j. For clarity of representation, solution and contact-resistance losses are omitted.

A key bottleneck in the construction of buried junction PEC devices is the development of catalysts that can perform the multiple proton-coupled electron transfer chemistry of water splitting. Added benefits are realized if the catalyst is composed of inexpensive, highly manufacturable materials that are easily integrated with the photovoltaic substrate, and is able to operate under benign conditions so as to engender better stability of the semiconductor substrates. To this end, we have recently described the self-assembly of a highly active cobalt-based oxygen-evolving catalyst that forms as a thin film when aqueous solutions of Co²⁺ salts are electrolyzed in the presence of phosphate (Co-P_i), borate (Co-B_i), or methylphosphonate (Co-MeP_i) (collectively termed Co-OEC) (11, 12). More recently, we have used a similar strategy to prepare a Ni-B_i catalyst (13). These catalysts model the oxygen-evolving complex of Photosystem II (14) because they: (i) self-assemble under mild conditions (11–13, 15); (ii) exhibit high activity in pH 7–9 water at room temperature (11, 12); (iii) are functional in a variety of water sources (12, 15); (iv) are comprised of inexpensive, terrestrially abundant materials (11, 12); and (v) self-heal by reversing catalyst corrosion at open circuit upon application of a potential (16, 17). Their ability to be interfaced easily with light-absorbing and charge-separating materials (18–24) has permitted the construction of a buried junction PEC device (25, 26). In the wireless configuration, the buried junction device captures many of the functional elements of the water-splitting chemistry of a leaf (27, 28). In this artificial leaf, the Co-OEC catalyst is interfaced through a thin-film transparent conductive oxide ohmic contact to a triple-junction Si PV cell to allow for the direct splitting of water under illumination with 1-sun AM 1.5 simulated sunlight.

We interrogate here the interplay of OER catalysis and photovoltaic performance in defining SFE of the artificial leaves based on Ni-B_i and Co-B_i catalysts. Building on the theoretical work of Hanna and Nozik (9) and adapting the engineering loss analysis model of Rocheleau and Miller (10), we use Ni-B_i and Co-B_i electrokinetic data as a basis for modeling the electrochemical load of water splitting in a PEC cell. We show that Ni-B_i and Co-B_i exhibit markedly different Tafel slopes, pointing to different mechanisms of oxygen evolution that translate into disparate electrochemical loads for water splitting. By assembling the electrochemical profiles of Ni-B_i and Co-B_i systems with multijunction PV components of similar power-conversion efficiency but disparate open-circuit voltages, V_oc, we show that OER-catalyst kinetics are a key determinant of SFE when water splitting is performed near its thermodynamic limit (i.e., low V_oc). This observation has not been broadly appreciated previously because most PEC cells have employed semiconducting materials with large band gaps that provide high voltages that are energetically far removed from the thermodynamic limit of water splitting.

Results and Discussion

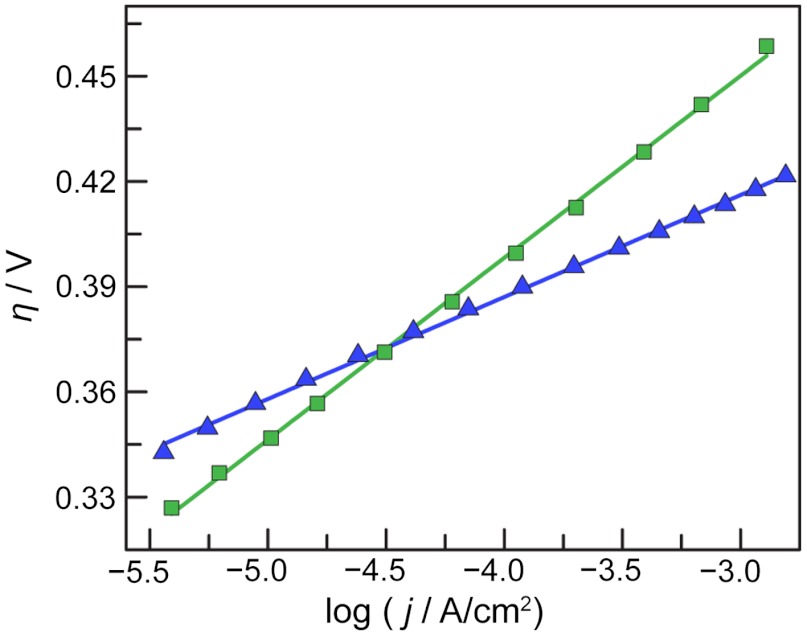
Water-splitting catalysts are deposited as thin films by controlled potential electrolysis of Co²⁺ and Ni²⁺ solutions in 0.1-M potassium borate electrolyte, pH 9.2 (B_i), at a potential of 0.92 and 1.15 V (vs. the normal hydrogen electrode, NHE), respectively (12, 13). Following electrodeposition, Co-B_i films may be rinsed and placed in electrolyte containing no additional Co²⁺ to yield steady-state current density values that are unchanged over time. The log of the steady-state current density of Co-B_i films versus the applied overpotential exhibits good linearity over an approximately 2.5-decade range in current density and yields a Tafel slope of 52 mV/decade (Fig. 2). This Tafel slope is similar to those previously observed for films grown from phosphate electrolyte at pH 7 (29), and it is diagnostic of a mechanism involving an equilibrium of a one-electron reaction that precedes a rate-limiting chemical step for oxygen evolution.

Fig. 2.

Tafel plot, η = (V_appl - iR - E⁰), of a Ni-B_i-catalyst film operated in 0.5-M B_i, pH 9.2 (blue triangles), and a Co-B_i-catalyst film operated in 1-M B_i, pH 9.2 (green squares). E⁰ is the thermodynamic potential of water splitting under the conditions of the experiment, η is the overpotential, and iR accounts for the uncompensated cell resistance. The slopes of the linear fits to the data are 52 mV/decade and 29 mV/decade for Co-B_i and Ni-B_i, respectively.

In contrast to Co-B_i films, which exhibit high initial OER activity that is sustained indefinitely, Ni-B_i requires preconditioning by anodic polarization in order to obtain steady-state current densities that are high and remain unchanged over time (13, 30). Over the course of this anodic preconditioning, Ni-B_i films exhibit a dramatic rise in activity and undergo structural changes reminiscent of a β-NiOOH to γ-NiOOH phase conversion (30). The logarithm of the steady-state current density of preconditioned Ni-B_i films versus the applied overpotential exhibits good linearity over an approximately 2.5-decade range in current density and yields a Tafel slope of 29 mV/decade (Fig. 2), in contrast to the value observed for Co-B_i under similar conditions. In our initial report of Ni-B_i (13), we examined very thick (> 1-μm thick) films, which, following preconditioning, exhibited a Tafel slope of approximately 60 mV/decade. The data in Fig. 1 are for ultrathin Ni-B_i films (< 8-nm thickness), suggesting that sluggish electron and/or ion transport in thick mesoporous Ni-B_i films inflate the Tafel slope. A thorough mechanistic investigation of thin Ni-B_i films reveals that the low Tafel slope for Ni implies a mechanism involving a two-electron equilibrium prior to the rate-limiting step of oxygen evolution, as opposed to the one-electron preequilibrium observed for the Co-B_i catalyst (29, 31).

The disparate Tafel behaviors of Ni-B_i and Co-B_i films are paramount to determining the anodic electrochemical load in an artificial leaf. Specifically, the electrochemical load of water splitting is described by the following equation (10):

[1]

where V_op is the overall operational voltage necessary for water splitting at a given current density j over area A, V⁰ is the thermodynamic potential stored in water splitting (1.23 V under standard conditions), and η_Ω represents the voltage required to overcome resistive losses in the device, including contact resistance between the components and ion transport resistance arising from the electrolyte solution. Typically these resistances are ohmic and therefore can be represented by the simple product of the net current (jA) and an aggregate cell resistance, R. The η_OER and η_HER terms represent the overpotential losses accompanying the oxygen-evolution and hydrogen-evolution half-reactions, respectively, and they are illustrated in Fig. 1. Both overpotential terms are functions of the current density as given by the Tafel law,

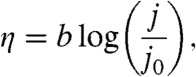[2]

in which b is the Tafel slope and j₀ is the exchange current density, representing the extrapolated rate at which the forward and back reactions occur under conditions of zero driving force, η = 0. Combining Eqs. 1 and 2 with consideration of the ohmic nature of the cell-resistance term engenders the following expression for the electrochemical load of water splitting,

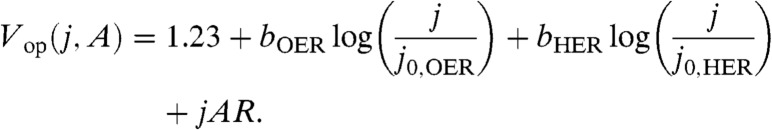[3]

In this expression, b_OER, j_0,OER, b_HER, and j_0,HER represent the Tafel slopes and exchange current densities of the OER and HER catalysts, respectively. In order to isolate the impact of disparate OER-catalyst kinetics, we chose to model the hydrogen-evolution catalyst using values both typical of the HER on high-surface area Ni electrodes (32, 33) and similar to those used in the artificial leaf (27), j_0,HER = 10 μA cm^-2 and b_HER = 30 mV/decade (32), and we also assume a conservative value of R = 10 Ω (A = 1 cm²) and note that resistive losses are highly dependent on cell geometry. Extrapolation of the Tafel data in Fig. 2 yields exchange current densities for Co-B_i and Ni-B_i of 2.1·10^-12 and 5.0·10^-18 A cm^-2, respectively. These values, taken together with the Tafel slopes of the two catalysts, yield the current density-voltage (j-V) curves shown in Fig. 3 for water splitting by Co-B_i and Ni-B_i. Consistent with the larger exchange current density for Co-B_i, the onset of appreciable water splitting occurs at a lower potential relative to Ni-B_i. However, the lower Tafel slope of Ni-B_i causes its j-V curve to rise far more steeply, requiring a lower voltage at high current density. In this treatment, we assume that the Tafel behavior shown in Fig. 2 is retained over the entire overpotential range and acknowledge that mass transport limitations and/or changes in OER mechanism at high overpotential may perturb the theoretical j-V behavior in Fig. 3. As further points of comparison, published Tafel data for RuO₂ (34) and LaMnO₃ (35) in 1 M NaOH are also overlaid on the graph to model the electrochemical load of water splitting using these catalysts. The reported Tafel data for RuO₂ and LaMnO₃ correspond to materials prepared by high-temperature calcination of metal salt precursors at > 350 °C. As such, these materials may not be suitable for integration into PV-PEC architectures, and we therefore include them in Fig. 3 as exemplars of high- and low-performance OER catalysts. Thus, they provide a benchmark for the impact of catalyst performance on SFE.

Fig. 3.

Electrochemical load of water splitting utilizing Co-B_i (dashed green line), Ni-B_i (dashed dark-blue line), RuO₂ (dashed red line), and LaMnO₃ (dashed light-blue line) oxygen-evolution catalysts and the j-V curve of an idealized model of an a-Si|nc-Si|nc-Si triple-junction photovoltaic displaying V_oc = 1.94 V, j_sc = 8.96 mA cm^-2 (solid black line) and an idealized hypothetical cell possessing V_oc = 2.13 V, j_sc = 8.15 mA cm^-2 (dashed black line). Open circles indicate operating current densities for the high V_oc cell and correspond to 10% SFE for all catalysts. Closed circles indicate operating current densities for the low V_oc cell for which SFE is sensitive to catalyst performance.

In the artificial leaf, the operating current density is given by the intersection of the j-V curve for the PV and the j-V curve representing the electrochemical load for water splitting. This operating current density multiplied by the thermodynamic potential of water splitting (1.23 V) defines the power stored in water splitting, and the ratio of this power to the incident power of the solar flux, 100 mW/cm², defines the SFE. For the purposes of illustration, we model in Fig. 3 the idealized PV behavior of a triple-junction amorphous Si (a-Si) | nanocrystalline Si (nc-Si) | nc-Si triple-junction cell stack (36) exhibiting V_oc = 1.94 V and j_sc = 8.96 mA cm^-2, and a hypothetical multijunction cell with V_oc = 2.13 V and j_sc = 8.15 mA cm^-2. Idealized behavior of the PV is modeled by ignoring efficiency losses caused by high series or low shunt resistances and assuming a diode ideality factor of 1 (details of PV modeling provided in Experimental Methods). Both idealized cells exhibit a power-conversion efficiency of 16%, but display dramatically different SFEs when paired with the various OER catalysts. For the cell possessing the lower V_oc, the electrochemical load curves for water splitting using Ni-B_i and Co-B_i intersect the j-V curve of the PV at 1.85 and 1.89 V (Fig. 3), respectively, which is beyond the maximum power point (V_mp = 1.83 V) of the PV. As the PV current density declines sharply beyond V_mp, an artificial leaf utilizing Co-B_i is expected to exhibit a lower hydrogen production current density (7.6 mA cm^-2) than one utilizing Ni-B_i (8.7 mA cm^-2). Water splitting stores 1.23 V and, thus, these current densities translate to SFE = 9.3% and 10.7% for Co-B_i and Ni-B_i, respectively. The SFE declines further for the case of LaMnO₃, which displays an overall water-splitting current density of 4.4 mA cm^-2 and SFE = 5.4%. In contrast, RuO₂, despite displaying greater OER-catalytic activity than thin-film Co-B_i and Ni-B_i exhibits only a marginally larger SFE = 11.1%. The artificial leaf becomes even more insensitive to OER-catalytic activity if the V_oc of the PV is increased (Fig. 3). For the higher V_oc cell, all of the catalysts exhibit SFE = 10.0%, highlighting the fact that good catalyst performance and high SFE are only mandated if a suitable PV with a V_mp matched to the electrochemical load can be designed near the thermodynamic potential of water splitting. The foregoing analysis assumes that the PV exhibits ideal diode behavior with minimal series and maximal shunt resistances. In practice, multijunction Si devices suffer from poor fill factors symptomatic of nonideal diode behavior and parasitic-resistance losses (36). Thus, we stress that the trends observed here are purely theoretical and that a more rigorous analysis performed on a specific PV/catalyst pairing would be necessary for device optimization. We do note, however, in a practical artificial leaf with minimized ohmic losses, an overall SFE = 5.2% has been observed for a PV cell of 7.7% efficiency (27).

In summary, we illustrate here that a key determinant of high SFE for artificial leaves, and more generally, photoelectrochemical cells, is the OER kinetic profile. In particular, thin Ni-B_i catalyst films exhibit a 29 mV/decade Tafel slope as compared to the 52 mV/decade slope observed for Co-B_i under similar electrolyte conditions. The disparate kinetics of Co-B_i and Ni-B_i translate into improved SFE of an artificial leaf utilizing the latter, suggesting that Ni-B_i is particularly well-suited to direct solar-to-fuels generation. We note that the critical role of catalysis in SFE has generally been underappreciated because PEC cells to date have generally relied on semiconducting materials with large band gaps (e.g., SrTiO₃, TiO₂, and WO₃ display band gaps, E_g > 2.5 V) that supply very high voltages to drive water splitting (37). These materials have typically been used as components of solution junction PEC devices rather than buried junction devices, complicating their analysis using the simple power matching model presented here (38). Notwithstanding, extremely poor catalytic activity of semiconducting oxides such as SrTiO₃, TiO₂, and WO₃ can be masked by the large voltages they deliver to drive water splitting via high overpotential pathways (e.g., hydroxyl radical formation) (37, 39). As illustrated in Fig. 4, qualitatively, large band gap oxide PEC devices can be viewed as exaggerated cases of the high V_oc PV we model in Fig. 3, wherein load curves for poor catalysts still intersect the j-V curve of the semiconductor at or below the V_mp. The maximum SFE of such cells, however, is intrinsically limited because of inefficient utilization of the solar spectrum. High SFEs can only be achieved for PVs operating near the thermodynamic potential of water splitting so that the absorption of the solar spectrum can be maximized. In this case, as illustrated in Figs. 3 and 4, the overall SFE becomes extremely sensitive to catalyst performance. These results show that the construction of efficient PEC devices such as the artificial leaf reduces to a problem of catalyst design. To this end, Co-B_i and Ni-B_i are ideal water-splitting catalysts when integrated to well-designed Si-junctions or other PV cells operating near the thermodynamic potential for water splitting. The results herein show that SFEs = 10% are easily within reach if Co-B_i and Ni-B_i catalysts are integrated with PV cells operating at 15% efficiency, thus highlighting the promise of artificial leaves as a low-cost method for direct solar-to-fuels production.

Fig. 4.

Low-SFE (dashed red with solid green line) and high-SFE PEC cells (solid red with solid blue or solid purple line). The j-V curves of a PV (dashed red line) of a typical metal oxide semiconductor operating at V_oc > 3.0 V and a PV (solid red line) operating near the region of thermodynamic potential for water splitting (gray bar) at arbitrary current density j overlaid with Tafel curves of catalysts exhibiting increasing performance (solid green to solid blue to solid purple lines). Note the sensitivity of the overall SFE to catalyst performance for PVs operating near the thermodynamic potential of water splitting.

Experimental Methods

Materials.

Ni(NO₃)₂•6H₂O 99.9985% and Co(NO₃)₂•6H₂O 99.999% were used as received from Strem. H₃BO₃ (99.5%) and KOH (85%) were used as received from Sigma-Aldrich. NaOH (99%) and KNO₃ (99%) were used as received from Mallinckrodt. All buffers were prepared with reagent-grade water (18 MΩ-cm resistivity; Ricca Chemical) or Millipore type I. Fluorine-tin-oxide (FTO)-coated glass slides (TEC-7) were purchased as precut pieces from Hartford Glass.

Electrochemical Methods.

All electrochemical experiments were performed at ambient temperature with a CH Instruments 760D potentiostat and a BASi Ag/AgCl reference electrode. All electrode potentials were converted to the NHE scale using E(NHE) = E(Ag/AgCl) + 0.197 V. Unless otherwise stated, the electrolyte was 0.1-M potassium borate at pH 9.2 (B_i).

Co-B_i-Catalyst Film Formation and Tafel Data Collection.

Bulk electrolyses were performed in a two-compartment electrochemical cell with a glass frit junction of fine porosity. For catalyst electrodeposition, the auxiliary compartment was charged with approximately 50 mL of 0.1-M B_i electrolyte and the working compartment was charged with approximately 50 mL of solution comprising 25 mL of 0.2-M B_i electrolyte and 25 mL of 1-mM Co²⁺ solution. The working electrode was a 1-cm by 2.5-cm piece of FTO-coated glass. The FTO-coated side was masked so as to expose a 1-cm² area of the electrode to the solution. Pt mesh was used as the auxiliary electrode. Electrolysis was carried out at 0.92 V on quiescent solutions without iR compensation and with the reference electrode situated 2–3 mm from the ITO surface. Electrolysis was continued until 24 mC of charge were passed.

Tafel data were obtained by conducting controlled-potential electrolysis in 1-M B_i electrolyte at a variety of applied potentials. Prior to film deposition, the solution resistance of the 1-M KB_i electrolyte to be used for Tafel data collection was measured using the iR test function. The electrolysis solution was exchanged with Co²⁺-containing 0.1-M B_i electrolyte without disturbing the relative positions of the working and reference electrodes. The film was prepared by controlled-potential electrolysis as described above. Following film preparation, the working electrode was rinsed in reagent-grade water and transferred without drying to the same electrolysis bath in which the solution resistance was measured. The electrode was allowed to equilibrate with the electrolysis solution for 5 min while being held at the open circuit potential. The solution was stirred and steady-state currents were then measured at applied potentials that descended from 1.17 V to 0.96 V in 10-to 30-mV steps. For currents greater than 10 μA cm^-2, a steady-state was reached at a particular potential in 400–600 s. For currents lower than 10 μA cm^-2, longer electrolysis times (15–20 min) were utilized to ensure that steady-state conditions had been achieved. The solution resistance measured prior to the data collection was used to correct the Tafel plot for ohmic potential losses.

Ni-B_i-Catalyst Film Formation, Anodization, and Tafel Data Collection.

Ni-B_i-catalyst films were prepared by controlled-potential electrolysis of 0.1-M B_i electrolyte solutions containing 0.4-mM Ni²⁺. To minimize precipitation of Ni(OH)₂ from these solutions, 25 mL of 0.2-M B_i was added to 25 mL of 0.8-mM Ni²⁺ solution. The deposition solutions were subsequently filtered through a 0.2-μm syringe filter (Pall Inc.) to remove any precipitated Ni(OH)₂ that formed. The solutions thus prepared remained clear over the course of all depositions, which were carried out using a piece of FTO-coated glass as the working electrode. These FTO-coated glass electrodes were rinsed with acetone and water prior to use in all experiments and the FTO-coated side was masked so as to expose a 1-cm² area of the electrode to the solution. Deposition by controlled-potential electrolysis was carried out on quiescent solutions at 1.15 V without iR compensation and with passage of 1 mC cm^-2. A typical deposition lasted 70 s. Following deposition, films were rinsed with 0.1-M B_i and subsequently anodized in 1-M B_i electrolyte by passage of 3.5-mA cm^-2 for 1 h with stirring.

Current-potential data were obtained by conducting controlled-potential electrolysis in 0.5-M B_i 1.75 M KNO₃ electrolyte at a variety of applied potentials. Prior to film deposition and anodization, the solution resistance of the electrolyte to be used for Tafel data collection was measured using the iR test function. The electrolysis solution was exchanged for Ni²⁺-containing B_i electrolyte without disturbing the relative positions of the working and reference electrodes. The film was prepared by controlled-potential electrolysis and anodized as described above. Following film preparation, the working electrode was rinsed in fresh Ni-free B_i electrolyte and transferred, without drying, to the same electrolysis bath in which the solution resistance was measured. The electrode was allowed to equilibrate with the electrolysis solution for 5 min while being held at the open circuit potential. The solution was stirred and steady-state currents were then measured at applied potentials that descended from 1.1 V to 1.00 V in 7-to 20-mV steps. For currents greater than 10 μA cm^-2, a steady-state was reached at a particular potential in less than 400 s. For currents lower than 10 μA cm^-2, longer electrolysis times (15–20 min) were utilized to ensure that steady-state conditions had been achieved. The solution resistance measured prior to the data collection was used to correct the Tafel plot for ohmic potential losses.

Current Density-Voltage Curve Modeling.

The j-V curve representing the electrochemical load of water splitting was calculated using Eq. 3 over a current density range from 10^-5 A cm^-2 to 10^-1 A cm^-2. A 10 Ω cell resistance was assumed along with j_0,HER = 10 μA cm^-2 and b_HER = 30 mV/decade. The Tafel slopes and exchange current density values for Co-B_i and Ni-B_i were taken from linear fits to the data in Fig. 2, whereas Tafel slopes and exchange current density values were taken from published data for RuO₂ (34) and LaMnO₃ (35).

The j-V curve representing idealized power output from a triple-junction Si photovoltaic stack was modeled using reported data for an a-Si|nc-Si|nc-Si cell (36), which exhibits V_oc = 1.94 V and j_sc = 8.96 mA cm^-2 (Fig. 3). These two experimental parameters were used to calculate the dark saturation current of an idealized cell, j₀, using the following equation:

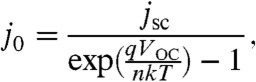[4]

where q is the fundamental charge of an electron, k is the Boltzmann factor, T is the temperature (taken as 300 K), and n is the diode ideality factor, taken as 1. Using the calculated value of j₀, the ideal j-V curve was calculated using

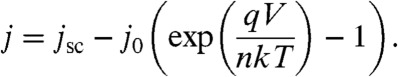[5]

The same analysis was applied to a hypothetical idealized cell with a 10% increase in V_oc and a concomitant 10% decrease in j_sc so as to preserve the same overall power-conversion efficiency of 16%. We note that the above equations produce upper-limit ideal behavior because they do not account for parasitic resistances that may exist within or between the individual p-n junction components of the triple-junction stack.