Abstract
Much of what we know and love about music is based on implicitly acquired mental representations of musical pitches and the relationships between them. While previous studies have shown that these mental representations of music can be acquired rapidly and can influence preference, it is still unclear which aspects of music influence learning and preference formation. This article reports two experiments that use an artificial musical system to examine two questions: 1) which aspects of music matter most for learning, and 2) which aspects of music matter most for preference formation. Two aspects of music are tested: melody and harmony. In Experiment 1 we tested the learning and liking of a new musical system that is manipulated melodically so that only some of the possible conditional probabilities between successive notes are presented. In Experiment 2 we administered the same tests for learning and liking, but using a musical system that is manipulated harmonically to eliminate the property of harmonic whole-integer ratios between pitches. Results show that disrupting melody (Experiment 1) disabled the learning of music without disrupting preference formation, whereas disrupting harmony (Experiment 2) does not affect learning and memory, but disrupts preference formation. Results point to a possible dissociation between learning and preference in musical knowledge.
Keywords: music, cognition, learning, preference, pitch, melody, harmony, grammar
1 Introduction
Cognitive science is fundamentally concerned with the possession of knowledge. In the musical world, this possession of knowledge requires the formation of accurate mental representations for sequential and simultaneous pitches. The sequential presentation of pitches gives rise to melody, which is thought of as the horizontal dimension of music. The simultaneous presentation of pitches gives rise to harmony, which is the vertical dimension of music (Piston & DeVoto, 1987; Tramo, Cariani, Delgutte, & Braida, 2001).
Much evidence has shown that the human brain possesses knowledge of vertical and horizontal musical structures. For instance, knowledge of musical harmony has repeatedly been demonstrated in both musically trained and untrained people (Krumhansl, 1990b). Reaction time and electrophysiological studies have shown that individuals from Western cultures readily form expectancies for melodic and harmonic sequences of pitches (Besson & Faita, 1995; Bigand & Parncutt, 1999; Koelsch, Gunter, Friederici, & Schroger, 2000; Loui & Wessel, 2007; Poulin-Charronnat, Bigand, Madurell, & Peereman, 2005), with effects that generally exist in persons with and without musical training (Bigand & Parncutt, 1999; Bigand & Poulin-Charronnat, 2006; Krumhansl, 1990a; Loui & Wessel, 2007). Developmental studies suggest that musical knowledge and expectations are already well-formed early in life (Koelsch et al., 2003; Schellenberg, Bigand, Poulin-Charronnat, Garnier, & Stevens, 2005; Schellenberg & Trehub, 1996; Trainor & Trehub, 1994). In addition, a number of researchers have compared findings in the Western harmonic system against musical systems of other cultures such as Indonesian scales (Castellano, Bharucha, & Krumhansl, 1984; Lynch, Eilers, Oller, & Urbano, 1990) and the North Sami Yoiks of Finland (Krumhansl et al., 2000). Findings confirm that individuals of other cultures demonstrate knowledge of the underlying statistics of their musical culture, much as do individuals exposed to the Western musical culture.
These results have led people to ask about the source of musical knowledge. One possibility is the existence of innate psychoacoustical principles (such as sensory consonance and dissonance) that underlie the perception of musical rules and structures. Another possibility is that knowledge of common practices in melody and harmony is learned via exposure to music in the culture. While many theorists agree that knowledge of the principles of melody and harmony can be implicitly acquired by humans via exposure to music (Huron, 2006; Meyer, 1956), the relative contributions of innate factors and acquired processes to musical knowledge remain unknown. The question of what musical knowledge is readily acquirable is fundamental to cognitive science as a computational problem, whereas the question of how one acquires such knowledge requires an algorithmic level of analysis. To address the topic of what and how musical knowledge is acquired, recent research has turned to the use of artificial grammars. Artificial grammar learning is a paradigm used extensively to address the form of knowledge acquired as a result of learning. It is thought to rely upon implicit learning (Reber, 1967), and the source of knowledge that is learned gives rise to theories of artificial grammar learning, including rule learning, similarity learning, and associative learning (Pothos, 2007). In the domain of music, studies have explored the learning of tone sequences with predictable structures (Saffran, Johnson, Aslin, & Newport, 1999), melodies formed from tones that are determined by grammatical structures (Rohrmeier, Rebuschat, & Cross, 2011), grammatical timbre sequences (Tillmann & McAdams, 2004), and even serialist musical strucutres (Dienes & Longuet-Higgins, 2004). Previous studies also investigated implicit learning of nonadjacent rules, showing that learning is somewhat dissociated when tested using the direct test of grammaticality judgment and the indirect test of preference ratings (Kuhn & Dienes, 2005). Importantly, this study found dissociated results between liking and recognition. In further work the same authors also found differences in the types of musical regularity that can be learnt in incidental vs. intentional learning conditions (Kuhn & Dienes, 2006).
In recent studies we have shown, using artificial musical grammars that are based on the Bohlen-Pierce scale, that people can rapidly acquire knowledge of, and form preferences for, novel melodies in a new musical system (Loui & Wessel, 2008; Loui, Wessel, & Hudson Kam, 2010; Loui, Wu, Wessel, & Knight, 2009). The present article describes two experiments in which, by systematically varying the Bohlen-Pierce scale input, we test for rapidly acquired knowledge of, and rapidly formed preferences for, melodic intervals and harmonic relations in music. The approach of an artificial musical system to investigate knowledge acquisition is an effective alternative to developmental and cross-cultural approaches, as it allows for a highly controlled environment where we can systematically manipulate the auditory input, and then observe the extent to which musical knowledge is acquired. This grammar was chosen such that it adheres to psychoacoustical and cognitive principles of musical systems (Krumhansl, 1987; Lerdahl & Jackendoff, 1983) but is also completely unfamiliar to participants; thus it offers a viable approach to testing rapid learning without the confounds of perceptual stability and long-term memory (Mathews, Pierce, Reeves, & Roberts, 1988). The artificial musical system we use is based on the Bohlen-Pierce scale. It has been described in previous studies (Loui & Wessel, 2008; Loui, et al., 2010; Loui, et al., 2009) but will be briefly described below.
1.1 A New Musical System for Studying Learning
Musical systems of the world are built around the octave, which is a two to one ratio in frequency. Given a starting point of 220 Hz (the musical A3), the equal-tempered Western scale has 12 logarithmic divisions within the 2:1 ratio, so that the formula for the frequency of each note is:
F = 220 * 2 ^ n/12
In contrast, the Bohlen-Pierce scale is based on the three to one ratio, and within the 3:1 ratio it is divided into 13 logarithmic steps, so that with the starting point of 220 Hz, the formula for the frequency of each note is:
F = 220 * 3 ^ n/13
Within this thirteen-tone scale, some of the notes have low-integer ratios in frequency, which sound consonant psychoacoustically when played together. For example, when n is 0, 6, and 10, the three resulting tone frequencies approximate a 3:5:7 (low-integer) ratio. Low-integer ratios in frequency are known since Pythagorean times to sound relatively consonant and harmonious (Kameoka & Kuriyagawa, 1969), and are preferred by humans even from infancy (Schellenberg & Trehub, 1996). The tones that form these low-integer ratios are chosen to be the “diatonic” version of the Bohlen-Pierce scale, and are relatively stable and consonant harmonic chord tones. The role of this consonance in learning and preference will be tested for in Experiment 2. Having defined three-note chords with low-integer harmonic ratios, it is possible to string these chords together to form a chord progression. In a four-chord progression, each pitch within each chord serves the function of one of 12 (4 × 3) nodes within an artificial finite-state grammar system. Melodies, which are strings of pitches, can be composed using the finite-state grammar by choosing one starting point as one of the three pitches in the first chord, which then can lead to either another pitch within the same chord or can move forward to any of the pitches within the next chord, which can, in turn, repeat to a pitch within the same chord or move forward to any pitch within the next chord, and so on until a melody is constructed as a string of pitches that follows a legal pathway through the chord progression. A large set of melodies can be composed this way, all of which are legal exemplars of the same pitch-based finite-state grammar. In contrast, another chord progression can be generated by reversing the original chord progression (such that the transitional probability between successive chords can be different but the frequency of appearance of each pitch is the same) and using the new, retrograde, chord progression as the basis of the finite-state grammar. This retrograde grammar, in turn, can generate another set of melodies that are different from the first set. In behavioral experiments investigating learning of the new musical system, participants are exposed to one of the two large sets of melodies. After exposure, learning is assessed using a two-alternative forced choice test where one melody is generated from the original chord progression whereas the other melody is generated from the retrograde chord progression. Accuracy in learning is defined as correct selection of the melody that is generated from the same chord progression that had generated the melodies presented during exposure. Thus, during the test phase, the correct answer for one group of subjects was the wrong answer for the other group, and vice versa. This two-alternative forced choice test of generalization is similar to those used in other studies that investigate learning in various domains.
Due to the unique psychoacoustical properties of the new musical systems, the artificial grammars described here have harmonic as well as melodic structures. In previous experiments we have tested and demonstrated successful learning of the Bohlen-Pierce scale given only 30 minutes of exposure to 400 non-repeated melodies (Loui, et al., 2010). In contrast, when given repeated exposure to only five melodies, participants did not learn the scale, but they did form an increased preference for the melodies after repeated exposure (Loui, et al., 2010). Furthermore, a no-exposure condition was also tested as a control condition in previous studies, verifying that performance showing successful learning occurred truly as a result of exposure rather than a product of incidental preferences for certain properties of test stimuli (Loui, 2007). In the current experiments we address an important follow-up question regarding the constraints of the learning system. To try to identify these constraints, we altered the learnable new musical system and then tested for people’s learning and preference formation when given the altered musical system. By disrupting the melodic intervals (Experiment 1) and the harmonic consonance (Experiment 2) of the Bohlen-Pierce scale system, our aim is to identify the acoustic and statistical conditions of the input under which learning and preference formation are affected.
2 Experiment 1. Effects of Melodic Intervals
A melody can be identified by its contour (the successive up-down patterns between notes) and its intervals (the pitch distances between successive notes). Past researchers have proposed that the sizes of melodic intervals play an important role in the perception of melody. The Implication-Realization Model (Narmour, 1990) and regression-to-the-mean model (Huron, 2006) have both related melody to Gestalt perceptual processes by proposing that the ability to perceive a melody as a holistic object, or its Gestalt, depends mostly on interval sizes. The rule of thumb governing successive intervals is a gap-fill model, where a large interval in a melody is usually followed by small intervals in the opposite direction (Krumhansl, 1995; Meyer, 1956). Gap fill and other melodic processes generally refer to transitions between sizes of melodic intervals, whereas melodic intervals themselves are transitions between successive notes. Thus, melodic processes such as gap fill can be conceptualized statistically as second-order transitions (i.e. transitions of transitions) between notes (Huron, 2006). The first-order transitions between notes, also known as melodic intervals, can be illustrated in a finite-state grammar diagram as pathways, or arrows, that connect the nodes, which represent tones. In order to investigate the effects of melodic intervals on learning, in the present experiment we change the exposure melodies by omitting the presentation of some of the legal pathways in the finite-state grammar, such that the exposure phase consists of only a subset of melodic intervals. If the transitional probabilities between successive pitches are important as a fundamental aspect of the input that triggers learning, then we would expect no generalization towards melodies that contain pathways that were not presented during the exposure phase. In contrast, if the material that is learned is independent of transitional probabilities between tones, then we would expect that knowledge will generalize successfully to melodies containing pathways that were not presented during the exposure phase. Similarly, if melodic intervals are important for preference formation, we would expect preferences to be increased for previously-presented melodies, whereas if melodic intervals are not important for preference formation, then we would expect no preference change for previously-presented melodies.
2.1 Methods
2.1.1 Participants
Twenty-four undergraduates from University of California at Berkeley participated in return for one hour of course credit. All participants reported having normal hearing. As previous experiments (Loui, et al., 2010) had shown no systematic differences between musicians and nonmusicians in learning a new musical system, participants in all experiments in this study were unselected for musical training.
2.1.2 Stimuli
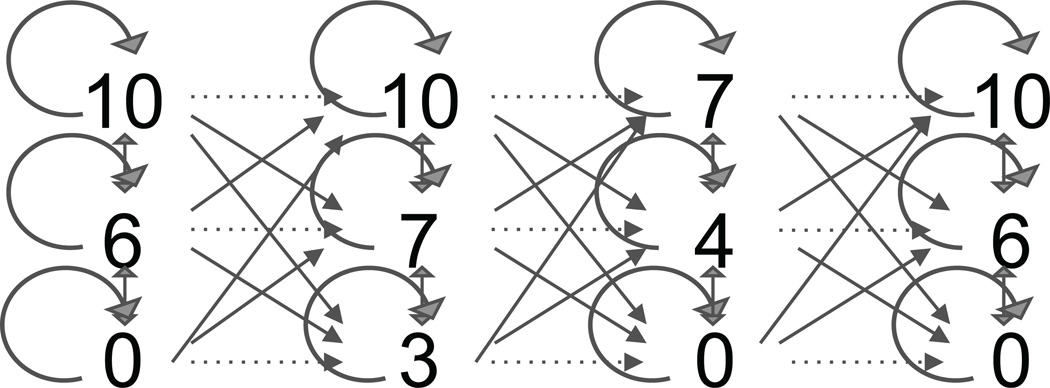
All auditory stimuli were presented using in-house software written in MaxMSP (Zicarelli, 1998) from a Dell PC through AKAI headphones at 70 dB. Strings of tones were generated, with each tone being 500 ms in length, including rise and fall times of 5 ms each. Five hundred melodies were generated from each of the two artificial grammars, with 400 melodies being used for training and 100 melodies for test. Melodies (strings of tones) contained eight tones each and were presented with a silent gap of 500 ms between successive melodies. Frequencies of the tones were determined by the artificial musical grammar shown in Figure 1, which is similar to previous studies except that nine horizontal pathways of the finite-state grammar were removed such that nine small intervals were omitted from melodies presented during the exposure phase. The intervals that were not used in exposure melodies, i.e. the horizontal pathways, were used to generate novel melodies for generalization tests (see Figure 1).
Figure 1.
The finite-state grammar with its omitted pathways in Experiment 1. These omitted pathways, shown here in dotted arrows, correspond to the pathways that were not presented during the exposure phase in Experiment 1.
2.1.3 Procedure
Informed consent was obtained from each participant prior to the start of the experiment. All experiments took place in a sound-attenuated chamber and included an exposure phase followed by a test phase with two-alternative forced choice tests and preference ratings.
Exposure was the half-hour phase of the experiment where participants were systematically exposed to a large set of melodies in one of the two grammars in the new music system. Four hundred melodies were presented once each for an overall duration of 30 minutes. Each melody contained only the intervals that are shown as solid black pathways in the finite-state grammar in Figure 1. Participants were told that they were about to be exposed to a new musical system: they were instructed to listen to the auditory stimuli without trying too hard to memorize or over-analyze the sounds. They were not allowed to make sounds, fall asleep, or seek external sources of stimulation (e.g. read or check their phones). To avoid boredom, they were provided with colored pencils and were given the option of drawing or writing on paper as a distracter task. Participants were monitored by an experimenter during the entire 30 minutes of the exposure phase. Sound examples of select musical stimuli are posted online in http://www.psycheloui.com/publications/downloads.
Two-alternative forced choice tests were conducted to assess learning and memory for the new musical system. Learning was assessed using a generalization test, whereas memory was assessed using a recognition test. Each of the recognition and generalization tests included 10 trials of a two-alternative forced choice task, where participants were presented with two melodies sequentially, and were asked to choose the melody that sounded more familiar. In the recognition test, one of the melodies in each trial belonged to the set of 400 melodies that participants had previously heard, whereas the other melody was not previously presented, and was generated from the other grammar. In the generalization test, each trial consisted of two melodies, neither of which had been presented during exposure, but one of which was constructed from the participant’s exposure grammar, whereas the other belonged to the other grammar. Both melodies contained pathways that were not presented during the exposure phase (white arrows outlined in Figure 1). For both recognition and generalization tests, participants’ task was to chose the melody that sounded more familiar. Each participant was exposed to one grammar and tested against another. Exposure and test grammars were reversed between participants, as was done in previous studies (Saffran, Johnson, Aslin, & Newport, 1999). Thus, during the test phase, the correct answer for one group of participants was the wrong answer for the other group, and vice versa. In thus way the impact of training on behavior is fairly independent of the stimuli or the testing conditions.
Preference ratings. Forty trials were presented, of which 20 trials were in the participants’ exposure grammar (“Grammatical”) and 20 trials were in the opposite grammar (“Ungrammatical”). Among the melodies in the exposure grammar, 10 melodies were previously presented (“Old”) whereas the other 10 were not previously presented in the exposure phase (“New”). This resulted in three categories of melodies for which participants had to make preference ratings: Old Grammatical, New Grammatical, and Ungrammatical. Comparisons between preference ratings for Old Grammatical and New Grammatical melodies would reveal whether a Mere Exposure Effect exists to boost participants’ preference for previously heard items, whereas comparing preference for New Grammatical and Ungrammatical items would reveal whether any change in preference generalizes towards previously-unencountered but grammatical items.
2.2 Results
2.2.1 Forced-choice tests
Forced choice tests of recognition and generalization were both at chance levels (Recognition: mean = 52.5%, SE = 2.9%; two-tailed t-test against chance: t(23) = 0.84, n.s.; Cohen’s d = 0.35. Generalization: mean = 55%, SE = 6.8%; t(23) = 0.73, n.s.; Cohen’s d = 0.30). Participants’ inability to remember and to learn the melodies, in contrast to previous studies in which they could both recognize and generalize, shows that the elimination of pathways in the finite-state grammar disrupts learning and memory for the new musical system.
2.2.2 Preference ratings
Results from preference ratings showed significantly different ratings for the three types of melodies (F(2, 69) = 5.39, p < 0.01). Pairwise t-tests further revealed that preference ratings were significantly higher for Old Grammatical melodies compared to New Grammatical melodies (Old Grammatical mean rating: 4.23, SE = 0.22; New Grammatical mean rating: 3.37, SE = 0.18; t(23) = 4.52, p < 0.001) and Ungrammatical melodies (Ungrammatical mean rating: 3.66, SE = 0.16; t(23) = 2.47, p = 0.02). Preference ratings for New Grammatical and Ungrammatical melodies did not differ significantly from each other (t(23) = 1.53, n.s., Cohen’s d 0.63), suggesting that preferences increased for previously-encountered items but did not generalize readily to other items that followed the same grammar.
2.3 Conclusion
In this experiment, pathways of the finite-state grammar were eliminated during exposure such that certain melodic intervals were not presented. This manipulation disrupted learning such that both recognition and generalization dropped to chance levels of performance. One possible reason for the disruption of learning arises from Gestalt theories of melody perception (Meyer, 1956). When pathways corresponding to smaller intervals are eliminated, the resulting melodies form either large intervals or repeated notes. This results in disjoint melodies, which have disrupted melodic grouping structure instead of a coherent gestalt percept. Past studies (Creel, Newport, & Aslin, 2004) have shown that statistical learning tends to be facilitated in items that can be easily perceived as gestalts, and relatively difficult for sounds that do not readily stay together in a coherent auditory stream. Thus the disjoint character of these melodies, leading to their disrupted grouping structure, may possibly hinder learning.
In contrast to the learning results, preference ratings showed that old melodies were more highly preferred than new melodies. However, this effect of preference formation for familiar items did not generalize towards melodies that adhered to the same grammar. This effect replicates the Mere Exposure Effect, where stimuli become more preferred after repeated exposure, sometimes without conscious awareness even of the repeated exposure (Zajonc, 1968). The lack of generalizability of this preference replicates our previous studies and is also to be expected given the unsuccessful generalization as shown in the forced choice data from this experiment. Taken together, Experiment 1 showed that participants did not learn to recognize or to generalize the new musical system when given disrupted melodic intervals, but they did form an increase in preference for old melodies, even without successful recognition. These results suggest that preference can be changed in the absence of conscious recognition or learning of musical material.
3 Experiment 2. Testing for Harmonicity
Having shown unsuccessful learning but significant preference formation after manipulating the horizontal dimension of musical melody, the next experiment concerns whether the same can be true of the vertical, harmonic dimension. In Experiment 2, we asked the question of whether a disruption in the harmonic ratios between tones in the Bohlen-Pierce scale might produce similar results to melodic disruptions.
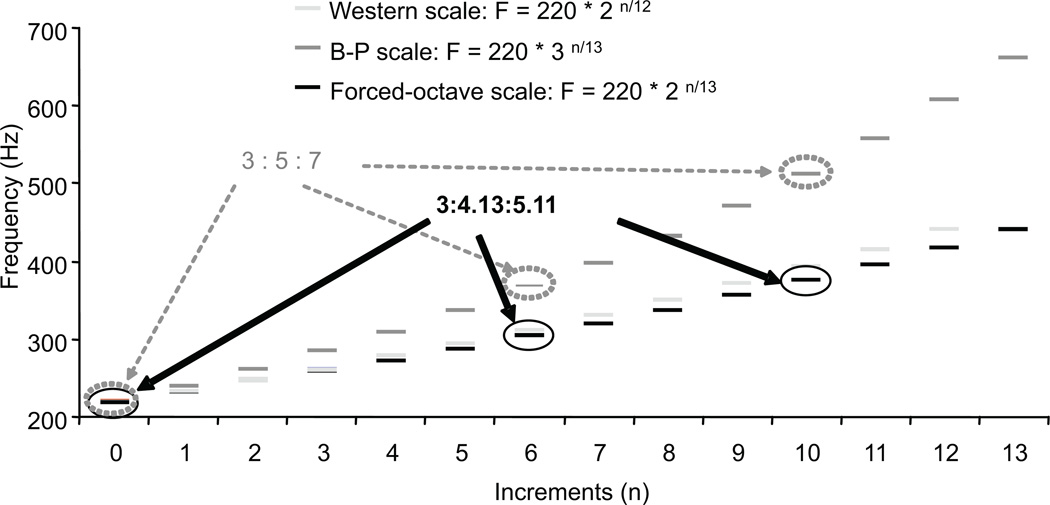
To test for the effect of disrupted harmonic ratios on learning and liking new music, we tested for artificial grammar learning and preference formation using another scale that did not contain harmonic relationships within its chords, but whose melodic principles, including all intervals and contours of the melodies, remained the same as previous studies. A forced-octave scale was created and the artificial grammars similar to previous studies (Loui, et al., 2010) were used. This force-fitted octave scale (Fig. 2) used the formula:
Frequency (Hz) = 220 * 2 ^ (n/13),
where all increments of the Bohlen-Pierce scale were fitted into the octave, such that the relative interval sizes were similar and all the melodies were the same in contour, but the tones chosen to be chords did not form low-integer harmonic ratios together.
Figure 2.
The Forced-octave scale, which was used for Experiment 2, in comparison to the Western and Bohlen-Pierce scales.
The forced-octave scale is used in contrast to previous experiments using the Bohlen-Pierce scale. In previous experiments, pitches were defined according to the Bohlen-Pierce scale formula: F = 220 * 3 ^ (n/13), which is itself a contrast to the Western scale, F = 220 * 2 ^ (n/12). In testing for harmonicity, the scale used in the present experiment is a newly defined forced-octave scale, where the number of steps in the scale was 13, same as the Bohlen-Pierce scale, but the numbers were fitted into a 2:1 (octave) frequency ratio. This new forced-octave scale results in pitches that do not fit together into whole-integer ratios of frequency, in contrast to the original Bohlen-Pierce scale (Fig. 2).
If the disruption of harmonic properties of a musical system disrupts learning, then we would expect to see no learning as shown by chance levels of performance in recognition and generalization tests. In contrast, if the disruption of harmony does not influence learning, then we would expect to see above-chance performance in recognition and generalization as in previous studies. Similarly for preference ratings, if the disruption of harmony also disrupts preference formation, then we would expect no Mere Exposure Effect: i.e. no significant change in preference ratings for previously-presented melodies. In contrast, if harmony does not affect preference formation, then we would expect a significant Mere Exposure Effect, i.e. increased preference for previously-presented melodies, even after this harmonic manipulation.
3.1 Methods
3.1.1 Stimuli
Five hundred melodies (eight tones each) were constructed from each of two artificial grammars, similar to Figure 1 (with all possible pathways) and to previous studies (Loui, et al., 2010), and therefore similar to Experiment 1 with all the horizontal pathways replaced in the exposure set. However, the pitches that represent each node in the artificial grammar are different in that the forced-octave scale is used instead of the Bohlen-Pierce scale for all melodies, as shown in Figure 2. Thus, frequencies of tones ranged from 220 Hz (220 Hz * 2^(0/13)) to 417 Hz (220 Hz * 2^(12/13)). Similar to Experiment 1, 400 melodies in each grammar were used for training in the exposure phase, whereas the remaining 100 melodies in each grammar were used for testing. All other acoustic parameters were also the same as Experiment 1.
3.1.2 Participants and Procedure
Twenty-four UC Berkeley undergraduates participated in Experiment 2, following recruitment procedures identical as Experiment 1. All testing procedures were also identical as Experiment 1. Procedures included three phases: 1) exposure, 2) two-alternative forced choice tests of recognition and generalization, and 3) preference ratings.
3.2 Results
3.2.1 Forced choice tests
Forced choice tests revealed successful recognition and generalization. Mean recognition performance was 57% (SE = 3.0%) and mean generalization performance was 63% (SE = 3.0%). Both were significantly above the chance level of 50% (recognition t(23) = 2.48, p < 0.05; generalization t(23) = 4.02, p < 0.01), but recognition and generalization results did not differ significantly from each other (t(23) = 0.26, n.s.; Cohen’s d = 0.10).
3.2.2 Preference ratings
Preference ratings were not significantly different across the three conditions of Old Grammatical melodies, New Grammatical melodies, and Ungrammatical melodies. Mean Old Grammatical rating was 4.1 (out of 7), SE = 0.21; mean New Grammatical mean rating was 4.0, SE = 0.22; mean Ungrammatical rating was 4.0, SE = 0.20. A one-way ANOVA comparing ratings for the three conditions was not significant (F(2, 69) = 0.1, n.s., Cohen’s d = 0.09), and neither were the t-tests between each pair of conditions (all p > 0.2).
3.3 Conclusion
By altering the tones from the tritave-based Bohlen-Pierce scale and forcing these tones to fit within a forced-octave scale, we tested for the effects of harmony on learning and liking. Despite the stimuli being inharmonic, participants were still successful in learning the grammatical structure. Thus the harmonicity of the scale appears to be relatively unimportant for learning, at least in situations where the stimuli were learned based on exposure to monophonic melodies. Instead of using the harmonicity of the scale as a cue for learning, it appears that participants were learning a structure of sequential probabilities in the style of finite-state grammar learning. However, no significant preference change was observed, suggesting that exposure did not influence participants’ preferences for previously presented items compared to novel or ungrammatical items, thus providing further evidence for the possible dissociation between learning and preference formation in music.
4 Discussion
The present study explored melodic intervals and harmonic consonance, two properties of the auditory input that are important in our mental representation of music. In previous experiments we had shown that after only 30 minutes of exposure, humans consistently demonstrate knowledge of an artificial musical system that is derived from the Bohlen-Pierce scale (Loui & Wessel, 2008; Loui, et al., 2010; Loui, et al., 2009). In this set of experiments, we tested for the contribution of statistical and acoustic properties of the input, and observed behavioral indices of learning including recognition, generalization, and preference formation. In Experiment 1, a subset of legal pathways was eliminated from the finite state grammar, thus disrupting melodic processes of the musical system. Results showed that participants did not recognize old melodies, nor did they demonstrate generalized knowledge of the musical grammar. However, a significant Mere Exposure Effect was observed, as assessed by a difference in preference ratings between old and new melodies. In Experiment 2, the harmonic property of the new musical system was manipulated by force-fitting the Bohlen-Pierce scale into an octave, thus forming the new forced-octave scale. Results showed successful learning; however, the Mere Exposure Effect was now eliminated. Taken together, combined results from Experiments 1 and 2 show that disrupting melodic properties resulted in unsuccessful learning, but a significant Mere Exposure Effect, whereas disrupting harmonic properties resulted in successful learning, but no Mere Exposure Effect.
Regarding the Mere Exposure Effect, one remaining issue concerns why preferences did not generalize towards grammatical but new items. The Mere Exposure Effect was first reported as increased preference towards repeatedly presented visual stimuli (Zajonc, 1968). As the increase in preference was observed even for subliminally presented stimuli, it was thought to be a result of implicit rather than explicit cognitive processes (Bornstein & D'Agostino, 1992; Monahan, Murphy, & Zajonc, 2000; Zizak & Reber, 2004). However, this increase in preference did not generalize to structurally similar but superficially different items, suggesting that the processes that underlie the Mere Exposure Effect may be different from the implicit learning mechanisms that subserve artificial grammar learning, in that they do not generalize towards new but structurally similar items (Newell & Bright, 2003). This dissociation was also observed in previous studies on music learning, where ratings of liking were sensitive to different types of learning than grammaticality judgment task (Kuhn & Dienes, 2005). In this regard, the present study converges with previous reports in showing that the implicit processes that give rise to learning and preference formation may be separate. Alternately, the lack of generalization of the Mere Exposure Effect may be simply due to the relatively short duration of the present experiment: given longer exposure, our affective responses might be changeable such that the effect of exposure on preference might generalize towards novel but structurally similar items. Another outstanding issue concerns why participants were unable to recognize and generalize melodies after removal of pathways in the grammar in Experiment 1. It was interesting that after melodic processes (which are equivalent to first-order conditional probabilities in this experiment) were disrupted, in addition to being unable to generalize to new melodies, participants also could not recognize previously heard melodies. This suggests that removing the pathways that correspond to small pitch intervals disrupted recognition as well as learning, possibly because of the change in perceptual Gestalt of the melody. In this regard, results are congruent with previous literature in showing that Gestalt properties affect learning of melodies (Creel, et al., 2004).
The experimental manipulations presented in this study can be considered from an artificial grammar perspective (conditional probabilities), from a musical perspective (melodic interval sizes), and from the perspective of Gestalt psychology (coherent percepts of auditory objects). While it is unclear which perspective is the correct one to take (if there even is a correct perspective), the musical artificial grammar approach does offer a valuable testing ground for questions from cognitive science, cognitive psychology, and music perception and cognition. Taken together, results from this study converge with previous literature (Kuhn & Dienes, 2005; Loui, et al., 2010) in suggesting that preference formation can occur in the absence of conscious recognition or learning, and that successful grammar learning may not co-occur with preference formation. Furthermore, the vertical and horizontal musical dimensions of harmony and melody are both important components of our mental representation of music. Melodic processes play a significant role in the learnability of new music, whereas harmonic consonance plays an important role on the likability of new music. Vertical and horizontal dimensions must be combined to give rise to our coherent representations of music in the natural world.
Acknowledgements
I would like to thank David Wessel, Ervin Hafter, and Carla Hudson Kam for helpful advice and valuable mentorship, Carol Krumhansl for helpful discussions, Gustav Kuhn and Emmanuel Pothos for helpful comments on a previous version of this manuscript, and Elaine Wu, Pearl Chen, Judy Wang, Shaochen Wu, and Charles Li for help with data collection. Data collection is supported by the UC Berkeley Academic Senate and a dissertation research grant from UC Berkeley Psychology. Writing of this manuscript is supported by NICHD R01 DC009823.
References
- Besson M, Faita F. An Event-Related Potential (ERP) Study of Musical Expectancy: Comparison of Musicians With Nonmusicians. Journal of Experimental Psychology: Human Perception and Performance. 1995;21(6):1278–1296. [Google Scholar]
- Bigand E, Parncutt R. Perceiving musical tension in long chord sequences. Psychol Res. 1999;62(4):237–254. doi: 10.1007/s004260050053. [DOI] [PubMed] [Google Scholar]
- Bigand E, Poulin-Charronnat B. Are we "experienced listeners"? A review of the musical capacities that do not depend on formal musical training. Cognition. 2006;100(1):100–130. doi: 10.1016/j.cognition.2005.11.007. [DOI] [PubMed] [Google Scholar]
- Bornstein RF, D'Agostino PR. Stimulus recognition and the mere exposure effect. J Pers Soc Psychol. 1992;63(4):545–552. doi: 10.1037//0022-3514.63.4.545. [DOI] [PubMed] [Google Scholar]
- Castellano MA, Bharucha JJ, Krumhansl CL. Tonal hierarchies in the music of north India. Journal of Experimental Psychology: General. 1984;113(3):394–412. doi: 10.1037//0096-3445.113.3.394. [DOI] [PubMed] [Google Scholar]
- Creel SC, Newport EL, Aslin RN. Distant Melodies: Statistical Learning of Nonadjacent Dependencies in Tone Sequences. JEP: Learning, Memory, and Cognition. 2004;30(5):1119–1130. doi: 10.1037/0278-7393.30.5.1119. [DOI] [PubMed] [Google Scholar]
- Dienes Z, Longuet-Higgins C. Can musical transformations be implicitly learned? Cognitive Science: A Multidisciplinary Journal. 2004;28(4):531–558. [Google Scholar]
- Huron D. Sweet Anticipation: Music and the Psychology of Expectation. 1 ed. Vol. 1. Cambridge, MA: MIT Press; 2006. [Google Scholar]
- Kameoka A, Kuriyagawa M. Consonance theory part II: consonance of complex tones and its calculation method. J Acoust Soc Am. 1969;45(6):1460–1469. doi: 10.1121/1.1911624. [DOI] [PubMed] [Google Scholar]
- Koelsch S, Grossmann T, Gunter TC, Hahne A, Schroger E, Friederici AD. Children processing music: electric brain responses reveal musical competence and gender differences. Journal of Cognitive Neuroscience. 2003;15(5):683–693. doi: 10.1162/089892903322307401. [DOI] [PubMed] [Google Scholar]
- Koelsch S, Gunter T, Friederici AD, Schroger E. Brain indices of music processing: "nonmusicians" are musical. J Cogn Neurosci. 2000;12(3):520–541. doi: 10.1162/089892900562183. [DOI] [PubMed] [Google Scholar]
- Krumhansl C. Cognitive Foundations of Musical Pitch. Oxford University Press; 1990a. [Google Scholar]
- Krumhansl C. Music Psychology and Music Theory: Problems and Prospects. Journal of the Society for Music Theory. 1995;17(1):53–80. [Google Scholar]
- Krumhansl CL. General properties of musical pitch systems: Some psychological considerations. In: Sundberg J, editor. Harmony and Tonality. Vol. 54. Stockholm: Royal Swedish Academy of Music; 1987. [Google Scholar]
- Krumhansl CL. Cognitive foundations of musical pitch. New York, NY US: Oxford University Press; 1990b. [Google Scholar]
- Krumhansl CL, Toivanen P, Eerola T, Toiviainen P, Jarvinen T, Louhivuori J. Cross-cultural music cognition: cognitive methodology applied to North Sami yoiks. Cognition. 2000;76(1):13–58. doi: 10.1016/s0010-0277(00)00068-8. [DOI] [PubMed] [Google Scholar]
- Kuhn G, Dienes Z. Differences in the types of musical regularity learnt in incidental- and intentional-learning conditions. The Quarterly Journal of Experimental Psychology. 2006;59(10):1725–1744. doi: 10.1080/17470210500438361. [DOI] [PubMed] [Google Scholar]
- Kuhn G, Dienes Zn. Implicit Learning of Nonlocal Musical Rules: Implicitly Learning More Than Chunks. Journal of Experimental Psychology / Learning, Memory & Cognition. 2005;31(6):1417–1432. doi: 10.1037/0278-7393.31.6.1417. [DOI] [PubMed] [Google Scholar]
- Lerdahl F, Jackendoff R. Generative Theory of Tonal Music. Cambridge, Mass: MIT Press; 1983. [Google Scholar]
- Loui P. Acquiring a New Musical System. Berkeley, CA: University of California at Berkeley; 2007. [Google Scholar]
- Loui P, Wessel D. Harmonic expectation and affect in Western music: Effects of attention and training. Perception & Psychophysics. 2007;69(7):1084–1092. doi: 10.3758/bf03193946. [DOI] [PubMed] [Google Scholar]
- Loui P, Wessel DL. Learning and Liking an Artificial Musical System: Effects of Set Size and Repeated Exposure. Musicae Scientiae. 2008;12(2):207–230. doi: 10.1177/102986490801200202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loui P, Wessel DL, Hudson Kam CL. Humans Rapidly Learn Grammatical Structure in a New Musical Scale. Music Perception. 2010;27(5):377–388. doi: 10.1525/mp.2010.27.5.377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loui P, Wu EH, Wessel DL, Knight RT. A Generalized Mechanism for Perception of Pitch Patterns. Journal of Neuroscience. 2009;29(2):454–459. doi: 10.1523/JNEUROSCI.4503-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch MP, Eilers RE, Oller DK, Urbano RC. Innateness, experience, and music perception. Psychological Science. 1990;1(4):272–276. [Google Scholar]
- Mathews MV, Pierce JR, Reeves A, Roberts LA. Theoretical and experimental explorations of the Bohlen-Pierce scale. J Acoustical Soc Am. 1988;84:1214–1222. [Google Scholar]
- Meyer L. Emotion and Meaning in Music. U of Chicago Press; 1956. [Google Scholar]
- Monahan JL, Murphy ST, Zajonc RB. Subliminal mere exposure: specific, general, and diffuse effects. Psychol Sci. 2000;11(6):462–466. doi: 10.1111/1467-9280.00289. [DOI] [PubMed] [Google Scholar]
- Narmour E. The Analysis and Cognition of Basic Melodic Structures: The Implication-Realization Model. Chicago: University of Chicago Press; 1990. [Google Scholar]
- Newell BR, Bright JE. The subliminal mere exposure effect does not generalize to structurally related stimuli. Can J Exp Psychol. 2003;57(1):61–68. doi: 10.1037/h0087413. [DOI] [PubMed] [Google Scholar]
- Piston W, DeVoto M. Harmony. WW Norton; 1987. [Google Scholar]
- Pothos EM. Theories of Artificial Grammar Learning. Psychological Bulletin. 2007;133(2):227–244. doi: 10.1037/0033-2909.133.2.227. [DOI] [PubMed] [Google Scholar]
- Poulin-Charronnat B, Bigand E, Madurell F, Peereman R. Musical structure modulates semantic priming in vocal music. Cognition. 2005;94(3):B67–B78. doi: 10.1016/j.cognition.2004.05.003. [DOI] [PubMed] [Google Scholar]
- Reber AS. Implicit learning of artificial grammar. Journal of Verbal Learning and Verbal Behaviour. 1967;6:855–863. [Google Scholar]
- Rohrmeier M, Rebuschat P, Cross I. Incidental and online learning of melodic structure. Consciousness and Cognition. 2011;20(2):214–222. doi: 10.1016/j.concog.2010.07.004. [DOI] [PubMed] [Google Scholar]
- Saffran JR, Johnson EK, Aslin RN, Newport EL. Statistical learning of tone sequences by human infants and adults. Cognition. 1999;70:27–52. doi: 10.1016/s0010-0277(98)00075-4. [DOI] [PubMed] [Google Scholar]
- Schellenberg EG, Bigand E, Poulin-Charronnat B, Garnier C, Stevens C. Children’s implicit knowledge of harmony in Western music. Developmental Science. 2005;8(6):551–566. doi: 10.1111/j.1467-7687.2005.00447.x. [DOI] [PubMed] [Google Scholar]
- Schellenberg EG, Trehub SE. Natural musical intervals: Evidence from infant listeners. Psychological Science. 1996;7(5):272–278. [Google Scholar]
- Tillmann B, McAdams S. Implicit Learning of Musical Timbre Sequences: Statistical Regularities Confronted With Acoustical (Dis)Similarities. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2004;30(5):1131–1142. doi: 10.1037/0278-7393.30.5.1131. [DOI] [PubMed] [Google Scholar]
- Trainor L, Trehub SE. Key membership and implied harmony in Western tonal music: developmental perspectives. Perception & Psychophysics. 1994;56(2):125–132. doi: 10.3758/bf03213891. [DOI] [PubMed] [Google Scholar]
- Tramo MJ, Cariani PA, Delgutte B, Braida LD. Neurobiological foundations for the theory of harmony in western tonal music. Ann N Y Acad Sci. 2001;930:92–116. doi: 10.1111/j.1749-6632.2001.tb05727.x. [DOI] [PubMed] [Google Scholar]
- Zajonc RB. Attitudinal Effects of Mere Exposure. Journal of Personality and Social Psychology. 1968;11:224–228. [Google Scholar]
- Zicarelli D. An extensible real-time signal processing environment for Max; Paper presented at the Proceedings of the International Computer Music Conference; Ann Arbor, USA: University of Michigan; 1998. [Google Scholar]
- Zizak DM, Reber A. Implicit preferences: The role(s) of familiarity in the structural mere exposure effect. Consciousness and Cognition. 2004;13(2):336–362. doi: 10.1016/j.concog.2003.12.003. [DOI] [PubMed] [Google Scholar]