Measurements of Street-Crossing Decision-Making in Pedestrians with Low Vision

Abstract

Purpose

Crossing the street is an important but risky activity of daily living. If a pedestrian makes a poor street-crossing decision, the consequence could be serious injury or death. In order to advance our understanding of how visual and auditory information is sampled and processed to make street-crossing decisions, an accurate, reliable, and sensitive psychophysical and/or psychometric method of measurement of the street-crossing decision variable must first be developed and validated. The aim of this paper is to develop and validate a new metric for this variable.

Methods

Using a 5 point rating scale, safety ratings for eight different vehicular gap times of different durations were recorded along an unsignalized, two-lane street of one-way traffic. Safety ratings were collected from 12 normally sighted and 10 visually impaired subjects. Receiver Operating Characteristic (ROC) curves were estimated for all possible gap pairs and the discriminability (d’) of the street-crossing decision variable for all gap pairs was estimated from the area under the ROC curve.

Results

We found that our data conform with the assumptions that the underlying distributions of the decision variable are continuous, monotonic and unbounded. Using the dissimilarity matrix of d’ values for each person (which were computed for all pairings of gap times) in a one-dimensional scaling model, we estimated the means of each distribution of the decision variable relative to a center of gravity (COG) for the person. When plotting the means of the distributions against vehicular gap time, the data are best described as a non-linear function symmetric about the COG. We showed that the x-intercept (t_COG) and slope from the non-linear function can be used to assess a person’s street-crossing decision-making performance for different amounts of sensory information. Using our newly developed metrics, we found no significant difference in t_COG (p=0.30) and in the slopes of the model (p=0.85) between normally-sighted and visually impaired subjects. In addition, both subject groups centered their t_COG close to their actual crossing time.

Conclusions

A newly developed model for measuring a street-crossing decision variable functions as a valid metric that can be used to quantify street-crossing decision making performance in pedestrians. Using this new metric, we observed that visually impaired subjects who travel independently are able to make street-crossing judgments that are comparable to those of normally sighted subjects.

1.0 Introduction

Crossing a non-signalized street is a high-risk activity that depends on the processing of complex sensory information before a crossing decision is made. The street-crossing environment is a very rich sensory environment that contains both visual and auditory information from vehicles and fellow pedestrians and tactile information from the movement and vibration of vehicles traveling along the roadway.

Traffic engineering for pedestrians at non-signalized intersections have included installing motorist and in-roadway warning lights and flashing beacons to alert drivers to expect and yield to pedestrians, improving driver and pedestrian visibility by removing objects that obstruct the line of sight as well as including roadway design elements such as crosswalk pavement markings, median refuge islands, curb extensions and traffic calming measures to reduce the vehicular speeds of drivers entering an intersection (Fitzpatrick et al. 2006). While these “treatments” assist and improve pedestrian safety (Fitzpatrick et al. 2006), they do not ensure complete pedestrian safety and / or tell the pedestrian when it is safe to cross. For example, Fitzpatrick et al. (2006) found that the percentage of drivers who yielded or stopped where required at a non-signalized intersection varied anywhere between 30% to 99% depending on the traffic engineering treatment. When drivers do yield, pedestrians may not always recognize that a driver has yielded since Ashmead et al. (2005) found that blind pedestrians at roundabouts failed to perceive drivers yielding. As a result, the burden of knowing when it is safe to cross at a non-signalized intersection often still lies with the pedestrian. Therefore, it is important to quantify how well pedestrians can discriminate vehicular gap times of different durations at non-signalized intersections.

Research on the gap acceptance of drivers at non-signalized intersections has shown that the existence of multiple vehicles waiting at the intersection (ie. a queue) and increased driver’s waiting time (Kittelson and Vandehey 1991; Lall and Lu 1994; Polus et al. 2003) and traffic flow (Lall and Lu 1994) result in drivers accepting a shorter gap in traffic when entering or turning into an intersection. Applying these research findings to pedestrians’ acceptance of gaps for street-crossing, one might expect that pedestrians may accept shorter and potentially unsafe gaps in vehicular traffic when there is heavy traffic flow and when they have been waiting for a long time by the curb to cross the street.

Previous studies have shown that the ability of pedestrians to make accurate street-crossing decisions becomes seriously compromised with impaired vision. Cheong et al. (2008) found that people with severe visual field loss from retinitis pigmentosa identified fewer crossable gaps and made significantly more unsafe street-crossing decisions compared to age-matched controls with normal vision. When using only auditory information, blind pedestrians require significantly more time to determine when it is safe to cross (Guth et al. 2003; Ashmead et al. 2005; Guth et al. 2005), make a higher percentage of unsafe gap determinations (Guth et al. 2003; Ashmead et al. 2005) and are more likely to miss detecting a crossable gap (Ashmead et al. 2005; Guth et al. 2005) compared to sighted pedestrians.

While these earlier studies show the effects of sensory vision loss on street-crossing decision-making, the psychophysical measures used were criterion-dependent because these studies dichotomized vehicular gap times into “crossable” and “uncrossable” gaps. A “crossable gap” is a vehicular gap time that is longer in duration than the time needed by the subject to cross the street (ie. the subject’s street-crossing time). Subjects were then required to indicate which of the presented vehicular gap times they felt were crossable. The psychophysical measures used in these previous studies are therefore measures of the subject’s personal definition of what they believed was “crossable”, and of the frequency of correctly identifying different intervals as crossable or uncrossable relative to their crossing time.

A limitation of using a criterion-dependent measure to assess street-crossing decision making behavior is that it is not possible to separate the subject’s ability to process and interpret the perceptual information pertinent to the task (ie. the subject’s ability to discriminate different vehicular gap times) from the subject’s own decision criteria for judging what is crossable. To separate these two factors, a criterion-free psychophysical measure must be utilized.

In order for a pedestrian to make a street-crossing decision, the pedestrian must estimate both the time it will take them to cross the street (ie. their street-crossing time) and the time available before the next vehicle reaches the crosswalk (ie. the vehicular gap time). Very little is known about how accurately and precisely different individuals estimate these variables and whether or not their accuracy and precision changes when using different sensory modalities. By using a criterion-free psychophysical method to quantify performance, one can assess how well subjects can discriminate vehicular gap times under different amounts of sensory information independent of their personal decision-making criteria.

The aim of this study is to develop and validate a new model for quantitatively assessing how pedestrians make street-crossing decisions. This model defines and offers a criterion-free method of measuring a latent street-crossing decision-making variable that can be used to study sensory information processing by pedestrians.

2.0 Materials and Methods

2.1 Subjects

Twelve normally-sighted and ten visually impaired adult subjects participated in the study. The normally-sighted subjects were recruited either from the community or through a relationship with another subject and the visually impaired subjects were recruited from the Wilmer Eye Institute’s Low Vision Clinic at the Johns Hopkins University.

Table 1 lists the ages and visual function measures for the two groups of subjects. There was no significant difference in age between the groups (Independent t-test t₂₀=0.58, p=0.57). There were significant differences between groups in visual acuity (VA) in the better eye, contrast sensitivity (CS) in the better eye and averaged visual field (VF) extent in the better eye (Wilcoxon Rank Sums Test z=3.93, p<0.0001; z= −3.83, p<0.0001; z = −2.43, p=0.015 for VA, CS and VF extent respectively).

Table 1.

Subject characteristics

Subject Group	# of Subjects	Age (years)	Parameter *
			Visual Acuity in Better Eye (Log MAR)	Contrast Sensitivity in Better Eye (Log CS)	Average VF Extent (diameter) in Better Eye (Degrees)
Normally Sighted	12	39.02 ± 16.74	−0.09 ± 0.11	1.83 ± 0.09	65.27 ± 4.16
Visually Impaired	10	42.73 ± 12.33	1.04 ± 0.16	0.85 ± 0.54	52.27 ± 15.27

^*Results listed as average ± 1 standard deviation

Visual acuity in each eye was measured using a Lighthouse ETDRS acuity chart (Ferris et al. 1982) transilluminated at approximately 100 cdm⁻² and reported as the logarithm of the minimum angle of resolution (log MAR) using the scoring of Bailey and Lovie (1976). Contrast sensitivity in each eye was measured at 1 m using the Pelli-Robson letter contrast sensitivity chart (Pelli et al. 1988) with overhead illumination of 85 cdm⁻² and scored using the method of Elliott et al. (1990; 1991). The VF in each eye of subjects was measured along 24 meridians from radii of 70⁰ vertically and 90⁰ horizontally using kinetic perimetry with a Goldmann perimeter (III4e target on a background luminance of 10 cdm⁻²). Subjects were instructed to fixate on a central target located within the bowl of the Goldmann perimeter. Subjects with central field loss were encouraged to maintain steady fixation, presumably with their PRL, during the VF assessment. VF extent and the position of any central scotoma were then recorded for all subjects and were reported as the average VF extent (radius) across all meridians from the better eye.

With the exception of five visually impaired subjects who were not tested, all subjects' hearing function was assessed as being ‘normal’ with pure tone air conduction threshold assessment. Normal hearing was defined as pure tone thresholds of 25 dB or less bilaterally for the frequency range from 500 to 8000 Hz. The hearing screening was performed by a certified clinical audiologist using a calibrated portable audiometer (Maico MA 40) and circumaural headphones in a sound-attenuated room. The untested subjects all self-reported that they had normal hearing, had no significant injuries or infections to their ears and did not use any auditory assistive devices such as a hearing aid.

All subjects self-reported that they traveled independently and crossed streets regularly without assistance. None of the subjects were familiar with the intersection used in the study. All subjects were free of physical and cognitive disorders that could affect their ability to walk or follow directions.

The study was designed in accordance to the tenets of the Declaration of Helsinki and was approved by the Institutional Review Board of the Johns Hopkins University School of Medicine. Informed consent was obtained from each subject after explaining the study.

2.2 Street Test Site

The test site used in this study was a residential street within Baltimore City, Maryland, USA. The street had a total of six lanes; 3 lanes on either side of a 1.75 m wide median strip. The three lanes on either side of the median strip were identical to each other except for the direction of traffic and consisted of an outer parking lane and two lanes of free-flowing, one-way traffic. The study was conducted along the curb from one side of the median strip (refer to Figure 1). Thus subjects made street-crossing decisions with traffic approaching from just one side of the street (ie. across two lanes). The width of the street from the curb of the median strip to the parked vehicles in the parking lane was ~6.5 m.

Figure 1. The street crossing test site showing two of the four sensors used in this study.

The star depicted on the median strip adjacent to the sensor positioned in the foreground is where subjects stood when making their street-crossing decisions.

The location at which subjects stood on the median strip for the study was called the crossing point (refer to Figure 1). From the crossing point, subjects’ line of sight was uninterrupted for at least 500 feet and in the absence of loud background (masking) sounds, subjects could hear approaching vehicles at a time that greatly exceeded the time it took them to actually cross that side of the street. Thus the physical and sensory characteristics of the street did not diminish the quality of available sensory information from which subjects could make a street-crossing decision.

2.3 Measurement of Physical Gap Time

Positioned at various locations along the street test site were four sensor systems that computed the vehicular speeds and physical gap times of approaching vehicles. The sensor system consisted of a low-powered laser (<5mW) positioned along the curb on one side of the street and its beam was aligned with a photo-detector positioned along the curb on the median strip (refer to Figure 2). Both the laser and photo-detector were positioned at a height of approximately 50 cm above the curb using tripods. Pilot data showed that at this height, the path of the laser beam was, on average, at the approximate height of a passing vehicle’s bumper bar. The four sensor systems were located approximately 213 m, 200 m, 12 m and 0 m to the right of the crossing point. The two farthest sensors wirelessly sent their recorded information to a portable computer while the two closest sensors were connected to the same portable computer via serial cables.

Figure 2. The set-up of the sensory system at the test site where subjects made their street-crossing decisions.

The dotted line in the picture represents the path of the laser beam emanating from the laser pointer on the far side of the street to the photo-detector within the sensor unit located on the median strip.

The star depicted on the median strip is where subjects stood when making their street-crossing decisions.

Each photo-detector was housed within a water- and light-proof box approximately fifteen by fifteen centimeters in size (refer to Figure 2). At the front of each box were two identically sized apertures that were vertically orientated with respect to each other. Positioned behind each aperture were two identical optical systems that directed and focused the light entering through the aperture onto the photo-detectors positioned at the rear of the box. Each optical path consisted of a 33 D Fresnel lens positioned just behind the aperture that focused incoming light in a plane just in front of the photo-detector. A translucent diffuser, placed at the focal length of the Fresnel lens, evenly diffused the light over the surface of the photo-detector. The photo-detector continuously recorded the incident light intensity and sent its output to a portable computer.

The bottom optical path was exposed to ambient (environmental) light as well as to the light emitted from the laser. The top optical path was exposed to ambient light only. The photo-detectors were calibrated so that their recordings were matched for the ambient illumination. During an experimental trial, readings from the top photo-detector were subtracted from the intensity readings from the bottom detector, with the difference representing the intensity of the laser light, which improved detection of the interruption of the laser beam by a moving vehicle.

When the path between the laser and photo-detector was broken by an approaching vehicle, the event was recorded, time stamped and sent (either wirelessly or by serial cable depending on the location of the sensor) to the portable computer. Vehicular velocity was computed by dividing the known distance separating two adjacent sensors by the time difference between the two sensor signals. The physical gap time was calculated as the difference between the time the prompt signal was given (see Experimental Procedure for an explanation of the prompt signal) and the time the approaching vehicle was first detected by the sensor system positioned by the crossing point.

2.4 Experimental Procedure

Four repetitions of subjects’ street crossing times were measured by recording the time it took subjects to walk, at their usual street-crossing pace, from the curb of the median strip to the parked vehicles in the parking lane (ie. the outermost third lane).

For the main experiment, subjects were positioned as close as possible to the crossing point. Numerous subjects could be assessed concurrently; however, for this study, we limited the number in a group of subjects to a maximum of four. To ensure that a subject’s vision and hearing were not obstructed by another participating subject, subjects’ positions were staggered such that they stood in front of, or off to the side of, the subject standing next to them.

Subjects stood by the crossing point where they viewed and listened to gaps in vehicular traffic for a given period of time. At the end of this period, an audible prompt signal was given and subjects had to immediately rate, using a 5-point ordinal rating scale, his/her perception of whether or not there was enough time to cross the street. A rating of 1 and 2 was used when subjects judged that the vehicular gap time was definitely or probably not enough time to cross respectively. A rating of 3 was used when subjects were uncertain whether there was enough time to cross. A rating of 4 or 5 was used when subjects judged that there was probably or definitely enough time to cross respectively. Street-crossing decisions were therefore made on subjects’ perception about whether they believed that the vehicular gap time was physically longer or shorter in duration than their own crossing time. Subjects responded by pressing a button that was attached to a portable computer. Subjects pressed the button one to five times to signal their chosen ordinal rating category. The number of button presses was automatically recorded for each subject and trial by custom software on the portable computer.

Crossability ratings were collected for eight different vehicular gap time intervals grouped in one second increments commencing from 0 – 1 sec with the eighth gap time category grouping together all gap times of 7 seconds or longer. The vehicular gap time was defined as the period of time between the prompt signal and the signal from the sensor located by the crossing point. The vehicular gap times were based on the day-to-day traffic flow of vehicles traveling along the test site (street). Thus the velocity, acoustical properties, and make and models of approaching vehicles changed from trial-to-trial. Sources of variability arising from varying vehicular speeds and acoustical variations from different vehicle makes and models do not need to be controlled as they simply combine with all other sources of variability in the decision variable. The average velocity (SD) of the approaching vehicles used to generate the different vehicular gap times in this study was 52.79 km/hr (8.77). The sign posted vehicular speed limit for the test site (street) was 56.33 km/hr (≡35 miles/hr).

A trial commenced when the experimenter, gave subjects an audible “get ready” signal followed by the prompt signal. The time between the “get ready” signal and the prompt signal was unpredictable. The time at which the prompt signal was given was estimated from the vehicle’s speed and varied across trials in order to collect crossability ratings for each gap time category. A minimum of 10 trials were collected for each gap time interval.

Subjects were instructed that they must give their rating immediately after hearing the prompt signal. This was done to prevent subjects from continuing to sample sensory information. Subjects were instructed to assume that they were crossing the street at their regular walking pace; not running or speeding up, and were able to reach the other side of the street by the parking lane, crossing at their usual comfortable pace, before the vehicle reached the crossing point. They also were instructed never to assume that the approaching vehicle(s) will slow down for them, or that they will yield to them.

In circumstances when subjects were prevented from making a judgment, subjects were instructed not to give a response (rating) and the trial was not used in any analyses. To minimize the confounding effects of background noise on subjects’ street-crossing decision making ability, trials were conducted only when the experimenter believed that there was minimal interference from masking sounds. If during the trial there was a sudden change in background noise (eg. an emergency vehicle siren), the trial was aborted by issuing an audible “cancel” signal.

Prior to starting data collection, all subjects were given practice trials to familiarize themselves with the experimental task, and to become familiar with the “get ready” and prompt signals. Test sessions were conducted on days that had clear weather and not on days when it rained (including drizzle), when there was heavy fog, snow, or when it was dark. All data were collected during off-peak traffic hours, typically between 11am – 4pm and the (average ± standard deviation) temperature across all test days was (21 ± 7)°C.

3.0 Measurement Model and Data Analysis

To develop the measurement model, we will consider the performance of subject n who makes crossability ratings for gap times that are of different duration. During the period of exposure to environmental sensory information following the get ready signal, we postulate that the stream of visual and auditory information in the street crossing environment is processed by subject n to obtain two estimates: 1) subject n’s estimate of the time it will take to cross the street (c_n) and 2) subject n’s prediction of the duration of the gap in the traffic on trial i (g_ni). These estimates must then be combined to produce a single latent decision variable, X_ni, that is used by subject n to decide whether or not there is enough time to cross the street on trial i. Presumably, this latent decision variable has a stochastic, but monotonic relationship to the actual gap in the traffic on that trial. When the prompt signal is given, subject n must then decide how much risk there is for crossing at that moment. Most likely, subject n does not consciously compute all of these variables in a way that could be verbalized, but instead responds to a level of anxiety associated with the command to cross.

For the purpose of this study, subject n’s subjective rating of the street’s crossability at that moment is based on a single decision variable X_ni, which may be considered equivalent to the difference between the subject’s estimates of the time it will take to cross the street (c_n) and the gap time for that trial (g_ni). The subject’s estimate of crossing time (c_n) is assumed to be constant across all gap durations since the same street was used for all trials. The subject’s estimate of the gap duration (g_ni) however is expected to vary with the actual duration of the gap being assessed. Both c_n and g_ni are fixed variables. Trial-to-trial fluctuations for a given person are captured in the random error term, e_ni, for which the probability density function is person-specific and gap duration-specific. Thus, subject n’s decision variable for gap time t(i) on trial i can be written as:

$$X_{\mathit{\text{ni}}}=g_{\mathit{\text{ni}}}-c_n-e_{\mathit{\text{ni}}}$$ (1)

Across trials having the same nominal gap time t, the street crossing decision variable, X_nt, will have a density function f(X_n|t) conditioned on gap time t. The mean of the street crossing decision variable distribution for gap time t is ${\overline{X}}_{\mathit{\text{nt}}}$ and is equal to:

$${\mathrm{X̄}}_{\mathit{\text{nt}}}=g_{\mathit{\text{nt}}}-c_n$$ (2)

assuming no bias, ie. the expected value of e_nt is 0, and the standard deviation is sd_nt.

For the purpose of assigning crossability ratings, the theory assumes that subject n divides the decision variable axis into five bins. All values of the decision variable less than some threshold, s_n1, will be called “definitely not enough time to cross” (rating category 1). Decision variable values greater than s_n1 but less than s_n2 will be called “probably not enough time to cross” (rating category 2). Other rating categories would be assigned to values of the decision variable, X_n, similarly: “unsure” (rating category 3) for s_n2<X_n< s_n3; “probably enough time to cross” (rating category 4) for s_n3<X_n< s_n4; and “definitely enough time to cross” (rating category 5) for all values of X_n greater than s_n4.

By integrating f(X_n|t) from negative infinity to s_n1, we obtain the theoretical probability that subject n will use rating category 1 for gap time i trials. Similarly, by integrating f(X_n|g_j) from negative infinity to s_n1, we obtain the theoretical probability that subject n will use rating category 1 for gap time j trials. If f(X_n|g_i) and f(X_n|g_j) are normal density functions, these probabilities can be transformed to z-scores for gap times i and j respectively:

$$z_{\mathit{\text{ni}}}=\frac{s_{n1}-{\mathrm{X̄}}_{\mathit{\text{ni}}}}{{\mathit{\text{sd}}}_{\mathit{\text{ni}}}}$$ (3a)

$$z_{\mathit{\text{nj}}}=\frac{s_{n1}-{\mathrm{X̄}}_{\mathit{\text{nj}}}}{{\mathit{\text{sd}}}_{\mathit{\text{nj}}}}$$ (3b)

Similarly, z-scores can be computed for the other rating categories by integrating from negative infinity to s_n2 (probability of using rating categories 1 or 2), to s_n3 (probability of using rating categories 1, 2, or 3), or to s_n4 (probability of using rating categories 1, 2, 3, or 4) for each of the two distributions (gap times i and j).

Replacing ${\overline{X}}_{\mathit{\text{ni}}}\text{ and }{\overline{X}}_{\mathit{\text{nj}}}$ in equations (3a) and (3b), respectively, with the definition in equation (2), we obtain:

$$z_{\mathit{\text{ni}}}=\frac{s_{n1}-(g_{\mathit{\text{ni}}}-c_n)}{{\mathit{\text{sd}}}_{\mathit{\text{ni}}}}$$ (4a)

$$z_{\mathit{\text{nj}}}=\frac{s_{n1}-(g_{\mathit{\text{nj}}}-c_n)}{{\mathit{\text{sd}}}_{\mathit{\text{nj}}}}$$ (4b)

Solving for s_nr (r = 1 to 4) in both equations, and equating them leads to:

$$z_{\mathit{\text{nj}}}=\frac{{\mathit{\text{sd}}}_{\mathit{\text{ni}}}}{{\mathit{\text{sd}}}_{\mathit{\text{nj}}}}{z}_{\mathit{\text{ni}}}+\frac{(g_{\mathit{\text{ni}}}-g_{\mathit{\text{nj}}})}{{\mathit{\text{sd}}}_{\mathit{\text{nj}}}}$$ (5)

Equation (5) describes the ROC curve for discriminating gap times i and j expressed in normal deviate (z-score) units. Equation (5) demonstrates that the ROC curve for discriminating gap times is independent of the subject’s estimate of the crossing time, c_n. If both density functions defining the ROC curve are normal, then z-scores for the observed cumulative response probabilities will fall on a line with the slope determined by the ratio of the distributions’ standard deviations and the horizontal intercept determined by the difference between the distributions’ means.

The person’s ability to discriminate gap times i and j in a two-alternative forced-choice task is equal to the area under the ROC curve (AUC) (Massof and Emmel 1987). If f(X_n|t) is normally distributed for both gap times, then the z-score for the AUC, z_AUC, is:

$$z_{\mathit{\text{AUC}}}=\frac{g_{\mathit{\text{ni}}}-g_{\mathit{\text{nj}}}}{\sqrt{{\mathit{\text{sd}}}_{\mathit{\text{ni}}}^2+{\mathit{\text{sd}}}_{\mathit{\text{nj}}}^2}}$$ (6)

which is a gap time discrimination index. However, z_AUC can be interpreted as an unbounded gap time discrimination index, even if f(X_n|t) is not normal. Therefore, to estimate the decision variable, we compute the AUC of the empirical ROC curve for each pair of gap times using the piecewise cubic hermite interpolating polynomial (pchip) in MATLAB and convert the area to a z-score. The result is a gap time dissimilarity matrix for each person with the absolute value of z_AUC defining the dissimilarity between each of 28 pairs of gap times. Multidimensional scaling (MDS), using Systat, then is applied to the dissimilarity matrix to estimate the one dimensional decision variable, ${\overline{X}}_{\mathit{\text{nt}}}$, for each gap time, t. Using the bivariate Gaussian model, the origin of the estimated scale, ${\overline{X}}_{\mathit{\text{nt}}}=0$, is interpreted as the value of the decision variable at which the estimated gap time equals the estimated crossing time for person n.

4.0 Results

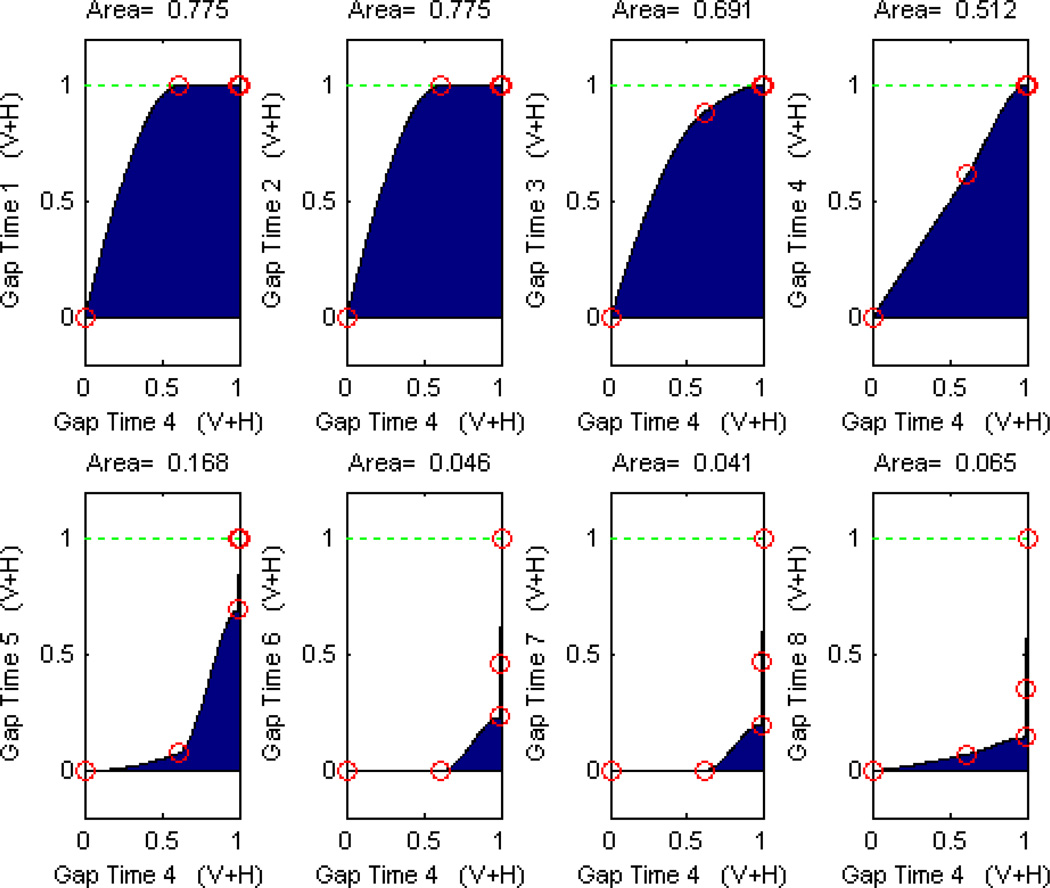
Receiver Operating Characteristic (ROC) curves were estimated from street-crossability ratings for all possible gap pairs for each subject. As illustrated in Figure 3, the discriminability of the street crossability decision variable for each gap pair was then calculated by estimating the area under the ROC curve and converting it to a z score (z_AUC). The z_AUC values were entered into a dissimilarity matrix for each subject and a one-dimensional scaling model (Guttman loss function) was used to estimate the mean of each distribution of the decision variable, ${\overline{X}}_{\mathit{\text{nt}}}=0$, relative to a “center of gravity” (COG). By using a one-dimensional scaling model, we implicitly assumed that the standard deviations of the eight distributions were equal, with only the means varying across gap times. The Guttman coefficients of alienation ranged from 0.0035 to 0.199 (median = 0.025) for normally sighted subjects and from 0.0064 to 0.165 (median = 0.038) for low vision subjects. The proportion of variance in z_AUC values explained by the estimated scale (ie. R² values) ranged from 0.921 to 0.99999 (median = 0.9994) for normally sighted subjects and ranged from 0.949 to 0.99996 (median = 0.9982) for low vision subjects.

Figure 3. Sample Receiver Operating Characteristic (ROC) curves estimated from street-crossability ratings for all gap pairs from one subject under the sensory modality condition of vision + hearing.

Area = area under the ROC curve

(V+H) = sensory modality condition of vision + hearing

Gap Time (for any given x and y axis label) = The gap time categories that frequency distributions were computed for using a subject’s crossability ratings in order to generate a ROC curve between two gap time categories (pair).

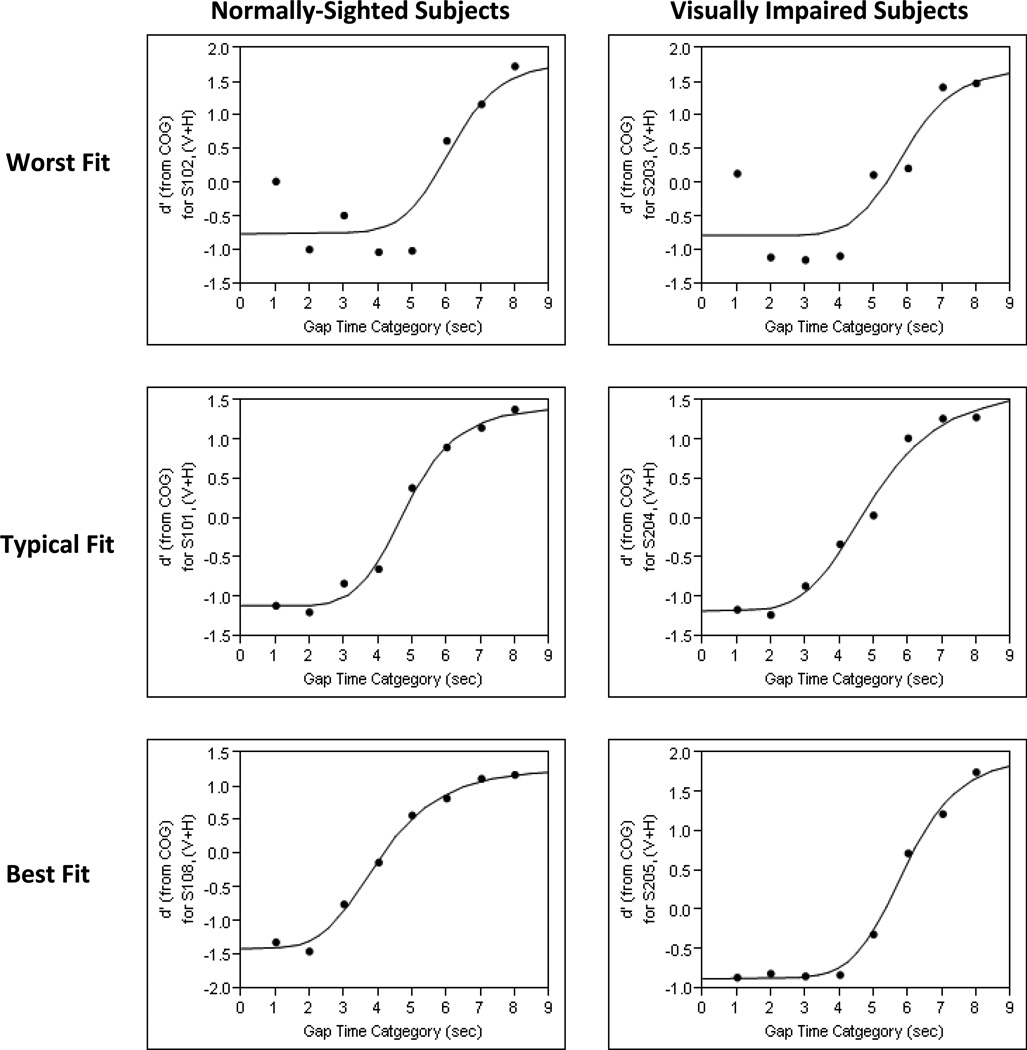
The estimated value of the decision variable relative to the COG, ${\overline{X}}_{\mathit{\text{nt}}}=0$, was plotted against gap time for each subject. As illustrated in Figure 4, the relationship is the same type of nonlinear function for each subject.

Figure 4. Sample non-linear functions from both subject groups.

d’ (from COG) = mean of each distribution of the decision variable relative to a center of gravity (COG)

(V+H) = sensory modality condition of vision + hearing

S101, S102, and S108 = subject ID codes for 3 normally-sighted subjects

S203, S204, and S205 = subject ID codes for 3 visually-impaired subjects

The function that best describes the data takes the form:

$$y=\frac{a_1{t}^{a_2}}{a_3+t^{a_2}}+a_0$$ (7)

where:

• y = street-crossing decision variable estimated from MDS

• t = gap time (in seconds)

• a₀ = is the y-intercept, ie. determines the gap time that corresponds to COG

• a₁ = is the difference between the intercept and the asymptote, ie. determines the maximum value of y.

• a₂ = controls the shape of the function

• a₃ = controls the relative slope of the rising portion of the function

The parameters of the best fitting function were estimated for each subject using non-linear regression (JMP). The sums of squares (SSE) for the fits to the data ranged from 0.009 to 1.45 (median = 0.16) for normally sighted subjects and from 0.04 to 1.58 (median = 0.19) for low vision subjects. Examples of good, bad, and typical fits of the nonlinear function to the estimated decision variables for individual subjects are illustrated in Figure 4. The SSE values for these examples are 1.45 for S102 (upper left panel), 1.58 for S203 (upper right panel), 0.06 for S101 (middle left panel), 0.13 for S204 (middle right panel), 0.05 for S108 (lower left panel), and 0.04 for S205 (lower right panel).

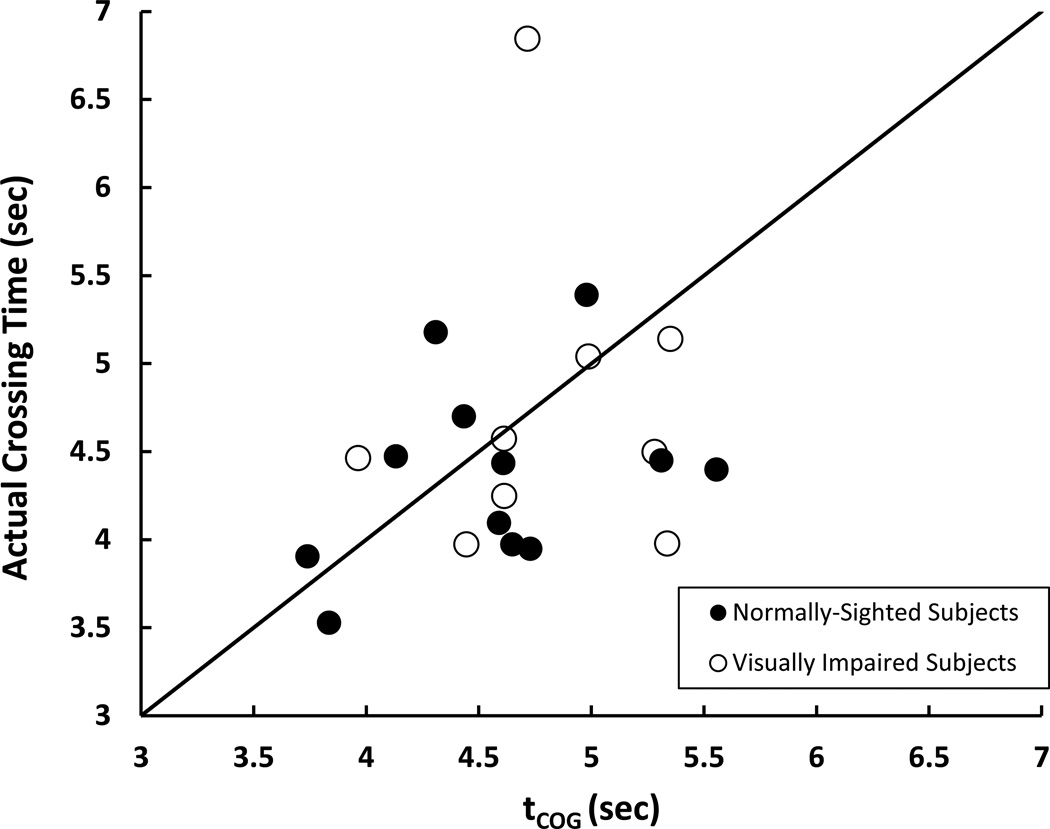
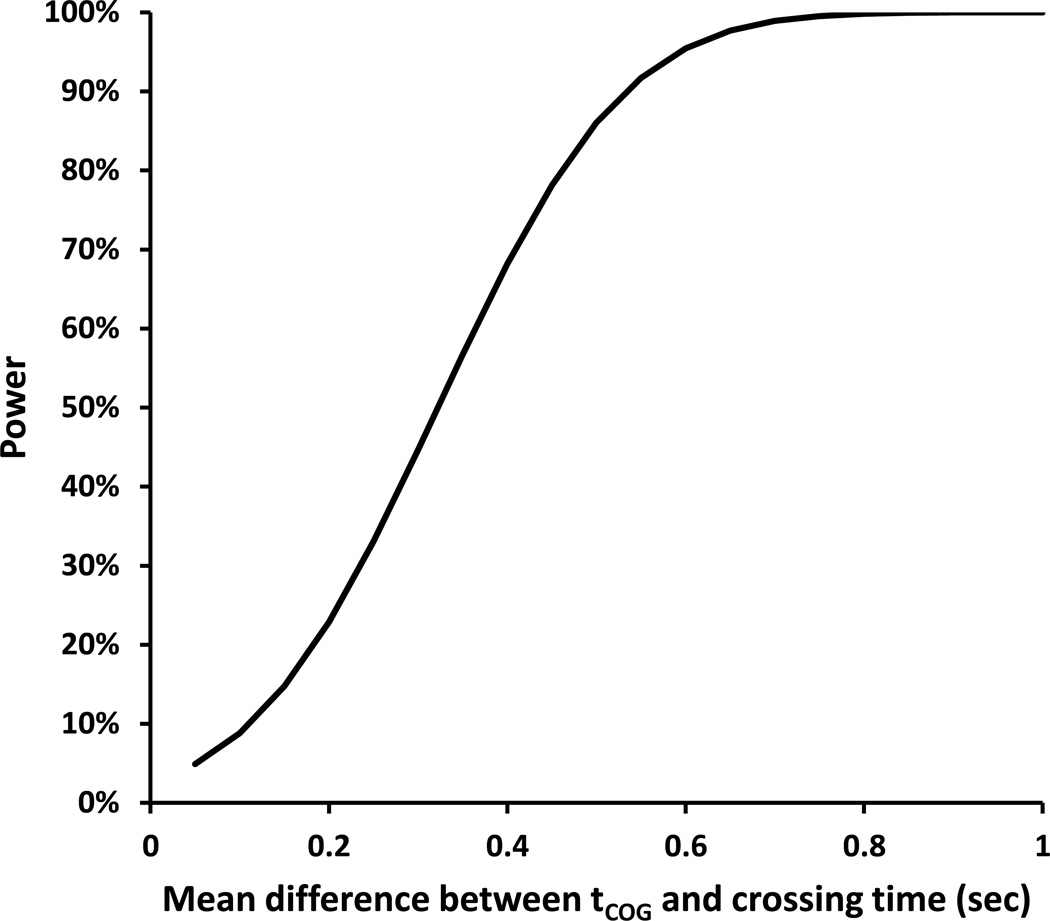
The best-fit functions then were used to calculate the x-intercept for each subject. The x-intercept is the estimated gap time for the COG, t_COG, which corresponds to the time (in seconds) at which the subject transitioned from classifying gap times as being “not enough time to cross” to being “enough time to cross”. If the model has criterion validity, the t_COG for each subject is expected to correspond to that subject’s street-crossing time, ie. the minimum time required to completely cross the street before the vehicle reaches the crossing point. Figure 5 illustrates a scatterplot of actual crossing time for each subject versus the subject’s t_COG estimate along with the identity line. The filled symbols are results for normally sighted subjects and the open symbols are results for low vision subjects. The average crossing times (SD) are 4.4 sec (0.54) for normally sighted subjects and 4.8 sec (0.88) for low vision subjects. The average t_COG values (SD) are 4.6 sec (0.54) for normally sighted subjects and 4.8 sec (0.47) for low vision subjects. The root mean squared error is 0.77 sec. There was no significant difference between the t_COG values (p = 0.30) or between the crossing times (p = 0.24) for the two groups of subjects. We also found no significant difference between subjects’ t_(COG) and their crossing time (p=0.42). By showing no significant difference between subjects’ t_(COG) and crossing time, we validate our model by demonstrating that it has criterion validity. As shown in Figure 6, even with the relatively small sample size employed in this study, it is possible to resolve a 0.50 second difference between subjects’ t_(COG) and crossing time with a power of approximately 86%.

Figure 5. Scatterplot between subjects’ actual crossing time and their t_COG.

t_COG = x-intercept of the non-linear function between the mean of each distribution of the decision variable relative to a center of gravity (COG) (ie. d’ relative to COG) and Gap Time category. The t_COG corresponds to the time (in seconds) at which the subject transitions from classifying gap times as being “not enough time to cross” to being “enough time to cross”.

Figure 6. Power (1−β) with a two-tailed test and α = 0.05 as a function of the difference between subjects’ t_COG and their actual crossing time.

The derivative of the nonlinear function in Figure 4 at t_COG is an indicator of uncertainty in gap time discrimination. Smaller values of the derivative indicate that there must be relatively larger changes in gap time to obtain a criterion change in the decision variable, and vice versa. The derivatives range from 0.42 to 4.89 for the normally sighted subjects and from 0.57 to 1.04 for the low vision subjects. Although three of the normally sighted subjects had derivatives that exceeded the maximum for low vision subjects, there was no significant difference between the distributions (2-sample KS, p = 0.85) which have similar medians (Normals = 0.75, LV = 0.79), first quartiles (Normals = 0.58, LV = 0.63), and third quartiles (Normals = 1.32, LV = 0.91).

5.0 Discussion

In this paper, we offer a model for estimating measures of a unidimensional latent perceptual variable in individual subjects from rating scale responses to a parameterized physical variable. The latent variable in the present study corresponds to the subject’s estimate of the difference between the time required to cross the street and the time available to cross before the next vehicle arrives at the crosswalk (ie. gap time). We assume this latent variable is the result of higher order cognitive processing of complex visual, auditory, and other sensory information about the moving vehicle and the environment. We also assume that subjects’ responses using ordinal categories represent stochastically uncertain magnitude estimates of the latent variable. The model is nonparametric in the sense that no specific assumptions are made about the probability distributions of the stochastic variables.

The unit of measurement is the z-score for the area under the empirical ROC curve for pairs of gap times, z_AUC. The empirical ROC curve describes the covariance of the cumulative frequencies of using the ordered response categories for each gap time in the pair. The cumulative frequencies are criterion-dependent, and the analysis assumes that expected values of a subject’s personal criteria for using the ordered response categories are the same for each gap time. Because the area under the ROC curve is the integral of the cumulative frequencies across all criteria, z_AUC is criterion-free. By transforming the area under the ROC curve to a z-score, the analysis makes the implicit assumption that the latent variable is normally distributed with constant variance across gap times, a requirement that must be met in order to estimate equal interval scales (Massof 2011). These assumptions are the same as those commonly used in signal detection theory to estimate d’ (Green and Swets 1966).

The z_AUC estimate for each pair of gap times represents the distance between the latent variable values for the two gap times on an interval scale. We assume that the subject’s responses to different gap times are governed by a common single variable. This assumption is validated by the low Guttman coefficients of alienation for estimated distance in one dimension. For each subject, one dimension was able to account for more than 92% of the variance in the estimated z_AUC values between gap times (in most cases one dimension accounted for more than 99% of the variance). Therefore, we conclude that the estimated measures are valid estimates of the latent street crossing decision variable on a unidimensional interval scale for both normally sighted and visually impaired people.

The origin of the estimated scale is the centroid of the latent variable estimates for the binned gap times (COG), which is equal to the average cumulative sum of latent variable intervals between successive gap times. For all subjects, the latent decision variable changes most rapidly with gap time in the neighborhood of the centroid, asymptotically approaches a positive ceiling value at long gap times, and approaches a negative floor value at short gap times. This observation suggests that beyond some gap time, all longer gap times are judged to be equally crossable, and less than some other gap time, all shorter gap times are judged to be equally uncrossable. With the most rapid change in the decision variable occurring at the centroid, one might expect the centroid to occur at a gap time (t_COG) that is equal to the person’s crossing time. That expectation was confirmed by the data since the average difference between subjects’ t_COG and their actual crossing time was 0.14 seconds for both the normally-sighted and visually impaired subjects. The ability of subjects to center their t_COG close to their actual crossing time was further demonstrated through the clustering of data points close to the identity line from the scatterplot between subjects’ actual crossing time and their t_COG (Figure 5) and that we found no significant difference between subjects’ t_COG values and their actual crossing times.

The rate of change in the latent decision variable as a function of gap time, as it ascends from the floor and approaches the ceiling, can be interpreted as an indicator of how discriminable gap times are in the neighborhood of the crossing time. It would be reasonable to expect visual impairments to reduce the discriminabilty of gap times. Although the steepest rates of change were observed in the group of normally sighted subjects, there was no significant difference between rates of change distributions for normally sighted and low vision subjects. In addition, there were no differences between normally sighted and low vision subjects in t_COG or crossing time distributions. These results suggest that the independent-traveling low vision subjects in our sample were able to compensate for their visual impairments and did not suffer a loss of ability to judge when it is safe to cross the street. However more research is required to confirm these findings since the statistical power of this study was low – ranging only between 18% - 26%. We would however like to emphasize that the primary aim of this study was to develop and validate a metric that can assess street-crossing decision making performance of pedestrians as opposed to conducting a study with the aim of testing for differences in performance between subject groups.

The metric that we have developed and validated has many applications for improving pedestrian safety. With this metric, we are now able to carry out systematic and parametric assessments of street-crossing performance of people with varying degrees of remaining vision and perception about their own ability. Understanding this information is important because it will show us the characteristics that predispose a person to make either risky or cautious street-crossing decisions. It also allows us to develop objective recommendations for low vision (LV) rehabilitation specialists regarding when to refer patients for orientation and mobility (O&M) training in street-crossing decision making.

Furthermore, this metric can be used to objectively measure and evaluate the success of existing street-crossing decision training programs, the effectiveness of electronic travel aids, and the impact of environmental changes designed to improve pedestrian safety. Currently, specially developed O&M training in street-crossing decision making, electronic travel aids and street-crossing traffic treatments have been proposed to increase pedestrian safety and accessibility. When measuring the effects of such interventions, it is important to separate the different variables that contribute to the effect. The metric we offer here can be used to separate effects that manifest in the person’s discrimination capabilities (eg. t_COG and the slope of the nonlinear function at the t_COG) from changes that manifest in the person’s decision criteria.

The relevance of this metric is not just limited to visually impaired and blind pedestrians. This metric can be applied to any situation that puts people at risk of making unsafe street-crossing decisions such as changes in the environment that affects the fidelity or interpretation of the sensory information. Additionally, this metric can be used in driver evaluation and education on gap acceptance since like pedestrians, drivers frequently have to make judgments regarding if the gap in vehicular traffic is large enough for them to safely cross an intersection or street or merge with flowing traffic.

6.0 Conclusions

In summary, this paper describes and validates a new model that provides a criterion-free method of measuring how pedestrians make street-crossing decisions. We show that two measurement parameters from this model, the x-intercept (t_COG) and the value of the slope at t_COG, can be used to quantify street-crossing decision making performance. The x-intercept of the model corresponds to the time at which subjects transition from classifying gap times as being “not enough time to cross” to being “enough time to cross” which ideally should coincide with the subject’s actual crossing time. The value of the slope of the model at t_COG is a measure of how well subjects can discriminate gap times that straddle the subject’s t_COG. Using this model, we found no significant differences in the slopes between normally-sighted and visually impaired subjects and that both subject groups’ t_COG was similar to the observed time it took them to cross the street. However, a targeted and adequately powered study would be required to confirm these preliminary observations before final conclusions about the effects of visual impairments on gap time judgment can be drawn.

Highlights.

• We developed a model for measuring street-crossing decision making-performance in pedestrians.

• The model’s x-intercept and slope assesses street-crossing decision-making performance.

• Visually impaired people make street-crossing judgments comparable to normally sighted people.