Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2013 Sep 12.
Published in final edited form as: J Am Chem Soc. 2012 Aug 31;134(36):14973–14981. doi: 10.1021/ja3052975

Diastereoselectivity in Lewis-Acid Catalyzed Mukaiyama Aldol Reactions: A DFT Study

Joshua M Lee 1, Paul Helquist 1,*, Olaf Wiest 1,2,*
PMCID: PMC3465709  NIHMSID: NIHMS404156  PMID: 22891640

Abstract

The basis for diastereoselectivity in Lewis acid-catalyzed Mukaiyama aldol reactions was studied using density functional theory. By exploring the conformations of the transition structures for the diastereodifferentiating step of seven different reactions, simple models were generated. The effects of varying the substituents on the enol carbon and the α-carbon of the silyl enol ether from methyl to tert-butyl groups and the substituent on the aldehyde between methyl and phenyl groups were investigated by comparison of the transition structures for different reactions. Expanding on the previous qualitative models by Heathcock and Denmark, we found that while the pro-anti pathways takes place via antiperiplanar transition structures, the pro-syn pathways prefer synclinal transition structures. The relative steric effects of the Lewis acid and trimethyl silyl groups and the influence of E/Z isomerism on the aldol transition state were investigated. By calculating 36 transition structures at the M06/6-311G*//B3LYP/6-31G* level of theory and employing the IEFPCM polarizable continuum model for solvation effects, this study expands the mechanistic knowledge and provides a model for understanding the diastereoselectivity in Lewis acid-catalyzed Mukaiyama aldol reactions.

INTRODUCTION

Since their first demonstration in 1973,1 aldol reactions of silicon-masked enolates in the form of enol silyl ethers2 and later silyl ketene acetals3 as well as thioester silyl ketene acetals4 have been convenient routes to form carbon-carbon bonds under mild conditions. These very commonly used reactions, an example of which is shown in Figure 1, have become known as Mukaiyama aldol reactions. As aldol reactions have the potential to set two stereocenters in one step, controlling the diastereoselectivity is important for realizing the full potential of this reaction.5–10 A better understanding of the mechanism and the structural origin of the diastere-oselectivity of the reaction would facilitate its further use in applications such as polyketide synthesis,11–16 but such aspects of this reaction have yet to be thoroughly understood. Surprisingly, relatively few quantum mechanical computational studies17,18 that would provide this information have been published for the Mukaiyama aldol reaction. Establishing a sound mechanistic basis for diastereoselectivity also provides a foundation for the control of enantioselectivity of these reactions. Many of these reactions employ chiral Lewis base or acid catalysts, which may be subject to improvement by rational, mechanism-based design,19–21 thus furthering the applicability of the Mukaiyama aldol reaction.

Figure 1.

Figure 1

Open in a new tab

Example of a Mukaiyama aldol reaction.1,2

While many aldol reactions and their stereoselectivity have been studied extensively using computational methods,22–34 only two quantum-mechanical studies of the Lewis-acid catalyzed Mukaiyama aldol reaction have been published to date.17,18 B3LYP and MP2 calculations performed by Wong and coworkers described simplified model systems for Lewis-acid catalyzed Mukaiyama aldol reactions. In these studies, Wong found that the metal chloride-promoted reactions of trihydrosilyl enol ethers with formaldehyde take place via a mechanism in which the rate-determining step includes a concerted carbon-carbon bond formation and chloride transfer to the silyl enol ether. Wong also found that a similar reaction promoted by diatomic halogens as Lewis acids takes place via a concerted carbon-carbon bond formation and trihydrosilyl transfer. Finally, the halogen-catalyzed reaction of benzaldehyde with the more representative TMS-protected silyl enol ether of acetophenone was found to take place via a stepwise mechanism, with carbon-carbon bond formation being the rate-determining step. Although this work provides a useful starting point in studying the reaction using computational methods, to the best of our knowledge, there has been no quantum mechanical computational study of the diastereoselectivity of Mukaiyama aldol reactions. While the reaction was studied using DFT methods, the models did not contain a prochiral α-carbon in any of the silyl enol ethers that were studied. Finally, the reaction has yet to be studied using a solvent model, which is likely to be important due to the formation of a zwitterionic intermediate species during the reaction.18

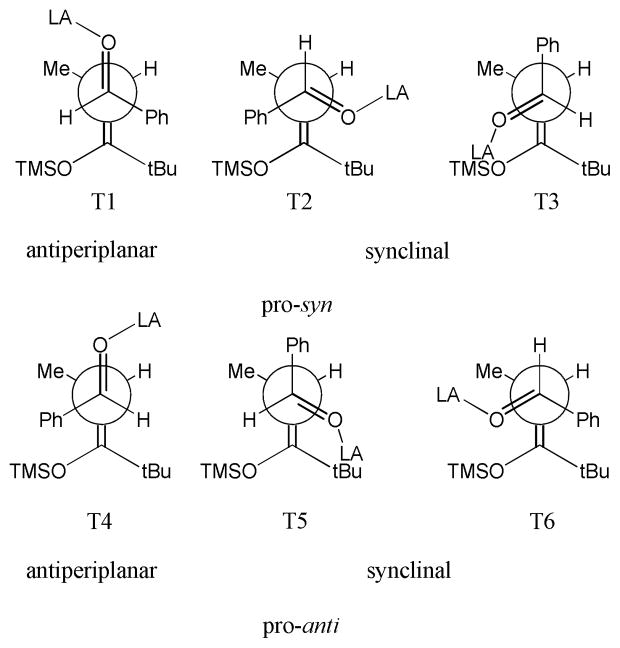
Experimentally, the mechanistic steps of the reaction are well enough understood for one to be confident that the diastereoselectivity is determined when an activated aldehyde35 forms a C—C bond with a silicon-masked enolate.36,37 For the Lewis acids used in this study, it has been shown that side reactions such as the formation of metal enolates do not occur.38 Early work by Heathcock provided transition state models that are still considered the standard model for this reaction. Current qualitative models for the stereoselectivity of the reaction, shown in Figure 2 and originally proposed by Heathcock39 and Denmark,40 discuss possible sources of selectivity and causes for difficulty in achieving high selectivity. Heathcock’s studies were accomplished by screening the reaction with various combinations of simple aldehydes and silyl enol ethers and rationalizing diastereoselectivity. Additionally, Denmark’s work on the reaction utilized an adamantane framework to limit the degrees of freedom of the reaction substrates and to force an intramolecular reaction in which the syn product can form via only a synclinal transition state and the anti product via an antiperiplanar transition state. This work suggests an antiperiplanar transition state preference due to the observation of anti selectivity. These studies, along with the present one, suggest that the reaction takes place via open transition states, in contrast with traditional ionic aldol reactions, which are usually thought to proceed through cyclic transition states. This lack of a Zimmerman-Traxler-type, chair-like transition state41 creates unique challenges for a full understanding of the Mukaiyama aldol reaction because the number of possible transition state conformations to be considered is much larger.

Figure 2.

Figure 2

Open in a new tab

Transition state models proposed by Heathcock.39

Based on the gas-phase computational studies, the large body of experimental work, and the qualitative models by Heathcock and Denmark, we set out to develop quantitatively accurate models for the Lewis-acid catalyzed Mukaiyama aldol reaction by calculating simple but realistic model reactions using density functional theory with an implicit solvent model. The geometric and electronic structures as well as the relative energies of the stable conformations of the relevant diastereomeric transition states would provide the basis for a quantitative analysis of the factors responsible for the diastereoselectivity of the reaction. Our aim was to develop a more general understanding of the reaction and the origin of its diastereoselectivity as well as to provide accurate transition structures that include solvation effects through an implicit solvent model. Finally, the method was validated against experimental values in the literature. The models presented serve both as tools for predicting diastereoselectivity and an advance in the understanding of the mechanism of the Mukaiyama aldol reaction.

COMPUTATIONAL METHODS

Starting from initial models for the model reactions shown in Figure 3, the transition structures were located through a combination of scans of dihedral angle and bond distance for the forming carbon-carbon bond. The model systems were designed to lead to diastereomeric products by selecting silyl enol ethers containing a substituted, prochiral α-carbon. The aldehydes that were studied include acetaldehyde and benzaldehyde, with boron trichloride used as a Lewis acid. Although boron trifluoride is experimentally used as a Lewis acid in these reactions,7,39 fluorine was substituted by chlorine to avoid some of the computational difficulties that we encountered due to the electronegativity of fluorine42 and to make the work more comparable to the results by Wong et al.17 Although boron trichloride is a stronger Lewis acid than boron trifluoride, our focus on relative rather than absolute activation energies allows for this approximation. Based on the experimental results,39 which show similar diastereoselectivities for a series of related Lewis acids such as BF3, TiCl4 and SnCl4, it is reasonable to expect that boron trichloride will be a reasonable model for the steric and electronic effects of other Lewis acids. This substitution should have little effect on diastereoselectivity based on the experimental literature, which indicates the reaction to have a tolerance to minor Lewis acid changes.39 We modeled this Lewis acid cis to the aldehyde hydrogen, as this configuration has been shown to be the most stable geometry for the Lewis acid:aldehyde complex.43,44

Figure 3.

Figure 3

Open in a new tab

(A) The general form of the Mukaiyama aldol reaction studied in this work. Substituents R1, R2, and R3 are varied throughout this study to explore their effects on the selectivity. (B) The three silyl enol ethers described in this study. (C) Depiction of our definition for the dihedral angle (ϕ) around the forming C—C bond. The antiperiplanar example shown corresponds to ϕ =180°.

All optimizations were performed using Gaussian 0945 at the B3LYP/6-31G* level of theory with an IEFPCM solvation model46 with solvent parameters chosen to represent diethyl ether. All transition structures reported are optimized without constraints and their identity was confirmed by harmonic frequency analysis and visual inspection of the imaginary frequency. In order to obtain more accurate final energies, single point energies of the optimized structures were calculated at the M06/6-311G* level of theory with an IEFPCM solvation model46 with solvent parameters for diethyl ether, and thermal corrections from the B3LYP/6-31G* level of theory were included. Using an implicit solvation model is essential to studying diastereoselectivity accurately, as dipole minimization has been shown to influence diastereoselectivity.40 Solvation presumably stabilizes different dipole alignments differently, making it unreasonable to assume this source of error in gas-phase calculations would be systematic. All energies are reported as Gibbs free energies in kcal/mol. All bond lengths are given in Ångstroms, the key dihedral angle is measured between the enol carbon and the aldehyde oxygen, increasing counterclockwise as shown in Figure 3C, and is reported in degrees.

RESULTS

The first step in our study of the Mukaiyama aldol reaction was the investigation of a simple yet physically realistic model system for which experimental data are available. In order to understand the energetics of this system, optimized energies were calculated for the reactants, transition structure, and preferred product of a previously reported anti-selective Mukaiyama aldol reaction.39 These calculations of (Z)-3 reacting with benzaldehyde differ from the reaction reported by Heathcock only in the choice of the Lewis acid BCl3 in place of BF3. The selectivity of (E)-3 was studied as well and is discussed later. As shown in Figure 4, the calculated activation energy is 5.7 kcal/mol and the overall reaction is calculated to be exothermic by 1.6 kcal/mol. Although no experimental activation parameters have been measured for this reaction, the results are in reasonable agreement with the fact that the BF3-catalyzed reaction gives a 95% yield after 4 h47 at −78 °C39 indicating a low activation energy. The calculated bond length for the forming carbon-carbon bond of 2.11 K is in agreement with a slightly exothermic reaction while the dihedral angle around the forming bond for this conformation resembles the antiperiplanar transition state in models by Heathcock and Denmark, shown in Figure 2.

Figure 4.

Figure 4

Open in a new tab

The reaction pathway for the C—C bond formation in the reaction of (E)-3 with benzaldehyde.

Starting from these results for an experimentally studied reaction, we systematically calculated the possible conformations for the transition structures for the relevant mechanistic step (Figure 3A) in several model systems. For the sake of direct comparison, the dihedral angle (ϕ about the two carbons forming a bond is measured in the same way for all transition states as defined in Figure 3C, where the silyl enol ether is positioned with its larger substituent on the α-carbon to the left and the aldehyde in front of it. In our calculations, these relative orientations lead to the five possible transition structures named TS1-5, shown in Figure 5.

Figure 5.

Figure 5

Open in a new tab

Transition structure conformations studied for the Mukaiyama aldol reaction. The conformations are similar for both silyl enol ether isomers.

As an initial model, the transition structure conformations for reactions in which R1=R2=R3=Me, i.e. (E)-1 and (Z)-1 reacting with acetaldehyde, were located. Results are reported in Table 1 and include the dihedral angle around the forming carbon-carbon bond ϕ as defined in Figure 3C, the distance between the reacting carbons, and relative free energy values for each transition state, which are referenced to the lowest energy transition state for each pathway for each silyl enol ether isomer. As is to be expected based on the experimentally observed effect of varying the size of the R3 substituent in (E)-silyl enol ethers,39 the data suggest that this model system in the case of (E)-1 has a free energy difference of approximately 0.0 kcal/mol between the pathways leading to anti and syn products and is therefore not significantly diastereoselective. For the reaction of (Z)-1, the syn pathway is favored by 1.5 kcal/mol. In addition, several additional transition structure conformations that are significantly higher in energy were located. The pro-anti and pro-syn pathways for both isomers of the silyl enol starting material show similar ϕ values in their transition states. The pro-anti pathways for both silyl enol ethers have transition states with dihedral angles ϕ of approximately 170°, 295°, and 330°, and (Z)-1 has an additional transition state with 15° geometry. The pro-syn pathway, interestingly, gives transition states with dihedral angles around 220° and 260° for both (E)-1 and (Z)-1 and an additional transition state at 86° for (Z)-1. The length of the forming C—C bond ranges from 2.37 to 2.66 Å, reflecting that the bond formation distance in the transition structure responds strongly to small steric and electronic effects.

While the pro-anti transition structures include antiperiplanar configurations close to 180°, as expected,40 the pro-syn transition states do not. Despite extensive searches, including a complete scanning of the potential energy surface for pro-syn transition structure geometries, no antiperiplanar transition structure could be located. The geometry closest to an antiperiplanar transition structure that we located has a dihedral angle of 220.3° for (E)-1 (entry 2), while the antiperiplanar configuration is closer to a local energy maximum (see Supporting Information Chart S1). This result is in in noteworthy contrast to the previously established models of the Mukaiyama transition state, which postulated an antiperiplanar transition state.39,40

With a better understanding of the potential energy surface of our first model reaction, we next studied model systems that are expected to show larger energy differences between different transition structure conformations and are consequently expected to be more diastereoselective. To deconvolute the steric effects of R2 and R3 substituents, we focused on bulky aliphatic groups. For this purpose, silyl enol ethers (E)-2, (Z)-2, (E)-3, and (Z)-3 that incorporate tert-butyl groups at different positions as shown in Figure 3B were chosen as model systems.

Similar to the first model, the possible transition structure conformations were calculated for these four silyl enol ethers with acetaldehyde. The results of these studies are summarized in Table 1, entries 13–31. As with the first model, pro-syn and pro-anti pathways generally show similar ϕ values in their transition states for both silyl enol ether geometries. For enol silyl ether 2, pro-anti pathways for both E and Z isomers showed transition states close to dihedral angles of 0° and 170°. Pro-syn pathways for both isomers showed transition states with ϕ values near 80° and 240°. The enol silyl ether (E)-2 showed an additional synclinal transition state near 275°. Compared to the reactions of (E)-1 and (Z)-1, the length of the forming C–C bond stayed relatively constant, ranging from 2.26 to 2.39 Å, and the potential energy surface did not change significantly with enol configuration. For (E)-2 and (Z)-2, the syn product was favored by 0.4 and 2.7 kcal/mol, respectively, which indicated higher diastereoselectivity than in the case of 1. While this result is to be expected qualitatively based on the larger steric bulk of the tert-butyl group, the significant difference between the diastereoselectivity of (E)-2 and (Z)-2 is interesting and will be discussed in more detail below.

Table 1.

Key parameters for transition structures of Mukaiyama aldol reaction

Entry Enol Ether/R1CHO Φ ΔΔGa Distance Product TSb
1 (E)-1/MeCHO 257.2 0.0 2.45 syn 2
2 (E)-1/MeCHO 220.3 0.6 2.37 syn 2
3 (E)-1/MeCHO 332.6 0.0 2.41 anti 5
4 (E)-1/MeCHO 171.0 0.1 2.46 anti 3
5 (E)-1/MeCHO 295.3 0.6 2.42 anti 5
6 (Z)-1/MeCHO 86.8 0.0 2.58 syn 1
7 (Z)-1/MeCHO 257.1 2.2 2.66 syn 2
8 (Z)-1/MeCHO 222.8 3.0 2.59 syn 2
9 (Z)-1/MeCHO 165.3 1.5 2.41 anti 3
10 (Z)-1/MeCHO 15.4 3.6 2.46 anti 4
11 (Z)-1/MeCHO 295.1 3.8 2.56 anti 5
12 (Z)-1/MeCHO 334.9 4.1 2.47 anti 5
13 (E)-2/MeCHO 80.5 0.0 2.39 syn 1
14 (E)-2/MeCHO 233.9 1.4 2.32 syn 2
15 (E)-2/MeCHO 276.0 2.9 2.26 syn 2
16 (E)-2/MeCHO 343.6 0.4 2.32 anti 4
17 (E)-2/MeCHO 179.6 1.6 2.29 anti 3
18 (Z)-2/MeCHO 83.4 0.0 2.36 syn 1
19 (Z)-2/MeCHO 244.1 4.2 2.39 syn 2
20 (Z)-2/MeCHO 5.1 2.7 2.37 anti 4
21 (Z)-2/MeCHO 163.9 3.3 2.32 anti 3
22 (E)-3/MeCHO 121.5 0.0 2.37 syn 1
23 (E)-3/MeCHO 190.3 2.7 2.28 syn 2
24 (E)-3/MeCHO 168.1 1.1 2.42 anti 3
25 (E)-3/MeCHO 40.5 2.3 2.45 anti -
26 (E)-3/MeCHO 280.1 2.5 2.28 anti 5
27 (Z)-3/MeCHO 173.1 0.0 2.27 anti 3
28 (Z)-3/MeCHO 338.4 4.0 2.27 anti 4
29 (Z)-3/MeCHO 16.8 5.3 2.32 anti 4
30 (Z)-3/MeCHO 78.7 0.2 2.30 syn 1
31 (Z)-3/MeCHO 257.1 1.1 2.32 syn 2
32 (Z)-3/PhCHO 168.6 0.0 2.11 anti 3
33 (Z)-3/PhCHO 339.0 4.2 2.16 anti 4
34 (Z)-3/PhCHO 67.9 1.2 2.18 syn 1
35 (Z)-3/PhCHO 109.4 2.5 2.09 syn 1
36 (Z)-3/PhCHO 276.3 5.3 2.25 syn 2
Open in a new tab
a

Free energies are relative to the lowest energy transition state for each independent pathway for each silyl enol ether isomer. The lowest energy syn and anti transition states for each case are shown in bold font.

b

For structural representation of the types of transition structures in the TS column, see Figure 5.

In the pro-anti pathways for compounds (E)-3 and (Z)-3, both isomers share similar transition state geometries with dihedral angles of approximately 170°. Additionally, transition structures with dihedral angles of 40.5° and 280.1° could be located for (E)-3 and 16.8° and 338.4° for (Z)-3. These additional transition structures for (E)-3 and (Z)-3 can be attributed to the substantially different steric effects of the tert-butyl group as compared to the OTMS group. The dihedral angles in the transition structures for the pro-syn pathway with (E)-3 are 121.5° and 190.3°, while (Z)-3 isomer shows transition states around 78.7° and 157.1°. While (E)-3 leads to syn selectivity with an energy difference of 1.1 kcal/mol, (Z)-3 favors the anti diastereomer by 0.2 kcal/mol.

Finally, in order to extend this study to a reaction for which experimental data are available, transition states were calculated for (Z)-3 reacting with benzaldehyde (entries 32-36). The located transition structures are similar to those discussed earlier in the reaction of (Z)-3 with acetaldehyde with the only differences affecting high-energy transition structures. The anti and syn products are produced by transition states that are similar to the reaction with acetaldehyde, with the pro-anti pathway now favored by 1.2 kcal/mol.

To reveal the structural origin of the calculated energy differences, we analyzed representative transition structures for the systems listed in Table 1, starting with the experimentally studied reaction shown in Figure 4. Figure 6 shows two views of the transition structures for the major and minor pathways of the reaction of benzaldehyde with (Z)-3 corresponding to the lowest pro-anti and pro-syn energy pathways, respectively (entries 32 and 34). In both cases, steric effects are minimized if the aldehyde oxygen is close to the α-hydrogen of the enol silyl ether. This placement occurs in most of the preferred transition states in this study and, by extension, in similar Mukaiyama aldol reactions. The space surrounding the silyl enol ether double bond is sterically crowded with the exception of the hydrogen substituent, opening up space to position the Lewis acid beyond this hydrogen. Also, it can be seen that the bulky group on the aldehyde is positioned away from methyl and TMS substituents to relieve steric strain. This effect is augmented by the incipient sp3 character of the aldehyde’s reacting carbon in the transition structure and the ability of the Lewis acid to utilize out-of-plane coordination to the aldehyde.35 This preference of the Lewis acid to be near the hydrogen on the α-carbon is essential to understanding the diastereoselectivity and allows a much more general description of the Mukaiyama aldol reaction.

Figure 6.

Figure 6

Open in a new tab

(A) Structure of entry 32, the transition state for the major anti-product in the reaction of (Z)-3 with benzaldehyde. (B) Side view of the structure of entry 32. (C) Structure of entry 34, the transition state for the minor syn-product in the reaction of (Z)-3 with benzaldehyde. (D) Side view of the structure of entry 34.

Next, we investigated the reaction of 1 with acetaldehyde, a system that is not expected to show the steric effects discussed above. Starting with the reaction of silyl enol ether (E)-1 with acetaldehyde, we found transition state structures (entries 1–5) corresponding to each of the model transition states in Figure 5, except for TS1. We were unable to locate a transition state similar to TS1, although it does not have any particularly destabilizing interactions. A relaxed scan about the dihedral angle of the forming C—C bond indicates a possible local minimum close to the ϕ angle of TS1, but transition state optimization calculations starting near this geometry failed to converge. This behavior is most likely due to a flat potential energy surface caused by the small barriers for bond rotation in this system containing R1=R2=R3=Me.

Finally, we investigated another system 2 with very large steric repulsion due to a tert-butyl group, but this time as the α-carbon substituent. For compounds (E)-2 and (Z)-2 reacting with acetaldehyde (Entries 13–21), all transition state models are accounted for, except for TS5, which could not be located presumably due to an unfavorable interaction between the Lewis acid and the tert-butyl group. While both (E)-2 and (Z)-2 preferentially form a syn product via TS1, TS4 is the lowest-energy pro-anti transition state. This preference is larger for compound (Z)-2 (Figure 7A-D). Although this eclipsed conformation might intuitively seem unstable, the optimized dihedral scan for this reaction (Supporting Information Chart S2) reveals that decreases in the ϕ angle create an unfavorable Lewis acid:tert-butyl interaction, while increases in this angle create an unfavorable methyl:tert-butyl interaction. A likely explanation for the stability of TS4 over TS3 is the destabilizing methyl:tert-butyl interaction in TS3 (Figure 7F) and possibly a favorable polar interaction between the overlapping π-electron systems on the nucleophile and electrophile in TS4. For larger aldehydes than acetaldehyde, this conformation is much less stable due to eclipsed interactions, and TS3 becomes more likely as the positioning of the Lewis acid near the α-hydrogen allows for relief of steric strain (Figure 7E,F). For this reason, it is useful to compare TS1 to TS3 as well as TS4. In the reaction of (Z)-2, while both TS1 and TS3 place the Lewis acid near the α-hydrogen of the silyl enol ether, TS1 is favored because the methyl and Lewis acid groups on the aldehyde are both further away from the large tert-butyl group on the α-carbon. The opposite is true for the TS3 structure, in which the R1 and R2 groups are within 2.18 Å of each other, as shown in Figure 7A,B. These structures thus represent a balance between the two repulsive interactions. Comparing the E and Z silyl enol ether isomers can also be useful in understanding dipole effects, as discussed below (Figure 7G,H).

Figure 7.

Figure 7

Open in a new tab

(A) Structure of entry 18 showing the lowest-energy pro-syn pathway for the reaction of (Z)-2 with acetaldehyde. (B) Side view of the structure of entry 18. (C) Structure of entry 20 showing the lowest-energy pro-anti pathway for this reaction. (D) Side view of the structure of entry 20. (E) Structure of entry 21, a minor pro-anti pathway, showing unfavorable interactions caused by proximity of aldehyde substituents to the tert-butyl group. (F) Side view of the structure of entry 21. The shortest distance between the aldehyde methyl group and the enol ether tert-butyl group is highlighted as 2.17 Å compared to 2.37 Å for the forming carbon-carbon bond. (G) Structure of entry 14 showing unfavorable interactions between the methyl group of acetaldehyde and the α-carbon hydrogen of the silyl enol ether and between the tert-butyl group and the Lewis acid. (H) Side view of the structure of entry 14.

DISCUSSION

With the quantitative information for the transition structures and their relative energies as well as the validation of the calculations by comparison to available experimental data in hand, a more detailed analysis of the interactions leading to the computed diastereoselectivities is possible. Shown in Figure 8 are the Newman projections for the transition structures of the reaction of (Z)-1 with acetaldehyde (Entries 6-12), which provide a starting point for a discussion of the general features of the transition states of the Mukaiyama aldol reaction. The main goal in developing the initial model was to determine the complete set of transition structures for the Mukaiyama aldol reaction. The small substituents on the substrates allow a larger number of possible transition structures while the larger substituents discussed later destabilize several of these structures.

Figure 8.

Figure 8

Open in a new tab

Newman projections for the transition states of the reaction of (Z)-1 with acetaldehyde.

The seven transition states for the reaction of (Z)-1 with acetaldehyde (entries 6-12) lead to the five main transition states shown in Figure 5. The pro-syn pathways with ϕ angles of 222.8° and 257.1° share similar interactions and can be combined into one model, TS2. The pro-anti transition state with a dihedral angle of 334.9° is much higher in energy and will therefore not be relevant. While Lewis acid-catalyzed Mukaiyama aldol transition states have been previously described as synclinal and antiperiplanar,39 several of the geometries shown in Table 1 do not fit these models.39 Furthermore, it is clear from the analysis of the transition structure energies and geometries in Table 1 that steric effects are not always minimized in the staggered geometries and that among the models in Figure 5, TS1 and TS3 represent the lowest energy transition structures that will in most cases determine the stereochemical outcome of the reaction. TS2, TS4, and TS5 show unfavorable interactions and lead to minor products in our representative model reactions, even though the wide substrate variability in the Mukaiyama aldol reaction make it conceivable that other substrate combinations could negate this bias.

The existing transition state models are based on steric interactions39 and dipole—dipole minimization.40 However, larger substituents on the aldehyde reacting with the same silyl enol ether did not lead to large changes in the geometries of the transition structures but did increase the energy differences between pathways. This is a consequence of the fact that independent of the size of R1, the Lewis acid is positioned near the α-hydrogen on the silyl enol ether. Comparison of the reactions of (Z)-3 with acetaldehyde and with benzaldehyde shows that while the transition structure geometries for both diastereomeric pathways are consistent in geometry and relative energy, the anti preference increases from 0.2 kcal/mol for acetaldehyde to 1.2 kcal/mol for benzaldehyde. In contrast, changing either of the two methyl groups on 1 to tert-butyl groups, thus generating 2 and 3, leads to significant geometric and energetic changes.

Based on previous models of the reaction,39,40 it is surprising that the lowest energy transition structure calculated for (E)-2 is TS1 placing both C—O dipoles in the same direction. This suggests that dipole minimization is less important than the steric effect caused by the introduction of the tert-butyl group. While TS2 would minimize dipole repulsion, the combined effects of the me-thyl:hydrogen and tert-butyl:Lewis acid interactions are too destabilizing, as seen in Figure 7G,H. In contrast, dipole—dipole interactions in the lowest energy transition structure explain why the reaction with (Z)-2 favors the pro-syn transition state by 2.7 kcal/mol while the reaction with (E)-2 favors the pro-syn transition state by only 0.4 kcal/mol. The quantitative analysis of the transition structure energies therefore suggests that dipole—dipole minimization has a 2.0-2.5 kcal/mol effect on transition state stability, demonstrating the usefulness of a quantitative rather than a qualitative approach to the conformational analysis of the stereodetermining transition structures.

Analysis of the results for the reaction of 3 also elucidate the steric effects of the substituents on the silyl enol ether. By replacing the R3 methyl group in 1 with a much larger tert-butyl group in 3, the steric effects of the OTMS substituent completely change in nature as indicated by the dihedral angles listed in Table 1. In going from entry 1 to entry 24, the introduction of the large tert-butyl substituent forces the TMS group to move toward the α-carbon, as shown in Figure 9. This effect is more pronounced for (E)-silyl enol ethers because silicon is on the same side of the double bond as the hydrogen rather than a methyl group. As a result of this finding, the preference for the Lewis acid to be close to the α-hydrogen in the transition state is smaller for silyl enol ethers with large R3 groups. While in previous examples, the Lewis acid is positioned in the open space around the α-hydrogen to minimize steric effects, this space becomes more crowded. Therefore, the results for (E)-3 do not match the transition state models in Figure 5 quite as well as data for other nucleophiles. This change in silyl enol ether geometry influences the potential energy surface for aldol reactions of (E)-3, but not as much for those of (Z)-3, for the reason previously described.

Figure 9.

Figure 9

Open in a new tab

Silyl enol ethers (E)-1 and (E)-3 from the transition structure Entries 1 and 24. The carbon-carbon-silicon angles are highlighted for comparison.

A comparison of the original qualitative models of Heathcock and the model outlined above with the data from the experimentally studied reaction of (Z)-3 with benzaldehyde39 demonstrates the utility of our model based upon the quantitative predictions of explicit electronic structure calculations. As shown in Figure 6, the Lewis acid is closer to the tert-butyl group in TS1 than it is in TS3, forcing the phenyl group on the aldehyde to be closer to the tert-butyl group. These destabilizing interactions are not present in TS3, leading to the observed diastereoselectivity. The same reasoning explains the syn selectivity for the case of 2 with large aldehydes. These conclusions from the model and from QM transition structures rationalize the experimental data, showing a 1.2 kcal/mol preference for the predicted product via TS3, giving a theoretical selectivity of 95:5 at − 78°C, which compares well with the reported >95:5 experimental selectivity.39

In comparison to Heathcock’s model for the reaction (Figure 2), which is based largely upon exclusion of possible transition states as discussed below, the rationale derived from the quantum mechanical calculations is more quantitative and includes energies for the minor as well as the major pathways. In the Heathcock model,39,48 T3, T4 and T5 are excluded due to dipole—dipole interactions, with T3 particularly unstable because of the phenyl:tert-butyl interaction. T2 is excluded due to steric repulsion between the tert-butyl and the Lewis acid. Finally, T6 is eliminated due to repulsive tert-butyl:oxygen interactions and phenyl:OTMS interactions, leaving T1 as the lowest energy transition state in this staggered model, which is therefore selected for the correct reasons. While this reasoning is useful, this model is difficult to use in a quantitatively predictive manner because it is difficult to estimate the impact of the destabilizing factors relative to each other. For example, our results indicate that the influence of dipole—dipole interactions is not necessarily decisive and interactions between groups attached to oxygen are difficult to quantify based on Newman projections alone. Finally, the previous analyses rely on the assumption that staggered transition states are preferred, but the electronic structure calculations indicate that some staggered structures are actually located in high-energy regions on the energy surface. T2, T3, and T4 are particularly far from transition states and closer to local maxima along the dihedral angle coordinate. T2 is destabilized by a tert-butyl-:Lewis acid interaction, and T3 and T4 are destabilized by phenyl-:tert-butyl interactions, as can be seen in the relaxed dihedral scans (Supporting Information Charts S1-S4).

Our computational findings also expand the previous work by Denmark that is based on an inherent preference for antiperiplanar transition states.40,48 To dissect the different possible influences, Denmark’s work on this reaction utilized a conformationally rigid adamantane-based framework with minimal steric bias which included an aldehyde and a silyl enol ether. This structure forced the reaction to take place via either an antiperiplanar transition state, leading to dipole minimization and an anti product preference in the reactions studied there, or a synclinal transition state, leading to a syn product. We find that while dipole minimization is preferred, it is not the deciding factor in selectivity, especially for bulky substrates, and that pro-syn pathways do not occur via anti-periplanar transition states because the Lewis acid is least hindered near the α-hydrogen, and a pro-syn antiperiplanar transition state does not allow this placement.

To demonstrate the generality of the transition state models, we calculated diastereomeric energy differences between the lowest-energy pro-anti and pro-syn product pathways for two other experimentally studied Mukaiyama aldol reactions. While the aldol reactions of (E)-1 and (Z)-1 are difficult to assess experimentally due to the technical difficulties forming these enol silyl ethers in isomerically pure form, the reaction of the similar ethyl-substituted (Z)-silyl enol ether with benzaldehyde has been shown to produce a 60:40 ratio of syn:anti products (Table 2, entry A).7 Our calculations indicate that the pro-syn TS1 for this reaction is 0.6 kcal/mol more stable than pro-anti TS3. As expected, replacement of the R3 methyl group from (Z)-1 with an ethyl group destabilizes TS1 and biases the reaction towards formation of more of the anti product by creating a nucleophile slightly more similar to (Z)-3. Our data for 2 compare well to analogous reactions in the literature, as well. These calculations suggest a preference for syn product formation, which is observed for the analogous ketene silyl acetal reaction (Table 2, entry B).8 Our calculated results for the reaction of this ketene silyl acetal with benzaldehyde indicate a 2.0 kcal/mol preference for the pro-syn TS1 over the pro-anti TS3. Although the calculations were performed with BCl3 rather than the experimental catalysts, similar minor changes have been suggested to have little influence on diastereoselectivity.39 An optimized scan about the dihedral angle of the forming C—C bond was used to verify that TS1 and TS3 are the lowest energy transition states for each product in this reaction (Supporting Information Chart S5). The agreement between these calculations and experimental data further strengthens our confidence in these transition state models.

Table 2.

Comparison of experimental and calculated results for additional enol derivatives.

Silyl enol ether Aldehyde Catalyst Selectivity: syn/anti Predicted Energy Difference
A graphic file with name nihms404156t1.jpg graphic file with name nihms404156t2.jpg BF3-OE2 60:40 0.6 kcal/mol
B graphic file with name nihms404156t3.jpg graphic file with name nihms404156t4.jpg Ticl4 >9208 2.0 kcal/mol
Open in a new tab

SUMMARY AND CONCLUSIONS

We have devised an enhanced model for studying the transition states in Mukaiyama aldol reactions based on a quantitative computational approach. This model provides quantitative information about the geometric and electronic structures of the major and minor transition states responsible for the selectivity in this reaction, demonstrating that computational methods can be used to rationalize and ultimately predict diastereoselectivities in these open transition states. The calculated results allow the analysis of the relative contributions of the steric effects of the Lewis acid and substituents on the silyl enol ether and the relative effects of dipole—dipole interactions. The reasons for and the extent of selectivity differences for E and Z isomers of silyl enol ethers are also rationalized. This work therefore adds to our knowledge of aldol reaction transition states, as it represents the first computational study of the Mukaiyama aldol reaction with physically realistic systems, solvation modeling, and density functional theory applied to substrates permitting a probe of diastereoselectivity. While the interactions in the Mukaiyama aldol reaction are complicated, and simple Newman projections are not enough to answer all questions about diastereoselectivity, the results presented here allow a better understanding of such models. In particular, the experimental chemist might make use these of these findings to assist in predicting diastereoselectivity using a relatively simple model based on the relative sizes of the substituents on the enol and α-carbon s of a given silyl enol ether and comparing the interactions in TS1 and TS3 rather than the full set of possible conformers. Two potential exceptions to this model are aldehydes with additional coordinating groups that can force the Lewis acid into a trans configuration relative to the aldehyde hydrogen44,49–52 and reactions involving aromatic substituents on both the aldehyde and the silyl enol ether due to π-stacking interactions.18 A future expansion of this study will be to investigate these effects and to exploit such interactions in designing enantioselective aldol reactions. This aim can be accomplished by the use of quantum mechanical results for the parameterization of transition state force fields20 for the screening of Mukaiyama aldol reactants and catalysts for the quantitative prediction of diastereoselectivity and eventually of enantioselectivity.53

Supplementary Material

1_si_001

Acknowledgments

We thank the U.S. National Science Foundation (NSF 1058075) for financial support and the TeraGrid (TG-CHE090124 and TG-CHE120050) and the Notre Dame Center for Research Computing for computational resources. J.M.L. thanks the Chemistry Biochemistry Biology Interface (CBBI) Program funded by NIH Training Grant T32GM075762 for a predoctoral fellowship. P.H. thanks the Research Council of Sweden for support as the Tage Erlander Guest Professor at Gothenburg University, Stockholm University, and the Royal Institute of Technology (Stockholm) during the conduct of this research. The authors thank Professor Timofei Privalov (Stockholm University) and Professor Per-Ola Norrby (Gothenburg University) for many helpful discussions regarding computational methods.

Footnotes

ASSOCIATED CONTENT

Additional computational data, including coordinates and energies for all described transition structures, and complete ref 45. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

References

  • 1.Mukaiyama T, Narasaka K, Banno K. Chem Lett. 1973;2:1011–1014. [Google Scholar]
  • 2.Mukaiyama T, Banno K, Narasaka K. J Am Chem Soc. 1974;96:7503–7509. [Google Scholar]
  • 3.Saigo K, Osaki M, Mukaiyama T. Chem Lett. 1975;4:989–990. [Google Scholar]
  • 4.Gennari C, Bernardi A, Cardani S, Scolastico C. Tetrahedron Lett. 1985;26:797–800. [Google Scholar]
  • 5.Mahrwald R. Modern aldol reactions. Wiley-VCH; Weinheim: 2004. pp. 139–140. [Google Scholar]
  • 6.Chan TH, Aida T, Lau PWK, Gorys V, Harpp DN. Tetrahedron Lett. 1979;20:4029–4032. [Google Scholar]
  • 7.Heathcock CH, Hug KT, Flippin LA. Tetrahedron Lett. 1984;25:5973–5976. [Google Scholar]
  • 8.Dubois JE, Axiotis G, Bertounesque E. Tetrahedron Lett. 1984;25:4655–4658. [Google Scholar]
  • 9.Gennari C, Beretta MG, Bernardi A, Moro G, Scolastico C, Todeschini R. Tetrahedron. 1986;42:893–909. [Google Scholar]
  • 10.Mahrwald R. Chem Rev. 1999;99:1095–1120. doi: 10.1021/cr980415r. [DOI] [PubMed] [Google Scholar]
  • 11.Casiraghi G, Battistini L, Curti C, Rassu G, Zanardi F. Chem Rev. 2011;111:3076–3154. doi: 10.1021/cr100304n. [DOI] [PubMed] [Google Scholar]
  • 12.Paterson I, Davies RDM, Heimann AC, Marquez R, Meyer A. Org Lett. 2003;5:4477–4480. doi: 10.1021/ol0357853. [DOI] [PubMed] [Google Scholar]
  • 13.Evans DA, Burch JD, Hu E, Jaeschke G. Tetrahedron. 2008;64:4671–4699. doi: 10.1016/j.tet.2008.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Troast DM, Yuan JY, Porco JA. Adv Synth Catal. 2008;350:1701–1711. doi: 10.1002/adsc.200800247. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Hassfeld J, Kalesse M. Tetrahedron Lett. 2002;43:5093–5095. [Google Scholar]
  • 16.Ehrlich G, Hassfeld J, Eggert U, Kalesse M. Chem Eur J. 2008;14:2232–2247. doi: 10.1002/chem.200701529. [DOI] [PubMed] [Google Scholar]
  • 17.Wong CT, Wong MW. J Org Chem. 2007;72:1425–1430. doi: 10.1021/jo062218v. [DOI] [PubMed] [Google Scholar]
  • 18.Wang L, Wong MW. Tetrahedron Lett. 2008;49:3916–3920. [Google Scholar]
  • 19.Brown JM, Deeth RJ. Angew Chem, Int Ed. 2009;48:4476–4479. doi: 10.1002/anie.200900697. [DOI] [PubMed] [Google Scholar]
  • 20.Donoghue P, Helquist P, Norrby PO, Wiest O. J Am Chem Soc. 2009;131:410–411. doi: 10.1021/ja806246h. [DOI] [PubMed] [Google Scholar]
  • 21.Weill N, Corbeil CR, De Schutter JW, Moitessier N. J Comput Chem. 2011;32:2878–2889. doi: 10.1002/jcc.21869. [DOI] [PubMed] [Google Scholar]
  • 22.Wong CT, Wong MW. J Org Chem. 2005;70:124–131. doi: 10.1021/jo048398v. [DOI] [PubMed] [Google Scholar]
  • 23.Cheong PHY, Legault CY, Um JM, Celebi-Olcum N, Houk KN. Chem Rev. 2011;111:5042–5137. doi: 10.1021/cr100212h. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Allemann C, Um JM, Houk KN. J Mol Catal A: Chem. 2010;324:31–38. doi: 10.1016/j.molcata.2010.03.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Duarte FJS, Cabrita EJ, Frenking G, Santos G. Eur J Org Chem. 2008:3397–3402. [Google Scholar]
  • 26.Denmark SE, Fan Y, Eastgate MD. J Org Chem. 2005;70:5235–5248. doi: 10.1021/jo0506276. [DOI] [PubMed] [Google Scholar]
  • 27.Branchadell V, Crevisy C, Gree R. Chem Eur J. 2004;10:5795–5803. doi: 10.1002/chem.200400466. [DOI] [PubMed] [Google Scholar]
  • 28.Clemente FR, Houk KN. Angew Chem, Int Ed. 2004;43:5766–5768. doi: 10.1002/anie.200460916. [DOI] [PubMed] [Google Scholar]
  • 29.Ruiz M, Ojea V, Quintela JM. Tetrahedron: Asymmetry. 2002;13:1863–1873. [Google Scholar]
  • 30.Arno M, Domingo LR. Theor Chem Acc. 2002;108:232–239. [Google Scholar]
  • 31.Bahmanyar S, Houk KN. Org Lett. 2003;5:1249–1251. doi: 10.1021/ol034198e. [DOI] [PubMed] [Google Scholar]
  • 32.Bouillon JP, Portella C, Bouquant J, Humbel S. J Org Chem. 2000;65:5823–5830. doi: 10.1021/jo005544y. [DOI] [PubMed] [Google Scholar]
  • 33.Yasuda M, Chiba K, Baba A. J Am Chem Soc. 2000;122:7549–7555. [Google Scholar]
  • 34.Bernardi A, Gennari C, Raimondi L, Villa MB. Tetrahedron. 1997;53:7705–7514. [Google Scholar]
  • 35.Shambayati S, Crowe WE, Schreiber SL. Angew Chem, Int Ed. 1990;29:256–272. [Google Scholar]
  • 36.Hollis TK, Bosnich B. J Am Chem Soc. 1995;117:4570–4581. [Google Scholar]
  • 37.Carreira EM, Singer RA. Tetrahedron Lett. 1994;35:4323–4326. [Google Scholar]
  • 38.Chan TH, Brook MA. Tetrahedron Lett. 1985;26:2943–2946. [Google Scholar]
  • 39.Heathcock CH, Davidsen SK, Hug KT, Flippin LA. J Org Chem. 1986;51:3027–3037. [Google Scholar]
  • 40.Denmark SE, Lee WS. J Org Chem. 1994;59:707–709. [Google Scholar]
  • 41.Zimmerman HE, Traxler MD. J Am Chem Soc. 1957;79:1920–1923. [Google Scholar]
  • 42.Chan JCC, Eckert H. J Mol Struc: THEOCHEM. 2001;535:1–8. [Google Scholar]
  • 43.Heathcock CH, Flippin LA. J Am Chem Soc. 1983;105:1667–1668. [Google Scholar]
  • 44.Reetz MT, Kesseler K, Jung A. Tetrahedron. 1984;40:4327–4336. [Google Scholar]
  • 45.Frisch MJ, et al. Gaussian 09 (Revision A.02) 2009. See Supporting Information for complete reference. [Google Scholar]
  • 46.Tomasi J, Mennucci B, Cammi R. Chem Rev. 2005;105:2999–3039. doi: 10.1021/cr9904009. [DOI] [PubMed] [Google Scholar]
  • 47.The reaction can most likely be completed in shorter times, the reaction time with TiCl4 achieves a 92% yield in 1 h.2
  • 48.Denmark SE, Lee WS. Chem Asian J. 2008;3:327–341. doi: 10.1002/asia.200700300. [DOI] [PubMed] [Google Scholar]
  • 49.Cram DJ, Kopecky KR. J Am Chem Soc. 1959;81:2748–2755. [Google Scholar]
  • 50.Reetz MT, Jung A. J Am Chem Soc. 1983;105:4833–4835. [Google Scholar]
  • 51.Reetz MT, Kesseler K, Schmidtberger S, Wenderoth B, Steinbach R. Angew Chem, Int Ed. 1983;22:989–990. [Google Scholar]
  • 52.Reetz MT. Angew Chem, Int Ed. 1984;23:556–569. [Google Scholar]
  • 53.Palomo C, Oiarbide M, Garcia JM. Chem Soc Rev. 2004;33:65–75. doi: 10.1039/b202901d. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

1_si_001
NIHMS404156-supplement-1_si_001.pdf (580KB, pdf)

RESOURCES