Specificity in Molecular Design: A Physical Framework for Probing the Determinants of Binding Specificity and Promiscuity in a Biological Environment

Abstract

Binding specificity is an important consideration in drug design. An effective drug molecule often must bind with high specificity to its intended target in the body; lower specificity implies the possibility of significant binding to unintended partners, which could instigate deleterious side effects. However, if the target is a rapidly mutating agent, a drug that is too specific will quickly lose its efficacy by not binding well to functional mutants. Therefore, in molecular design, it is crucial to tailor the binding specificity of a drug to the problem at hand. In practice, specificity is often studied on a case-by-case basis, and it is difficult to create general understanding of the determinants of specificity from the union of such available cases. In this study, we undertook a comprehensive, general study of molecular binding with emphasis on understanding the determinants of specificity from a physical standpoint. By extending a theoretical framework grounded in continuum electrostatics and creating an abstracted lattice model that captures key physical aspects of binding interactions, we systematically explored the relationship between a molecule’s physical characteristics and its binding specificity toward potential partners. The theory and simulated binding interactions suggested that charged molecules are more specific binders than their hydrophobic counterparts for several reasons. First, the biological spectrum of possible binding characteristics includes more partners that bind equally well to hydrophobic ligands than to charged ligands. Also, charged ligands, whose electrostatic potentials have strong orientational dependence, are more sensitive to shape complementarity than their hydrophobic counterparts. Ligand conformational and orientational flexibility can further influence a charged molecule’s ability to bind specifically. Interestingly, we found that conformational flexibility can increase the specificity of polar and charged ligands, by allowing them to greatly lower the binding free energy of a select few interactions relative to others. Additionally, factors such as a molecule’s size and the ionic strength of the solution were found to predictably affect binding specificity. Taken together, these results — all of which stemmed from a unified theoretical framework — provide valuable physical insight into the general determinants of binding specificity and promiscuity in a biological environment. The general principles discussed here could prove useful in the design of molecules with tailored specificities, leading to more effective therapeutics.

1 Introduction

Molecules in a biological environment have a myriad of potential binding partners. The problem of designing effective drug molecules therefore must involve developing ligands that bind not only with high affinity to a desired target or collection of targets, but also with the appropriate level of specificity. Often, it is narrow specificity that is desired. For example, certain kinase inhibitors developed to treat cancer, autoimmune diseases, and other disorders must be highly specific for their intended targets, as the ATP-binding sites of kinases with different functions are highly similar and may cause unwanted side interactions and drug toxicity¹. However, there are situations where a more promiscuous drug — one that can recognize multiple targets — may be beneficial. In the case of a rapidly mutating target, such as HIV-1 protease, a drug molecule that can effectively bind to and inactivate many variants would likely be less susceptible to drug resistance².

The ability to rationally design therapeutics with tailored specificities requires an understanding of the physical, chemical, and biological determinants of binding between a molecule and its potential partners. To begin to gain such an understanding, one might first study Nature’s own molecules, as their varied functions require a broad range of specificities. For example, the aminoacyl tRNA synthetases specifically recognize their appropriate amino acids, with some synthetases having additional “proofreading” mechanisms structurally incorporated to ensure translational fidelity^3,4. A lack of specificity due to mutation in such enzymes has been implicated in the synthesis of mis-folding proteins and neurodegeneration⁵. As another example, zinc-finger binding proteins recognize specific DNA sequences with high selectivity⁶. At the same time, there are molecules for which promiscuity is crucial for proper function. The pregnane-X receptor (PXR) helps mediate the metabolic pathway responsible for breaking down many potentially harmful substrates, and so it is advantageous to be promiscuous to effectively carry out this function^7,8. Promiscuous scavenger receptors endocytose diverse modified lipoproteins and play numerous other functions, such as host defense⁹. In some cases, a delicate balance between specificity and promiscuity is important; interactions between peptide-major histocompatibility complexes and T-cell receptors are both specific and promiscuous, and the precise balance is thought to aid in their efficient and accurate discrimination between foreign and self peptides¹⁰. Sometimes, the lack of proper binding specificity is a cause or consequence of disease, such as undesirable interactions leading to autoimmune illnesses¹¹ or the extreme case of protein protofibrillar aggregations that are implicated in neurodegenerative disorders, such as Parkinson’s and Alzheimer’s diseases¹².

There have been many studies aimed at developing a physical understanding of the binding preferences of natural molecular systems. Here we highlight some basic trends encountered in the literature. Many of these studies were done on natural receptors as opposed to smaller molecules that would more closely mirror drug molecules, but here we assume that many physical attributes of molecular recognition could nevertheless apply to ligands and receptors alike. First, several systems use conformational flexibility to bind to multiple partners. Systems such as PXR, cytochrome P450 3A4, fibroblast growth factor, certain antibodies, aldose reductase, and the DNA binding domain of the Bacillus subtilus protein AbrB exhibit varying degrees of mobility, flexibility, or “induced fit” mechanisms to achieve their promiscuous functions^{8, 13-17}. Conformational changes, perhaps mediated in part by a glycine-rich flexible loop, have been implicated in altering the specificity of protein-peptide recognition of thimet oligopeptidase^18,19. Structural plasticity, exemplified by “floppy” methionine residues and mobile hinge domains, may enable promiscuous binding²⁰. Clusterin’s disordered, “molten globule-like” binding site is thought to enable it to bind to many partners that are often hydrophobic²¹. Indeed, hydrophobic surfaces in multiple systems appear to confer promiscuity^22-24, with the small number of electrostatic interactions in such systems potentially contributing to specificity²⁴. In PXR, changes in specificity have been introduced by altering only the polar residues⁸, suggesting that polar residues could be responsible for existing selectivity. In fact, the lack of specificity-inducing hydrogen bonds and the small buried surface area between interleukin-2 (IL2) and the γ_c subunit of its receptor have been used to explain its promiscuous interactions with several cytokines²⁵. Indeed, general electrostatic interactions can confer specificity; long-range electrostatics via Mg²⁺ ions have been shown computationally to play a role in the specificity of aspartyl-tRNA synthetase toward aspartate over asparagine²⁶. Thus, studies on natural systems show the trend that mobile and hydrophobic surfaces are generally more promiscuous, while salt-bridge, hydrogen-bond, or charge interactions can confer specificity.

Nevertheless, there are also examples where highly electrostatic interactions can be promiscuous. Direct hydrogen-bonding interactions in drug-kinase systems confer promiscuity because of the very conserved hydrogen-bonding patterns such kinases exhibit, and more subtle, indirect desolvation of intramolecular hydrogen-bonded kinase residues upon binding may determine drug-kinase specificity²⁷. The DNA-binding surface of p53 core domain contains “promiscuous” arginine residues that mediate its binding to several peptides²⁸. The legume lectin UEA-II exhibits promiscuity toward certain carbohydrates in the primary site presumably because of sub-optimal hydrogen bonding that can be achieved by a variety of ligands, none of which can achieve fully compensated interactions²⁹. However, the ability to make various types of strong hydrogen-bonding interactions can also confer promiscuity; in the SPE7 antibody system, diverse ligands make a variety of different hydrogen-bonding interactions in a relatively rigid binding cleft, and promiscuity arises from the large number of possible polar interactions^{30, 31}. Thus, polar and charged interactions can be satisfied in a variety of ways, leading to an electrostatic promiscuity that may be more difficult to engineer than “hydrophobic stickiness.”

In addition to conformational flexibility and hydrophobicity, other physical characteristics of a molecule and its surroundings have been implicated in mediating binding specificity or promiscuity. The ability of water at a binding interface to confer both promiscuity and specificity through its versatility and ability to easily reorient itself to mediate strong interactions has been reviewed³². Also, it has been suggested that molecules with asymmetric functional groups can bind well to multiple partners by presenting different shape and charge patterns to partners upon changing orientation². The examples provided here by no means exhaust the vast literature on natural systems; nevertheless, to our knowledge, there has not been a unified, physics-based approach to analyze the observations that may come out of the union of such studies.

Many successful molecular design applications have focused on tailoring the specificity of the designed molecule to the problem at hand. O’Shea et al. used electrostatics to create a specific heterodimeric coiled-coil; one monomer contained interfacial acidic residues, while the other contained basic residues such that the two homodimeric states yielded electrostatic repulsions and the heterodimeric state was highly favored³³. Havranek and Harbury explicitly considered competing states in order to design coiled coils that would specifically homodimerize rather tha heterodimerize, aggregate, or unfold³⁴. through analyzing parallel designs of SspB heterodimers, one of which was optimized for stability and the other accounting for competing homodimeric states, Bolon et al. demonstrated that negative design — explicitly designing against related, undesired states — is often crucial in obtaining desired narrow specificity³⁵. Shifman and Mayo, through rational design, increased the specificity of calmodulin toward one of its many potential partners³⁶, while Green et al. designed a mutually specific calmodulin/target-peptide variant pair³⁷. Using multiple rigid binding conformations in their designs, Joachimiak et al. redesigned the E7 DNase-Im7 interface to make a highly specific pair³⁸. Todorov et al. addressed both broad and narrow specificity, designing ligand candidates predicted to bind to multiple members of the cyclin-dependent kinase (CDK) family³⁹. Experimental data has suggested physical characteristics that correlate with broad recognition, including drug molecular weight and lipophilicity⁴⁰, in addition, experimental and structural data have guided computational virtual screening and QSAR approaches to predict off-target binding of potential drug molecules with promiscuous receptors such as PXR, cytochrome P450, and P-glycoprotein (see reference⁴¹ for a review). In epitope-based vaccine design, multiple computational methods, such as TEPITOPE and MULTIPRED, have been developed and applied to determine epitope sequences that could be promiscuous with respect to immunological recognition^42-46. In spite of this progress, the systematic, physics-based incorporation of tailored specificity or promiscuity in molecular design is still a relatively new prospect, and a fundamental understanding of the molecular determinants of binding specificity may be of use in automating such a process.

Previous theoretical studies on model systems have probed various aspects of binding specificity. A lattice model was used to probe fold specificity, and it was found that salt bridges, while not generally energetically stabilizing, can increase the specificity of a particular fold⁴⁷. Kangas and Tidor developed a framework through which a ligand can be electrostatically optimized to bind promiscuously to a number of targets while avoiding unwanted interactions with “decoys”⁴⁸. This framework was applied in the analysis of HIV-1 protease inhibitors⁴⁹. Eaton et al. performed simulations to probe effects of nonspecific binding in a biological environment⁵⁰.

Taken together, the large collection of experimental and theoretical studies leads to some anecdotal trends for binding specificity involving physical characteristics such as polarity, flexibility, and size. However, a systematic, unified study of binding specificity can be more powerful, as it can provide fundamental insights that are grounded in more broadly applicable physico-chemical principles. Our goal was to test anecdotal observations and derive general insight by extending existing theory in continuum electrostatics and molecular packing and applying it to representative model system. In this work, we systematically explored physical properties that can affect a ligand’s binding specificity in a biological environment. Some of these properties are intrinsic to the ligand molecule, such as charge distribution, size, and rigidity; others are not, such as the characteristics of the possible binding partners and the surrounding environment. In addition to theory, we used interacting lattice-model molecules to computationally study each of these physical properties in turn. The model molecules captured major physico-chemical properties of actual biological molecules, in that they could vary in size, shape, charge distribution, and conformational flexibility, but they were not limited by the constraints of chemical bonding and functionality. As a result, the properties of these molecules could be systematically and exhaustively varied, and the dependence of ligand specificity on these properties could be analyzed.

We found that molecules that were more hydrophobic, smaller, or could present multiple distinct binding faces were generally more promiscuous than their counterparts. In particular, we found that hydrophobicity could increase a molecule’s promiscuity for multiple reasons, including a tolerance for multiple shape complementarities with potential partners, and the higher abundance of equally tight binding partners. Surprisingly, we found that increasing conformational flexibility for charged and polar ligands led to enhanced specificity, as they were able to assume conformations that yielded highly favorable electrostatic interactions toward a select number of binding partners. These interactions were made at the expense of smaller magnitude, unfavorable van der Waals interactions. A small number of bound states were greatly stabilized relative to others, leading to greater overall specificity. The theoretical framework presented here provides for a physical understanding of these and other results.

2 Methods

In this work, two parallel approaches were used to explore the physical determinants of binding specificity and promiscuity. The first was theoretical (analytical) and provided a visual and mathematical interpretation of the specificities of molecules as a function of their physical characteristics. The second was a series of computational experiments on latticemodel molecules, which served to demonstrate the principles predicted by the theory and also to determine outcomes when analytical theory dis not offer a clear prediction.

In both approaches, a metric that quantified a molecule’s specificity or promiscuity was required for analyses. In addition, an energy function comprised of physics-based terms was used to compute binding free energies between potential partners. The following sections define the promiscuity metric and energy function used, and outline the applied theoretical and model frameworks.

2.1 Promiscuity Metric

When presented with multiple binding partners, a specific ligand binds to one molecule with far greater affinity than it binds to the others. A promiscuous ligand, on the other hand, binds to many partners with near-equal affinity. In order to evaluate and compare the binding spectra of different ligands in a standardized way, we defined a simple promiscuity metric that captures this idea.

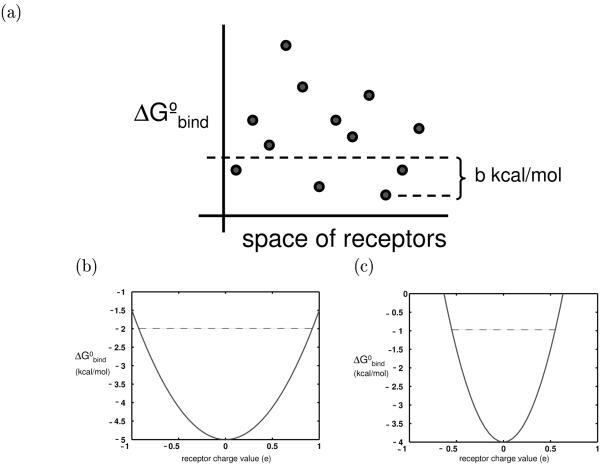
Given a ligand and a set of possible binding partners (called “receptors” for the remainder of this work), the promiscuity_B or Π_B of the ligand is the number of receptors within the set whose binding energy is within B kcal/mol of the affinity to the tightest binder in the set. In mathematical notation,

$${\Pi }_b=(\text{number of receptors}{\mathrm{r}}_{\mathrm{i}}\mathrm{s}.\mathrm{t}.\Delta G_{\mathrm{bind},\mathrm{i}}^0-mi{n}_i\left(\Delta G_{\mathrm{bind},\mathrm{i}}^0\right)\le b)$$ (1)

Figure 1 shows a pictorial representation of this definition.

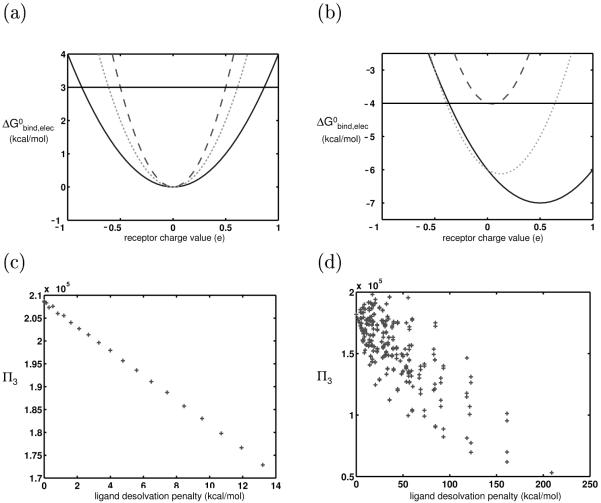
Figure 1.

(a) Graphical representation of the promiscuity metric; the ligand represented here has a promiscuity of 4. (b), (c) The binding profiles of two hypothetical ligands toward an infinite panel of identically-shaped receptors, using a continuum electrostics framework. for ease of visualization, the receptors have only one charged atom so that a ligand’s binding profile is a function of only one value. The profile shown in (b) represents a more promiscuous ligand that that shown in (c). The dotted line in each indicates the possible receptors that can contribute to each ligand’s promiscuity, using a 3 kcal/mol threshold, Π₃.

There are other definitions that capture the nature of binding promiscuity. In our study, we also considered a Boltzmann-weighted definition of promiscuity, φ_b,

$${\Phi }_b=\sum _{(i,s.t.\Delta G_{\mathrm{bind},\mathrm{i}}^0-mi{n}_i\left(\Delta G_{\mathrm{bind}}^0\right)<b)}{e}^{-\frac{(\Delta G_{\mathrm{bind},i}^0-mi{n}_i\left(\Delta G_{bind}^0\right))}{kT}},$$ (2)

using a fixed unbound state for a given ligand. Qualitative results achieved with this definition from pilot studies were similar to those using the simpler definition, and therefore, the first definition presented will be used throughout the following.

These definitions account for relative and not absolute binding affinities between a ligand and possible receptors. A measure or relative binding in useful when one is concerned about how discriminating a ligand is toward multiple receptors. Moreover, the relative equilibrium fractions of ligand bound to each receptor will be independent of ligand concentration. Nevertheless, for most design applications, it is also valuable to consider the absolute binding affinities with which the ligand binds the receptors. To that end, we define the coverage, C_b, of a ligand as the number of receptors within the set to which it binds with absolute binding free energy difference of less than or equal to B kcal/mol.

$$C_b=(\text{number of receptors}{\mathrm{r}}_{\mathrm{i}}\mathrm{s}.\mathrm{t}.\Delta G_{bind,i}^0\le b).$$ (3)

2.2 Choice of Energy Function

The function used to calculate binding free energies between model ligands and receptors consisted of physics-based contributions,

$$\Delta G_{\mathrm{bind}}^0=\Delta G_{\mathrm{vdW}}^0+\Delta G_{\mathrm{int}}^0+\Delta G_{\mathrm{SASA}}^0+\Delta G_{\mathrm{elec}}^0$$ (4)

where ΔG⁰_vdW is the van der Waals (vdW) energy, for which a Lennard-Jones 6-12 potential was used; ΔG⁰_int is the internal conformational energy of the ligand, and, analogously to the bond, angle, and dihedral deformation terms in molecular mechanics, it is a function of the geometry and is charge-independent; ΔG⁰_SASA accounts for the solvent entropy gain upon complex formation, as well as the loss of dispersion interactions between solvent and solute; and ΔG⁰_elec accounts for the electrostatic component of the binding free energy. The ΔG⁰_SASA term is a function of the change in the solute’s solvent accessible surface area (SASA), as is commonly done in molecular mechanics studies^51,52. To compute ΔG⁰_elec, We used a continuum electrostatic model that accounts for both electrostatic desolvation and solvent-screened interaction; the change in electrostatic binding free energy was calculated by solving the linearized Poisson-Boltzmann equation for the unbound and bound states of the species involved. The continuum electrostatic model, while directly contributing to only $\Delta G_{\mathrm{elec}}^0$, provides a useful starting point for understanding the relationship between many ligand properties and promiscuity.

2.3 A Continuum Electrostatic Framework Allows for Analysis of Ligand Promiscuity

Here, we outline the theoretical framework, based on previous work from our group^48,53-55, that was extended for our analyses. Consider the reversible reaction between a ligand and receptor to form a complex, l + r ⇌ c, in aqueous solution, for which we wish to calculate ΔG⁰_elec. Rigid binding is assumed for the discussion here, although we loosened this assumption as part of this study. The ligand and receptor are modeled as low-dielectric cavities in a high-dielectric solvent that may contain mobile ions.

In the individual ligand and receptor unbound states, each is surrounded entirely by solvent, whereas in the complexed state, each is partially desolvated by the other. Because the solvent has a higher dielectric than the solutes, this desolvation energy is always nonnegative under the rigid binding assumption. At the same time, charges on the ligand interact with receptor charges through a solvent-screened Coulombic interaction. Let q_l and q_R be vectors representing the partial charges on ligand and receptor atoms, respectively. Using the linearized Poisson-Boltzmann equation, the total electrostatic binding free energy — the sum of these desolvation and interaction components — can be written as

$$\Delta G_{\mathrm{elec}}^0=q_l^{T}L{q}_l+q_r^{T}R{q}_r+q_r^{T}C{q}_l.$$ (5)

The first term represents the ligand desolvation penalty, the second the receptor desolvation penalty, and the third the screened interaction between the charges on the ligand and receptor L and R are the ligand and receptor desolvation matrices, respectively, and account for the loss in the interaction with solvent and the change in the screened interaction between charges within the molecule upon binding. Specifically, the ij^th element of the L matrix is one-half of the potential difference upon binding at the i^th ligand charge component due to a total charge of +1.0e on the j^th ligand component. The factor of one-half exists for the off-diagonal elements to avoid double-counting, while the diagonal elements are halved because the free energy of a point charge interacting with its reaction field potential is 05.qφ, where q is the charge value and φ is the reaction field potential generated⁵⁴. The R matrix is defined analogously for the recepotor. The L and R matrices are positive semidefinite, as the cost to desolvate a ligand with arbitrary charge distribution is nonnegative. C is a matrix that accounts for the solvent- and ion-screened Coulombic interactions between the species; the ij^th element of C is the potential difference upon binding at the i^th receptor component due to a charge of +1.0e on the j^th ligand component. All three matrices depend on the shapes of the ligand, receptor, and complex and are independent of the charge distributions involved in the binding reaction.

The framework presented readily allows for an interpretation of ligand promiscuity. Suppose a ligand is presented with an ensemble of identically-shaped receptors differing in their charge distributions. In this thought experiment, every possible receptor charge distribution is available. Because q_l is fixed, and the receptor and complex shapes do not vary, the electrostatic binding free energy (Eq. 5) is a quadratic funciton of only q_R. As R is positive semidefinite, $\Delta G_{\mathrm{elec}}^0$ as a function of q_R is a k-dimensional paraboloid, where k is the number of receptor charge components. The q_R corresponding to the minimum of this paraboloid is the receptor charge distribution to which the ligand will bind most tightly and is mathematically found by minimizing $\Delta G_{\mathrm{elec}}^{0}w.r.t.q_r:(q_{r,\mathrm{opt}}=\frac{1}{2}{R}^{-1}C{q_l}^{55})$.

The promiscuity of the ligand in this thought experiment directly relates to the paraboloid representing its binding energy profile toward all receptors, as shown in Figure 1. Recall above that Π_b was defined as the number of receptors that bind to the ligand within B kcal/mol of the best binder in the space. Here, the best binder in the space is the receptor corresponding to the minimum point of this paraboloid. The promiscuity of the ligand, therefore, is proportional to the volume of the hyperelliptical cross-section B kcal/mol above its minimum, as this corresponds to the size of the set of receptors whose binding affinity lies in this range. In this thought experiment a ligand will be more specific if the paraboloid is very “skinny”, so that there are few receptors whose affinities are near the optimal affinity. Conversely, a ligand is promiscuous if the paraboloid is very wide (Figure 1). Mathematically, the promiscuity of a ligand in this system is wholly determined by the R matrix, as it geometrically determines the curvature of the binding free energy paraboloid. One goal, then, is to relate physical characteristics of a ligand-receptor interaction to mathematical properties of this matrix. Interestingly, previous work has discussed the relationship between the properties of the L matrix and the sensitivity of the binding free energy to charge values at one or more ligand charge centers^56-61; this relationship allows one to interpret the charges at certain ligand atom centers as being more crucial for achieving near-optimal binding free energy toward a receptor, potentially focusing a design problem down to one in which only a few key charge values need be optimal for tight binding. The current application to promiscuity is different from that of achieving optimally tight binding to one receptor. Here, we are interested in the relationship between ligand binding free energy and receptor charge distributions, which is encoded in the properties of the R matrix. Moreover, the interest spans high specificity and high promiscuity (low specificity).

The thought experiment above involved several assumptions — the space of receptors was infinite and shape-invariant, and the binding between ligands and receptors was rigid. In this work, we systematically relaxed each of these assumptions in turn, extending the theory and the model system to treat them and to explore ligand specificity in a more realistic biological context.

2.4 Model Molecules

Model ligand and receptor molecules were used to validate the ideas developed by extending the theoretical framework. They captured much of the physical richness of real biological molecules; various molecular shapes, charge distributions, conformations, and complexes could easily be created, but the lack of chemical constraints allowed for the variation of such characteristics systematically, exhaustively, and effeciently.

The model molecules used for the results shown here were built up from atom-sized spheres (2.0-Å radius). These spheres were “bonded” into rods, using typical heavy-atom bond lengths (1.5 Å). Figure 2 shows a sample binding complex between a model receptor (shown in green) and a model ligand (show in yellow). Differently-shaped and -sized molecules were generated by moving the rods along the axis of cylindrical symmetry in increments, or by adding and removing spheres or entire rods. The centers of spheres could be charged to arbitrary values to generate complex charge distributions. The qualitative conclusions and the theory developed were insensitive to the base size and shape of model ligands and receptors, so we chose to work with systems containing relatively few variable components for ease of implementation and interpretation.

Figure 2.

Sample model molecules. A bound model ligand and receptor are shown in yellow and green, respectively. The model molecules represent portions of a biological ligand-receptor interface. The spheres marked with ‘*’ on the receptor were allowed to bear charge in the numerical simulations. All ligand atoms could bear charge.

The model molecules were intended to represent essential features of small ligand region interacting with its immediate environment on a potential receptor. A subset of pilot studies was also performed with a larger model system to represent features of larger-scale protein-protein interactions; sphere radii and bond lengths were scaled up by a factor of four from the smaller system. The charge on each sphere could now be thought to capture the overall monopole of collections of atoms on a part of the protein. The qualitative relationships between physical characteristics and binding promiscuity demonstrated with the larger model molecules were similar to those using the small molecules, and we therefore show results from investigating the small molecules.

2.5 Implementation Details

Generation of Model Receptors and Ligands

The model molecules used in numerical experiments were composed of spheres bonded together to form rods. Receptors were composed of four rods of bonded spheres of van der Waals radius 2.0 Å and well-depth −0.1200 kcal/mol to model typical biological heavy atoms. The two long receptor rods were offset along the binding axis by 0.2 Å to break the molecular symmetry such that pairs of charge distributions were no longer related by a rotation. The bond length between each bonded sphere pair was 1.5 Å. The two central rods contained two spheres each, while the two outer rods contained five spheres each (see Figure 2). Rods were offset 4.0 Å from each other. To generate 144 different receptor shapes, each outer rod was allowed to move parallel to the bonding axis at 0.6-Å intervals to four total positions, while the shorter rods were allowed to be at three positions at 0.3-Å intervals. As these molecules represented local environments of protein-protein interfaces, these translations were chosen to simulate local “complementarities” between binding partners. In some cases, small clashes were created as a result of the translation, while in other cases small gaps were created between ligand and receptor.

Each ligand was composed of two rods of two spheres each, assembled in the same way as described above. For nonrigid binding analyses, each rod was allowed to move parallel to the binding axis to five total positions at 0.3-Å intervals, for a total of 9 distinct ligand conformations and 25 bound-state conformations. The ligands used to probe the effect of ligand size on specificity were made up of eight spheres. To generate the protein-domain-sized ligands and receptors, all spheres and bond lengths were multiplied by 4.

To approximately model an infinite ensemble of receptors containing every receptor from a continuous, unbounded charge space, the charges at each basis point on the receptor shape took on values from −7.15e to +7.15e in increments of 0.1e for a total of 20,736 receptors for any given receptor shape. These bounds were chosen to generate results nearly identical (in several cases, exactly identical) to those generated from an unbounded space; as long as the receptors outside the bounds do not significantly add to the promiscuity of any ligand, the receptor charge space essentially behaves as if it is unbounded. For a subset of the nonrigid binding calculations, a larger range of charges was needed to model an unbounded space (−11.25e to +11.25e was used, with increments of 0.25e for a faster implementation). We restricted the number of charged atoms on the receptor to the two at the binding interface pocket even though the receptors contained many more atoms. As the theoretical conclusions herein are independent of the number of basis points used, and computational time to enumerate all binding energies increases exponentially as the number of basis points is increased, a relatively simple system that highlighted the theoretical points of interest was used. Moreover, a subset of coarsely sampled pilot studies was performed with six possible receptor basis points, and results were qualitatively the same.

Continuum Electrostatics

The L, R, and C matrices for each ligand shape-receptor shape pair and the desolvation matrix for each ligand shape were calculated using a locally-modified version of the DELPHI computer-program package ^62-64. The linearized Poisson-Boltzmann equation was solved in the same manner as described in ⁶⁵, except for these systems, a 129×129×129 point grid was used for complexes, corresponding to approximately 6.5 grids/Å for a typical complex. For calculating ligand desolvation penalties, a 65×65×65 grid was used, corresponding to 5.9 grids/Å for the ligand alone. For nonrigid calculations, a 73×73×73 grid was used for the unbound state so that the grid resolutions for the bound and unbound states were approximately equal. In all cases, three translations of the grids were used and averaged. A two-tiered focusing procedure was used, in which the molecules occupied 23% and then 92% percent of the calculation volume. The solvation radii of the spheres was set to 2.0 Å, and the molecular surface was generated using a 1.4-Å sphere. The solute dielectric was set to 4.0 and the solvent dielectric to 80.0. For runs with nonzero ionic strength, a Stern layer of 2.0 Å was used. For each run, one atom center was charged to +1.0e and the potential was calculated in the bound and unbound states. These potential difference values were used in the assembly of the matrices, as explained in reference ⁴⁸.

Calculation of the van der Waals and SASA Contributions

van der Waals and SASA calculations of the bound and unbound states of ligand-receptor interactions were done with the CHARMM molecular mechanics software package⁶⁶, using the van der Waals and radius parameters described above. The SASA energies of the bound and unbound molecules were found by computing (5 cal/Ų) × (SASA) + 860 cal⁶⁷, where SASA was the solvent accessible surface area of the molecule (or complex), using a 1.4-Å probe radius.

Binding Free Energy Calculations

The assembly of the energy function terms to compute binding free energies and promiscuities was accomplished with MATLAB⁶⁸. We also used MATLAB to generate the plots shown here.

Nonrigid Binding Calculations

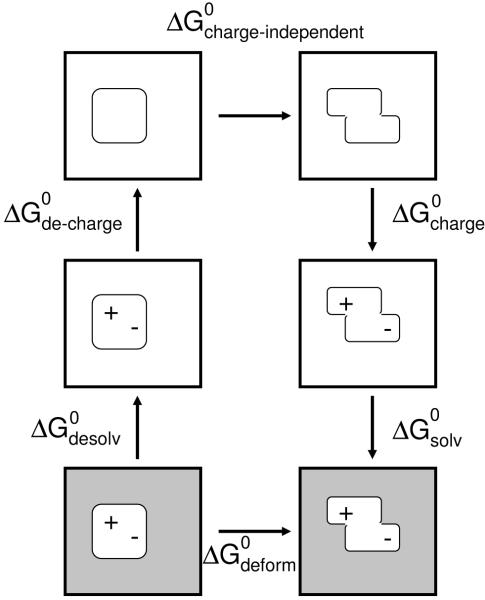
Using the thermodynamic cycle shown in Figure 7, deformation energies for the nine conformations were calculated. Solvation L matrices (used to calculate $\Delta G_{\mathrm{desolv}}^0$ and $\Delta G_{\mathrm{solv}}^0$ shown in Figure 7) were calculated for each conformation using DELPHI as described above. Matrices were also generated to account for the Coulombic change in ligand intramolecular interactions upon deformation (i.e. to compute $\Delta G_{\mathrm{de}-\text{charge}}^0$ and $\Delta G_{\text{charge}}^0$, in which each off-diagonal element $a_{ij}=0.5\ast \left(\frac{1}{4\Pi {\in }_0\in r_{ij}}\right)$ (the diagonal elements were set to zero). In addition, van der Waals and SASA state energies for each ligand conformation were found using CHARMM as described above. An internal energy associated with each ligand conformation was created that was proportional to the square of the displacement of one rod relative to the other. The proportionality constants used here were 5 and 0.25 kcal/Ų. Together, the van der Waals, SASA, and internal terms comprise the ${\Delta }_{\text{charge}-\text{independent}}^0$ portion of the cycle. MATLAB was used in computing and assembling the terms.

Figure 7.

Thermodynamic cycle used for computing the total deformation energy of ligands. $\Delta G_{\mathrm{deform}}^0$ was found by taking the sum over all other ΔG⁰’s indicated in the cycle. Solvation and Coulombic matrices were generated to compute the charge-dependent portions of the cycle. The charge independent portion consisted of van der Waals, SASA, and internal energy contributions.

Determining Empirical Receptor Charge Space

To estimate amino acid frequencies used in the analysis of receptor charge space, the Protein Data Bank (http://www.rcsb.org/pdb) was culled for all structures with less than 90% identity that contained only protein chains (i.e. no DNA or RNA) from source organism Homo sapiens (the structures from “genetically modified source” were selected, as this resulted in a far larger dataset than choosing the sequences catagorized as “natural source”). This selection resulted in 2656 structures (as of April 8, 2007). The sequences from every chain in these structures were used in the estimation of amino-acid frequencies; structural information was not used here, so there was no need to repair or patch missing residues. To assign partial atomic charges, histidines were assumed to be tautomerized and protonated according to their estimated thermodynamic frequencies in protein environments as pH 7.4⁶⁹, and standard charged N- and C-termini were assumed. The slightly different charge values resulting from proline and glycine N-termini were neglected, as such small changes were not expected to alter the overall trends observed.

The same set of proteins was used to estimate the distribution of protein monopoles. Monoples were computed for each individual protein chain in the Protein Data Bank structures, again using only their sequence information. Histidines were charged to a value of +0.09e based on the approximate probability of histidine side chain protonation at pH 7.4.

To estimate the frequencies of partial atomic charges at protein surfaces, 20 structures of human proteins with crystallographic resolution less than or equal to 1.5 Å were prepared (PDB ID’s 1aap, 1bkr, 1d4t, 1e87, 1eaj, 1ek6, 1slk, 1st1, 1f86, 1fcy, 1fj2, 1fl0, 1g1t, 1g9o, 1gd0, 1ggz, 1gk7, 1gqv, 1hd2, and 1hdo). All hetero-atoms (i.e. small molecule ligands, phosphates, etc.), including water molecules, were removed, leaving only protein. REDUCE⁷⁰ was used to build all hydrogen atom positions, to analyze asparagine, glutamine, and histidine side chains for possible flipping, and to determine the tautomerization states for histidines. Calculation of the accessible surface area was done using CHARMM, with CHARMM22 parameters for atomic radii⁷¹ and a 2.0-Å probe radius. Each protein chain was considered separately, i.e., any protein complexes were rigidly separated into unbound species for analyses, even if they were homodimers. The exposure for each atom was calculated by dividing its accessible surface area in the protein by the accessible surface area of the isolated atom (i.e., the area of a sphere of radius r = (2 + atomic radius)). The exposures for each partial atomic charge value were then summed over all protein atoms and all protein structures, and then normalized by the sum over all exposures to yield surface frequencies. Because the radii of certain hydrogen atoms allow for their complete envelopment by bound atoms, the exposure of any hydrogen atom with zero exposure was set to the exposure of the atom to which it was bound. For comparison, results were also generated in which no corrections were made for hydrogens with zero exposure; this yielded very similar results for promiscuity trends, i.e., the trend in Fig. 5 showed only subtle differences (data not shown), although the charge space was less symmetric because the highly polar hydrogens within hydroxyl groups were generally undercounted.

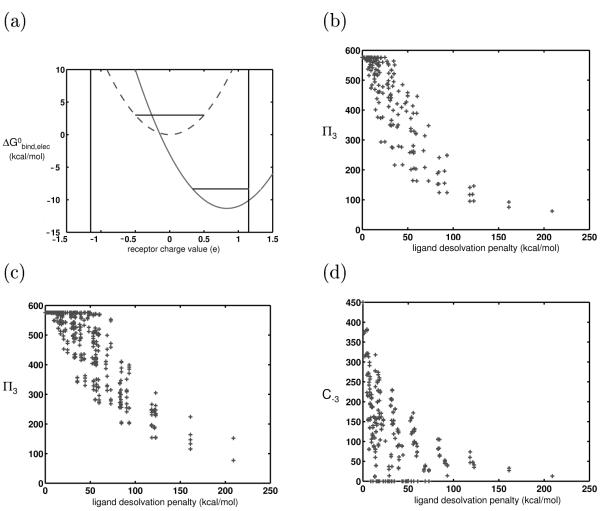
Figure 5.

Effect of adding bounds to receptor charge space. (a) The vertical lines represent bounds that lower the number of competing receptors for a highly charged/polar ligand (represented by solid-line parabola) more than it does for an uncharged ligand (represented by dashedline parabola). Therefore, polar/charged ligands are less promiscuous in a symmetrically bounded space. (b) Numerical experiment showing the promiscuities of model ligands varying only in charge and rigidly binding to identically-shaped model receptors in a bounded charge space. (c) Same as (b), except the receptor charge space at the two basis points is sampled from the distribution shown in Figure 4b. (d) C₋₃, values are plotted against ligand desolvation penalty. The receptor panel used was the same as that used to generate the results shown in (b). Now that the receptor charge space is bounded, the charged and polar receptors are able to bind to few receptors with high affinity, unlike those analyzed in Figure 3d.

Visualization Software

All images of model molecules were made with the program VMD⁷². In addition, Raster3D was used in rendering images of model molecules⁷³.

3 Results and Discussion

The goal of this study was to explore physical determinants of binding specificity and promiscuity through application of theory and computation on model molecules. In order to determine the individual contributions of each physical characteristic toward ligand promiscuity, the basic approach taken here was to begin with a control system in which all ligands were equally promiscuous. By modifying physical characteristics of the ligands and receptors in the control system, the effect of each potential determinant on the collection of ligands could be studied in turn.

3.1 A Control System in Which Various Ligands Are Equally Promiscuous

Our control system was identical to the one described in the thought experiment described in the Methods Section; ligands could rigidly bind in a fixed orientation to identically-shaped receptors, forming identically-shaped complexes, and every possible receptor charge distribution was available in the set.

Theory

In this system, the binding profile of a ligand to the receptor ensemble is a multi-dimensional paraboloid in receptor charge space, as described in the Methods Section. A ligand’s promiscuity depends on the curvature of this paraboloid, which is completely determined by the R matrix. Suppose the promiscuity of one ligand in this system is compared to that of a second ligand differing only in its charge distribution. According to Eq. 5, the free energy profiles of both ligands are paraboloids, and they are translated relative to each other, according to their different ql values. The curvatures of the two paraboloids are identical, as that is determined by the R matrix. The promiscuities, therefore, of these two ligands — and of all identically-shaped ligands in such a system — are equal (Figure 3a).

Figure 3.

Theory and results for the control system: (a) Binding free energy profiles for two hypothetical ligands differing in charge and binding in fixed orientation to identically-shaped receptors. Though these ligand have different absolute affinities to the panel of receptors, they have identical promiscuities (π₃), as shown by the black horizontal lines. This plot shows the hypothetical electrostatic binding affinity, but as the shapes of all receptors and complexes are identical, the van der Waals and SASA contributions will not contribute toward promiscuity. (b) Plot of promiscuity vs. ligand hydrophilicity (as measured by desolvation penalty) for 625 simulated ligands varying only in charge and binding to simulated receptors meant to recreate the space described in (a). (c) The results in (b) (black + ’s) are compared to ones in which the two receptor rods marked with a ‘*’ in Fig. 2 were translated 0.3 Å closer to the ligand, thus increasing receptor desolvation by the ligand (gray o’s). As the R matrix for this new system has larger elements, the ligands are all more specific toward their panel of receptors. (d) Ligand coverage (C₋₃) is plotted against its desolvation penalty. In this control system, highly charged and polar ligands are able to bind to many receptors with high affinity, when compared to hydrophobic ligands. Chapter 3 provides the theoretical framework for understanding why this is the case in this system.

Numerical Experiment

A computational approximation of this control system was implemented to serve as a baseline for the next steps in the study and to compare with the theory. We generated a library of model ligands varying only in charge, and a large set of model receptors that approximated the theoretical, infinite set containing all receptor charge distributions from a continuous, unbounded charge space (see Methods). The ligands each had four charge basis points (one at each sphere center) that could independently vary from −1e to +1e 0.5e increments, for a total of 625 ligands (considering each ligand orientation distinct). The receptors each had two charge basis points at the binding interface (sphere centers indicated by ‘*’ in Figure 2). We generated the receptor ensemble by exhaustively sampling receptor charge space in 0.1^e increments at these two points. The upper-bound charge magnitude on the spheres was chosen to be large enough that the results would be identical to those generated from using an unbounded space (see Methods). We did not constrain the total charge on each binding partner to be integral, as these model molecules could represent regions of larger systems, with the values at basis points representing partial atomic charges. The free energy of binding of every ligand-receptor pair was calculated according to Eq. 4. Because the ligands and receptors were all identically shaped and the binding was rigid, the only term that contributed to promiscuity was the electrostatic term. For each ligand, a II₃ value was computed. Figure 3b is a plot of the II₃ of each ligand versus its desolvation free energy (the free energy required to transfer it from a completely solvated state to a completely desolvated state, modeled by a medium of dielectric 4). The desolvation penalty is a measure of a ligand’s hydrophilicity and, for identically-shaped ligands, depends only on its charge distribution. The completely uncharged ligand had a desolvation penalty of 0 kcal/mol, while the ligands with +1e (or −1e) on all basis points had the highest desolvation penalty of 209 kcal/mol.

Consistent with theory, promiscuity in this system did not depend on ligand charge distribution (Figure 3b). Each ligand bound to approximately 1470 receptors within 3 kcal/mol of its tightest binder. There was a small (±5) variation in the ligands’ promiscuity values because of the discretization in our model of the continuous receptor charge space. The result that all ligands have identical promiscuities was insensitive the promiscuity cutoff chosen.

The precise value of II₃ attained by all ligands in the control system was determined by the R matrix, which was in turn determined by the physical properties of the ligand-receptor interaction. The R matrix, and therefore the sensitivity of the binding energy to receptor charge distribution, is influenced by the complementarity between the ligand and receptor shapes, the locations of the charge centers on the receptor, and the extent to which each basis point is desolvated upon binding. Generally, the more desolvated a receptor charge basis point is upon binding, the more sensitive the binding free energy will be to that charge value. Therefore, ligands will be more specific toward a receptor set when they highly desolvate the variable receptor charges upon binding (Figure 3c). Put into a biological context, a group that closly interacts across an interface, such as a tight hydrogen bonding group that highly desolvates its partner, can increase the specificity of the overall interaction. Of course, in situations where there are many potential receptors with highly similar, direct hydrogen-bonded groups across the interface, as with kinases, such interactions may not increase specificity because of the lack of target variation in charge distribution at the direct interface. As noted, such systems may achieve specificity by the differences in the desolvation of pre-existing receptor hydrogen-bonded groups upon binding²⁷; these effects are mathematically captured by the off-diagonal elements of the R matrix, and therefore the physical phenomenon of desolvating such intramolecular hydrogen bonds upon binding can also greatly affect the properties of the R matrix — and therefore specificity — within our framework.

Figure 3d shows that while the ligands all have the same promiscuities, their absolute affinities to the set of receptors greatly varied. Some ligands had very high coverage (C_B, b = −3 here); others did not. In our control system, highly charged and polar ligands had greater coverages; these ligands were able to obtain highly favorable electrostatic energies with a number of appropriately highly-charged receptors, due to the closely interacting nature of the charges on the opposite partners.

In this section we established a control system for which we found the promiscuities of an ensemble of ligands to be equal. In what follows, by varying the physical properties of the ligands and receptors relative to this control, an understanding of the relationship between physical properties of the system and ligand promiscuity will be developed.

3.2 Hydrophobic Ligands Are More Promiscuous Because They Are Far From the Edges of Biological Charge Space

In the control system, the charge space of the receptors was unbounded, continuous, and uniformly sampled. Here we argue that such an assumption is likely implausible for biological molecules, and we examine the consequences of a bounded charge space on ligand specificity. To better understand the receptor charge space that a ligand “sees” in a biological environment, we used varying methods to qualitatively characterize the biological charge space of proteins. We focus on proteins here, noting that nucleic acids, lipids, and other biological molecules can also be potential binding partners. As the primary goal of this study was to extract trends and their basis, rather than pure quantitation, these methods were applied to provide very general guidelines.

The simplest approach used was to estimate the relative abundances of amino acids and use parameterized partial atomic charges (here, from the CHARMM22 parameter set⁷¹) to generate a histogram of protein partial atomic charge frequencies at the atomic level (Figure 4a). Amino-acid frequencies were estimated using 2656 protein structures and complexes culled from the Protein Data Bank (see Methods). Expectedly, we found that the space is bounded, is reasonably symmetric, and has a mode near a charge of zero (these corresponded to aliphatic hydrogens on nonpolar side chains, which were parameterized to generally have a charge of +0.09e). This approach did not differentiate between buried atoms and atoms at the surface. To roughly estimate the distribution of partial atomic charges on protein surfaces (i.e., the charges with which a potential ligand would likely directly interact), a second approach was used in which the exposure of every atom from 20 human protein molecules and complexes (excluding non-protein atoms such as metal ions, cofactors, water molecules, small-molecule ligands, etc.) was calculated (see Methods). Exposure was defined as the ratio of an atom’s accessible surface area in the protein to its accessible surface area if it were an isolated atom. A probe radius of 2.0 Å was used to compute the accessible surface areas, to model typical heavy atom interactions. Figure 4b shows a plot of exposure as a function of charge. Here, exposures have been normalized to obtain relative frequencies. This plot also reveals a bounded, fairly symmetric space, though not surprisingly, higher magnitude partial charges occurred more on the protein surfaces than in proteins overall. Finally, to gauge the relative sizes of monopoles on overall proteins, the sequences of each chain from the 2656 protein structures were evaluated fro their overall monopoles. The resulting distribution of protein monopoles is shown in Figure 4c and shows a relatively tight distribution around approximately 0. Again, we did not account for non-protein species such as metal or phosphate ions, but one might expect them to decrease the effect of the overall protein monopoles on average.

Figure 4.

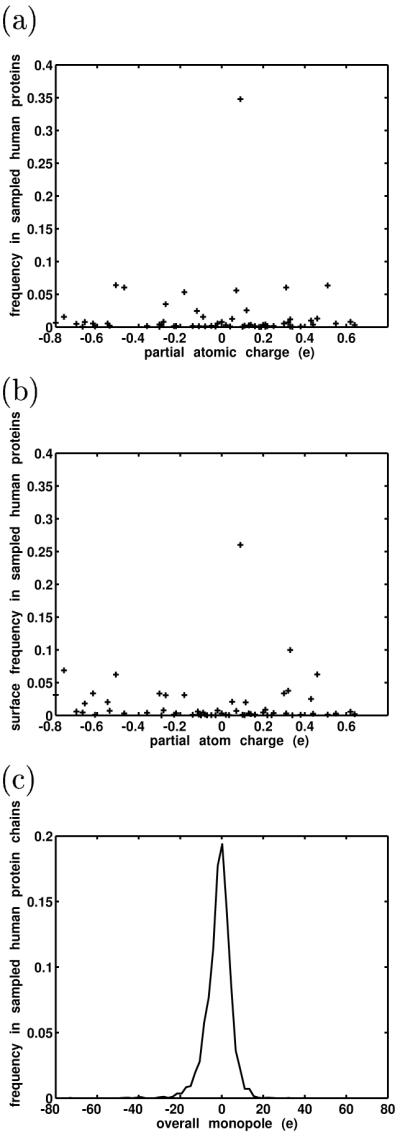
Three qualitative methods were used to estimate the magnitudes and distribution of charge values in proteins (a) Estimated frequencies of partial atomic charge values in human proteins. (b) Estimated frequencies of partial atomic charges at protein surfaces. (c) Estimated monopole frequencies of human protein sequences.

Taken together, these assessments, while qualitative, showed that at both the atomic and molecular level, the biological charge space of proteins is bounded — there is an upper limit to the magnitudes of partial charges and protein monopoles. Moreover, the distribution of partial atomic charges and monopoles peaks around zero.

Theory

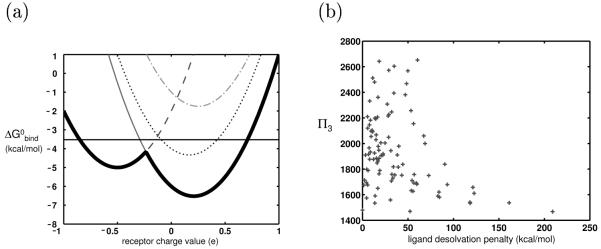
We applied the continuum electrostatics framework to analyze the effect of a bounded receptor charge space on ligand promiscuity. First consider two ligands from our control system, one completely hydrophobic and one charged. Figure 5a shows the binding profiles corresponding to these two ligands. The best binder to the hydrophobic ligand is the completely hydrophobic receptor, while the best binder to the charged ligand is a receptor with nonzero charges at its basis point(s). As shown in the previous section, when the receptor charge space is unbounded, both ligands will have the same promiscuity. When symmetric bounds are imposed on this space, all ligands no longer have equal promiscuities. Many of the potential binding partners for the charged or polar ligands are now excluded from the space, and as a result, these ligands have lower promiscuities than their hydrophobic counterparts (shown schematically in Figure 5a).

Numerical Experiment

A bounded receptor charge space was constructed by constraining receptor basis point charges to magnitudes less than or equal to 1.15e in 0.1e increments, for a total of 576 receptors. Figure 5b shows a plot of the π₃ of each ligand against its desolvation penalty. Overall, hydrophobic ligands were clearly more promiscuous than highly charged ligands.

To more qualitatively account for the distribution of receptor partial atomic charges, a second experiment was done in which the charges at the two spheres were independently chosen according to probabilities determined from Figure 4b, for each of the 576 receptors. Figure 5c shows the results, and again, the general trend of charged and polar ligands having decreased promiscuity was borne out. To ensure that this trend was not an artifact of allowing only two spheres to bear charge, we did a parallel simulation in which all eight spheres that made direct contact with the ligand upon binding could bear a charge value sampled from this distribution; the trend was robust to such perturbations, and was even stronger in this case (data not shown). Overall, these results suggest one reason for the observed higher specificity of polar and charged molecules in the literature; they are near the edges of the biochemical charge space, so there are fewer molecules to which they can bind with near-equal affinity.

Figure 5d, which shows coverage values toward the receptor panel in a bounded charge space, demonstrates that a finite receptor charge space significantly affects not only the promiscuities of charged and polar ligands, but also their coverage values. While in the unbounded charge space, polar and charged ligands had substantially more higher-affinity interactions, now they have substantially fewer than their hydrophobic counterparts.

3.3 Hydrophobic Ligands Are More Promiscuous Because They Are Not as Sensitive to the Shapes of Potential Binding Partners

In a biological environment, potential binding partners differ in shape as well as charge distribution. To probe the effect of differing receptor shapes on ligand promiscuity, we examined the effects of adding an ensemble of receptor shapes to the control system. In order to isolate the effect of shape variation, an infinite number of receptors was allowed for each shape in theory, sampling every point in continuous, unbounded charge space; the shape variation was therefore the only difference between the control system and this experiment.

Theory

Currently, a full analytical treatment of this scenario is not possible because allowing receptors to vary in shape results in R matrices that are no longer identical for all interactions; therefore the binding profile of a ligand to the collection of receptors must be represented by multiple paraboloids of different curvatures. Nevertheless, the continuum electrostatics framework suggests that in general, charged ligands may be more specific toward a set of receptors varying in shape than hydrophobic ligands because the electrostatic component of the binding free energy for charged ligands is more sensitive to shape differences than it is for their hydrophobic counterparts. For example, consider a ligand in which all partial atomic charges are zero. No matter the shape of its possible binding partner, if it is completely uncharged as well, it will be the optimal binder of that particular shape to the ligand, and the pair will have an electrostatic free energy of binding of 0 kcal/mol. While the paraboloids corresponding to each receptor shape have different curvatures, their minima are all 0 kcal/mol, if only the electrostatic portion of the binding free energy is considered. Under this assumption, every shape will contain some charge distributions that will contribute to its promiscuity (Figure 6a). This is not necessarily true for a charged or polar ligand (Figure 6b). The electrostatic binding free energies to the optimal receptors for each receptor shape vary greatly such that few receptor shapes can contribute to a ligand’s promiscuity.

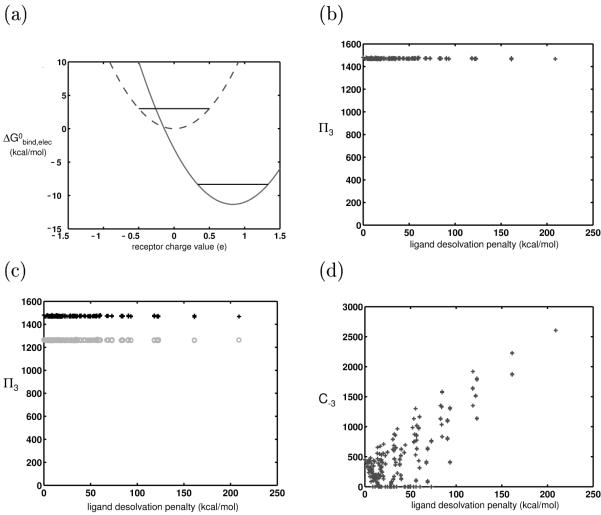
Figure 6.

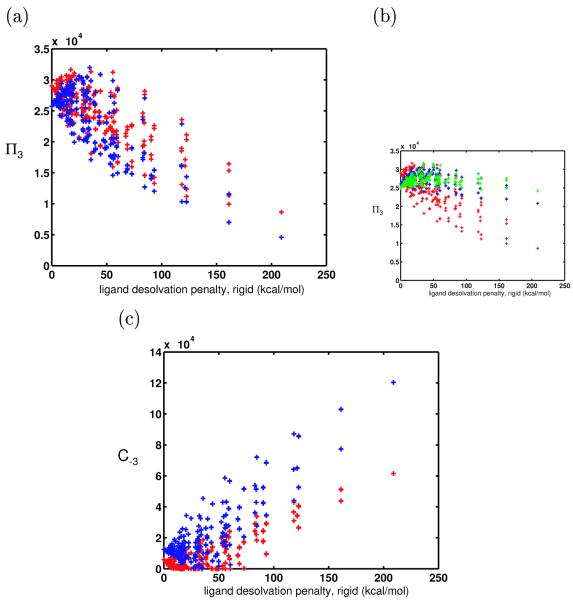
Effect of having multiple receptor shapes and charge distributions in the system: (a-b) Schematic electrostatic binding profiles of a hypothetical hydrophobic ligand (a) and charged ligand (b) to three differently-shaped sets of receptors. Each parabola represents the electrostatic binding profile toward identically shaped receptors varying in charge; there are three different shapes of receptors, leading to the three different parabolas. Note that the hydrophobic ligand has far more receptors in the space within b kcal/mol from the best binder — all three receptor shapes contribute to its promiscuity, and it is more promiscuous. Only two receptor shapes (represented by the solid and dotted parabolas) contribute to the promiscuity of the charged ligand, and it is therefore less promiscuous. (c) Plot of promiscuity vs. ligand desolvation penalty for ligands varying linearly in their charge distribution and binding rigidly to receptors varying both in their shape and charge distribution (in an unbounded charge space). Only the electrostatic component of binding was calculated in this plot. (d) Promiscuities of the 625 model ligands toward the ensemble of differently-shaped and -charged receptors are plotted against ligand desolvation penalty. Here, the full energy function was used.

The difference in the electrostatic contribution to promiscuity can be analytically derived for ligands whose charge distribution varies purely linearly. Recall that for a given ligand binding to identically shaped-receptors, the charge distribution of the tightest-binding receptor is:

$$q_{r,\mathrm{opt}}=-\frac{1}{2}{R}^{-1}C{q}_l.$$ (6)

Substituting this charge distribution for q_r into Equation 5 yields the optimal free energy of binding to a given ligand, assuming constant shapes for ligand, receptor, and complex:

$$\Delta G_{\mathrm{opt},\mathrm{elec}}^0=q_l^T(L-\frac{1}{4}{C}^T{R}^{-1}C)q_l=q_l^{T}M{q}_l,$$ (7)

where $M=L-\frac{1}{4}{C}^T{R}^{-1}C$. When the shapes of the receptor and complex are changed, M changes accordingly. The sensitivity to shape can be thought of as the difference in the optimal binding free energy for a ligand binding to two arbitrarily shaped receptors, 1 and 2.

$$\Delta \Delta G_{\mathrm{opt},\mathrm{elec}}^0=q_l^T(M_1-M_2)q_l$$ (8)

For any two arbitrary shapes, Equation 8 shows that the difference between the optimal electrostatic binding free energies for an uncharged ligand is zero. Both shapes can therefore contribute to the ligand’s promiscuity, unless van der Waals and SASA energies are substantially different. For ligands with nonzero charges, there will be nonzero sensitivity. Moreover, Equation 8 shows that doubling every charge on the ligand makes the ligand four times more sensitive electrostatically to shape differences. The promiscuity due to electrostatics toward a set of arbitrarily-shaped receptors therefore decreases quadratically as the charges on the ligand are linearly increased. When comparing the promiscuities of ligands whose charges do not differ linearly, we cannot make any quantitative statements. Also, the addition of the nonelectrostatic components of binding may also significantly affect the general trends. We therefore used numerical experiments on our model system to generalize this trends to the case of ligands with arbitrary charge distributions interacting via the full potential represented by Equation 4.

Numerical Experiment

To isolate the effect of receptor shape variation, the control system was modified to include 144 different receptor shapes (see Methods). For each shape, a large set of recepter charges at the two basis points was allowed (to approximate a continuous, unbounded charge space, analogously to what was done for the control system), and the rigid binding and fixed orientation assumptions were maintained. To first demonstrate the quantitative relationship derived above, 21 ligands that varied linearly in charge (ql = a[−1 + 1 − 1 + 1], where a varied from 0 to 1e in increments of 0.05e) were bound in a fixed orientation to this ensemble of receptors, and the electrostatic component of their binding free energies was calculated. Theory predicted a quadratic dependence of promiscuity on the charge magnitude a, and therefore a linear dependence on ligand desolvation penalty because the ligand desolvation penalty also varies quadratically as the ligand charge distribution is varied linearly. The expected linear dependence was found (Figure 6c).

If ligands differ nonlinearly in their charge distributions, the quantitative theoretical conclusions no longer hold. Also, the van der Waals and SASA contributions to the energies will affect relative promiscuities. We therefore used numerical experiments to account for these effects. The results of binding the complete set of 625 identically-shaped ligands described above to the set of receptors described in the previous paragraph resulted in a fairly strong trend, as shown in Figure 6d. The trend was no longer linear, however, with there being a large spread in promiscuity values for ligands with similar hydrophilicities. Nevertheless, hydrophobic molecules were generally more promiscuous than their highly charged counterparts. This shows that simply the variation in shape of biological molecules is one reason for increased specificity of charged molecules relative to hydrophobic molecules. Moreover, in this experiment, the inclusion of van der Waals and SASA components did not change the overall trend that was predicted from an analysis of the electrostatic component alone.

3.4 Ligand and Bound-State Conformational Flexibility May Further Increase the Specificity of Charged and Polar Ligands

Results to this point considered only rigid binding and showed that charged and polar ligands were more sensitive to shape differences in their potential binding partners. We next addressed whether conformational flexibility, of both the ligand and the complexed state, could allow these ligands to bind more promiscuously to receptors of different shape.

Theory

As demonstrated earlier, a small deviation from shape complementarity may cause a large variation in the optimal binding affinity achievable toward a charged or polar ligand. A flexible ligand, by achieving shape complementarity to more receptors, may be able to achieve similar optimal binding energies to more receptor shapes, thereby regaining promiscuity relative to its hydrophobic counterparts. Recently, the charge optimization framework was extended to a nonrigid binding model in which the complexed state was invariant and the unbound ligand conformation was allowed to vary⁶¹. It was shown that well-defined, optimal charge distributions may not exist in this scenario when the matrix determining the quadratic dependence on charge is no longer positive semi-definite; nevertheless, useful insights were achieved through constrained numerical studies on a biomolecular system. For example, the stationary point ligand charges from constrained optimization depended highly on the particular conformation used to model the unbound state. Also, numerical minimizations of the binding free energy tended to yield charge distributions that stabilized the bound ligand conformation relative to the unbound ligand conformation, therefore suggesting that a ligand with such a charge distribution would not adopt the assumed unbound conformation in reality. These results highlight the importance of sampling multiple conformations of the unbound state in a nonrigid binding model and explicitly accounting for the free energy of the unbound state when computing or optimizing binding free energies. In this work, we compute free energies over multiple conformations in both the unbound ligand and the complexed states. The R, L, and C matrices are different for each bound-state conformation, as opposed to only ligand-associated matrix elements changing when the bound state conformation is fixed and the unbound state varies in conformation. The parabolic free energy landscapes do not hold in such a model, and therefore numerical experiments were carried out to achieve insight.

Numerical Experiment

To test the effect of conformational freedom on ligand promiscuities, ligands were now allowed to exist in nine unique conformations, created by moving one rod of spheres relative to the other, with a harmonic internal energy penalty associated with this movement. The bound state was allowed to exist in multiple conformations as well, consisting of rigid translations oif ligand conformations relative to the receptor. There was a total of 25 complex conformations for each ligand-receptor pair. Binding free energies were calculated using the thermodynamic cycle shown in Figure 7. The reference state ligand conformation was the one used for the rigid binding calculations discussed previously. The total deformation energy of each of the ligand conformations was calculated by summing the van der Waals, SASA, internal, and electrostatic contributions relative to the reference state. The free energy of the unbound state was then calculated by

$$G^0=-kT\ln Q,$$ (9)

where Q is the partition function obtained from the Boltzmann-weighted sum of the conformational energies associated with each ligand, k is the Boltzmann constant, and T is the absolute temperature (set to 300 K). The free energy of the bound state was calculated analogously, summing over the Boltzmann factors of the twenty-five bound-state geometries to obtain the bound-state partition function. The free energy of binding for each ligand-receptor pair was then the difference of the bound and the unbound state free energies.

The binding free energy for each of the 625 flexible ligands was found to the panel of 144 receptor shapes, with each shape set containing a large set of receptor charges to approximately model a continuous, unbounded charge space (see Methods). Figure 8a shows a comparison of the promiscuities of the rigid ligands (red) and flexible ligands (blue). Surprisingly, many of the flexible ligands — especially the charged or highly polar ones — were less promiscuous than their rigid counterparts.

Figure 8.

(a) Promiscuities toward a receptor ensemble (whose members differ in both shape and charge) when ligands and bound states are conformationally flexible (blue) and rigid (red), plotted against their desolvation penalties. (b) Promiscuities when ligands and bound states are conformationally flexible (blue and green) and rigid (red), except now, flexible ligands are not allowed to have any unfavorable van der Waals interactions with receptors upon binding. Ligands with high flexibility (internal constant = 0.25 kcal/Ų) are shown in green, and those with moderate flexibility (internal constant = 5 kcal/Ų) are in blue. (c) C₋₃ values for conformationally flexible (blue) and rigid (red) ligands.

To understand this somewhat counterintuitive result, we looked at the preferred conformations of ligand molecules in the system. We found that when a ligand was bound to a receptor with which it could have electrostatically favorable interactions, it tended to prefer a bound-state conformation that has somewhat unfavorable van der Waals interactions in order to maximize these electrostatic interactions. The gain in electrostatics more than out-weighed the van der Waals penalty, so the actual binding free energy was greatly improved as a result of ligand and bound-state conformational flexibility. This parallels hydrogen bond and salt bridge formation at protein interfaces, in which very close contacts between binding partners are made. Because a select few binding free energies were highly stabilized in this way for each ligand, the ligand became more specific. In other words, ligand and bound-state conformational flexibility allowed ligands to get as close as possible to their most desirable partners, thereby increasing their affinities to those partners even more relative to other possible targets.

To further test this hypothesis, we redid the numerical experiment using flexible ligands, but we disallowed any bound-state conformations that would create unfavorable van der Waals interactions, i.e. where the Lennard-Jones potential energy between any ligand and receptor sphere was positive. The results are shown in Figure 8b. When ligands and bound states were allowed to be flexible but could not form unfavorable van der Waals interactions, the charged and polar ligands were nearly as promiscuous as their hydrophobic counterparts (blue and green crosses, representing moderate and low internal energy penalties, of 5 and 0.25 kcal/Ų, respectively). Charged ligands could not gain extra electrostatic affinity to a few desirable receptors at the expense of unfavorable van der Waals interactions, so their promiscuity was not decreased by the existence of such higher-affinity interactions; in fact, they were able to form complementary conformations to the receptor shapes and decrease their sensitivity to shape, making them more promiscuous than they would be if the binding was completely rigid (red crosses). These results were therefore in line with our original intuition that conformational flexibility would increase polar and charged molecule’s promiscuities. This test system demonstrated that in our actual system that interacted via the Lennard-Jones potential, the trade-off between unfavorable van der Waals interactions and favorable electrostatics was responsible for the surprising result that conformational flexibility increases the specificity of charged and polar ligands.

Overall, these data show that the balance between attractive charge-charge interactions and repulsive steric interactions is subtle but extremely important in determining both affinities and specificities; the effect of flexibility on ligand promiscuity may not be robust to the quantitative details of this trade-off. In most molecular mechanics calculations, the repulsive part of the Lennard-Jones function, which models the Pauli repulsion between atoms interacting at very close distances, is somewhat arbitrarily set to have a $\frac{1}{r^{12}}$ dependence. During preliminary analysis, we varied the exponent on this term to see how exponents of 14 and 16 affected the specificities of ligands in our model system (keeping other parameters and the functional form unchanged). As the repulsive term became stronger, the promiscuities resembled those of the ligands unable to form any unfavorable van der Waals interactions more and more (data not shown). The trade-off between electrostatic interactions and the Pauli repulsions modeled by the Lennard-Jones repulsive term therefore appears to play an extremely important role in determining binding affinities and specifities, and the nature of this trade-off warrants further study.

Figure 8 shows the C₋₃ values for rigid and nonrigid ligands in this system. The flexible ligands generally had greater coverage values than their rigid counterparts, with the highly charged and polar ligands showing the greatest effect. Again, this is likely due to the electrostatic stabilization of the bound states of these ligands that results from the added flexibility.

3.5 Smaller Ligands Are More Promiscuous Than Larger Ligands

We considered the effect of ligand size on specificity by increasing the number of spheres used to generate our model ligands. We allowed these additional atoms to bear charge (in the form of extra basis points).

Theory

Recall that the R matrix determines the promiscuity of a ligand when presented with identically-shaped receptors. When bulk is added to a ligand at any location, the ligand will desolvate the receptor more upon binding, for a given receptor charge distribution. This makes the binding free energy increase (i.e., affinity decrease) more steeply as the receptor charges deviate from the optimal receptor charge distribution, resulting in lowered promiscuity. Stated mathematically, the elements of R will generally increase (the diagonal elements always increase), making the ligand’s binding free energy paraboloid steeper. Because a ligand’s promiscuity toward identically-shaped receptors increases with the width of its free energy parabola, this larger ligand will be less promiscuous than its smaller counterpart. Moreover, allowing the added bulk to take on an arbitrary charge distribution will not additionally affect ligand specificity (assuming an unbounded receptor charge space) because the ligand’s charge distribution does not affect the elements of the R matrix. Conceptually, one can argue that a bigger ligand — because it desolvates its receptor more upon binding — is much more sensitive to the charge values on potential receptors, with fewer receptors contributing to near-optimal binding toward it.

Numerical Experiment

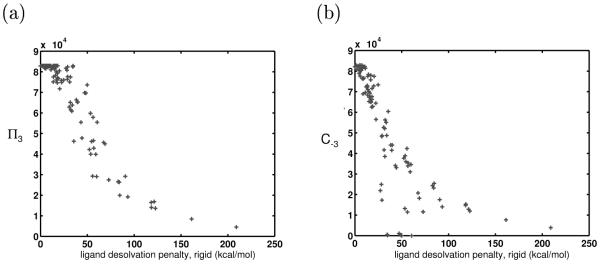
Four extra atoms were added to each of the 625 model ligands from the control system (Figure 9a). In the results shown in Figure 9b, the four added ligand atoms bore no charge. The binding free energies of these larger ligands were computed toward the set of receptors in the control system. When compared with their smaller counterparts, these ligands were all less promiscuous. When some of the added ligand atoms were allowed to take on nonzero charge values, their promiscuities were unchanged, as the theory would predict. These data, in agreement with anecdotal evidence, show that toward the same panel of receptors, smaller ligands are more promiscuous than larger ligands. Indeed, the R matrix corresponding to complexation with the larger ligand had elements that were more than twice those of the R matrix from the control system. As expected, larger ligands are more specific because their high desolvation of the receptor makes the resulting binding free energies very sensitive to receptor charge values.

Figure 9.

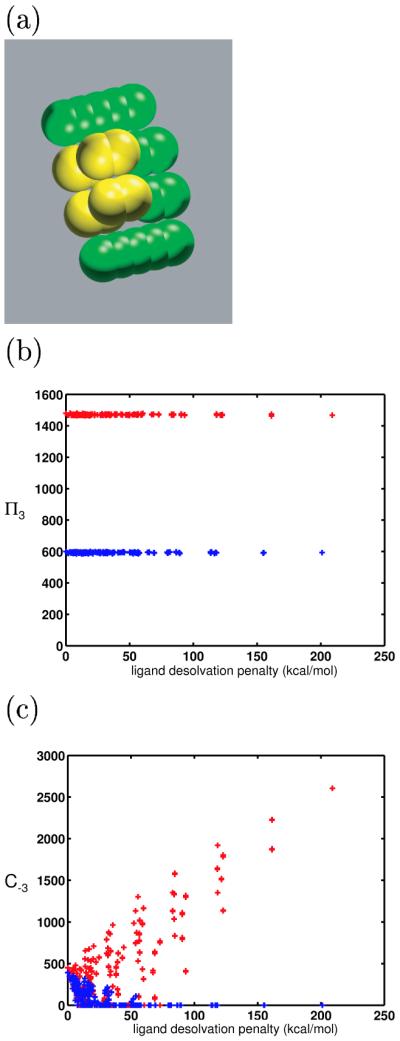
(a) Representation of the larger ligand molecules used to study the effect of ligand size on promiscuity. These ligands were composed of eight spheres. The first four were located identically to those in the control ligand. The second four were offset by 4 Å above the others, and by 1.5 Å along the bonding axis. These locations were chosen such that the added spheres would highly desolvate the receptor upon binding, such that large differences in the promiscuity values could be seen. (b) The π₃ values for two sets of ligands toward the same receptor set, plotted against each ligands desolvation energy. One set (red) is composed of “small” ligands, made up of four model atoms. The other set (blue) is composed of larger ligands, of shape shown in (a). This data supports the theoretical prediction that generally, smaller molecules are more promiscuous than large ligands toward the same receptor set. (c) C₋₃ values are shown for each of the smaller (red) and larger (blue) ligands. Few of the larger ligands are able to bind with high affinity to many of the receptors in the panel.

Figure 9c shows that in this system, when the extra spheres on the large ligand did not bear charge, the smaller ligands often had higher coverages than large ligands. Although they were unable to make as favorable van der Waals interactions with the receptors, their relative lack of sensitivity to receptor charge distribution often dominated and allowed for more higher-affinity binding partners.

3.6 Increased Ionic Strength Can Slightly Increase Ligand Promiscuity

All of the above computations were made in zero ionic strength. Here we analyzed how ligand promiscuity is altered by the ionic strength of its surrounding medium.

Theory

The C matrix depends the most on the ionic strength, as it captures the solvent-screened interactions between the ligand and receptor. The elements of the C matrix are generally reduced because salt screens interactions. The R and L matrices are very slightly affected, and their diagonal elements are generally increased, because it costs more energy to remove both salt and water from around a molecule than only water. We have found using our model systems that the reduction in the elements of the C matrix dominates over the increase in the elements of the L and R matrices (data not shown). Moreover, because the R matrix does not appreciably change as ionic strength is increased, changing the ionic strength from 0 M to 0.145 M had no significant effect on promiscuity in our control system (data not shown).

However, when multiple receptor shapes are introduced, theory may suggest that molecules have altered promiscuities when the ionic strength is increased to a nonzero value. This is because the C matrix plays a role in defining the spread in the optimal binding energies of a given ligand to differently-shaped receptors, as Eq. 7 shows. When the elements of the C matrix are made smaller for the interactions with each receptor shape, the spread in energies as a function of shape may change as well. Because promiscuity is directly related to the spread in energies, one might expect that ligands will have different promiscuities toward a panel of differently-shaped receptors as a function of ionic strength.

Numerical Experiment

The ionic strength was increased from zero to 0.145 M to the model system containing 625 ligands varying only in charge. The receptor set used contained 144 receptor shapes and the large set of receptor charges for each shape. Figure 10 is a plot of the Π₃ values of the 625 ligands in a nonzero ionic strength compared with their promiscuities in zero ionic strength (the latter is the same data shown in Figure 6c). Addition of salt usually increased promiscuity, especially for the most charged ligands, though the effect is small. Note that for highly charged species in an ionic solution, the linearized Poisson-Boltzmann equation may not be a quantitative approximation for electrostic binding free energies. While some model molecules were highly charged, our interest was in making qualitative statements, so the lack of quantitative accuracy was not of concern here.

Figure 10.

The π₃ values for ligands plotted against ligand desolvation free energy. Here, the receptor set consists of 144 different shapes and an “unbounded” charge space for each shape. Systems with ionic strengths of 0.0 M (red) and 0.145 M (blue) are plotted. For ease of comparison, the desolvation energy plotted for both systems is the desolvation energy in an ionic strength of 0.0 M.

These data suggest that often, a high ionic strength slightly reduces the specificities of charged or polar ligands in a biological environment.

3.7 Ligands With Asymmetric Charge Distributions Can Achieve Higher Promiscuities

In the control system, each ligand bound in only one orientation to each receptor. In reality, a ligand will most likely bind in the orientation that minimizes the energy of the bound state conformation. Here we loosened the orientation constraint by allowing the ligand to bind in any of its shape-invariant orientations. We used shape-invariant orientations here to separate the effects of orientational freedom and shape differences, which were considered in a previous section.

Theory

Consider a ligand with charge distribution ql. The shape invariant orientations of this ligand can be represented by different ql values, as rotating the ligand amounts to permuting the labels on the ligand basis points. Figure 11a shows the free energy parabolas in a 1-D receptor charge space for the orientations of a hypothetical ligand (the model ligands used in this work had four shape-invariant orientations). For ease of visualization, assume the zero temperature limit, such that the binding free energy of a ligand to each receptor in the space will be the minimum of the four possible binding free energies at each point. Therefore, the binding free energy profile will trace out the minimum of the union of paraboloids. Two conditions are necessary for ligand orientational freedom to confer increased promiscuity:

1. The lowest minima corresponding to orientations of the ligand must be at similar energies, and

2. These minima should correspond to receptor charge distributions that are far away from one another in receptor charge space; otherwise, even though the binding energies in these orientations are similar, they are similar toward the same receptor subset, and promiscuity is not increased.

Note that for the completely uncharged ligand or a ligand in which every basis point has the same charge, all orientations are equivalent, so the four paraboloids are exactly the same; no promiscuity is gained in these situations because no new receptors in the space can contribute to the ligand’s promiscuity as a result of its orientational freedom. In these cases, the first criterion is satisfied, but the second one is not. Conversely, a ligand with one highly charged face and one hydrophobic face is expected to have very different minimum values corresponding to these two orientations; in this case, while the second criterion might be satisfied, the first one is not. Therefore, one might expect asymmetric and fairly — but not completely — hydrophobic ligands to gain the most promiscuity once orientational freedom is introduced.

Figure 11.

Effect of ligand orientational freedom (multiple binding modes): (a) Free energy paraboloids for multiple binding orientations of a hypothetical ligand to a set of identically-shaped receptors in an unbounded charge space. The thick, solid trace represents the zero temperature limit of the binding energy of the ligand to receptors bearing the corresponding charge distrbutions. This ligand is able to achieve increased promiscuity by binding to members of the receptor panel in two distinct modes. (b) Plot of promiscuity against ligand hydrophilicity for model ligands allowed to bind in shape-invariant orientations to a set of identically-shaped receptors in an unbounded charge space.

Numerical Experiment

Each of the 625 ligands was rigidly docked in its four shape-invariant orientations into each of the receptors in the control system, and the binding free energy in each orientation was calculated. The graphical view explained above did not account for the entropy due to these four binding modes at nonzero temperatures. To include this component of entropy, we calculated the binding partition function for each ligand over its i orientations (i = 4 in this case), noting that the unbound state is invariant:

$$Q=\sum _i{e}^{-\frac{\Delta G_{\mathrm{bind},i}^0}{kT}}$$ (10)

The free energy of binding in this system is then

$$\Delta G_{\mathrm{bind}}^0=-kT\ln Q.$$ (11)

T was set to 300 K. We did not remove duplicate bound states resulting from orientational symmetry from our calculations, as actual biological molecules would likely have isotopic variation or more realistic geometries that would break perfect symmetry. Figure 11b shows the Π₃ of each ligand in this system against its desolvation penalty. As expected, the extremely hydrophobic and hydrophilic ligands showed the lowest promiscuities once orientational freedom was introduced. The most promiscuous molecules still had a relatively low desolvation penalty. these molecules generally had alternating charges that break symmetry, such that by reorienting themselves, they could bind well to a completely different set of receptors with nearly the same affinity.

3.8 Multiple Factors in Combination

In this work, we created a control system based on several assumptions about the ligands, receptors, and their interactions. Each assumption was loosened in turn to probe various molecular determinants of binding specificity individually. We now loosened multiple assumptions simultaneously, to simulate a more realistic picture of ligands in a biological environment. Our system here contained a finite set of differently-shaped receptors. Ligands had varied conformational flexibility, translational, and orientational freedom with respect to the receptors, and the ionic strength of the system was nonzero. We did not vary ligand size here because this would result in an exponential increase in the number of Poisson-Boltzmann calculations needed; we presumed that the trends for ligand size would not be different from what was seen when ligand size was varied in the control system, i.e. larger ligands would be less promiscuous than smaller ligands.

Numerical Experiment

This numerical experiment combined various aspects of the previous numerical experiments shown above. Each of the 625 ligands was allowed to exist in 9 unbound conformations and 25 bound conformations, as outlined above in the section on conformational flexibility. Ligands were allowed to bind in 4 different orientations to the receptor, also detailed in the appropriate section above. Now, however, because the ligands were flexible, these orientations were not shape-invariant, so the van der Waals and SASA energies associated with each appropriate shape, as well as the coresponding L, C, and R matrices, were used as necessary. The charge space of the receptors was bounded exactly as was done in the appropriate section above, and all 144 receptor shapes were used, for a total of 82,944 receptors. The ionic strength of the system was 0.145 M.

Figure 12 shows the Π₃ for the 625 ligands, plotted against their desolvation energies. There is a very strong trend — with the Π₃ of many of the most hydrophobic ligands equal to the total number of receptors and falling off rapidly as hydrophilicity increased. This final system captures many relevant characteristics of an actual biological environment: flexible ligands encounter a panel of differently-shaped receptors in an aqueous, ionic environment, and they are free to bind to these receptors in multiple orientations. We have demonstrated that in this system, hydrophobic molecules are far more promiscuous than their charged counterparts, and we have systematically explored the physical reasons for this result. In addition, a similar trend holds for absolute affinity in this system (Figure 12), suggesting that polar and charged ligands not only bind to molecules more specifically, but they also bind to a select few with high absolute affinity.

Figure 12.

(a) π₃ of ligands plotted against their desolvation energies (when in the conformation taken by their rigid counterparts). In this system, ligands and bound states are conformationally flexible, and ligands can bind in any of four orientations to receptors, as described in the text. The receptors have bounded charge magnitudes at each basis point and differ in shape, also as described in the text. The ionic strength is 0.145M. The total number of receptors in the system is 82,944. Some of the most hydrophobic receptors have promiscuity values of 82,944 - that is, they bind to all receptors in the space with affinities that lie within a 3 kcal/mol spread. (b) C₋₃ is plotted against ligand desolvation penalty for this system.

4 Conclusions

Through developing a unified physical framework, we have systematically analyzed the effect of several ligand and receptor properties on binding promiscuity. In general, our results are in agreement with case-specific studies from the literature: hydrophobic, small, and asymmetric molecules are generally more promiscuous. Our study provided physics-based explanations and numerical experiments for understanding these trends. In addition, we surprisingly found that conformational flexibility can increase the specificity of polar and charged ligands, and this is because they can achieve high affinities to a few partners by trading off unfavorable van der Waals interactions for favorable electrostatic interactions. The sensitivity of this trade-off was found to be important, and understanding this trade-off more will be important for future computational design and analysis efforts on specific systems.

This study focused on the physics of binding interactions by using model molecules that were free from the constraints of chemistry. By separating the physics from such contraints, a systematic analysis of the determinants of specificity and promiscuity was achieved on a physical level. However, the constraints imposed by chemically reasonable charge distributions and shapes can potentially affect some of the conclusions here. Such chemically realistic models will eventually be necessary to yield specific insights that can be directly applicable to drug design applications; the work developed here is intended to provide an initial foundation for such practical applications.

While there is plenty of precedent to support the analysis presented here, there are also interesting apparent exceptions. For example, staurosporine, a kinase inhibitor with extremely broad recognition⁷⁴, is neither small nor very hydrophobic, and so it clearly does not possess the general characteristics shown here to lead to promiscuity. However, ATP-binding sites of kinases comprise a very small, highly-concentrated region of receptor charge space complementary to ATP, smaller than the range of variability considered here. It would be interesting in future work to analyze the kinase “charge space” on its own, within the framework developed here and to determine whether staurosporine’s optimal binders lie in the center of this subspace. Moreover, a rationalization of staurosporine’s large size will require a careful delineation between promiscuity and coverage as defined here, as it can be argued that staurosporine’s broad recognition is more a statement about its coverage than its promiscuity. In our model systems, larger ligands had lower coverage values because their increased nonpolar interactions were not enough to overcome the desolvation penalty incurred by the receptors. An analysis of this trade-off in kinase binding sites will shed light on the effect of molecular size on molecular recognition in this special system. Such an analysis could also provide a complementary perspective on the observed increased specificity of a methylated (and therefore larger) staurosporine analog toward Src kinase, which has been attributed to its dehydration of a nonconserved pre-formed kinase intramolecular hydrogen bonding pair upon binding⁷⁵.

Finally, one limitation of this study was the small degree to which molecular shapes varied as well as the small shape changes incurred by the modeled conformational flexibility; the binding sites of actual biological molecules show great diversity in shape and mobility. It remains to be seen if numerical experiments involving very large molecular rearrangements and shape variation will qualitatively agree with the conclusions of the numerical experiments shown here. In future work, a model with such additional features will add further dimensions to our understanding of the physicochemical determinants of binding specificity. Overall, this work introduced an expandable framework that allows for explanation and understanding of the physical determinants of specificity, and it provides for a mechanism to interpret future case studies of specificity and promiscuity.