Abstract
Accurate computation of free energy changes upon molecular binding remains a challenging problem, and changes in configurational entropy are especially difficult due both to the potentially large numbers of local minima, anharmonicity, and high-order coupling among degrees of freedom. Here we propose a new method to compute molecular entropies based on the maximum information spanning tree (MIST) approximation that we have previously developed. Estimates of high-order couplings using only low-order terms provide excellent convergence properties, and the theory is also guaranteed to bound the entropy. The theory is presented together with applications to the calculation of the entropies of a variety of small molecules and the binding entropy change for a series of HIV protease inhibitors. The MIST framework developed here is demonstrated to compare favorably with results computed using the related mutual information expansion (MIE) approach, and an analysis of similarities between the methods is presented.
Keywords: maximum information spanning trees (MIST), mutual information expansion (MIE), Bethe approximation, configurational entropy
Introduction
A fundamental goal of computational chemistry is the calculation of changes in thermodynamic properties for physical processes, such as chemical potential, enthalpy, and entropy changes. Accurate calculation of such properties can enable computational design and screening at a scale infeasible experimentally, and provides tools for detailed computational analysis of molecules and processes of interest. Design work often focuses on evaluating single configurations in the bound and unbound state, frequently representing the global minimum energy conformation, for instance; however, after filtering out infeasible candidates, additional effort may be warranted to investigate configurational ensemble properties, with significant corrections resulting from entropic or en-thalpic sources possible.1–3 This work, as well as recent experimental studies using NMR, has so far highlighted the importance of configurational solute entropy in a variety of systems.1,4 As such, improving the accuracy and speed of molecular ensemble based calculations, particularly in larger systems, is an area of active research.
One class of approaches for computing configurational averages centers around the use of sampling based simulations, such as molecular dynamics (MD) and Monte Carlo. Such methods may be particularly well suited for larger systems, including proteins, where explicit enumeration and characterization of all relevant minima is infeasible.2 One of the better known methods in this field is the quasiharmonic approximation, which approximates the system as a multidimensional Gaussian using the covariance matrix computed across aligned simulation frames.3 While successful in many cases, the quasiharmonic approximation has been shown to significantly overestimate entropies in systems containing multiple unconnected minima, which are poorly modeled by a single Gaussian.5,6 Recent phrasings have instead focused on more directly estimating probability densities over the configurational space of a molecule using the frames from MD simulations.2,7 As system size grows, however, direct estimation of the density over all molecular degrees of freedom (DOF) becomes infeasible, due to exponential scaling of the sampling requirements with respect to the effective dimensionality of the system.8
While estimates of the probability distribution over all DOF of reasonably-sized molecules generally cannot reach convergence given current sampling capabilities, the distributions over each individual DOF, or the joint distribution for groups of small numbers of DOF at a time may converge with the sample sizes accessible from MD simulations.9 Because of this, recent directions have focused on taking advantage of the entropies computed over these subsets (also called marginal entropies). In general, the motiviation for such methods is to combine these well-converged low-order marginal entropies of pairs or triplets of DOF in a molecule to provide an approximation of the ensemble properties of the full molecular system; rather than estimating higher-order contributions directly, they are approximated from low-order terms or neglected through assumptions of the theory. Essentially, these methods effect a trade-off by introducing errors due to theoretical approximations, yet recouping enhanced convergence by avoiding direct estimation of the high-order terms. A net benefit results if the approximation errors introduced are smaller than the estimation (convergence) errors avoided.
One such method is the mutual information expansion (MIE) approximation, recently developed by Gilson and co-workers, which enables approximation of configurational entropies as a function of lower-dimensional marginal entropies.2 This method expresses the configurational entropy of a system as a series of couplings between all possible subsets of degrees of freedom, placed in order from lowest to highest order. To provide a low-order approximation, and typical for an expansion, MIE assumes the higher-order terms expressed in its expansion can be neglected and truncates all couplings including a large number of DOF (generally omitting all sets of 4 or more DOF). The MIE framework has proved accurate in the analysis of a variety of small-molecule systems, 2 and it has been combined with nearest-neighbor methods to improve convergence.10 It has also been used in the analysis of side-chain configurational entropies to identify residue–residue coupling in allosteric protein systems.11
In parallel work developed in the context of gene expression and cell signaling data, we have generated a similar framework, maximum information spanning trees (MIST), that provides an upper bound to Shannon’s information entropy as a function of lower-order marginal entropy terms.12 For multiple synthetic and biological data sets, we found that, in addition to acting as a bound, the MIST approximations generated useful estimates of the joint entropy. Due to the mathematical relationships between information theory and statistical mechanics, application of MIST to the calculation of molecular entropies proved feasible with relatively little adaptation. While similar in spirit to MIE, MIST represents a distinct framework for approximating high-dimensional entropies by combining associated low-order marginal entropies. In particular, whereas MIE explicitly includes all couplings of a particular order in the approximation (e.g., accounting for the couplings between all pairs of DOF), MIST chooses a subset of the same couplings to include so as to maintain a guaranteed lower bound on the entropic contribution to the free energy. In effect, MIST can be thought to infer a model of relevant couplings between molecular degrees of freedom and only include these couplings in the approximation.
Here we examine the behavior of MIST when used to calculate molecular configurational entropies from MD simulation data and also in the context of idealized rotameric systems. The behavior of MIST is compared directly to MIE in both of the scenarios for a number of systems, and exaplanations for the differences between the two methods are explored.
Theory
In this section, we review the Maximum Information Spanning Tree (MIST) approximation in the context of configurational entropies. Further details of MIST have been published previously in the context of analyzing mRNA expression data for cancer classification.12 In addition, we highlight the theoretical differences between MIST and MIE. In both cases, the goal is to generate an approximation to the confiugrational entropy of a molecule by combining marginal entropy terms calculated over subsets of the degrees of freedom. In so doing, one seeks to introduce a small approximation error, in favor of faster convergence relative to calculations over all degrees of freedom.
The information theoretic phrasing of the calculation of configurational entropies has been well described previously.2 The key step of the phrasing comes from representing the partial molar configurational entropy, S°, of a molecule as
| (1) |
where R is the gas constant, T is the absolute temperature, C° is the standard state concentration, and ρ is the probability density function (PDF) over the configurational degrees of freedom, r. For the purposes of this report, r is represented in a bond–angle–torsion (BAT) coordinate system, as opposed to Cartesian coordinates. BAT coordinates tend to be less coupled than Cartesian coordinates for molecular systems and are thus well suited for low-order approximations.13 The first term on the RHS represents the entropic contribution of the six rigid translational and rotational degrees of freedom and is found via analytical integration, assuming no external field. When negated, the second term can be recognized as the continuous Gibbs entropy,14 which is also identical to RT times the continuous information entropy, S, as described by Shannon,15 providing the equation
| (2) |
| (3) |
This relationship allows techniques developed in the context of information theory to be used for the calculation of configurational entropies. Also note that here we generally report the configurational entropy contribution to the free energy or free energy change (−TS° or −TΔS°), which we refer to as the entropic free energy (change).
The MIST framework provides an upper bound to the information entropy using marginal entropies of arbitrarily low order. The approximation arises from an exact re-expression of the entropy as a series of conditional entropies, or alternatively, as a series of mutual information terms,
| (4) |
| (5) |
where Ii (ri; r1,…,i−1) is the mutual information (MI) between DOF ri and all DOF that have already been included in the sum. Throughout this section, subscripts on S or I are included to indicate the order of the term (i.e., the number of dimensions in the PDF needed to compute the term). Notably, while these MI terms are functions of probability distributions of dimension i, they are still pairwise mutual information terms between the single variable ri and the set of variables represented by r1,…,i−1, in contrast to the multi-information terms employed in the MIE expansion. As a result, these high-dimensional terms maintain key properties of mutual information, including non-negativity.16 The MI phrasing can be thought of as adding in the entropy of each DOF one at a time (S1 terms in Eq. (4)), then removing a term corresponding to the coupling between that DOF and all previously considered DOF (Ii terms).
The MIST approximation consists of limiting the number of DOF included in these information terms. For example, for the first-order approximation, all coupling is ignored, and the I term is completely omitted from the formulation. By the non-negativity of MI,16 the first-order approximation is thus an upper bound to the exact entropy
| (6) |
where the superscript MISTi indicates the MIST approximation of order i.
For the second-order approximation, when each DOF is added, its coupling with a single previously chosen DOF is accounted for, as opposed to considering the coupling with all previously included terms
| (7) |
Comparing Eq. (4) to Eq. (7), one can see that the I2(ri; rj) replaces Ii (ri; r1,…,i−1) in the summation. This replacement provides the upper-bounding behavior of MIST2 due to the fact that I(ri; rj) ≤ I(ri; rj, rk), for all vectors ri, rj, and rk.16 Additional discussion and demonstration of this relationship can be found in the supplementary information.
To generate approximations of arbitrarily high order k, we include an increasing number of DOF in the mutual information term,
| (8) |
where rj is a vector of length k′ −1 representing any subset of DOF ∈ {r1, … , ri−1}. As with Eq. (7), the bounding properties of the approximation are guaranteed by the fact that including additional DOF in the MI terms can not decrease the information.
The ordering of terms to consider in the summation over i, and the terms included in the MI terms, j, in Eq. (7) and Eq. (8) may impact the resulting approximation. Because any choice of ordering and information terms will still result in an upper bound to the true entropy, the choices that minimize this expression will provide the best approximation. For small systems, exhaustive enumeration of ordering of indeces and information terms may be feasible, but for larger systems, an optimization method is called for. Here, we have chosen to employ a greedy selection scheme that maximizes the information term selected in each step of the summation,
| (9) |
| (10) |
Thus, a third-order approximation is constructed by stepping through each degree of freedom in sequence and adding the S1 (ri) one-dimensional entropy for that degree of freedom to and subtracting one pairwise third-order mutual information term I3 (ri; rj) from the accumulated sum. The term subtracted is the one that gives the largest mutual information between the current DOF ri and a pair of previously considered DOF rj; for the first DOF considered there is no mutual information term, for the second degree of freedom the mutual information term is just the second-order mutual information between the second and first DOF I2 (r2; r1), and for the third degree of freedom there is no choice in the pairwise third-order mutual information term as there is only one possibility. Higher-order approximations are constructed in the same manner, but the bulk of the pairwise mutual information terms are order k for a k-th order approxmation, with lower-order mutual information terms used for the first k−1 DOF considered.
In the context of approximations to thermodynamic ensemble properties, MIST bears a strong resemblance to the Bethe free energy (also known as the Bethe approximation).17 In fact, the second-order MIST approximation is equivalent to the Bethe approximation, and the full MIST framework may thus be thought of as a high-order generalization of the Bethe free energy. While a full comparison of MIST and the Bethe approximation is outside the scope of the current work, a number of modifications and applications of the Bethe approximation have been explored that may be extensible to MIST.18,19
In contrast to MIST, MIE2 expands the entropy as a series of increasingly higher-order information terms, as previously formulated by Matsuda:20
| (11) |
where M is the multi-information, defined as
| (12) |
and the second summation runs over all possible combinations of k DOF from the full set of {r1, … , rn}. Note that for n = 1, the multi-information is equivalent to entropy, and for n = 2, it is equivalent to the mutual information defined in Eq. (5). MIE generates a kth-order approximation to the full entropy by truncating all terms of order larger than k in Eq. (11). The approximation will converge to the true entropy when no relationships directly involving more than k DOF exist in the system. Notably, MIE does not carry any bounding guarantees, but it does not require the optimization utilized in MIST.
Despite relying on different expansions, MIST and MIE share many similarities. The first-order approximation is identical in both cases (summing all first-order entropies). For the second-order approximation, MIE adds in all first-order entropies and subtracts off all possible pairwise mutual information terms,
| (13) |
In contrast, MIST adds in all first-order entropies, and then subtracts off n−1 of the information terms (where n is the number of DOF in the system), as is seen in Eq. (9). These terms are chosen to account for as much information as possible, while still guaranteeing an upper bound. The second-order approximations highlight the theoretical differences between MIST and MIE. Whereas MIE removes all pairwise couplings, effectively assuming that that all couplings are independent of each other, MIST removes a subset of couplings, effectively assuming a network of higher-order dependencies in which each DOF is primarily coupled to the system through a single dominant interaction. In particular, MIST can provide a good approximation if the majority of the degrees of freedom in the system are directly coupled only to a small number of other DOF. Such a system can be well covered by the n−1 terms included in MIST. The maximization procedure leading to the tightest upper bound effectively selects these direct couplings when sufficient data exist to accurately estimate their relative magnitudes.
In contrast, MIE may not provide a good approximation in such a system due to indirect couplings that are likely to exist between DOF, and must be removed by higher-order terms. These indirect couplings arise when the configuration of a DOF is coupled to a second DOF only through its interactions with a third intermediate DOF. In such a case, all three DOF will exhibit pairwise coupling with each other, as well as a strong third-order coupling. In MIE, these high-order couplings may be missed, whereas in MIST, one of the pairwise terms may be omitted, providing the possibility for a good approximation of highly coupled triplets of DOF, even when using a second-order approximation. Alternatively, in systems containing a larger number of direct pairwise interactions and relatively few higher-order couplings, MIST may provide a poor approximation relative to MIE. Given these differences in representation, we have performed a series of computational experiments to evaluate the performance of MIST and MIE in a variety of molecular systems, which have helped to reveal how coupled coordinates contribute to configurational entropy.
Methods
Molecular dynamics simulations of small molecules
All molecular dynamics simulations were run using the program CHARMM21,22 with the CHARMm22 all-atom parameter set.23,24 Partial atomic charges were fit using the RESP procedure25,26 and the program GAUSSIAN 03,27 with the 6–31G* basis set.26 All simulations were run at a temperature of 1000 K using a distance-dependent dielectric of 4r with a 1-fs time step, Langevin dynamics, and the leapfrog integrator. A 1-ns equilibration was performed prior to a 50-ns production run from which frames were extracted at a frequency of 1 frame per 10 fs, yielding 5 million frames per simulation.
For each molecule, an internal coordinate representation was chosen in the BAT framework. The internal coordinate representation consisted of the selection of three seed atoms, as well as a single bond, angle, and torsion term for each subsequent atom so as to use improper dihedrals whenever possible, and to place heavy atoms prior to hydrogens. Improper torsions were selected to produce an effect similar to the phase angle approach used by Abagyan and co-workers and Gilson and co-workers.2,28 Only bond, angle, and torsion terms between chemically bonded atoms were allowed as coordinates. Other than these restrictions, the specific coordinates were chosen arbitrarily. The values of each bond, angle, and torsion were extracted from the simulations and binned. Marginal PDFs of all single, pairs of, and triplets of coordinates were computed using the frequencies from the simulation. These PDFs were then used to compute the first-, second-, and third-order entropies and information terms. All first- and second-order terms were computed using 120 bins per dimension, and all third-order terms were computed using 60 bins per dimension. In both cases, the ranges of the bins were defined by the minimum and maximum value observed in the simulation. For MIE, third-order information terms containing any bond or angle DOF were set to zero, as was done previously to improve convergence.2 For MIST, all third-order terms were included, as doing so did not dramatically impact numerical stability. All calculations included a Jacobian term of where bi and θi are the bond length and bond angle used to place atom i, and the product runs over all DOF included in the marginal term.
Mining minima implementation
In order to enable comparison to the Mining Minima (M2) method using our specific parameters and energy function, we implemented a version of the method within CHARMM consistent with the original method as described.1,29 Briefly, a list of candidate minima was first identified by combinatorially combining all observed minima in each torsional degree of freedom from the MD simulations. Each minimum was then further minimized in CHARMM and duplicates were omitted. For each remaining minimum the Hessian was computed in Cartesian coordinates in CHARMM and converted to the same BAT coordinate system used for analysis with MIST. The energy of each minimum was also extracted. The BAT Hessians were diagonalized, and the product of the eigenvalues computed, with a correction applied to include no more than 3 standard deviations or 60° in any dimension along each eigenvector. Modes with force constants less than 10 kcal/mol were also integrated numerically to check for anharmonicities. For the current work, no modes were found to differ from the harmonic approximation by more than 1 kcal/mol, so the integrated results were not used in the final calculation. Finally, the ensemble average energy was computed and subtracted from the potential to yield the entropic contribution to the free energy, −TS.
Discrete rotameric treatment of HIV protease inhibitors
Discrete rotameric systems representing four candidate HIV protease inhibitors, either unbound or in the binding pocket of a rigid HIV-1 protease were generated. Each system consists of the 5 × 104 lowest-energy rotameric configurations, accounting for > 99% of the contributions to the free energy at 300 K in all cases. For the current work, these 5 × 104 configurations were treated as the only accessible states of the system, enabling exact calculation of all ensemble properties.
The low-energy configurations were determined via a two-step, grid based, enumerative configurational search. All ligands are comprised of a common chemical scaffold with potentially variable functional groups at 5 possible positions (see Figure 5). We first collected an ensemble of low-energy scaffold conformations using an enumerative Monte Carlo (MC) search. Ten independent simulations of 5 × 104 steps were performed for each ligand in both the bound and unbound states, and the external and scaffold degrees of freedom of all collected configurations were idealized to a uniform grid with a resolution of 0.1 Å and 10° or 20° (bound or unbound state, respectively). All simulations were performed using CHARMM21 with the CHARMm22 force field30 and a distance-dependent dielectric constant of 4r. The result of the first step was a set of energetically accessible rotameric scaffold configurations.
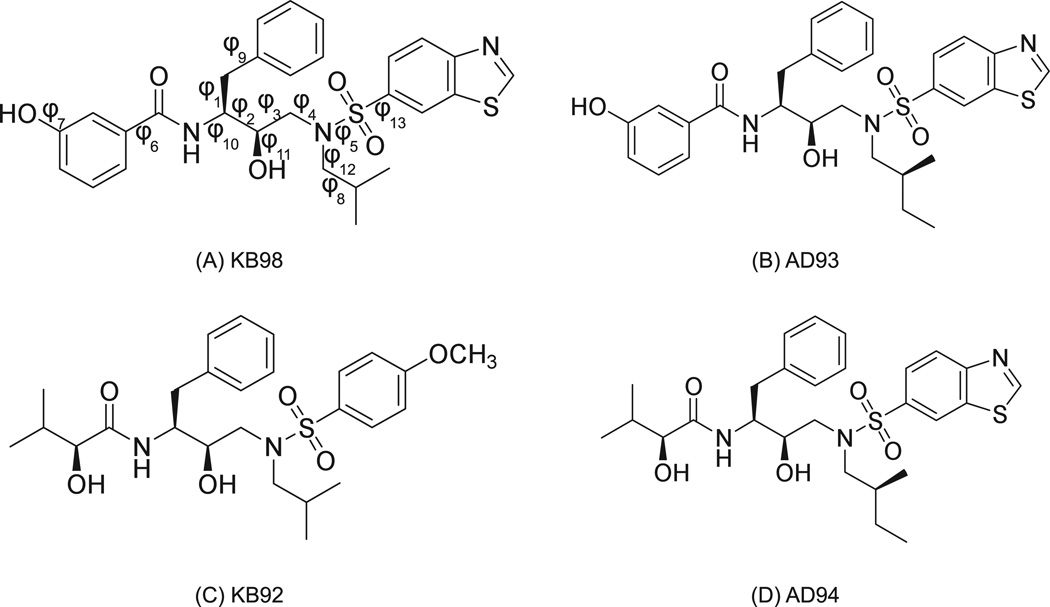
Figure 5. Chemical structures of HIV-1 protease inhibitors.
The four molecules shown were previously designed as candidate HIV-1 protease inhibitors.35 For the current work, idealized rotameric systems in which the exact energies of 50,000 rotameric states were generated in both bound and unbound states, as described in Methods. All torsional degrees of freedom for each inhibitor were rotamerized, and all other DOF (bonds, angles, impropers) were fixed to idealized values. In the bound state overall translations and rotations (external DOF) were also enumerated. Torsions about the bonds labeled in (A) correspond to numbering used in Figure 8.
The second step exhaustively searched the configurational space of the remaining functional group degrees of freedom for each collected scaffold using a combination of the dead-end elimination (DEE)31–33 and A* algorithms34 as described previously.35 For high throughput energy evaluations, a pairwise decomposable energy function was used that included all pairwise van der Waals and Coulombic, intra- and inter-molecular interactions, computed with the CHARMm22 force field and a distance-dependent dielectric. Uniformly sampled rotamer libraries for each functional group with resolutions of 15° or 60° for the bound or unbound states, respectively, were used. The 5 × 104 lowest-energy configurations across all scaffolds were enumerated and their energies computed.
These lowest-energy configurations from each ensemble were re-evaluated using a higher resolution energy function to account for solvation effects and to obtain a more accurate estimate of the energy. The enhanced energy function included all pairwise van der Waals interactions, continuum electrostatic solvation energies collected from a converged linearized Poisson–Boltzmann calculation using the Delphi computer program,36,37 and solvent accessible surface area energies to model the hydrophobic effect.38 Solvation energies were calculated using an internal dielectric of 4 and a solvent dielectric of 80. A grid resolution of 129 × 129 × 129 with focusing boundry conditions39 was used, along with a Stern layer of 2.0 Å and an ionic strength of 0.145 M.
Given the energies of all configurations in the idealized rotameric systems, entropies of arbitrary order were computed analytically by integrating through the Boltzmann distribution determined from the 5 × 104 molecular configurations included in the ensemble. To evaluate the convergence properties of the metrics in the context of the discrete rotameric systems, we randomly drew from the 5 × 104 structures representing each system with replacement according to the Boltzmann weighted distribution. The resulting samples were then used to estimate the single, pair, and triplet PDFs as for the MD systems. Because the exact marginal entropies are analytically computable, convergence for these systems was examined with respect to the same approximation computed using the analytically-determined marginal terms. No symmetry adjustments were applied for the discrete systems.
Results
Molecular dynamics simulations of small molecules
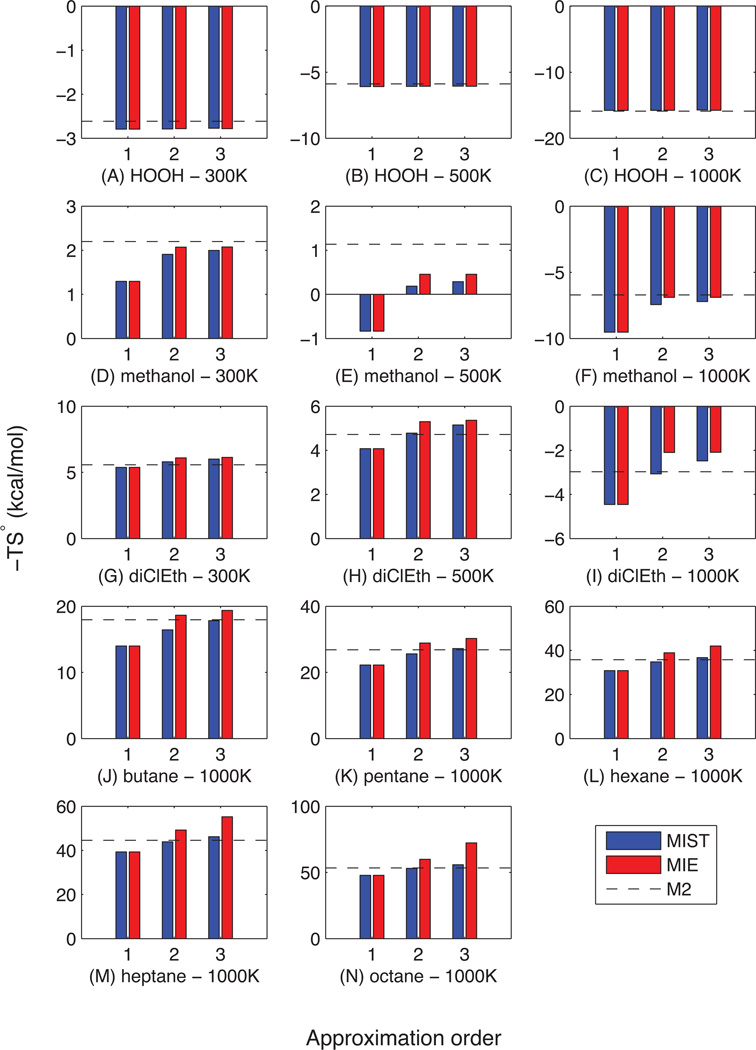
To investigate the behavior of the MIST framework in the context of configurational entropies, we first examined a set of small molecules including hydrogen peroxide, methanol, 1,2-dichloroethane, and linear alkanes ranging in size from butane to octane. Configurational entropies for all of these systems have been previously computed using MIE and were shown to agree well with M2 calculations. 2 As was done in those studies, we collected 5 × 106 frames from a 50-ns molecular dynamics trajectory for each molecule and computed the single, pair, and triplet entropies of all BAT degrees of freedom as described in Methods. We then combined these marginal entropies according to the MIST (Eq. (8)) or MIE (Eq. (11)) framework, using approximation orders of one, two, or three. The resulting values for the entropic contribution to the free energies, −TS° (computed using Eq. (2)), are shown in Figure 1, where they are compared to the gold standard estimation from the M2 method.
Figure 1. MIST and MIE results for small alkanes.
Hydrogen peroxide, methanol, 1,2-dichloroethane and five linear alkanes ranging in size from butane to octane were simulated using MD, and the resulting 5 × 106 frames were used to estimate the marginal entropies. These entropies were then combined according to MIST (blue bars) or MIE (red bars) to generate the first-, second-, or third-order approximation to the configurational entropy of each molecule. Results are compared to calculations using the Mining Minima method (dashed black line).
As seen in the previous studies using MIE (red bars), the second-order approximation (MIE2) shows good agreement with M2 (dashed line) for all molecules, particularly the smaller systems. MIE3 generally shows similar agreement with M2 for the small molecules and worse agreement (> 10 kcal/mol in some cases) for the alkanes, while MIE1 shows worse agreement in all cases. The MIST approximations (blue bars) show somewhat different behavior than MIE. As inherent in the theory, the first-order MIST and MIE approximations are identical. MIST2, shows somewhat larger deviations fromM2 for the smallest molecules compared to MIE2 but provides better agreement for 1,2-dichloroethane and the linear alkanes. Also, whereas MIE3 generally shows worse agreement with M2 than MIE2, MIST3 improves upon MIST2 for many systems, showing deviations from M2 less than 1.0 kcal/mol for all systems other than heptane and octane, where the deviations are 1.6 and 2.4 kcal/mol, respectively. While MIST3 is guaranteed to yield at least as accurate a result as MIST2 when both are fully converged, here we see that behavior in the context of finite sample sizes.
Convergence for small molecules
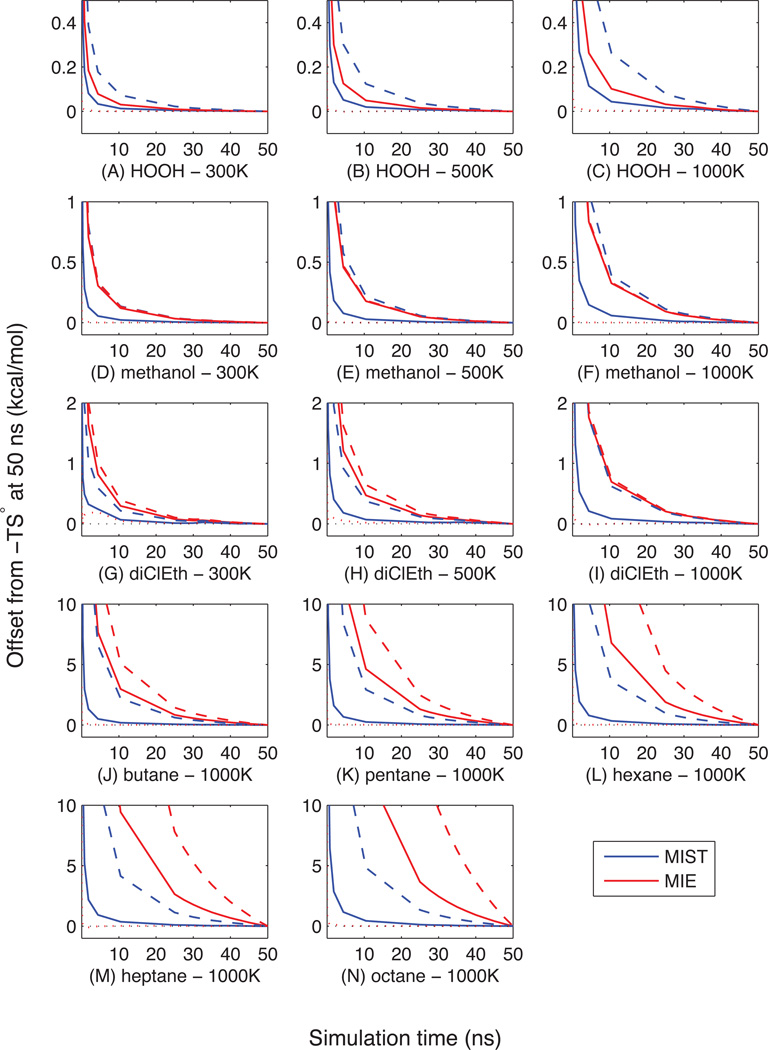
In addition to looking at the MIE and MIST values computed using the full 50-ns simulation, we also examined the behavior of the approximations when using only frames corresponding to shorter simulation times, obtained by truncating the existing simulations. Because each approximation order is converging to a different value and the fully converged values are not known, we track the approach to the value computed with the full 50 ns. The results are shown in Figure 2 and Table 1. For all systems, MIST2 (solid blue lines) exhibits faster convergence than MIE (red lines). While the third-order approximations (dashed lines) converge more slowly than the corresponding second-order ones (solid lines), MIST3 demonstrates comparable convergence to MIE2 for hydrogen peroxide, methanol, and 1,2-dichloroethane and faster convergence for the alkanes.
Figure 2. Convergence of MIST and MIE for small molecules.
MD simulations of various small molecules were subsampled to include frames corresponding to shorter simulation times, and the resulting sets of frames were used to compute the MIST (blue lines), and MIE (red lines) approximations. The convergence of first- (dotted line), second- (solid lines), and third-order (dashed lines) approximations is shown. Each line shows the deviation from the same value computed using the full 50-ns trajectory. MIE3 overlaps MIE2 for HOOH and methanol because each system contains only a single torsional term.
Table 1.
Change in estimation of −TS° from 40 ns–50 ns (kcal/mol)
| molecule | T (K) | MIST1=MIE1 | MIST2 | MIST3 | MIE2 | MIE3 |
|---|---|---|---|---|---|---|
| HOOH | 300 | −0.00 | −0.00 | −0.01 | −0.00 | −0.00 |
| HOOH | 500 | −0.00 | −0.00 | −0.01 | −0.00 | −0.00 |
| HOOH | 1000 | −0.00 | −0.00 | −0.02 | −0.01 | −0.01 |
| methanol | 300 | 0.00 | −0.00 | −0.01 | −0.01 | −0.01 |
| methanol | 500 | −0.00 | −0.00 | −0.02 | −0.01 | −0.01 |
| methanol | 1000 | 0.00 | −0.00 | −0.03 | −0.02 | −0.02 |
| diClEth | 300 | −0.01 | −0.01 | −0.02 | −0.02 | −0.03 |
| diClEth | 500 | −0.01 | −0.02 | −0.04 | −0.04 | −0.06 |
| diClEth | 1000 | −0.00 | −0.01 | −0.05 | −0.05 | −0.06 |
| butane | 1000 | 0.00 | −0.01 | −0.15 | −0.21 | −0.37 |
| pentane | 1000 | −0.01 | −0.03 | −0.20 | −0.34 | −0.64 |
| hexane | 1000 | 0.00 | −0.02 | −0.23 | −0.48 | −1.15 |
| heptane | 1000 | −0.01 | −0.03 | −0.29 | −0.68 | −2.01 |
| octane | 1000 | 0.00 | −0.03 | −0.34 | −0.93 | −3.67 |
Previous work showed that MIE3 was poorly converged for many of the alkanes, particularly the larger ones, as is observed here.2 Over the last 10 ns of the hexane, heptane, and octane simulations, the MIE3 estimate changes by 1.0–3.5 kcal/mol. Notably, the third-order MIE approximation already omits a number of terms to improve numerical stability (all three-way information terms containing a bond or an angle are set to zero). In contrast, the third-order MIST implementation shown here includes all of these terms, and still demonstrates significantly faster convergence. Though we have not explored higher-order MIST approximations for these systems, the good convergence of MIST3 suggests that fourth- or fifth-order approximations may be feasible.
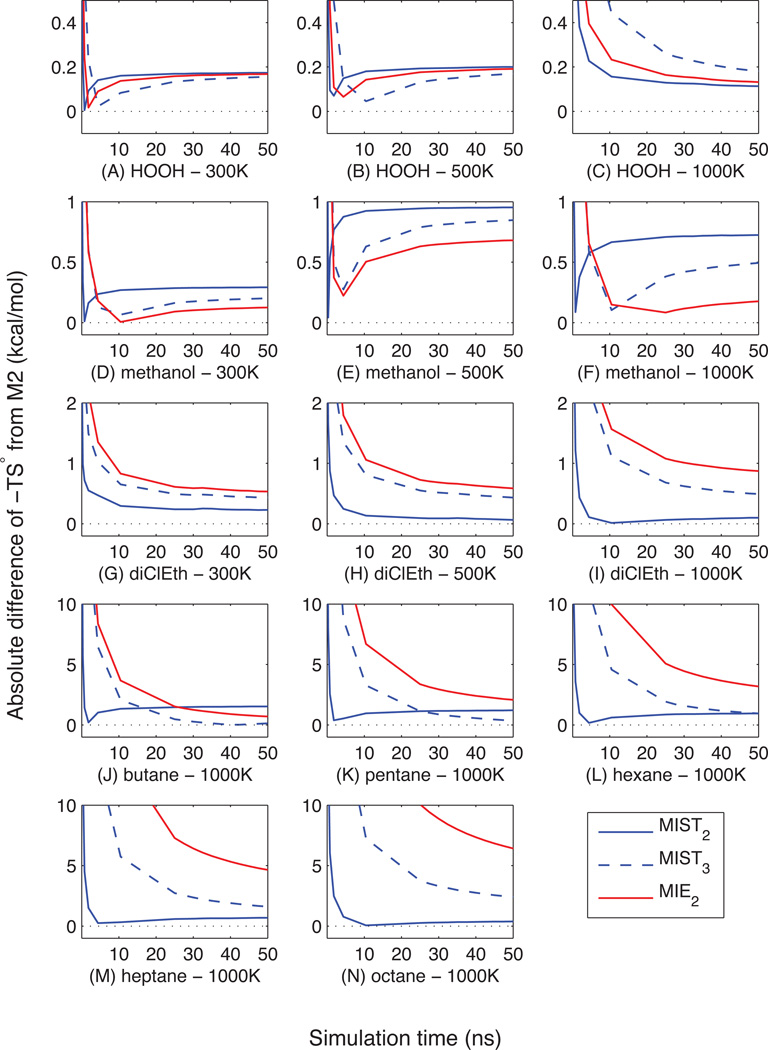
Taken together with the previous section demonstrating the agreement between MIST, MIE, and M2, the results show that sampling regimes may exist in which any of the MIE or MIST approximations give the smallest error. To gain a sense of how the approximations may behave in this regard, we can treat M2 as a comparison point. Although the M2 result may not be equivalent to the full entropy to which MIE and MIST would ultimately converge, treating it as a standard can be instructive about the combined behavior of the methods when weighing accuracy and convergence. To this end, Figure 3 shows the absolute error of the approximations as a function of simulation time when treating M2 as a gold standard.
Figure 3. Agreement with M2 across sampling regimes.
MIST (blue lines) and MIE (red lines) approximations were computed as a function of simulation times as described in Figure 2, and the absolute deviation from M2 results were plotted, demonstrating that different approximations provide the best agreement with M2 in different sampling regimes.
For hydrogen peroxide regimes exist for which MIST2, MIST3, or MIE2 provide the smallest error. In particular, the rapid convergence of MIST2 produces the best agreement with M2 for very short simulation times. With more samples MIE2 tends to reach adequate convergence to provide the best estimate until MIST3 converges to the point that it provides the closest agreement. For methanol, the faster convergence of MIST2 again provides the best agreement for small sample sizes before MIE2 converges to give the best agreement. Across 1,2-dichloroethane and the alkanes, MIST provides better agreement than MIE2. Either MIST2 or MIST3 provides the best agreement depending on the number of samples. In particular, MIST3 seems to provide better overall agreement with M2 when converged, but the fast convergence of MIST2 again creates regimes for which it demonstrates the best agreement. For heptane and octane (the largest systems examined here), MIST2 provides the best agreement even after 50 ns, possibly due to MIST3 having not fully converged.
Source of differences between MIE2 and MIST2 for small molecules
To understand the differences in accuracy and convergence between MIE and MIST, we examined the terms of the expansions that differ between the two approximation frameworks. In particular, for the second-order approximations, MIST2 includes a subset of the mutual information terms considered by MIE2, as can be seen by comparing Eq. (13) and Eq. (7). As such, these omitted terms are entirely responsible for the differences between the two approximations. The values of the terms used for both approximations when applied to butane are shown in Figure 4.
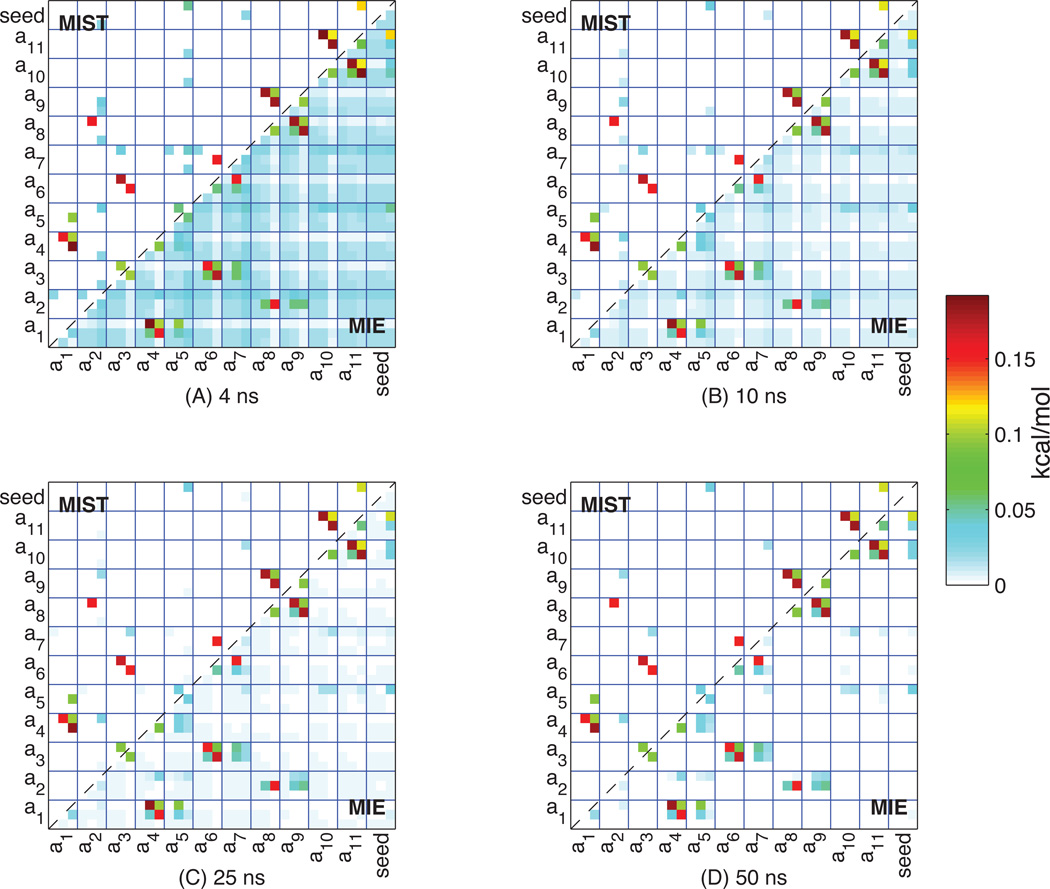
Figure 4. Convergence of MI matrix for butane.
The pairwise mutual information terms between all pairs of degrees of freedom in butane computed using the first (A) 4 ns, (B) 10 ns, (C) 25 ns, or (D) 50 ns are show in the lower triangles. The upper triangles indicate the terms that were chosen to be included in the second-order MIST approximation, according to Eq. (7). The dark blue lines separate the atoms from each other, with each atom being represented by three degrees of freedom associated with its placement (bond, angle, torsion from bottom to top and left to right in each box). All values are reported in kcal/mol.
For each plot, the lower triangle of the matrix shows the pairwise mutual information between each pair of degrees of freedom, all of which are included in the calculation of MIE2. The upper triangle shows the subset of these terms that are used by MIST2, chosen to minimize Eq. (7) while maintaining an upper bound on the entropy. Focusing on panel D, which shows the results using the full 50-ns simulation, one can see that most of the terms omitted in MIST2 are relatively low in value, whereas the high MI terms are included (to satisfy the maximization in Eq. (7)). Panels A–C show the same information computed over the first 4, 10, or 25 ns of the simulation, respectively. In contrast to the 50-ns results, the shorter simulations show dramatic differences between MIST2 and MIE2. While roughly the same set of terms is omitted by MIST2 in these cases as in the 50-ns case (because the largest MI terms come from the same couplings in the shorter and 50-ns calculations), the omitted terms are much larger, due to their relatively slow convergence. These plots indicate that slow convergence of MIE2 relative to MIST2 is a result of the many terms in the MI matrix that are slowly converging to very small values. In particular, because MI values tend to be consistently overestimated, the quadratic number of MI terms included in MIE2 slow convergence more than the linear number of MI terms included in MIST2. Furthermore, the terms that are included by MIST2 are the larger MI terms which tend to converge more quickly than small MI terms. For sufficiently short simulations neglecting these small and slowly converging terms (as done by MIST2) appears to be better than trying to estimate them (as done by MIE2).
To further examine the source of differences between MIST2 and MIE2, we looked at how much of the difference between the approximations was accounted for by terms of various sizes for the linear alkanes. The results of this analysis using the full 50-ns simulations are shown in Table 2. As suggested by Figure 4, much of the difference between MIST2 and MIE2 comes from the large number of omitted small terms. For example, for butane 39.9% of the 2.22 kcal/mol difference comes from MI terms with magnitudes less than 0.01 kcal/mol. Furthermore, the importance of these small terms grows as the system size increases, accounting for nearly 60% of the disparity for octane. Taken in conjunction with the slow convergence of these small terms, these results suggest that, while some real representational differences do exist between MIE and MIST, much of the difference may in fact be explained by differences in convergence, even at 50 ns.
Table 2.
Percentage of (MIE2 − MIST2) accounted for by terms of various magnitudes
| molecule | x ≥ 0.05 | 0.05 > x ≥ 0.01 | 0.01 > x ≥ 0.00 |
|---|---|---|---|
| butane | 29.7 | 30.4 | 39.9 |
| pentane | 28.4 | 30.1 | 41.5 |
| hexane | 24.4 | 26.7 | 49.0 |
| heptane | 19.5 | 26.3 | 54.2 |
| octane | 17.5 | 23.8 | 58.7 |
Discretized inhibitor molecules as an analytical test case
While the good agreement that both MIST and MIE show with the M2 results is an important validation step in evaluating the overall accuracy of the approximations, some fundamental differences in the methodology can make the results somewhat difficult to evaluate. There are two primary issues that can confound the interpretation. Firstly, M2 calculations and MD simulations represent similar but ultimately different energy landscapes. Whereas the MD landscape represents the exact energy function, M2 approximates the landscape by linearizing the system about a set of relevant minima. Although mode-scanning is employed to account for some anharmonicities in the systems, M2 still operates on an approximation of the energy landscape sampled during MD. As such, even given infinite samples, and without making any truncation approximations (i.e., directly generating ρ(r) for use in Eq. (1)), the entropy estimate would not necessarily converge to the M2 result. Secondly, because application of MIST and MIE relies upon estimating the low-order marginal entropies from a finite number of MD frames, it is difficult to separate the error introduced by the approximation framework from the error introduced by estimating the marginal terms.
To address these issues, we examined MIST and MIE in the context of a series of discrete rotameric systems in which the energy of all relevant states was calculated directly. Given this distribution of rotameric states, the full configurational entropy and all marginal entropies can then be computed exactly. As such, for these systems we can separately evaluate the approximation errors due to the MIST or MIE frameworks as well as sampling errors due to estimating the marginal terms; here the marginal terms are known exactly. These discrete ensembles were originally generated to analyze a series of candidate HIV-1 protease inhibitors,35 but their primary importance for the current work is as a test case in which entropies of arbitrary order can be computed exactly. The chemical structures of the four inhibitors are given in Figure 5. Additional details on the generation of these systems is described in Methods.
We employed eight different discrete ensembles, representing bound and unbound states of the four inhibitors. All bonds, angles, and non-torsional dihedrals were idealized and fixed, leaving 13–15 torsional degrees of freedom in each inhibitor. We also included an additional variable (referred to as external or ext) representing the six translational and rotational degrees of freedom in the bound cases to model the position of the inhibitor with respect to the rigid binding pocket. For each system we computed exactly all entropy terms containing 1, 2, 3, 4, or 5 degrees of freedom by marginalizing the full Boltzmann distribution of each ensemble, which consisted of the 5 × 104 lowest-energy molecular configurations. We then computed approximations to the total entropy of each system using either MIST or MIE. As such, we were able to examine the approximation error associated with both methods when the low-order terms are known exactly. The results are shown in Figure 6. For all eight systems the MIST approximations (blue lines, ×’ s) monotonically approach the full entropy (dashed black line) as the approximation order increases. All MIST approximations also provide a lower bound to the entropic free energy (or an upper bound to the associated Shannon entropy) when the low-order terms are known exactly. Both of these properties are guaranteed for MIST when the marginal terms are known exactly, so seeing them hold in our test system is important validation but not surprising. For all cases the second-order MIST approximation provides an estimate within 1.2 kcal/mol of the full analytic entropic free energy, with particularly good performance in the bound systems (top row of Figure).
Figure 6. Accuracy in rotameric systems.
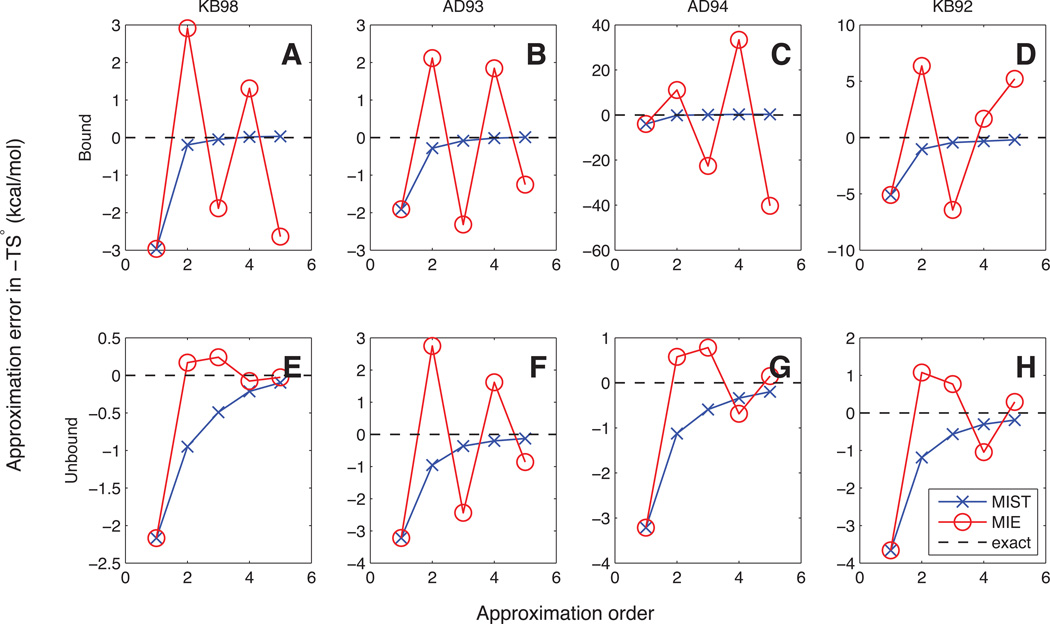
For each of the four inhibitors, either in the unbound state (bottom row), or in the context of a rigid binding pocket (top row), we computed the exact marginal entropies for all combinations of 1–5 torsions, according to the Boltzmann distribution across the 5 × 104 configurations representing each system. Using these exact marginal entropies we computed the MIST (blue lines) or MIE (red lines) approximations to the entropy (−TS°) of each system. The convergence as a function of approximation order is shown in comparison to the analytically determined entropy of the full system (dashed black line).
For the four unbound systems (bottom row of Figure 6), MIE (red lines, °’s) shows similar accuracy to MIST, generating a lower-error estimate once (KB98, panel E), a worse estimate once (AD93, panel F), and comparable error for two cases (AD94 and KB92, panels G and H). Unlike MIST, MIE is not guaranteed to monotonically reduce the approximation error as the order increases, and in some cases, such as unbound KB98 and AD94, the third-order approximation performs worse than the second-order one. In general, however, for the unbound cases the MIE approximations converge towards the true entropy as the approximation order is increased, with exact low-order terms.
In contrast to its performance in the unbound systems, MIE demonstrates erratic behavior in the bound systems. For all four inhibitors and all approximation orders, MIST results in considerably lower error than the corresponding MIE approximations. Furthermore, increasing the approximation order does not dramatically improve the performance of MIE in the bound systems, and actually results in divergent behavior for orders 1–5 in AD94 (panel C). Notably, the bound systems represent identical molecules to those in the unbound systems; the only differences lie in the level of discretization, and the external field imposed by the rigid protein in the bound state.
Convergence properties in discrete systems
Having investigated the error due to the MIST and MIE approximation frameworks in our analytically exact discrete systems, we next looked to explore the errors associated with computing the approximations from a finite number of samples. To do this we performed a series of computational experiments in which we randomly drew with replacement from the 50,000 structures representing each system according to the Boltzmann distribution determined by their energies and a temperature of 300 K. For each system we drew 106 samples, and estimated the PDF over the 50,000 states using subsets of the full 106. These PDFs were then used to compute the marginal entropies used in MIST and MIE. For each system this procedure was repeated 50 times to evaluate the distribution of sampling errors for the two methods.
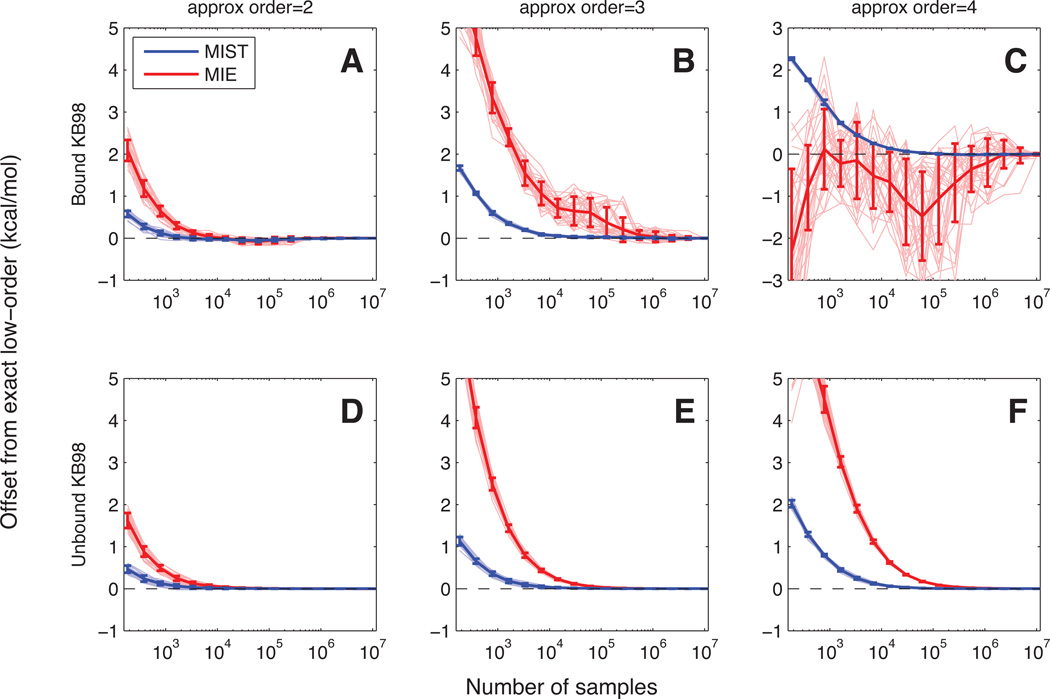
In order to quantify the sampling error separately from the approximation error (which we examined in the previous subsection), we compared the approach of each approximation to the value computed when using the exact low-order terms (i.e., we examined the convergence of each approximation to its fully converged answer, as opposed to the true joint entropy). The results for the bound and unbound KB98 systems are shown in Figure 7. Results for the other inhibitors were similar and are shown in Figures S1, S2, and S3. As expected, the lower-order approximations converge more quickly, as the low-order PDFs require fewer samples to estimate accurately. For the unbound case (bottom row), both MIE (red) and MIST (blue) exhibit consistent steady convergence for all 50 runs. For the bound case (top row), while MIST exhibits similar convergence behavior as in the unbound system, MIE shows much larger variations across the 50 runs. As with the MD analysis, MIST demonstrates considerably faster convergence than MIE for all approximation orders examined and all systems.
Figure 7. Convergence in KB98 rotameric systems.
For each of the eight idealized rotameric systems, we sampled with replacement from the 5 × 104 configurations representing the system, according to the Boltzmann distribution determined by the relative energies of each configuration. These samples were then used to estimate the marginal entropies of all combinations of 1–4 torsions prior to application of MIST (blue lines) or MIE (red lines) to compute −TS°. This procedure was repeated 50 times for each system, and the deviation of each run from the exact result to the same order approximation are shown (pale lines), as well as the mean and standard deviation across the 50 runs (thick lines). Results for bound (top row) and unbound (bottom row) KB98 are shown here. Results for other molecules were similar and can be seen in Figures S1, S2, and S3.
Source of differences between MIE2 and MIST2 for discrete systems
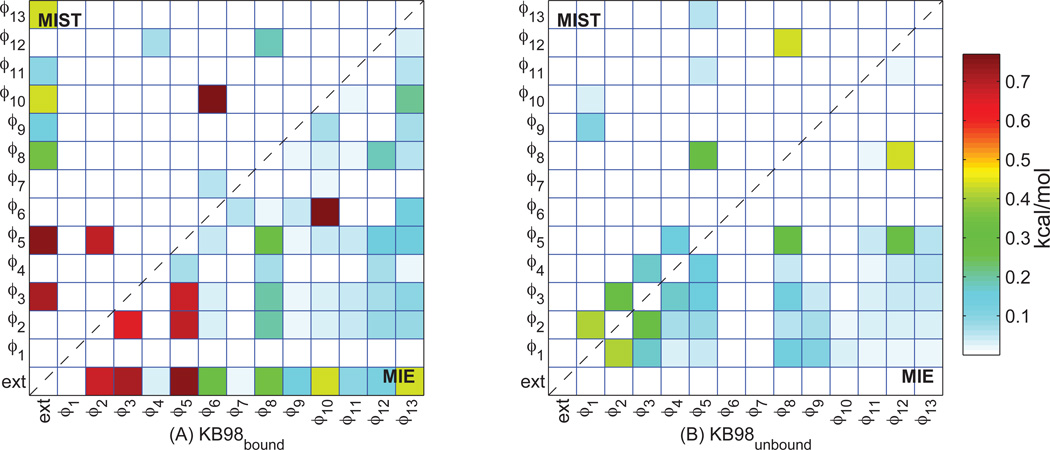
We next examined the MI terms accounting for differences between the two approximation frameworks. As with the analysis of the alkanes, the similarities between the second-order approximations enable a direct comparison of the MI terms that are included by MIE but omitted in MIST. Unlike the alkane studies, however, because the low-order terms can be determined directly for these discrete cases, the convergence errors, which played an important role in differences for the alkanes, can be eliminated in the current analysis. Doing so allows direct examination of the differences for the two approximation frameworks, independent of errors introduced due to sampling. The MIs between all pairs of degrees of freedom for bound and unbound KB98, as well as the terms chosen by MIST2 are shown in Figure 8.
Figure 8. MI matrix for discretized KB98.
The pairwise mutual information terms between all pairs of degrees of freedom (DOF) in (A) bound or (B) unbound KB98 are show in the lower triangles. The upper triangles indicate the terms that were chosen to be included in the second-order MIST approximation to −TS°, according to Eq. (7). All values are reported in kcal/mol. Numbering of DOF corresponds the labels in Panel A of Figure 5.
The results for the unbound case (panel B), for which MIE2 provides lower error, are qualitatively similar to those seen for the alkanes. Most of the differences between MIE2 and MIST2 in the unbound inhibitor arise from the omission of a number of relatively small terms, less than 0.2 kcal/mol each. The larger MI terms are all included in both approximations. In contrast, the differences between the two methods for the bound case come from a different source: MIST2 omits three of the seven largest MI terms in the bound system, together accounting for nearly 2 kcal/mol of the 2.91 kcal/mol difference between MIE2 and MIST2. In particular, whereas all six pairwise relationships among the external, ϕ2, ϕ3, and ϕ5 degrees of freedom show strong (and nearly equivalent) couplings, MIST2 only includes three of these terms.
The qualitative differences in the terms accounting for the disparity between MIST2 and MIE2 in bound KB98 compared the unbound KB98 and the alkanes may be particularly relevant given the relatively poor accuracy of MIE for the bound systems. The strong couplings between the four degrees of freedom of focus (external, ϕ2, ϕ3, and ϕ5), suggest a high-dimensional transition in which all four DOF are tightly coupled to each other and must change in concert to adopt different energetically relevant states. In particular, the values of the couplings, all of which are near RT ln2, are consistent with these four degrees of freedom together occupying two dominant states. Furthermore, the coupling between all subsets of three, and the full set of four DOF also are near RT ln2, further demonstrating the strong high-dimensional coupling between these four. Due to the structure of the MIE approximation, in which all low-order couplings are treated as independent from each other, a highly coupled system may result in errors due to the double-counting of low-order relationships. In contrast, the MIST approximation, which treats each DOF to be predominantly coupled to the system through a single low-order coupling, can appropriately describe such a highly-coupled system with a small number of effective states.
Discussion
Here we have examined the behavior of our Maximum Information Spanning Trees (MIST) approximation framework in the context of computing molecular configurational entropies. Though we originally developed MIST to pursue high-dimensional information theoretic phrasings in the analysis of experimental biological data, the generality of the method, coupled with the mathematical relationships between information theory and statistical mechanics, enabled application to molecular configurational entropy with relatively little modification. The adaptation of the method was largely inspired by the approach taken previously with the Mutual Information Expansion (MIE) method.2 We have compared to both MIE and the well established Mining Minima (M2) method in the context of MD simulations of a variety of small molecules. While MIE showed better agreement with M2 for some systems (notably methanol simulated at various temperatures), the MIST approximations tended to provide improved agreement, particularly for larger systems. Furthermore, for all but the smallest molecules, both MIST2 and MIST3 demonstrated faster convergence than the MIE approximations. While MIST3 seemed to provide the best converged answers across all systems, the fast convergence of MIST2 resulted in it providing better agreement in many sampling regimes, particularly for the larger alkanes. These results suggest that the MIST approximations are likely to be particularly useful in larger systems where simulation times may be limiting.
While the agreement with M2 is an important validation for the overall accuracy of the methods, it does not provide an ideal testing framework, as M2 and the MD simulations represent different energy landscapes. As such, separate examination of the errors due to approximation and sampling was not possible. To address this we also examined MIST and MIE in the context of a series of idealized rotameric systems for HIV protease inhibitors in which the exact entropies could be computed directly. In these systems, we observed that while MIE and MIST both showed good behavior in systems representing unbound molecules, MIE demonstrated poor accuracy in the more restricted bound systems, even for the fifth-order approximation with exactly determined marginal terms. In contrast MIST exhibited small approximation errors in the bound systems, even for the second-order approximation. Furthermore, when sampling from the known analytical distribution, the fast convergence of MIST relative to MIE seen in the MD systems was also observed for these discretized molecular systems.
In addition to improved convergence, MIST carries useful properties that are not shared by MIE. For fully converged systems, the approximation error of MIST is guaranteed to monotonically decrease with increasing approximation order. This behavior can be easily seen for the discrete systems in Figure 6, and stands in contrast to the behavior of MIE in the same systems. In application to novel systems where the behavior of the approximations is untested, this property means that the highest approximation order to have reached convergence provides the best estimate of the full entropy. In the absence of such a guarantee, it is unclear how to select the appropriate approximation order.
Furthermore, all converged MIST approximations provide a lower bound on the entropic contribution to the free energy, −TS° (or an upper bound on the Shannon information entropy, S). The bounding behavior may prove particularly useful in identifying optimal coordinate representations. In the previous MIE work the choice of coordinate system has been demonstrated to significantly impact the quality of the approximation.2 In particular, removing high-order couplings between coordinates, such as those present in Cartesian coordinates, can dramatically improve the accuracy of low-order approximations like MIST and MIE. Because MIST applied to any valid coordinate system will still provide a lower bound on −TS°, a variety of coordinate systems may be tested, and the one that yields the largest converged answer is guaranteed to be the most accurate. While additional work is needed to fully enable such a method, even brute-force enumeration is likely to improve performance.
The results of MIE and MIST in the context of the discrete systems also highlight the ability of MIST to provide a good approximation at low orders, even when direct high-order couplings are known to exist. As has been described previously,2,20 low-order MIE approximations truncate terms in Eq. (11) representing only direct high-order relationships. The poor accuracy of low-order MIE metrics for the bound idealized systems therefore implies that these systems contain significant high-order terms. Despite the presence of such complex couplings, MIST still provides a good approximation in these same systems. For systems such as proteins that are known to exhibit high-dimensional couplings, the ability to capture high-order relationships in the context of a low-order approximation may prove crucial.
Since the original development of the MIE framework, additional work has been done to extend and apply the method. Nearest-neighbor (NN) entropy estimation has been used to compute the low-order marginal terms utilized by the MIE framework, resulting in significantly improved convergence.10 Given that MIST relies upon the same low-order marginal terms as MIE, it is likely that NN methods would also be useful in the context of MIST. MIE has also been used to analyze residue side-chain configurational freedom from protein simulations.11 These studies were able to identify biologically relevant couplings between distal residues in allosteric proteins. Given the relative computational costs of simulating large proteins, and the strong high-dimensional couplings that surely exist in the context of proteins, application of MIST in similar studies may be particularly useful. Preliminary results from ongoing studies have proved promising in the calculation of residue side-chain configurational entropies in the active site of HIV-1 protease.
Conclusion
In summary, we have adapted our existing information theoretic-based approximation framework to enable calculation of configurational entropies from molecular simulation data. Having characterized its behavior in a variety of molecular systems, we believe MIST can serve as a complement to existing methods, particularly in poorly sampled regimes. A variety of existing extensions and applications for MIE are also likely to be useful in the context of MIST, though further exploration is needed. Finally, in addition to improved convergence, MIST carries monotonicity and bounding guarantees that may prove valuable for future applications.
Supplementary Material
Acknowledgement
We thank Michael Gilson, Vladimir Hnizdo, Andrew Fenley, Adam Fedorowicz, Dan Sharp, and Jay Bardhan for helpful disucssion and thoughtful comments on the manuscript. This work was partially supported by the National Institutes of Health (GM065418 and GM082209) and the National Science Foundation (0821391).
Footnotes
Supporting Information Available
Figures showing the convergence plots of the additional HIV-1 protease inhibitors are available as supporting information. This material is available free of charge via the Internet at http://pubs.acs.org/.
References
- 1.Chang C, Gilson MK. J. Am. Chem. Soc. 2004;126:13156–13164. doi: 10.1021/ja047115d. [DOI] [PubMed] [Google Scholar]
- 2.Killian BJ, Kravitz JY, Gilson MK. J. Chem. Phys. 2007;127:024107–024116. doi: 10.1063/1.2746329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Karplus M, Kushick JN. Macromolecules. 1981;14:325–332. [Google Scholar]
- 4.Lee AL, Kinnear SA, Wand AJ. Nat. Struct. Biol. 2000;7:72–77. doi: 10.1038/71280. [DOI] [PubMed] [Google Scholar]
- 5.Chang C, Chen W, Gilson MK. J. Chem. Theory Comput. 2005;1:1017–1028. doi: 10.1021/ct0500904. [DOI] [PubMed] [Google Scholar]
- 6.Hnizdo V, Darian E, Fedorowicz A, Demchuk E, Li S, Singh H. J. Comput. Chem. 2007;28:655–668. doi: 10.1002/jcc.20589. [DOI] [PubMed] [Google Scholar]
- 7.Hnizdo V, Fedorowicz A, Singh H, Demchuk E. J. Comput. Chem. 2003;24:1172–1183. doi: 10.1002/jcc.10289. [DOI] [PubMed] [Google Scholar]
- 8.Scott DW. Multivariate Density Estimation: Theory, Practice, and Visualization. New York: John Wiley and Sons; 1992. [Google Scholar]
- 9.Walton EB, Van Vliet KJ. Phys. Rev. E. 2006;74 061901. [Google Scholar]
- 10.Hnizdo V, Tan J, Killian BJ, Gilson MK. J. Comput. Chem. 2008;29:1605–1614. doi: 10.1002/jcc.20919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.McClendon C, Friedland G, Mobley D, Amirkhani H, Jacobson M. J. Chem. Theory Comput. 2009;5:2486–2502. doi: 10.1021/ct9001812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.King BM, Tidor B. Bioinformatics. 2009;25:1165–1172. doi: 10.1093/bioinformatics/btp109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Potter MJ, Gilson MK. J. Phys. Chem. A. 2002;106:563–566. [Google Scholar]
- 14.Gibbs JW. Elementary Principles in Statistical Mechanics. C. Scribner’s sons; 1902. [Google Scholar]
- 15.Shannon C. Bell System Technical Journal. 1948;27:379–423. 623–656. [Google Scholar]
- 16.Cover TM, Thomas JA. Elements of Information Theory. 2nd ed. Hoboken, N.J.: Wiley-Interscience; 2006. [Google Scholar]
- 17.Bethe HA. Proc. R. Soc. Lond. A. 1935;150:552–575. [Google Scholar]
- 18.Montanari A, Rizzo T. J. Stat. Mech.: Theory Exp. 2005;2005:P10011. [Google Scholar]
- 19.Yedidia JS, Freeman WT, Weiss Y. Bethe free energy, Kikuchi approximations and belief propagation algorithms. Technical Report 16, Mitsubishi Electric Research Lab. 2001
- 20.Matsuda H. Phys. Rev. E. 2000;62:3096. doi: 10.1103/physreve.62.3096. [DOI] [PubMed] [Google Scholar]
- 21.Brooks BR, Bruccoleri RE, Olafson BD, States DJ, Swaminathan S, Karplus M. J. Comput. Chem. 1983;4:187–217. [Google Scholar]
- 22.Brooks BR, Brooks CL, III, Mackerell AD, Jr, Nilsson L, Petrella RJ, Roux B, Won Y, Archontis G, Bartels C, Boresch S, et al. J. Comput. Chem. 2009;30:1545–1614. doi: 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.MacKerell AD, Jr, Bashford D, Bellott M, Dunbrack RL, Jr, Evanseck JD, Field MJ, Fischer S, Gao J, Guo H, Ha S, et al. J. Phys. Chem. B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 24.MacKerell AD, Jr, Feig M, Brooks CL., III J. Comput. Chem. 2004;25:1400–1415. doi: 10.1002/jcc.20065. [DOI] [PubMed] [Google Scholar]
- 25.Bayly CI, Cieplak P, Cornell W, Kollman PA. J. Phys. Chem. 1993;97:10269–10280. [Google Scholar]
- 26.Green DF, Tidor B. J. Phys. Chem. B. 2003;107:10261–10273. [Google Scholar]
- 27.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Montgomery JA, Jr, Vreven T, Kudin KN, Burant JC, et al. Gaussian 03. Wallingford, CT: Gaussian, Inc.; 2004. [Google Scholar]
- 28.Abagyan R, Totrov M, Kuznetsov D. J. Comput. Chem. 1994;15:488–506. [Google Scholar]
- 29.Chang C, Potter MJ, Gilson MK. J. Phys. Chem. B. 2003;107:1048–1055. [Google Scholar]
- 30.Momany FA, Rone R. J. Comput. Chem. 1992;13:888–900. [Google Scholar]
- 31.Desmet J, Maeyer MD, Hazes B, Lasters I. Nature. 1992;356:539–542. doi: 10.1038/356539a0. [DOI] [PubMed] [Google Scholar]
- 32.Dahiyat BI, Mayo SL. Protein Sci. 1996;5:895–903. doi: 10.1002/pro.5560050511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Dahiyat BI, Mayo SL. Science. 1997;278:82–87. doi: 10.1126/science.278.5335.82. [DOI] [PubMed] [Google Scholar]
- 34.Leach AR, Lemon AP. Proteins. 1998;33:227–239. doi: 10.1002/(sici)1097-0134(19981101)33:2<227::aid-prot7>3.0.co;2-f. [DOI] [PubMed] [Google Scholar]
- 35.Altman MD, Ali A, Reddy GSKK, Nalam MNL, Anjum SG, Cao H, Chellappan S, Kairys V, Fernandes MX, Gilson MK, et al. J. Am. Chem. Soc. 2008;130:6099–6113. doi: 10.1021/ja076558p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Gilson MK, Honig B. Proteins. 1988;4:7–18. doi: 10.1002/prot.340040104. [DOI] [PubMed] [Google Scholar]
- 37.Nicholls A, Honig B. J. Comp. Chem. 1991;12:435–445. [Google Scholar]
- 38.Sitkoff D, Sharp KA, Honig B. J. Phys. Chem. 1994;98:1978–1988. [Google Scholar]
- 39.Gilson MK, Sharp KA, Honig BH. J. Comp. Chem. 1988;9:327–335. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.