Abstract
In the context of cell signaling, kinetic proofreading was introduced to explain how cells can discriminate among ligands based on a kinetic parameter, the ligand-receptor dissociation rate constant. In the kinetic proofreading model of cell signaling, responses occur only when a bound receptor undergoes a complete series of modifications. If the ligand dissociates prematurely, the receptor returns to its basal state and signaling is frustrated. We extend the model to deal with systems where aggregation of receptors is essential to signal transduction, and present a version of the model for systems where signaling depends on an extrinsic kinase. We also investigate the kinetics of signaling molecules, “messengers,” that are generated by aggregated receptors but do not remain associated with the receptor complex. We show that the extended model predicts modes of signaling that exhibit kinetic discrimination for some range of parameters but for other parameter values show little or no discrimination and thus escape kinetic proofreading. We compare model predictions with experimental data.
An important feature of receptor-mediated cell signaling pathways is the capacity to discriminate between different ligands that bind to the same receptor. McKeithan introduced a kinetic proofreading model to explain such discrimination in T cell activation (1). In the model, the bound receptor must complete a series of modifications (e.g., phosphorylations, associations with kinases, phosphatases, adapter molecules) for a particular cellular response to occur. If the ligand dissociates before the full set of modifications is completed, the receptor reverts to its basal state. The model explains in part the correlation between the ability of peptide-MHC to activate T cells and the lifetime of the bond formed between the clonotypic T cell antigen receptor (TCR) and the peptide-MHC (2). In kinetic proofreading, cells discriminate between ligands based on a kinetic parameter, the dissociation rate constant, rather than on the equilibrium binding properties of the ligands.
Recent experiments (3, 4) investigated the extent to which kinetic proofreading controls cellular responses induced by FcɛRI, a receptor homologous to TCR and other multichain immune recognition receptors (MIRR; ref. 5), which binds IgE with high affinity. Multivalent antigen, binding to the IgE, aggregates the FcɛRI and initiates cellular responses (6, 7). The experiments in ref. 3 showed that certain cellular responses induced by FcɛRI were consistent, qualitatively, with predictions of McKeithan's kinetic proofreading model (1). In the accompanying paper (4), newer studies support and extend the earlier ones, but also reveal a response that escapes kinetic proofreading, in the sense that ligands with widely different dissociation rate constants induce the same level of response. The authors propose an escape route—a branch from the chain of modifications of aggregated receptors, corresponding to a reaction in which a modified aggregate generates a “messenger” that mediates the response.
To test this idea, we expand McKeithan's kinetic proofreading model in several ways. We allow for a branch reaction, in which a modified receptor aggregate acts as an enzyme on an intracellular substrate, generating a messenger. In addition, to model the FcɛRI system, and potentially other systems where receptor aggregation is required for signaling, we include ligand-induced aggregation of receptors explicitly as the primary event in the signaling pathway (8, 9). We also present a version of the model where aggregated receptors must be associated with a kinase before any receptor modification can occur. The models allow us to study differences between receptors that are intrinsic kinases, such as growth factor receptors (10), and receptors that require an external kinase to initiate signaling, such as cytokine receptors (11), FcɛRI, and related receptors.
We will show that the models predict ways to escape kinetic proofreading. In particular, as proposed in the accompanying paper (4), the extent of production of a messenger can be insensitive to the dissociation rate constant of the ligand that induces and maintains aggregation of receptors. Depending on the other parameters of the system, the relation between messenger production and the ligand/receptor dissociation rate constant can be strong or weak. The two extremes are evident in two gene induction responses measured in ref. 4.
Models and Results
The kinetic proofreading models we present are implemented in simulation software available on discs for Windows-based or Macintosh computers. For information on requesting the software, and for detailed documentation of the models and software, go to http://www.t10.lanl.gov/teams/signaling.html.
Intrinsic Kinase (IK) Model.
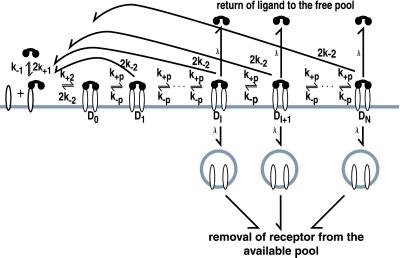
Fig. 1 shows the states and rate constants for the basic model we consider. We treat the simplest case of ligand-induced aggregation of receptors, a symmetric bivalent ligand interacting with a monovalent receptor. The prototypic example is a homodimeric form of platelet-derived growth factor (PDGF) interacting with a homogeneous population of PDGF receptors (12). There are also a number of ways to mimic such a system by using FcɛRI. When a bivalent ligand binds to monovalent receptors, the only aggregate that can form is a dimer, i.e., a pair of receptors, each bound to one of the binding sites on a single ligand. Receptor dimers are subject to reversible modifications. We refer to this model as the intrinsic kinase model (IK model) because, like the growth factor receptors, which have intrinsic kinase activity and transphosphorylate each other on aggregation (10), dimerized receptors in the model become modified without the help of an external initiating enzyme. The model assumes that signaling requires receptor aggregation. If a dimer breaks up, the receptors revert to the unmodified state.
Figure 1.
The IK model. A bivalent ligand binds to monovalent receptors, aggregating pairs of receptors into dimers. The single site forward and reverse rate constants for ligand/receptor binding are k+1 and k−1 when the ligand binds singly, from solution, and k+2 and k−2 for the surface reaction when the second site on a singly bound bivalent ligand binds to a second receptor. Receptor dimers undergo a sequence of reversible modifications, with forward and reverse rate constants k+p and k−p. The final activated state is numbered N. The model allows for the possibility that, beyond some level of modification, dimers are subject to down-regulation. Dimers in states i ≥ I are removed at a rate λ.
In restricting the model to the case where dimers are the only aggregates that form, we gain insight into the effect of aggregation while avoiding ambiguities that would arise, regarding the state of modification of an aggregate, in a model where large aggregates undergo modifications and then break up into smaller aggregates.
In many systems, receptor aggregation leads to a reduction in the number of receptors, “down-regulation,” most commonly by internalization. The model allows for down-regulation by an unspecified mechanism. In the model, receptors are subject to down-regulation only if they are in dimers that have undergone a specified number of modifications.
In McKeithan's formulation (1), the key quantity in predicting the steady state concentration of activated receptors (i.e., receptors that have completed the full sequence of modifications), is α = k+p/(k+p + k−1) where k−1 denotes the rate constant for ligand/receptor dissociation and k+p is the rate constant for each modification. The ratio α can be interpreted as the probability that the next receptor modification will occur before the ligand dissociates (in which case the unbound receptor returns to the unmodified state). For the model in which receptors must be in dimers to undergo modifications (Fig. 1), the rate at which a dimer breaks up, 2k−2, plays an analogous role to k−1 in ref. 1.
In the special case where modifications are reversed only when dimers dissociate or are down-regulated (i.e., k−p = 0 in Fig. 1), the probability that a dimer in an intermediate state of modification goes on to the next state, before the dimer breaks up or is removed in the down-regulation process, is
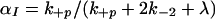 |
1 |
where λ is the rate constant for down-regulation. For dimers that are not subject to down-regulation, λ = 0 in Eq. 1. When down-regulation is negligible (i.e., when λ = 0 for all dimers), the system reaches a steady state. The steady state fraction of dimers that have completed all N modifications is α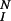 .
.
In the case where modification reactions are reversible, i.e., k−p ≠ 0 (13), the expression for the fraction of dimers that become activated is more complex, with α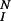 as an upper bound. In all cases, if dissociation is rapid relative to modification, and if there are enough steps in the activation cascade, few receptors become activated.
as an upper bound. In all cases, if dissociation is rapid relative to modification, and if there are enough steps in the activation cascade, few receptors become activated.
Extrinsic Kinase (EK) Model.
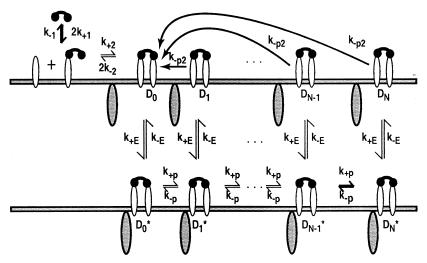
Unlike the receptors for growth factors, multichain immune recognition receptors do not encode a kinase as an intrinsic part of their structure. Instead, they associate with an Src family kinase, which phosphorylates tyrosines on the receptor (14). In at least one system, experimental and computational analyses suggest that the kinase is limiting (15, 16). We have, therefore, extended the model to explore the effects such a constraint places on the system. We refer to this extension as the extrinsic kinase (EK) model (Fig. 2). The model also applies to cytokine receptors, which must associate with Janus kinases (JAKs) to activate signal transducers and activators of transcription (STATs) and mediate signal transduction (11).
Figure 2.
The EK model. Dimers must associate with a surface-associated cytoplasmic enzyme before any further modifications can occur. Association with the enzyme is reversible. When the enzyme is present, dimers undergo reversible modifications. If the enzyme dissociates from a modified dimer, the modifications are reversed rapidly. Down-regulation and dissociation of dimers are omitted from the figure. When dimers are lost, associated enzyme is not down-regulated but returns to the pool of free enzyme.
The requirement that an initiating enzyme must associate with a dimer for receptor modification to begin has two major effects when enzyme is limiting: it reduces the total concentration of receptors that undergo modification and it affects how receptors progress through the series of modifications required for signaling. The probability that an enzyme-associated dimer undergoes the next modification before down-regulation or loss of all previous modifications is
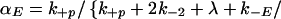 |
2 |
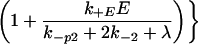 |
in the special case where modifications of enzyme-associated dimers are irreversible (k−p = 0). When k−p ≠ 0, the probability of progression before reversal of all modifications depends on the state of modification and is less than αE. In the model, when the modified dimer loses its associated enzyme (rate constant k−E), modifications are reversed (rate constant k−p2), unless the dimer associates with another enzyme molecule before reversal occurs. The forward rate constant for enzyme/dimer association is k+E, and E denotes the concentration of free enzyme. Because the dissociation of either the ligand or the enzyme can reverse receptor modification, the requirement for an initiating enzyme raises the possibility that there is an upper bound to the expected lifetime of a receptor in an aggregate, beyond which kinetic proofreading no longer occurs. If the initiating enzyme is available in excess, then Eq. 2. reduces to Eq. 1. In this case, the requirement for the enzyme does not affect the progression of dimers through the sequence of modifications leading to activation.
Parameter Estimates Used in the Simulations
The standard set of parameters used in simulations is given in Table 1. The figure legends indicate any variation in the values used. Where available, we have chosen values determined experimentally for FcɛRI on the extensively studied line of rodent mast cells, RBL-2H3 (17, 18), as summarized in ref. 16. The cells express ≈3 × 105 FcɛRI.
Table 1.
Parameter values
| Rate constants used in simulations | ||
| k+1, 1/Ms | 1.0E+6 | Binding, high affinity ligand |
| k−1, 1/s | 5.0E−2 | Dissociation, high affinity ligand |
| k+2RT, 1/s | 1.5E−1 | Formation of dimer |
| k−2, 1/s | 5.0E−2 | Dissociation of dimer |
| k+p, 1/s | 5.0E−1 | Modification of dimer |
| k−p, 1/s | 1.0E−1 | Reversal of modification |
| k−p2, 1/s | 5.0E−2 | Reversal after loss of enzyme |
| k+EET, 1/s | 2.0E+0 | Enzyme/dimer association |
| k−E, 1/s | 2.0E−2 | Enzyme/dimer dissociation |
| λ, 1/s | 1.0E−3 | Down-regulation |
| Other parameters | ||
| ρ, cells/ml | 2.0E+6 | Cell density |
| LT, M | 1.0E−9 | Concentration of high affinity ligand |
| RT | 3.0E+5 | Receptors per cell |
| ET | 3.0E+4 | Initiating enzyme molecules per cell |
| N | 9 | Number of modifications |
The following points played a role in the choice of the parameters governing binding and aggregation. The concentration and rate constants for the ligand are estimates for the high affinity ligand used in the experiments in ref. 4. We take the rate of opening of a ligand–receptor bond to be the same whether the ligand is bound through one site or two, i.e., k−1 = k−2 (19). For a bivalent ligand and monovalent receptor, at equilibrium, dimer formation is maximal when the total ligand concentration LT = 1/(2K1)+(RT/2)(ρcell/6.02 × 1020), where ρcell is the concentration of cells in cells/ml (20). At this ligand concentration, there is substantial aggregation at equilibrium when K2RT ≥ 1, where K2 = k+2/k−2 is the equilibrium aggregation constant. Only for a few ligands that aggregate surface IgE has K2 been determined (21, 22). For ligands that activate the full range of RBL cell responses, we expect that K2RT ≥ 1. For the parameters in Table 1 characterizing the high affinity ligand, K2RT = 3.
In RBL-2H3 cells, the kinase that initiates FcɛRI phosphorylation, Lyn (23), appears to be limiting, with a ratio of available Lyn to receptor of about 0.1 (15, 16, 24). We take the total initiating enzyme concentration ET = 0.1RT. Only one Lyn per aggregate is required to initiate phosphorylation of receptors (25). k+E is the forward rate constant for the association of the initiating enzyme with a receptor in a dimer, a reaction between two surface associated molecules. Lyn associates weakly with unphosphorylated receptors; on receptor aggregation, Lyn phosphorylates the receptor, leading to a stronger association of Lyn (24, 26, 27). For the questions we address in this paper, which deal with the signaling pathway after receptor aggregation, it suffices to include only the high affinity interaction in the model.
In the models, each receptor modification is governed by the same rate constants, k+p and k−p. In a true activation, distinct steps are different in character and occur at different rates. k+p and k−p are therefore average quantities. We use values estimated from measurements of the phosphorylation and dephosphorylation of receptor tyrosines (13, 28). We obtained a lower bound of 0.06–0.12 s−1 for the rate constant for dephosphorylation of FcɛRI dissociated from an aggregate (16). Because Lyn is limiting on RBL cells, to get sufficient receptor phosphorylation for activation, we expect that most receptors in aggregates associated with Lyn are phosphorylated, so that k+p > k−p. In the EK model, if the initiating enzyme dissociates from a dimer, the dimer decays to an unmodified dimer at a rate k−p2, which is taken to be independent of how many modifications the receptors in the dimer have undergone.
The model parameter N is the maximum number of modifications a receptor can undergo. In a signaling cascade, receptors go through numerous modifications of differing duration. In the model, the rate constants for all modifications are identical. Therefore, there is not necessarily a one-to-one correspondence between a true modification and a modification step in a kinetic proofreading scheme. We expect that the slowest modification steps will have the strongest influence on determining the values of N, k+p, and k−p, but as yet there are no rules for how to choose these values. On receptor aggregation, receptor phosphorylation rises and then usually decreases. The molecular events that account for this phenomenon are largely unknown. In the model, the only reaction that can lead to a loss of receptor phosphorylation is the down-regulation process (Fig. 1). The phenomenological parameter λ, the rate constant for down-regulation of receptors, is estimated from the decaying portion of the time course of receptor phosphorylation in figure 1 of ref. 4.
Kinetic Proofreading Controls Signaling by Fully Modified Aggregates.
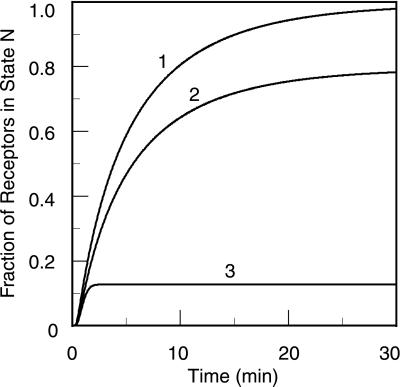
Following McKeithan (1), we first consider the case where a response is generated by receptors in the Nth state, the last state in the chain of modifications. As the lifetime of a receptor in a dimer, 1/(2k−2), increases, the concentration of the Nth state increases. Maximal concentration of the Nth state is achieved when the lifetime is infinite, i.e., when k−2 = 0. In the absence of down-regulation, a steady state is reached. If k−2 = 0, the modifications are irreversible (k−p = 0), and the initiating enzyme is in large excess, then αE = 1 (Eq. 2) and in the steady state, all of the dimers are in state N. If k−p ≠ 0, then αE < 1, the steady-state concentration of the Nth state is reduced, and the states from N − 1 to 0 become populated. If enzyme is limiting, there is a further reduction in the concentration of the Nth state. Fig. 3, generated by using the EK model, illustrates these cases. The figure shows how reversible modifications and limiting extrinsic kinase can affect signaling, even when the ligand aggregates receptors irreversibly.
Figure 3.
Predicted kinetics of receptor modification when binding is irreversible (k−1 = k−2 = 0). The curves were obtained by solving numerically the set of ordinary differential equations that describe the EK model (see Models and Results). Plotted is the fraction of receptors in dimers that have undergone nine modifications, for the following cases: (i) excess initiating enzyme and k−p = 0; (ii) excess initiating enzyme and k−p = 0.01 s−1; (iii) limiting initiating enzyme and k−p = 0.01 s−1. Other parameters are given in Table 1 and discussed in Parameter Estimates Used in the Simulations.
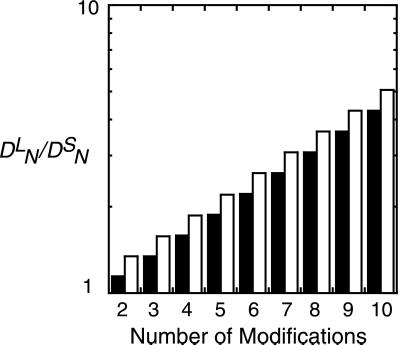
Whether or not the initiating enzyme is limiting, kinetic proofreading is robust, in the sense that, as the number of modifications increases, discrimination between ligands with different dissociation rates increases. In Fig. 4, we show that kinetic proofreading models can even discriminate between two ligands whose rate constants differ by a factor of two but whose equilibrium binding and aggregation constants are identical, so that in the steady state the concentration of receptor dimers is the same for both ligands.
Figure 4.
Kinetic discrimination as a function of N, the number of modifications required to produce a signaling state. Two ligands, referred to as long (L) and short (S) lived, have the same equilibrium binding and aggregation constants, i.e. K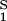 = K
= K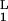 and K
and K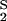 = K
= K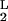 , so that, in the steady state (λ = 0), they produce the same total concentration of dimers. Their rate constants differ by a factor of two, with k
, so that, in the steady state (λ = 0), they produce the same total concentration of dimers. Their rate constants differ by a factor of two, with k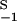 = 2k
= 2k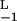 and k
and k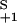 = 2k
= 2k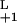 . k−1 = k−2 for both ligands. Plotted is the ratio of the concentrations in the Nth state, D
. k−1 = k−2 for both ligands. Plotted is the ratio of the concentrations in the Nth state, D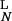 /D
/D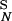 , a measure of discrimination, vs. N. The filled bars correspond to excess initiating enzyme (ET ≫ RT) and the open bars to limiting enzyme (ET = 0.1RT). Parameters are given in Table 1.
, a measure of discrimination, vs. N. The filled bars correspond to excess initiating enzyme (ET ≫ RT) and the open bars to limiting enzyme (ET = 0.1RT). Parameters are given in Table 1.
Signaling by Messenger Can Escape Kinetic Proofreading.
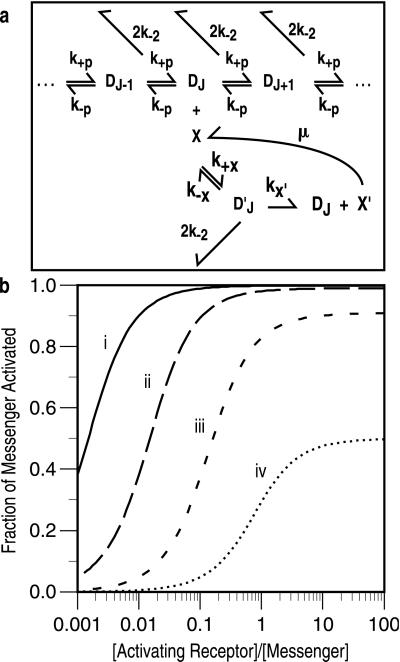
To test the proposal in ref. 4—that production of a messenger can allow a receptor-mediated cellular response to escape kinetic proofreading—we add a branch to the IK and EK models (Figs. 1 and 2). Fig. 5a shows a reaction scheme in which a modified dimer activates a component in a signaling pathway that serves as a messenger. The messenger is not associated with the receptor complex. For example, the signal transducers and activators of transcription (STATs) associate with aggregated cytokine receptors, become activated, and translocate to the nucleus (11).
Figure 5.
(a) Production of messenger. Dimers in the Jth state of modification mediate production or activation of an intracellular “messenger.” The Jth dimer (DJ) acts as an enzyme, and the inactive messenger (X) as the substrate. The dimer and the inactive messenger combine reversibly to form a complex (D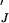 ), which then yields the activated messenger (X′) and the activating dimer. Active messenger decays back to the inactive form at a rate μ. In the case of the EK model (Fig. 2), we assume that both forms of the Jth dimer (i.e., associated or not associated with an initiating enzyme) can activate messenger. (b) Activated messenger as a function of the steady-state level of activating receptor dimers. The curves depend only on two parameters, kx′/μ and XT/Km, where XT is the total concentration of messenger and Km = (k−x + kx′ + 2k−2)/k+x. When k−2 = 0, Km is the usual Michaelis-Menten constant. For these plots XT/Km = 1 and kx′/μ has the values: (i) 1000, (ii) 100, (iii) 10, and (iv) 1. The plots are identical for the IK and EK models.
), which then yields the activated messenger (X′) and the activating dimer. Active messenger decays back to the inactive form at a rate μ. In the case of the EK model (Fig. 2), we assume that both forms of the Jth dimer (i.e., associated or not associated with an initiating enzyme) can activate messenger. (b) Activated messenger as a function of the steady-state level of activating receptor dimers. The curves depend only on two parameters, kx′/μ and XT/Km, where XT is the total concentration of messenger and Km = (k−x + kx′ + 2k−2)/k+x. When k−2 = 0, Km is the usual Michaelis-Menten constant. For these plots XT/Km = 1 and kx′/μ has the values: (i) 1000, (ii) 100, (iii) 10, and (iv) 1. The plots are identical for the IK and EK models.
Analysis of the extended model indicates that a response can escape kinetic proofreading if that response depends on a messenger whose activation saturates as the dissociation rate constant k−1 = k−2 decreases. This result is illustrated in Fig. 5b for the case where down-regulation is negligible. For convenience in describing the production of activated messenger, we will refer to the precursor as inactive messenger. The total concentration of messenger, XT, includes the inactive and active forms, as well as messenger complexed with the activating dimer, the Jth dimer in Fig. 5a. One sees in Fig. 5b that the fraction of total messenger that is activated saturates as a function of the concentration of the activating receptor dimer. The plots in Fig. 5b show that ligands with differing dissociation rate constants, that populate the Jth dimer state at different levels, can produce similar concentrations of the activated messenger. The sensitivity of a response to the ligand/receptor dissociation rate constant depends on the rate constants that characterize messenger activation, the lifetime of the activated form, and relative amounts of the reactants. The four curves in Fig. 5b are generated by using four different values for the ratio of two key parameters, the rate of activation, kx′, and the rate of inactivation, μ. As expected intuitively, levels of activation plotted in Fig. 5b increase as the ratio kx′/μ increases. More interestingly, the curves show that, if activation is rapid or decay to the inactive state is slow (corresponding to large values of kx′/μ), the production of activated messenger saturates over a wider range of concentrations of the activating dimer and is therefore less sensitive to differences in the ligand/receptor dissociation rate.
Kinetic Proofreading and Messenger Kinetics Characterize Distinct RBL Cell Responses.
We shall now describe to what extent the models can predict several results observed experimentally by Liu et al. (4).
Result 1.
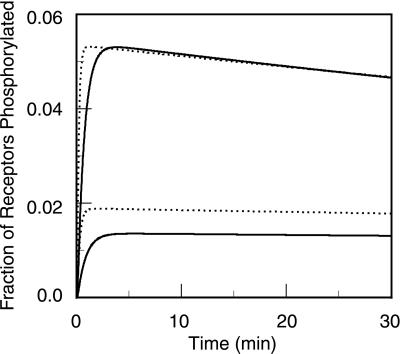
Cells exposed to appropriately chosen concentrations of two ligands having similar binding rate constants (k+1) but widely different dissociation rate constants (k−1) generate approximately equivalent levels of tyrosine-phosphorylated FcɛRI. Five-fold reductions in the concentrations of the ligands lead to 4-fold reductions in the phosphorylation of the receptors.
Fig. 6, generated from the EK model, is analogous to figure 1 in ref. 4, showing the kinetics of phosphorylation of receptor tyrosines. Concentrations of ligands with the same forward rate constant but differing reverse rate constants are adjusted so that both ligands induce similar levels of receptor phosphorylation (upper curves). When each ligand concentration is reduced 5-fold, the levels of receptor phosphorylation remain similar for the two ligands (lower curves).
Figure 6.
Predicted kinetics of phosphorylation of receptor tyrosines, for two ligands with different dissociation rate constants, at two concentrations (LT): (i) k−1 = k−2 = 0.05, LT = 10−9 M (solid upper curve); (ii) k−1 = k−2 = 0.05, LT = 2 × 10−10 M (dotted upper curve); (iii) k−1 = k−2 = 0.11, LT = 10−8 M (solid lower curve); (iv) k−1 = k−2 = 0.11, LT = 2 × 10−9 M (dotted lower curve). Additional parameters are given in Table 1. Time courses are simulated by using the EK model. Receptor phosphorylation is taken to be the first modification that dimers undergo. Plotted is the fraction of all receptors that are modified (i.e., receptors in all dimers except D0 and D*0 in Fig. 2).
In Fig. 6, which shows only the first 30 min of the predicted time course, receptor phosphorylation rises and peaks much more rapidly than in the corresponding experiments (4). A possible explanation for this discrepancy is that we have not included transport effects when modeling the binding. In the model, the binding of ligand to the receptor occurs in a thoroughly mixed system whereas in the experiments the binding occurs in a well with adherent cells on the bottom surface. For this geometry and the large ligands used, we expect transport effects to slow the kinetics of binding and, consequently, the kinetics of phosphorylation.
Result 2.
Several distal responses such as the phosphorylation of Syk, the generation of mRNA for c-fos, and degranulation were much less efficiently stimulated by the low affinity ligand than by the high affinity ligand, qualitatively consistent with the kinetic proofreading model. However, induction of transcription of the MCP-1 gene, unlike the other RBL cell responses investigated by Liu et al. (4) and Torigoe et al. (3), appears to largely escape the control of kinetic proofreading. At least at higher doses, the ligand with the high dissociation rate constant is just as effective as the ligand with the lower dissociation rate constant in inducing the formation of monocyte chemoattractant protein 1 (MCP-1) mRNA and secretion of MCP-1 protein.
As we have shown, a response that depends on receptor-mediated activation of a messenger can escape kinetic proofreading. Fig. 5b shows that, even if low and high affinity ligands produce substantially different numbers of receptors in complexes capable of generating a messenger, both amounts may be in the range where production of messenger saturates (i.e., toward the right on the axis labeled “activating receptor/messenger”). In this case, the low and high affinity ligands generate approximately the same amount of messenger. However, at lower concentrations of both ligands, the production of activating receptor complexes is reduced and there can be a wide gap between the amounts of messenger generated by the two ligands. This predicted shift is seen in the dose-dependence of the production of mRNA for MCP-1, shown in figures 5 and 6 of the accompanying paper (4). Kinetic proofreading is not evident at higher concentrations of the ligands but is observed at lower concentrations. Levels of secretion of the MCP-1 protein reported in ref. 4 also show this pattern.
There is an alternative explanation for the MCP-1 data. It is possible that, even at the higher concentrations of the ligands, the amounts of messenger produced are quite different for the two ligands but both are above a threshold amount needed for maximal induction of transcription of the MCP-1 gene.
Result 3.
As noted in ref. 4, the kinetics of phosphorylation of Syk show some distinctive features, and we can ask whether these are predicted by our model. The response of the more rapidly dissociating ligand is reduced relative to that induced by the more slowly dissociating ligand, and, for a system constrained by kinetic proofreading, this is as expected. Two other phenomena are not anticipated. The kinetics appear to be slowed in the case of the low affinity ligand. This result is surprising because binding should equilibrate more rapidly for the ligand with the higher dissociation rate constant and higher concentration. Also, the decrease in phosphorylation observed for each of the ligands, when the ligand concentration is reduced 5-fold, is smaller than expected if the phosphorylation of Syk was identified with a sum of dimer states (as in the treatment of receptor phosphorylation in Fig. 6).
The models allow us to test a possible explanation for the unexpected features of the phosphorylation of Syk. These features are consistent with messenger kinetics, for certain parameters. It may be reasonable to model Syk as a messenger, in the limited sense of a component that becomes altered (phosphorylated) at the receptor complex but then dissociates. Using conventional methods for assessing phosphorylated Syk, virtually all of it is found in the cytosol, although as noted elsewhere (29), it is possible that this observation is at least in part related to the disruption induced by the experimental procedures. However, for the model to predict a time course for the phosphorylation of Syk corresponding with the experimental observations, the time Syk stays phosphorylated after dissociating from the receptor complex would have to be much longer (about 15 min, on average) than estimated from observations of the dephosphorylation of Syk after hapten-induced disaggregation of FcɛRI (about 20 s; ref. 28). A different kind of model, one that treats Syk explicitly and includes details of the interactions of Syk with other components in the signaling pathway, will be required to test alternative mechanisms of Syk regulation and to arrive at a consistent explanation of all of the experimental data.
Another Escape Route.
The kinetic proofreading models reveal a second way, besides messenger kinetics, for a cellular response to escape kinetic proofreading under the experimental conditions in (4). When ligand concentrations are adjusted so that two ligands with similar association but different dissociation rate constants give equal degrees of receptor phosphorylation, the models make different predictions for signals that depend on fully modified aggregates and those that depend on intermediate states in the signaling pathway. Concentrations of terminal states are lower, but concentrations of some earlier (less modified) states are higher, for the low affinity ligand than for the high affinity ligand. Consequently, responses initiated by intermediate states can be as high for the low affinity ligand as for the high affinity ligand, possibly higher.
Discussion
The accompanying paper (4) and the model-based analysis we have presented here show that two broad classes of cell signals can be distinguished by a set of kinetic properties. As McKeithan pointed out for T cell activation (1), if a receptor/ligand complex must be stable enough to persist through a sequence of biochemical modifications to generate a ligand-induced cellular response, then this response is subject to kinetic proofreading. Cellular responses that are under the strict control of kinetic proofreading are critically dependent on the lifetime of the ligand/receptor bond. Other responses that use the same receptor but that result from production of an intracellular messenger can be stimulated by a broader range of ligands. Even if the messenger is generated at a late stage in the modification pathway, the efficiency of activation, lifetime of the activated state, total amount of messenger, and possible saturation of the cellular response can result in escape of the response from kinetic proofreading.
In the models we have presented, where cellular responses depend on receptor aggregation, fractions of receptor aggregates that complete a chain of biochemical modifications differ widely for ligands with high and low dissociation rates, under conditions where the extent of the initial modification is the same for both ligands. In the corresponding experiments (4), concentrations of two ligands, with slow and fast rates of dissociation from IgE bound to FcɛRI on RBL cells, were adjusted so that both ligands induced the same level of receptor tyrosine phosphorylation. The late responses that were reduced significantly in the case of the more rapidly dissociating ligand, relative to levels induced by the slowly dissociating ligand, were degranulation and induction of c-fos mRNA. These responses appear to depend strongly on receptor aggregates that remain intact throughout a sequence of biochemical modifications. In contrast, the induction of MCP-1 mRNA by the two ligands is consistent with a signal generated by a messenger, under conditions where the concentration of messenger is relatively insensitive to the kinetics of the modified receptor aggregate that activates the messenger. The induction of c-fos mRNA must also depend on the release of a messenger from a modified receptor complex, but the kinetics of messenger production in this case, unlike for MCP-1, must be strongly coupled to the kinetics of the receptor complex.
For other receptor systems, experiments designed similarly to those of Torigoe at al (3) and Liu et al. (4) may provide clues to the structure of the signaling pathway leading to a particular response.
Models like those we have presented simplify signaling pathways to focus on key aspects of signal transduction. They can reflect qualitative properties of the system, but the simplification limits the quantitative correspondence between the model and a specific experimental system and limits the range of questions that can be addressed. An alternative approach that permits investigation of the roles and interactions of components of a particular signaling pathway is to construct, test, refine, and expand detailed models of known or hypothesized reactions among specific signaling molecules (e.g., ref. 16). Potentially, such models can be used to provide accurate quantitative predictions of cellular responses.
Acknowledgments
This work was supported in part by National Institutes of Health Grant GM35556 and National Science Foundation Grant MCB9723897.
Abbreviations
- FcɛRI
the high affinity receptor for IgE
- MCP-1
monocyte chemoattractant protein 1
- IK
intrinsic kinase
- EK
extrinsic kinase
Footnotes
See commentary on page 6989.
References
- 1.McKeithan T W. Proc Natl Acad Sci USA. 1995;92:5042–5046. doi: 10.1073/pnas.92.11.5042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lyons D S, Lieberman S A, Hampl J, Boniface J J, Chien Y, Berg L J, Davis M M. Immunity. 1996;5:53–61. doi: 10.1016/s1074-7613(00)80309-x. [DOI] [PubMed] [Google Scholar]
- 3.Torigoe C, Inman J K, Metzger H. Science. 1998;281:568–572. doi: 10.1126/science.281.5376.568. [DOI] [PubMed] [Google Scholar]
- 4.Liu Z-J, Haleem-Smith H, Chen H, Metzger H. Proc Natl Acad Sci USA. 2001;98:7289–7294. doi: 10.1073/pnas.121171998. . (First Published May 22, 2001; 10.1073/pnas.121171998) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Keegan A D, Paul W E. Immunol Today. 1992;13:63–68. doi: 10.1016/0167-5699(92)90136-U. [DOI] [PubMed] [Google Scholar]
- 6.Ishizaka K, Ishizaka T. Ann N Y Acad Sci. 1971;190:443–456. doi: 10.1111/j.1749-6632.1971.tb13554.x. [DOI] [PubMed] [Google Scholar]
- 7.Metzger H. Adv Immunol. 1974;18:169–207. doi: 10.1016/s0065-2776(08)60310-7. [DOI] [PubMed] [Google Scholar]
- 8.Metzger H, Alcarez G, Hohman R, Kinet J-P, Pribluda V, Quarto R. Annu Rev Immunol. 1986;4:419–470. doi: 10.1146/annurev.iy.04.040186.002223. [DOI] [PubMed] [Google Scholar]
- 9.Klemm J D, Schreiber S L, Crabtree G R. Annu Rev Immunol. 1998;16:569–592. doi: 10.1146/annurev.immunol.16.1.569. [DOI] [PubMed] [Google Scholar]
- 10.Lemmon M A, Schlessinger J. Trends Biochem Sci. 1994;19:459–463. doi: 10.1016/0968-0004(94)90130-9. [DOI] [PubMed] [Google Scholar]
- 11.Leonard W J, O'Shea J J. Annu Rev Immunol. 1998;16:293–322. doi: 10.1146/annurev.immunol.16.1.293. [DOI] [PubMed] [Google Scholar]
- 12.Heldin C H, Östman A, Rönnstrand L. Biochim Biophys Acta. 1998;1378:F79–F113. doi: 10.1016/s0304-419x(98)00015-8. [DOI] [PubMed] [Google Scholar]
- 13.Kent U M, Mao S-Y, Wofsy C, Goldstein B, Ross S, Metzger H. Proc Natl Acad Sci USA. 1994;91:3087–3091. doi: 10.1073/pnas.91.8.3087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Thomas S M, Brugge J S. Annu Rev Cell Dev Biol. 1997;13:513–609. doi: 10.1146/annurev.cellbio.13.1.513. [DOI] [PubMed] [Google Scholar]
- 15.Torigoe C, Goldstein B, Wofsy C, Metzger H. Proc Natl Acad Sci USA. 1997;94:1372–1377. doi: 10.1073/pnas.94.4.1372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wofsy C, Torigoe C, Kent U M, Metzger H, Goldstein B. J Immunol. 1997;159:5984–5992. [PubMed] [Google Scholar]
- 17.Kulczycki A, Jr, Metzger H. J Exp Med. 1974;140:1676–1695. doi: 10.1084/jem.140.6.1676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Barsumian E L, Isersky C, Petrino M G, Siraganian R P. Eur J Immunol. 1981;11:317–323. doi: 10.1002/eji.1830110410. [DOI] [PubMed] [Google Scholar]
- 19.Subramanian K, Holowka D, Baird B, Goldstein B. Biochemistry. 1996;35:5518–5527. doi: 10.1021/bi9523522. [DOI] [PubMed] [Google Scholar]
- 20.Goldstein B, Wofsy C. In: Cell Biology. Goldstein B, Wofsy C, editors. Vol. 24. Providence, RI: Am. Math. Soc.; 1994. pp. 109–135. [Google Scholar]
- 21.Xu K, Goldstein B, Holowka D, Baird B. J Immunol. 1998;160:3225–3235. [PubMed] [Google Scholar]
- 22.Hlavacek W S, Perelson A S, Sulzer B, Bold J, Paar J, Gorman W, Posner R G. Biophys J. 1999;76:2421–2431. doi: 10.1016/s0006-3495(99)77397-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Eiseman E, Bolen J B. Nature (London) 1992;355:78–80. doi: 10.1038/355078a0. [DOI] [PubMed] [Google Scholar]
- 24.Yamashita Y, Mao S-Y, Metzger H. Proc Natl Acad Sci USA. 1994;91:11251–11255. doi: 10.1073/pnas.91.23.11251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Wofsy C, Vonakis B M, Metzger H, Goldstein B. Proc Natl Acad Sci USA. 1999;96:8615–8620. doi: 10.1073/pnas.96.15.8615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Pribluda V S, Pribluda C, Metzger H. Proc Natl Acad Sci USA. 1994;91:11246–11250. doi: 10.1073/pnas.91.23.11246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Vonakis B M, Chen H, Haleem-Smith H, Metzger H. J Biol Chem. 1997;272:24072–24080. doi: 10.1074/jbc.272.38.24072. [DOI] [PubMed] [Google Scholar]
- 28.Mao S-Y, Metzger H. J Biol Chem. 1997;272:14067–14073. doi: 10.1074/jbc.272.22.14067. [DOI] [PubMed] [Google Scholar]
- 29.Peirce M, Metzger H. J Biol Chem. 2000;275:34976–34982. doi: 10.1074/jbc.M005819200. [DOI] [PubMed] [Google Scholar]