Separating Fluid Shear Stress from Acceleration during Vibrations in Vitro: Identification of Mechanical Signals Modulating the Cellular Response

Abstract

The identification of the physical mechanism(s) by which cells can sense vibrations requires the determination of the cellular mechanical environment. Here, we quantified vibration-induced fluid shear stresses in vitro and tested whether this system allows for the separation of two mechanical parameters previously proposed to drive the cellular response to vibration – fluid shear and peak accelerations. When peak accelerations of the oscillatory horizontal motions were set at 1g and 60Hz, peak fluid shear stresses acting on the cell layer reached 0.5Pa. A 3.5-fold increase in fluid viscosity increased peak fluid shear stresses 2.6-fold while doubling fluid volume in the well caused a 2-fold decrease in fluid shear. Fluid shear was positively related to peak acceleration magnitude and inversely related to vibration frequency. These data demonstrated that peak shear stress can be effectively separated from peak acceleration by controlling specific levels of vibration frequency, acceleration, and/or fluid viscosity. As an example for exploiting these relations, we tested the relevance of shear stress in promoting COX-2 expression in osteoblast like cells. Across different vibration frequencies and fluid viscosities, neither the level of generated fluid shear nor the frequency of the signal were able to consistently account for differences in the relative increase in COX-2 expression between groups, emphasizing that the eventual identification of the physical mechanism(s) requires a detailed quantification of the cellular mechanical environment.

Introduction

Exposure to vibrations is ubiquitous during daily activities and includes externally generated signals such as road noise during car rides¹⁸ or internal signals such as muscular vibrations generated during postural activities.²³ Because of the physiologic nature of the signal, it may not be surprising that a large number of tissues and cell types are capable of responding to vibrations. Exploiting this cellular mechano-sensitivity at high-frequencies, benefits of vibrations have been suggested for a wide range of applications – from athletic training³⁶ to the treatment of Parkinson’s²⁰ or cardiovascular diseases.³⁵ The potential anabolic and anti-catabolic effects of vibrations on the musculoskeletal system to maintain and enhance tissue quality and quantity have received particular attention,^22,28,44 facilitated by the high level of transmissibility of the oscillatory signal (20 to 90Hz) through the lower and axial skeleton (> 90% transmissibility at ankle and knee).²⁹

The physical mechanisms by which cells can perceive and respond to low-intensity vibrations are largely unknown. In bone, accelerations of up to 0.5g induce matrix deformations of less than 10με, at least two orders of magnitude below those strains that are typically considered osteogenic when the frequency of the mechanical signal is less than 10Hz.⁵³ Emphasizing that matrix deformations are unlikely required in the mechanotransduction of vibrations, low-intensity vibrations applied as simple oscillatory motions to freely moving limbs (“shaking”), rather than induced by whole-body vibrations against the gravitational force of the body, result in matrix strain magnitudes of less than 1με.¹⁹ That vibrations can engender a biologic response even at these extremely small deformation magnitudes³⁸ suggests that the deformation-response relation proposed for lower frequency mechanical signals⁴⁹ does not apply to high-frequency mechanical signals.²⁷

While the extremely small matrix deformations associated with low-level vibrations are insufficient to create pressure gradients large enough to cause local fluid flow in the matrix or canalicular system,⁵¹ oscillatory accelerations will generate relative motions between cells and the surrounding fluid. Thus, cells residing in most tissues and cavities will be subjected not only to accelerations transmitted from the vibrating device but also to fluid shear. As both fluid shear and direct forces acting on the cell have been suggested as modulators of mechanotransduction, it becomes necessary to decouple them for identifying their respective roles in driving the biologic response to vibrations.

Exploiting the opportunities of cell culture systems to investigate the underlying mechanisms, distinct cell types including osteoblasts,² osteocytes,³¹ myoblasts,⁵⁰ chondrocytes,⁴⁷ or progenitor cells⁴⁵ have been shown to respond to vibrations in vitro. While providing important data on the biologic response of cells to vibrations, the identification of the specific component(s) of the vibratory signal that modulates the response requires the quantification of the cellular mechanical environment. Here, we mechanically characterize an in vitro model of vibrations in which, similar to in vivo vibrations, cells are exposed to both accelerations and fluid shear forces. As an example of using this model, we collected data from osteoblast like MC3T3-E1 cells to test whether fluid shear generated by high-frequency oscillations may alter transcriptional levels of cyclooxygenase-2 (COX-2), a gene implicated in regulating mechanically induced bone formation.^8,16

Methods

Experimental Design

To generate in vitro fluid shear magnitudes similar to those estimated in vivo,¹¹ cell culture plates were oscillated in the horizontal, rather than vertical, direction. Horizontal oscillations may engender fluid shear by sloshing, similar to recently analyzed fluid filled structures such as road tankers⁴³ or nuclear reactor design.⁴⁸ The mechanical environment of cells during in vitro vibrations, including fluid motions and fluid shear, was measured with particle image velocimetry (PIV) and modeled with the finite element method (FEM). Speckle photography, an analytical sloshing model, and PIV were used to validate the FEM. Fluid shear within an oscillating cell culture well was determined as a function of vibration magnitude, frequency, fluid viscosity, and total fluid volume in the well. Fluid viscosity was altered by the addition of dextran to the culture medium⁴² and measured by a viscometer (ASTM D455). All data were quantified in a sagittal plane through the center of the well that was positioned in the direction of the imposed oscillatory motion. Shear was reported primarily in the horizontal direction because of the horizontal alignment of the cell layer and the much smaller values for vertical shear.

Vibrating stage

A stage was constructed capable of transmitting the sinusoidal oscillations from the actuator at frequencies between 10–400Hz and peak accelerations up to 1.8g (400Hz) or 3g (10Hz). However, frequencies above 250Hz created secondary vibrations of the whole system which were eliminated by selecting 100Hz as the maximal frequency. A linear actuator (NCM15, H2W Technologies Inc., CA) controlled by a signal generator was attached to a platform mounted onto a linear frictionless slide (NK2-110B, Schneeberger GmbH, Germany) which horizontally constrained the motion. An accelerometer (CXL10, Moog Crossbow Inc., CA) attached to the oscillating platform recorded accelerations in three orthogonal directions in real-time. Up to three 24-well cell culture plates (CLS3527, Corning, NY) were firmly secured to the platform to avoid any secondary vibrations.

Particle image velocimetry (PIV)

PIV was used to experimentally measure vibration induced fluid velocity gradients and the resultant shear rates in the close vicinity of the cell layer at 37.5, 75, 112.5, and 150μm from the well bottom for a well filled with 2.5mm of fluid. A well filled up to 5mm fluid was used to validate shear rates calculated by FEM at 150, 300, 450 and 600μm from the well bottom. A glass fluid chamber was fixed on a single glass slide, attached to the actuator and mounted under a fluorescent microscope. One-micron fluorescent polystyrene microspheres (Fluorospheres-580/605, Invitrogen, CA) served as markers for tracking motions during 60Hz vibrations. Microspheres were uniformly distributed at the bottom of the fluid chamber at a concentration of 37×10⁶/cm² to establish a reference coordinate system on the bottom of the well. In the absence of fluid in the well, the vibration (60Hz) induced motion of the slide was visualized and recorded (250fps) with a high-speed camera (Motion-scope, Redlake Digital Imaging Systems, FL) using a 20X objective (Fig. 1a). The absence of fluid increased the fluorescent signal intensity of the polystyrene beads, enabling the verification of the sampling rate by comparing it to 500fps. Motions recorded at 250fps were not different from those recorded at 500fps. Fluid containing 40,000 spheres/ml to reach fill heights of either 5mm (1000μl fluid) or 2.5mm (500μl fluid) was then added and particle motions were tracked at the horizontal planes specified above (250fps). Acceleration was varied through the output voltage of the function generator. Above 0.6V, our ability to accurately track particles decreased considerably due to total particle travel being larger than field of view. Thus, 0.6V was used as the maximal voltage, corresponding to 0.86g at a vibration frequency of 60Hz.

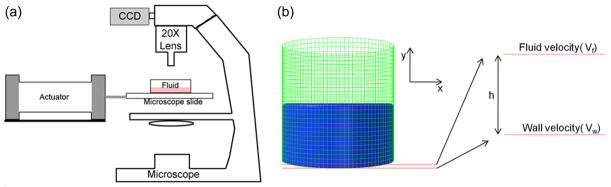
Figure 1. Experimental and computational methods used to describe fluid motions at the well bottom.

(a) Schematic of the Particle Image Velocimetry (PIV) setup. A high-speed camera recorded the motions of 1μm red fluorescent polystyrene particles vibrating within a fluid filled chamber attached to a microscope slide. Fluid shear was quantified by comparing the motion of the slide surface to the particle motions measured at 37.5μm distance intervals. (b) A fluid filled cell culture well was modeled as viscous fluid within a rigid well with the Finite Element Method (FEM). Vibration induced fluid shear at the bottom of the well was calculated by computing the relative velocity between wall and fluid assuming linear velocity gradients.

Finite element modeling (FEM)

FEM (Abaqus 6.9.1, Simula, RI) was used to determine the 3D fluid flow field within the modeled cell culture well and to investigate how changes in vibration frequency, acceleration magnitude, fluid viscosity and fluid volume alter flow patterns (Fig. 1b). To accommodate the computational resources, the distance between fluid nodes was set to 150μm, creating 861,888 fluid nodes. Fluid shear acting on the bottom of the well was calculated through the relative velocity magnitude between the bottom and the adjacent fluid layer. To maintain continuity of velocity between the bulk motion of the fluid and the bottom (Fig. 1b), a linear velocity gradient between the wall and the first fluid layer was assumed similar to Couette flow,²⁴

$$\tau (y)=\frac{\mu (V_w-V_f)}{h},$$ (1)

where τ(y)= fluid shear, μ = viscosity, V_w= velocity of well bottom, V_f= fluid velocity, and h= distance between fluid layer and the well bottom. Results were obtained for vibration frequencies of 30, 60, 75, and 100Hz, acceleration magnitudes of 0.01, 0.1, 0.5, and 1.0g, and normal (0% dextran) and viscous mediums (6% dextran). Data acquired at a level of 150μm from the well bottom were extrapolated to the cell vicinity of 37.5μm from the bottom through the PIV defined spatial gradient pattern (Fig. 2).

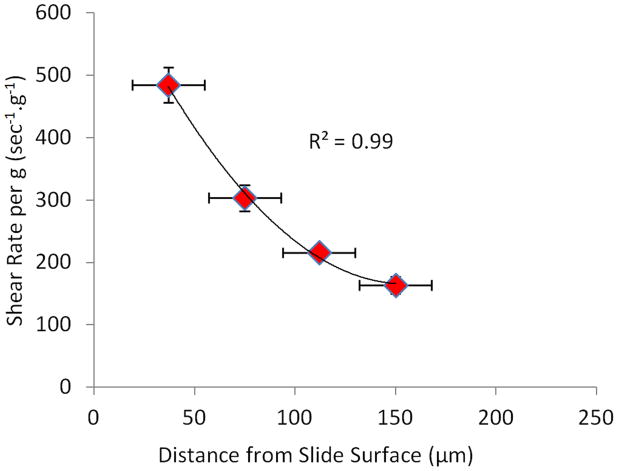
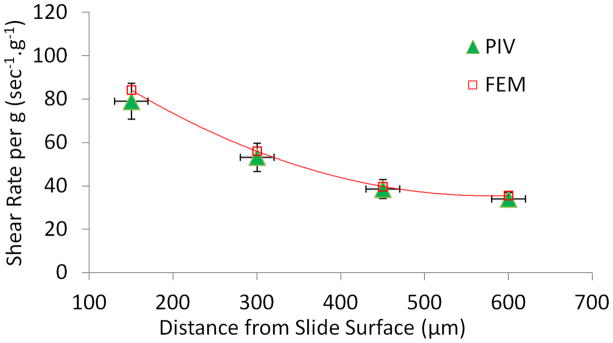
Figure 2. Shear rates between fluid and the well bottom as determined by PIV.

PIV showed a steep non-linear increase in shear rate towards the surface of the glass slide (bottom of the well).

The model was validated by comparing shear rates between FEM and PIV at 150, 300, 450 and 600μm from the well bottom. Further validation of FEM was performed by comparing bulk motions of the fluid to speckle photography and an analytical sloshing model.

Speckle photography

Speckle photography^4,6,7 was performed to quantify the motion of the well and the relative motion of the fluid within the well during high-frequency oscillations. An acrylic well was casted (18mm wide and 2mm deep), filled with culture medium (α-MEM, Invitrogen, CA) to reach 5mm in height and attached to a horizontally vibrating plate. Mixtures of silicon carbide (SiC) and talc speckles ranging in size from 3 to 20μm were suspended in the medium to facilitate the tracking of fluid motions throughout the well. The well was vibrated at 60Hz and 1g acceleration. A high-speed camera (Motion-scope, Redlake Digital Imaging Systems, FL) recorded motions of the vibrating well section and its fluid at 250fps. During the analysis, two consecutive frames (720×630 pixels) were extracted and segmented into sets of 16×16 pixel sub-images. The displacement vectors for the speckles within the sub-image were determined with a two-step fast Fourier transform algorithm.⁷

Linear sloshing analytical model

A linear wave theory solution was used to analytically describe the fluid motions caused by the horizontal oscillations.⁵ Briefly, we assumed that the fluid will have a relative velocity u = ∇ϕ with respect to the well during oscillations. The relative velocity potential of a fluid ϕ(x,y;t) with a depth (H) in a rectangular container with a width of 2a that is vibrating horizontally at an acceleration of G̈_x(t) is,

$$\varphi (x,y;t)=\sum _{n=0}^{\infty }{\stackrel{.}{C}}_n(t)sin({\alpha }_{n}x)cosh({\alpha }_n(y+H))$$ (1)

where C_n can be determined by the following differential equation.

$${\ddot{C}}_n+2{\zeta }_n{\omega }_n{\stackrel{.}{C}}_n+{\omega }_n^2{C}_n=\frac{{(-1)}^{n+1}2}{{\alpha }_n^{2}acosh({\alpha }_{n}H)}\ddot{G}(n=1,2,\dots )$$ (2)

Here, α_n = (2n−1)π/2a and w_n = α_ngtanh(α_n H) are the n^th wave number and natural frequency, respectively. ζ_n is a damping ratio to simulate the viscosity of the fluid. Taking the partial derivative of the velocity potential ϕ(x,y;t) with respect to x and y yielded the relative velocity of the fluid in the well at any given time t. Input parameters were: H=5mm, a=7mm, ζ_n=1, G=9.81m/s² and w=367.99 rad/s (60Hz). At n>3, the higher-order terms did not significantly contribute to the solution and, therefore, n=3 was used.

In vitro COX-2 experiments

As an application of the model developed above, we tested whether increasing fluid shear, independent of the peak acceleration that the cell receives, increases COX-2 gene expression levels in osteoblast like MC3T3-E1 cells. COX-2 is an enzyme that directly produces PGE₂ and thereby plays a key role in mechanically induced bone formation.^8,16 Inhibition of COX-2 and PGE₂ blocks new bone formation by mechanical signals in vivo.³³ Cells were subjected to vibrations for 30min at frequencies of either 10, 30, 60 or 100Hz in standard or viscous medium that contained 6% dextran (n=9 per group). The peak acceleration of the sinusoidal oscillatory signal was selected as 1g because data from our model indicated that this acceleration level can generate fluid shear stresses that are similar to those generating a MC3T3-E1 response in previous fluid shear investigations.^1,26 Experiments were performed at a fluid height of 2.5mm within each well to maintain optimal oxygen diffusion (Corning Inc.). Cells in the control groups were subjected to identical procedures as those in the vibration groups but the oscillating stage was not turned on.

MC3T3-E1 cells (CRL-2593, ATCC, Manassas, VA) were cultured in culture dishes (100mm, Corning Inc., NY) using α-MEM supplemented with 10% fetal bovine serum (FBS, Gibco, CA) and 1% Penicillin-Streptomycin (PS, Gibco, CA) and incubated at 37°C, 5% CO₂. Medium was changed every 48h. Cells were sub-cultured prior to reaching confluence. Cells were then seeded in 24-well plates (CLS3527, Corning Inc.) using 0.5ml of culture medium at a density of 140,000 cell/ml. Cells were then incubated at 37°C and 5% CO₂ for 24h to facilitate attachment. Prior to exposure to the mechanical signal (1g peak acceleration at 10, 30, 60, or 100Hz), the fluid in each well was aspirated out and cells were supplied with new culture medium containing 2% FBS and 1%PS. Fluid shear was modulated by increasing the viscosity of the culture medium via the addition of 6% (w/v) dextran (Molecular Weight ~70,000, Sigma, Lot#0001352455). Upon vibrating the cell culture dishes for 30 minutes, all fluid was aspirated from the wells and cells were supplemented with a culture medium without dextran containing 2% FBS and 1% PS.

Following a 30min incubation period at 37°C and 5% CO₂, cells were treated with 600ml of TRIzol (Ambion, TX) and stored at −80°C. Total RNA was isolated (RNeasy Mini Kit, Qiagen, CA) and its quality and concentration were determined (NanodropND-1000, Thermo Scientific, NY). Upon reverse transcription (High Capacity RNA to cDNA kit, Applied Biosystems, CA), RT-PCR was performed (Step-One Plus, Applied Biosystems, CA) using Taqman primer probes (Applied Biosystems, CA) for COX-2 (Mm_00478374_m1_Ptgs2) and 18S (Mm_03928990_g1_Rn18s) that served as referent. Expression levels were quantified with the delta-delta CT method.³⁴ Experiments were repeated three times with n=3 each. Results were presented as mean ± SD. Differences between groups were identified by one-way analysis of variance (ANOVA) followed by Newman-Keuls post-hoc tests. P-values of less than 0.05 were considered significant.

Results

Mechanical signals in the immediate vicinity of the cell layer

Particle image velocimetry (PIV) allowed the quantification of fluid velocities in close proximity of the well bottom. In wells filled up to 2.5mm, the shear rate between layers at 37.5, 75, 112.5 and 150μm from the bottom of the well was non-linear (R²=0.99 for 2^nd degree polynomial fit, Fig. 2), reaching peak shear stresses of up to 0.47Pa at 37.5μm and 0.15Pa at 150μm. Increasing fluid fill height from 2.5mm to 5mm decreased the shear rate almost 2-fold as a result of decreased relative fluid velocity, from 163 to 79sec⁻¹.g⁻¹.

Bulk motion of the fluid within the well

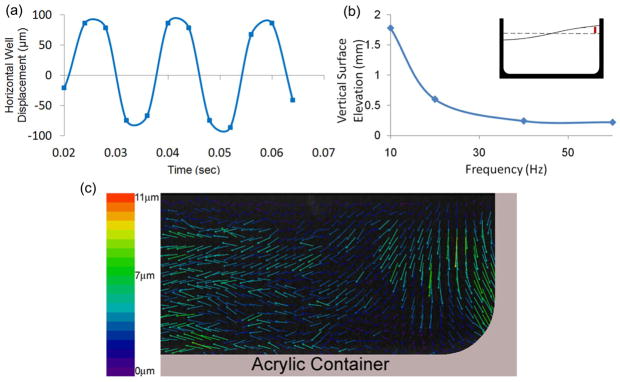
Data from the accelerometer and speckle photography confirmed that the horizontal oscillation of the well was sinusoidal with an amplitude of 152±8.2μm (Fig. 3a). By step-wise decreasing the oscillation frequency from 60 Hz to 10Hz and measuring the free surface elevation near the side wall of the well, the resonance frequency was determined to be equal or smaller than 10Hz (Fig. 3b). Thus, frequencies at 30Hz or above did not induce large nonlinear motions typically observed at resonance.^3,9,14,30 Speckle photography also quantified the oscillation-induced relative motion of the fluid within the well. The relative displacement of fluid within the well was 7.1μm±1.3 μm on average, corresponding to a phase shift of $\frac{\pi }{10.5}$ radians over a 60Hz, 1g cycle (2π) (Fig. 3c). This phase shift matched the results from the FEM that was $\frac{\pi }{10}$ radians (Fig. 4a), corresponding to 7.5μm of fluid displacement. As visualized by speckle photography, the oscillatory motion caused the direction of the fluid displacement vectors to shift to a vertical direction near the side wall, justifying the selection of a previously described two-dimensional linear model of fluid sloshing in a horizontally oscillating well.⁵

Figure 3. Motions of the well and the fluid as determined by speckle photography.

(a) Displacement of the well, during 1g, 60Hz oscillatory motions. (b) Elevation of the fluid surface near the side-wall of the well (vertical red line in inset) as a function of vibration frequency. Non-linear surface motions at frequencies around 10Hz are indicative of resonance behavior. (c) Upon completion of one full oscillatory cycle, out-of-phase fluid displacements relative to the well demonstrated sloshing behavior are visualized in the mid-sagittal plane of the well.

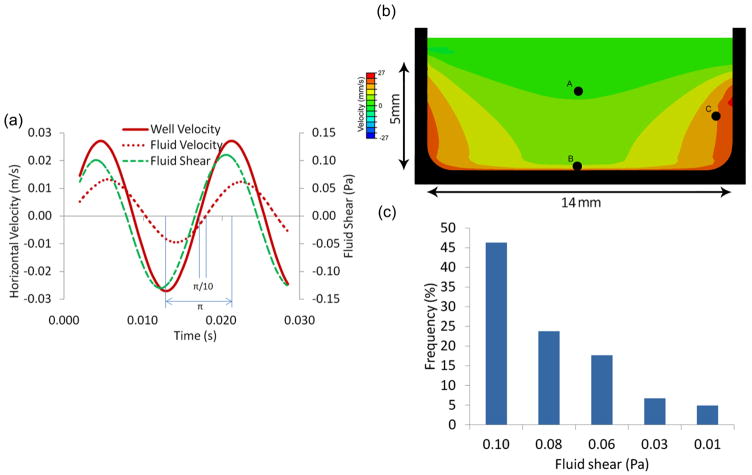
Figure 4. Fluid velocities and shear stress determined by FEM.

(a) Velocity profile of the rigid well (solid-red), fluid velocity (dashed-red), and fluid shear at Point B (see Figure 4b) during a 60Hz, 1g oscillatory motion. The phase difference between the well and the fluid was $\frac{\pi }{10}$ radians. (b) The velocity profile of the viscous fluid at t=0.005s during the 1g, 60Hz oscillatory motion of the rigid well (in black). Shown is a mid-sagittal plane of the well. Points A, B, and C were used to compare relative fluid velocities against the linear solution depicted in Table 1. (c) Histogram with the distribution of fluid nodes subjected to a given level of fluid shear at t=0.005s. In spite of spatial non-uniformity, approximately 75% of the well surface received shear stresses within 20% of the peak shear stress magnitude.

Bulk fluid motion was compared between the analytical closed-form solution and the FEM to test for potential discrepancies. Relative fluid velocities quantified at three random points within the well (Fig. 4b) were in good agreement between the two methods even though the analytical model was 2D and not 3D (Table 1). Similar to speckle photography (Fig. 3c), horizontal components of the relative fluid velocities determined by FEM decreased in the vicinity of the walls (Fig. 4b). The inhomogeneity of the flow field was reflected in the histogram of fluid shear stress magnitudes in a plane 150μm from the well bottom wall at t=0.005sec (π/4). 70% of the fluid nodes in a vertical plane experienced fluid shear between 0.10 and 0.08Pa with shear at the remaining fluid nodes decreasing to 0.01Pa at the side wall (Fig. 4c). The central region of the well was subjected to maximal fluid shear values. At 150μm from the well bottom, peak fluid shear stresses in the center reached up to 0.13Pa during a 60Hz, 1g vibration cycle (Fig. 4a). There were also vertical motions of the fluid surface due to sloshing. However, the vertical motions of the fluid surface did not propagate to layers in the proximity of the cells (well bottom) and peak vertical fluid shear was at least two orders of magnitude smaller than peak horizontal fluid shear.

Table 1.

Comparison between the linear and finite element solutions at different spatial locations as specified in Figure 3 during 60Hz, 1g oscillations. Results are represented as percentages of the peak well velocity of 0.027m/s.

	Point A	Point B	Point C
Linear Solution	98.6%	72.6%	20.7%
Finite Element	88.5%	70.4%	15%

Modulation of fluid shear stress via viscosity and vibration acceleration/frequency

FEM defined how changes in vibration frequency, acceleration magnitude, fluid viscosity and fluid volume modulated fluid shear in the vicinity of the cell layer. For a fill height of 5mm, shear rates showed an excellent agreement between FEM and PIV at distances up to 600μm from the bottom (Fig. 5). Similar agreement was observed at 2.5mm fluid fill height. For instance at 150mm from bottom wall, FEM showed a shear rate of 150 sec⁻¹.g⁻¹, compared to the experimental shear rate of 163 sec⁻¹.g⁻¹.

Figure 5. Validation of FEM simulations by PIV.

Comparison of shear rates between FEM and PIV at heights of 150, 300, 450 and 600μm from the well bottom. Measurements were taken in a well with a total fluid height of 5mm.

To increase fluid shear without altering any variable defining the vibratory signal, fluid viscosity of the medium was increased. The addition of every 3% (v/w) dextran approximately doubled the fluid viscosity from 1.05cP at 0%, to 2.12cP at 3% and 3.58cP at 6% dextran. Independent of the applied frequency and acceleration, the greater viscosity of the fluid slightly decreased fluid shear rates because of greater fluid density. However, the modest decrease in shear rates was over-compensated by the large increase in fluid shear resulting from the greater fluid viscosity. For example, the resulting peak fluid shear stresses measured at 150μm from the well bottom increased from at 0.13Pa at 0%, to 0.22Pa at 3%, and 0.33Pa at 6% dextran during 60Hz, 1g oscillations.

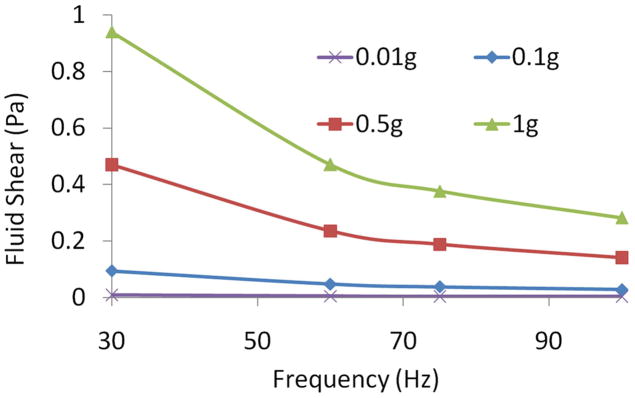
Increasing vibration frequency nonlinearly increased fluid shear. At an acceleration magnitude of 1g, fluid shear stress at 30Hz (0.94Pa) decreased by 70% when raising signal frequency to 100Hz. Increasing acceleration magnitude linearly increased fluid shear. At a vibration frequency of 60Hz, the fluid shear stress increased an order of magnitude from 0.047Pa to 0.47Pa when the acceleration magnitude was increased from 0.1g to 1g (Fig. 6).

Figure 6. Modulation of fluid shear by vibration parameters.

Peak fluid shear stress was modulated by vibration acceleration magnitude and vibration frequency, demonstrating that different combinations of frequency and acceleration can produce identical shear stress values.

Modulation of COX-2 mRNA levels by vibration frequency, acceleration, and fluid viscosity

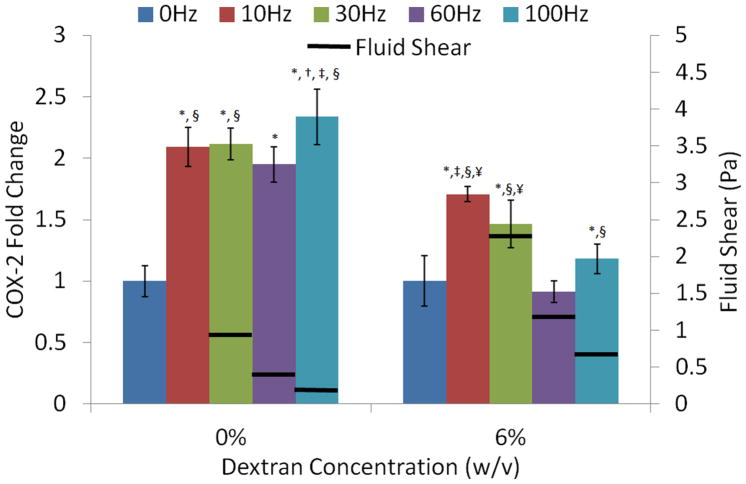
COX-2 mRNA expression was determined after a 30min exposure to a signals of 1g peak acceleration at four different frequencies (10, 30, 60 and 100Hz). Cells were oscillated in fluid viscosities of 1 or 3.5cP, corresponding to 0 and 6% dextran solutions. Cells did not lift off the well bottom during vibrations in either medium. Compared to controls, all frequencies significantly increased COX-2 gene expression except the 60Hz, 6% dextran group (Fig. 7). In standard culture medium viscosity, COX-2 transcriptional level were the highest in the 100Hz group (p<0.01). This difference in COX-2 could not be attributed to an increase in fluid shear since fluid shear stress was the smallest at 100Hz (0.28Pa). Increasing the viscosity from 1cP to 3.5cP via the addition of dextran greatly increased fluid shear stress; at an oscillation frequency of 30Hz, peak fluid shear at the well bottom increased from 0.94Pa to 2.6Pa. While control COX-2 levels were not significantly different between the 0% and 6% dextran groups, COX-2 levels increased less with vibrations in the more viscous medium. In contrast to the relatively similar COX-2 levels across the frequency spectrum in normal culture medium, there was a trend towards lower COX-2 expression in the higher frequency groups in the 6% medium; COX-2 expression in the 10Hz and 30Hz groups was significantly greater (p<0.001) than in the 60Hz and 100Hz groups (Fig. 7).

Figure 7. Change in COX-2 expression of MC3T3-E1 cells exposed to five different frequencies under low-shear (0% dextran) and high-shear (6% dextran) conditions.

Fluid shear for each frequency is represented by horizontal black bars. Shear at 10Hz could not be quantified because of resonance behavior of the fluid at this frequency. P<0.05: * against 0Hz, † against10Hz, ‡ against 30Hz, § against 60Hz, ¥ against 100Hz.

Discussion

Particle image velocimetry and finite element modeling were used to characterize mechanical signals, in particular fluid shear, that the cell layer in a culture well experiences during high- frequency vibrations. FEM, speckle photography, and an analytical sloshing model characterized the motion of the bulk flow. Cellular fluid shear stress was modulated by fluid viscosity, fluid volume, vibration frequency and acceleration. At 30Hz and 1g, shear stresses reached up to 1Pa. Tripling vibration frequency decreased shear more than 2-fold while decreasing acceleration magnitude to 0.1g reduced shear by an order of magnitude. To highlight potential applications of this model, we tested whether vibration induced fluid shear in pre-osteoblasts drives the expression of a gene known to be responsive to low-frequency fluid shear. In regular culture medium, the group that experienced the smallest amount of fluid shear (100Hz) showed the greatest increase in COX-2 expression. Increasing fluid viscosity and fluid shear muted, rather than increased, COX-2’s response to vibrations. Within this high fluid shear (viscosity) group, shear stress was negatively associated with vibration frequency and there was a trend towards greater COX-2 transcriptional levels with greater shear stresses. The absence of consistent associations between COX-2 and the mechanical variables considered here indicates that the physical mechanism by which pre-osteoblasts sense and respond to high-frequency mechanical signals in vitro is not defined by fluid shear or signal frequency.

Several limitations should be considered when interpreting our findings. The full-field velocity solutions for the well showed that shear stress is distributed spatially non-uniform with the greatest stresses at the center. While this heterogeneity precludes determination of the precise level of any given mechanical parameter that cells responded to during vibrations, it allows conclusions regarding the change in the cellular response when altering vibration parameters. Micron-sized surface features of the cell may alter local fluid shear gradients ¹⁷ but the resolution of PIV was not sufficient to capture these local variations. Thus, shear stresses quantified here via linear assumptions may slightly underestimate the true shear magnitudes experienced by cells. Lastly, the 10Hz vibration group was included in the cell culture experiments but the non-linear fluid sloshing effects at this frequency did not permit an accurate assessment of fluid shear. Thus, cells subjected to 10Hz oscillations in either the normal or dextran medium experienced much greater shear levels than the higher-frequency groups and may give an indication of the cellular response to the maximal level of fluid shear that our in vitro system can generate at a given acceleration magnitude.

Cell culture studies using vibrations as mechanical input for regulating cell activity are becoming increasingly popular.^{25,31,32,41,47,50} While these studies have been defining the biochemical response of the cell, the physical mechanism by which the signal is sensed and transduced is typically neglected. Primarily based on in vivo investigations, direct and indirect mechanisms have been suggested including out-of-phase acceleration of the cell nucleus ³⁸ or fluid shear.⁵¹ Unlike in vivo experiments in which these variables are difficult to separate, the mechanical characterization of our horizontally oscillating cell culture system demonstrates that this can be readily achieved in vitro. Vibrating the cells horizontally represents a physiologically more relevant model by creating substantial amounts of fluid shear compared to vertical vibration which primarily generates fluid shear by straining the well wall but not by vertical motions.¹⁰ A model capable not only of generating but also of precisely controlling fluid shear is critical for studying many cell types/tissues including bone in which the high viscosity of the bone marrow and the geometry of the surrounding trabecular bone can give rise to significant fluid shear during vibrations in vivo.¹¹

In contrast to the frequently used parallel plate assumption,²⁶ experimental data showed that fluid shear stress magnitude spatially increased nonlinearly towards the cell layer, perhaps a consequence of the high frequency of the fluid motion which behaved like a harmonic oscillator.⁵ Because the bone marrow cavity is entirely filled with fluid, the sloshing motion created by in vitro oscillations is different from fluid motions in vivo. The fluid within the bone marrow, however, is 40 to 400 times more viscous than water,²¹ linearly raising fluid shear caused by fluid motions. Thus, even though the space in the marrow cavity is fully filled and fluid motions induced by vibrations are much smaller than generated here, the resulting fluid shear stresses are significant.¹¹ In contrast, vibrations produce only negligible fluid shear in a fully filled cell culture well,^2,31,32 precluding comparisons to the in vivo mechanical environment. While increasing the in vitro viscosity of the fluid will increase shear, the viscosity of bone marrow cannot be modeled by the addition of dextran because of cell death at high dextran concentrations.¹⁵ Thus, the large difference between in vitro and in vivo fluid viscosities necessitates an in vitro model that raises fluid motions in an open well to generate levels of fluid shear similar to those encountered in vivo.

The most comprehensive analysis of vibration induced fluid shear stress in vivo was performed with a computational model based on mixture theory.¹¹ In this model, accelerations applied to a bone induce strain in the bone matrix which, in turn, leads to fluid shear. In this study, fluid shear was positively correlated with both viscosity and vibration frequency. In our study, fluid shear was also positively correlated with viscosity but in contrast, a negative correlation was observed between fluid shear and vibration frequency. This discrepancy is likely accounted for by differences in how confounding variables were treated. In our model, we kept acceleration magnitude constant when increasing vibration frequency, causing a decrease in peak fluid velocity and resulting fluid shear. In the previous study, however, matrix strain was kept constant when frequency was increased. As the conservation of momentum dictates that all inertial forces have to be balanced with strains, increasing the frequency decreases peak velocity (i.e., linear momentum). Thus, matrix strains can only remain constant if linear momentum is increased, implying that acceleration magnitudes increased concomitantly with frequency in their model. Our model however separated the role of accelerations from frequency and derived fluid shear stresses from relative motions of the fluid rather than from relying on very small matrix deformations.

Our COX-2 expression data from cells subjected to relatively low-shear in normal culture medium showed that shear stress was unrelated to vibration induced differences in transcriptional activity. These results are similar to those from in vivo low-intensity vibration studies, demonstrating that bone has the ability to sense vibrations over a wide range of frequencies⁵² and that higher-frequency vibrations generating less fluid shear, rather than more, can be more effective in initiating new bone for a given peak acceleration.²⁸ Increasing the viscosity of the medium by adding dextran significantly increased shear stress at all frequencies. For these high-shear conditions and in contrast to the low-shear conditions, the vibration induced increase in COX-2 expression was moderately associated with the level of shear generated, consistent with an in vivo study in which the application of large-magnitude vibrations produced a skeletal response that was dependent on shear stress (i.e., acceleration magnitude) that cells were exposed to.³⁷

Previous studies that demonstrated a frequency-dependency of COX-2 expression in bone cells used completely filled and sealed containers, largely eliminating fluid shear.^2,31 Here, using an in vitro system that allowed us to generate fluid shear magnitudes similar to those experienced in vivo (~0.1–2Pa),¹¹ we showed that amplifying fluid shear 2.6-fold via dextran decreased and not increased, COX-2 transcriptional levels. The differential response between the two distinct viscosity groups was independent of differences in osmolarity as COX-2 levels in the two control groups were identical. Ostensibly, the lower responsiveness in the higher viscosity group could be attributed to decreased chemotransport.¹³ In low-frequency fluid shear studies, 0.5–1Pa are required to elicit a biologic response in osteoblast like cells in vitro,⁴⁰ but the typically used pulsating or continuous flow profiles may provide a more potent stimulus to cells than oscillating flow generated here.²⁶ Further, a cell’s responsiveness to flow may decrease at high frequencies.¹² As peak shear generated at 30Hz in normal medium was at least 0.94Pa and no influence of shear on COX-2 was observed, our data suggest that fluid shear must reach levels of at least 1Pa for fluid shear to play a significant role in defining the cellular response to vibrations.

The only group in which vibrations did not increase transcriptional levels of COX-2 was the 60Hz, 6% dextran group. In the 0% dextran 60Hz group, the COX-2 response was not abolished but merely lower than for the other frequencies and, therefore, cells clearly have the ability to respond to this specific frequency. It is entirely possible that the (unknown) mechanism which senses and orchestrates the cellular response to vibrations is less sensitive to a 60Hz frequency. Considering that the COX-2 response was greater at 100Hz than at 60Hz at both dextran concentrations, it is also possible that this cellular mechanism is particularly sensitive to 100Hz vibrations (e.g., cytoskeletal resonance⁴⁶), and that the lack of a response in the 60Hz group, 6% dextran group merely follows the downward trend in cellular responsivity defined by the 10Hz and 30Hz signals. Previous studies indicated that the cellular responsiveness to mechanical signals can be increased by incorporating rest periods, independent of signal frequency.^39,45 Whether the addition of rest period could normalize the COX-2 response in the 60Hz, 6% dextran group remains to be determined.

In summary, we characterized the mechanical environment of cells in vitro during horizontal vibrations that exposed cells not only to oscillatory accelerations but also to oscillatory fluid shear. In this system, fluid shear can be controlled precisely and independently by acceleration magnitude, vibration frequency, fluid viscosity and fluid volume and may allow for the potential identification of the specific mechanical parameter(s) that cells respond to during the exposure to vibrations. As an example of an application of this system, we subjected an osteoblast-like cell line to four different frequencies under two distinct fluid viscosities. Under low viscosity conditions, fluid shear was a poor predictor of the molecular response. Under high fluid shear conditions, shear stress emerged as a variable that may have played at least a role in modulating COX-2 expression levels. These data suggest that other mechanical factors such as the out-of-phase acceleration of the cell nucleus^2,19 may need to be considered for investigating oscillatory mechano-transduction in cells. The identification of these mechanical factor(s) and their effects and interactions under different vibration conditions will be critical to advance our understanding of the mechanisms by which cells in different tissues respond to high-frequency mechanical signals.