Evaluation of the Technical Adequacy of Three Methods for Identifying Specific Learning Disabilities Based on Cognitive Discrepancies

Abstract

This study used simulation techniques to evaluate the technical adequacy of three methods for the identification of specific learning disabilities via patterns of strengths and weaknesses in cognitive processing. Latent and observed data were generated and the decision-making process of each method was applied to assess concordance in classification for specific learning disabilities between latent and observed levels. The results showed that all three methods had excellent specificity and negative predictive values, but low to moderate sensitivity and very low positive predictive values. Only a very small percentage of the population (1%–2%) met criteria for specific learning disabilities. In addition to substantial psychometric issues underlying these methods, general application did not improve the efficiency of the decision model, may not be cost effective because of low base rates, and may result in many children receiving instruction that is not optimally matched to their specific needs.

The statutory definition of specific learning disabilities (SLD) states that the term “means a disorder in one or more of the basic psychological processes involved in understanding or in using language, spoken or written, which may manifest itself in an imperfect ability to listen, speak, read, write, spell, or do mathematical calculations” (U.S. Office of Education, 1968, p. 34). Advocates for a cognitive discrepancy framework to identifying SLD focus on the component of the statutory definition indicating that SLD involves psychological processes, arguing that these processes should be directly assessed (Hale et al., 2010; Reynolds & Shaywitz, 2009). Considerable evidence shows that cognitive processes are associated with different types of SLD, especially when the definition specifies an academic component skill as a primary characteristic (e.g., word recognition, reading comprehension, math calculations; Compton, Fuchs, Fuchs, Lambert, & Hamlett, 2012; Fletcher, Lyon, Fuchs, & Barnes, 2007).

Despite this correlational evidence, efforts to relate cognitive patterns of strengths and weaknesses (PSW) to identification or treatment have met with limited success, especially when the focus is on individual profiles. Kavale and Forness (1984) conducted a meta-analysis of 94 studies of the validity of the Wechsler Intelligence Scales for Children—Revised (Wechsler, 1974) subtest regroupings for differential diagnosis of SLD and found that “no recategorization profile, factor cluster, or pattern showed a significant difference between learning disabled and abnormal samples” (p. 136). Similarly, Kramer, Henning-Stout, Ullman, and Schellenberg (1987) reviewed studies of scatter analysis of Wechsler Intelligence Scales for Children—Revised subtests and concluded that these measures were “unrelated to diagnostic category, academic achievement, or specific remedial strategies” (p. 42). Research with the third edition of the Wechsler Intelligence Scales for Children (WISC-III; Wechsler, 1991) found that the subtest profiles of 579 students replicated across test–retest occasions at chance levels (Mdn_K = 0.02; Watkins & Canivez, 2004).

Simulation studies represent “best-case” scenarios for an association of a cognitive pattern and SLD because simulations are not subject to errors in administration, interpretation, referral bias, and other factors that affect the observed performance of the child. However, Macmann and Barnett (1997) simulated both test–retest and alternate form reliability of WISC-III scale differences, factor index-score differences, and ipsative profile patterns; they found that the decision reliability was too poor for these techniques to be interpreted with confidence by practitioners.

Despite the poor performance of WISC profiles in both empirical and simulation studies, many practicing psychologists believe that cognitive profiles are useful for diagnostic and treatment planning purposes and patterns from the fourth edition of the Wechsler Intelligence Scale for Children (WISC-IV; Wechsler, 2003) are prominent in one PSW method (Hale et al., 2008). A survey of 354 certified school psychologists on the usefulness of WISC-III profile analysis found that 70% listed profile analysis as a beneficial feature of the test for identification and educational placement (Pfeiffer, Reddy, Kletzel, Scmelzer, & Boyer, 2000); a similar survey of SLD professionals argued for an approach to identification “that identifies a pattern of psychological processing strengths and deficits, and achievement deficits consistent with this pattern of processing deficits” (Hale et al., 2010, p. 2). The survey results suggested that the respondents believed that PSW assessments were essential for identification, indicating that there was a research base supporting this implementation of cognitive discrepancies.

Cognitive Discrepancy (PSW) Methods

Three contemporary methods that focus on evaluating the patterns of cognitive process strengths and weaknesses in conjunction with academic achievement have been proposed (Flanagan & Alfonso, 2010) and have been recommended for the identification of children with SLD in different practice documents (e.g., Hanson, Sharman, & Esparza-Brown, 2008). The three methods of cognitive PSW are the Concordance-Discordance Method (C-DM; Hale et al., 2008), the Discrepancy/Consistency Method (D/CM; Naglieri & Das, 1997a, 1997b;), and the Cross Battery Assessment (XBA; Flanagan, Ortiz, & Alfonso, 2007). Beyond correlational studies demonstrating associations of cognitive test performance and achievement, and single-case studies showing relations of profile patterns and intervention outcomes, these PSW methods have not been extensively studied in relation to identification or intervention.

Description of PSW Methods

All three methods are aimed at evaluating broad profiles of strengths and weaknesses in cognitive skills. Multiple cognitive skills are usually identified with a goal of uncovering a weakness that is related to an achievement domain. However, the weakness must exist within a set of strengths for the identification of SLD to be tenable. The tests recommended are usually highly reliable and norm referenced, based on nationally representative standardizations. A theory of human ability organization underlies each of the methods. The three methods assume that factors expressed in most definitions of learning disabilities as exclusionary have been ruled out (e.g., low achievement because of vision, hearing, or other disabilities; economic disadvantage; minority language status). They all assume that discrepancies in cognitive abilities are related to low achievement, but have different definitions of strengths and weakness in cognitive abilities and definitions of low achievement.

The C-DM method applies tests of significance to the differences between each pair of measures using the standard error of the difference (Anastasi & Urbina, 1997). The standard error of the difference represents the average amount of difference expected between two test scores if the true difference is zero and only unreliability is the cause of any observed difference. The C-DM thus requires a significant difference between the two cognitive processes, a significant difference between a cognitive process (strength) not related to the achievement measure, and no significant difference between a cognitive process (weakness) related to the academic weakness. There are no formal definitions of low achievement other than discrepancy from cognitive performance. Hale et al. (2008) proposed a z test where the standard error of the difference between any pair of results is calculated and then multiplied by the z value that gives the desired Type I error rate.

The D/CM developed by Naglieri and Das (1997a, 1997b) assesses the differences between achievement and abilities using specific tests, preferring the Planning, Attention, Simultaneous, and Successive (PASS) factors of intelligence measured by the Cognitive Assessment System (CAS; Naglieri & Das, 1997a, 1997b) and the Woodcock-Johnson tests of achievement (WJIII; Woodcock, McGrew, & Mather, 2001) because the achievement tests were administered to the same sample as the CAS norming sample. Thus, high-quality correlations among measures are available; all have high reliabilities and the test scores are expressed on the same scale. If SLD is present, there should not be differences between factors and achievement for those factors known to be highly related to the achievement domain in question (a consistency should be observed) and there should be a discrepancy between achievement and factors not as strongly related to the achievement domain. There should also be discrepancies among the PASS factors. Differences are evaluated by comparing them to tables of critical values using either standard score or regression score discrepancies. The method recognizes both significant relative weaknesses and cognitive weaknesses, where the low value in question is not just discrepant, but falls below a standard score of 90.

The XBA method for implementing the PSW framework (Flanagan et al., 2007), based on the Cattell-Horn-Carroll (CHC) theory of intelligence, includes seven cognitive clusters from the CHC. Although this method initially provided coverage of CHC constructs with tests from different batteries, the WJIII made this less important because all critical CHC clusters are measured by this battery. The XBA method does not focus exclusively on intraindividual differences in subtests or clusters, but rather on normative deficits. Flanagan et al. (2007) defined the null hypothesis as assuming that the scores will be in the normal range (85–115) until there is evidence of a deficit in the form of a score below the average range. To meet criteria for SLD with this method: (a) Low achievement is established in a given domain; (b) the child is then assessed for cognitive deficiencies, defined as a cluster score below the average range of 85–115; (c) CHC theory and research are used to determine whether any observed cognitive deficiencies are related by research to the domain in which low achievement was observed. Results from the seven clusters in the CHC model are dichotomized into below-average range and within- or above-average range. These results are then combined, using a weighting scheme based on g loadings (McGrew & Woodcock, 2001) and a g value ranging from 0.09 to 1.64 is calculated. A value ≥1 suggests that the cognitive deficiencies occur within an otherwise normal cognitive profile; a score of <1 indicates that evaluation for an intellectual disability should be considered because the profile contains many cognitive deficiencies.

Differences in the Three Methods

The C-DM has no preferred tests, whereas the D/CM relies on the CAS and prefers the WJIII achievement tests. The XBA method can use tests across different assessment batteries, but is optimized by the WJIII because it assesses all of the CHC constructs. For decision making, the C-DM uses an ipsative or within person approach and does not take into account the correlations among the cognitive and achievement variables. In contrast, the D/CM combines ipsative and normative approaches and permits corrections for the correlation of IQ and achievement tests. PASS factor scores are compared to the mean of the four PASS factor scores or to each other, which is ipsative. Naglieri and Das (1997b) also recognized that there is a distinction between a relative weakness and a cognitive weakness, the latter showing both an ipsative and a normative discrepancy. The regression portion of the D/CM is ipsative, requiring a within-person comparison. Finally, the XBA method is predominantly normative because an individual with scores in the average range on either the achievement measures or the cognitive measures should not be considered to have a disability.

Why Simulate PSW Methods? The Gold Standard Problem

Simulation techniques are typically used to assess the extent to which new statistical procedures accurately capture population values, especially when performance of the procedure does not lend itself to an analytic approach (Mooney, 1997). Simulations have been used to determine the technical adequacy of severe discrepancy score classification (Francis et al., 2005; Macmann & Barnett, 1985, 1997), to compare classification agreement between regression score and standard score discrepancies (Macmann, Barnett, Lombard, Belton-Kocher, & Sharpe, 1989), and to compare the effect of the use of alternate achievement measures on classification agreement (Macmann et al., 1989). Using IQ-achievement discrepancy methods as an example, simulations suggested that there was likely weak validity of these methods, which has been confirmed by meta-analyses showing small aggregated effect size differences in cognitive processes between IQ-discrepant and low-achieving poor readers (Stuebing et al., 2002).

Simulations of psychometric methods are important because all tests are indicators of constructs and must be adequately reliable and valid to measure the true state at the latent level. Thus, few would dispute that IQ or LD exists, but our measures of these latent constructs are imperfect because of either measurement error or construct under-representation. In its simplest form, the SLD pattern in a PSW model would include three variables. There is a low cognitive ability and a low achievement and a high cognitive ability. The observed scores arising from this latent profile will differ from it because of random measurement error. Less reliable measures will have larger deviations. Measures that are more highly correlated with each other are likely to have smaller observed differences from each other than measures that are less correlated when reliabilities are held constant. Because of this random measurement error, some observed profiles are visually consistent with the underlying pattern and some are not. In actual efforts to identify children with SLD based on these patterns, errors will occur because of these measurement problems.

Empirical evaluation of the diagnostic accuracy of PSW and other identification methods is difficult because of the lack of an agreed upon operational gold standard for SLD (Hale et al., 2010; VanDerHeyden, 2011). A simulation approach solves this problem by generating both latent and observed values from the known correlations among and reliabilities of the necessary variables. The gold standard is then the latent profile. To classify latent profiles as being consistent with SLD, we have to consider the magnitude of latent differences (effect sizes) between latent cognitive abilities or between a cognitive strength and low achievement that are large enough to be consistent with our definition of SLD. We also have to consider the size of a latent difference between achievement and the cognitive weakness that is small enough to be ignored, i.e., treated for all practical purposes as if it is zero. This is necessary because at the latent level there will be no zero differences given that the distribution of the differences of two continuous variables is also continuous and the frequency of any discrete value in a continuous distribution is zero. Arriving at the SLD designation at the latent level requires setting cutoffs for true differences large enough to warrant identification. We will call this an important difference (Thompson, 2002). It is also necessary to decide the size of a difference that is small enough to be of no consequence, or an ignorable difference (Bondy, 1969). A pattern of two predicted differences of important size and one difference of ignorable size would result in a designation of SLD at the latent level. Cases that did not meet the criteria would be designated Not SLD.

This classification is the simulated gold standard against which observed classifications can be compared. The percentage of cases that are classified as SLD at the latent level gives an estimate of prevalence or base rate for each combination of important and ignorable differences. When the simulated latent gold standard is crossed with the decisions made for each case by applying the diagnostic rules of each method, information about diagnostic accuracy (sensitivity and specificity) is obtained. The combination of diagnostic accuracy measures and the base rate for each method yields estimates of positive and negative predictive values and efficiency (Meehl & Rosen, 1955). The predictive values give the clinician information about how much confidence to place in the result of the test. Efficiency allows for evaluation of the number of errors made compared to other tests, including no test.

Research Questions

In the absence of adequate validity research and as a precursor to conducting actual classification studies, a simulation study will allow exploration of the following research questions: (1) What is the diagnostic accuracy of these three models of PSW? (2) What proportion of cases meets the definitions of SLD at the latent level? (3) How confident can practitioners be that the test results (both positive and negative) are correct? (4) Does the addition of a PSW evaluation improve on the efficiency of existing tests or classification scheme, given plausible base rates of SLD prevalence?

Method

Assumptions and Definitions

It was assumed that (a) the underlying characteristics (i.e., latent variables) used by each method are continuous and normally distributed and that multivariate normal data adequately represent the constructs and measures in which we are interested; (b) correlations from the test manuals are adequate representations of population correlations among the observed variables; and (c) reliabilities from the manuals are adequate representations of population reliabilities for the observed variables. For convenience and without loss of generality, a z score metric was used (μ = 0, σ = 1). Observed scores were composed of two parts: the latent or true part plus random error. The variance of the error was a function of the reliability of the test, which was taken from the published literature on the observed tests employed by each method. Again, for convenience and without loss of generalization, the observed scores were scaled to a mean = 100 and SD = 15.

The magnitude of a nonzero difference is critical: Surely a true difference of 0.01 z scores between two latent abilities is less likely to be related to SLD than a difference as large as 1.0 z scores, all other things being equal. This assertion implies that the latent abilities follow a multivariate distribution that is not explained by a single underlying latent dimension, i.e., we do not expect all abilities for a typically developing individual to be equal. Rather, some nonzero magnitude of difference between any two latent abilities is expected. Levels of important and ignorable levels of latent differences were chosen to span the range of plausible values or to be consistent with the decisions specified by each method.

In the absence of the empirical data necessary to choose “important” difference levels, we used a range of values consistent with the latent differences implied by the statistical tests used in the methods. For example, the difference required for statistical significance between the WISC-IV Verbal Comprehension Index (VCI) and Perceptual Reasoning Index (PRI) is ±11.0 standard score points. The mean latent difference in z scores associated with an observed difference of −11 given the reliabilities of VCI and PRI and their correlation is −1.01. The range of the latent scores for these observations is −3.6 to 0.7 and 90% of the cases fall between −1.9 and −0.26. Because this pair of variables has reliabilities for tests typically used for these methods, and because the moderate correlation between the variables is also typical for tests used in these methods, we included levels of important difference between −0.25 and −25 incrementing by 0.25. Too few cases fell below the −1.25 level to include more extreme differences as important.

In practice, the choice of an ignorable level of difference is a clinical rather than a statistical decision (Bondy, 1969). For this simulation, we looked at the distributions of latent differences between VCI and PRI and chose cutoffs that included various proportions of the population where 0.1% of the cases fall in the interval between −0.001 and 0.001, 1% fall between −0.01 to 0.01, and 14.6% of the cases fall within the −0.15 to 0.15 interval. Pairs of variables with different reliabilities but the same latent correlations would have similar proportions of the population in these bands on the latent variables. We chose −0.01 to 0.01 as the smallest level of ignorable difference to simulate because a narrower band would include too small a proportion of the population to be meaningful. We also chose several bands of larger magnitudes of ignorable difference that included larger proportions of the population. These were −0.05 to + 0.05 (9.6%), −0.15 to + 0.15 (28.24%), −0.25 to + 0.25 (45.4%), −0.50 to + 0.50 (77.2%), −0.75 to + 0.75 (93%), and −1.00 to + 1.00 (98.4%). These bands represent the full relevant spectrum where at the lower end, differences are very close to zero and at the upper end nearly 100% of the population of differences was included.

All values of important and ignorable differences were crossed and simulations were run within each combination, except for combinations that did not make sense. For example, it does not make sense to say that a difference is ignorable when it is <0.75, but important when it is ≥0.50. Each pairing of important and ignorable levels represents a plausible definition of SLD at the latent level.

D/CM and XBA use low-performance cut points (at the observed level) with a scale score of below either 85 (−1 SD in the XBA) or 90 (−0.67 SD in the D/CM) representing below-average performance. All three methods require absence of intellectual deficiency, which we defined as a composite IQ below 70. Discussion of the latent-level implementation of these cutoffs is contained within the descriptions of each specific method.

Generating the Data

Generating latent and observed variables

The correlations among the constructs for each method were calculated by disattenuating an observed large population correlation by dividing it by the product of the square roots of the reliabilities of the two measures to obtain the latent correlation, rho.

$${\mathrm{\rho }}_{\mathit{\text{xy}}}=r_{\mathit{\text{xy}}}/(\sqrt{{\mathit{\text{rel}}}_x}*\sqrt{{\mathit{\text{rel}}}_y})$$ (1)

Latent variables in z score metric with the correlational structure implied by observed correlations and reliabilities were generated using the latent variable correlation matrix and a Cholesky factorization approach (Mooney, 1997) with SAS IML (SAS Institute, Inc., 2008). The observed variables were created by generating independent random errors for each individual and variable, and creating a weighted composite where the weight for the latent variable is the square root of the reliability and the weight for the error is the square root of 1 − reliability.

$$Y_{\mathit{\text{ij}}}=\sqrt{{\mathit{\text{reliability}}}_j}*t_{\mathit{\text{ij}}}+\sqrt{1-{\mathit{\text{reliability}}}_j}*e_{\mathit{\text{ij}}}$$ (2)

Where Y_ij is the observed variable j for person i, t_ij is the latent score for person I on variable j, and e_iy is a random error.

Transforming the data

At this step Y, t, and e were all in z score metric. The observed scores were then rescaled to mean of 100, standard deviation of 15. The scores were rounded to whole numbers and extreme values outside of the published ranges for any given variable included in the method (e.g., <40 or >160 for Full Scale IQ) were truncated so that values below the minimum were reset to 40 and those above the maximum were set to 160. This process yielded observed variables with the same means, variances, reliabilities, and covariances as are found in the test manuals. A population of 1 million cases was generated for each method to ensure adequate precision (Schneider, 2008) in our estimates of classification accuracy, predictive values, and efficiency. Note that batches of observations were not analyzed separately as might be done in simulations testing the efficiency of a statistic summarizing group-level data. These methods are typically applied and decisions are made at the level of the individual, and thus this study includes 1 million replications for each method.

Creating and Evaluating Classifications

To simulate the effectiveness of each method, we applied compound rules and conditions to both the latent and observed values. The first step for each method was to reduce the 1 million observations by removing any observation where the observed Full Scale IQ (FSIQ) < 70, or fell in the range associated with intellectual disabilities. Cases where the achievement variable in question was average or above (standard score > 89) were also removed so that the set of observations would represent cases likely to have failed to respond adequately to instruction, following decisions made in other studies of instructional response (Fletcher et al., 2011; Vellutino, Scanlon, Small, & Fanuele, 2006).

The classification rules for each method were applied to arrive at classes that did (SLD) and did not (Not SLD) meet criteria for SLD. The parallel set of rules was next applied to the latent-level values, also resulting in each case being classified as SLD or Not SLD at the latent level. Cross tabs of these two classifications allowed for estimation of the true base rate of SLD for each definition as well as sensitivity, specificity, positive predictive value (PPV), and negative predictive value (NPV). Base rate is the proportion of the population designated SLD. Sensitivity is the number of method-identified true SLD cases divided by the total number of true SLD cases and is comparable to hit rate in decision theory. Specificity is the number of method-identified true Not SLD cases divided by the total number of true Not SLD cases. Positive predictive value is the proportion of method-identified true SLD cases out of the total number of cases that were method identified as SLD. Given a test that has a PPV of .85 for a given base rate, we could assume that out of every 100 cases diagnosed as SLD by our test, 85 of them are correct and 15 are false positives. The NPV is the number of method-identified true Not SLD cases divided by the total number of cases identified as Not SLD by the method. An NPV of .90 tells us that for every 100 cases where our test gives us a Not SLD result, 90 of them are correct and 10 are false negatives. Finally, we estimated the change in efficiency that would result if these methods were implemented compared to the efficiency of the decision process when the tests are not used. Meehl and Rosen (1955) defined efficiency as the proportion of correct decisions made. If no test is administered and all students were assumed to be Not SLD, the efficiency would be 1 minus the base rate of SLD in that population for that definition. Once the test is added to the decision-making process, efficiency is the sum of the true positives and the true negatives. In situations where base rate is low, it is almost impossible to develop a test that improves efficiency (Meehl & Rosen, 1955).

Results

Diagnostic Accuracy of C-DM

To simulate the C-DM, we followed an example from Hale et al. (2008) and generated 1 million observations using the reliabilities for and correlations among the WISC-IV VCI and PRI indices, FSIQ, and the Wechsler Individual Achievement Test (WIAT-II; Wechsler, 2001, reading achievement composite). (Code to generate all simulations in this study is posted on www.texasldcenter.org.) All obtained correlations among simulated data adequately reproduced target correlations (mean difference −0.0004, SD = 0.0007), indicating that the simulated data adequately reproduced the structure of the data within the norming sample. Observations where the FSIQ score was < 70 and where the WIAT-II reading achievement score was ≥90 were deleted, resulting in 221,285 cases in our referred for testing sample. The observed differences among VCI and PRI, VCI and WIAT-II, PRI and WIAT-II were calculated and compared to the cut point required for significance using the standard error of the difference approach recommended by Hale et al. (2008). At the observed level, we classified cases as SLD when three criteria were met: (a) The difference between VCI and PRI was significant and VCI was lower than PRI: (b) the difference between VCI and WIAT-II Reading was not significant; and (c) the difference between PRI and WIAT-II Reading was significant and in the expected direction. If these three criteria were not met, we classified the case as Not SLD at the observed level. For the C-DM method, 34,465 cases (15.6%) met criteria for SLD and 186,820 (84.4%) did not. At the latent level, we classified the case as SLD when: (a) The latent difference between VCI and PRI was greater than the important difference value and was in the expected direction; (b) the latent difference between VCI and WIAT-II Reading was within the ignorable band; and (c) the latent difference between PRI and WIAT-II Reading was greater than the important level and in the right direction. If these three criteria were not met, we classified the case as Not SLD at the latent level. The process was repeated within each combination of important and ignorable differences.

The results of the simulation of the C-DM are in Table 1, which shows that across different combinations of ignorable and important differences, the base rates tend to be low or very low except for definitions where the important and ignorable criteria are identical or very close. Specificity and especially NPV are very high, indicating that decisions about Not SLD tend to be highly accurate and that both false negative and false positive rates are low relative to true negatives. Sensitivity is moderate to high, rising as the effect to be detected becomes larger (i.e., larger important values). PPV tends to be low, and gets lower as the effect to be detected gets larger, which is a problem. Although not many cases are identified as SLD, those that are identified tend to be wrong (false positive errors). Because of low base rates, the efficiency or number of correct classifications without the test (E1) tends to be high, so that adding the test leads to reductions in efficiency and more incorrect classifications (E2).

Table 1.

Technical Adequacy of Concordance-Discordance Method

Ignorable Differencea	Important Differenceb	Base Rate %c	Sensitivityd	Specificitye	PPVf	NPVg	E1h	E2i
.01	.25	.6	.51	.85	.02	.99	99.4%	84.4%
	.5	.5	.65	.85	.02	.99	99.5%	84.6%
	.75	.3	.79	.85	.02	.99	99.7%	84.6%
	1.0	.2	.86	.85	.01	.99	99.8%	84.6%
	1.25	.1	.92	.85	.01	.99	99.9%	84.5%
.05	.25	3.0	.52	.86	.10	.98	97.0%	84.6%
	.5	2.3	.65	.86	.09	.99	97.2%	85.1%
	.75	1.5	.78	.85	.08	.99	98.5%	85.3%
	1.0	1.0	.87	.85	.05	.99	99.0%	85.2%
	1.25	.6	.93	.85	.03	.99	99.4%	84.9%
.15	.25	8.8	.53	.88	.30	.95	91.2%	84.9%
	.5	6.5	.66	.88	.27	.97	93.5%	86.5%
	.75	4.4	.78	.87	.22	.99	95.6%	86.9%
	1.0	2.7	.88	.86	.15	.99	97.3%	86.5%
	1.25	1.5	.93	.86	.09	.99	98.5%	85.7%
.25	.25	14.1	.52	.90	.47	.92	85.9%	85.1%
	.5	10.3	.65	.90	.43	.96	89.7%	87.6%
	.75	6.9	.78	.89	.35	.98	93.1%	88.3%
	1.0	4.2	.87	.88	.24	.99	95.8%	87.5%
	1.25	2.4	.91	.86	.14	.99	97.6%	86.4%
.5	.5	17.9	.62	.94	.71	.92	82.1%	88.6%
	.75	11.9	.73	.92	.56	.96	88.1%	89.9%
	1.0	7.1	.81	.89	.37	.98	92.9%	88.8%
	1.25	3.9	.85	.87	.21	.99	96.1%	87.2%
.75	.75	14.7	.67	.93	.63	.94	85.3%	89.4%
	1.0	8.7	.74	.90	.41	.97	91.3%	88.6%
	1.25	4.7	.78	.88	.24	.99	95.3%	87.1%
1.0	1.0	9.5	.69	.90	.42	.97	90.5%	88.1%
	1.25	5.1	.74	.88	.24	.98	94.9%	86.9%

Note. These results apply to the 221,285 cases out of 1,000,000 that remained after applying achievement (<90) and mental ability (>69) cutoffs. At the observed level there were 34,465 cases (15.6%) of SLD and 186,820 (84.4%) of Not SLD. This is the same over all latent definitions.

^aIgnorable Difference is the latent z score difference that is small enough to ignore.

^bImportant Difference is the latent z score difference that is large enough to be considered a cause of SLD.

^cBase Rate % is percentage of cases in the sample selected for low achievement but of average mental ability classified as SLD at the latent level.

^dSensitivity is the proportion of true SLD cases identified as such by the method.

^eSpecificity is the proportion of true Not SLD cases identified as such by the method.

^fPPV is Positive Predictive Value or the probability of being truly SLD given a positive test result.

^gNPV is Negative Predictive Value or the probability of being truly Not SLD given a negative test result.

^hE1 is the efficiency or percent of correct classifications made without applying the test. It is equal to 1- Base Rate %.

ⁱE2 is the efficiency or percent of correct classifications made when the test is used and is the sum of the percent of True Positives and True Negatives.

To understand these numbers, consider the implications for the cell that represents the conditions within the simulation where the ignorable difference had to be no larger than ±0.25 and the important difference had to be at least 1. The actual frequencies for this method are presented in Table 2, which shows the concordance at the observed and latent levels. The first thing to note is that 9,377 of our selected subsample of 221,285 meet this criterion at the latent level, meaning a prevalence rate of 4.24% of the tested sample and a little less than 1% of the population of 1 million. Next, the NPV value is high (99%). Thus, a negative test result will only very infrequently be wrong (in this case only 1,246 times out of 186,820). The PPV, however, is low at 24%, indicating that for this definition only about 1 out of 4 cases identified as SLD at the observed level are actually SLD at the latent level. The sensitivity of 87% indicates that we have correctly found 8,131 of the 9,377 true SLD cases. The PPV of 24% indicates that this group of 8,131 true positives is accompanied by 26,334 false positives. The specificity of .88 indicates that the classification Type I error rate for the method (not for individual tests of differences) is 12%. The efficiency or percent of correct decisions if no test is given and all observations are classified as Not SLD is 96% or 1 minus the base rate. The efficiency drops to 88% if the test is used. This value is the sum of the true positives and true negatives. More generally, these patterns are apparent across different definitions/combinations of important and ignorable differences in the C-DM: a negative identification (Not SLD) will most likely be correct, but a result of SLD is likely to be incorrect, especially when values very close to 0 are required for the ignorable difference and large differences are required for the important difference. Efficiency does not improve over the no test condition except for in the few conditions where the ignorable and important differences are identical or very close.

Table 2.

Cross Tabulation of Latent and Observed Classifications When the Ignorable Difference is .25 and Important Difference is 1.0 for the Concordance-Discordance Method

	Latent Classification
Observed Classification	Not SLD Frequency (%)	SLD Frequency (%)	Total Frequency (%)
Not SLD	185,574 (83.86%)	1246 (.56%)	186,820 (84.42%)
SLD	26,334 (11.90%)	8131 (3.67%)	34,465 (15.57%)
Total	211,908 (95.76%)	9377 (4.24%)	221,285 (100%)

Note. 221,285 cases remained after applying achievement (<90) and mental ability (>69) cutoffs to a population of 1,000,000. Observed classification as SLD required specific pattern of 2 significant differences and one nonsignificant difference among two cognitive variables and one achievement variable. Latent classification required specific pattern of two differences larger than 1.0 and one difference no larger in an absolute sense than .25. Cases not meeting these criteria were classified as Not SLD. For this definition, Sensitivity = .87, Specificity = .88, PPV = .24, NPV = .99, and base rate = 4.24%.

Diagnostic Accuracy of D/CM

For the D/CM simulation, the four PASS scales from the V (Naglieri & Das, 1997a,b), FSIQ based on the four PASS scales, and WJIII Basic Reading (WJBR) using correlations found in Naglieri and Das (1997b) were generated for a population of 1 million cases. All obtained correlations among simulated data adequately reproduced target correlations (mean difference −0.001, SD = 0.004), indicating that the simulated data adequately reproduced the structure of the data within the norming sample. After deleting low IQ and average and above WJBR, 221,598 observations remained. The same ignorable and important levels as in the C-DM simulation were used; for simplicity, we modeled only one cognitive characteristic, the Simultaneous scale, because it has the highest correlation with WJBR. All four PASS scales were simulated because their mean is required by the method. In the D/CM, Simultaneous processing can only be a cognitive weakness if it is significantly different from the average of all four of the PASS scales and if it is below the average range (i.e., < 90). The other comparisons made to determine SLD are that the achievement variable is not significantly different from the cognitive weakness, but that it is significantly different from FSIQ. We modeled the regression-based approach, which takes advantage of the known correlation between the PASS variables and the achievement measure and tests for differences between actual reading and reading predicted by either the cognitive weakness or the PASS cognitive composite IQ. We used published criteria for observed differences (Naglieri & Das, 1997a) and adopted a cut point of <90 to indicate a cognitive weakness if Simultaneous processing had already been found to be a relative weakness. At the latent level, we chose −0.667 SD as the cut point, which is consistent with an observed cut point of 90 for Simultaneous scores to be a cognitive weakness. This was only done after it had passed the test of being found a relative weakness by comparing its deviation from the average PASS score to the ‘important difference’ at each level of the simulation. This same important difference level was used when we compared WJBR as predicted by CAS composite and WJBR at the latent level.

At the observed level, we classified cases as SLD when three criteria were met: (a) The difference between Simultaneous and the mean PASS scale score was significant and Simultaneous was lower and was <90; (b) the difference between WJBR and WJBR predicted by Simultaneous was not significant; and (c) the difference between WJBR and WJBR as predicted from the CAS composite was significant and in the right direction. If the three criteria were not met, we classified the case as Not SLD. At the observed level, 6,693 cases (3%) met criteria for SLD and 214,905(97%) were Not SLD. These numbers are the same over all latent definitions. At the latent level, we classified the case as SLD when: (a) The latent difference between Simultaneous and the average of the four PASS latent variables was greater than the important level with Simultaneous being lower and less than −0.667; (b) the latent difference between Simultaneous and latent Basic Reading was within the ignorable band; and (c) the difference between the average of the four PASS latent variables and latent Basic Reading was larger than the important level and in the right direction. If these three criteria were not met, we classified the case as Not SLD at the latent level.

The results for the simulations involving this method are found in Table 3. In general, the results show a pattern similar to that observed in the C-DM simulation, characterized by high values of NPV, low values of PPV, moderate to low sensitivity, and very high specificity within comparable cells. The base rates are also low in general, although the highest rates (in the definitions where ignorable and important cutoffs are the same) are not as high as in the C-DM method. Efficiency without the test is high because of low base rates and the test improves over no test in only four definitions where the ignorable and important are identical or very close.

Table 3.

Technical Adequacy of Discrepancy/Consistency Method (D/CM)

Ignorable Differencea	Important Differenceb	Base Rate %c	Sensitivityd	Specificitye	PPVf	NPVg	E1h	E2i
.01	.25	6.3	.19	.97	.33	.95	93.7%	92.5%
	.5	3.2	.27	.98	.27	.98	96.8%	95.0%
	.75	1.4	.47	.97	.18	.99	98.6%	96.3%
	1.0	.5	.66	.97	.09	.99	99.5%	97.5%
	1.25	.2	.82	.97	.04	.99	99.8%	96.5%
.05	.25	6.9	.19	.98	.37	.94	93.1%	92.1%
	.5	3.6	.31	.97	.31	.97	96.4%	95.0%
	.75	1.6	.47	.97	.21	.99	98.4%	96.3%
	1.0	.6	.66	.97	.11	.99	99.4%	96.6%
	1.25	.2	.82	.97	.04	.99	99.8%	96.5%
.15	.25	8.5	.19	.98	.46	.93	91.5%	91.2%
	.5	4.6	.31	.98	.39	.97	95.4%	94.6%
	.75	2.0	.48	.97	.28	.99	97.9%	96.3%
	1.0	.8	.66	.97	.14	.99	99.2%	96.6%
	1.25	.2	.80	.97	.05	.99	99.8%	96.5%
.25	.25	10.2	.19	.98	.54	.91	87.8%	90.2%
	.5	5.6	.31	.98	.48	.96	94.4%	94.3%
	.75	2.5	.48	.98	.34	.99	97.5%	96.3%
	1.0	.9	.67	.97	.17	.99	99.1%	96.7%
	1.25	.3	.79	.97	.06	.99	99.7%	96.5%
.5	.5	7.4	.32	.99	.65	.95	92.6%	93.7%
	.75	3.3	.49	.98	.45	.99	96.7%	96.3%
	1.0	1.2	.66	.97	.21	.99	98.8%	96.8%
	1.25	.4	.76	.97	.07	.99	99.7%	96.6%
.75	.75	3.8	.49	.98	.51	.98	96.2%	96.3%
	1.0	1.3	.64	.97	.23	.99	98.7%	96.7%
	1.25	.4	.74	.97	.08	.99	99.6%	96.6%
1.0	1.0	1.4	.62	.97	.24	.99	98.6%	96.7%
	1.25	.4	.71	.97	.08	.99	99.6%	96.5%

Note. These results apply to the 221,598 cases out of 1,000,000 that remained after applying achievement (< 90) and mental ability (> 69) cutoffs. At the observed level there were 8031 cases (3.6%) of SLD and 213,567 (96.4%) of Not SLD.

^aIgnorable Difference is the latent z score difference that is small enough to ignore.

^bImportant Difference is the latent z score difference that is large enough to be considered a cause of SLD.

^cBase Rate % is percentage of cases in the sample selected for low achievement but of average mental ability classified as SLD at the latent level.

^dSensitivity is the proportion of true SLD cases identified as such by the method.

^eSpecificity is the proportion of true Not SLD cases identified as such by the method.

^fPPV is Positive Predictive Value or the probability of being truly SLD given a positive test result.

^gNPV is Negative Predictive Value or the probability of being truly Not SLD given a negative test result.

^hE1 is the efficiency or percent of correct classifications made without applying the test. It is equal to 1- Base Rate %.

ⁱE2 is the efficiency or percent of correct classifications made when the test is used and is the sum of the percent of True Positives and True Negatives.

Diagnostic Accuracy of XBA

The XBA (Flanagan et al., 2007) is a more complex method than C-DM and D/CM because of the number of cognitive measures included, the method of finding a cognitive deficiency within an otherwise normal profile of abilities, and the generally normative rather than ipsative approach to identifying cognitive deficiencies. The XBA requires the user to choose an age range, so we generated a population of 1 million cases for the 7 cognitive clusters as well as FSIQ and WJBR using the correlations and reliabilities for 7-year-olds in the WJIII technical manual (McGrew & Woodcock, 2001), an arbitrary decision we selected as the earliest age at which SLD might be determined. All obtained correlations among the simulated data adequately reproduced target correlations (mean difference −0.0004, SD = 0.0005). After deleting cases where the FSIQ was below 70 and WJBR was in the average range or above, 223,607 observations remained. We then applied decision rules to both observed and latent variables according to the steps outlined in the earlier description of the XBA method.

At the observed level, most of the steps within XBA involve comparisons of an observed score to a preestablished cut point value of 85 where scores below the cut point are considered low achievement or low ability. We used a range of cut point values at the latent level to establish deficiency choosing −1 (which corresponds to the observed cut point of 85, which is 1 SD below the observed mean) and −1.25 and −0.75. Each of the seven clusters was coded as a 1 (at or above the cut point) or a 0 (below the cut point) and the weights derived from the SLD Assistant version 1.0 (Flanagan et al., 2007) for 7-year-olds in second grade were applied to these codes and the products summed into the g value (Flanagan et al., 2007). A g value ≥1 indicates a profile of normal ability. A g value <1 indicates that the profile has many low values

At the observed level, we classified cases as SLD when three criteria were met: (1) Low achievement was established on WJBR, defined as a score below the average range (85–115); (2) a cognitive deficiency was found in a cluster that is theoretically related to reading for this age group; (3) the profile of cognitive abilities is otherwise normal. We ran separate simulations for four of the clusters listed as critical to early reading development in Flanagan et al. (2007): Ga (phonological awareness/processing), Gc (language development, lexical knowledge, and listening ability), Gsm (memory span), and Glr (naming facility or “rapid automatic naming”). We tested within each simulation whether the cluster in question was below 85. We determined that the cognitive deficiency existed within an otherwise “normal” profile, indicated by a g value ≥1. If all three criteria were not met, the observation was coded as Not SLD at the observed level. Otherwise, it was coded SLD. For Ga, 15,165 (6.78%) met criteria for SLD and 208,442 (93.22%) did not. For Gc, 11,493 (5.14%) met criteria and 212,114 (94.86%) did not. For Gsm, 17,099 (7.65%) met criteria and 206,508 (92.35%) did not. For Glr, 19,899 (8.9%) met criteria and 203,708 (91.1%) did not.

At the latent level, a similar three-step process occurred. We used a value of −1 as the cut point for the reading achievement latent variable in all permutations of this simulation. The WJBR test is highly reliable (r = .97), and the expected true score equivalent of a score of 85 is −0.97, which we rounded to −1.0 for convenience. After applying the latent cut points, we coded each cluster score as 1.0 if it was at or above the cut point, and as 0 otherwise, and then applied the same weights as described earlier to arrive at a latent g value. Observations were coded as SLD at the latent level when the latent Basic Reading fell below −1.0, when the cluster score was below the latent cut point, and when the g value was ≥1.0, indicating that the deficient cluster score existed within an otherwise normal profile. If these three criteria were not met, the observation was coded Not SLD at the latent level.

The pattern of results for the XBA method is similar to the other two methods with high specificities and NPVs (Table 4). The base rate is low, but with more consistency across definitions than for the C-DM or D/CM methods. The larger the low-performance deficit criterion, the more cases are included within the SLD group. This counter-intuitive result makes sense because in order to be considered SLD, most cognitive characteristics in a profile must be “normal.” When the criterion for below normal is very low, e.g., −1.25 z scores below the mean, many characteristics will be higher than this cut point and thus coded as normal.

Table 4.

Technical Adequacy of Cross-Battery Method (XBA)

Cognitive Abilitya	Low Construct Cutoffb	Base Rate %c	Sensit.d	Specif.e	PPVf	NPVg	E1h	E2i
Phonemic Awareness	−.75	5.4	.47	.96	.38	.97	94.6%	92.9%
	−1.00	6.5	.54	.97	.52	.97	93.5%	93.8%
	−1.25	6.8	.51	.96	.51	.96	93.2%	93.3%
RANj	−.75	7.0	.46	.94	.36	.96	93.0%	90.6%
	−1.00	8.6	.55	.95	.53	.96	91.4%	91.9%
	−1.25	9.1	.51	.95	.52	.95	90.9%	91.2%
Verbal	−.75	3.7	.46	.96	.33	.98	96.3%	94.6%
	−1.00	4.9	.51	.97	.48	.97	95.0%	94.9%
	−1.25	5.7	.44	.97	.49	.97	94.3%	94.2%
Memory	−.75	6.3	.47	.95	.38	.95	93.7%	91.9%
	−1.00	7.6	.54	.96	.53	.96	92.4%	93.0%
	−1.25	7.8	.51	.96	.51	.96	92.2%	92.4%

Notes:

^aCognitive Ability is the deficient variable for a given model.

^bLow Construct Cutoff is the z score cutoff used to define low ability at the latent level.

^cBase Rate % is percentage of cases in the sample selected for low achievement but of average mental ability classified as SLD at the latent level.

^dSensitivity is the proportion of true SLD cases identified as such by the method.

^eSpecificity is the proportion of true Not SLD cases identified as such by the method.

^fPPV is Positive Predictive Value or the probability of being truly SLD given a positive test result.

^gNPV is Negative Predictive Value or the probability of being truly Not SLD given a negative test result.

^hE1 is the efficiency or percent of correct classifications made without applying the test.

ⁱE2 is the efficiency or percent of correct classifications made when the test is used.

^jRAN = rapid automatic naming.

Sensitivities are moderate, ranging from .46 to .52, signifying that about half of the observations that are truly SLD at the latent level are missed. Specificity is high for all conditions, meaning that the proportion of false positives to true negatives is very low. PPV is medium small to medium, indicating that between 33% to 54% of the cases that are SLD at the observed level are truly SLD at the latent level. However, the rest are false positives, meaning that the proportion of false positives to all cases scored as positives is high. As with the other methods, many true positives are not detected and when SLD is indicated, the decision is often wrong. NPV is high across combinations, meaning that as with C-DM and D/CM, a negative result is rarely a false negative. Finally, efficiency is high for all definitions without testing, and testing improves efficiency slightly for phonological awareness, rapid automatic naming, and memory, when the low cutoff is −1.0 or lower.

Discussion

We simulated three methods for identification of SLD based on the assessment of patterns of strengths and weaknesses in cognitive processes. For each simulation, we estimated the sensitivity, specificity, PPV and NPV, and change in efficiency relative to giving no test. We also estimated the proportion of cases meeting the definition for SLD within each definition of the simulation. Such an approach is necessary because there is no gold standard for identifying SLD. Thus, the simulations allowed us to cross classify each observation as SLD or Not SLD at both the observed and latent levels, and then calculate the extent to which each method recaptured the true or latent condition as defined by that particular approach.

Overall, we found the three methods were all very good at identifying Not SLD observations. Specificity was generally higher than .85 and NPV was uniformly above .90. Sensitivity, however, varied from poor (.17) to excellent (.91) across conditions; PPV was typically quite low and never better than moderate. If the three methods are correct, only a very small proportion of the population meets the criteria for true SLD. Although the high NPV and specificity values are desirable, especially for a test that is used to “rule in” SLD as proposed for the PSW methods, with low sensitivity we are unlikely to find all of the observations that truly meet the method definition of SLD. With low PPV, we will classify many cases as SLD that are truly Not SLD. A rule-in test requires high sensitivity in the context of a moderate base rate.

To be concrete, consider what happens with a referred sample of 10,000 cases with below-average reading and average IQ. If we believed because of theory or research that a latent difference ≤0.01 SD met our definition of consistency and that a latent difference of 0.75 SD or larger met our definition of discrepancy, the C-DM would result in only 31 out of the 10,000 tested cases being SLD at the latent level. Our assessment would detect 25 out of these 31 (good sensitivity of .79). We would correctly identify 8,436 of the 9,969 who are truly Not SLD (good specificity of .85). Our assessment would indicate that 8,443 cases are Not SLD at the observed level. Only 7 of these are incorrect (false negatives), or cases that are truly SLD, but not detected by this method (high NPV of .99). The problematic number is the PPV. Our tests will identify 1,558 cases as SLD. Only 25 of these will be correct (poor PPV of .016). This leaves 1,533 cases that are wrongly labeled as SLD. If we had assumed that all 10,000 children were Not SLD, the efficiency would have been 99.7%. Adding the test drops efficiency, or the percent of correct decisions, to 85%.

If we use the D/CM within the same cell, 217 out of 10,000 meet the definition at the latent level. Our assessment would allow us to identify 89 of these cases (low to moderate sensitivity of .41). We would correctly identify 9,510 of the 9,783 who are truly Not SLD (excellent specificity of .97). The assessment would identify 9,638 cases as Not SLD. Only 128 of these decisions are incorrect (false negatives), or cases that are truly SLD, but not detected by this test (excellent NPV of .99). The problematic number is again the PPV. The assessment will identify 362 cases as SLD and only 89 of these will be correct (poor PPV of .24). This leaves 273 cases that are wrongly labeled as SLD. Thus, of 10,000 assessments, 362 are identified as SLD and only 89 of these 362 are correct.

In the XBA method, there is no ignorable value, so we cannot choose a parallel cell. Using the cell where the middle value, a normative deficit of −1 latent SDs is required and the discrepant cognitive characteristic is phonological awareness (Ga), we find that of 10,000 cases, 651 would meet the SLD definition at the latent level. The assessment would allow us to identify 353 of these 651 cases (moderate sensitivity of .54). We would correctly identify 9,024 of the 9,349 who are truly Not SLD (excellent specificity of .97). Our assessments would identify 9,322 cases as Not SLD. Only 298 of these are incorrect (false negatives), or cases that are truly SLD, but not detected by this method (excellent NPV of .97). PPV (.52) is again problematic. Our assessment will identify 678 cases as SLD, but only 353 of these will be correct, which leaves 325 cases that are wrongly labeled as positives.

Improving PSW Research

Proponents of cognitive assessments make strong assertions at national (Hale et al., 2010) and state levels (Hanson et al., 2008) about the need to use cognitive discrepancies for identification purposes. The Oregon report (Hanson et al., 2008), for example, identified all three of these methods as “research based” and immediately applicable to practice. However, as these simulations demonstrate, the three methods have serious problems that limit their applicability. One of the factors that weaken the methods and provides opportunities for improvement is the misinterpretation of tests of significance. In each example, the p value is interpreted as a statement about the probability of the alternative hypothesis, which is an inverse probability error (Cohen, 1994). All the p value indicates is the probability of obtaining data at some level of extremity, given that the null is true. What is needed for this application is the probability that the condition exists, given that the test is positive, which is what PPV tells us.

The three PSW methods also do not adequately address the fact that the cognitive and achievement constructs are correlated. Hale et al. (2008), following Anastasi and Urbina (1997), may confuse issues related to the correlation of errors of measurement and the correlation of the tests themselves. Although the errors of measurement might be uncorrelated, the underlying variables are correlated. If the correlations are known, the proportion of cases that will have differences equal to or greater than any given magnitude at the latent level can be estimated and used as the base rate of the number of cases that have discrepancies of a given size. In our simulations, the PPV is the probability that the case is true SLD given that the observed test results indicate that the case is SLD.

The three methods also prioritize Type I errors at the cost of significant risk for Type II errors, which may lead to the low base rates and low PPVs associated with each method. The consequence is a great deal of testing to determine not SLD. A stronger focus on the relation of Type I and II errors is needed.

The need to relate identification to intervention is especially urgent for PSW methods, which are motivated in part by an aptitude by treatment interaction paradigm (ATI), which Hale et al. (2010) and Reynolds and Shaywitz (2009) affirmed, but others have long questioned (Braden & Shaw, 2009; Reschly & Tilly, 1999). Pashler, McDaniel, Rohrer, and Bjork (2009) were not able to locate evidence that interventions chosen based on hypothesized group by treatment interactions (e.g., learning styles, ATI) produced better outcomes. In the case of the PSW methods examined here, the low base rate or percentage of true SLD paired with the high cost of testing is potentially concerning. If the ATI component of these methods is correct, in that only an individualized intervention that matches a specific cognitive profile will allow optimal learning for each child, then the large numbers of false positives will receive interventions matched to them at the observed level, but mismatched and thus suboptimal at the true or latent level. False positive errors would lead to effects that are iatrogenic given the premise of the ATI model, which predicts poorer outcomes when profile and treatment are mismatched.

Limitations of the Study

The present study made specific assumptions and decisions for evaluating the decision-making processes of the three methods. More complex methods based on different tests, with different covariance structures and reliabilities, may yield somewhat different results. However, the examples we chose were derived directly from research by the proponents of the methods, the correlations and reliabilities come from the test manuals, and latent cut points and effect sizes were chosen to reflect the full range of plausible values.

These results represent a simulation and actual data might perform differently. However, the data we generated closely replicated the published correlations, means, and SDs. If our assumptions hold in the actual observations, major differences would not be expected. Years of factor analytic work on variables such as these have made the same assumptions.

Similarly, we simulated the minimum number of variables needed to test each method. For the C-DM, we chose just one strength (PRI) and one weakness (VCI) and paired it with one academic outcome. For the D/CM, we looked at deficits in Simultaneous only rather than in all four of the PASS variables. Actual implementation might allow for the discovery of SLD on more than the 4 variables for C-DM, 7 variables for D/CM, and 11 variables for XBA; we have not assessed the degree of overlap within a method using different cognitive characteristics.

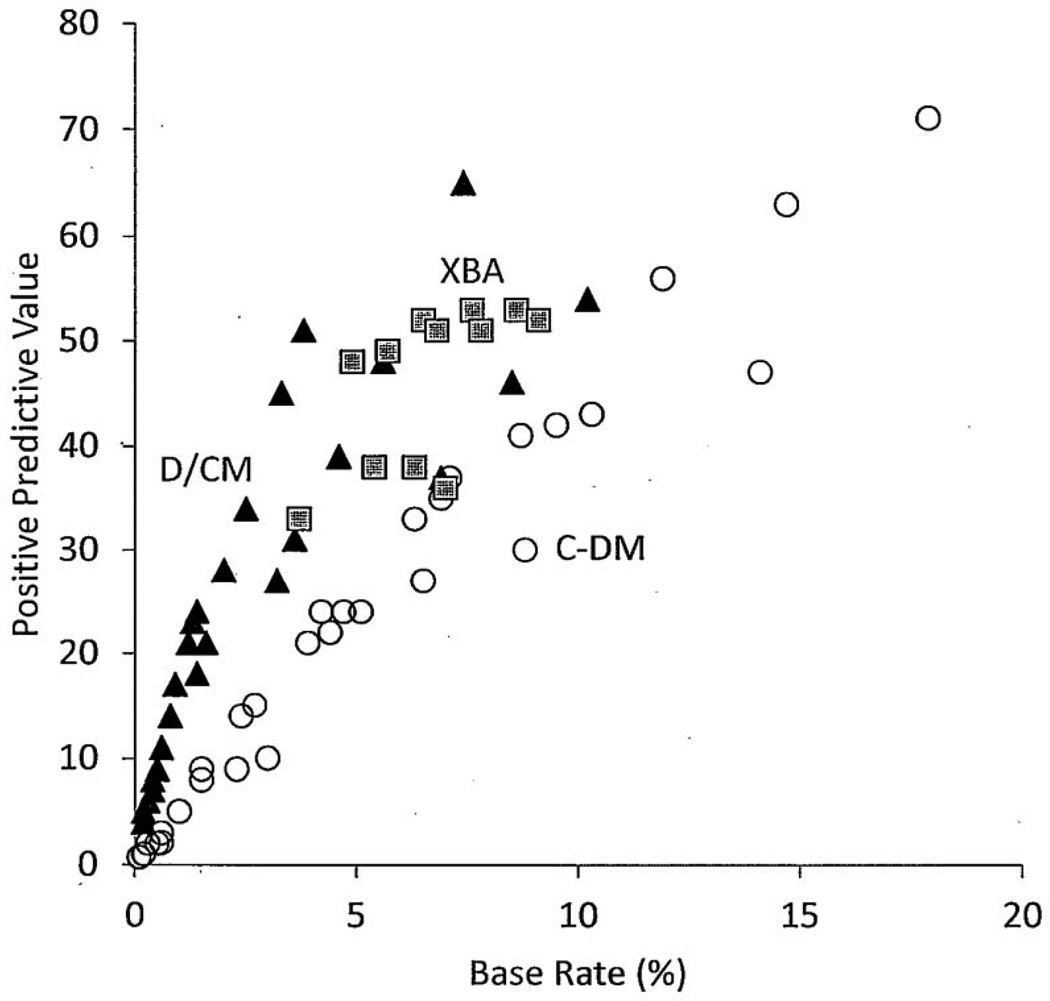
It was not possible in this study to evaluate agreement across PSW methods. In each method, the SLD type is specific to the cognitive characteristics being evaluated and to whether the method involves within person or between person comparisons. At the construct level, a deficit in latent VCI is not the same as a deficit in latent Simultaneous, or in latent Gc. A method that uses primarily normative criteria is not likely to agree with one that uses ipsative criteria on which cases represent true SLD. Finally, the base rates across the methods vary. If the problematic PPV is plotted against base rate across all definitions in the simulation for all three methods, we see (Figure 1) that the PPV for the D/CM or regression based model is highest for most levels of base rate, XBA is next highest and C-DM tends to be lowest.

Figure 1.

Comparison of positive predictive value when base rate is held constant. Note. C-DM = Concordance-Discordance Method; D/CM = Discrepancy/ Consistency Method; XBA = Cross Battery Assessment. In general, for any given base rate, D/CM has higher PPV than either XBA or C-DM, and XBA has higher PPV than C-DM.

Although this investigation began each simulation with a population of 1 million cases, the actual evaluation was done on the segment of this population representing those with low achievement. A cut point for low performance at the 25th percentile was chosen based on the literature (Fletcher et al. 2011; Vellutino et al., 2006). Other low-performance cutoffs could have been chosen, e.g., reading performance below 85, or the 16th percentile. We simulated the effect of using a cut point of 85 across the three methods for a number of cells and found that the effect was to improve sensitivity from 7 to 15 points across cells, without changing specificity, NPV, and PPV >1%–2%. We also ran additional simulations within the cells described earlier for the C-DM model after deleting only low-ability cases (IQ < 70) because the C-DM model does not require low performance for SLD. Sensitivity dropped 1–5 points, specificity improved about 5 points, and PPV, NPV, and base rate were virtually the same.

In practice, it is possible that some cases we included in our pool that had not responded (based on low achievement) would have been eliminated from consideration for further testing because of application of exclusionary criteria, such as economic disadvantage or another disability. What is unknown is whether this culling would result in differential removal of observations with and without the SLD profiles. Future simulations should include data about the relation of latent SLD profiles and exclusionary criteria. In addition, it is possible that only a subset of the cases included in our pool because of low achievement would have been referred by parents or teachers for further testing. For this to bias our results, we would have to demonstrate that parents and teachers are able to distinguish between LD and low-achieving students. Gresham and MacMillan (1997) reported that although teachers are accurate in distinguishing poor performers from controls, they were not able to distinguish between LD and low achieving.

Naglieri and Das (1997b) and Flanagan et al. (2007) both emphasized relations of outcomes and intervention with cross-person factor structures addressing the construct validity of the cognitive tasks. These simulations are also based on latent cross-person factor structures. However, it is not clear that this type of correlational data are adequate for within person methods. For example, how well does a cross-person factor structure represent the cross-time relations? This larger question of whether interindividual data are appropriate for studying intraindividual methods needs further consideration (Molenaar, 2004).

Finally, this study began with the assumption that is shared by the majority of the research on these constructs, which is that these abilities and achievement constructs are dimensional and that SLD exists on this continuum of multivariate normal space. An alternative starting place begins with a mixture of populations where the multivariate normal relations are specific to each population and the primary difference across populations is in the covariance structure rather than mean vectors.

Conclusions

The current study does not question that cognitive processes underlie academic skills or their manifestations as SLD. However, the idea that cognitive processes make SLD “qualitatively and functionally different from low achievement only” (Hale et al., 2010, p. 3) has not been established and would seem particularly challenging given the dimensional nature of the attributes of SLD and the lack of evidence for qualitative cognitive processing differences between adequate and inadequate responders (Fletcher et al., 2011; Vellutino et al., 2006). These present simulations suggest that a great deal of expense could be needed just to determine who is eligible for certain interventions and that much of that expense would be for naught as the methods yield far too many false positive cases to be cost effective. However, the cost effectiveness of the PSW method was not evaluated with the current data and suggests an area for future research. Ironically, testing would match the false positives with a form of instruction that does not optimally support their learning. Thus, these PSW methods may not be a solution for the problems associated with identification of SLD and certainly do not appear to be strong implementations of the PSW framework. To make progress, it is likely that the dimensional nature of SLD needs to be rigorously addressed and multiple criteria used with a focus on an appropriate balance of false positive and negative errors.

Biographies

Karla K. Stuebing, PhD, is a research professor at the Texas Institute for Measurement, Evaluation, and Statistics, Department of Psychology, University of Houston. Her research focuses on measurement issues in development disorders.

Jack M. Fletcher, PhD, is a Hugh Roy and Lillie Cranz Cullen Distinguished Professor of Psychology at the University of Houston. He is the principal investigator of the NICHD-funded Texas Center for Learning Disabilities. His research addresses classification and definition and the neuropsychological and neurobiological correlates of learning disabilities.

Lee Branum-Martin, PhD, is a research assistant professor at the Texas Institute for Measurement, Evaluation, and Statistics, Department of Psychology, University of Houston. His research focuses on multilevel and latent variable measurement issues in literacy.

David J. Francis, PhD, is a Hugh Roy and Lillie Cranz Cullen Distinguished Professor and Chairman of Psychology at the University of Houston. He is the director of the Texas Institute for Measurement, Evaluation, and Statistics, with a long-term focus on measurement issues in learning disabilities.