Abstract
Background
Radial movement of the arterial wall is a well-known indicator of the mechanical properties of arteries in arterial disease examinations. In the present study, two different motion estimation methods, based on the block-matching and maximum-gradient algorithms, were examined to extract the radial displacement of the carotid artery wall.
Methods
Each program was separately implemented to the same axial consecutive ultrasound images of the carotid artery of 10 healthy men, and the radial displacement waveform of this artery was extracted during two cardiac cycles. The results of the two methods were compared using the linear regression and Bland-Altman statistical analyses. The maximum and mean displacements traced by the block-matching algorithm were compared with the same parameters traced by the maximum-gradient algorithm. The frame numbers in which the maximum displacement of the wall occurred were compared too.
Results
There were no significant differences between the maximum and the mean displacements traced by the block-matching algorithm and the same parameters traced by the maximum-gradient algorithm according to the pair t-test analysis (p value > 0.05). There was a significant correlation between the radial movement of the common carotid artery measured with the block-matching and maximum-gradient methods (with a correlation coefficient of 0.89 and p value < 0.05). The Bland-Altman analysis results confirmed a good agreement between the two methods in measuring the radial movement, with a mean difference and limits of agreement of 0.044 ± 0.038. The results showed that both methods found the maximum displacement occurring in the same frame.
Conclusion
Both block-matching and maximum-gradient algorithms can be used to extract the radial displacement of the carotid artery wall and in addition, with respect to the pixel size as error, the same results can be obtained.
Keywords: Ultrasonography, Carotid arteries, Motion, Algorithms
Introduction
Sclerotic and ageing changes in the human cardiovascular system are well reflected by the status and structure of carotid arteries. The elastic properties of the carotid artery are affected by different physiological states and external stimuli. The carotid artery wall structure, thickness, and stiffness are good indicators for the estimation of the risk of stroke, myocardial infarction, and vascular disease. This artery is well accessible by ultrasonic investigation and also is the main vessel supplying blood to the brain; ultrasonic investigations of the carotid artery have, therefore, been the target of numerous attempts.1, 2
Arteries in the human body are constantly moving due to the mechanical stresses to which they are subjected. In fact, blood pressure, blood flow, and tethering to the surrounding tissue cause stresses on the arterial wall, resulting in its motion. Stresses can lead to strains in three directions which, in relation to a B-mode ultrasonic image, correspond to changes in the radius of the vessel, changes in the axial length, and movement out of the B-mode section.3 This motion may be responsible for tissue rupture and cerebrovascular symptoms.
The high resolution B-mode ultrasonic imaging of the carotid artery is widely used in the diagnosis of atherosclerosis as it allows non-invasive measurements of the intima-media thickness and lumen diameter and assessment of the degree of stenosis as well as of plaque morphology. In addition to this, temporal sequences of ultrasound images can be employed to estimate the movement of the carotid artery wall.4, 5 It has been confirmed that B-mode ultrasonic images, in combination with appropriate image-processing methods, may be utilized to extract useful physiological indices of the carotid artery wall, including anatomical, texture, and elasticity features (Grava C, Gacsádi A, Gavriluţ I. Arterial elasticity maps obtained by using basic block-matching methods. IEEE 2009;151–154. & Stoitsis J, Golemati S, Koropouli V, Nikita KS. Simulating dynamic B-mode ultrasound image data of the common carotid artery. IEEE Workshop Imag Syst Tech 2008;144–148.). But because of the nature of ultrasound imaging, there are regions in the image with insufficient image data to guide fully automated methods. However, with minimal operator input, semi-automated methods work well and provide reproducible estimates of luminal and vessel dimensions under realistic conditions (Herrington DM, Johnson T, Santago P, Snyder WE. Semi-automated boundary detection for intravascular ultrasound. IEEE 1992;103–106.).
Boundary-detection algorithms often have been applied just to measure the intima-media thickness and internal diameter of arteries. We assessed the diameter changes of the carotid artery from consecutive ultrasonic B-mode images using the maximum-gradient algorithm.6 Since motion analysis results have a significant role in diagnostic interpretation and different motion analysis methods may result in different findings, a comparative study of the block-matching and maximum-gradient algorithms for the estimation of the carotid artery wall motion in the radial direction is presented.
Methods
In the present study, two different methods are employed for a quantitative analysis of the carotid artery wall motion in the radial direction. The first method is based on the block-matching algorithm.7, 8 In the block-matching algorithm, as long as the brightness intensity is assumed to be constant, given a block of pixels or reference block in the current frame, matching consists in finding the block in the next (or previous) frames that best matches the block in the reference frame. The method requires a good measure of match. In order to avoid the incorrect matches, the search for the best-matched block is typically constrained to a searching window, the size of which has to be appropriately chosen because it may affect the motion analysis results. The information obtained from a single pixel is not discriminatory enough to ensure unique matches. This is why the supplementary assumption is made that all the neighbor pixels in a block have the same movement. Thus, instead of one pixel, a block of pixels centered in the current pixel is considered (the reference block). Another assumption for correlating the movement of echo patterns to the associated tissue motion is that motions are in plane and are small. The displacement vector is estimated by matching the information content of a measurement window with that of a corresponding measurement window within a search area, placed in the previous frame.
In the block-matching motion estimation methods, the best match is found by maximizing a similarity measure.9 The maximization of appropriate correlation measures or coefficients can be also used in the block-matching methods.10 This algorithm allows the automatic motion tracking of one or more region(s) of interest [ROI(s)] on the vessel wall, in a sequence of ultrasound images.9, 10
The second method is edge detection based, which is a combination of dynamic programming and maximum gradient. The dynamic programming algorithm is an optimization of the cost function by finding optimal polyline, corresponding to the artery boundary. Within a rectangular region close to the boundary searched for, local measurements of echo intensity, intensity gradient, and boundary continuity are extracted and included as weighted terms in a cost function. Each image point of the search region then gets a specific cost. The points are thereafter connected by lines forming a polyline, and the scanning of the image line by line in horizontal direction is performed. The optimal polyline is the one that minimizes the cost function. The maximum-gradient algorithm searches along a path perpendicular to the boundary and picks up the point of maximum intensity gradient. The reference points are placed in the middle of the artery. The points are subsequently connected by lines, and the scanning of the image line by line in the horizontal direction is performed. The gradient of each vertical line is calculated. The boundaries are searched for the local maximums of the image line’s gradient to the left and to the right from the predefined middle line. This algorithm has been previously validated by the manual method.6 Since the dynamic programming algorithm has the highest accuracy and the maximum-gradient algorithm requires no training to perform measurements,1, 4, 11 we combined them and designed new software in which the reference points were selected as the maximum-gradient algorithm and the points with maximum gradients were picked up. Afterward, the best candidates were those with the least cost function. The cost function was defined according to the dynamic programming algorithm.
The ultrasonic examination of the right common carotid artery of 10 healthy men (aged 41 ± 2 years) with no history of cardiovascular disease, hypertension, or diabetes2 was performed. All the subjects gave informed written consent for the examination. Before ultrasonography, the subjects rested for at least 10 minutes in the supine position until their heart rate and blood pressure reached a steady state. The common carotid artery of the subjects, 2–3 cm proximal to the bifurcation, was examined with a Sonoline Antares (Siemens, Germany) ultrasound system equipped with a 5 – 13 MHz linear transducer. the audio video interleave (AVI) format of the consecutive images of the common carotid artery with a frame rate of 30 frames per second was transferred to a PC for post processing. Each recording contained two cardiac cycles, and the right common carotid artery was scanned in the longitudinal direction. The software was designed in MATLAB software to extract consecutive images in the bitmap image file (BMP) format from the AVI movies. This software provided the image dimensions (the images were 547 × 692 pixel2), image type (B-mode), and pixel dimensions (0.063 × 0.063 mm2).
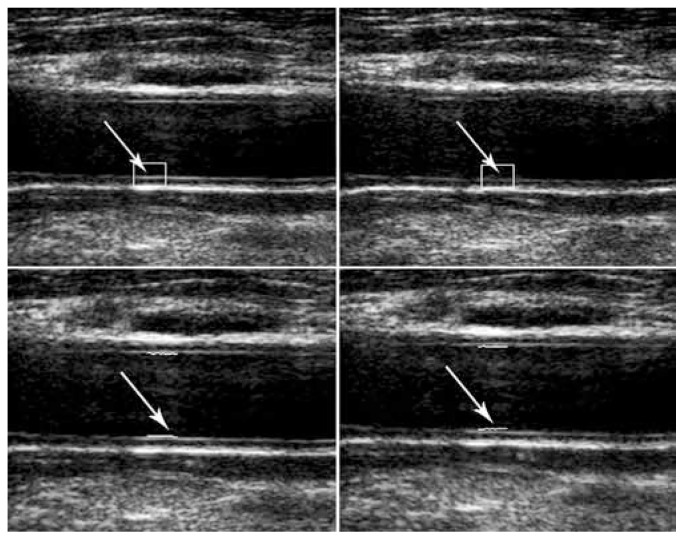
Because the far wall has better reflections due to the interface blood-intima-media layers and the arterial wall on the far side from the transducer are thus more convenient for measurements,1 the measurement of the radial movement based on the block-matching algorithm was performed using ROI with a size of approximately 53 × 42 pixel2 on the intima-media thickness of the posterior wall of the artery. The second algorithm was thereafter implemented; the reference points were selected in the first frame approximately at the center of the reference block of the block-matching algorithm. Then the blood-intima boundary was searched in the perpendicular direction and the points with maximum gradients were picked up, with the best candidates being those with the least cost function (Figure 1).
Figure 1.
Wall motion detection in two sequential frames by block-matching algorithm (A), and maximum-gradient algorithm (B). Arrows show region of interest
Our ultrasonic image pixel had a dimension of 0.06 × 0.06 mm2. By interpolating, 100 boundary points were obtained; and by considering the measurements in two cardiac cycles, measuring error would become less than 0.003 mm.
All the data are expressed as mean ± standard deviation (SD). The data were tested for normal distribution and homogeneity of variance by the Kolmogorov-Smirnov test (K-S) and Levene test, respectively. In the pilot study, we extracted 200 arterial displacements from the images of 4 subjects. The maximum sample size for the Pearson correlation analysis was estimated on 11 images with a confidence level of 95% and power of test of 90%. The Pearson linear correlation and the Bland-Altman analysis12 with a 95% limit of agreements (LOA) (i.e., mean difference ± 1.96 SD of the difference) were calculated to assess the relationships between the two methods, block-matching algorithm and combination of dynamic programming and maximum-gradient algorithm for the motion estimation of the arterial walls. A comparison of the differences of the maximum and the mean of the radial displacements of the right common carotid artery was done with the paired samples t-test. The results were considered significant when the probability value was < 0.05. Intraobserver and interobserver variability was defined as differences between the two measured methods and expressed as a percentage error of the means and was carried out as follows:
The images of one random subject were examined by two observers: the person who had examined all the other images and another observer. Each of them evaluated the radial movement of the arterial wall three times using each algorithm. The percentage of the coefficient of variation was defined as:
Where SD and mean value are standard deviation and mean value of the measurements using each algorithm, respectively.
All the statistical analyses were performed using the SPSS software package (SPSS Inc. Chicago, IL, USA).
Results
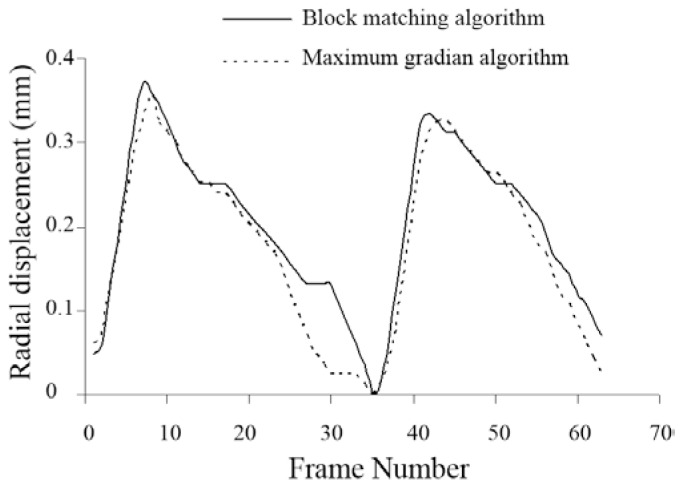
For one of the subjects, the radial displacement waveforms at each frame via the block-matching and maximum-gradient algorithms are depicted in Figure 2, which demonstrates a good agreement between the waveforms.
Figure 2.
Radial displacement waveform (mm) of the carotid artery wall obtained from the block-matching and maximum-gradient algorithms
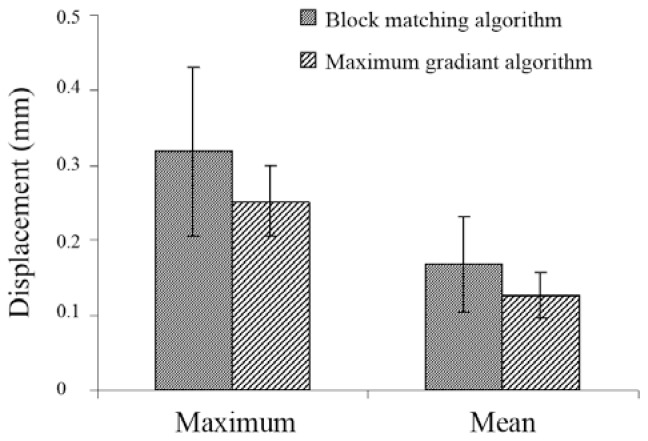
The maximum and the mean of the radial displacements of the right common carotid artery were extracted throughout two heart cycles via the block-matching algorithm and maximum-gradient algorithm in the 10 healthy subjects. The results are shown in Figure 3. The measurements of the maximum and the mean radial displacements using the block-matching algorithm are respectively 0.06 and 0.04 mm greater than the values obtained from the maximum-gradient algorithm.
Figure 3.
The mean ± standard deviation of the maximum and mean radial displacement of the carotid artery wall for the 10 subjects obtained via the block-matching and maximum-gradient algorithms
The statistic analysis showed no differences between the two methods of the block-matching and the maximum-gradient algorithms (p value > 0.05). The coefficients of variation percent (CV %) for the arterial displacements in the block-matching and the maximum-gradient algorithms were 0.47% and 0.04%, respectively.
This study compares the relation between radial displacements measured by automated methods, i.e. the block-matching and the maximum-gradient algorithms. The correlation between the values of the block-matching analysis and the maximum-gradient tracing was assessed by the Pearson correlation analysis. The Pearson linear correlation coefficients were calculated to analyze the similarity between the displacement waveforms acquired from the two methods for our 10 subjects with 200 frames for each ones (Table 1).
Table 1.
The Pearson linear correlation coefficients and p values for the wall radial movement of the common carotid artery of the 10 healthy subjects
| Subject | Correlation coefficient | P value |
|---|---|---|
|
|
|
|
| 1 | 0.876 | 0.000 |
| 2 | 0.966 | 0.000 |
| 3 | 0.938 | 0.000 |
| 4 | 0.969 | 0.000 |
| 5 | 0.901 | 0.000 |
| 6 | 0.908 | 0.000 |
| 7 | 0.868 | 0.000 |
| 8 | 0.777 | 0.000 |
| 9 | 0.988 | 0.000 |
| 10 | 0.848 | 0.000 |
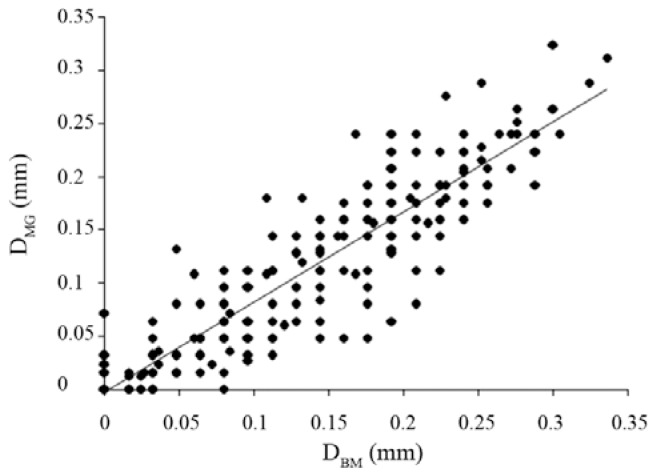
There was a high correlation between the radial displacement as measured by the two methods, namely the block-matching algorithm and the maximum-gradient algorithm (R = 0.89, p value < 0.05) (Figure 4).
Figure 4.
Scatter plot demonstrating the correlation between the radial displacements (mm) of the right common carotid artery as measured by the block-matching method (DBM) and the maximum-gradient method (DMG)
By the linear regression analysis, the regression function between the radial displacements measured by the block-matching and the maximum-gradient tracing methods was predicted as: DMG = 0.847 × DBM − 0.003, where DMG and DBM are radial displacements measured by using the maximum-gradient and block-matching algorithms, respectively. The radial displacements in the right common carotid artery measured by the block-matching algorithm method were significantly correlated to the radial displacements measured by the maximum-gradient algorithm manual method (p value < 0.05).
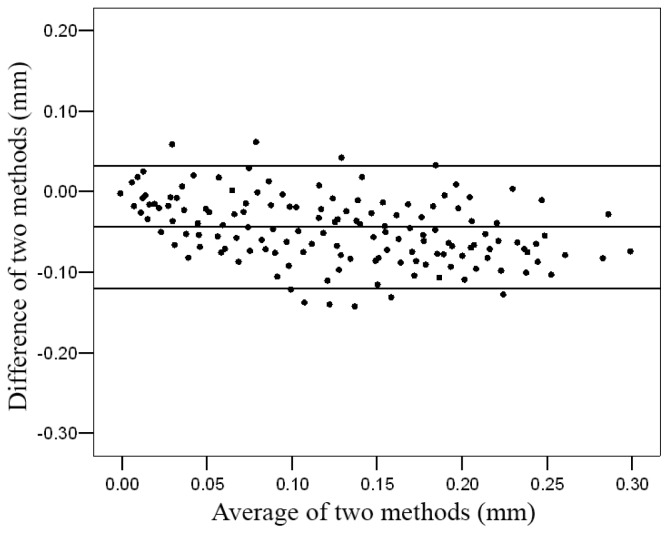
For the Bland-Altman analysis, the difference between the arterial wall displacement changes estimated from the regression function and changes displacement measured by using the block-matching algorithm was plotted against the average of both observations. The middle line indicates the average difference between the two methods, whereas the outer lines represent 2SD or the 95% limits of agreement (LOA) (Figure 5).
Figure 5.
Relative Bland-Altman plot of the difference between arterial wall displacement changes estimated based on the block-matching method and maximum-gradient method. The outer lines represent 2 standard deviation or the 95% limits of agreement
Confidence interval was 95%. There was a high agreement between the two methods. The mean difference between the estimated displacement and measured displacement was −0.044 ± 0.038 mm. The Bland-Altman analysis results confirmed a good agreement between the two methods in measuring the radial movement (Figure 5).
Table 2 shows the frame number in which maximum displacement of each cardiac cycle of the subjects occurred for both algorithms. As it can be seen, both methods found the maximum displacement occurring in the same frames (± 1 frame) and just in three cycles; this difference is more than one frame.
Table 2.
Frame number in which maximum displacement was found by each algorithm
| First maximum(Frame No.) | Second maximum (Frame No.) | |||
|---|---|---|---|---|
|
|
|
|||
| Subject | Block matching algorithm | Maximum gradient algorithm | Block matching algorithm | Maximum gradient algorithm |
|
|
|
|
|
|
| 1 | 16 | 15 | 53 | 50 |
| 2 | 8 | 8 | 31 | 32 |
| 3 | 9 | 9 | 39 | 40 |
| 4 | 7 | 7 | 42 | 43 |
| 5 | 8 | 8 | 37 | 36 |
| 6 | 16 | 17 | 39 | 40 |
| 7 | 13 | 10 | 40 | 40 |
| 8 | 8 | 8 | 31 | 31 |
| 9 | 6 | 6 | 31 | 31 |
| 10 | 7 | 7 | 34 | 37 |
The intraobserver and interobserver variability of maximum and mean radial displacement was 0.47% and 0.48% for the block-matching algorithm and 0.04% and 0.09% for the maximum-gradient algorithm, respectively.
Discussion
Because of the important role of the arterial wall motion in discriminating mechanical properties between healthy and diseased vessels, several methods have been used for evaluating the mechanical properties of arteries.13–15 Among them, ultrasonography, as a non-invasive, safe, and cost-effective method, has always been of great interest for estimating both motion amplitude and direction from temporal consecutive images.16–18
In this study, we showed that high resolution B-mode ultrasound can be used to evaluate the mechanical properties of the arterial wall by calculating the displacement of the arterial wall during cardiac cycles using a computerized analyzing method. The interface location is commonly determined by using computer-based interactive tracing systems. Efforts have been made to make the measurement less operator-dependent by introducing automated image analysis procedures. The two methods of block-matching algorithm and a combined algorithm of dynamic programming and maximum-gradient are implemented for measuring the arterial wall changes of the common carotid in healthy subjects.
Two-dimensional block-matching time domain approaches to speckle tracking have found widespread application because of their inherent simplicity and relative immunity to noise.7 Golemati et al. demonstrated that the two-dimensional motion of the normal and diseased arterial wall as well as the surrounding tissue can be accurately quantified through cross-correlation.5, 19 They compared block matching and optical flow and the effect of the block size on the arterial wall motion estimation of 10 healthy subjects in both radial and axial directions.3 They also attempted to combine a FIELD-∏ software based ultrasound simulation approach with mathematical modeling of the arterial wall motion. The simulated sequential image data may be used to evaluate the performance of motion analysis algorithms.7 Persson et al. designed and demonstrated a new non-invasive method for longitudinal and circumferential movement estimation.20 Cinthio et al. evaluated this echo-tracking system based on block matching for measuring radial and longitudinal movements of small regions of the intima-media complex of the arterial wall. They subsequently used this to estimate the longitudinal movement and resulting shear strain of the arterial wall.21
Other different image analysis algorithms have been investigated for automated ultrasonic boundary detection. These are the dynamic programming, maximum gradient, model-based, and matched filter algorithms. These methods were implemented to measure the intima-media thickness and internal diameter of arteries; and among them, dynamic programming and maximum gradient have the highest accuracy.1, 4, 22
Wendelhag et al. used the dynamic programming algorithm for developing a computerized analyzing system to evaluate the boundaries of the intima-media.23 Chang et al. proposed an automatic system for detecting the intima-media thickness of the common carotid artery using the snake techniques. They showed that the computerized system had the potential in automatically detecting the intimal and adventitial layers without any manual correction.24 Jegelevicius et al. employed the dynamic programming and maximum-gradient algorithms for measuring the intima-media thickness in a single frame, separately.
They suggested the maximum gradient for intima-media thickness measurement.15 But all of the above-mentioned studies, was used the computerized analyzing method for detecting the lumen diameter or intima-media thickness in a single frame, and method for making the actual measurements over the entire cardiac cycle to capture the dynamic nature of the vessel are spars.
In the present study, we detected the absolute carotid artery wall displacement in the radial direction by tracking the location of a block and using a maximum-gradient-based algorithm. The echo-tracking algorithm has been used most frequently in the studies on the arterial wall motion due to its computational simplicity and accuracy. On the other hand, ultrasonic boundary detection algorithms based on the maximum gradient and dynamic programming have been rarely used to extract arterial wall motion. The results of the present study showed that in conjunction with the arterial intima-media thickness and internal diameter measurements, boundary detection algorithms can be used for arterial wall motion detection. From the computation complexity view, maximum gradient was higher than block matching, and it required manually placing the approximate boundary points and was more time-consuming. The most important advantage of maximum gradient over block matching is its ability to detect the coincidental waveforms of the anterior and posterior wall motion and thus the arterial diameter changes.
The results of the presents study showed that the maximum and mean radial displacements acquired from block matching were respectively 0.06 and 0.04 mm greater than the values gained from maximum gradient. Regarding the pixel size, the differences had the order of one pixel size. The greater values of the block-matching measurements can be related to its more accurate searching method. In the block-matching techniques, the intensity of a block of pixels is compared with the reference frame and the best match is found by maximizing the similarity. Consequently, more accurate two-dimensional tracking is possible. But in maximum-gradient-based algorithms, searching is performed in just one direction, perpendicular to the boundary, and the point of maximum intensity gradient is picked up. Thus, with the presence of echo-dropout, it fails to track the boundary and the average of neighboring points is replaced.
Our regression analysis demonstrated a good correlation, with a correlation coefficient of 0.89, between the two methods in measuring the radial displacement of the carotid artery wall. The Bland-Altman statistical analysis, with the mean difference and limits of agreement of −0.044, −0.12 and 0.032 respectively, confirmed this correlation. Low dispersion coefficients showed high reproducibility of both methods, higher for the maximum-gradient method.
Despite the differences in the radial displacements obtained from the two algorithms, it is notable that in seventeen out of twenty cardiac cycles, maximum displacements occurred in the same (± 1) frame, showing the coincidence of cardiac events for both algorithms.
Conclusion
The results of the present study showed that both block-matching and maximum-gradient algorithms can be used to extract the radial displacement of the carotid artery wall; and regarding the pixel size as error, the same results can be obtained. In spite of the two-dimensional searching of the block-matching algorithm, maximum gradient seems to have higher reproducibility and is more user-friendly. Thus we suggest the maximum-gradient algorithm for further studies on the radial movement of the arterial wall.
Acknowledgment
We want to thank Dr S. Shams Hakimi for their valuable technical assistance. This study has been approved by Institutional Review Board and Ethics Committee of Tarbiat Modarres University.
References
- 1.Jegelevicius D, Lukosevicius A. Ultrasonic measurements of human carotid artery wall intima-media thickness. Ultragras. 2002;2:43–47. [Google Scholar]
- 2.Schmidt-Trucksäss A, Grathwohl D, Schmid A, Boragk R, Upmeier C, Keul J, Huonker M. Assessment of carotid wall motion and stiffness with tissue Doppler imaging. Ultrasound Med Biol. 1998;24:639–646. doi: 10.1016/s0301-5629(98)00023-4. [DOI] [PubMed] [Google Scholar]
- 3.Golemati S, Sassano A, Lever MJ, Bharath AA, Dhanjil S, Nicolaides AN. Carotid artery wall motion estimated from B-mode ultrasound using region tracking and block matching. Ultrasound Med Biol. 2003;29:387–399. doi: 10.1016/s0301-5629(02)00760-3. [DOI] [PubMed] [Google Scholar]
- 4.Gustavsson T, Abu-Gharbieh R, Hamarneh G, Liang Q. Implementation and comparison of four different boundary detection algorithms for quantitative ultrasonic measurements of the human carotid artery. IEEE Comp Cardiol. 1997;24:1–4. [Google Scholar]
- 5.Stoitsis J, Golemati S, Dimopoulos A, Nikita K. Analysis and quantification of arterial wall motion from B-mode ultrasound images comparison of block-matching and optical flow. Conf Proc IEEE Eng Med Biol Soc. 2005;5:4469–4472. doi: 10.1109/IEMBS.2005.1615459. [DOI] [PubMed] [Google Scholar]
- 6.Rafati M, Mokhtari-Dizaji M, Saberi H, Grailu H. Automatic measurement of instantaneous changes in the walls of carotid artery with sequential ultrasound images. Iran J Physiol Pharmacol. 2009;13:308–318. [Google Scholar]
- 7.Yeung F, Levinson SF, Parker KJ. Multilevel and motion model-based ultrasonic speckle tracking algorithms. Ultrasound Med Biol. 1998;24:427–441. doi: 10.1016/s0301-5629(97)00281-0. [DOI] [PubMed] [Google Scholar]
- 8.Yeung F, Levinson SF, Fu D, Parker KJ. Feature-adaptive motion tracking of ultrasound image sequences using a deformable mesh. IEEE Trans Med Imaging. 1998;17:945–956. doi: 10.1109/42.746627. [DOI] [PubMed] [Google Scholar]
- 9.Boukerroui D, Noble JA, Brady M. Velocity estimation in ultrasound images: a block matching approach. Inf Process Med Imaging. 2003;18:586–598. doi: 10.1007/978-3-540-45087-0_49. [DOI] [PubMed] [Google Scholar]
- 10.Chen Z. Efficient block matching algorithm for motion estimation. Intenat J Sig Proc. 2009;5:133–137. [Google Scholar]
- 11.Barrett WA, Mortensen EN. Interactive live-wire boundary extraction. Med Image Anal. 1997;1:331–341. doi: 10.1016/s1361-8415(97)85005-0. [DOI] [PubMed] [Google Scholar]
- 12.Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1986;1:307–310. [PubMed] [Google Scholar]
- 13.Vaitkevicius PV, Fleg JL, Engel JH, O’Connor FC, Wright JG, Lakatta LE, Yin FC, Lakatta EG. Effects of age and aerobic capacity on arterial stiffness in healthy adults. Circulation. 1993;88:1456–1462. doi: 10.1161/01.cir.88.4.1456. [DOI] [PubMed] [Google Scholar]
- 14.Nagai Y, Fleg JL, Kemper MK, Rywik TM, Earley CJ, Metter EJ. Carotid arterial stiffness as a surrogate for aortic stiffness: relationship between carotid artery pressure-strain elastic modulus and aortic pulse wave velocity. Ultrasound Med Biol. 1999;25:181–188. doi: 10.1016/s0301-5629(98)00146-x. [DOI] [PubMed] [Google Scholar]
- 15.Arnett DK, Evans GW, Riley WA. Arterial stiffness: a new cardiovascular risk factor? Am J Epidemiol. 1994;140:669–682. doi: 10.1093/oxfordjournals.aje.a117315. [DOI] [PubMed] [Google Scholar]
- 16.Tortoli P, Bettarini R, Guidi F, Andreuccetti F, Righi D. A simplified approach for real-time detection of arterial wall velocity and distension. IEEE Trans Ultrason Ferroelectr Freq Control. 2001;48:1005–1012. doi: 10.1109/58.935717. [DOI] [PubMed] [Google Scholar]
- 17.Ramnarine KV, Kanber B, Panerai RB. Assessing the performance of vessel wall tracking algorithms: the importance of the test phantom. J Phys. 2004;1:199–204. [Google Scholar]
- 18.Sunagawa K, Kanai H, Tanaka M. Simultaneous measurement of blood flow and arterial wall vibrations in radial and axial directions. IEEE Ultrason. 2000;2:1541–1544. [Google Scholar]
- 19.Golemati S, Stoitsis J, Nikita KS. Motion analysis of the carotid artery wall and plaque using B-mode ultrasound. Vasc Dis Prev. 2007;4:1–7. [Google Scholar]
- 20.Persson M, Ahlgren AR, Jansson T, Eriksson A, Persson HW, Lindström K. Non-invasive measurement of arterial longitudinal movement. IEEE Ultrason. 2002;2:1783–1786. [Google Scholar]
- 21.Cinthio M, Ahlgren AR, Jansson T, Eriksson AW, Persson H, Lindstrom K. Evaluation of an ultrasonic echo-Ttracking method for measurements of arterial wall movements in two dimensions. IEEE transact ultrason ferroelec freq contr. 2005;52:1300–1311. doi: 10.1109/tuffc.2005.1509788. [DOI] [PubMed] [Google Scholar]
- 22.Liang Q, Wendelhag I, Wikstrand J, Gustavsson T. A multiscale dynamic programming procedure for boundary detection in ultrasonic artery images. IEEE Transact med img. 2000;19:127–142. doi: 10.1109/42.836372. [DOI] [PubMed] [Google Scholar]
- 23.Wendelhag I, Liang Q, Gustavsson T, Wikstrand J. A new automated computerized analyzing system simplifies readings and reduces the variability in ultrasound measurement of intima-media thickness. Stroke. 1997;28:2195–200. doi: 10.1161/01.str.28.11.2195. [DOI] [PubMed] [Google Scholar]
- 24.Cheng DC, Schmidt-Trucksass A, Cheng KS, Burkhardt H. Using snakes to detect the intimal and adventitial layers of the common carotid artery wall in sonographic images. Comput Methods Programs Biomed. 2002;67:27–37. doi: 10.1016/s0169-2607(00)00149-8. [DOI] [PubMed] [Google Scholar]