Probing hybridization parameters from microarray experiments: nearest-neighbor model and beyond

Abstract

In this article, it is shown how optimized and dedicated microarray experiments can be used to study the thermodynamics of DNA hybridization for a large number of different conformations in a highly parallel fashion. In particular, free energy penalties for mismatches are obtained in two independent ways and are shown to be correlated with values from melting experiments in solution reported in the literature. The additivity principle, which is at the basis of the nearest-neighbor model, and according to which the penalty for two isolated mismatches is equal to the sum of the independent penalties, is thoroughly tested. Additivity is shown to break down for a mismatch distance below 5 nt. The behavior of mismatches in the vicinity of the helix edges, and the behavior of tandem mismatches are also investigated. Finally, some thermodynamic outlying sequences are observed and highlighted. These sequences contain combinations of GA mismatches. The analysis of the microarray data reported in this article provides new insights on the DNA hybridization parameters and can help to increase the accuracy of hybridization-based technologies.

INTRODUCTION

Hybridization of single-stranded nucleic acids to form a duplex is a reversible chemical reaction, which is at the basis of many processess and techniques currently used in biotechnology, as for instance PCR (1). Due to its central importance, hybridization has been intensively studied in experiments (focusing on the thermodynamics (2,3) or kinetics of the process) and also in computer simulations (4).

The thermodynamics of DNA hybridization is usually described by the nearest-neighbor (NN) model (5). This model assumes that the free energy of a duplex can be expressed as a sum of dinucleotide stability parameters; it is therefore based on the principle of additivity. From the NN parameters one can, for instance, estimate melting temperatures, compute melting curves and predict secondary structures in which RNA molecules fold (6,7). In the folding problem, many different local conformations arise as single nucleotide mismatches, bulges, stem–loop structures, etc. Describing these conformations in the framework of the NN model is very challenging and requires a large number of parameters (6). However, only a limited number of them have been measured directly in experiments (8). In addition, one may also wonder whether additivity holds in such cases. To investigate a large number of different conformations, it would be very advantageous to have access to high-throughput measurements, provided that they are sufficiently accurate.

In this article, we quantitatively determine free energy penalties for mismatches using microarray data obtained from a set of optimized and dedicated experiments. In DNA microarrays, several thousand of different sequences can be spotted at a surface, hence a large number of hybridization reactions takes place simultaneously. We use two different approaches: the first one is based on a linear regression of a large set of experimental data points (≈1000) to fit 58 NN dinucleotide parameters. The second method relies on the computation of the logarithm of the ratios of fluorescent intensities measured from different spots of the arrays. We show that both methods provide highly correlated set of NN parameters. In addition, the second approach allows to probe the limitations of the NN model. It is found that when two mismatches are closer than 5 nt, additivity breaks down and the free energy of the duplex is not equal to the sum of the two separate contributions of isolated mismatches. We also quantify the influence of mismatches close to the edge of the double helix and show that the free energy penalty is much weaker in those cases. Overall, this work provides new insights on DNA hybridization thermodynamics and can help to increase the accuracy of hybridization-based technologies.

MATERIALS AND METHODS

The experiments were performed on custom Agilent arrays, following a standard protocol, which is discussed in (9). In each experiment, a single target sequence in solution was hybridized at concentrations ranging typically from ∼10 picoM to ∼2 nanoM. In total, three different sets of experiments were performed using the target sequences shown in Table 1. These sequences were selected from 25-mers human DNAs using Optimal Design methods (10). The theory of Optimal Design provides some criteria of selecting an optimal set of measurements, which minimize the uncertainties in the parameters of a statistical model (see Supplementary Data).

Table 1.

Target sequences used in the experiments

t1:	5′–CTGGTCTTAGATGCAGCGACTGTTT–poly(A)–3′–Cy3
t2:	5′–CTGCACAATTCCGGAGCTATGAATT–poly(A)–3′–Cy3
t3:	5′–AATAATGCTCATTAGGCACCGGGAA–poly(A)–3′–Cy3

At the 3′ side of each sequence a 20-mer poly(A) is attached, terminating with a Cy3 fluorophore. The targets were selected from Optimal Design criteria (10) (Supplementary Data). Each target is hybridized separately on specific microarrays containing mismatched probes with up to two mismatches with respect to the target. Note that t₁ and t₂ share a common triplet of nucleotides AGC at the same sequence position (in bold characters). The mismatches centered around this triplet will be discussed in some details in the ‘Results’ Section.

From the targets of Table 1, three different microarrays were designed and used for hybridization to either t₁, t₂ or t₃. Each microarray contains probes with either zero, one or two mismatches with respect to the given target, covering all possible mismatch combinations. In a stretch of N nucleotides, there can be 3N single mismatch probes and 9N(N − 1)/2 double mismatch probes. For N = 25, this gives in total 2776 different sequences, which were spotted in the microarray. The sequences were replicated 15 times to fill up completely a 44K custom Agilent array. Another design was also used in which mismatches have a minimal distance of 4 nt from the border and a minimal relative distance of 5 nt. In this case, the total number of sequences is 646. These sequences were replicated 23 times to fill a 15K custom arrays. We considered hybridizing sequences of 25 nt. This is because in the previous studies (11), these sequences were found to attain thermodynamic equilibrium after ∼3 h of hybridization (in the experiments, the hybridization time is of 17 h, hence thermodynamic equilibrium is guaranteed). A hybridization experiment provides a large number of fluorescence intensities: the highest intensity is from spots containing perfect match sequence, whereas the intensity decreases with the number and type of mismatches. The reduction of the intensity provides an estimate of the hybridization free energy. We use two different methods to obtain the NN parameters, as discussed in the next sections.

RESULTS

Nearest-neighbor parameters from linear regression

Equilibrium thermodynamics predicts that the measured fluorescence intensity from a spot i equals to:

(1)

where ΔG_i is the hybridization free energy between the target sequence and a probe sequence in i, A is a parameter, which sets the intensity scale, c the target concentration, R the gas constant and T the temperature (experiments are performed at T = 65°C = 338K, which is the value of the temperature used in the rest of the analysis). Although the data analyzed are background-subtracted from the Agilent scanner, there remains always some small aspecific signal, which we denote by I₀ in Equation (1). In the experiments, I_i is obtained from the average over typically approximately 15 replicated spots. One should note that Equation (1) is valid at sufficiently low target concentrations, i.e. when only a limited fraction of probes is hybridized in a spot, hence far from chemical saturation. On the other hand, at very low concentrations, the specific signal, i.e. the second term in Equation (1), can become comparable to I₀. Therefore, for the analysis of the data we restricted ourselves to intermediate concentrations and intensities for which we explicitly verified that the intensities scale linearly with concentrations, as predicted by Equation (1) (more details can be found in the Supplementary Data). In the intensity scale of the experiments I₀ ≈ 1, whereas the values used in the analysis are I_i ≳ 20. In practice, the large majority of the intensities in experiments with target concentration c = 100 pM or higher are above this threshold value.

In the following, we will consider the logarithm of the intensities measured with respect to the perfect match (PM) intensity. Using Equation (1), for I_i ≫ I₀ we get:

(2)

which defines the free energy penalty of probe i with respect to the perfectly matching probe. This penalty can be expressed as a sum of NN dinucleotide parameters. Consider, for instance, the example of a probe i with a single mismatch of type A with respect to the target nucleotide G and with neighboring nucleotides G and T. We have:

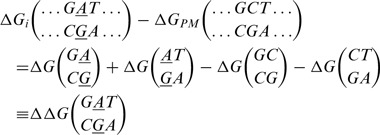(3)

We use the following notation: the target sequence is the bottom strand and the probe sequence, which is oriented from 5′ – 3′, is the top strand. This example corresponds to target t₁ or t₂ at position 10, counting from 3′ end (the triplet of nucleotides are indicated in bold in Table 1). In Equation (3) ΔΔG is defined as the free energy penalty of an isolated mismatch in a DNA duplex. This penalty is expected to be a local effect. In the NN model, this locality is inherent: the dots in Equation (3) indicate identical nucleotides in the two sequences, their contribution cancels out and leaves per isolated mismatch only four dinucleotide parameters around the mismatch position. There are in total only 58 such dinucleotide parameters: 10 perfect match parameters and 48 single mismatch parameters (taking into account symmetries). The dinucleotide parameters are not directly experimentally accessible and are not unique (12), e.g. they can be shifted by some constant value such that the physically accessible ΔΔG remains unchanged (see Supplementary Data).

Equations (2) and (3) define a linear problem: each measured y_i can be expressed by a linear combination of dinucleotide parameters. In order to extract the parameters from the data, we combined the results of the three experiments and performed a least square minimization of Equation (2). Mismatches closer than five sites from the helix edges were excluded from the analysis, as well as pairs of mismatches with a distance smaller than 5 nt.

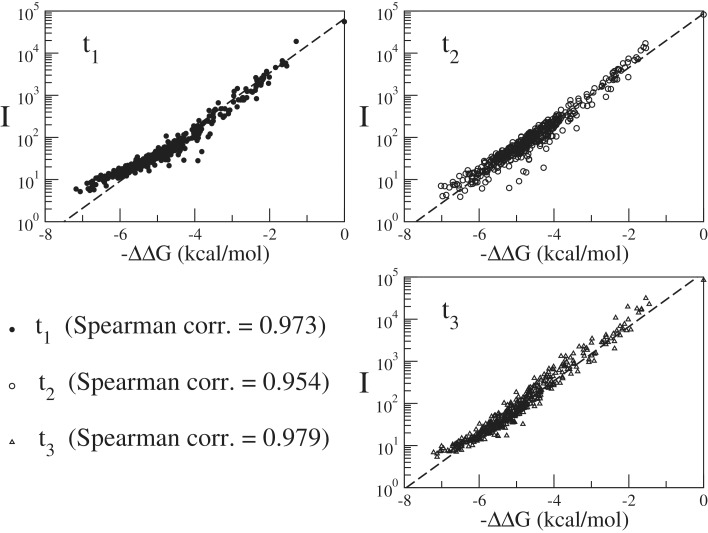
The 58 adjustable parameters were fitted on a set of about a thousand of experimental data points above the intensity threshold. The fitted parameters then applied to produce the plot as shown in Figure 1 for all available intensities of the experiments in which either sequence t₁, t₂ or t₃ was hybridized on its corresponding microarray at a concentration of c = 100 pM. The data are plotted as a function of the unique ΔΔG for triplets defined as in Equation (3). We note that there is very good agreement between the data and the thermodynamic model of Equation (1). The experiments follow the equilibrium isotherm (a straight line with a slope equal to 1/RT) for a range of intensities of more than four orders of magnitude. A previous study (9) in which hybridizing strands were 30-mers did not provide a single straight line in a ln I versus ΔΔG plot. Deviations due to lack of thermodynamic equilibrium were observed in the high-intensity range, as discussed in (11,13).

Figure 1.

Plot of the Intensities for concentrations c = 100 pM from the experiments using hybridization of targets t₁, t₂ or t₃, as a function of the ΔΔG parameters obtained from least-squared minimization. The data agree well with hybridization isotherm given in Equation (2), shown as a straight line in the linear-log scale.

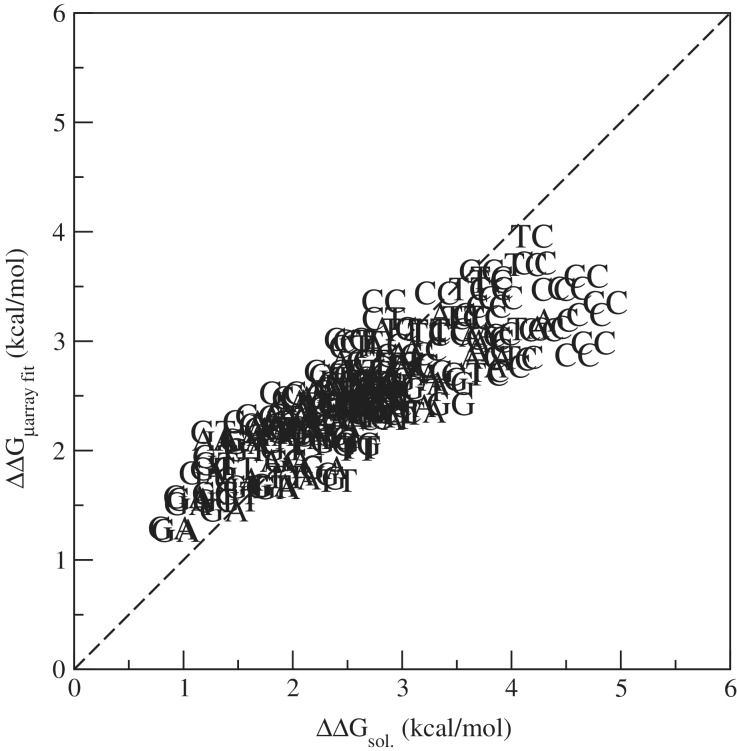
Further, it is important to note that we do not only find internally consistent results, but that our microarray-derived free energy parameters also correlate to a fair degree with those reported in literature for hybridization in solution (8). Figure 2 shows a correlation plot of the free energy penalties [i.e. the ΔΔG defined as in the example of Equation (3)] obtained from the microarray data analysis and those from SantaLucia et al. from (8). The Spearman correlation coefficient is equal to 0.855. This clearly shows that free energy parameters for DNA features measured by the presented microarray approach also apply for thermodynamic properties in solution. This opens the highly parallelled microarray toolbox for the study of thermodynamics of DNA structures. An example is discussed in the next section.

Figure 2.

Plot of free energy penalties ΔΔG for triplets obtained from the microarray fit versus those from hybridization in solution (8). The central mismatching nucleotides of the triplet [underlined in Equation (3)] are indicated in the plot.

Nearest-neighbor parameters from ratios of intensities: probing additivity

The crucial assumption of the NN model is additivity of local free energy contributions. We probe here the limits of additivity of free energy penalties as a function of the distance between two mismatches. We will access the free energy parameters by comparing ratios of intensities measured from different spots in the microarray.

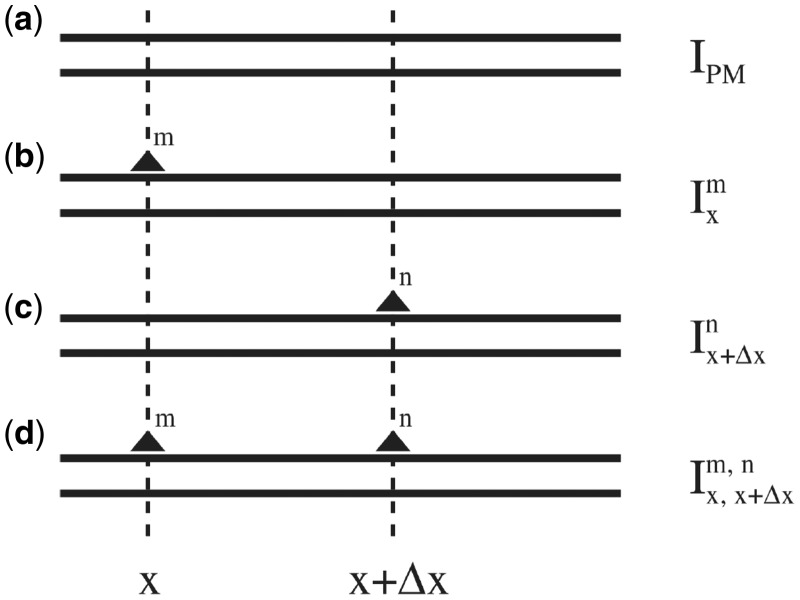
Hereto, we combine microarray spots that contain probes with zero, one or two mismatches with respect to the target and we denote the location of the mismatch by x or x + Δx, as illustrated in Figure 3. The associated free energy penalties can then be derived from the intensity measurements as follows

(4)

(5)

(6)

in which the superscript m and n represent the three possible mismatching nucleotides at location x and x + Δx, respectively. If the additivity of the NN model holds, the free energy penalty of Equation (6) should equal the sum of the individual penalties of Equations (4) and (5). To test this, we introduce

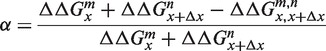(7)

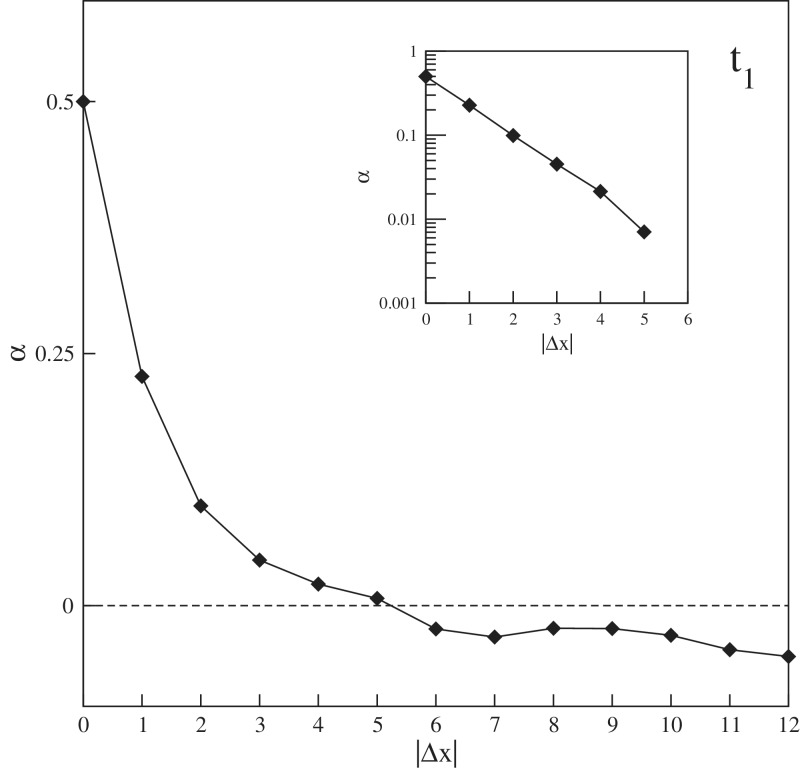
which measures the relative deviation from additivity. Figure 4 shows the experimental results for α in which we averaged over x, m and n, leaving α as a function of the distance |Δx| between two mismatches. From this data, we notice that α has a value of about zero when the mismatches are separated by ≥5 nt, but a clear positive value for smaller Δx. Apparently, the free energy penalty of two nearby mismatches is smaller than the sum of the two individual contributions, resulting in a positive α. Furthermore, the inset from Figure 4 shows that the relationship is linear in a semi logarithmic plot, hence α decays exponentially with |Δx|. Note that at Δx = 0 only one mismatch is present, hence m = n and α will be identical to 1/2 according to Equation (7). All these observations result from direct measured values, containing no fitting parameters and strongly suggest that in double-stranded DNA mismatches have a physical interaction with each other, which decays exponentially to zero over a distance of about five nucleotides.

Figure 3.

Schematic representation of hybridizing strands in the microarray experiment. From the appropriate ratios of intensities measured from these spots, the free energy parameters can be determined and the additivity principle can be tested. As in the rest of the article, the lower strand is the fixed target sequence. The upper strand is the probe sequence. The filled triangles denote mismatching nucleotides. In the four examples from the top we show: (a) hybridization with a PM probe, (b and c) hybridization with a single mismatch probe where the mismatching nucleotides are m and n at positions x and x + Δx, respectively, (d) hybridization with a probe carrying two mismatches. We use the notations 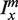, 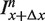and 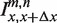to denote the corresponding intensities measured in the experiment.

Figure 4.

Parameter α, the relative deviation from additivity, from the experiment of target t₁, averaged over x, m and n as a function of the distance |Δx| between two mismatches. The inset shows the plot with α in log scale.

These results are setting some limitations on the additivity of the NN model. However, outside this interaction region of 4 nt, we expect the NN model to hold i.e. α should be zero and mismatches can be considered as isolated. This can be explicitly checked in a very direct way. When α = 0, we get from Equation (7)

(8)

The free energy penalty 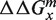of a mismatch m at location x, which we will call the focus mismatch (m, x), can be estimated either directly using Equation (4) or via a second mismatch (n, x + Δx) using Equations (5) and (6) for any choice of n and Δx > 4. Hence, the free energy penalty of the focus mismatch can be estimated from measurements in many independent ways and they should provide the same answer if additivity holds. Note that, using Equations (5) and (6) I_PM drops out in the right hand side of Equation (8).

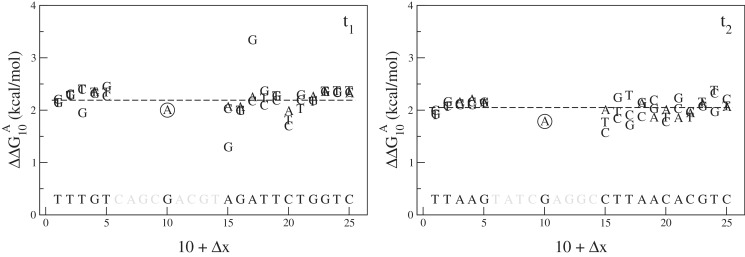
Figure 5 illustrates how Equation (8) can be used to estimate the ΔΔG using different combinations of n and Δx. In this specific example, we consider 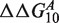, which corresponds both for target t₁ and t₂ to 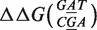(in the Supplementary Data, we show other examples featuring additivity for different focus mismatches).

Figure 5.

Free energy penalty 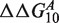for focus mismatch (m = A, x = 10) derived from experimental intensities according to Equation (8) as a function of the location x + Δx of the second mismatch (n, x + Δx). For each |Δx > 4| the three values, one per possible mismatch, are indicated by the letter representing the mismatching nucleotide n of the probe. The target sequence is written in top of the x-axis in 3′ – 5′ notation, t₁ in left pane, t₂ in right pane. The dotted line corresponds to the median value of the 48 estimates. The circled point is the estimate without second mismatch coming from Equation (4). For this particular mismatch, the free energy penalty for both t₁ and t₂ is identical and corresponds to .

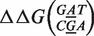In the pane for target t₂, all the estimates of the free energy penalty are close the each other, the 48 + 1 estimates tightly lie around a median value, in this case, ∼2.1 kcal/mol, is indicated by the dotted line. The picture in the right pane is a typical one, which we observe for any focus mismatch (m, x). This confirms that additivity holds in the regime Δx > 4, i.e. when mismatches are separated by >4 nt. Moreover, it shows that the microarray measurement is internally consistent. Second, the left pane, i.e. experiment t₁, provides the same median value for the free energy penalty, showing also the robustness of the microarray approach to estimate free energies of DNA structures. However, this figure was chosen because it is atypical in the sense that one notices two pronounced outlying values. They correspond to a sequence where both the focus mismatch and the second mismatch are of type AG. Since, they clearly deviate from an otherwise nicely consistent picture, we believe there must a physically underlying reason for it. We will come back to this point in the section where we discuss thermodynamic outliers.

Note that with this second method, we accessed values for the free energy penalties of isolated mismatches without using any multiple regression or fitting procedure, but we simply compared the ratios of intensities, Equations (4–6), to get a consistent set of independent estimates. The free energy penalties are then obtained from the median over all data points. We compared the free energy penalties obtained from this method (median) with those obtained from linear regression as discussed in the previous section. The two sets of data are well correlated with a Pearson correlation coefficient equal to 0.966 (see Supplementary Data). This correlation shows the equivalence of the two approaches. In this analysis, we restricted ourselves to mismatches in the bulk of the sequence, i.e. x is >5 nt from the border. Closer to the border, we observe boundary effects, which are covered in the next section.

Boundary effects

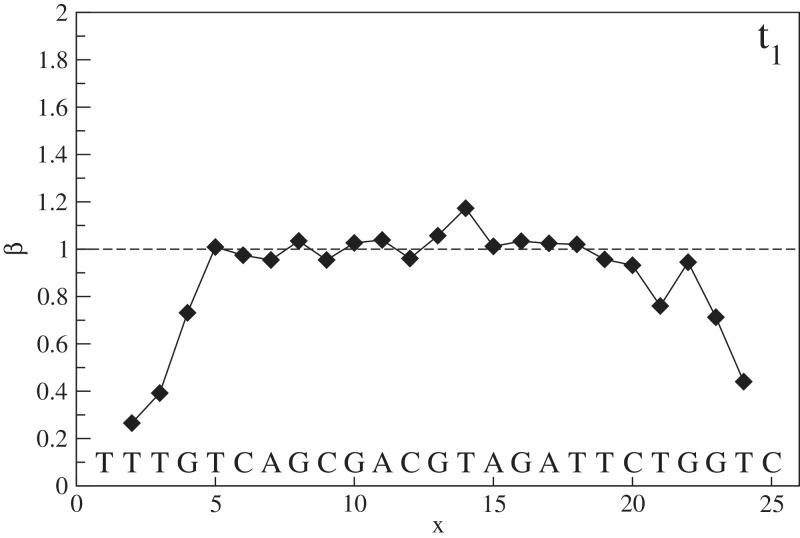
The previous section ended by showing the equivalence of both approaches to access free energy penalties of an isolated mismatch, provided the data are restricted to bulk mismatches. The direct median method of the previous section can also assess penalties of mismatches close to the boundary, whereas on the contrary, the fitting method cannot by construction. The latter, however, has the advantage of fitting a full parameter set of the NN model and as such can easily provide bulk values for the free energy penalty of any isolated mismatch. The combination of both methods now provides an elegant way to assess the effect of boundary proximity on an isolated mismatch. Hereto, we introduce the parameter β as the relative reduction of free energy penalty of a mismatch when compared to its bulk value.

(9)

In Figure 6, the parameter β is shown as a function of x after averaging over m. It is clear that, as expected, β is approximately equal to one in the bulk, whereas when approaching the boundary, a reduction of free energy penalty occurs which reaches up to 80%. Note that for mismatches at the boundary, x = 1 and x = 25, the NN model is not applicable and no data are presented. Figure 6 shows that the range of boundary effect is about 4 nt.

Figure 6.

Boundary effect: β, the relative reduction of mismatch free energy penalty, as a function of location for experiment with target t₁. Each point is the average of three estimates, one per possible mismatch. Data are absent for the extremal locations x = 1 and x = 25, since no value can be calculated by the NN model.

Thermodynamic outliers

As a final result of this article, we come back to the two outliers observed in Figure 5(a); the same deviations are found in replicated experiments at different concentrations: therefore, they are unlikely due to experimental errors. For these two cases, we find 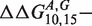 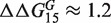kcal/mol and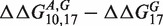 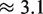 kcal/mol, strongly deviating from the median value (≈2.1 kcal/mol). The common feature of these two sequences is that they involve GA mismatches. The two set of mismatches are arranged in an antiparallel way i.e. one G and one A are on the same strand. Mismatches of GA type in DNA and RNA helices have been the subject of several studies in the past (14–21). In the RNA folding, it is known that GA pairs contribute substantially to the RNA helix stability. Their contribution is comparable to that of a canonical AT pair. As AT pairs, GA form two hydrogen bonds, but can also assume four different conformations (14). The microarray data suggests that the antiparallel combination of GA and AG pairs of mismatches have a long range interaction effect, which is probably a signature of some structural conformational change of a double helix containing these pairs. Next-nearest neighbor effects extending up to 4 nt distance for antiparallel GA mismatches have been reported in the case of RNA duplexes in (19) (longer distances were not considered that case). We investigated antiparallel GA and AG pairs of mismatches also in sequences t₂ and t₃, but found no anomalous behavior in those cases. This suggests that the nucleotide sequences between the two GA/AG pairs plays an important role in the overall stability of the duplex.

As a further proof of the outlying behavior of antiparallel GA/AG pairs, we show in Figure 7 a plot of free energy penalties for tandem mismatches (neighboring double mismatches). These are again obtained from Equation (6) for different m and n mismatching nucleotides, where in the case of tandem mismatches, Δx is equal to 1. On each location of the sequence our data set contains nine different types of tandem mismatch. A clear boundary effect is noticeable, but when looking at the bulk data points tandem mismatch of the type GA/AG are again outlying, they appear to be particularly stable with a free energy penalty ∼2 kcal/mol below average.

Figure 7.

The free energy penalty of tandem mismatches from experiment with target t₁: 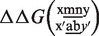, where x′ and y′ are complementary to x and y, respectively. ab denoted above the x-axis are the fixed nucleotides in the target. mn is a tandem mismatch in the probe and the vertical position of these letters in the plot give the associated free energy penalty. Note the low free energy penalty for 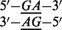mismatches (encircled).

DISCUSSION AND CONCLUSION

In this article, we have analyzed DNA hybridization reactions in microarrays and quantified free energy penalties of single and double mismatches. We have shown that the experimental data are very precise and reproducible. The microarray data follow an equilibrium isotherm over a range of four orders of magnitude in the fluorescence intensities and allow the extraction of accurate thermodynamic parameters. First, the analysis provides a database with a large number of NN parameters for isolated mismatches. These parameters correlate well with those reported in the literature from hybridization experiments in solution. Second, the experiments contain systematic measurements of hybridization with two mismatches, which allowed us to probe the validity limit of the NN approximation. We showed that when two mismatches are separated by a distance of ≥ 5 nt their effect is additive, allowing a standard approach with the NN model. However, for shorter distances, the additivity is no longer valid and we found that duplexes with neighboring mismatches are more stable than expected from additivity. This interaction was shown to decay exponentially as a function of the distance between mismatches. Further, we investigated the behavior of mismatches close to the helix edges, and showed that their free energy penalty is reduced up to 80% when compared to the bulk behavior. The boundary effect was observable up to 4 nt from the helix edge. Finally, we also found some thermodynamic outliers, sequences involving two antiparallel GA mismatches, in which the mismatch interaction appears to persist beyond 5 nt. These outliers were not related to experimental error indicating a signature of some structural conformational change of a double helix containing these mismatch pairs.

Overall, the analysis of the microarray data reported in this article provides new quantitative insights on the DNA hybridization parameters, on the NN model and its present limitations. Our study is in line with a number of recent papers, which have been dedicated to the investigations of fundamental physico-chemical properties of DNA arrays [(22–31)]. Due to the relevance of hybridization in many technologies, going from PCR (1) to recent developments in biosensors, e.g. (32), a good thermodynamic model is also important from the application point of view. A precise quantification of interaction free energies involved in the hybridization will help to increase the accuracy of microarrays and other hybridization-based technologies, so that these devise could realize their full potential, for instance, for clinical applications (33). For these applications, an increase in specificity and sensitivity is very important and can be achieved through better understanding of fundamental properties of hybridization in these devices.

There has been considerable attention in recent years (9,22,24–34) in understanding the fundamentals of hybridization in DNA microarrays and its impact in data analysis. Here, we have shown that microarrays are a reliable and high-throughput tool to gain insight on DNA hybridization thermodynamics. The same method could be used to screen other types of defects, as bulges. Indeed, it was recently used for understanding loop conformations (22).

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online: Supplementary Figures 1–4.

FUNDING

FWO Vlaanderen [G.0311.08]; KULeuven [STRT1/09/042]; VITO [ZL39010200-401]. Funding for open access charge: KULeuven [STRT1/09/042].

Conflict of interest statement. None declared.