Abstract
Chromatin is a multiscale structure on which transcription, replication, recombination and repair of the genome occur. To fully understand any of these processes at the molecular level under physiological conditions, a clear picture of the polymorphic and dynamic organization of chromatin in the eukaryotic nucleus is required. Recent studies indicate that a fractal model of chromatin architecture is consistent with both the reaction-diffusion properties of chromatin interacting proteins and with structural data on chromatin interminglement. In this study, we provide a critical overview of the experimental evidence that support a fractal organization of chromatin. On this basis, we discuss the functional implications of a fractal chromatin model for biological processes and propose future experiments to probe chromatin organization further that should allow to strongly support or invalidate the fractal hypothesis.
INTRODUCTION
The structure of chromatin in vivo remains one of the major unsolved problems in biology, despite its eminent importance as template onto which transcription, replication, recombination and repair occur. Chromatin is a hierarchical structure, and the nucleosome, which consists of ∼150 bp of deoxyribonucleic acid (DNA) wrapped around an octamer of histone proteins, is its constitutive basic element. The nucleosome structure has been resolved with atomic precision by X-ray diffraction (1,2), and its biological function has been extensively studied by molecular biology and biophysics techniques over the past three decades. Beyond the nucleosome level, chromatin structure is far less characterized. Condensed nucleosome arrays that fold into a ‘30 nm fiber’ have been described long ago using electron microscopy of chromatin spread at moderate ionic strength (3), yet their exact structure still remains strongly debated (4), and 30 nm fibers were not convincingly detected in vivo using high-resolution electron microscopy of thin nuclear sections, which rather pointed to the existence of fibers with a variety of diameters, none particularly resonant with a hierarchical organization built on a 30 nm structural element (5). At larger scales, chromatin is arranged in three dimensions (6), allowing for crosstalk between distant chromatin loci in cis and in trans that participate in large-scale expression regulation (7). Although this architectural level seems to be crucial for genomic transactions, as is its conservation through cell cycle (8), the multiscale structure of chromatin is still hotly debated (9), and the topological parameters characterizing this organization remain unknown.
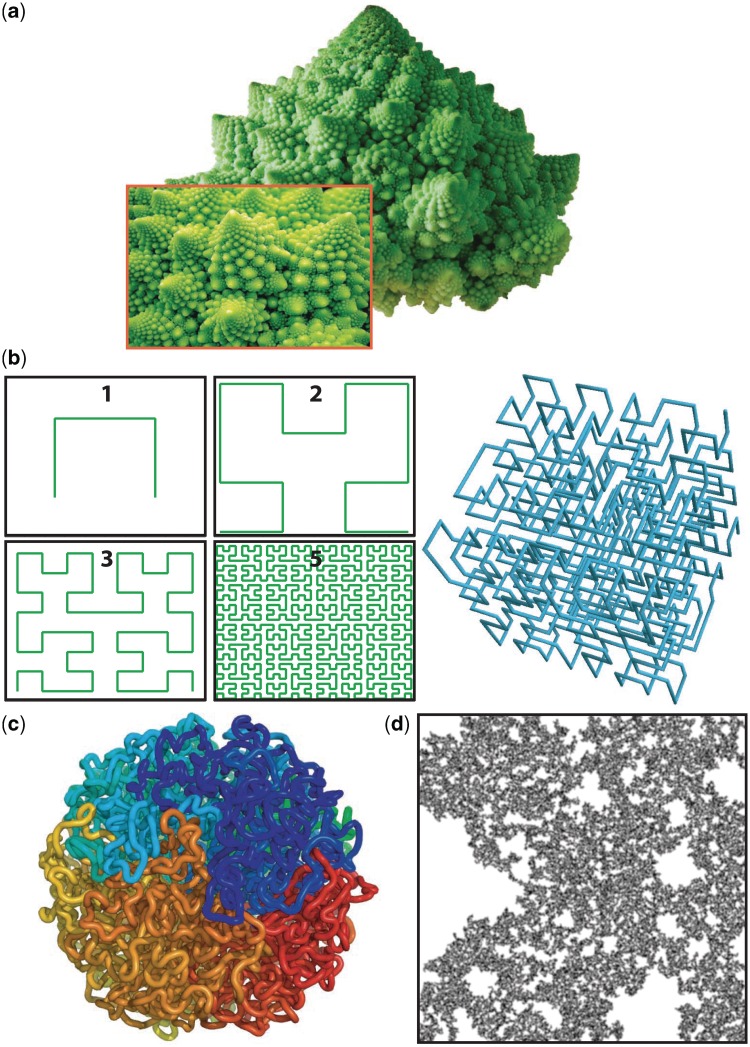
Recent studies indicated that a fractal model of chromatin architecture is consistent with structural data on chromatin interminglement (10) and with the diffusion and binding properties of chromatin interacting proteins (11). Fractal structures are self-similar, meaning that they consist of characteristic patterns that can be repeatedly observed after zooming in on any part of it at any magnification. The fractal formalism has been successfully used to describe numerous natural shapes [Figure 1a, (12–14)], and several studies have invoked this model in the nuclear context. For instance, the analysis of genomic DNA sequences by statistical methods showed long-range correlations, which are characteristic of fractal geometries, although the biological origin and function of this organization remain unclear (15–21). The three-dimensional (3D) spatial organization of the genome was also proposed to be fractal based on the hypothesis that chromosomes are unknotted structures so as to prevent the formation of glass-like architectures that are inconsistent with the dynamic and reconfigurable properties of chromatin for expression regulation (22), and each chromosome was proposed to adopt a crumpled globule conformation (23). Interestingly, a fractal organization of chromosomes fits well with the polymeric nature of chromatin, as generic fractal models were successfully applied to describe polymer conformations (24).
Figure 1.
Examples of 2D and 3D fractals. (a) The romanesco broccoli is one of the most popular natural fractal architecture. (b) The left panel shows the first, second, third and fifth iterations for the recursive construction of a 2D Hilbert fractal. The right panel is a 3D Hilbert curve, which fractal dimension is equal to f = 3. These two examples constitute deterministic fractals. (c) The picture represents a 3D crumpled globule polymer conformation (with permission from the AAAS (11)), which is a maximally compact, knot-free and fractal architecture. (d) Dark pixels form a 2D percolation cluster, which is obtained by clustering randomly distributed elements using nearest-neighbor connections. The fractal dimension of a percolation cluster is f = 2.5.
A few reviews recently discussed the relevance of the crumpled globule model for chromosome architecture (25–27). In this study, we provide an overview of the experimental results that support a fractal organization in the nucleus. We show that the term fractal refers to several architectural components of the nucleus, including the DNA or protein components of chromosomes, for which fractal structural characterizations are not equivalent. We then explore the implications of a fractal nuclear organization for biological processes, and we give an outlook on future experiments that should provide additional insights on chromatin organization and allow to validate or falsify the fractal model of chromatin.
A FEW FACTS ON FRACTALS AND THEIR APPLICATION TO CHROMOSOMES
The romanesco broccoli is a popular example of fractal object, in which one structural pattern is repeatedly observed at all scales [(28), Figure 1]. The evaluation of the contour length of the outline of this structure leads to a surprising outcome: as we increase the resolution (equivalently the zoom factor), we detect a growing number of structural elements, so that this line cannot be mapped with a finite number of geometrical objects (Figure 1b), and its length is infinite. The morphology of this object can nevertheless be characterized by the fractal dimension f, which can be measured by assessing the mass distribution (i.e. the number of structural elements N) at a given zoom factor R according to the following relationship:
| (1) |
The fractal dimension of the outline of the romanesco broccoli is a non-integer number of ∼1.26, and more generally, this parameter somewhat varies between 1 and 2 for a line in 2D. Interestingly, the case of a fractal line with an integer dimension of 2 or 3 corresponds to a space filling object, as shown with the 2D or 3D Hilbert curve shown in Figure 1b or c, respectively. The Hilbert curve is a deterministic fractal, meaning that its structure is obtained by a recursive process in which each repetition is built on the previous result (Figure 1b), but the concept can be generalized to random fractals (Figure 1c and d), in which case the fractal dimension is defined statistically by measuring the average number of structural elements for a given zoom.
Mathematical fractals are invariant over an unlimited range of scales, but natural fractals are self-similar only within a spatial domain with upper and lower scaling limits that typically spread over two or three orders of magnitude. Chromatin is a long polymer that fills the nuclear volume at an estimated concentration from ∼100 to 200–400 mg/ml (29,30). It is constituted by a series of structural elements including DNA, the nucleosome, the chromatin fiber, higher order chromatin loops, coils or folds, chromosome territories and the nucleus itself, which are associated to different spatial scales of ∼2 nm, 10 nm, 30 nm, 200 nm, 1 µm and 20 µm, respectively. Therefore, chromatin architecture spans four orders of magnitude. To the best of our knowledge, there are currently no methods to probe chromatin organization in living cells over this complete spectrum, most techniques rather providing structural information over two orders, and we will, therefore, survey the experimental evidence for the fractal organization of chromatin specifying their spatial relevance.
The fractal dimension is a static architectural parameter, which does not provide information on how dynamical processes, e.g. transport by molecular diffusion, occur in fractal environments (31). In the specific case of diffusion, which, together with the binding properties, determines the behavior of nearly every nuclear protein (32), the analysis of the motion of inert tracers in fractal environments based on the temporal evolution of the average mean square displacement (L2) for a given time lag Δt generally exhibits anomalous subdiffusive behaviors:
| (2) |
with γ the anomaly parameter and γ ≥ 2. Note that the anomaly parameter is equal to 2 for normal diffusion in free space. The anomalous response in fractal environments is due to the existence of spatial heterogeneities that create dead ends and impede the progression of tracers (33). Interestingly, f refers to the geometry of a fractal structure and γ to dynamical processes occurring within this architecture. Although these quantities can be related for some theoretical structures (34), there are no general rules to relate them, so they are generally treated independently for experimental studies.
EVIDENCE FROM IMAGE ANALYSIS
Image analysis provided the first evidence for a fractal organization of chromatin architecture, which was associated to a fractal dimension of f ∼ 2.5 in the 0.15–2.7 µm spatial range, using bright field microscopy on breast epithelial cells obtained by fine-needle aspiration biopsies and stained with ultrafast Papanicolaou protocol [(35), Table 1]. A number of subsequent studies performed with confocal microscopy, that is with a better axial resolution, supported the large scale fractal organization of chromatin and the estimate for the fractal dimension f ∼ 2.4–2.5 (39,40). It has now become relatively common in clinical diagnosis to incorporate fractal analysis into image analysis devices for cancer cell classification (41–43). Textural analysis was also applied to transmission electron micrographs of cell nuclei stained with uranyl acetate as a contrast agent (44), and a fractal spatial organization of chromatin was detected. Although optical imaging at these resolutions provides only a 2D projection, either of the entire nucleus or a relatively thick optical section within it fractal properties of 2D images are good indicators of a 3D optical organization, as it has been shown that 2D intensity images exhibit fractal patterns only if the corresponding 3D architecture is fractal in the general case of Brownian self-similarity (45), which is a reasonable model for polymeric chromatin.
Table 1.
Summary of fractal dimensions characterizing the mass distribution [f in Eq. (1)] and the line of polymer in space [ε in Eq. (3)] and the associated measurement technique for DNA, chromatin, proteins and the nucleoplasm, which are represented in black, green, red and blue, respectively. Note that these results have been sorted according to their respective length scales
| Technique | Mass fractal dimension | Line fractal dimension | Spatial length scale | Tentative interpretation | Limitations |
|---|---|---|---|---|---|
| Neutron scattering (36) | 2.2 | 0.02–0.4 µm | Random or swollen polymer chains | Direct evidence but isolated nuclei | |
| Neutron scattering (36) | 2.4 | 0.02–0.4 µm | Percolation cluster | Direct evidence but isolated nuclei | |
| FISH (37,38) | 2.0–2.2 | 0.15–1 µm | Random or swollen polymer chains | Fixed cells | |
| Neutron scattering (36) | 2.5 | 0.02–10 µm | Percolation cluster | Direct evidence but isolated nuclei | |
| Textural analysis (35) | 2.4–2.5 | 0.3–3 µm | Percolation cluster | Mostly in fixed cells. Problem of chromatin reporter | |
| Hi-C (10) | 3 | 3 | 0.4–3 µm | Crumpled globule or random loops | Indirect evidence based on contact probability |
| Neutron scattering DNA (36) | 3.1 | 0.4–10 µm | Crumpled globule or random loops | Direct evidence but isolated nuclei | |
| Neutron scattering (36) | 2.9 | 0.4–10 µm | Crumpled globule or random loops | Direct evidence but isolated nuclei | |
| FISH (37,38) | 3.2 | 1–5 µm | Crumpled globule or random loops | Fixed cells | |
| Rheology: euchromatin (11) | 2.6 | 0.02–0.2 µm | Less compact exploration | Indirect evidence in living cells | |
| Rheology: heterochromatin (11) | 2.2 | 0.02–0.1 µm | Compact exploration | Indirect evidence in living cells |
EVIDENCE FROM NEUTRON SCATTERING
Neutron scattering is presumably the optimal method to probe chromatin fractal organization over a broad spatial range, because it can cover the length scale spectrum from 15 nm to 10 µm (36, 46). This technique, however, is not applicable to intact cells because the contributions of cytoplasm and the nucleoplasm scattering cannot be differentiated. Lebedev et al. thus set out to perform neutron scattering on isolated chicken erythrocyte nuclei and observed that the relationship between the scattering intensity and the scattering vector follows a power law scaling, which is characteristic of a fractal organization. A bi-phasic response with a fractal dimension of f ∼ 2.4 in the length spectrum 15–400 nm and f ∼ 2.9 for larger length scales was detected. The response could then be studied in finer details by assaying the contribution of DNA architecture that also exhibited two different regimes of fractality with a fractal dimension of f ∼ 2.2 in 15–400 nm space domain and a f ∼ 3.2 exponent for larger length scales [(36), Table 1]. Intriguingly, neutron scattering is the only technique that provides quantitative information on the organization of nuclear proteins, which is also associated to a fractal behavior with an exponent of f ∼ 2.5 over the full length spectrum.
EVIDENCE FROM CHROMOSOME CONFORMATION CAPTURE
A number of methods have been established to map chromosome large scale organization based on the capture of spatially adjacent chromatin segments after crosslinking in fixed cells using spatially constrained ligation followed by locus-specific polymerase chain reaction (47). Recent developments (Hi-C) enable an unbiased identification of chromatin interactions across an entire genome with a precision of ∼ 1 Mbp (10). This technique showed that even for distances larger than ∼200 Mb, the intra-chromosomal contact probability is greater than the average contact probability between different chromosomes, suggesting that they are arranged in discrete entities, the so-called chromosome territories (9). Moreover, the intra- and inter-chromosomal interaction pattern could be decomposed into two compartments, within which contacts were enriched. This dual compartimentalization seemed to be closely associated to the bi-partite organization of chromosomes in euchromatin (less compact and enriched in active genes) and heterochromatin (more compact and transcriptionally mostly silent). Finally, Hi-C was applied to assess intra-chromosomal contact probabilities in human lymphoblastoids, unraveling a power law scaling associated to a slope of −1.08 in the range 500 kb to 7 Mbp, that corresponds to a spatial range of ∼500 nm–2 µm. This structural property seemed to be consistent with a fractal organization of DNA in a crumpled globule conformation characterized by a fractal dimension of f ∼ 3.
EVIDENCE FROM NUCLEAR RHEOLOGY
Structural insights on nuclear organization may be inferred from rheological measurements because nuclear proteins diffuse in the inter-chromatin space, and their motion is hindered by the obstruction of chromatin fibers (48–50). At length scales larger than ∼500 nm, photoperturbation techniques have consensually demonstrated that diffusion is normal (32,51), whereas complex behaviors, which were interpreted in terms of anomalous diffusion or multiple-component diffusion, were observed at smaller length scales of ∼100–200 nm using single particle tracking or fluorescence correlation spectroscopy (11,52–54). Our group observed that the diffusive hindrance and anomalous diffusion exponent γ of Green Fluorescent Protein (GFP) multimers containing 1, 2, 5 and 10 GFPs in tandem were size independent, suggesting that the nucleoplasm architecture is fractal because these structures have no characteristic length scale, so diffusing molecules encounter the same obstructions regardless of their size. Furthermore, the fractal dimension of the accessible nucleoplasm could be derived from quantitative modeling of interaction kinetics, revealing that the fractal architecture of nucleoplasm euchromatin and heterochromatin were markedly distinct and associated to fractal dimensions of f ∼ 2.6 and 2.2, respectively, in the 2–100 nm space domain.
The fact that both the chromatin and the nucleoplasm exhibit fractal architectures seems contradictory from a mathematical standpoint, because the dimension of the complement of a fractal is 3 (28). Two, not mutually exclusive, hypotheses can explain this apparent paradox. First, fractals and their complements may both exhibit mass fractal properties when they span only a limited spatial range (55,56). In support of this hypothesis, molecular dynamic simulations have shown that size independent anomalous diffusion occurs for finite sized random walkers in the presence of fractal obstacles (49), in clear contradiction with the theoretical expectation that unobstructed diffusion should occur in the complement of a fractal, which is of dimension 3. Second, one may conceive that nuclear diffusion involves a combination of diffusion in the chromatin-free space and some degree of longitudinal movements (or sliding) along the fractal ‘surface’ of chromatin, which together give the appearance of a fractal architecture of the nucleoplasm. Interestingly, this proposition leads to the intriguing consequence: proteins might sense different nuclear environment depending on their interaction dynamics with chromosomes. In line with this speculative model, we note recent Brownian dynamics simulations performed on GFP diffusion in an atomically detailed model of bacterial cytoplasm including the 50 most abundant types of macromolecules revealed that attractive interactions between GFP and cytoplasmic macromolecules were necessary to reproduce the slow diffusion of GFP in these cells (57).
FIRST COMMENTS ON THE FRACTAL MODEL
Several experimental lines of evidence support the fractal organization of the nucleus (Table 1). The available experimental data provides a complex picture because fractality refers to DNA, chromatin, the nucleoplasm or the whole nucleus, which exhibit markedly different architectures as exemplified by the unrelated fractal structural parameters detected by neutron scattering for the DNA or protein component of chromosomes in the nucleus (Table 1). Moreover, the fractal exponents inferred from the different assays do not characterize the geometrical organization of chromatin over the same spatial range. Interestingly, a survey on the use of fractal models for physical systems pointed out the narrow spectrum (sometimes less than one order of magnitude) on which fractal properties were detected (58), although these models should be applied to structures self-similar over broad physical lengths. This concern holds for chromatin architecture as power-law scalings are observed in the range ∼2–200 nm and 200 nm–2 µm (i.e. over two or one order of magnitude, respectively). Thus, the term fractality may be misleading, although power-law scaling behaviors are clearly observed for the different nuclear components. Bearing this limitation in mind, fractal models, even valid on a limited spatial range, call into question the textbook picture of a clear hierarchical folding of chromatin, which is formed by discrete structures at different length scales, because a fractal geometry is similar at all length scales where it applies. A fractal nuclear architecture would naturally connect the different chromatin structural levels in a common organization without sharp boundaries, rather than artificially segmenting chromatin into discrete and separate entities, e.g. nucleosomes, nucleosome arrays or chromatin loops.
Now, one may wonder whether the fractal dimensions reported in the literature can be linked to specific geometries. This assignment is, however, impossible in most cases because a variety of structures can be imagined to match a given fractal dimension. Nevertheless, we note that the fractal dimension somewhat varies between three main values f ∼ 2, 2.5 and 3 for small, intermediate and large length scales, respectively (Table 1). f ∼ 3 corresponds to a space-filling line in space, which can be a topologically entangled state or a crumpled globule (see discussion later). f ∼ 2.5 is reminiscent of the exponent observed for percolation clusters, which is the example of Brownian self-similarity depicted in Figure 1d. Percolation clusters are generic models to study diffusion in porous materials (59) or to describe the architecture of condensed polymers (60). Note that these architectures are detected for the protein component of chromosomes or for chromatin but not for DNA organization in chromosomes. Finally, f ∼ 2 is the fractal dimension of a Gaussian chain, which is the ideal polymer conformation typically detected in high-concentration polymer solutions (61), a situation relevant for the nuclear environment.
Fractal models of chromatin should be judged based on the accuracy of their predictions regarding nuclear organization or the molecular processes occurring in the nuclear context. Interestingly, the fractal parameters that describe the DNA component or the nucleoplasm are not equally insightful in terms of functional consequences for biological transactions. For instance, when diffusive processes or target-search mechanisms of nuclear proteins such as transcription factors are investigated, it is appropriate to consider the fractal architecture of the chromatin-free space, which is the medium available for diffusive movement. On the other hand, to understand large-scale chromosome organization and the structural determinants of interactions between distant genomic loci the fractal architecture of DNA is the relevant. In the following, we, therefore, discuss the predictions of fractal models for DNA architecture and the chromatin-free space at large and small length scales, respectively.
FUNCTIONAL IMPLICATIONS OF A FRACTAL MODEL FOR THE NUCLEOPLASM AT SMALL LENGTH SCALES
The fractal dimensions of the nucleoplasm measured in (11) for euchromatin and heterochromatin are 2.6 and 2.2, respectively. Because the fractal dimension exactly matches the intuitive notion of textural roughness (45), these values are somewhat consistent with the idea that heterochromatin is more condensed than euchromatin: the topography of the complement of heterochromatin is smooth and poorly branched, thus leaving a smaller part of chromatin surface for transcription factors to scan for target sites. By contrast, nucleoplasm in euchromatin is defined by a larger fractal dimension, occupying more of the total volume and, therefore, giving access to a larger part of the rough chromatin surface for scanning chromatin interacting proteins.
Moreover, it was recently shown that the comparison of the fractal dimension f to the anomaly parameter γ provides general predictions regarding the target-search mechanism in fractal environments (62–64). When γ > f, exploration by diffusion is compact, meaning that diffusing molecules systematically visit their neighboring sites and oversample their surrounding environment. On the contrary, the time to reach a target locus is independent on the distance from the initial position for f ≥ γ, so diffusing molecules rapidly sample large environments although they may overlook nearby sites, referred to as non-compact exploration. This model has intriguing consequences for hetero- and eu-chromatin (Table 1). Given that similar anomaly parameters are detected in both compartments (11) and the fractal dimension of the heterochromatin nucleoplasm is lower, exploration is expected to be more compact in heterochromatin. Thus, chromatin interacting proteins should systematically bind to all their available binding sites in heterochromatin, in agreement with the long residence of generic chromatin binding proteins observed in heterochromatin (11) and with the higher frequency of transient protein trapping in heterochromatin (53). In addition, such binding enhancement could be involved in heterochromatin maintenance in a silent state: specific histone modifications that create stereo-specific binding sites are known to be required for the formation of this compartment (65,66) and compact exploration could ensure a positive feedback for their maintenance (11). On the contrary, the target search strategy in euchromatin seems to favor a faster non-compact exploration with less redundancy in the scanning, which is presumably adapted to scan for comparatively rare cis regulatory elements in the genome. It was formerly suggested that a local change in the fractal landscape of chromatin could result in a change of local attractor for proteins, which might in turn account for repression or expression of a region (67). Chromatin might thus be able to switch the expression of different loci by altering its fractal structure. We note that the prediction of this model was recently tested in a theoretical work that showed a link between the compact/non-compact exploration of transcription factors and the kinetics of transcriptional response (68).
FUNCTIONAL IMPLICATIONS OF A FRACTAL MODEL FOR CHROMATIN AT LARGE LENGTH SCALES
A number of models for the large-scale architecture of chromosomes have already been proposed and investigated experimentally using in situ hybridization of oligonucleotides targeted to specific genomic sequences in fixed cells (Fluorescent In Situ Hybridization, FISH). The physical distance between genomic loci (L) was mapped as a function of genomic distances (G) (37,38,69):
| (3) |
with ε the fractal dimension of the line of polymer in space, which is a priori unrelated to f (A. Grosberg, personal communication). In the 150 nm–1 µm spatial range, ε was ∼2, and it increased to ∼3.2 above 1 µm (note that a fractal dimension larger than 3 is somewhat surprising and would deserve further investigations). A confinement for distances larger than 2–3 µm, which is consonant with the existence of chromosome territories of finite dimension in interphase (9), was recently detected (70). Albeit the fact that FISH is an artifact-prone technique that strongly alters chromatin structures smaller than ∼1 Mb mainly during the harsh thermal denaturation step (71), different models were built on chromatin loops that were either of ∼1 Mbp in length (37,38) or of ∼200 kb and bundled in groups of ∼5 (69). However, their consistency with respect to polymer physics predictions so far remains limited because it was recently demonstrated that confined polymer models could equally well reproduce FISH data (72). A new dynamic loop model was recently proposed assuming that the formation of chromosome loops is a random diffusion-driven process and that loops occur transiently (73, 74). This model, which leads to the formation of loops of random sizes, relies on two fitting parameters, namely the loop formation probability on collision of two chromatin loci and the loop lifetime. Notably, the looping probability is set to low values ∼10−4, so as to avoid the formation of collapsed, highly entangled, polymer chains. Using an appropriate set of parameters, it was shown that this model reproduces experiments of FISH and Hi-C and the general topography of chromosome territories (74).
Interestingly, structural insights obtained by Hi-C lead to an alternative model of chromosomes architecture called the crumpled globule, which is a space filling conformation characterized by a fractal dimension of f = 3. The crumpling was originally imagined to explain relaxation kinetics of polymers rapidly brought in poor solvent conditions (23). The crumpled conformation is transient and ultimately collapses into an equilibrium globule, which is the stable configuration in poor solvent. The crumpled globule is not entangled, and large scale loops should be reorganized at a low energetic cost with no need to break physical contacts to liberate genomic sequences. In addition, the crumpled globule favors long-range intra-chromosomal interactions, as shown by the power-law dependence of −1 for contact probabilities in comparison with −1.5 for equilibrium globules (10). Despite these attractive predictions, it remains elusive whether a crumpled conformation can be stabilized over long time periods in vivo. Interestingly, Rosa et al. (75) proposed that the organization of chromosomes in discrete territories was unstable from a thermodynamic standpoint yet maintained throughout interphase kinetically. One may then speculate that crumpling occurs during the post-mitotic decondensation of chromosomes due to the topological constraints in the nuclear volume, and these long polymer chains remain unentangled and segregated in territories throughout the period of interphase.
Overall, the dynamic loop and the crumpled globule models seem to account for experimental data on chromatin large scale organization, though the former is a steady-state model built on transient loops, whereas the latter is kinetically unstable. Despite these differences, it remains unclear whether the structures proposed by Bohn and Heermann (74) or Mirny and coworkers (10) share similarities or not, and one future study comparing their conformations is thus needed.
Because the fractal description of the different structural elements in the nucleus remains far from complete, we propose a roadmap of future experiments to validate the fractal model of nuclear architecture and determine its properties more precisely.
ROADMAP TO SUPPORT OR INVALIDATE THE FRACTAL MODEL
A convergence of experimental data obtained from Hi-C, image analysis and neutron scattering supports the fractal architecture of nuclear DNA mass distribution at length scales larger than 300 nm, but a consensus about the nature of the underlying structure at smaller scales is still lacking (see column f in Table 1). Image analysis of confocal or electron micrographs of individual fixed cells remain to be improved due to the potential artifacts associated to the staining protocol (76). Fluorescent cell-permeable stoichiometric DNA intercalators, such as Hoechst 33342 (77) or DRAQ5 (78) could be used to characterize DNA architecture. In addition, labeling the DNA backbone with fluorescent nucleotide analogs is possible in living cells (79). Core histones, such as H2B, could be simultaneously fluorescently labeled (chemically or with GFP) to directly test whether the fractal dimensions of the DNA and the protein component of chromatin differ in individual cells, as expected from neutron scattering (Table 1). It may also prove useful to compare chromatin texture based on transmission electron micrographs and correlative H2B-GFP fluorescent images, given that the distribution of H2B-GFP is correlated with electron-dense chromatin regions (80). Electron spectroscopy imaging (ESI) is another powerful technique to study the nuclear interior using nitrogen and phosphorus mapping, which enables to delineate protein from nucleic acids without contrast agents (81,82). Interestingly, all these techniques allow to derive the mass fractal distribution of different nuclear components, yet this quantity is not relevant to strengthen the crumpled globule hypothesis vs. dynamic looping. In fact, the crumpled globule conformation can be unambiguous demonstrated by determining ε, which is equal to 3 only for this architecture (A. Grosberg, personal communication). FISH represents the most straightforward technique to measure ε, but the artifacts of fixation have always raised concerns on the reliability of FISH data (70). Thus future experiments should ideally be performed in living cell using, e.g. PNA as hybridization probes (83), or developing new fluorescent nucleotide incorporation regimes in different colors into the DNA backbone. Finally, the probability of intra-chromosomal contacts could be scanned by Hi-C in cells treated to control the degree of nuclear confinement using, e.g. hypo/hypertonic media (84), or drug treatments such as aphidicolin, which induces an increase in nuclear volume while preventing DNA replication (Sébastien Huet and J.E., unpublished results). The changes in chromatin folding could then be analyzed with the crumple globule and the dynamic loop models to compare the relevance of their predictions.
At scales <300 nm, experimental data on chromatin fractal architecture is still sparse (Table 1), and electron microscopy or ESI of thin nuclear sections clearly constitutes methods of choice to probe the DNA or protein structures of chromatin at small length scales. Conventional preparation protocols, which involve fixation, dehydration, embedding in plastic for sectioning and staining with heavy metals, may, however, distort cellular structures (85), and other methods of sample preparation have been explored, one of which, cryofixation, has received much attention. Cryofixation that relies on the rapid freezing of the specimen has emerged as a powerful solution to observe samples in their fully hydrated 3D structure (86), although the lack of staining has to be compensated by sophisticated image analysis and reconstruction (87). Notably, these techniques could also prove useful to characterize the architecture of the nucleoplasm using, e.g. textural analysis of inverted contrast images, and the spatial resolution should be sufficient to zoom at the level of nuclear compartments, such as euchromatin and heterochromatin, and ascertain whether they exhibit significantly different fractal architectures. Moreover, the recent advent of super-resolution microscopy techniques, e.g. PhotoActivated Localization Microscopy/Stochastic Optical Reconstruction Microscopy/Ground State Depletion microscopy followed by Individual Molecule return, which achieve spatial resolutions of ∼20 nm (88–91), and which have been applied to cell lines for instance expressing H2B tagged GFP (92) and with a moiety that can be labeled with a bright organic fluorophore (93), or could be applied to DNA stained cells, constitutes an interesting prospect to strengthen or invalidate the fractal model. Notably, the diffusion coefficient of genomic loci of ∼10−2 µm2/s, meaning that they explore ∼100 nm in 1 s, is rapid (94,95), and optimal resolutions in super-resolution microscopy are reached only after fixation of the cells, thus suggesting that cryofixation will be a relevant tool for the observation of small chromatin features.
We envisioned several consequences of chromatin fractal organization for euchromatin and heterochromatin in terms of target search strategies. Transcription factors are indeed expected to exhibit dramatically different behaviors in hetero- and eu-chromatin in terms of the compactness of their exploration by random motion. Interestingly, it was recently shown that the movement of transcription factors could be tracked spatially with exquisite precision at the single molecule level in living bacteria (96). These experiments are, however, limited to ∼5 images before fluorophores bleach, and this time frame is likely insufficient to assay the compactness of a trajectory. Stable inorganic probes, such as quantum dots or nano-crystals (97,98), or new generations of stable organic dyes, such as Atto 647 (99), are expected to greatly improve acquisition conditions and to pave the way to a direct validation of these propositions.
CONCLUSION
Beyond the discussion on the relevance of a fractal nuclear organization, one may speculate on why chromatin has evolved toward a fractal architecture. This question was raised in the seminal work of Grosberg et al. (22), who proposed that DNA primary sequence, which exhibits self-similar properties (15–20), and its spatial structure were created together as a result of a self-similar evolution process. Loops may indeed be stabilized by DNA sequences non-randomly repeated along chromosomes, as suggested by the spatial correlation between CTCF binding sites and contacts between DNA fragments derived from Hi-C (100). The crumpled globule architecture may have been selected due to its optimal packing of chromosomes, while maintaining them in a dynamic and accessible state. Whether these properties are essential for genomic transactions are unclear, and it remains to be assessed whether chromosome adopt a fractal conformation in every eukaryotes. In addition, it was recently shown that the facilitated diffusion model, which describes the search for a target site based on alternating phases of free diffusion in the bulk and sliding diffusion of a bound complex, is a robust mechanism for a fractal template such as chromatin (101). In turn, this study shows that the exploration strategy can be finely tuned, and the first passage time at a target site greatly accelerated, by adjusting the molecular interactions of a complex and the fractal characteristics f and γ of the template. Consequently, the fractal hypothesis seems to be adding a new line to the already rich palette of structural polymorphism of chromatin, which appears to be reconfigurable from the nucleosomal to the nuclear level.
FUNDING
Funding for open access charge: CNRS funding.
Conflict of interest statement. None declared.
ACKNOWLEDGEMENTS
The authors are particularly grateful to Alexander Grosberg for enlightening comments. They also thank Raphaël Voituriez and Jean-Marc Victor for critical comments on the manuscript, Nathalie Daigle for proofreading, and the Nuclear Architecture and Dynamics research network (CNRS GDR 3536) for discussions.
REFERENCES
- 1.Luger K, Mader AW, Richmond RK, Sargent DF, Richmond TJ. Crystal structure of the nucleosome core particle at 2.8 A resolution. Nature. 1997;389:251–260. doi: 10.1038/38444. [DOI] [PubMed] [Google Scholar]
- 2.Harp JM, Hanson BL, Timm DE, Bunick GJ. Asymmetries in the nucleosome core particle at 2.5 A resolution. Acta. Crystallogr. D Biol. Cyrstallogr. 2000;56:1513–1534. doi: 10.1107/s0907444900011847. [DOI] [PubMed] [Google Scholar]
- 3.van Holde KE. Chromatin. New York, NY: Springer; 1989. [Google Scholar]
- 4.van Holde K, Zlatanova J. Chromatin fiber structure: where is the problem now? Semin. Cell. Dev. Biol. 2007;18:651–658. doi: 10.1016/j.semcdb.2007.08.005. [DOI] [PubMed] [Google Scholar]
- 5.Woodcock CL, Ghosh RP. Chromatin higher-order structure and dynamics. Cold Spring Harb. Perspect. Biol. 2010;2:a000596. doi: 10.1101/cshperspect.a000596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Cook PR. The organization of replication and transcription. Science. 1999;284:1790–1795. doi: 10.1126/science.284.5421.1790. [DOI] [PubMed] [Google Scholar]
- 7.Göndör A, Ohlsson R. Chromosome crosstalk in three dimensions. Nature. 2009;461:212–217. doi: 10.1038/nature08453. [DOI] [PubMed] [Google Scholar]
- 8.Gerlich D, Ellenberg J. 4D imaging to assay complex dynamics in live specimens. Nat. Cell. Biol. 2003;(Suppl):S14–S19. [PubMed] [Google Scholar]
- 9.Cremer T, Cremer M, Dietzel S, Muller S, Solovei I, Fakan S. Chromosome territories—a functional nuclear landscape. Curr. Opin. Cell. Biol. 2006;18:307–316. doi: 10.1016/j.ceb.2006.04.007. [DOI] [PubMed] [Google Scholar]
- 10.Lieberman-Aiden E, van Berkum NL, Williams L, Imakaev M, Ragoczy T, Telling A, Amit I, Lajoie BR, Sabo PJ, Dorschner MO, et al. Comprehensive mapping of long-range interactions reveals folding principles of the human chromosome. Science. 2009;326:289–293. doi: 10.1126/science.1181369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bancaud A, Huet S, Daigle N, Beaudouin J, Mozziconacci J, Ellenberg J. Molecular crowding affects diffusion and binding of nuclear proteins in heterochromatin and reveals the fractal organization of chromatin. EMBO J. 2009;28:3785–3798. doi: 10.1038/emboj.2009.340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Goldberger AL. Non-linear dynamics for clinicians: chaos theory, fractals, and complexity at the bedside. Lancet. 1996;347:1312–1314. doi: 10.1016/s0140-6736(96)90948-4. [DOI] [PubMed] [Google Scholar]
- 13.Havlin S, Buldyrev SV, Goldberger AL, Mantegna RN, Ossadnik SM, Peng CK, Simons M, Stanley HE. Fractals in biology and medicine. Chaos Solitons Fractals. 1995;6:171–201. doi: 10.1016/0960-0779(95)80025-c. [DOI] [PubMed] [Google Scholar]
- 14.Heymans O, Fissette J, Vico P, Blacher S, Masset D, Brouers F. Is fractal geometry useful in medicine and biomedical sciences? Med. Hypotheses. 2000;54:360–366. doi: 10.1054/mehy.1999.0848. [DOI] [PubMed] [Google Scholar]
- 15.Buldyrev SV, Goldberger AL, Havlin S, Peng C, Simons M, Sciortino F, Stanley HE. Long-range fractal correlations in DNA. Phys. Rev. Lett. 1993;71:1776. doi: 10.1103/PhysRevLett.71.1776. [DOI] [PubMed] [Google Scholar]
- 16.Cristea P, Popescu G. 1st SouthEast European Symposium on Interdisciplinary Approachees in Fractal Analysis. Bucharest, Romania: 2003. pp. 131–134. [Google Scholar]
- 17.Garte S. Fractal properties of the human genome. J. Theor. Biol. 2004;230:251–260. doi: 10.1016/j.jtbi.2004.05.015. [DOI] [PubMed] [Google Scholar]
- 18.Nicolay S, Brodie Of Brodie EB, Touchon M, Audit B, d'Aubenton-Carafa Y, Thermes C, Arneodo A. Bifractality of human DNA strand-asymmetry profiles results from transcription. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2007;75:032902. doi: 10.1103/PhysRevE.75.032902. [DOI] [PubMed] [Google Scholar]
- 19.Voss RF. Evolution of long-range fractal correlations and 1/f noise in DNA base sequences. Phys. Rev. Lett. 1992;68:3805–3808. doi: 10.1103/PhysRevLett.68.3805. [DOI] [PubMed] [Google Scholar]
- 20.Borovik AS, Grosberg A, Frank-Kamenetskii MD. Fractality of DNA texts. J Biomol. Struct. Dyn. 1994;12:655–669. doi: 10.1080/07391102.1994.10508765. [DOI] [PubMed] [Google Scholar]
- 21.Arneodo A, Vaillant C, Audit B, Argoul F, d'Aubenton-Carafa Y, Thermes C. Multi-scale coding of genomic information: from DNA sequence to genome structure and function. Phys. Reports. 2011;498:45–188. [Google Scholar]
- 22.Grosberg AY, Rabin Y, Havlin S, Neer A. Crumpled globule model of the three-dimensional structure of DNA. Europhys. Lett. 1993;23:373–378. [Google Scholar]
- 23.Grosberg AY, Nechaev SK, Shakhnovich EI. The role of topological constraints in the kinetics of Collapse of macromolecule. Le J. Phys. 1988;49:2095–2100. [Google Scholar]
- 24.Witten TA. Polymer solutions: a geometric introduction. Rev. Mod. Phys. 1998;70:1531–1544. [Google Scholar]
- 25.McNally JG, Mazza D. Fractal geometry in the nucleus. EMBO J. 2010;29:2–3. doi: 10.1038/emboj.2009.375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Mirny LA. The fractal globule as a model of chromatin architecture in the cell. Chromosome Res. 2011;19:37–51. doi: 10.1007/s10577-010-9177-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Sanyal A, Bau D, Marti-Renom MA, Dekker J. Chromatin globules: a common motif of higher order chromosome structure? Curr. Opin. Cell. Biol. 2011;23:325–331. doi: 10.1016/j.ceb.2011.03.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Mandelbrot BB. In: The Fractal Geometry of Nature. Freeman WF, editor. 1982. San Francisco. [Google Scholar]
- 29.Daban JR. Physical constraints in the condensation of eukaryotic chromosomes. Local concentration of DNA versus linear packing ratio in higher order chromatin structures. Biochemistry. 2000;39:3861–3866. doi: 10.1021/bi992628w. [DOI] [PubMed] [Google Scholar]
- 30.Bohrmann B, Haider M, Kellenberger E. Concentration evaluation of chromatin in unstained resin-embedded sections by means of low-dose ratio-contrast imaging in STEM. Ultramicroscopy. 1993;49:235–251. doi: 10.1016/0304-3991(93)90230-u. [DOI] [PubMed] [Google Scholar]
- 31.Cassi D, Regina S. Spectral dimension of branched structures: universality in geometrical disorder. Phys. Rev. Lett. 1993;70:1647–1649. doi: 10.1103/PhysRevLett.70.1647. [DOI] [PubMed] [Google Scholar]
- 32.Beaudouin J, Mora-Bermudez F, Klee T, Daigle N, Ellenberg J. Dissecting the contribution of diffusion and interactions to the mobility of nuclear proteins. Biophys. J. 2006;90:1878–1894. doi: 10.1529/biophysj.105.071241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Saxton MJ. Anomalous diffusion due to obstacles: a Monte Carlo study. Biophys. J. 1994;66:394–401. doi: 10.1016/s0006-3495(94)80789-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Ben-Avraham S, Havlin S. Diffusion and Reactions in Fractals and Disordered Systems. Cambridge: Cambridge University Press; 2000. [Google Scholar]
- 35.Einstein AJ, Wu H-S, Sanchez M, Gil J. Fractal organization of chromatin appearance for diagnosis in breast cytology. J. Pathol. 1998;185:366–381. doi: 10.1002/(SICI)1096-9896(199808)185:4<366::AID-PATH122>3.0.CO;2-C. [DOI] [PubMed] [Google Scholar]
- 36.Lebedev DV, Filatov MV, Kuklin AI, Islamov AK, Ketzinger E, Pantina R, Toperverg BP, Isaev-Ivanov VV. Fractal nature of chromatin organization in interphase chicken erythrocyte nuclei: DNA structure exhibits biphasic fractal properties. FEBS Lett. 2005;579:1465–1468. doi: 10.1016/j.febslet.2005.01.052. [DOI] [PubMed] [Google Scholar]
- 37.Yokota H, van den Engh G, Hearst JE, Sachs RK, Trask BJ. evidence for the organization of chromatin in megabase pair-sized loops arranged along a random walk path in the humand G0/G1 interphase nucleus. J. Cell. Biol. 1995;130:1239–1249. doi: 10.1083/jcb.130.6.1239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Sachs RK, van den Engh G, Trask B, Yokota H, Hearst JE. A random-walk/giant-loop model for interphase chromosomes. Proc. Natl Acad. Sci. USA. 1995;92:2710–2714. doi: 10.1073/pnas.92.7.2710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Tóth KF, Knoch TA, Wachsmuth M, Frank-Stöhr M, Stöhr M, Bacher CP, Müller G, Rippe K. Trichostatin A-induced histone acetylation causes decondensation of interphase chromatin. J. Cell. Sci. 2004;15:4277–4287. doi: 10.1242/jcs.01293. [DOI] [PubMed] [Google Scholar]
- 40.Huisman A, Ploeger LS, Dullens HF, Poulin N, Grizzle WE, van Diest PJ. Development of 3D chromatin texture analysis using confocal laser scanning microscopy. Cell Oncol. 2005;27:335–345. doi: 10.1155/2005/494605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Ferreira RC, de Matos PS, Adam RL, Leite NJ, Metze K. Application of the Minkowski-Bouligand fractal dimension for the differential diagnosis of thyroid follicular neoplasias. Cell Oncol. 2006;28:331–333. doi: 10.1155/2006/634840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Mello MR, Metze K, Adam RL, Pereira FG, Magalhaes MG, Machado CG, Lorand-Metze I. Phenotypic subtypes of acute lymphoblastic leukemia associated with different nuclear chromatin texture. Anal. Quant. Cytol. Histol. 2008;30:92–98. [PubMed] [Google Scholar]
- 43.Metze K, Ferreira RC, Adam RL, Leite NJ, Ward LS, de Matos PS. Chromatin texture is size dependent in follicular adenomas but not in hyperplastic nodules of the thyroid. World J. Surg. 2008;32:2744–2746. doi: 10.1007/s00268-008-9736-0. [DOI] [PubMed] [Google Scholar]
- 44.Castelli C, Rosa GA. Ultrastructural complexity of nuclear components during early apoptotic phases in breast cancer cells. Anal. Cell. Pathol. 2001;23:1–9. doi: 10.1155/2001/828309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Pentland AP. Fractal-based description of natural scenes. IEEE Trans. Pattern Anal. Mach. Intell. 1984;6:661–674. doi: 10.1109/tpami.1984.4767591. [DOI] [PubMed] [Google Scholar]
- 46.Lebedev DV, Filatov MV, Kuklin AI, Islamov AK, Stellbrink J, Pantina R, Denisov YY, Toperverg BP, Isaev-Ivanov VV. Structural hierarchy of chromatin in chicken erythrocyte nuclei based on small-angle neutron scattering: fractal nature of the large-scale chromatin organization. Crystallogr. Reports. 2008;53:110–115. [Google Scholar]
- 47.Dekker J. The three ‘C’s of chromsome conformation capture: controls, controls, controls. Nat. Methods. 2006;3:17–21. doi: 10.1038/nmeth823. [DOI] [PubMed] [Google Scholar]
- 48.Weiss M, Elsner M, Kartberg F, Nilsson T. Anomalous subdiffusion is a measure for cytoplasmic crowding in living cells. Biophys. J. 2004;87:3518–3524. doi: 10.1529/biophysj.104.044263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Saxton MJ. Lateral diffusion in an archipelago. Dependence on tracer size. Biophys. J. 1993;64:1053–1062. doi: 10.1016/S0006-3495(93)81471-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Guigas G, Weiss M. Sampling the cell with anomalous diffusion—the discovery of slowness. Biophys. J. 2008;94:90–94. doi: 10.1529/biophysj.107.117044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Seksek O, Biwersi J, Verkman AS. Translational diffusion of macromolecule-sized solutes in cytoplasm and nucleus. J. Cell. Biol. 1997;138:131–142. doi: 10.1083/jcb.138.1.131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Pack C, Saito K, Tamura M, Kinjo M. Microenvironment and effect of energy depletion in the nucleus analyzed by mobility of multiple oligomeric EGFPs. Biophys. J. 2006;91:3921–3936. doi: 10.1529/biophysj.105.079467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Grunwald D, Martin RM, Buschmann V, Bazett-Jones DP, Leonhardt H, Kubitscheck U, Cardoso MC. Probing intranuclear environments at the single-molecule level. Biophys. J. 2008;94:2847–2858. doi: 10.1529/biophysj.107.115014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Wachsmuth M, Waldeck W, Langowski J. Anomalous diffusion of fluorescent probes inside living cell nuclei investigated by spatially-resolved fluorescence correlation spectroscopy. J. Mol. Biol. 2000;298:677–689. doi: 10.1006/jmbi.2000.3692. [DOI] [PubMed] [Google Scholar]
- 55.Crawford J, Matsui N. Heterogeneity of the pore and solid volume of soil: distinguishing a fractal space from its non-fractal complement. Geoderma. 1996;73:183–195. [Google Scholar]
- 56.Dathe A, Thullner M. The relationship between fractal properties of solid matrix and pore space in porous media. Geoderma. 2005;129:279–290. [Google Scholar]
- 57.Mc Guffee SR, Elcock AH. Diffusion, crowding & protein stability in a dynamic molecular model of the bacterial cytoplasm. PLoS Comput. Biol. 2010;6:e1000694. doi: 10.1371/journal.pcbi.1000694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Avnir D, Biham O, Lidar D, Malcai O. Is the geometry of nature fractal? Science. 1998;279:39–40. [Google Scholar]
- 59.Schaefer DW, Keefer KD. Structure of random porous materials: silica aerogel. Phys. Rev. Lett. 1986;56:2199. doi: 10.1103/PhysRevLett.56.2199. [DOI] [PubMed] [Google Scholar]
- 60.Schaeffer DW, Keefer KD. Fractal geometry of silica condensation polymers. Phys. Rev. Lett. 1984;53:1383–1386. [Google Scholar]
- 61.de Gennes P-G. Scaling Concepts in Polymer Physics. Ithaca: Cornell university press; 1979. [Google Scholar]
- 62.Condamin S, Tejedor V, Voituriez R, Bénichou O, Klafter J. Probing microscopic origins of confined subdiffusion by first-passage observables. Proc. Natl Acad. Sci. USA. 2008;105:5675–5680. doi: 10.1073/pnas.0712158105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Bénichou O, Chevalie C, Klafter J, Meyer B, Voituriez R. Geometry-controlled kinetics. Nat. Chem. 2010;2:472–477. doi: 10.1038/nchem.622. [DOI] [PubMed] [Google Scholar]
- 64.Condamin S, Bénichou O, Tejedor V, Voituriez R, Klafter J. First-passage times in complex scale-invariant media. Nature. 2007;450:77–80. doi: 10.1038/nature06201. [DOI] [PubMed] [Google Scholar]
- 65.Rea S, Eisenhaber F, O'Carroll D, Strahl BD, Sun ZW, Schmid M, Opravil S, Mechtler K, Ponting CP, Allis CD, et al. Regulation of chromatin structure by site-specific histone H3 methyltransferases. Nature. 2000;406:593–599. doi: 10.1038/35020506. [DOI] [PubMed] [Google Scholar]
- 66.Trojer P, Reinberg D. Facultative heterochromatin: is there a distinctive molecular signature? Mol. Cell. 2007;28:1–13. doi: 10.1016/j.molcel.2007.09.011. [DOI] [PubMed] [Google Scholar]
- 67.Spinelli G. Heterochromatin and complexity: a theoretical approach. Nonlinear Dynamics Psychol. Life Sci. 2003;7:329–361. doi: 10.1023/a:1025980007520. [DOI] [PubMed] [Google Scholar]
- 68.Meyer B, Bénichou O, Kafri Y, Voituriez R. Geometry-induced bursting dynamics in gene expression. Biophys. J. 2012;102:2186–2191. doi: 10.1016/j.bpj.2012.03.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Munkel C, Eils R, Dietzel S, Zink D, Mehring C, Wedeman G, Cremer T, Langowski J. Compartmentalization of interphase chromosomes observed in simulation and experiment. J. Mol. Biol. 1999;285:1053–1065. doi: 10.1006/jmbi.1998.2361. [DOI] [PubMed] [Google Scholar]
- 70.Mateos-Langerak J, Bohn M, de Leeuw W, Giromus O, Manders EM, Verschure PJ, Indemans MH, Gierman HJ, Heermann DW, van Driel R, et al. Spatially confined folding of chromatin in the interphase nucleus. Proc. Natl Acad. Sci. USA. 2009;106:3812–3817. doi: 10.1073/pnas.0809501106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Solovei I, Cavallo A, Schermelleh L, Jaunin F, Scasselati C, Cmarko D, Cremer C, Fakan S, Cremer T. Spatial preservation of nuclear chromatin architecture during three-dimensional fluorescence in situ hybridization (3D-FISH) Exp. Cell Res. 2002;276:10–23. doi: 10.1006/excr.2002.5513. [DOI] [PubMed] [Google Scholar]
- 72.Emanuel M, Rajda NH, Henriksson A, Schiessel H. The physics behing the larger scale organization of DNA in eukaryotes. Phys. Biol. 2009;6:025008. doi: 10.1088/1478-3975/6/2/025008. [DOI] [PubMed] [Google Scholar]
- 73.Bohn M, Heermann DW. Conformational properties of compact polymers. J. Chem. Phys. 2009;130:174901. doi: 10.1063/1.3126651. [DOI] [PubMed] [Google Scholar]
- 74.Bohn M, Heermann DW. Diffusion-driven looping provides a consistent framework for chromatin organization. PLoS One. 2010;5:e12218. doi: 10.1371/journal.pone.0012218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Rosa A, Everaers R. Structure and dynamics of interphase chromosomes. PLoS Comput, Biol. 2008;4:e1000153. doi: 10.1371/journal.pcbi.1000153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Metze K, Adam RL, Vido JR, Lorand-Metze IG. The influence of staining characteristics on nuclear texture features in cytology. Anal. Quant. Cytol. Histol. 2009;31:241–246. [PubMed] [Google Scholar]
- 77.Latt SA, Wohlleb JC. Optical studies of the interaction of 33258 Hoechst with DNA, chromatin, and metaphase chromosomes. Chromosoma. 1975;52:297–316. doi: 10.1007/BF00364015. [DOI] [PubMed] [Google Scholar]
- 78.Martin RM, Leonhardt H, Cardoso MC. DNA labeling in living cells. Cytometry A. 2005;67A:45–52. doi: 10.1002/cyto.a.20172. [DOI] [PubMed] [Google Scholar]
- 79.Zink D, Sadoni N, Stelzer E. Visualizing chromatin and chromosomes in living cells. Methods. 2003;29:42–50. doi: 10.1016/s1046-2023(02)00289-x. [DOI] [PubMed] [Google Scholar]
- 80.Monier K, Armas JC, Etteldorf S, Ghazal P, Sullivan KF. Annexation of the interchromosomal space during viral infection. Nat. Cell. Biol. 2000;2:661–665. doi: 10.1038/35023615. [DOI] [PubMed] [Google Scholar]
- 81.Bazett-Jones DP, Li R, Fussner E, Nisman R, Dehghani H. Elucidating chromatin and nuclear domain architecture with electron spectroscopic imaging. Chromosome Res. 2008;16:397–412. doi: 10.1007/s10577-008-1237-3. [DOI] [PubMed] [Google Scholar]
- 82.Dellaire G, Kepkay R, Bazett-Jones DP. High resolution imaging of changes in the structure and spatial organization of chromatin, gamma-H2A.X and the MRN complex within etoposide-induced DNA repair foci. Cell Cycle. 2009;8:3750–3769. doi: 10.4161/cc.8.22.10065. [DOI] [PubMed] [Google Scholar]
- 83.Molenaar C, Wiesmeijer K, Verwoerd NP, Khazen S, Eils R, Tanke HJ, Dirks RW. Visualizing telomere dynamics in living mammalian cells using PNA probes. EMBO J. 2003;22:6631–6641. doi: 10.1093/emboj/cdg633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Richter K, Nessling M, Lichter P. Macromolecular crowding and its potential impact on nuclear function. Biochim. Biophys. Acta. 2008;1783:2100–2107. doi: 10.1016/j.bbamcr.2008.07.017. [DOI] [PubMed] [Google Scholar]
- 85.Glauert AM, Lewis PR. Biological Specimen Preparation for Transmission Electron Microscopy. Princeton: Princeton University Press; 1998. [Google Scholar]
- 86.Dubochet J. The physics of rapid cooling and its implications for cryoimmobilization of cells. Methods Cell. Biol. 2007;79:7–21. doi: 10.1016/S0091-679X(06)79001-X. [DOI] [PubMed] [Google Scholar]
- 87.Dubochet J, Zuber B, Eltsov M, Bouchet-Marquis C, Al-Amoudi A, Livolant F. How to “read” a vitreous section. Methods Cell. Biol. 2007;79:385–406. doi: 10.1016/S0091-679X(06)79015-X. [DOI] [PubMed] [Google Scholar]
- 88.Betzig E, Patterson GH, Sougrat R, Lindwasser OW, Olenych S, Bonifacino JS, Davidson MW, Lippincott-Schwartz J, Hess HF. Imaging intracellular fluorescent proteins at nanometer resolution. Science. 2006;313:1642–1645. doi: 10.1126/science.1127344. [DOI] [PubMed] [Google Scholar]
- 89.Hell SW. Toward fluorescence nanoscopy. Nat. Biotech. 2003;21:1347–1355. doi: 10.1038/nbt895. [DOI] [PubMed] [Google Scholar]
- 90.Rust MJ, Bates M, Zhuang X. Sub-diffraction-limit imaging by stochastic optical reconstruction microscopy (STORM) Nat. Methods. 2006;3:793–795. doi: 10.1038/nmeth929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Fölling J, Bossi M, Bock H, Medda R, Wurm CA, Hein B, Jakobs S, Eggeling C, Hell SW. Fluorescence nanoscopy by ground-state depletion and single-molecule return. Nat. Methods. 2008;5:943–945. doi: 10.1038/nmeth.1257. [DOI] [PubMed] [Google Scholar]
- 92.Bohn M, Diesinger P, Kaufmann R, Weiland Y, Müller P, Gunkel M, von Ketteler A, Lemmer P, Hausmann M, Heermann DW, et al. Localization Microscopy Reveals Expression-Dependent Parameters of Chromatin Nanostructure. Biophys. J. 2010;99:1358–1367. doi: 10.1016/j.bpj.2010.05.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Wombacher R, Heidberder M, van de Linde S, Sheetz MP, Heilemann M, Cornish VW, Sauer M. Live-cell super-resolution imaging with trimethoprim conjugates. Nat. Methods. 2010;7:717–719. doi: 10.1038/nmeth.1489. [DOI] [PubMed] [Google Scholar]
- 94.Hajjoul H, Kocanova S, Lassadi I, Bystricky K, Bancaud A. Lab-on-chip for fast 3D particle tracking in living cells. Lab. Chip. 2009;9:3054–3058. doi: 10.1039/b909016a. [DOI] [PubMed] [Google Scholar]
- 95.Levi V, Ruan Q, Gratton E. 3-D particle tracking in a two-photon microscope: application to the study of molecular dynamics in cells. Biophys. J. 2005;88:2919–2928. doi: 10.1529/biophysj.104.044230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Elf J, Li G-W, Xie XS. Probing transcription factor dynamics at the single molecule level in a living cell. Science. 2007;316:1191–1194. doi: 10.1126/science.1141967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Harke B, Ullal CK, Keller J, Hell SW. Three-dimensional nanoscopy of colloidal crystals. Nano. Lett. 2008;8:1309–1313. doi: 10.1021/nl073164n. [DOI] [PubMed] [Google Scholar]
- 98.Dahan M, Lévi S, Luccardini C, Rostaing P, Riveau B, Triller A. Diffusion dynamics of glycine receptors revealed by single-particle quantum dot tracking. Science. 2003;302:442–445. doi: 10.1126/science.1088525. [DOI] [PubMed] [Google Scholar]
- 99.Bruckbauer A, James P, Zhou H, Yoon JW, Excell D, Korchev Y, Jones R, Klenerman D. Nanopipette delivery of individual molecules to cellular compartments for single molecule fluorescence tracking. Biophys. J. 2007;93:3120–3131. doi: 10.1529/biophysj.107.104737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Botta M, Haider S, Leung IX, Lio P, Mozziconacci J. Intra- and inter-chromosomal interactions correlated with CTCF binding genome wide. Mol. Syst. Biol. 2010;6:426. doi: 10.1038/msb.2010.79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Benichou O, Chevalier C, Meyer B, Voituriez R. Facilitated diffusion of proteins on chromatin. Phys. Rev. Lett. 2011;106:038102. doi: 10.1103/PhysRevLett.106.038102. [DOI] [PubMed] [Google Scholar]