Abstract
The co-regulation of transcription factors (TFs) has been widely observed in various species. Why is such a co-regulation mechanism needed for transcriptional regulation? To answer this question, the following experiments and analyses were performed. First, examination of the human gene regulatory network (GRN) indicated that co-regulation was significantly enriched in the human GRN. Second, mathematical simulation of an artificial regulatory network showed that the co-regulation mechanism was related to the biphasic dose–response patterns of TFs. Third, the relationship between the co-regulation mechanism and the biphasic dose–response pattern was confirmed using microarray experiments examining different time points and different doses of the toxicant tetrachlorodibenzodioxin. Finally, two mathematical models were constructed to mimic highly co-regulated networks (HCNs) and little co-regulated networks (LCNs), and we found that HCNs were more robust to parameter perturbation than LCNs, whereas LCNs were faster in adaptation to environmental changes than HCNs.
INTRODUCTION
Biological organisms have evolved huge and complex gene regulatory networks (GRNs) to properly respond to external and internal changes. These huge and complex GRNs comprise transcription factors (TFs) that control the expression levels of a genome and the target genes (TGs) controlled by the TFs. It is well known that the TGs are usually controlled not by a single TF but by multiple TFs (1–5). This leads to the question of what kind of dynamical properties of a GRN are responsible for the evolution of such a co-regulation mechanism.
One clue to the responsible dynamic properties of the co-regulation mechanism is that GRNs of more complex organisms show higher degrees of co-regulation (3). This has led to speculation that the co-regulation mechanism might be enriched for dynamic properties specifically related to eukaryotes rather than prokaryotes, and multicellular organisms rather than single-celled organisms. Many studies support such speculation. First, the co-regulation mechanism of the yeast GRN participates in major eukaryotic signaling systems such as ubiquitin pathways and protein kinase cascades. It also integrates disparate cellular processes (1). Second, the co-regulation mechanism of the GRNs of multicellular organisms plays an important role in the control of tissue-specific gene expression during the differentiation of various cell types (4,6,7). Third, the division of network components into three levels (top, middle and bottom) in a hierarchical context illustrates that the co-regulation mechanism is more enriched in the middle level than in the other levels (3). This third evidence supports the aforementioned speculation since more complex organisms show more hierarchical levels in their GRNs (3,8,9). All these observations provide some clues as to the nature of the co-regulation mechanism in terms of comparative genomics or network topologies. However, no satisfactory explanation has emerged yet regarding the evolutionary design principles or dynamic properties underlying the development of such a co-regulation mechanism.
In this article, we exploited the dynamic properties related to the co-regulation mechanism and obtained the following results: (i) co-regulation is enriched in the human GRN, and this enrichment is related to a high rate of evolution and multicellular organismal processes such as developmental processes; (ii) the co-regulation mechanism of a TF can cause a biphasic dose–response curve and (iii) the co-regulation mechanism can enhance the robustness, but can also attenuate the adaptability of a GRN. Taken together, these results suggest that complex biological organisms evolved the co-regulation mechanism for their GRNs by inducing or increasing biphasic behavior in order to enhance robustness while sacrificing adaptability.
MATERIALS AND METHODS
Statistical analysis
A one-sided, one-sample z-test was performed to evaluate the statistical abundance of the sum of weights of each TF in TF co-regulation networks. A one-sided two-sample t-test was used to evaluate the evolutionary rate, tissue variability, messenger RNA (mRNA) abundance, topological properties, adaptability and robustness. For the regulation coherency index (RCI), a two-sided paired t-test was applied. Fisher’s exact test was used to evaluate the enrichment of ligands, extracellular proteins, receptors and membrane proteins in the TGs of the biphasic TFs (BTFs) and the TGs of the monophasic TFs (MTFs).
Evolutionary rate and tissue variability
Evolutionary rates were defined by the ratios of the non-synonymous substitution rates (dN) and synonymous substitution rates (dS) for homologous gene pairs in humans and mice and were retrieved from the Human PAML Browser (10). The tissue variability of a gene is defined as the standard deviation of mRNA expression abundance in 79 human tissues (11).
Mathematical model of the artificial network with eight TFs
We constructed a nonlinear ordinary differential equation (ODE) model as follows:
 |
 |
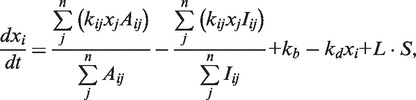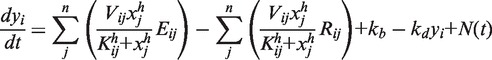where xi denotes the concentration of the active form of a signaling protein, yi denotes the expression level of a gene, kij denotes the rate constant of signaling in the range of 0.9–1.1, Aij denotes the activation matrix, Iij denotes the inhibition matrix, kb denotes the basal level of the production rate, kd denotes the degradation rate, S denotes the stimulus level, n denotes the number of nodes, Vij denotes the maximum velocity constant of gene expression in the range of 0.9–1.1, Kij denotes the dissociation constant of gene expression in the range of 0–1, h denotes the Hill coefficient, Eij denotes the expression matrix, Rij denotes the repression matrix and N(t) denotes the random noise function in the range of 0–0.1, and L = 1 for i = 1 and L = 0 for i ≠ 1. We set kb = kd = 1 and h = 4.
Cell culture and tetrachlorodibenzodioxin treatment
HepG2 cells were cultured in Dulbecco’s modified Eagle’s medium (WelGENE) supplemented with 10% fetal bovine serum (FBS) (WelGENE). The cells were grown in 6 cm dishes and treated with 0.1, 1 and 10 nM tetrachlorodibenzodioxin (TCDD) or with an equal volume of toluene and were then collected at the indicated times. Total RNA was extracted from the TCDD-treated cells using TRIzol reagent (Invitrogen). After DNase I (Takara) treatment, total RNA was isolated by phenol extraction.
Reverse transcription polymerase chain reaction
Reverse transcription to generate the first strand complementary DNAs was performed using oligo-dT primers and SuperScript RT-II (Invitrogen). Primers used for polymerase chain reaction amplification were as follows: CYP1A1, 5′-CCG ACC TCT ACA CCT TCA CCC T-3′ (forward) and 5′-TGT ACC CTG GGG TTC ATC ACC A-3′ (reverse); Caspase-4, 5′-AAC GTA TGG CAG GAC AAA TGC T-3′ (forward) and 5′-CCT TCT CCA CGT GGG TCT TGT A-3′ (reverse); BDH1 (3-hydroxybutyrate dehydrogenase), 5′-ATG GAG ACC TAC TGC AGC AGT G-3′ (forward) and 5′-ATC TCC GGA GAG ATA GAT TCA CCA-3′ (reverse); LMO7 (Homo sapiens LIM domain 7), 5′-CAA ATG TGC TTT CTG TAT CCT TCC-3′ (forward) and 5′-ATG CAA TTG AAC AGA AAG GCT CAC-3′ (reverse) and GAPDH, 5′-CCC ATC ACC ATC TTC CAG GAG TGA GTG GAA GAC-3′ (forward) and 5′-CGC CCC ACT TGA TTT TGG AGG GAT CTC GCC TAC CG-3′ (reverse).
Microarray experiments and data analysis
Gene expression data were obtained from 96 Affymetrix HG-U133 Plus 2.0 arrays (four doses × eight temporal variations × three replicates). For analysis, gene expression data were first normalized using R 2.6.1 with Robust Multi-array Averaging normalization (12). Second, differentially expressed gene (DEG) sets of the TCDD-treated cells were identified by comparing with the control cells (toluene-treated) for each of the concentrations (0.1, 1 and 10 nM) at each time point (0, 2, 8, 12, 16, 24, 36 and 52 h) using three different methods (linear models for microarray analysis (LIMMA) (13), EBarray (14) and the fold-change method). In the LIMMA, P-values were corrected using the Benjamini and Hochberg procedure (15) and identified DEGs using the P < 0.05 criteria. In the EBarray, DEGs were identified using a posterior probability threshold of 0.99 in both the gamma–gamma model and the lognormal–normal model. For the fold-change method, DEGs were identified using 3-fold change criteria. Twenty-four DEG sets were identified that met the criteria for significance using all three methods for each concentration and at each time point. Finally, the 24 DEG sets were combined into a single set consisting of the 183 DEGs.
Protein types
The ligands, extracellular proteins, receptors and membrane proteins were selected as the nodes with corresponding genes classified into one of four GO terms: ‘receptor binding (GO:0005102)’, ‘extracellular region (GO:0005576)’, ‘receptor activity (GO:0004872)’ and ‘membrane (GO:0016020)’ (16), respectively.
GO analysis
GO analysis was performed as follows: first, 67 GO terms were selected with the criterion that, among the GO terms classified as involved in a biological process in one of the three branches of the ontology, the number of corresponding genes must be>1000. Second, the enrichment of BTFs and MTFs (the exclusive TGs of the BTFs and those of the MTFs) in the 67 GO terms was examined by performing Fisher’s exact test using the union of the BTFs and MTFs (the exclusive TGs of the BTFs and those of the MTFs) as a background set.
Adaptability, robustness and diversity
Adaptability was defined as follows:
 |
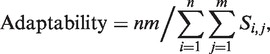where n denotes the number of TFs, m denotes the number of TGs, Si,j denotes the saturation time of TG j obtained from the simulation in which only TF i was stimulated for 100 time steps, and the initial state was given by the last state (100th time step) of the simulation result obtained for the stimulation of TF i−1 alone. For i = 1, the initial values were obtained from the simulation involving the stimulation of TF n alone. The saturation time of a TG was defined as the first time step at which the value of the TG was within a 0.0001 threshold of the last value of the TG.
Robustness was defined as follows:
 |
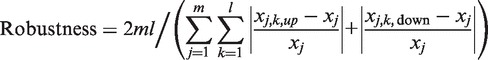where m denotes the number of TGs, l denotes the number of parameters in the ODE model, xj denotes the steady-state value of the TG j, and xj,k,up and xj,k,down denote the steady-state values of the TG j upon a 10% up/down perturbation of the parameter k, respectively.
Diversity was defined as follows:
 |
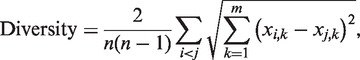where n denotes the number of TFs, m denotes the number of TGs, xi,k denotes the steady-state values of the TG k obtained from the simulation in which only TF i was stimulated for 100 time steps.
Evolution of artificial networks
For the evolution of artificial networks, a biological network evolution scheme was used (17,18) based on a genetic algorithm (GA) (19). For the evolution of n-node artificial networks composed of n/2 TFs and n/2 TGs, where n is an even number, 100 vectors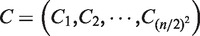 
were generated with entries of any number between 0 and 1. The vectors represent the initial chromosomes. Each vector was transformed into a network structure as follows:
- From each vector, a regulation matrix
was constructed, where
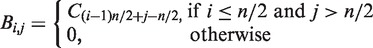
From each regulation matrix, an expression matrix
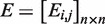and a repression matrix 
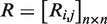were constructed, where 
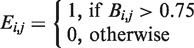and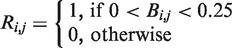 
.
If a network transformed from a chromosome contained isolated nodes, it was replaced with a newly generated chromosome with a transformed network that contained no isolated nodes. This constraint was checked at each generation of GA. Next, the fitness of each initial chromosome based on the ODE model simulation was evaluated using each transformed expression matrix and repression matrix. The fitness for adaptability, robustness or diversity of each chromosome was defined by the average of 100 adaptability/robustness/diversity values obtained by running the ODE simulation model 100 times with random parameter values. Starting with the initial chromosome, GA was performed using a mutation rate of 0.05.
RESULTS
Enrichment of co-regulatory interactions between human TFs
First, to examine how human TFs participate in co-regulation mechanisms, the human GRN was constructed on the basis of direct genetic regulation information with experimental evidence in the literature (see Supplementary Table S1 for details) by referring to KEGG (20) and TRANSFAC (21) and then transformed into a human TF co-regulation network (1) (Figure 1A and B). Within the human TF co-regulation network, each node denotes a TF, each link denotes a co-regulatory interaction between two different TFs, and the thickness of each link is proportional to the ‘weight’ of the interaction, defined by the number of co-regulated TGs between the two TFs. Next, the enrichment of the sum of the weights for each TF in the human TF co-regulation network was examined by performing z-tests for empirical distributions of the sum of these weights (see ‘Materials and Methods’ section and Supplementary Table S2). The empirical distributions were constructed by randomizing 100 networks while preserving the out-degree of each TF. Enrichment analysis showed that the ratio of co-regulation-enriched TFs (CETFs) was more than twice that of the ratio of co-regulation-depleted TFs (CDTFs). A CETF (CDTF) is defined as a TF with a z-score such that the sum of weights is more (less) than 0. As shown in Figure 1C, the number of co-regulatory interactions was significantly enriched in some TFs, including TCF7L2, CTNNB1, NFKB1, STAT1, SP1, RXRA and BRCA1, but was significantly depleted in other TFs, including HNF1A and TP53 (P < 0.01). The enrichment of co-regulatory interaction in the GRN of Escherichia coli obtained from RegulonDB (22), one of the simplest organisms, was examined for comparison, and the results showed that the ratio of CETFs (36.7%) was almost half of the ratio of CDTFs (63.3%) in the E. coli GRN (Supplementary Figure S1 and Supplementary Table S3). Consistent with the previous result (3), this implies that the co-regulation mechanism is evolutionarily conserved in multicellular eukaryotes (human), whereas it is evolutionarily depleted in prokaryotes (E. coli).
Figure 1.
Enrichment of co-regulations of human TFs. (A) Schematic diagram showing network transformation from a GRN to a TF co-regulation network. Green nodes denote TFs and cyan nodes denote TGs. (B) A human TF co-regulation network (418 nodes and 4124 links). (C) Enrichment of co-regulations of the 418 human TFs. Red nodes in Panel B or red bars in Panel C denote TFs with significantly enriched co-regulation and blue nodes in Panel B or blue bars in Panel C denote TFs with significantly depleted co-regulation (P < 0.01).
If co-regulation is enhanced during the evolution of multicellular eukaryotes, then there should be contrasting evolutionary features between the CETFs and CDTFs in the human GRN. To clarify this, 190 significant CETFs (red nodes in Figure 1B and red bars in Figure 1C) and 22 significant CDTFs (blue nodes in Figure 1B and blue bars in Figure 1C) were identified with the criterion of P < 0.01. Second, 430 exclusive TGs in the significant CETF group and 170 exclusive TGs in the significant CDTF group were identified. The evolutionary rates between the two exclusive TG sets (see ‘Materials and Methods’ section) were then compared. From the comparison, we found that the TGs of the significant CETFs had significantly higher evolutionary rates than those of the significant CDTFs (P = 4.42E−5; Supplementary Figure S2A), implying that the genes controlled by the CDTFs are evolutionarily conserved. Moreover, we explored the tissue variability of the two gene groups under the hypothesis that the co-regulation mechanism is related to multicellularity and found that the TGs of the significant CETFs showed a considerably greater degree of tissue variability than those of the significant CDTFs (P = 2.85E−4; Supplementary Figure S2B). This result implies that the genes transcribed by CETFs are expressed with a larger variation in different tissues and related to multicellular processes. In summary, this result suggests that the co-regulation mechanism is enriched for the regulation of tissue-specific gene expression which is an essential feature of multicellular organisms (4,11). In other words, our result suggests that multicellular organisms might have evolved their GRNs toward having more co-regulations to increase the variability of gene expressions, which is required for multicellular functioning.
We can classify TF co-regulations into two types: co-regulation by TFs separately binding to DNA (non-complex-type co-regulations) and co-regulation by complexes of TFs (complex-type co-regulations). How different are these two types of co-regulations in view from molecular evolution? To answer this question, we first identified 293 non-complex-type TFs (i.e. TFs that do not form any complex) and 125 complex-type TFs (i.e. TFs that form a complex) (Supplementary Table S2) based on the information on TF complexes from TRANSFAC (21) and BIND (23) and then compared the numbers of CETFs and CDTFs in the two types of TFs. As a result, we found that the numbers of CETFs in both types of TFs were much larger than those of CDTFs (Supplementary Figure S3), which means that both types of co-regulation are evolutionarily conserved in the human GRN. Second, we compared the evolutionary rate and tissue variability of the TGs of non-complex-type CETFs and CDTFs and then also compared those of complex-type CETFs and CDTFs. As a result, we revealed the following: (i) the TGs of non-complex-type CETFs have significantly higher evolutionary rates (P = 2.48E−3; Supplementary Figure S4A) and tissue variability (P = 1.19E−3; Supplementary Figure S4B) than those of non-complex-type CDTFs; (ii) the evolutionary rates of the TGs of complex-type CETFs and CDTFs do not significantly differ (P = 3.43E−1; Supplementary Figure S5A) and (iii) the TGs of complex-type CETFs have significantly higher tissue variability than those of complex-type CDTFs (P = 2.36E−4; Supplementary Figure S5B). These results imply that the non-complex-type co-regulation mechanism might have been evolved toward enhancing both evolutionary rate and tissue variability of TGs, whereas the complex-type co-regulation mechanism might have been evolved toward enhancing only tissue variability of TGs.
A mathematical model of an artificial regulatory network combining interactions related to signal transduction and genetic regulation
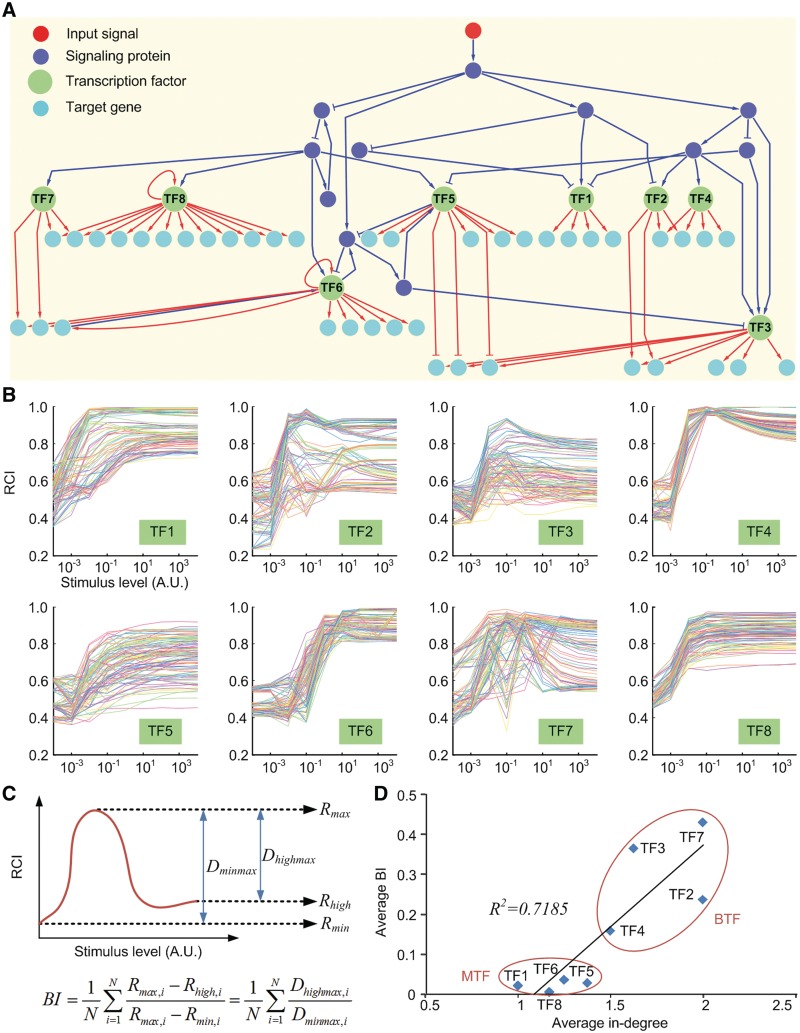
The previous section showed that co-regulatory interactions were enriched in the human GRN and that CETFs were evolutionarily conserved. However, the role of the co-regulation mechanism, and the reason for the conservation of this mechanism in the human GRN, remains unclear. To investigate this, an ODE model of an artificial regulatory network composed of 61 nodes (12 signaling proteins, 8 TFs and 41 TGs) and 86 links (32 signal transductions and 54 genetic regulations) was constructed (see Figure 2A and ‘Materials and Methods’ section). In this ODE model, the random noise effect (24,25) for the non-complex-type co-regulation was considered. We first simulated the ODE system for 100 time steps with zero initial values (no stimulation provided). Next, the ODE system was stimulated for 10 time steps with initial values set to the last values of the previous simulation, where the stimulus was given by a sustained type. This ODE model was used to calculate the RCI of each TF for nine stimulus levels (x-axis in Figure 2B) and 100 randomly generated parameter sets (each colored line in Figure 2B). The RCI of a TF is defined as follows:
 |
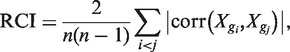where n denotes the number of TGs of the TF, Xgi denotes the temporal expression profile of the TG gi and 
denotes the Pearson correlation coefficient of the two expression profiles Xgi and Xgj. The RCI was measured for each TF because this index represents the activity or influence of the TF. The simulation revealed that the RCI patterns for TF1, TF5, TF6 and TF8 were monotonic and increasing for all parameter sets, whereas those for the other TFs (TF2, TF3, TF4 and TF7) were biphasic for most parameter sets (Figure 2B). Next, the biphasic index (BI) was defined to quantify these biphasic patterns as described in Figure 2C. Figure 2D shows that the average in-degree of TGs is highly related to the average BI of TFs. This result suggests that the co-regulation mechanism of TFs induces the dose-dependent biphasic regulation coherency among them. We obtained the same result from a mathematical model of the complex-type co-regulations (see Supplementary Methods and Figure S6).
Figure 2.
Mathematical model of an artificial regulatory network and the simulation results. (A) A diagram of an artificial regulatory network. Red nodes denote input signals, blue nodes denote signaling proteins, green nodes denote TFs and cyan nodes denote TGs. Blue (red) arrows and blue (red) blunt arrows denote the activation and inhibition of signal transduction (genetic regulation), respectively. (B) RCI profiles of the eight TFs along with the stimulus level. Each line denotes the RCI profile for a random parameter set. (C) Schematic illustration of the measurement of BI. N denotes the number of random parameter sets. (D) Scatter plot of average BI versus average in-degree of the TGs for the eight TFs.
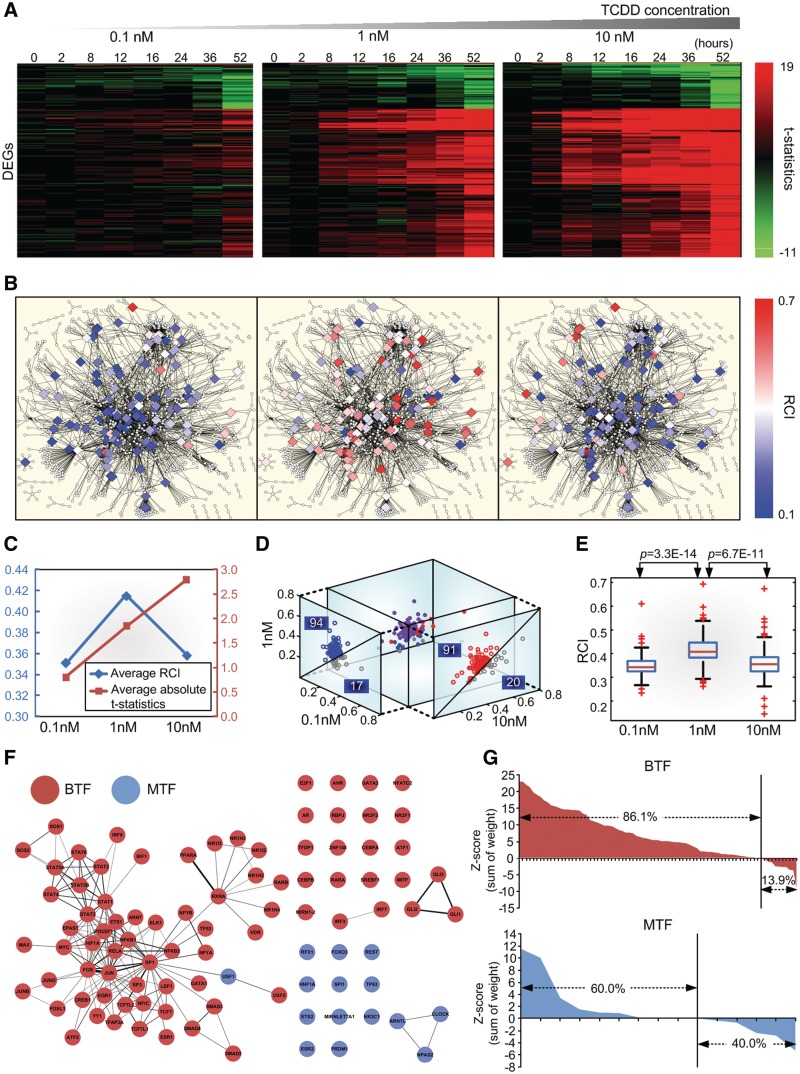
Biphasic dose–response pattern of TFs in the human GRN
In the previous section, we showed that the biphasic dose–response pattern was caused by the co-regulation mechanism. To verify this, we first investigated changes in gene expression in HepG2 cells at three different doses (0.1, 1 and 10 nM) of the toxicant, TCDD. Temporal variations (0, 2, 8, 12, 16, 24, 36 and 52 h) were also examined using microarray experiments (see ‘Materials and Methods’ section). The three different doses and the temporal variations were selected according to the previous study (26). Figure 3A shows changes in the expression of 183 DEGs, along with doses and temporal variations. Second, the RCIs of 111 TFs that have no less than five TGs in the human GRN were calculated, along with the level of stimulation provided by the three different doses, using gene expression (log2 ratios) profiles and network information. The large, diamond-shaped nodes in Figure 3B denote the 111 TFs; the RCI for each TF is colored. The results of this analysis showed that, in most cases, the RCI displayed a biphasic pattern according to the stimulus level. In contrast, the overall expression changes of 183 DEGs increased with the stimulus level (Figure 3C). In other words, the RCIs of 91 TFs increased from the low dose (0.1 nM) to the middle dose (1 nM) and those of 94 TFs decreased from the middle dose to the high dose (10 nM) (Figure 3D). The dose-dependent biphasic RCI from the low dose to the middle dose was statistically significant (P = 3.3E−14) and from the middle dose to the high dose (P = 6.7E−11) (Figure 3E). Third, the TFs were classified into two groups, BTFs, showing a biphasic behavior and MTFs, showing a monotonically increasing behavior. The human GRN was then transformed into a TF co-regulation network comprising only BTFs, MTFs and links with co-regulation weights >4 (Figure 3F). Figure 3F shows that BTFs have more links than MTFs and that each group is well-clustered within the TF co-regulation network. Furthermore, the percentage of BTFs that were also CETFs (86.1%) was higher than the percentage of total TFs that were also CETFs (67.2%; Figure 1C), whereas that of the MTFs (60.0%) was lower than that of the total TFs (Figure 3G). These results indicate that the dose-dependent biphasic pattern in the human GRN is positively related with co-regulation and is in agreement with the simulation results reported in the previous section.
Figure 3.
Biphasic dose–response of TFs in the human GRN. (A) Heat map of t-statistics for 183 DEGs along with three different doses of a toxicant (TCDD) and eight temporal variations (see ‘microarray experiment and data analysis’ in ‘Materials and Methods’ section). Each row represents a DEG. (B) The human GRN (1100 nodes and 2532 links). Diamond-shaped nodes denote 111 TFs with no less than five TGs and circle nodes denote the rest of the TFs. The color of each diamond-shaped node represents the RCI of each TF. The subfigures represent data for each dose (0.1 nM for left, 1 nM for center and 10 nM for right). (C) Average RCI of the 111 TFs and the average of the mean absolute t-statistics over the 183 DEGs, eight temporal variations and three doses. Note that the average RCI shows a biphasic dose–response pattern, while the average absolute t-statistics show a monophasically increasing dose–response pattern. (D) 3D scatter plot of the RCI of the 111 TFs with projections onto a 0.1–1 nM 2D plane and a 10–1 nM 2D plane. (E) Box plot of the RCI and the three doses. (F) TF co-regulation network composed of 79 BTFs and 15 MTFs and links with co-regulation weights >4. The thickness of each link denotes the co-regulation weight between the two different TFs. (G) Enrichment of the co-regulation weight of BTFs and MTFs.
Biphasic versus monophasic TFs
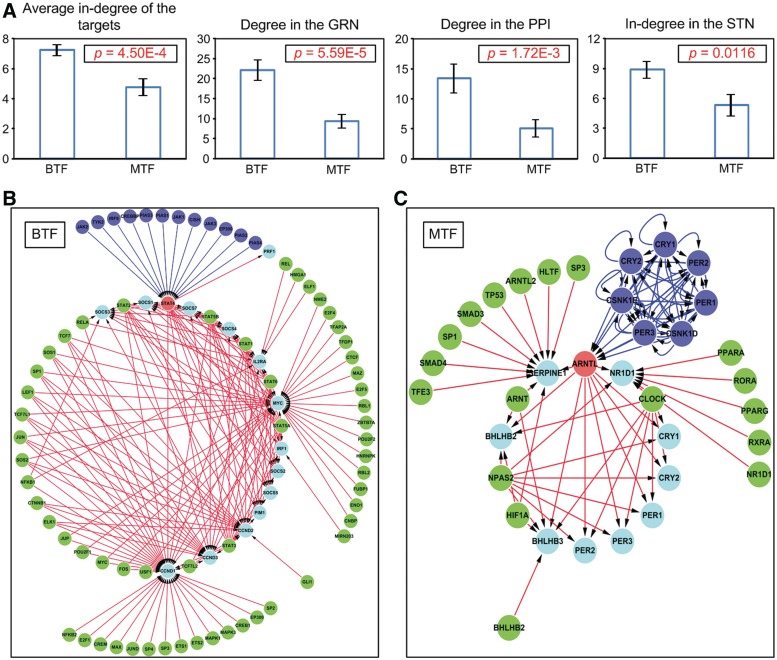
Because each type of TF was well-clustered within the human TF co-regulation network, we speculated that these two types of TFs might be topologically different. To clarify this, the average in-degrees of the TGs of the 79 BTFs and the 15 MTFs of the human GRN were compared using a statistical test (see ‘Materials and Methods’ section). As expected, the average in-degrees of the TGs of the BTFs were significantly higher than those of the MTFs (P = 4.50E−4; the first bar plot in Figure 4A). Not only that, but the degrees for the GRN, the degrees for the human protein–protein interaction (PPI) network and the in-degrees for the human signal transduction network (STN) of the BTFs were significantly higher than those of the MTFs, indicating that a BTF is more likely to be a hub gene or protein than an MTF in many biomolecular interaction networks (P = 5.59E−5 for the GRN, P = 1.72E−3 for the PPI and P = 0.0116 for the STN; see the last three bar plots in Figure 4A). These contrasting topological features imply that BTFs respond to a greater variety of signals and control a greater variety of TGs than MTFs (Figure 4B and C).
Figure 4.
Two types of TFs. (A) Topological properties of the two types of TFs. Error bars denote standard errors. (B) An example of a BTF-centered network. (C) An example of an MTF-centered network. In the example networks of (B) and (C), red nodes denote BTFs or MTFs; cyan nodes denote the TGs of the red nodes; green nodes denote other TFs targeting the cyan nodes; blue nodes denote upstream signaling proteins of the red nodes; blue lines denote signal transduction and red lines denote genetic regulation.
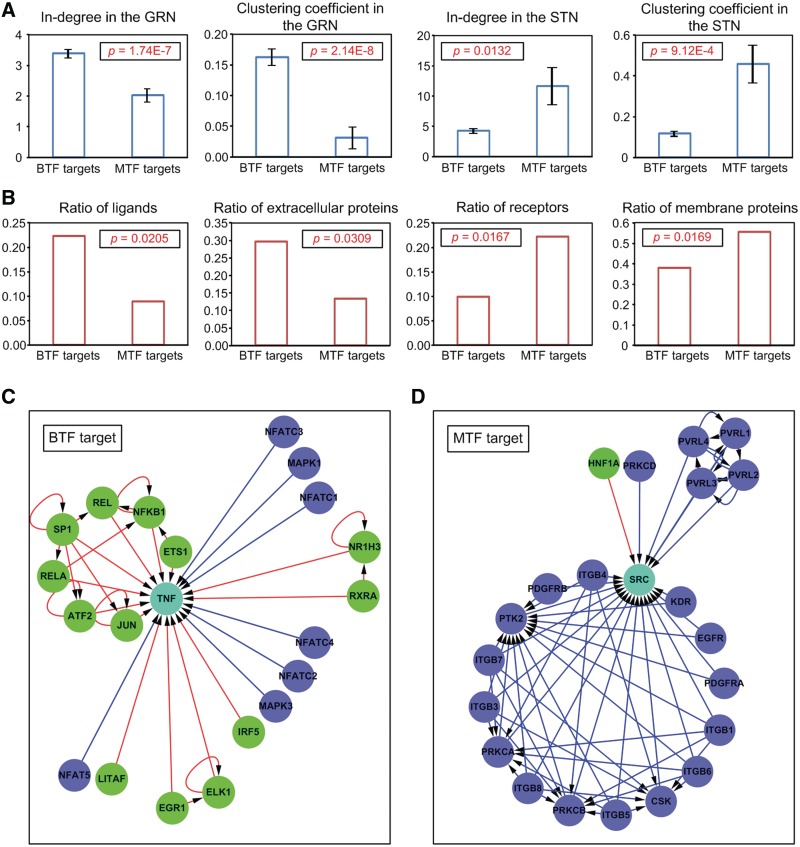
If BTFs and MTFs are structurally different, the TGs of these two types of TF may also be structurally different. To explore this possibility, four topological characteristics (in-degree and clustering coefficient for the human GRN and in-degree and clustering coefficient for the human STN) were compared between the 533 TGs exclusive with the BTFs and the 45 TGs exclusive with the MTFs. The results showed that the in-degrees and clustering coefficients of the TGs exclusive to the BTFs were significantly greater than those exclusive to the MTFs in the human GRN, whereas the in-degrees and clustering coefficients of the TGs exclusive to the BTFs were significantly smaller than those of the TGs exclusive to the MTFs in the human STN (Figure 5A). This indicates that, in the GRN, the TGs of the BTFs are controlled by more TFs and show more complex neighbor structures than those of the MTFs, whereas in the STN, the TGs of the BTFs are less controlled by signaling proteins and show a sparser neighbor structure than the TGs of the MTFs. To clarify the meaning of this result, we compared protein types between TGs of the BTFs and those of the MTFs (see ‘Materials and Methods’ section). The results showed that the TGs of the BTFs included more ligands or extracellular proteins than those of the MTFs, whereas the TGs of the MTFs included more receptors or membrane proteins than those of the BTFs (Figure 5B). These results imply that most of the TGs of the BTFs are ligands controlled mainly at the level of expression, i.e. they are controlled by genetic regulation rather than signal transduction. On the other hand, most of the TGs of the MTFs were receptors controlled mainly at the level of protein activity, i.e. they are controlled by signal transduction rather than genetic regulation (Figure 5C and D). Taken together, the results suggest that when a cell receives a middle-dose signal (normal environment), BTFs are mainly activated and regulate their TGs (mostly ligands), and then the transcriptionally controlled ligands change the cellular state by controlling their target receptors (TGs of MTFs) at the protein activity level. On the other hand, when a cell receives a high-dose signal (extreme environment), MTFs are mainly activated and regulate their TGs (mostly receptors), and then the transcriptionally controlled receptors change the cellular state by altering the ligand sensitivity. These results imply that the human GRN responds to extracellular signals in two different ways depending on signal strength through two different types of TFs (BTF and MTF) and the enrichment of TF co-regulation might be responsible for the origination of such a response strategy.
Figure 5.
TGs of the two types of TFs. (A) Topological properties of the TGs of the two types of TFs. Error bars denote standard errors. (B) Protein types for the TGs of the two types of TFs. (C) An example of a BTF-target-centered network. (D) An example of an MTF-target-centered network. In the networks in (C) and (D), the cyan node denotes an example of a TG of a BTF or an MTF; the blue node denotes a signaling protein that regulates the cyan node; the green node denotes a TF that targets the cyan node; the blue line denotes signal transduction and the red line denotes genetic regulation.
Furthermore, gene ontology (GO) analysis revealed that significantly enriched functions related to BTFs include development, differentiation and signal transduction (Table 1), and that those related to the TGs of BTFs include signal transduction and the regulation of biological processes (Table 2). In contrast, those related to the TGs of MTFs involve metabolic processes and transcription (Table 3). This implies that regulatory systems that include BTFs are related to biological processes exclusive to multicellular organisms, whereas regulatory systems that include MTFs are related to biological processes that take place in both single-celled and multicellular organisms.
Table 1.
GO terms significantly related to BTFs
| GO terms |
P-value |
|
|---|---|---|
| BTF | MTF | |
| Cell differentiation | 0.0029 | 1.0000 |
| Cellular developmental process | 0.0029 | 1.0000 |
| Organ development | 0.0042 | 0.9997 |
| Cell surface receptor-linked signal transduction | 0.0306 | 1.0000 |
| Anatomical structure development | 0.0322 | 0.9933 |
| System development | 0.0391 | 0.9914 |
| Multicellular organismal process | 0.0444 | 0.9891 |
Table 2.
GO terms significantly related to TGs of BTFs
| GO terms |
P-value |
|
|---|---|---|
| TGs of BTFs | TGs of MTFs | |
| Cell surface receptor-linked signal transduction | 0.0166 | 0.9958 |
| Negative regulation of cellular process | 0.0354 | 0.9867 |
| Positive regulation of cellular process | 0.0375 | 0.9844 |
| Positive regulation of biological process | 0.0477 | 0.9788 |
| Negative regulation of biological process | 0.0498 | 0.9793 |
Table 3.
GO terms significantly related to TGs of MTFs
| GO terms |
P-value |
|
|---|---|---|
| TGs of BTFs | TGs of MTFs | |
| Regulation of transcription, DNA-dependent | 0.9987 | 0.0040 |
| Regulation of RNA metabolic process | 0.9987 | 0.0040 |
| Transcription | 0.9988 | 0.0049 |
| Regulation of transcription | 0.9960 | 0.0107 |
| Regulation of nitrogen compound metabolic process | 0.9925 | 0.0183 |
| Gene expression | 0.9938 | 0.0193 |
| Regulation of macromolecule biosynthetic process | 0.9894 | 0.0247 |
| Regulation of nucleobase, nucleoside, nucleotide and nucleic acid metabolic processes | 0.9878 | 0.0284 |
| Cellular biosynthetic process | 0.9875 | 0.0285 |
| Cellular macromolecule biosynthetic process | 0.9873 | 0.0338 |
| Regulation of gene expression | 0.9817 | 0.0404 |
| Cellular biopolymer biosynthetic process | 0.9833 | 0.0442 |
| Biopolymer biosynthetic process | 0.9833 | 0.0442 |
| Regulation of biosynthetic process | 0.9787 | 0.0455 |
| Macromolecule biosynthetic process | 0.9807 | 0.0480 |
| Biosynthetic process | 0.9771 | 0.0485 |
Evolutionary design principles underlying the co-regulation mechanism
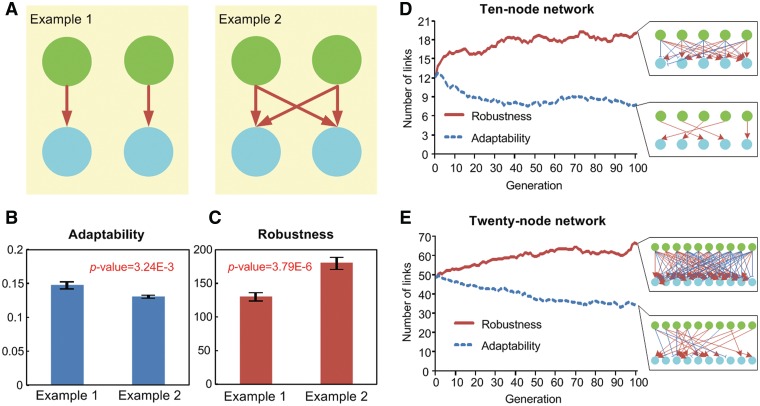
The two previous sections show that the co-regulation mechanism of a TF can induce dose-dependent biphasic behavior in the TF, and that this dynamic behavior is related to multicellular organismal processes. How, then, is this biphasic behavior helpful to multicellular organismal processes? What is the evolutionary design principle of this co-regulation mechanism? To answer these questions, we investigated the robustness and adaptability of the transcriptional regulation systems using mathematical models and simulations, since the biphasic behavior of a transcriptional regulation system can increase the robustness of a system (27,28), and trade-offs between adaptability and robustness are related to the evolutionary dynamics (29–31). Two contrasting ODE models were constructed, each comprising two TFs and two TGs: a little co-regulated network (LCN; the left subfigure in Figure 6A) and a highly co-regulated network (HCN; the right subfigure in Figure 6A). We considered the non-complex-type co-regulation for the second model (see Supplementary Methods). These ODE models incorporated 100 randomly selected parameter sets, which were used to measure adaptability and robustness. The results show that the adaptability of the LCN is greater than that of the HCN (Figure 6B), whereas the robustness of the LCN is lower than that of the HCN (Figure 6C). To verify that this contrasting feature between LCNs and HCNs can be selected by evolution, we evolved artificial networks with non-complex-type co-regulation based on the 10-node ODE model with the preference for adaptability or robustness. These networks comprised five TFs and five TGs. When the artificial networks were selected to enhance adaptability, the number of links decreased. In contrast, the number of links increased when the networks were selected to enhance robustness (Figure 6D). The same result was obtained using a 20-node ODE model comprising 10 TFs and 10 TGs (Figure 6E). This result implies that the co-regulation mechanism is beneficial for robustness, but disadvantageous for adaptability. Hence, GRNs might evolve to increase the degree of co-regulation in order to enhance robustness in multicellular organisms, but in single-celled organisms, they might evolve to decrease the degree of co-regulation in order to enhance adaptability. In other words, single-celled organisms might have evolved their GRNs with high adaptability to cope with rapidly changing external environment (18), whereas multicellular organisms might have evolved their GRNs with high robustness for differentiation into various cell types in an exact time and space irrespective of intrinsic variations (18,32–34). So, the co-regulation mechanism might have been evolutionarily depleted in the GRNs of single-celled organisms but conserved in the GRNs of multicellular organisms. This is concordant with our finding that the co-regulation mechanism is enriched in the human GRN (Figure 1B and C), but depleted in the E. coli GRN (Supplementary Figure S1).
Figure 6.
LCN and HCN models. (A) Example networks for LCN (Example 1) and HCN (Example 2). (B) Adaptability and (C) robustness of Examples 1 and 2. The average number of links during the artificial evolution of 10-node (D) and 20-node (E) networks with the preference for adaptability or robustness. We used 100 random parameter sets and 100 chromosomes for the artificial evolution. Each network in each subfigure represents the network with the best fitness for each evolution. Green nodes denote TFs, cyan nodes denote TGs, red arrows denote activation and blue blunt end arrows denote inhibition in each network. In B and C, error bars denote standard errors.
To investigate the evolutionary design principle of the complex-type co-regulation, we have artificially evolved networks of 10-nodes and 20-nodes with the preference of adaptability or robustness of the responses, respectively. When the networks were evolved toward enhancing adaptability, the number of links varied little in the 10-node network (Supplementary Figure S7A), but increased in the 20-node network (Supplementary Figure S7B). The number of links also increased when the networks were evolved toward enhancing robustness in both 10-node (Supplementary Figure S7C) and 20-node networks (Supplementary Figure S7D). These results imply that the complex-type co-regulation is beneficial for both robustness and adaptability in large networks. Then, why are there only 3.32% of complex-type co-regulating TFs in the human GRN (Supplementary Tables S4 and S5)? To answer this question, we evolved networks with the preference of response diversity. When networks were evolved toward enhancing diversity, the number of links increased for the non-complex-type co-regulation, but decreased for the complex-type co-regulation in both 10-node (Supplementary Figure S7E) and 20-node networks (Supplementary Figure S7F). This result implies that the non-complex-type co-regulation is beneficial for diversity whereas the complex-type co-regulation is not. Together, we infer that the complex-type co-regulation is not a major co-regulation type since it is not beneficial for diversity although it is advantageous for adaptability and robustness.
DISCUSSION
In this study, we used mathematical modeling to show that the co-regulation mechanism of TFs induces dose-dependent biphasic behavior in the TFs. Furthermore, the relationship between the co-regulation mechanism and biphasic behavior was confirmed by microarray experiments. Previous studies of this biphasic behavior only focused on network motifs such as incoherent feed-forward loops (35,36). Here, we undertook a genome-scale analysis of the co-regulation mechanism and the biphasic behavior of TFs in the human GRN using whole-genome expression data. Furthermore, we also showed that the TFs in the human GRN can be classified into two types (BTF and MTF) according to the presence or absence of biphasic behavior, that these two types of TFs control different groups of TGs and that BTFs are related to multicellular organismal processes. These results imply that the biphasic behavior of TFs induced by the co-regulation mechanism might play a pivotal role in phylogeny building of the two sets of genes.
The classification of TFs into two types (BTF and MTF) might also be useful for developmental studies in view of the attractor landscape. Several studies suggested that the co-regulation mechanism is related to democratic dynamics, hence causing attractors in the transcriptional state space (2,3). Each attractor represents a cell type in a developmental lineage. In this regard, the BTFs and the TGs of the BTFs could be candidate key factors determining attractor landscapes and the corresponding cellular development patterns.
Several studies reported that the co-regulation mechanism tends to be enhanced in the GRNs of more complex organisms (1,3) and that this is also related to multicellular organismal processes such as developmental processes (7) and immune processes (37,38). In this regard, we suggested that the co-regulation mechanism and dose-dependent biphasic behavior in a GRN may enhance robustness, but may also undermine adaptability in terms of evolutionary dynamics. Although previous research results (1,3) on the co-regulation mechanism were also based on genome-scale analysis, all these studies considered the GRN as a static topology. In contrast, we studied the co-regulation mechanism while considering evolutionary changes in the GRN. Hence, this study regarding the relationship between dynamic properties and the co-regulation mechanism provides new insights that may help to unravel the evolutionary design principles underlying the co-regulation mechanism.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online: Supplementary Tables 1–5, Supplementary Figures 1–7 and Supplementary Methods.
FUNDING
Funding for open access charge: National Research Foundation of Korea (NRF) grants funded by the Korean Government, the Ministry of Education, Science and Technology (MEST) [2009-0086964 and 2010-0017662]; WCU (World Class University) program through the NRF funded by the MEST [R32-2008-000-10218-0].
Conflict of interest statement. None declared.
Supplementary Material
ACKNOWLEDGEMENTS
We thank Sang-Mok Choo and Arthur D. Lander for their valuable comments on this article.
REFERENCES
- 1.Balaji S, Babu MM, Iyer LM, Luscombe NM, Aravind L. Comprehensive analysis of combinatorial regulation using the transcriptional regulatory network of yeast. J. Mol. Biol. 2006;360:213–227. doi: 10.1016/j.jmb.2006.04.029. [DOI] [PubMed] [Google Scholar]
- 2.Bar-Yam Y, Harmon D, de Bivort B. Attractors and democratic dynamics. Science. 2009;323:1016–1017. doi: 10.1126/science.1163225. [DOI] [PubMed] [Google Scholar]
- 3.Bhardwaj N, Yan KK, Gerstein MB. Analysis of diverse regulatory networks in a hierarchical context shows consistent tendencies for collaboration in the middle levels. Proc. Natl Acad. Sci. USA. 2010;107:6841–6846. doi: 10.1073/pnas.0910867107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ravasi T, Suzuki H, Cannistraci CV, Katayama S, Bajic VB, Tan K, Akalin A, Schmeier S, Kanamori-Katayama M, Bertin N, et al. An atlas of combinatorial transcriptional regulation in mouse and man. Cell. 2010;140:744–752. doi: 10.1016/j.cell.2010.01.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ronen M, Botstein D. Transcriptional response of steady-state yeast cultures to transient perturbations in carbon source. Proc. Natl Acad. Sci. USA. 2006;103:389–394. doi: 10.1073/pnas.0509978103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Davidson EH, Rast JP, Oliveri P, Ransick A, Calestani C, Yuh CH, Minokawa T, Amore G, Hinman V, Arenas-Mena C, et al. A genomic regulatory network for development. Science. 2002;295:1669–1678. doi: 10.1126/science.1069883. [DOI] [PubMed] [Google Scholar]
- 7.Inoue T, Wang M, Ririe TO, Fernandes JS, Sternberg PW. Transcriptional network underlying Caenorhabditis elegans vulval development. Proc. Natl Acad. Sci. USA. 2005;102:4972–4977. doi: 10.1073/pnas.0408122102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bhardwaj N, Kim PM, Gerstein MB. Rewiring of transcriptional regulatory networks: hierarchy, rather than connectivity, better reflects the importance of regulators. Sci. Signal. 2010;3:ra79. doi: 10.1126/scisignal.2001014. [DOI] [PubMed] [Google Scholar]
- 9.Cosentino Lagomarsino M, Jona P, Bassetti B, Isambert H. Hierarchy and feedback in the evolution of the Escherichia coli transcription network. Proc. Natl Acad. Sci. USA. 2007;104:5516–5520. doi: 10.1073/pnas.0609023104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Nickel GC, Tefft D, Adams MD. Human PAML browser: a database of positive selection on human genes using phylogenetic methods. Nucleic Acids Res. 2008;36:D800–D808. doi: 10.1093/nar/gkm764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Su AI, Wiltshire T, Batalov S, Lapp H, Ching KA, Block D, Zhang J, Soden R, Hayakawa M, Kreiman G, et al. A gene atlas of the mouse and human protein-encoding transcriptomes. Proc. Natl Acad. Sci. USA. 2004;101:6062–6067. doi: 10.1073/pnas.0400782101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Irizarry RA, Bolstad BM, Collin F, Cope LM, Hobbs B, Speed TP. Summaries of Affymetrix GeneChip probe level data. Nucleic Acids Res. 2003;31:e15. doi: 10.1093/nar/gng015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Smyth GK, Michaud J, Scott HS. Use of within-array replicate spots for assessing differential expression in microarray experiments. Bioinformatics. 2005;21:2067–2075. doi: 10.1093/bioinformatics/bti270. [DOI] [PubMed] [Google Scholar]
- 14.Kendziorski CM, Newton MA, Lan H, Gould MN. On parametric empirical Bayes methods for comparing multiple groups using replicated gene expression profiles. Stat. Med. 2003;22:3899–3914. doi: 10.1002/sim.1548. [DOI] [PubMed] [Google Scholar]
- 15.Benjamini Y, Hochberg Y. Controlling the false discovery rate—a practical and powerful approach to multiple testing. J. Roy. Stat. Soc. B Methodol. 1995;57:289–300. [Google Scholar]
- 16.Consortium TGO. The Gene Ontology project in 2008. Nucleic Acids Res. 2008;36:D440–D444. doi: 10.1093/nar/gkm883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kim J, Kim TG, Jung SH, Kim JR, Park T, Heslop-Harrison P, Cho KH. Evolutionary design principles of modules that control cellular differentiation: consequences for hysteresis and multistationarity. Bioinformatics. 2008;24:1516–1522. doi: 10.1093/bioinformatics/btn229. [DOI] [PubMed] [Google Scholar]
- 18.Kim TH, Kim J, Heslop-Harrison P, Cho KH. Evolutionary design principles and functional characteristics based on kingdom-specific network motifs. Bioinformatics. 2011;27:245–251. doi: 10.1093/bioinformatics/btq633. [DOI] [PubMed] [Google Scholar]
- 19.Beasley D, Bull DR, Martin RR. An overview of genetic algorithms. 1. Fundamentals. U. Comput. 1993;15:58–69. [Google Scholar]
- 20.Kanehisa M, Goto S, Kawashima S, Nakaya A. The KEGG databases at GenomeNet. Nucleic Acids Res. 2002;30:42–46. doi: 10.1093/nar/30.1.42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Matys V, Fricke E, Geffers R, Gossling E, Haubrock M, Hehl R, Hornischer K, Karas D, Kel AE, Kel-Margoulis OV, et al. TRANSFAC: transcriptional regulation, from patterns to profiles. Nucleic Acids Res. 2003;31:374–378. doi: 10.1093/nar/gkg108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gama-Castro S, Salgado H, Peralta-Gil M, Santos-Zavaleta A, Muniz-Rascado L, Solano-Lira H, Jimenez-Jacinto V, Weiss V, Garcia-Sotelo JS, Lopez-Fuentes A, et al. RegulonDB version 7.0: transcriptional regulation of Escherichia coli K-12 integrated within genetic sensory response units (Gensor Units) Nucleic Acids Res. 2011;39:D98–D105. doi: 10.1093/nar/gkq1110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Bader GD, Betel D, Hogue CW. BIND: the biomolecular interaction network database. Nucleic Acids Res. 2003;31:248–250. doi: 10.1093/nar/gkg056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Elowitz MB, Levine AJ, Siggia ED, Swain PS. Stochastic gene expression in a single cell. Science. 2002;297:1183–1186. doi: 10.1126/science.1070919. [DOI] [PubMed] [Google Scholar]
- 25.Swain PS, Elowitz MB, Siggia ED. Intrinsic and extrinsic contributions to stochasticity in gene expression. Proc. Natl Acad. Sci. USA. 2002;99:12795–12800. doi: 10.1073/pnas.162041399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Gim J, Kim HS, Kim J, Choi M, Kim JR, Chung YJ, Cho KH. A system-level investigation into the cellular toxic response mechanism mediated by AhR signal transduction pathway. Bioinformatics. 2010;26:2169–2175. doi: 10.1093/bioinformatics/btq400. [DOI] [PubMed] [Google Scholar]
- 27.Mayya V, Loew LM. STAT module can function as a biphasic amplitude filter. Syst. Biol. 2005;2:43–52. doi: 10.1049/sb:20045037. [DOI] [PubMed] [Google Scholar]
- 28.Zawalich WS, Yamazaki H, Zawalich KC. Biphasic insulin secretion from freshly isolated or cultured, perifused rodent islets: comparative studies with rats and mice. Metabolism. 2008;57:30–39. doi: 10.1016/j.metabol.2007.07.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Chandra FA, Buzi G, Doyle JC. Glycolytic oscillations and limits on robust efficiency. Science. 2011;333:187–192. doi: 10.1126/science.1200705. [DOI] [PubMed] [Google Scholar]
- 30.Kurata H, El-Samad H, Iwasaki R, Ohtake H, Doyle JC, Grigorova I, Gross CA, Khammash M. Module-based analysis of robustness tradeoffs in the heat shock response system. PLoS Comput. Biol. 2006;2:e59. doi: 10.1371/journal.pcbi.0020059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Gerhart J, Kirschner M. The theory of facilitated variation. Proc. Natl Acad. Sci. USA. 2007;104(Suppl. 1): 8582–8589. doi: 10.1073/pnas.0701035104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Chickarmane V, Troein C, Nuber UA, Sauro HM, Peterson C. Transcriptional dynamics of the embryonic stem cell switch. PLoS Comput. Biol. 2006;2:e123. doi: 10.1371/journal.pcbi.0020123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Huang S. Reprogramming cell fates: reconciling rarity with robustness. Bioessays. 2009;31:546–560. doi: 10.1002/bies.200800189. [DOI] [PubMed] [Google Scholar]
- 34.Nijhout HF. The nature of robustness in development. BioEssays. 2002;24:553–563. doi: 10.1002/bies.10093. [DOI] [PubMed] [Google Scholar]
- 35.Kim D, Kwon YK, Cho KH. The biphasic behavior of incoherent feed-forward loops in biomolecular regulatory networks. BioEssays. 2008;30:1204–1211. doi: 10.1002/bies.20839. [DOI] [PubMed] [Google Scholar]
- 36.Shin SY, Yang HW, Kim JR, Do Heo W, Cho KH. A hidden incoherent switch regulates RCAN1 in the calcineurin-NFAT signaling network. J. Cell Sci. 2011;124:82–90. doi: 10.1242/jcs.076034. [DOI] [PubMed] [Google Scholar]
- 37.Chen L, Glover JN, Hogan PG, Rao A, Harrison SC. Structure of the DNA-binding domains from NFAT, Fos and Jun bound specifically to DNA. Nature. 1998;392:42–48. doi: 10.1038/32100. [DOI] [PubMed] [Google Scholar]
- 38.Thanos D, Maniatis T. Virus induction of human IFN beta gene expression requires the assembly of an enhanceosome. Cell. 1995;83:1091–1100. doi: 10.1016/0092-8674(95)90136-1. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.