Developing a denoising filter for electron microscopy and tomography data in the cloud

Abstract

The low radiation conditions and the predominantly phase-object image formation of cryo-electron microscopy (cryo-EM) result in extremely high noise levels and low contrast in the recorded micrographs. The process of single particle or tomographic 3D reconstruction does not completely eliminate this noise and is even capable of introducing new sources of noise during alignment or when correcting for instrument parameters. The recently developed Digital Paths Supervised Variance (DPSV) denoising filter uses local variance information to control regional noise in a robust and adaptive manner. The performance of the DPSV filter was evaluated in this review qualitatively and quantitatively using simulated and experimental data from cryo-EM and tomography in two and three dimensions. We also assessed the benefit of filtering experimental reconstructions for visualization purposes and for enhancing the accuracy of feature detection. The DPSV filter eliminates high-frequency noise artifacts (density gaps), which would normally preclude the accurate segmentation of tomography reconstructions or the detection of alpha-helices in single-particle reconstructions. This collaborative software development project was carried out entirely by virtual interactions among the authors using publicly available development and file sharing tools.

Electronic supplementary material

The online version of this article (doi:10.1007/s12551-012-0083-x) contains supplementary material, which is available to authorized users.

Introduction

Three-dimensional (3D) cryogenic Electron Microscopy (cryo-EM) has emerged as a powerful imaging technology in structural biology, due to its ability to determine the structure of large biomolecular complexes in vivo or in a near native, vitreous ice environment (Baumeister 2002; Frank 2006). Macromolecular assemblies are essential for most subcellular processes, yet many such complexes are either too heterogeneous or too large in size to be routinely analyzed by traditional atomic resolution structure determination techniques such as NMR or X-ray crystallography.

The cryo-EM tomograms or micrographs are of low contrast, since the electron optics essentially produces a phase object, i.e. the electron wave front passing through the specimen is not absorbed but its phase is shifted according to the projection of the electrostatic potential of the traversed specimen. The electron microscope is then defocused, which makes phase objects visible, but individual particle projections are still barely discernible on the raw micrograph relative to the surrounding ice at the optimum defocus for biological specimens. An even bigger constraint for imaging is the noise introduced by the low electron dose, which is necessary to protect the biological specimen from radiation damage (Frank 2006). At low dose conditions, the resulting images show a very low signal-to-noise ratio (SNR; see Online Resource Section 1).

Careful noise reduction is essential prior to the extraction of biologically relevant information from tomographic 3D reconstructions (Frangakis and Hegerl, 2001). In single-particle cryo-EM, high noise levels in the micrographs also limit the resolution of the resulting volumetric data, in particular for asymmetric systems. Recent advances in instrumentation and algorithm development have led to the determination of high resolution volumetric maps for some specialized systems exhibiting symmetry. These reconstructions are approaching a level of detail previously only seen in X-ray crystallography data (Zhang et al. 2008). This high resolution is also typically a result of a correction of the contrast transfer function (CTF) of the microscope. In particular, a compensation of the CTF envelope function, which is attenuated at high frequencies, will sharpen the map considerably and may amplify high frequency noise together with bona fide features. Therefore, experimental single-particle 3D maps can often benefit from the removal of the remaining noise, e.g., in visualization or when performing a map analysis that is very noise sensitive such as secondary structure prediction (Jiang et al. 2001).

This review describes the Digital Path Supervised Variance (DPSV) filter (Szczepanski et al. 2004; Smolka 2008; Szczepanski 2008) which was recently adapted by us for tomography applications (Rusu and Wriggers 2012). In DPSV, the intensity of a focal pixel (voxel) is a weighted mean over a set of neighboring pixels similar to the bilateral filter (see Online Resource Section 1). The weights, however, are calculated from cost values assigned to paths emanating from the focal pixel. Thereby, paths with high noise are discarded with the use of a discriminant function, whereas object edge detail is preserved by those paths that follow the edge. The DPSV filter is efficient, and practical applications depend on only three user-defined parameters.

This paper also describes the technical means which enabled the interactions of the authors during the DPSV software development. In the course of our work, we were confronted with unusual challenges due to a reorganization at the School in Houston, resulting in an abrupt loss of the computational laboratory where we began our collaboration. Although our personal experiences differed in many respects (Z.S. was supported by a fellowship from Poland and continued the work seamlessly in a new laboratory, M.R. and M.W. took on new positions with new roles, whereas W.W. had relocated earlier to New York City), we were jointly committed to continuing our work while minimizing the impact to the users of our software. Within a few weeks, we salvaged all data from backups and server hard disks and moved the entire project into the cloud where we continued the collaboration in our free time. The transition to a “distributed laboratory” (we have never met as a team at one location) was helped by publicly available tools on the internet that enabled us to work efficiently. We hope our experience inspires other scientists to seek computing opportunities that transcend institutional and geographic barriers.

The remainder of this paper is organized as follows. In “Software development in the cloud”, we describe the collaborative technology that enabled this work. In “Overview of DPSV filtration, we summarize the concepts of DPSV. The sections “Denoising of 3D maps for visualization purposes” and “Helix detection enhanced by denoising” contain the results of applications of DPSV to 3D cryo-EM and to tomography data. In “Denoising and averaging of raw data”, we summarize tests erformed on 2D micrographs. We conclude with a discussion and implementation details in “Conclusions”. The Online Resource provides a mathematically complete description of the DPSV theory and more details on the 2D application examples.

Software development in the cloud

In the absence of a central physical laboratory, we used locally available personal computers for our software development. Instead of a dedicated server, we used the following services to facilitate our remote collaboration (these tools are freely available for academic users at the cited web sites). The free CVS software revision control system (GNU Savannah 2012) is running on a mini server at the home of one of us. As a future alternative in the cloud, we are exploring to move this central repository to the free Google Code developer site (Google 2012). We also use free file hosting services such as Dropbox (Dropbox 2012) that allow us to share and to synchronize documents and data files. The free Asana (Asana 2012) service supports task management and project coordination. For more than a decade, our laboratory had controlled its own webspace and e-mail services, with the http://www.biomachina.org domain hosted at a commercial site. The web server was and is managed by one of us, using the free HTML editor Nvu (Glazman 2012) as well as PHP and CGI scripts written by the group.

Sculptor (http://sculptor.biomachina.org) is a complex software package with more than 150,000 lines of source code. It leverages a range of external libraries for parallel computing, graphics rendering, and the user interface. During our salvage operation, one of us explored the varying software dependencies on the different operating systems and hardware architectures, and documented them for future releases. In the absence of physical machines with these different architectures, Sculptor builds for development, testing, and release purposes are compiled on virtual machines using the free VirtualBox software (Oracle 2012). Situs (http://situs.biomachina.org) is a more compact command-line package traditionally managed by one of us. Situs was recently added to the CVS repository to facilitate code sharing with Sculptor.

Overview of DPSV filtration

The DPSV filter is one of the advancements arising from the described remote collaboration. Below follows an abridged summary of the filter as established in earlier work. A complete and mathematically rigorous review of the DPSV theory, applied to cryo-EM and tomography maps, is given in Online Resource Section 2.

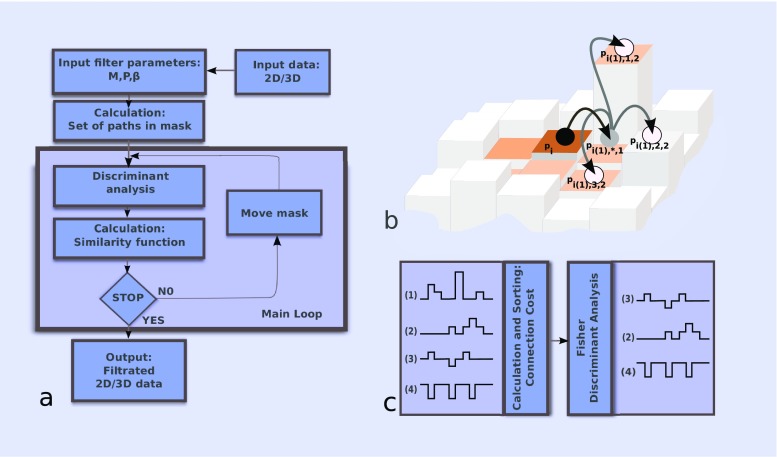
DPSV proceeds by a self-avoiding walk on a (square or cubic) lattice using a specific neighborhood model (4-neighbor or 8-neighbor in 2D; 6-neighbor or 26-neighbor in 3D). The reach of the filter is determined by the dimension M of a (square or cubic) mask, and the length P of the paths taken within the mask. Small mask sizes and long paths sample curved or bent features, whereas shorter walk lengths P ≤ (M - 1)/2 are unrestricted by the mask and better suited for straight edges. In Fig. 1b, we show a 2D example of a digital walk along a path through one of four nearest neighbors, where M = 5 and P = 2. Each path starts in the central pixel p _i, where i is the counter for the translational scan of all voxels. The distinction between different paths passing through the same n-th closest neighbor is introduced by l in the notation p _i(n),l,1 (when we do not differentiate between those paths, we use the notation \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {{p}_{{i(n),*,1}}} $$\end{document}). The virtual particle (black circle) is initially at position p _i, subsequently takes a step through the first neighbor \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {p_{{i(1), *, 1}}} $$\end{document} (gray), and then further through its second neighbor (white). For all four neighbors, there will be a total of 12 paths. During each step along the path, the virtual particle is defined by its spatial position and the intensity value.

Fig. 1.

a Block diagram of the filtering method. b Example of the 2D digital walk along a path through one of the four nearest neighbors. c Illustration of discriminant analysis (FDA) of the set of four paths. As a result of FDA, only the path with index 1 was excluded

A “connection cost” Λ is computed for all paths (see Online Resource Section 2). For the l-th path, this is defined as the maximum cost observed among pixels which are linked by one path, where the individual connection cost is defined as the absolute difference of (normalized) intensities between the center pixel p _i and a linked pixel p _i(n),l,k, (Fig. 1b) divided by their Euclidean distance.

Fisher’s discriminant analysis (FDA) is used to separate the set of paths into two classes which ideally correspond to signal and noise (see Online Resource Section 2 for details). The class with higher connection cost is then excluded from further consideration. This way, the algorithm should ideally preserve only the information that belongs to relatively smooth intensity landscapes and suppress areas affected by noise. In Fig. 1c, an input set of four hypothetical paths is sorted with respect to the connection cost. After applying FDA, only paths 2, 3, and 4 remain for further analysis.

The output intensity (of the central pixel) is finally calculated as a cost-weighted mean of the surviving paths (termed “Similarity Function” in Online Resource Section 2). We use an exponential weight for the cost-based averaging, K(β, Λ) = e ^−βΛ. The parameter β defines a “sharpening” effect, with higher β indicating more sharpening. Empirical tests in Online Resource Section 4 suggest useful values (that maximize SNR) in the range of 0.01–0.0001. The averaging is performed only over immediately neighboring voxels, but the information from more distant voxels is considered indirectly by means of the cost function Λ.

In the following, we provide application and performance examples of the DPSV filter. We begin with straightforward applications to experimental 3D maps from single particle cryo-EM and tomography, before describing tests on 2D micrographs.

Denoising of 3D maps for visualization purposes

As a first application of DPSV, we demonstrate its ability to enhance the recognition of the protein backbone in single-particle reconstructions. High resolution density maps have a great number of bona fide details but can contain artifacts and noise due to the reconstruction scheme.

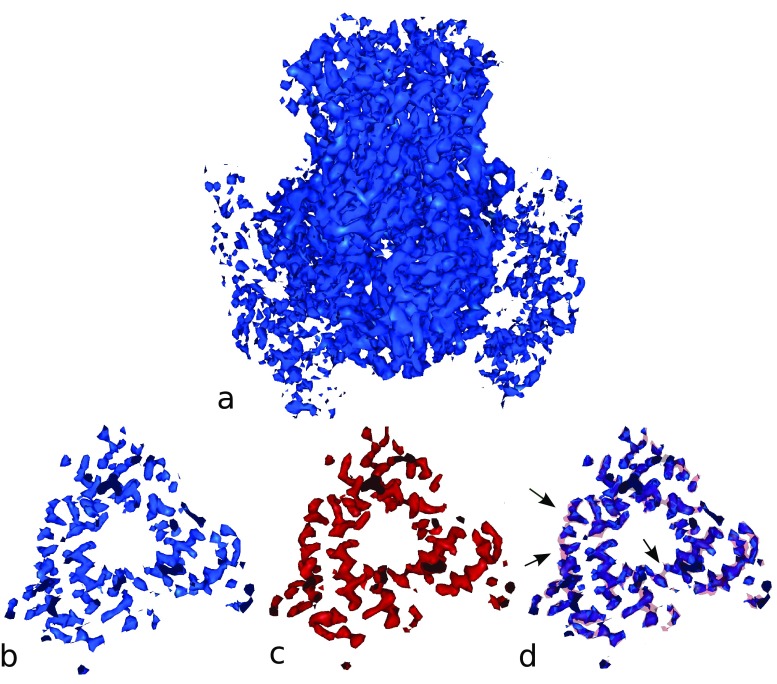
We tested our approach on a 3D reconstruction of viral protein VP6 with resolution 3.8 Å determined by Zhang et al. (2008). The full cryo-EM map (EMDB ID 1461) of VP6 is presented in Fig. 2a. The lower subsection of the map was selected to show visible discontinuities of long helices in Fig. 2b. The results after DPSV filtration (with mask size M = 5, path length P = 3, 6-neighbor model, filter parameter β = 0.0002) are presented in Fig. 2c. A comparison is shown in Fig. 2d, where solid transparent red indicates the structures after filtering, the blue solid surface represents the original map and the black arrows indicate the areas where the gaps in the density are filled during filtering. The results demonstrate that the filter is able to fill density gaps where needed without strong blurring of neighboring densities.

Fig. 2.

a Visualization of the cryo-EM reconstruction of viral protein 6 (VP6; blue) at 3.8 Å resolution (EMDB ID 1461; volume size 122 × 106 × 134). b Lower section (blue) with visible discontinuity of long helices (isolevel 1.4). c Lower section (red; isolevel 1.0) after filtering with DPSV filter (M = 5, P = 3, β = 0.0002, 6-neighbor model). d Comparison of results (b) and (c). The transparent red isocontour presents densities after filtering. The black arrows show areas where the filter algorithm fills gaps in helices. The isolevels in (b–d) were matched to yield the same helix thickness. All molecular graphics in the paper were created using Sculptor software (Birmanns et al. 2011)

Due to the importance of denoising prior to the interpretation of tomographic maps (Frangakis and Förster 2004), we also tested DPSV on a 3D reconstruction from electron tomography. Figure 3 shows the results of DPSV filtration of an HIV-1 virion map (Briggs et al. 2007) using one or two successive applications. The HIV-1 map is a frequently used test system for denoising (van der Heide et al. 2007; Fernandez 2009; Wei and Yin 2010); therefore, our results can be compared to those in the literature. Our DPSV filter is quite effective, even after one application with relatively short paths P = 2 (see also Rusu et al. 2012 for a comparison with Gaussian filtering). The filtered cross-sections (Fig. 3e, f) clearly show the conical core of the virion, including a region of high density within the core (near the broad end), likely representing the ribonucleoprotein complex of the viral genome with the nucleocapsid domain (Briggs et al. 2007).

Fig. 3.

Example of DPSV filtration results for one and two iterations. Shown is the isosurface of the 3D electron tomography reconstruction of unstained HIV-1 virion (EMDB ID 1155; cropped to volume size 141 × 91 × 281). a Original data, isolevel 140. b DPSV filter (M = 5, P = 2, β = 0.001) applied to (a), isolevel 134. c DPSV filter (M = 5, P = 2, β = 0.001) applied to (b), isolevel 132. d Cross-section of (a). e Cross-section of (b). f Cross-section of (c). The DPSV filter uses a 26-neighbor model. The raw reconstruction (Briggs et al. 2007) was cropped, inverted, and shifted so that the background is black and at zero, and the features are lighter color and positive. Scale bar (a, d): 10 × 100 nm

Helix detection enhanced by denoising

To demonstrate the benefits of DPSV denoising of higher resolution 3D maps, we present here the accuracy of alpha-helix detection afforded by the filter. Recently, we introduced VolTrac, a technique for the annotation of alpha-helical regions in cryo-EM maps (Rusu and Wriggers 2012). VolTrac combines a genetic algorithm with a so-called bidirectional expansion (a cylindrical template trace that crawls in both directions from a start position). The method reliably predicted helices with seven or more residues in experimental and simulated maps. The observed success rates, ranging from 70.6 to 100 %, depended on the map resolution and reconstruction quality of the experimental maps, especially in the higher 4-7 Å resolution range.

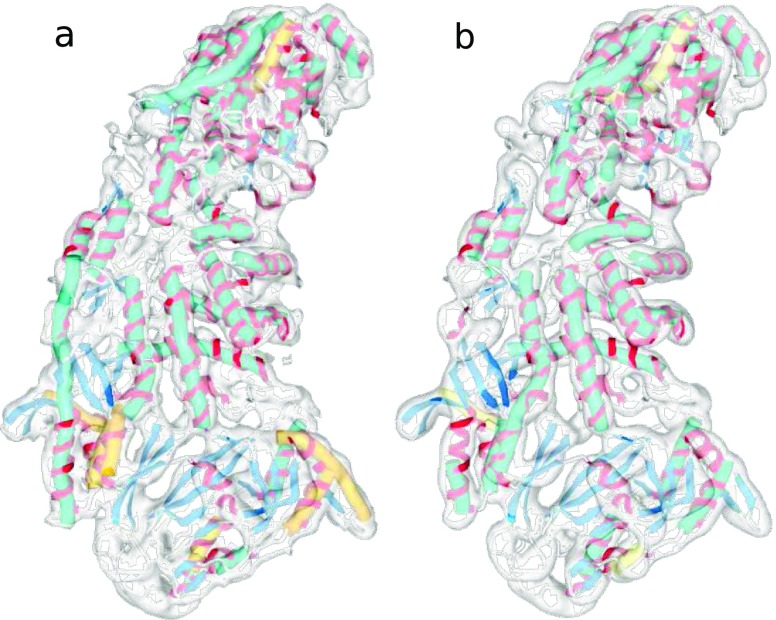
Here, we applied VolTrac to the experimental map depicting the P3A subunit of the Rice Dwarf Virus (EMDB ID 1376) by Liu et al. (2007). As shown in Fig. 4, the structure was solved at 7.9 Å resolution, with a voxel size of 1.49 Å. To demonstrate the ability of the DPSV filter to improve the extraction of α-helices, we executed VolTrac on (1) the raw map (without filtration), (2) after DPSV filtration, (3) after a local normalization (a useful filter that extracts positive densities and evens out their variations across the map, see Rusu and Wriggers 2012), and (4) when combining the local normalization with DPSV filtration. The score threshold in the bidirectional expansion (which terminates when the observed cross-correlation falls below the threshold) was set to 85 % in cases (1) and (2) and 70 % in cases (3) and (4), to account for the enhanced noise after local normalization (decreasing the value of the parameter reduces the risk of false negatives but increases the length of the predicted helices, so there is a tradeoff between tolerance and helical length; see Rusu and Wriggers 2012).

Fig. 4.

a Raw unfiltered map (EMDB ID 1376; volume size 128 × 128 × 128) of the P3A subunit of Rice Dwarf Virus with VolTrac results for locally normalized map (as in Rusu and Wriggers 2012; hSe = 78.8 %). b Locally normalized and DPSV filtered map with corresponding VolTrac results (hSe = 84.4 %). The crystal structure of the subunit (from PDB ID 1UF2) is shown as a ribbon with helices depicted in red and beta sheets in blue. Green tubes represent VolTrac predictions within the top 33 scoring solutions (where 33 is the known number of helices in the atomic structure), yellow tubes represent correct predictions that were found lower in list of solutions

In each case, we compared the VolTrac-predicted helices with the actual helices of the Rice Dwarf Virus (as known from the crystal structure, PDB ID 1UF2). We quantified the helix sensitivity (hSe) as the ratio of true positive predicted helices of 7 or more residues to the total number of 33 such helices in the crystal structure. The DPSV filter was executed on a 26-neighbor model with a mask size of M = 5, path length of P = 2, and β = 0.0001. The resulting sensitivities for the above four cases were: (1) hSE = 72.7 %, (2) hSE = 78.8 %, (3) hSE = 78.8 %, and (4) hSE = 84.8 %. Individually, the DPSV filter and the local normalization each improved the detection of α-helices when compared to the original unfiltered map (Fig. 4a), but combining them showed a dramatic synergistic effect on the detection sensitivity (Fig. 4b).

Denoising and averaging of raw data

The applications of DPSV in this review are focused mainly on 3D maps, but it is worthwhile to consider the effects of applying DPSV directly to the noisy raw image data. As an extension of this paper, we demonstrate in the Online Resource the utility of DPSV for denoising single 2D micrographs (Online Resource Section 3) and for denoising stacks of images used in class averaging (Online Resource Section 4). Our evaluation shows a signal-to-noise ratio (SNR) gain of 9–18 dB compared to unfiltered images and a gain of more than 3 dB compared to a Gaussian filter in the image stack tests.

For an individual 2D micrograph where no further processing is possible (and likewise for a finalized 3D tomogram or cryo-EM map), it is relatively easy to make a case for the use of DPSV, even if there are distortions present due to the non-linear filtration process. The case is far less clear when averaging of non-linear filtered data is being performed. The averaging of such filtered images would be different from the non-linearly filtered average of raw images. Our demonstration (Online Resource Section 4) suggests that DPSV may demonstrate utility when averaging is performed (in cases where the final performed analysis is the determination of 2D class-averages themselves, and the resolution is not expected to be high). However, before considering using DPSV as a preprocessing technique in a single-particle cryo-EM context, it would need to be validated further (in future research, a raw dataset should be processed conventionally and after filtration, and the final 3D structures should be compared to a known higher resolution structure).

Conclusions

We reviewed a signal preserving DPSV denoising filter for 2D and 3D data from cryo-EM and tomography. In contrast to other locally adaptive nonlinear methods, our filtering approach uses information gathered during virtual walks along all generated digital paths in a local neighborhood. The analysis of the variance of different paths allows us to segment out localized areas that are corrupted by high noise levels and to estimate pixel/voxel intensity based on a weighted mean of intensities obtained from low variance paths. The filter also reduces the number of parameters needed to three (path length P, mask width M, kernel parameter β), which is a relatively small set of parameters compared to previous methods.

We showed applications to both simulated and experimental 2D and 3D data from single-particle cryo-EM and tomography. One desired outcome is the capability of filling gaps in protein backbones that would preclude the visualization and secondary structure detection in single-particle 3D maps. The performance is evident from a visual comparison of single-particle and tomographic maps before and after filtering, and from the improved performance of a helix detection algorithm, especially in combination with a local normalization filter. The effects of DPSV filtering may depend on specific 3D reconstruction techniques and the accuracy of the 3D maps, but our results are consistent with prior work by other groups (Online Resource Section 1).

For the most part, the above review summarizes the already known benefits of denoising of 3D maps (Jiang et al. 2003) in the application areas of visualization and secondary structure prediction. The results in the Online Resource further demonstrate the utility of DPSV for denoising single 2D micrographs, and they suggest that in future work DPSV could be tried as a preprocessing technique in a 3D reconstruction context. Although the application was not discussed here, effective filtering techniques can also help significantly in particle boxing software (Yu and Bajaj 2004), making an automatic particle picking approach more robust and free of false positives, which would help in the classification of heterogeneous data into homogeneous sets. Finally, we mention feature tracing in filtered electron tomography reconstructions as an important application area of DPSV (Rusu and Wriggers 2012).

Our software was developed in C++ using free or inexpensive collaborative services on the internet. The DPSV filter is implemented in version 2.1 of the multi-scale modeling and visualization package Sculptor and is freely available at http://sculptor.biomachina.org. The computing times on an 4-core Linux workstation (Intel i5, 2.4 MHz, 8 GB RAM) were 28, 246, and 128 s for the VP6 (Fig. 2), HIV (Fig. 3), and P3A (Fig. 4) maps, respectively. Because Sculptor is primarily intended to function as an interactive graphics program, it can become impractical to wait several minutes when applying DPSV to larger maps. Therefore, we have implemented a new command-line tool volfltr that can be run in the UNIX shell. The volfltr tool is part of version 2.7 of the Situs package, freely available at http://situs.biomachina.org. Both Situs and Sculptor implementations were optimized for shared memory parallel processing using OpenMP (OpenMP Architecture Review Board 2012).

Electronic Supplementary Material

Below is the link to the electronic supplementary material.