Prognostic Significance of Growth Kinetics in Newly Diagnosed Glioblastomas Revealed by Combining Serial Imaging with a Novel Bio-mathematical Model

Abstract

Glioblastomas (GBMs) are the most aggressive primary brain tumors characterized by their rapid proliferation and diffuse infiltration of the brain tissue. Survival patterns in patients with GBM have been associated with a number of clinico-pathologic factors, including age and neurological status, yet a significant quantitative link to in vivo growth kinetics of each glioma has remained elusive. Exploiting a recently developed tool for quantifying glioma net proliferation and invasion rates in individual patients using routinely available magnetic resonance images (MRIs), we propose to link these patient-specific kinetic rates of biological aggressiveness to prognostic significance. Using our biologically-based mathematical model for glioma growth and invasion, examination of serial pre-treatment MRIs of 32 GBM patients allowed quantification of these rates for each patient’s tumor. Survival analyses revealed that even when controlling for standard clinical parameters (e.g., age, KPS) these model-defined parameters quantifying biologically aggressiveness (net proliferation and invasion rates) were significantly associated with prognosis. One hypothesis generated was that the ratio of the actual survival time after whatever therapies were employed to the duration of survival predicted (by the model) without any therapy would provide a “Therapeutic Response Index” (TRI) of the overall effectiveness of the therapies. The TRI may provided important information, not otherwise available, as to the effectiveness of the treatments in individual patients. To our knowledge, this is the first report indicating that dynamic insight from routinely obtained pre-treatment imaging may be quantitatively useful in characterizing survival of individual patients with GBM. Such a hybrid tool bridging mathematical modeling and clinical imaging may allow for statifying patients for clinical studies relative to their pretreatment biological aggressiveness.

MAJOR FINDINGS

Biomathematical modeling combined with routinely available serial pre-treatment MRIs can be used to quantify patient-specific kinetic rates of net glioma cell proliferation and invasion that are prognostically significant even when controlling for standard prognostic clinical parameters. Although further patient studies are necessary, these results illustrate that this bio-mathematical model provides a unique tool for quantifying the glioma phenotype for each individual patient and suggest a role for the development of patient-specific “virtual controls” for treatment design and assessment of treatment effects.

QUICK GUIDE TO EQUATIONS AND ASSUMPTIONS

The initial goal of our research was to see if we could develop a mathematical model of gliomas that would provide helpful insight into how gliomas behave. We decided to build the model from the bottom up, adding new features only as they became necessary, beginning with the definition of a cancer cell as proliferating without control, invading locally and metastasizing distantly, the last feature being unnecessary to consider further for glioma cells since they generally do not metastasize.

The resultant minimal model we chose was a reaction-diffusion partial differential equation (1, 2) used to describe the density of glioma cancer cells (c) in terms of two net rates: motility (D) and proliferation (ρ).

$$\stackrel{\text{rate of change of glioma cell density}}{\overbrace{\frac{\partial c}{\partial t}}}=\stackrel{\text{net dispersal of glioma cells}}{\overbrace{\nabla ·(D(\mathbf{x})\nabla c)}}+\stackrel{\text{net proliferation of glioma cells}}{\overbrace{\rho c(1-\frac{c}{k})}}$$ Equation 1

In words, at every location in the brain (x), the model equates the rate of change of the glioma cell density (c) at that location with the net dispersal (D) of the glioma cells near that location plus the net proliferation (ρ) of glioma cells locally. This model describes the density of tumor cells (and not individual cells), and therefore reflects net rates of proliferation and motility for the entire population of tumor cells. That is, these net rates are the net effects of and down-stream from actual determinants (genetic or other) of individual-cell behavior. The Brain Web (3, 4) provides the anatomic link (accurate to 1 mm³) between virtual and real images. What this all means is that we can predict and follow the growth of any glioma from its point of origin on an anatomically-accurate brain phantom through those first two pre-treatment scans and throughout the tumor’s subsequent natural history, including some of the theoretically simpler treatments such as surgical resection (5, 6).

Major Assumptions of the Model

Fickian diffusion has been used to quantify the random motility of a variety of invading cells (7) and is implemented in our model to represent the spatial invasion of the glioma cells at a rate D (mm²/yr). This rate can vary depending on the location in the brain (x), quantifying the observation that glioma cells migrate more quickly in white matter than they do in grey (8, 9). The net proliferation term includes mitosis, apoptosis and other cell loss mechanisms and is assumed to be logistic such that the net proliferation rate (ρ, 1/yr) is lower in regions of high cell density (where c ≈ K) than in regions of low cell density (where c <<K), K being the carrying capacity of the brain tissue. All glioma cells are assumed to be identical, about 20 µm in diameter, but do not affect the environment of grey and white matter in which they move freely. Although these last assumptions are quite unrealistic, they can be modified, if necessary, but they have served us well in capturing tumor dynamics in vivo thus far (2, 10, 11) in many iterative comparisons of theory and the real world as reviewed by Harpold et al (10).

Although there are certainly a variety of cellular subpopulations involved in GBM growth, ρ is a net measure of the proliferative capacity and D is a net measure of the invasive capacity of the overall dominant phenotype. As explored in detail elsewhere (2), an intuitive (and mathematical) analysis of polyclonal tumors within a confined space, with each subclone having a quantitatively different biological aggressiveness (quantified by net rates of migration and proliferation), typically leads to the overall pattern of growth being dominated by the most aggressive clone (2). This practical intuition is used routinely in cancer research labs to (partially) explain the observation that serial passages (even only a few) of a cell line leads to identification of the most aggressive phenotype since it dominates each culture. Conversely, others have suggested that microenvironmental influences exert selection pressures on the subclones, resulting in dominance of the most aggressive clone (12). Thus, under a variety of explanations, it is intuitive that a single measure of the dominant net proliferation rate ρ and the dominant net migration rate D would be considered as candidates for prognostic markers.

The first formulation (equation 1) led to Fisher's approximation $(\mathit{\nu }=2\sqrt{\mathit{D}\mathit{\rho }})$ and the suggestion that the radius should increase linearly with time (asymptotically) as the "traveling wave" (13) spreads forward. This was the first suggestion that the classical simple exponential doubling of the volume was far from correct and was soon proved correct for low- and high-grade gliomas (13, 14). The next suggestion was that less than "gross total resection" (GTR) produced no improvement in duration of survival and GTR not much more, recurrences occurring where the residual glioma was most concentrated, typically at the surgical margin (5, 15). We assume that D and ρ remain constant for long segments of the tumor’s course which is consistent with our data for long term untreated follow up of gliomas (10).

INTRODUCTION

Glioblastomas (GBMs) are the most aggressive primary brain tumors characterized by their rapid and diffuse infiltration of the adjacent normal-appearing brain tissue. Several clinico-pathologic factors have been found to allow stratification of glioma patients according to probable survival times: 1) as to the tumor: type and grade, size and site, and 2) as to the patient: age and neurological functioning, and history of previous treatment (extent of surgery, x-irradiation, chemotherapy) (16). None of these factors concerns patient-specific measures of the in vivo kinetics of the tumor itself - partially a result of the lack of tools to quantify overall growth kinetics of a tumor capable of both extensive invasion peripheral to the imaging abnormality as well as aggressive rates of cellular proliferation. We have recently developed a novel bio-mathematical model for glioma growth and invasion that allows the translation of routinely available, serial pre-treatment magnetic resonance images (MRIs) into patient-specific net rates of proliferation and dispersal of glioma cells (5, 17). It is the purpose of this presentation to demonstrate statistically that these two new measures of biological aggressiveness offer prognostic information independent of the classic clinico-pathologic features and thus allow a more accurate prediction of the duration of survival of GBM patients.

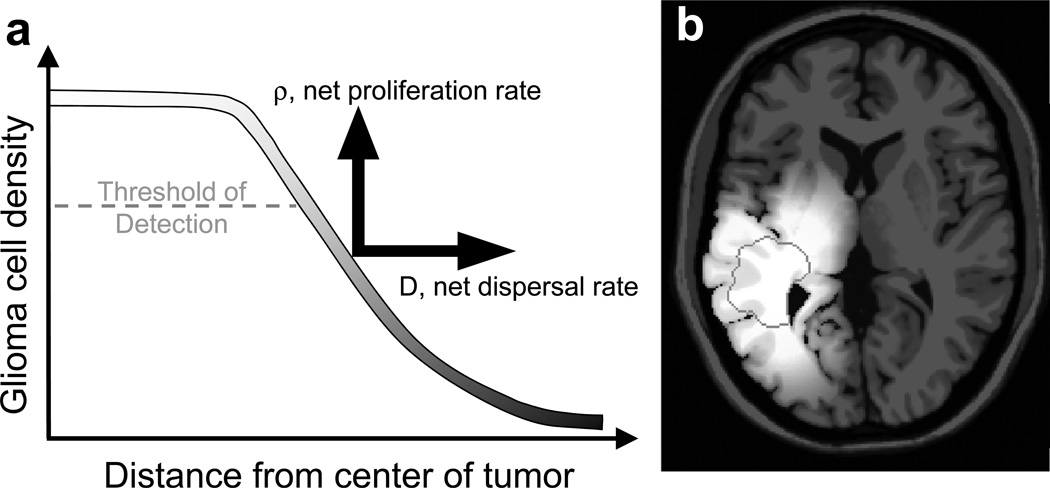
The cell density gradient implicit to these invasive tumors suggests that imaging reveals only the “tip of the iceberg” of each glioma with a significant portion of the glioma cells already invaded peripheral to the imaging abnormalities as shown in Figure 1a. The bio-mathematical model, combining two key net rates of proliferation (ρ) and invasion (D), has accurately quantified the diffuse invasion as well as the overall growth kinetics of gliomas (5, 17). Specifically, based on this model, we have developed a technique for translating changes seen on serial MRIs pre-treatment into measures of net proliferation and net invasion of glioma cells (17). Figure 1b shows the model-predicted diffuse gradient of glioma cells predicted by simulation of the bio-mathematical model with patient-specific model parameters (D and ρ) shown in Table 1 for patient 11. The grey-scale gradient in Figure 1b represents the model-simulation of glioma cellular density and reveals the diffuse nature of the lesion imaged as a nodule corresponding to the T1-Gd MR image surrounded by the white contour and dark grey contours which correspond to the T2 MRI abnormality. The ratio ρ/D can be interpreted as the relative steepness of the gradient of invading cells peripheral to the frank abnormality seen on T1Gd imaging (gross pathology or histology). Alternatively, the inverse of this ratio (D/ρ) has been termed the “Invisibility Index” and can be used to estimate the number of the diffusely invaded tumor cells peripheral to (and therefore invisible to) the imaging abnormality (10). Autopsy studies have revealed the remarkable accuracy of these model-predicted gradients of invasion in other glioblastoma cases for which autopsy was available (13).

Figure 1.

a) “Tip of the iceberg” analogy showing a threshold of detection based on concentrations of tumor cells (as well as leaky blood vessels) contributing to a gradient of glioma cells extending well beyond the T1-Gd MRI-defined threshold of detection and even beyond the T2-defined threshold. Our biologically-based mathematical model quantifies this growth and invasion of the glioma cells contributing to this overall profile by rates of net proliferation (ρ) driving the concentration of cells up and net dispersal (D) driving the concentration of cells peripherally. b) Model-predicted diffuse T2 gradient of glioma cells predicted by simulation of the bio-mathematical model on an anatomically-accurate brain phantom (3, 4) using model parameters (D and ρ) specific to Patient 11 in Table 2. The T1Gd MRI-detectable edge of the lesion is superimposed as a dark grey contour.

Table 1.

Summary of patient data.

No.	Age (yrs)	Sex	KPS	EOR	RT Dose (Gy)	Survival (days)	RPA Class	TMZ	T1Gd Radius (mm)	T2 Radius (mm)	T1Gd Velocity (mm/yr)	D (mm2/yr)	ρ (1/yr)	Time to FTB		TRI Cells	TRI Radius
														Cells (days)	Radius (days)
1	54	F	80	GTR	61.2	1027*	IV	no	7.5	11.2	67	19.4	57.3	160	151	6.4	6.8
2	44	F	80	STR	61.2	410	IV	no	13.4	21.8	469	316.7	173.6	16	17	25.6	24.4
3	40	F	100	STR	60.4	617	III	yes	6.8	10.8	16	5.1	12.3	686	656	0.9	0.9
4	73	F	80	Biop	48.6	91	V	no	27.2	33.7	33	17.4	15.4	81	87	1.1	1.0
5	47	M	70	STR	61.2	551	IV	yes	12.4	15.2	54	11.5	64.0	163	152	3.4	3.6
6	63	M	90	Biop	59.4	115	V	yes	20	20.8	38	1.3	272.7	119	144	1.0	0.8
7	53	F	70	Biop	61.2	377	V	yes	5.5	19.6	53	50.7	13.9	171	203	2.2	1.9
8	70	M	70	Biop	61.2	691*	V	yes	16.6	23.1	40	21.0	18.8	170	169	4.1	4.1
9	51	F	100	STR	59.4	1273	IV	no	8.3	13.7	9	3.9	5.5	1092	1048	1.2	1.2
10	76	M	80	GTR	61.2	351	IV	no	7.5	7.6	10	0.3	81.7	732	1057	0.5	0.3
11	65	F	70	GTR	61.2	446*	IV	yes	11.2	15.8	40	15.2	26.7	226	216	2.0	2.1
12	57	M	90	GTR	61.2	518*	IV	yes	17.4	27.7	57	47.1	17.3	99	113	5.2	4.6
13	60	M	90	GTR	61.2	491*	IV	yes	10.3	16.1	29	13.0	15.8	325	314	1.5	1.6
14	63	F		STR	60	91		no	12.9	28.9	25	29.4	5.1	238	329	0.4	0.3
15	52	M	90	GTR	60	345*	IV	yes	3.8	9.6	12	5.0	7.3	971	941	0.4	0.4
16	74	F	60	GTR	61.2	572	V	no	18.1	21.6	3	0.9	2.9	2052	1928	0.0	0.0
17	51	M	70	STR	60	347*	IV	yes	14.8	22.7	19	12.0	7.5	377	390	0.9	0.9
18	47	M	90	GTR	60	191*	III	yes	19.2	30	58	49.9	16.8	84	100	2.3	1.9
19	53	M	90	GTR	61.2	417	IV	yes	9.7	22.3	31	28.6	8.2	261	302	1.6	1.4
20	49	F	80	STR	61.2	483	IV	no	21.8	30.8	98	71.0	33.8	44	49	11.0	9.8
21	74	M	80	Biop	59.4	823	V	no	0	19	14	15.5	2.9	539	946	1.5	0.9
22	58	M	90	Biop	65	453	V	yes	8.6	16.2	11	6.2	4.6	902	909	0.5	0.5
23	58	M	70	STR	59.4	700	IV	yes	23	32.1	43	31.9	14.5	86	102	8.1	6.9
24	57	M	90	STR	59.4	2048*	IV	yes	21.8	28.4	7	3.9	3.3	655	679	3.1	3.0
25	58	F	80	Biop	69	375	V	yes	7.3	9.2	23	3.3	40.3	462	442	0.8	0.8
26	45	M	100	STR	61.2	334	III	yes	10.7	15.3	39	14.4	25.6	242	230	1.4	1.4
27	49	F		GTR	60	543	III / IV	no	10.3	14.5	26	8.5	19.8	368	348	1.5	1.6
28	50	M		STR	60	399		no	15.3	19.9	27	9.7	18.3	284	270	1.4	1.5
29	22	M		STR	60	415	III / IV	no	16.4	24.1	43	27.0	17.3	152	157	2.7	2.6
30	64	M		Biop	60	82	V	no	21.5	26.1	24	9.1	15.8	216	206	0.4	0.4
31	71	M		STR	60	260		no	18.1	29.7	23	21.6	6.2	217	266	1.2	1.0
32	50	M		Biop	60	487	V	no	20.9	29.9	54	40.0	18.3	85	95	5.7	5.1

^*Indicates censored data

In addition to quantifying the diffuse extent of gliomas, a novel prediction of the model’s combination of an exponential net proliferation rate (for low cell densities) and a diffuse invasion pattern is an asymptotic overall linear pattern of radial expansion of the detectable abnormality on imaging, dependent on both dispersal, D, and proliferation, ρ, with an overall velocity defined by Fisher’s approximation: $\mathit{\nu }=2\sqrt{\mathit{D}\mathit{\rho }}$. This consistent growth pattern has been validated in a variety of gliomas (13, 14) and already been shown to be a prognostic indicator in low-grade gliomas (18, 19). In addition to relating the overall velocity of radial expansion on MRI to a net combination of the invasiveness and net proliferation of the glioma cells, the individual parameter values, D and ρ, can be calculated from serial pre-treatment imaging for each individual contrast-enhancing glioma (5, 13, 20, 21). These parameters are characteristic for each patient’s tumor and allow for a dynamic characterization of disease response to any given treatment by providing an untreated virtual control (UVC) against which to compare actual tumor behavior. We will refer to this ratio as the “Therapeutic Response Index” (TRI) which is described as a fraction of the “Fatal Tumor Burden” (FTB).

Our hypothesis is that our bio-mathematical model-based net measures of proliferation and invasion rates provide novel insight into the overall glioma phenotype for each patient in vivo and are thereby prognostically significant. In this study, we considered 32 GBM patients with serial pre-treatment imaging to allow quantification of a net proliferation rate and a net invasion rate for each glioma. Using proportional hazard survival analyses, we first assessed the prognostic significance of these bio-mathematical model parameters relative to standard clinico-pathologic parameters. Next, using the model-predicted survival of each patient’s UVC, we assessed the net increase in actual survival (with treatment) for each patient. Complementary to the proportional hazard survival analysis, we found that those patients with the highest net proliferation rate were most likely to benefit significantly from therapy consistent with our recent finding regarding radiotherapy (22). That some GBMs do not respond significantly to cytotoxic therapies merely confirms the wide range of growth rates, extending into the low ranges, where XRT and chemotherapy are generally thought be less effective; the only problem with that thought being that net proliferation rates of gliomas could not previously be accurately measured.

MATERIALS AND METHODS

Patient Population

The two main criteria for inclusion in the patient population were: 1) a diagnosis of WHO grade IV GBM and 2) at least two gadolinium-enhanced T1-weighted (T1Gd) and T2-weighted (T2) MRIs prior to any surgical or treatment intervention in order to calculate the velocity of radial expansion and the bio-mathematical model parameters: D and ρ. To control for the role of heterogeneity in the primary treatment as it affects survival, we accepted only patients receiving standard conformal radiation therapy to a dose of at least 48 Gy (1 patient, others 59.4–69 Gy). Of the 32 patients identified, 17 received concurrent radiation and temozolomide (TMZ) chemotherapy as their primary therapy (summarized in Table 1). Twenty-one of the patients were diagnosed and treated at the University of Washington Medical Center, 6 at the SFC Brain Imaging Research Centre at the University of Edinburgh (20) and the remaining 5 at the UCLA Medical Center. Patient data were accrued under IRB-approved protocols.

As outlined in Table 1, 25 of the 32 patients had KPS scores at diagnosis ranging from 60 to 100 (median 80) and 32 had ages ranging from 22–76 (median 55); 22 received either a biopsy or subtotal resection (STR) and the other 10 received a gross total resection (GTR). Radiation Therapy Oncology Group (RTOG) recursive partitioning classification (RPA) ranged from class III (17.1 months expected median survival), and IV (11.2 months) to V (7.5 months) (23). Due to the fairly small number of patients in each RPA class, the survival analysis was performed treating RPA as a dichotomous variable, dividing at RPA III and IV (n=19) vs RPA V (n=10).

MRI Segmentation and Tumor Growth Kinetics of the Untreated Virtual Control

Model parameters for tumor growth kinetics (D and ρ) were calculated from two pretreatment MRIs as reviewed in Harpold et al (10) and applied in Swanson et al (5, 13, 21) to defined tumor volumes seen on T1Gd and T2. Velocities of radial expansion were computed as the average linear rate of increase in mean radius between two pre-treatment observations on T1Gd. The ratio ρ/D was determined from comparison of the tumor volumes seen on T1Gd and on T2 at a single time point. Details of the sensitivity of model parameters to uncertainty in the MR tumor volume measurements are provided in the Supplementary text and the Table S1.

Predicting Untreated Survival Time of Untreated Virtual Controls and the Therapeutic Response Index

Following (19), the untreated survival time for the UVC was estimated by developing the concept of a “fatal tumor burden” (FTB), either a size (35 mm radius) of the “solid tumor” as seen on T1Gd MRI or a total number of cells visible or invisible (1.1 × 10¹¹) (20) – see Table 1, Supplementary Table 1 and Supplementary Figure 1. The Munro-Kellie hypothesis (24) explains why brain tumors might actually have a FTB with a fixed volume of the skull. Both FTB endpoints yield the practically the same answer (see Supplementary Figure 1) and leads naturally to the Therapeutic Response Index (TRI). The TRI is the ratio of the actual survival of the patient to the model-predicted survival of that patient’s UVC.

Statistical Methods

Survival analysis was performed using Cox proportional hazard regression (25) implemented in S-PLUS (26). For patients still alive, standard censoring procedures were taken using survival in days from the date of operation or biopsy. Significance was determined by logrank p-values.

RESULTS

Table 1 summarizes the pre-treatment clinical characteristics and treatment details of the patients as well as the MRI measurements and related biomathematical model parameter estimates of proliferation and migration kinetics for each patient characterizing their untreated virtual control (UVC). The median net proliferation rate, ρ, of 15/yr corresponds to a net cellular doubling time of 17 days and are consistent with reported estimates (27). The net migration rates, D (3.2 – 468.9 mm²/day, median = 29.7 mm²/day) are similar to the random motility rate estimates of glioma cells observed under a variety of experimental conditions (9).

Survival Analysis Suggests that the UVC Proliferation and Invasion Kinetics are Significant

The results of univariate Cox proportional hazard analysis are summarized in the Table 2. In univariate analysis, the only significant predictors found were the UVC estimates for tumor net proliferation and invasion kinetics: ρ and ρ/D (p < 0.04 and p < 0.02). Amongst the standard clinico-pathologic factors, RPA was the closest to reaching significance in univariate analysis (p < 0.06)

Table 2.

Univariate analysis of survival for standard clinical parameters as well as parameters used by or generated from the bio-mathematical model.

Cox Model Covariates	Log hazard ratio coefficient (SE)		p-value
Clinical Parameters
RPA	0.84	(0.45)	0.05
Concurrent Chemotherapy	−0.53	(0.43)	0.21
KPS	−0.01	(0.02)	0.79
EOR (BX/STR vs GTR)	−0.09	(0.45)	0.85
age	−0.002	(0.02)	0.91
Modeling/Imaging Parameters
rT1Gd (mm)	0.02	(0.03)	0.58
rT2 (mm)	0.02	(0.03)	0.58
T1Gd Velocity (mm/yr)	0.002	(0.00)	0.47
T2 Velocity (mm/yr)	0.004	(0.00)	0.21
D (mm2/yr)	0.003	(0.00)	0.35
ρ (1/yr)	0.01	(0.00)	0.03
ρ/D (1/mm2)	0.01	(0.00)	0.01

Although there are a variety of multivariate models to consider, given the limited size of our population, we retained only the terms that were closest to significance in the univariate analysis. To control for these known prognostic factors, multivariate survival analysis (Table 3) was performed controlling specifically for RPA classification and the model-defined UVC measures. Consistent with the finding of Stupp et al (28) showing improved survival (17 patients who received TMZ concurrent with primary radiotherapy), a chemotherapy flag was added to the multivariate analysis (28). Even when controlling for these known clinical factors in multivariate analysis, the bio-mathematical model parameters for tumor kinetics, ρ and ρ/D, remained significant (p<0.02) while neither RPA nor the concurrent chemotherapy flag attained further significance. The log hazard ratio coefficients resulting from the multivariate Cox model indicate that a 19 /year increase in ρ (equivalent to a decrease of 13 days in the glioma cell doubling time) or a 1.3 /mm² increase in ρ/D would be associated with a 50% decrease in survival. Comparison between the ρ and ρ/D multivariate models (in terms of the logarithm of the partial likelihood) shows no clear advantage for either measure of glioma growth kinetics. Further analysis is required to reveal the relative importance of these two means of quantifying glioma aggressiveness.

Table 3.

Multivariate analysis of survival with RPA, a flag for receiving TMZ chemotherapy concurrent with primary radiotherapy, and the bio-mathematical model parameters for net rates of invasion (D) and proliferation (ρ). The log partial likelihood is used to assess the significance of the entire model while the log hazard ratio coefficients are used to assess the relative significance of each covariate.

Cox Model Covariates		Log hazard ratio coefficient (SE)	p-value
RPA		0.89 (0.47)	0.06
Concurrent Chemotherapy		−0.19 (0.47)	0.68
D		0 (0.00)	0.2
log-partial likelihood =		5.1
RPA		0.88 (0.45)	0.05
Concurrent Chemotherapy		−0.32 (0.45)	0.48
ρ		0.01(0.00)	0.02
log-partial likelihood =		7.94
RPA		0.87 (0.46)	0.06
Concurrent Chemotherapy		−0.22 (0.46)	0.63
ρ/D		0.01(0.00)	0.02
log-partial likelihood =		7.63

Untreated Virtual Controls in Predicting Patient-specific Survival

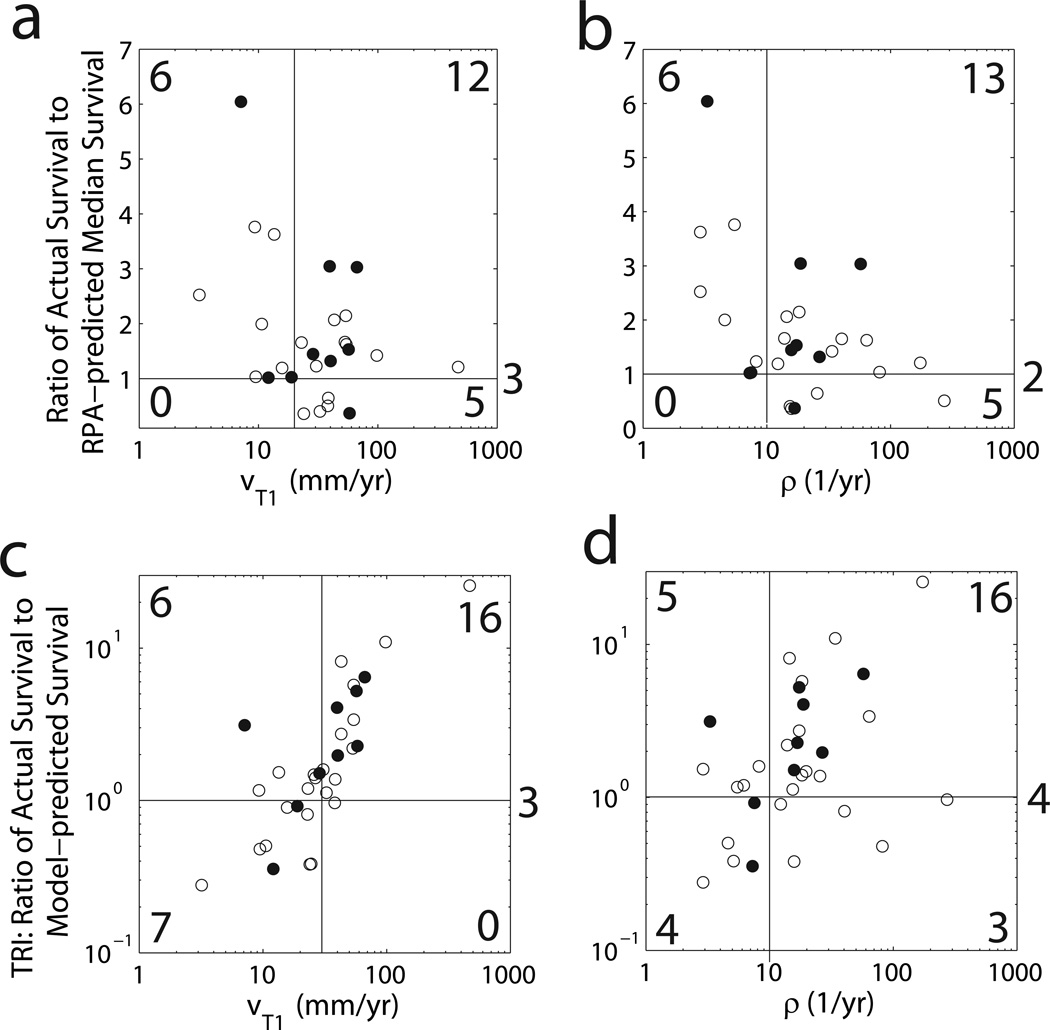
Next, we asked the question: does the baseline untreated growth and invasion kinetics of each patient’s UVC differentiate patients that will survive longer or shorter than that would be expected by their RPA classification (Figure 2)? We used the RPA-associated median survival times to divide each group into 2 sub-groups, short and long survivors relative to their RPA-associated median survival. A comparison of the ratio of the patient’s actual survival time to the median survival associated with each patient’s RPA classification compared with each patient’s UVC’s velocity (Figure 2a) or proliferation rate ρ (Figure 2b) reveals a striking pattern, suggesting that only tumors with low velocity of radial expansion on T1Gd (v<20 mm/yr in Figure 2a) or low net proliferation rate (ρ<10/yr in Figure 2b) survive longer than the median RPA prognosis. Further, only patients with high velocity (v>20 mm/yr in Figure 2a) or high net proliferation rate (ρ>10/yr in Figure 2b) survived less than the median RPA prognosis.

Figure 2.

a) The ratio of the actual survival to the RPA-predicted median survival vs. the velocity of radial growth seen on T1Gd MRI and b) vs the net proliferation rate ρ. c) The Therapeutic Response Index (TRI), the ratio of the actual survival to the model-predicted untreated survival, vs the velocity of radial growth seen on T1Gd MRI and d) vs the net proliferation rate ρ.

Therapeutic Response Index is Elevated in Highly Proliferative Tumors

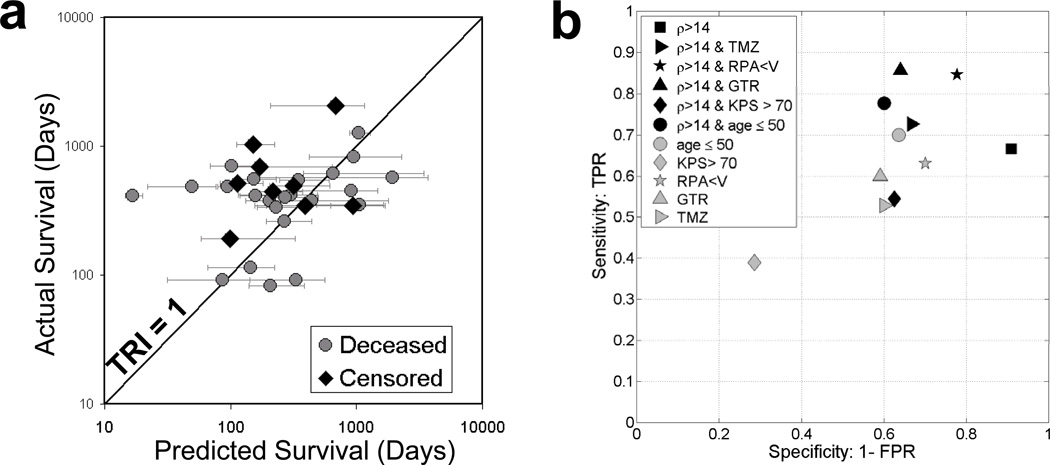
Each patient’s UVC also allows for estimation of a model-predicted untreated survival time for the UVC. This allows creation of a “Therapeutic Response Index” (TRI) defined as the ratio of the patient’s actual survival to the survival of their UVC defined as the time required to attain an appropriate fatal tumor burden (Table 1). Using our TRI, we begin our analysis of individual patients. A quick glance at Figure 3a suggests a random distribution of the actual (treated) survival vs predicted (untreated) survival of the UVCs with 8 patients practically on the line of equality of predicted and actual (TRI=1.0), 6 below the line and 18 above the line. By contrast, Figures 2c and d show that those tumors that are most likely to have a TRI significantly greater than 1 are those with a high velocity (v>30 mm/yr in Figure 2c) and an elevated net proliferation rate (ρ>10/yr in Figure 2d).

Figure 3.

a) Actual survival time vs predicted survival time of the untreated virtual control (UVC) showing the line of identity corresponding to a Therapeutic Response Index of 1.0. b) Sensitivity and specificity of standard clinical parameters and patient-specific model parameters in predicting the patients who will respond to treatments and survive longer than 150% of their baseline (untreated) model-predicted survival (TRI > 1.5).

A closer analysis of the individual results allows estimates of the specificities and sensitivities of potential predictors of good response to therapy (TRI > 1.5, those surviving 50% longer then their virtual control if untreated). These estimates are plotted in Figure 3b. That is, we hypothesize that since both radio- and chemo-therapies predominantly target proliferating cells, those tumors with high net rates of proliferation (high ρ) will have the largest TRI (largest deviation from their untreated virtual control), although they may not survive the longest overall since high ρ tumors are aggressive overall (Tables 2 and 3). A similar analysis was performed with patients with KPS with a cutoff of 70, RPA with a cutoff of V, GTR vs BX/STR and whether the patient received the Stupp protocol of XRT concurrent with TMZ chemotherapy as their primary therapy. This analysis (Figure 3b) reveals that using only a single parameter, ρ with a cutoff of 14/yr is the most sensitive and specific in predicting those patients who will have a TRI > 1.5. We explored the benefit of combining this threshold for ρ with the standard clinical parameters (KPS, RPA, EOR and Stupp protocol) to find any synergistic effect on combining these markers. Figure 3b shows that the most favorable combination is a threshold of 14/yr for ρ and RPA < V.

DISCUSSION

The real world can be divided into two unequal populations: a relatively large number of patients and a relatively small number of therapists. Most likely, from time to time, many individuals in both groups probably ask if there are any controls that have taken this treatment and gotten better and other controls who have gotten worse. Both “controls” being exactly like the patient about to be treated, not just an average individual who might not even resemble the present patient as to age, gender, etc, even more importantly with exactly the same disease, at the same location and at the same stage, etc. Wouldn’t it be nice to have an untreated virtual control (not a real live twin who could not be ethically treated or not)? Such has been the target of our research for the last several years to develop such a control for each of our patients with a glioma, especially a glioblastoma. To develop a virtual control that has all the necessary and sufficient characteristics of the glioma that could be treated or not to compare with the real patient at hand. We believe we have such a model and have given it a trial in the present manuscript: 32 real glioblastomas each matched exactly with those characteristics that should repeat the real course from its origin through diagnosis and treatment to death. In summary, all we need are two sets of MRIs (pre-treatment) from which to measure the velocity of radial expansion and to calculate the net rates of dispersal and proliferation of the UVC.

Because the concept of a virtual control (our UVC) is new, perhaps even unique to our investigative group, we began the presentation of our results with classical statistics with which the reader might be more familiar in order to show that our criteria have some comparability in the standard scheme of survival analysis as well as having some value in searching for other interesting details. These details concerning the evaluation of the individual patients cannot be approached by ordinary statistical approaches but can be by our novel bio-mathematical model.

Stratification of GBM patients according to probable prognosis has relied predominantly on clinico-pathologic factors including age, neurological status, KPS, EOR (29–32), and RPA (23). The relatively few studies that have sought to estimate the proliferative aggressiveness of GBMs in vivo have focused on tissue-based histologic analysis, such as MIB-1 labeling index (33, 34), or novel imaging agents, such as 18F-fluorothymidine PET (35–37). Histologic estimates for proliferation rate with the Ki-67 (MIB-1) labeling index, bromodeoxyuridine (BrdU) labeling index, and flow cytometry have predominantly suggested differences in these measures across grades of gliomas but not necessarily amongst WHO grade IV GBMs (33, 34, 36). Imaging cellular proliferation using FLT-PET (36) has been found to result in prognostically significant estimates of proliferation across grades of gliomas. In addition to their limited application to GBMs, each of these measures is difficult to quantify in individual cases as they are highly spatially variable and only representative of the positive component (mitosis) of the proliferation rate (ρ) without counting the negative component resulting from apoptosis or other cell death mechanisms. Further, none of these measures directly considers the role of invasiveness in the overall growth pattern.

Based on injections of intravenous iododeoxyuridine (IudR) and bromeodeoxyuridine (BudR) into patients prior to tumor resection, Hoshino et al. (27) reported a potential doubling time of gliomas ranging from 2 days to 1 month. Our patient-specific estimates of the net proliferation rate ρ corresponding to doubling times ranging from 1 to 87 days with a median of 17 days are thus consistent with these ranges. Furthermore, we have shown a similar agreement between our patient-specific estimates of D and that estimated from in vitro data (9).

We used proportional hazard analysis of newly diagnosed GBM patients considering the prognostic impact of tumor measures such as MRI-detectable tumor radius, tumor radial expansion velocity, and the model-defined net rates of dispersal and proliferation (10, 18–21). We found that, in our patient population, model parameters for these rates of net dispersal and proliferation of glioma cells were strong predictors of survival with only RTOG ‘s RPA classification (amongst the standard clinic-pathologic parameters considered) nearing significance (a marginal p-value (< 0.06) in univariate analysis. Multivariate analysis reveals that the significance of the bio-mathematical model biological aggressiveness parameters remains even when controlling for age, RPA classification as well as the existence of concurrent chemotherapy during primary radiotherapy. Further study on a larger patient population is required to enforce this significance and any role these measures may play in the routine clinical management of GBM patients.

For this patient population, the net invasiveness (D) only reaches prognostic significance when considered in combination with (ρ). The ratio ρ/D gives a measure of not only the steepness of the gradient of the invading cells peripheral to the T1-Gd edge, but also the net proliferation rate normalized to the net diffuse invasion, which and has been shown to be associated with increased hypoxic burden in GBMs (38). Thus high ρ/D tumors would be expected to show not only rather distinct borders on histology but also more necrosis associated with hypoxia due to the crowding and other microenvironmental constraints inherent to a highly proliferative tumor with a relatively low invasion. The present analysis suggests that prognostically significant measures of biological aggressiveness can be quantified from routinely-available pretreatment MR imaging of GBMs.

It is difficult to tease out subpopulations of patients with varying degrees of responsiveness in standard clinical study approaches. We have presented a method to predict the patient’s course without any treatment and to compare how the predicted result compares with the actual outcome. Our hypothesis is that ρ and D are sufficient to create such a UVC, but as we gain more experience in making such comparisons, we are willing to admit that there may be other factors that will improve the comparability of the real patient with the virtual control. At the current state, we have a tool that we believe represents an advance over the current techniques.

Following the vein of our early work (1, 2, 15, 39, 40), a number of model extensions and novel approaches to modeling gliomas have been explored by us (41) and others (42–45). Most others have focused on modeling the experimental setting in which, for instance, tumor spheroid data are analyzed (43, 46) but some have considered realistic patient geometries (42, 44, 47). Most of these are impractical for direct application to individual patients because of the need to estimate numerous patient-specific parameter values from scant data (42, 44) and none have applied their techniques to any significantly-sized patient data sets to yield patient-specific predictions that can be tested, validated and used to improve the care of glioma patients.

Other than our recent report on a small subset of 8 of these patients (20), to our knowledge, this is the first time in which routine clinical MRIs pre-treatment have been translated to prognostically significant net rates of GBM proliferation and invasion. Such a novel tool for quantifying glioma growth kinetics has numerous potential applications focusing on the creation of an untreated virtual control for each glioma against which treatment effects in each patient can be measured (6, 48, 49) and in which novel treatment approaches can be optimized.

We have developed a novel tool to potentially identify each individual patient who did or did not respond to treatment (through the TRI). Since all patients received XRT, what radiotherapist would like to learn is that his/her therapy (even with all the others combined) did or did not work in particular patients who can now be specifically identified? And that the addition of chemotherapy did or did not matter very much? And that high ρ was associated with longer survival and low ρ with only average survival? If the treatment(s) cannot provide a longer survival then the untreated virtual control, then that treatment can be discarded or retained to better suit the dynamics of the tumor growth. These general finding are consistent with our more detailed analysis of an extended model including a term to quantify the effect of RT and patient-specific radiation dose plans (48, 49).

This study highlights the novel role for a bio-mathematical model that takes into account both net tumor cell proliferation as well as net tumor cell invasion to allow for translation of information provided by routine serial (pre-treatment) MR imaging to overall tumor growth kinetics or phenotype in vivo. Thus, dynamic insight from routinely available pretreatment imaging may be useful both in predicting and assessing individual patients. Further, these results suggest that these measures of kinetics are important for the accurate prediction of disease course independent of the routine clinical parameters currently relied upon.