Robust Closed-Loop Minimal Sampling Method for HIV Therapy Switching Strategies

Abstract

The emergence of drug-resistant strains of HIV during antiretroviral therapy is a major cause of treatment failure and disease progression. Development of a resistant strain necessitates switching to a new antiretroviral regimen composed of novel drugs. Recent work has shown that current methods of switching antiviral therapies carry significant unnecessary risk of subsequent failures, and optimal switching schedules to minimize this risk have been proposed. These switching schedules require frequent sampling of viral load during an induced phase of transient viral load reduction, with the goal of switching to the new antiviral regimen at an induced viral load minimum. The proposed frequent sampling carries an unacceptable level of cost both in terms of measurement expense and inconvenience to the patient. In this paper we propose a closed-loop sampling algorithm to reduce the number of samples required to achieve the desired reduction in risk. We demonstrate through Monte-Carlo analysis that the proposed method is able to robustly achieve an average 50% reduction in the number of required samples while maintaining a reduction in the risk of subsequent failure to under 3%, despite experimentally verified levels of model and measurement uncertainty.

I. Introduction

Human Immunodeficiency Virus (HIV) is a retrovirus that infectsCD4+ T cells and macrophages producing chronic immunodeficiency, and, if untreated, death. Due to the very high likelihood of resistance being present to any one-drug antiviral treatment, multi-drug therapy is the modern strategy used to control HIV infection. This treatment, called combined antiviral therapy (cART) employs a cocktail of three or more drugs designed to interfere with multiple different steps in the HIV life cycle [1], [2], [3]. This approach has been successful in the sense that it has transformed HIV infection from a death sentence to a chronic and manageable disease [2].

Using a multiple drug regimen increases the mutational barrier to escape while suppressing the overall virus replication rate. Multiple mutations are necessary to confer resistance to the drugs, making it extremely unlikely for resistant viruses to be generated by random chance. The choice of these drugs is complicated by the possibility of cross-resistance between drugs in the current regimen and previously used drugs, leading to the possibility of lower mutational barriers than anticipated [1], [4].

Despite the success of this regimen at suppressing the virus in the short-term, many patients suffer viral load rebound, due to the emergence of a viral mutant resistant to all three components of their cART regimen. When this resistant mutant emerges, it becomes necessary to switch to a new three-drug regimen, whose components exhibit no cross-resistance with the failed three-drug regimen [4].

It has been shown in [5], [6] that a resistant virus is more likely to preexist a new therapy rather than emerge during successful treatment, resulting in treatment failure soon after switching antiviral regiments, and that the risk of this occurring is directly proportional to viral load. Thus, high viral loads increase the risk of early failure by increasing the probability that viruses carrying resistance mutations are randomly generated during replication. An intervention that reduces the viral load prior to introducing a new treatment will reduce the risk of developing resistance to the new treatment, preserving future treatment options. The same models predict that switched schedules of antiviral therapies may also reduce the risk of virological failure, an idea explored in [7], [8].

Our previous work introduced novel methods that employ either timed treatment interruptions or permuted antiviral regimens in order to induce a transient reduction in the viral load, using only previously failed antiretrovirals. By switching to the new therapy at the minimum of this transient drop, the failure risk due to preexisting resistance can theoretically be reduced by an order of magnitude [9], [10], [11], [12], [13].

These methods require the detection of the transient viral load minimum. Frequent sampling of the viral load, at least twice-weekly, is sufficient to find the viral load minimum within an acceptable margin. However, sampling the viral load is expensive and invasive, motivating the development of a method that finds the minimum while using the fewest possible number of viral load measurements.

In this paper we propose a closed-loop sampling algorithm using recursive simulated annealing parameter estimation for a reduced order viral load model in order to decrease the number of required samples with no degradation in performance compared to fixed sampling on a 3-day interval. This work has appeared in preliminary form using a normally distributed noise model with a standard deviation of 5% of the nominal measurement tested against a single nominal patient model in [14], [15], and with a novel clinically validated model of viral-load measurement uncertainty in [16]. In this paper, we introduce an updated form of the algorithm and use a recently developed library of patient models identified from experimental data to test the algorithms robustness to both measurement noise and model uncertainty using a Monte-Carlo approach.

The paper is organized as follows: We first introduce the resistance emergence risk probability model. Then we briefly summarize the optimal switching strategy for minimizing the risk of subsequent failure due to resistant virus fully described in [9]. Third, we describe the log-normal model for the viral load measurement uncertainty. Fourth, we introduce the closed loop algorithm for efficient sampling, finding the transient viral load minimum using a reduced number of viral load samples. Finally we demonstrate the algorithm’s robustness using a Monte-Carlo approach.

II. Resistance Emergence Risk Model

The risk of drug resistance emerging to a new regimen is the probability of mutation between the current dominant virus strain and the nearest genetic variant conferring resistance to the new regimen. As shown in previous studies [9], if a constant mutation rate is assumed, a Poisson distribution can be used to model the probability of resistant virus emerging. The probability of preexisting resistant viruses depends upon two variables: the total number of active virions for each type of virus present in an infected host, v₁, v₂, …v_n, and the point genetic distances g₁, g₂, …g_n where g_i is the genetic distance between virus, v_i, and a potential emerging resistant virus, v_e. The total active viral load can be calculated as the measurement of virions per ml multiplied by the volume distribution of total body extracellular fluid which is 25–30% of body mass. Assuming a constant point mutation rate of μ, the probability of v_e existing at time t_s is given by Equation (1):

$$\begin{array}{l}P(v_e(t_s)\ne 0\mid v_i(t_s))=1-e^{-{\mathrm{\Lambda }}_r}\\ {\mathrm{\Lambda }}_r={\sum }_{i=1}^n{v}_i(t_s){\mu }^{g_i}\end{array}$$ (1)

where v_i(t_s) is the measured viral load of viral strain v_i at the switching time t_s when the naive regimen is introduced. A resistant viral strain is almost certain to preexist when the genetic distance is 1, and extremely unlikely to preexist if the genetic distance is 3 or more. For a genetic distance of 2, the probability of preexistence depends on the virus load. Note that this model assumes low fitness of intermediate forms of the virus; a more general model is described in [17].

III. Viral strain competition model

The intrahost dynamics of multiple strains of HIV can be modeled by Equation (2) as in [9]:

$$\begin{array}{l}\stackrel{.}{\mathbf{x}}=\lambda -d\mathbf{x}-\sum _{0\le j\le n}{\beta }_j{\mathbf{xv}}_j(\prod _{0\le i\le n}(1-{\eta }_{j,i}{u}_i))\\ {\stackrel{.}{\mathbf{y}}}_k={\beta }_k(1-f_k)(\prod _{0\le i\le n}(1-{\eta }_{k,i}{u}_i)){\mathbf{xv}}_{\mathbf{k}}+{\alpha }_k{\mathbf{l}}_{\mathbf{k}}-a_k{\mathbf{y}}_{\mathbf{k}}\\ {\stackrel{.}{\mathbf{l}}}_k={\beta }_k{f}_k(\prod _{0\le i\le n}(1-{\eta }_{k,i}{u}_i)){\mathbf{xv}}_{\mathbf{k}}+g_k{\mathbf{l}}_{\mathbf{k}}-{\alpha }_k{\mathbf{l}}_{\mathbf{k}}\\ {\stackrel{.}{\mathbf{v}}}_k={\gamma }_k{\mathbf{y}}_{\mathbf{k}}-{\omega }_k{\mathbf{v}}_{\mathbf{k}}\end{array}$$ (2)

The states of this model are x, the concentration of healthy CD4+ T cells that are susceptible to infection; y_k, the concentration of CD4+ T cells infected by the virus strain v_k; l_k, the concentration of quiescent CD4+ T cells infected by the virus v_k; and v_k, the concentration of the k^th genetic variant of the virus present in the patient. A particular drug regimen u_i suppresses infection for a strain v_j with a maximum efficacy η_j,iu_i. Healthy CD4+ T cells decay exponentially at a rate dx and are regenerated at a rate λ. Virus of type k infects the cells in the absence of treatment at a rate β_kxv_k. A fraction f_k of these infected cells become quiescent, with the remainder actively producing virus. Actively infected cells of type k lyse at an exponential rate a_ky_k, and can be regenerated by quiescent infected cells becoming active at a rate α_kl_k. Quiescent infected cells can either exponentially decay through cell death or expand through cell division, for a net growth or decay rate of g_kl_k. Actively infected cells produce free virus at a rate γ_ky_k, which decays exponentially at a relatively fast rate ω_kv_k. A complete description of the model parameters can be found in [9], [11].

During the initial evolution of a resistant strain, intermediate forms of the virus carrying a subset of the necessary mutations for resistance can significantly alter the dynamics of resistance emergence, resulting in dynamically distinct multi-step or stochastic tunneling emergence phenomenon, depending on the relative fitness of the intermediate strains [17], [18]. These intermediate forms can dramatically alter the expected time to emergence of a resistant strain. In our proposed methods, however, viral strains resistant to all components of the transitional regimens used to induce a transient minimum in virus load have all previously appeared in the patient. Our model assumes that the fittest form of the virus resistant to the transitional regimen preexists the introduction of the transitional regimen, and will out-compete any previously generated transitional forms of the virus. This assumption allows us to reduce Equation (2) to the special case with only two virus populations: v_w, which is the fittest virus under the initial treatment conditions, and v_r, the fittest virus under the treatment regimen introduced to induce the transient minimum. While the slow decay rates of the quiescent infected cell populations l_k will ensure the persistence of any viral strains which have been previously selected for, only these two strains will exist at any significant level. Under these conditions, the dynamics simplify to Equation (3)

$$\begin{array}{l}\stackrel{.}{\mathbf{x}}=\lambda -d\mathbf{x}-{\beta }_w(1-{\mathbf{u}}_{\mathbf{1}})(1-{\mathbf{u}}_{\mathbf{2}}){\mathbf{xv}}_{\mathbf{w}}-{\beta }_r(1-{\mathbf{u}}_{\mathbf{2}}){\mathbf{xv}}_{\mathbf{r}}\\ {\stackrel{.}{\mathbf{y}}}_w={\beta }_w(1-{\mathbf{u}}_{\mathbf{1}})(1-{\mathbf{u}}_{\mathbf{2}}){\mathbf{xv}}_{\mathbf{w}}-a_w{\mathbf{y}}_{\mathbf{w}}+{\lambda }_w\\ {\stackrel{.}{\mathbf{y}}}_r={\beta }_r(1-{\mathbf{u}}_{\mathbf{2}}){\mathbf{xy}}_{\mathbf{r}}-a_r{\mathbf{y}}_{\mathbf{r}}+{\lambda }_r\\ {\stackrel{.}{\mathbf{v}}}_w={\gamma }_w{a}_w{\mathbf{y}}_{\mathbf{w}}-u_w{\mathbf{v}}_{\mathbf{w}}\\ {\stackrel{.}{\mathbf{v}}}_r={\gamma }_r{a}_r{\mathbf{y}}_{\mathbf{r}}-u_r{\mathbf{v}}_{\mathbf{r}}\end{array}$$ (3)

where v_w, y_w are the concentrations of virus type 1 and cells infected by virus type 1 that are susceptible to both treatment regimens u₁ and u₂; v_r and y_r are the concentrations of virus type 2 and cells infected by virus type 2 resistant to u₁. x is the concentration of the uninfected CD4+ T target cell population. The latent cell populations are assumed to be essentially constant on the experimental time scale, with λ_w = α_wl_w and λ_r = α_rl_r. The other parameters are as defined in Equation (2). It should be notes that the initial numbers of v_r can be very low, causing a violation of the large-number approximation inherent to the ODE formulation. However, the measurable effect of this sampling-error phenomenon is a slight change in the estimated initial value of v_r, with no significant effect on the methods presented here. A complete description of the parameters can be found in [9].

The parameters of this model were identified from viral load data from six patients subjected to a series of treatment interruptions and reintroductions [19], using modified Markov-Chain Monte-Carlo (MCMC) methods as described in [10]. The MCMC methods, instead of a single model fit, returns the posterior distribution of the parameter vectors, which describes the entire set of probable model fits to the observed data. This posterior distribution is sampled to provide the test population for the Monte-Carlo testing strategy in this work.

IV. Methods for Inducing Transient Drops in Viremia

In this section, we briefly describe the methods used to induce a transient drop in viremia prior to switching to a new regimen. We encourage to readers to examine the full description of the methods in [9]. Depending on whether the patient has failed multiple previous antiviral regimens or only a single antiviral regimen, two different strategies exist for creating a transient drop in the total viral load; the methods presented in this paper will then be used to switch to the new antiviral therapy at the time where a viral load minimum is reached.

A. Multiple Failed Treatment Strategy

When a patient has failed more than one regimen, the number of remaining regimens is reduced and the importance of preserving the remaining regimens is increased. However, these additional failed regimens provide additional intervention options, which allow for an increased reduction in failure risk in a shorter time with lower systemic cost than in the case of only a single previously failed regimen.

The optimal strategy for inducing a transient reduction in viral load when a patient has failed multiple previous antiviral regimens consists of applying permuted drug combinations of failed regimens. We assume that for each previously failed three drug regimen u_i consisting of the three component antivirals {a_i + b_i + c_i} there exists a resistant virus v_i. If resistant virus exists to regimen u₁ and regimen u₂, then both v₁ and v₂ will initially be susceptible to the permuted regimen a₁ + b₂ + c₂. However, as only one mutation is necessary to confer resistance to this permuted regimen, it is assumed that a very small population of virus v₃ resistant to the permuted regimen already exists. This implies that introducing this permuted regimen will result in a transient reduction of the total viral load. In this case, the states of Equation (3) are defined as v_w = v₂, v_r = v₃. There is a very small probability that v₃(0) = 0, in which case the viral load will not rebound. The best strategy under these circumstances is still to switch to a new antiviral therapy once the viral load drops below the limit of detection, as there is no way to distinguish between a slow-rebounding resistant strain and the unlikely event that no resistant strain exists.

B. One Failed Treatment Strategy

The switching strategy proposed in [9], [10], [12] for the case where the patient has experienced only one virological failure involves switching from a failing regimen u₁ to a successful regimen u₂ In this case, a transient reduction in total viral load can be induced through a schedule of treatment interruptions using the failing regimen. This method is as follows:

1. Interrupt antiviral therapy.

2. Wait for the wild-type virus to re-establish dominance.

3. Re-introduce the failed regimen u₁

4. Following reintroduction there is a transient reduction in total viral load as the wild-type virus decays and the resistant virus re-establishes dominance. Switch to the new antiviral regimen u₂ at the minimum.

In this case, rebound is certain, as the virus resistant to regimen u₁ already exists. In this case, the states of Equation (3) are defined as v_w, the wild-type virus, and v_r, the virus strain resistant to regimen u₁.

C. Sampling Issues for Implementation

Both strategies result in the creation of a transient drop in viral load; for maximum benefit, the treatment must be switched at the minimum of this induced transient drop. The problem can written finding the optimal switching time t̂ as described by Equation (4):

$$\widehat{t}=arg\underset{t}{min}\{{\mathbf{v}}_w(t)+{\mathbf{v}}_r(t)\}$$ (4)

This can be implemented by sampling frequently on a fixed schedule; however, the time to minimum following reintroduction can vary from weeks to months, so the potential number of expensive and invasive measurements can be quite large. To find the minimal viral load time using the minimal number of samples, we propose a novel closed loop sampling algorithm which recursively estimates the minimum time, and uses these estimates to plan the next sample time. This sampling algorithm will be described in the next section.

V. Model of Viral Load Measurement Uncertainty

The principal aim in this work is to find the time where the viral load reaches a minimum following an intervention using the strategies proposed above. Since the parameters of Equation (3) were identified using MCMC methods, the identified posterior distribution can be sampled in order to simulate inter-patient variation of the behavior of the measured viral load v_r and v_w during the transient viral load reduction. To test the robustness of the method, we corrupt these simulated viral loads according to a realistic model of the uncertainty in the standard Polymerase Chain Reaction (PCR) HIV RNA quantification, as characterized in [20], given by Equation (5).

$${log}_{10}\mathbf{v}(\mathbf{t})={log}_{10}({\mathbf{v}}_w(\mathbf{t})+{\mathbf{v}}_r(\mathbf{t}))+r{\stackrel{\sim }{\sigma }}_v(({\mathbf{v}}_w(\mathbf{t})+{\mathbf{v}}_r(\mathbf{t}))$$ (5)

where σ_v((v_w(t) + v_r(t)) is the observed log-normal standard deviation of HIV PCR measurement, r is a zero-mean, unity standard deviation normal random number, t is the set of time for sampling and v_w(t) + v_r(t) is the simulated total viral load obtained from Equation (3) at t. The value of the standard deviation was shown to vary according to the values in Table I by Perrin et al. [20]. The value for σ_v((v_w(t)+v_r(t)) is calculated by linearly interpolating (on a log scale) between the characterized values in Table I.

TABLE I. Viral Load Standard Deviations.

Adapted from Perrin et al.

log10(vw(t) + vr (t))	σv(log10(vw(t) + vr (t))
1.7	0.25
2.0	0.20
3.0	0.11
4.0	0.07
5.0	0.08
6.0	0.14
6.7	0.17

VI. Approximate Solution for Sampling

All the methods described in Section IV achieve a transient crash in the viral load, and maximum benefit is achieved if the treatment is switched at or near the minimum of this crash, before rebound. Model uncertainty due to inter-patient parameter variation makes a priori calculation of the minimum time impossible. Frequent sampling makes it possible to find the minimum, but the samples are expensive and invasive, so this should be avoided. Therefore, an estimation method using the smallest number of samples it is necessary to find the time of minimal viral load after reintroduce the failed regimen.

Online estimation provides a useful framework for this; however, the full model of Equation (3) has too many parameters to allow for quick convergence of an online estimator. Under the conditions induced by the switching algorithms described above, a simplified approximate solution to the model described in Equation (3) for the total virus load v_w(t) + v_r(t) after the failed regimen has been reintroduced and is given by the function:

$$\widehat{\mathbf{v}}(t,\mathit{\theta })={\widehat{v}}_w(t_0)e^{-k_w(t-t_0)}+{\widehat{v}}_r(t_0)e^{k_r(t-t_0)}$$ (6)

where t₀ is the time when the failed regimen is reintroduced and θ = (v_w(t₀), k_w, k_r) is the vector of parameters to be estimated (v̂_r(t₀) is omitted because v̂ (t₀, θ) = v̂_w(t₀)+ v̂_r(t₀) and v̂(t₀, θ) is known). This is an exact solution of Equation (3) when u_w ≫ a_w, u_r ≫ a_r, λ_w ≈ 0, λ_r ≈ 0, and x is approximately constant for the duration of the experiment. The first four conditions are satisfied in general, but x approximately constant is only approximately satisfied, as changes in the target cell population can be significant when the viral load rebound is slow. However, this approximate solution performs well in Monte-Carlo testing, so its accuracy is sufficient.

This simplified model has only four parameters, so the proposed online estimation method will converge in only a few samples. Once this has converged, it is used to iteratively estimate the optimal switching time t̂ using a closed-loop method described in the next section.

VII. Closed Loop Method

Achieving a minimal number of samples for the problem defined above requires a closed-loop method, where following an initial set of m samples, approximate values of t̂ are iteratively calculated, given the current set of samples (v̂,t). Depending on the estimated value of t̂, the uncertainty in the estimate, and the likelihood of resistance emergence related to this time, the algorithm computes the next sample time. The iterative estimation procedure continues until certain stop criteria are met. The iterative update algorithm and the stop criteria are described in the following sections.

A. Simulated Annealing Based Estimation of t̂

Following some m = 4 initial measurements (v,t), a nonlinear least-squares estimation approach is used to determine the next sampling point. To overcome problems with local minima in the fit encountered while using steepest-descent based methods, a simulated annealing algorithm is used to obtain the parameter vector θ̂= (v_w(t₀), k_w, k_r) such that

$$\widehat{\mathit{\theta }}=arg\underset{\mathit{\theta }}{min}f\{\mathbf{v},\widehat{\mathbf{v}}(\mathbf{t},\mathit{\theta })\}$$ (7)

where

$$f\{\mathbf{v},\widehat{\mathbf{v}}(\mathbf{t},\mathit{\theta })\}=ln\sum _{i=1}^m\mid \mathbf{v}({\mathbf{t}}_i)-\widehat{\mathbf{v}}({\mathbf{t}}_i,\mathit{\theta })\mid$$ (8)

subject to

$$\begin{array}{lllll}\hfill 0.95\times \mathbf{v}(t_0)& \le \hfill & \hfill {\widehat{v}}_w(0)\hfill & \le \hfill & \mathbf{v}(t_0)\hfill \\ \hfill 0& \le \hfill & \hfill k_w\hfill & \le \hfill & 1\hfill \\ \hfill 0& \le \hfill & \hfill k_r\hfill & \le \hfill & 1\hfill \end{array}$$ (9)

We used the built-in MATLAB implementation simulannealbnd with default settings, enforcing upper and lower bounds on the parameters as above and a terminal function value tolerance of 10⁻²⁰. This step is repeated J = 100 times with random noise added to the sampled data v(t_i) according to Equation (5), and J estimated viral-load minimum times $t_j=\frac{1}{k_r(j)+k_w(j)}ln(\frac{k_w(j){\widehat{v}}_{w0}(j)}{k_r(j){\widehat{v}}_{r0}(j)})$ are calculated.

The set {t_j} is the posterior distribution of t̂ subject to the known measurement uncertainty. In order to determine the next sampling point, a trade off must be made between the posterior mean and the standard deviation of the set {t_j} in order to create a conservative estimate for the minimum time t̂ that balances the goal of minimizing the number of samples with the goal of minimizing the risk of overshooting the try minimum. The conservative estimate of t̂, denoted t̆, is given by Equation (10):

$$\stackrel{⌣}{t}=\stackrel{\sim }{t}-\alpha \stackrel{\sim }{\sigma }$$ (10)

where t̃,σ are the mean and standard deviation of the set {t_j} and α is a tunable weighting parameter. Therefore, depending of the value of α > 0 the estimation of t̆ allows the algorithm be more or less conservative regarding the risk of emergence of resistance. An alternative method would involve directly computing a time t̆ from {t_j} such that P(t̂ < t̆) < K, where K is some given percentage. This is equivalent to the method of Equation (10) if the distribution of {t_j} is Gaussian. We plan to explore this alternative formulation in future work.

B. Calculation of Next Sample Time t_s

In order to avoid either sampling too frequently or overshooting the minimum, a minimum interval of T_min days and a maximum interval T_max days are defined. After m initial samples spaced at T_min are achieved, parameter estimation is performed as described above. Then, when t̂ is estimated three options to obtain the time of the next sample are proposed:

1. If t̆ > t_s−1 + T_max, where t_s−1 is the current sample time, the next sample is taken at t_s = t_s−1 + T_max.

2. If t̆ < t_s−1 + T_min, the next sample is taken at t_s = t_s−1 + T_min.

3. If t_s−1 + T_min < t̆ < t_s−1 + T_max, the next sample is taken at t_s = t̆.

Depending on whether the stop criterion has been reached, the algorithm ends or takes a new sample at the calculated time t_s.

C. Stop Criterion

Using the information in the posterior distribution {t_j} two criterion are defined where, if either is satisfied, the algorithm should be terminated and the patient switched to the new antiviral regimen.

The first criterion is if the last sample achieved for v has reached the viral load limit of detection (< 50 copies/mL), the algorithm terminates.

The second criterion uses the information in the estimated viral load posterior distribution. v_j = v(t_j) is calculated for all t_j corresponding to the standard deviation interval t̃ ± σ̃. Assuming a genetic distance g = 2 between the current dominant virus strain and a strain conferring resistance to the novel antiviral therapy to be introduced, the risk of preexistence for each component of the set {v_j} is calculated according to Equation (1). If the risk corresponding to the current measurement is between the minimum and maximum risk of this set, we conclude that the current sampling time is already within one standard deviation of the achievable minimum, and continuing to sample carries more risk than reward, therefore the algorithm terminates.

VIII. Results

A. An Illustrative Example

In order to illustrate the algorithm, step by step, we randomly choose one row of the parameter set and simulate the measurements according to Equation (5) using the viral model of Equation (3). Using the methods described in section III, starting when the failing regimen is reintroduced, we initially take 4 measurements using a minimum sampling time of three days.

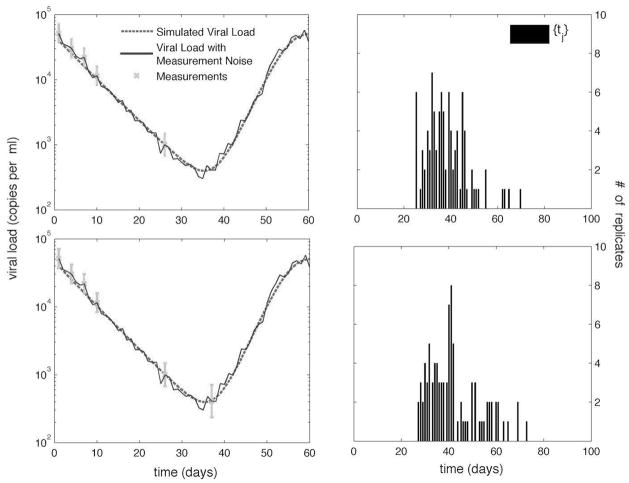
From these measurements we obtain the set {t_j} for j = 1,…, 100. The next sampling time t_s is calculated, with bounds of T_min = 3 and T_max = 21 days. The algorithm continues making samples as is shown in Fig. 1. In this example, the algorithm stops after the sixth sample because the second stop criterion is satisfied. The histograms of the posterior distributions {t_j} used to calculate sample times five and six are shown in the second column of Fig. 1.

Fig. 1. Sampling timest_s and the corresponding histogram of the set {t_j } for samples 5 and 6, respectively.

Measurements are shown with error bars corresponding to the uncertainty.

B. Robustness

In order to test the robustness of this method, the posterior distribution of parameter values for Equation (3) obtained from the MCMC estimation techniques described in [9] was randomly sampled. This posterior distribution is a set of 60,000 parameter sets representing feasible fits to patient viral load data from six different patients. The sets of parameter values reflect the natural uncertainty in the model parameters due to measurement noise and inter-patient variation.

The algorithm is tested in a Monte-Carlo fashion by randomly choosing a parameter set from the 60,000 parameter sets described above and randomly varying the initial conditions for v_w and v_r. Equation (3) is then used to generate simulated patient viral load measurements, to which log-normal noise is added according to Equation (5). The algorithm is applied to the simulated patient dataset.

The value of α for Equation (10) is calculated as follows: α_j = κc_v, where c_v is the coefficient of variation of the set {t_j} and κ = 4, so that Equation (10) becomes:

$$\stackrel{⌣}{t}=\stackrel{\sim }{t}-\kappa c_v\stackrel{\sim }{\sigma }.$$ (11)

By multiplying by the coefficient of variation, the flatness of the distribution from first few iterations of the algorithm is taken into account, and the algorithm samples at conservative intervals until enough information is available to generate a more normal posterior distribution. The alternative method discussed previously would make this correction unnecessary.

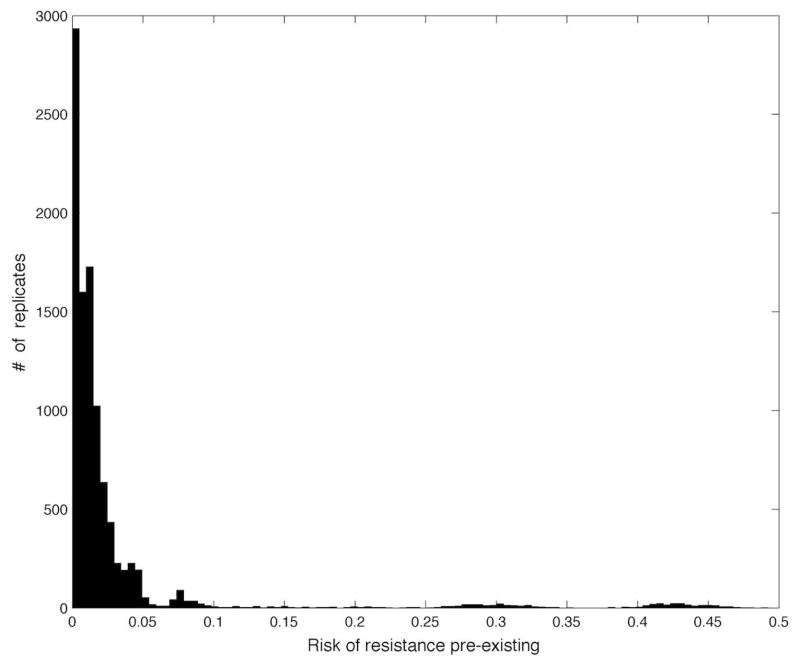
In order to evaluate the robustness of the closed-loop algorithm 10000 rows were randomly chosen from the 60000 row parameter set. The actual minimal time t̂, the achieved risk and the number of samples used were computed for each iteration. The histogram of the achieved risk corresponding to the viral load at switching is shown in Fig. 2. On average, the algorithm achieved a viral load at switching of under $1000\frac{\mathit{copies}}{mL}$ (compared to a baseline viral load of $>50,000\frac{\mathit{copies}}{mL}$), corresponding to a preexistence risk at switching of < 3% (compared to a baseline risk of > 95%), assuming a genetic distance of 2. The long-tail of this histogram represents conservative early terminations of the algorithm, where noise on the initial measurements make it appear as though the viral load is rebounding early. While this could be compensated for, this is actually a safety feature of this method, as it is impossible to distinguish between measurement noise and a true early rebound of virus due to unexpectedly high levels of drug resistant virus.

Fig. 2.

Histogram for probability of preexistence of resistant virus for the actual switching times, calculated from the corresponding viral load at switching according to Equation (1).

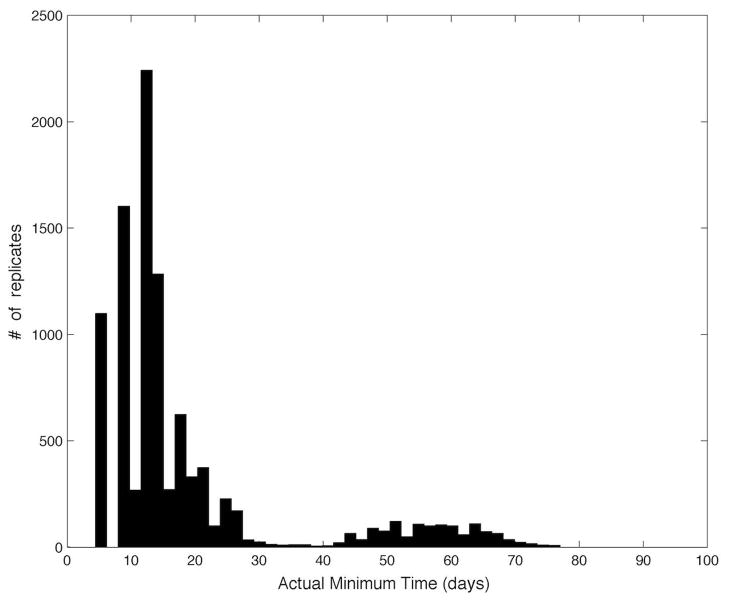
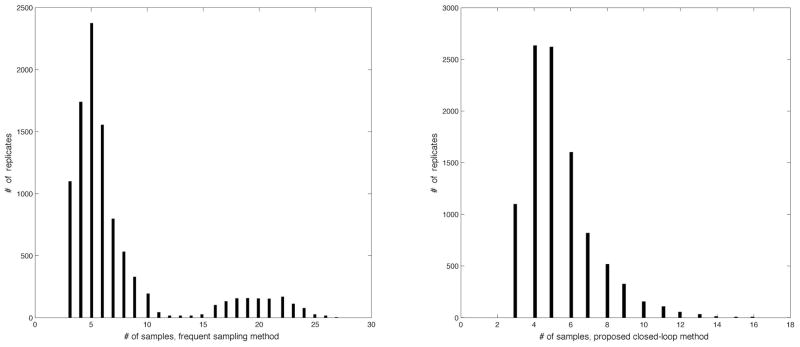
The main purpose of the proposed algorithm is to reduce the number of samples needed compared to a naive frequent-sampling approach. The histogram of true minimum times for the Monte-Carlo samples is shown in Fig. 3; these vary between 5 and 80 days. However, when measurement noise makes it appear as though the viral load is rebounding after the first few samples, both the closed-loop algorithm and the naive frequent-sampling algorithm will result in a conservative early exit. The histogram of the number of samples used for the naive frequent-sampling algorithm and the proposed closed-loop algorithm is shown in Fig. 4. In the case where a conservative early exit occurs (the total number of samples is five or less), both algorithms use approximately the same number of samples. When the first five samples do not trigger a conservative early exit, the proposed algorithm significantly reduces the total number of samples used, with an average reduction in the number of samples of 51%. In addition to the systemic cost of frequent blood draws, each quantitative HIV-1 PCR test costs approximately $250, leading to a savings of thousands of dollars per patient by using the proposed algorithm.

Fig. 3.

Histogram of the actual minimum times {t̂} for the 10000 samples of the parameter dataset.

Fig. 4.

Histogram of the number of samples required for a naive frequent sampling algorithm and the proposed closed-loop algorithm.

IX. Conclusions

In this paper we introduced a novel closed-loop sampling algorithm for a previously published HIV treatment switching problem. The algorithm is designed to allow robust switching to a novel antiviral regimen at the minimum of an induced transient crash in the viral load using a reduced number of samples. The algorithm is based on a recursive parameter estimation scheme using a approximate-solution model of viral dynamics.

The algorithm’s performance was tested in a Monte-Carlo fashion against an experimentally validated model of inter-patient parameter uncertainty and measurement uncertainty. The results of Monte-Carlo testing show that the algorithm was able to reduce the risk of resistant virus preexisting the new regimen to less than 3% on average assuming a genetic distance of 2 between the currently dominant virus strain and a strain carrying resistance to the new antiviral regimen. This may be compared to the currently used approach of switching at high viral loads, which has a corresponding average risk of over 95%, assuming a genetic distance of 2. The algorithm achieved this reduction in risk while using on average less than 50% of the HIV-1 quantitative PCR measurements needed by a naive frequent-sampling method to achieve the same average risk reduction.

This reduction in the number of samples needed represents significant reduction in monetary and systemic cost to the patient compared to the naive sampling algorithm. The reduced number of required HIV-1 PCR measurements represents thousands of dollars in reduced cost. The benefits of the method in terms of reduced patient morbidity and mortality related to subsequent virological failures are also very significant. The adaptive sampling algorithm proposed in this paper enables the use of our previously described risk-reduction strategies by reducing to an acceptable level the viral-load sampling burden.

Biographies

E. Fabian Cardozo E. Fabian Cardozo is a Ph.D. student in Electrical and Computer Engineering at the University of Delaware. He received his B.S. in Systems Engineering from the Universidad Industrial de Santander in Bucamaranga, Columbia in 2008 and his M.S. in Systems Engineering and Computer Science from the Universidad Industrial de Santander in 2012.

Ryan Zurakowski Ryan Zurakowski is an Assistant Professor in Electrical and Computer Engineering and a Faculty Fellow of the Delaware Biotechnology at the University of Delaware. He received his Ph.D. in Electrical and Computer Engineering from the University of California, Santa Barbara in 2004. Prior to joining the University of Delaware in 2006, he studied as a postdoctoral scholar with the department of Ecology and Evolutionary Biology at the University of California, Irvine.