Influence of graded facetectomy and laminectomy on spinal biomechanics

Abstract

Facetectomy and laminectomy are techniques for decompressing lumbosacral spinal stenosis. Resections of posterior bony or ligamentous parts normally lead to a decrease in stability. The degree of instability depends on the extent of resection, the loading situation and the condition of the intervertebral discs. The correlation between these parameters is not well understood. In order to investigate how these parameters relate to one another, a three-dimensional, non-linear finite element model of the lumbosacral spine was created. Intersegmental rotations, intradiscal pressures, stresses, strains and forces in the facet joints were calculated while simulating an intact spine as well as different extents of resection (left and bilateral hemifacetectomy, hemilaminectomy and bilateral laminectomy, two-level laminectomy), disc conditions (intact and degenerated) and loading situations (pure moment loads, standing and forward bending). The results of the modelling showed that a unilateral hemifacetectomy increases intersegmental rotation for the loading situation of axial rotation. Expanding the resection to bilateral hemifacetectomy increases intersegmental rotation even more, while further resection up to a bilateral laminectomy has only a minor additional effect. Hemilaminectomy and laminectomy only differ in their effect for ventriflexion and muscle-supported forward bending. Two-level laminectomy increases the intersegmental rotation only for standing. Degenerated discs result in smaller intersegmental rotations and higher disc stresses at the respective levels. Decompression procedures affect the examined biomechanical parameters less markedly in degenerated than in intact discs. Resection of posterior bony or ligamentous elements has a stronger influence on the amount than on the distribution of stresses and deformations in a disc. It has only a minor effect on the biomechanical behaviour of the adjacent region. Spinal stability is decreased after a laminectomy for forward bending, and after a two-level laminectomy for standing. For axial rotation, spinal stability is decreased even after a hemifacetectomy. Patients should therefore avoid excessive axial rotation after such a treatment.

Introduction

Severe spinal stenosis or ruptured/herniated discs are often treated by dorsal decompression. Although non-operative treatment and disc microsurgery are becoming increasingly popular, conventional open techniques are often regarded as the gold standard of treatment [3, 4]. The degree of stenosis determines the indication for mono- or bilateral hemifacetectomy, mono- or bilateral laminectomy or even laminectomy on two levels. A meta-analysis of the literature from 1975 to 1995 revealed that decompressive laminectomy is only optimal for degenerative spinal stenosis if symptoms have a duration of less than 8 years [13]. Another meta-analysis also showed that decompressive laminectomy can benefit many patients with lumbar spinal stenosis by reducing pain and increasing function [22]. Resecting a facet capsule and posterior bony parts of a vertebra reduces spinal stability and may thus increase deformation and loads at that level. Knowing the degree of instability caused by these procedures can help the surgeon decide whether fusion is necessary. Determining the mechanical behaviour of the lumbosacral spine would reveal which patients' activities and extents of posterior resection are most responsible for decreasing stability and increasing local loads.

Several groups [1, 10, 12, 16] have quantified the degree of instability caused by resecting dorsal parts. Quint et al. [16] loaded six human lumbar spine specimens with pure moments in the three main anatomic planes, recorded load-deformation hysteresis curves and measured the neutral zone and range of motion in relation to the extent of resection. Besides the intact specimens, four extents of resection were examined: left and bilateral hemifacetectomy, left hemilaminectomy and laminectomy at L4/L5. They found an increased range of motion for all loading situations and concluded that a laminectomy leads to marked instability. Abumi et al. [1] investigated spinal stability by applying pure moments together with an axial preload to intact functional spinal units and to those with division of posterior ligaments and medial or total facetectomies. They found an increased range of motion for the loading situation of flexion after unilateral medial facetectomy and for that of axial rotation after unilateral total facetectomy. The range of motion was not affected by extension or lateral bending.

It is difficult to perform reproducible experimental investigations or to apply physiological loads when using cadaver specimens. The finite element method allows the calculation of stresses, strains and movements in the different structures involved. The advantage of the analytical over the experimental approach is that no new specimens are needed to modify particular parameters such as the degree of resection, the loads or the boundary conditions. The process of comparing numerical to experimental data and subsequently adjusting the computer model makes the finite element method a powerful tool for analysing such biomechanical problems, as other studies have shown [6, 7, 11, 19, 25, 26].

The aim of the present finite element study was to determine the way in which different extents of posterior resection influence various mechanical properties of the lumbosacral spine.

Materials and methods

Finite element model

The study was performed after creating a three-dimensional, non-linear computational spine model from L2 to the upper endplate of the S1 vertebra (Fig. 1). The finite element mesh of the vertebrae is based on the L4 model created by Smit [21]. The geometry of the vertebrae was adapted using data from computed tomographic (CT) scans and the literature. The intact global model consists of more than 8,000 elements and has about 24,000 degrees of freedom. Results were calculated in the L4/5 disc after creating a sub-model with twice as many elements in each direction, i.e. nearly 4,000 elements and more than 6,000 degrees of freedom. In both the global model and the sub-model, the annuli fibrosi were simulated by volume elements with superimposed spring elements representing the fibres, and the nuclei were simulated by incompressible fluid-filled cavities. A degenerated disc was simulated by removing nuclear incompressibility, by using an elastic modulus of the annulus twice as high as that for intact discs and with fibres carrying loads only after a certain initial strain. The geometry of the degenerated disc was not modified. The modifications only imperfectly describe a grade 3 disc [2], but should be suitable for indicating trends. Besides intact discs, degenerated ones were simulated at the levels where dorsal parts were resected. The facet joints have a gap of 0.5 mm in an unloaded state and could only transmit compressive forces. Their spatial orientation was modelled according to measurements reported by Panjabi et al. [14]. The capsule of the facet joints and the six ligaments of the lumbar spine were included in the computer model. The mostly non-linear material properties of all tissues were chosen from the literature [8, 9, 20]. More details about the finite element model are given elsewhere [25, 26].

Fig. 1.

Finite element mesh of the ligamentous spinal segment from L2 to the upper endplate of S1 with dorsal muscle fibres

The study was performed using the finite element programme ABAQUS, and the pre- and postprocessor MSC/PATRAN. The highly non-linear computer model allows large deformations and is able to simulate contact behaviour at the facet joints. The intact model was validated on the basis of experimental data from in vitro measurements [17, 18] and a high degree of conformity was found.

Extent of resection

The different treatment situations studied were simulated by removing corresponding posterior parts of the finite element model.

1. Left hemifacetectomy: removal of the left superior articular process of L5 with the corresponding facet capsular ligament.

2. Bilateral hemifacetectomy: removal of the left and right superior articular processes of L5 with the corresponding facet capsular ligaments.

3. Left hemilaminectomy: same as (2) plus removal of the left inferior articular process and the left lamina of L4, resulting in a gap between the spinous process and the superior articular process, and removal of the left part of the flaval ligament between L3 and L5.

4. Laminectomy: same as (3) plus removal of the spinous process of L4, the right lamina and the right inferior articular process (Fig. 2). The supraspinous, flaval and intraspinous ligaments were removed between L3 and L5.

5. Two-level laminectomy: same as (4) plus removal of the corresponding bony and ligamentous elements at L5/S1.

Fig. 2.

Finite element mesh of the lumbosacral spine with laminectomy between L4 and L5

Boundary and loading conditions

The upper endplate of the S1 vertebral body was fixed to prevent movement. Eight different loading situations were studied. For validation of the finite element models, pure moments of 7.5 Nm were applied in the main anatomic planes to cause ventriflexion (referred to as flexion), extension, left and right lateral bending, and left and right axial rotation. In addition, the physiological loading cases standing and forward bending of the upper body were studied by applying upper body weight (400 N) and muscle forces. Upright standing was simulated by loading 70 local muscle fibres [5, 6, 25] with 5 N each (Fig. 1). The global dorsal muscle force representing the erector spinae was 300 N [25]. For 30° forward bending in an upright body position, the local muscle fibres were loaded with 10 N each, while a global dorsal muscle force of 900 N was chosen to counterbalance the moment caused by the upper body weight. Details regarding muscle forces for standing and upper-body inclination are given elsewhere [25].

Only the L4/5 disc was assumed to be degenerated for the intact model and the models with resection between the L4 and L5 vertebral body. For the two-level laminectomy, the L5/S1 disc was also simulated in a degenerated state.

Evaluation

The validity of the intact computer model has been previously demonstrated [17, 18]. To validate the modified models for the different degrees of resection, the intersegmental angle between the L4 and L5 vertebral body was compared to that measured in vitro by Quint et al. [16].

Calculated values

Finite element simulations have the advantage of rendering all mechanical field variables accessible and allowing the acquisition of any given value. Here the following were considered to be significant: the values for the intersegmental angle between the L4 and L5 vertebral body, the von Mises equivalent stresses and the strains in the annuli, the pressures in the nuclei, and the contact forces in the facet joints.

Results

Validation of the model

In 23 of 30 cases (76.7%), load-related intersegmental rotation angles in the loading plane calculated at L4/L5 lay within the ranges measured by Quint et al. [16] for the corresponding situation (Fig. 3). The highest values were found for flexion and rotation. Neither facetectomy nor laminectomy had a noticeable effect on intersegmental rotation for extension and lateral bending. Intersegmental rotation increased markedly for flexion after bilateral laminectomy, but it increased for axial rotation even after a hemifacetectomy. In the latter case, further resection of posterior elements had little additional influence on the intersegmental rotation angle.

Fig. 3.

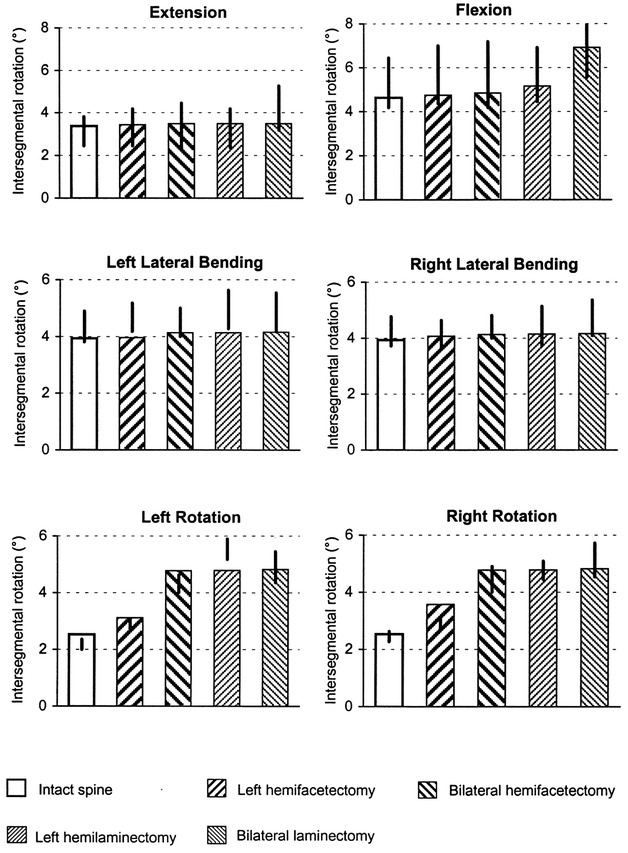
Intersegmental rotation in the loading plane between L4 and L5 for pure moment loads and different degrees of decompression. The in vitro results reported by Quint et al. [16] are marked by vertical lines

Simulation of physiological loads

Intersegmental rotation in the sagittal plane

For standing, the calculated intersegmental rotation angle in the L4/5 functional unit changed by 0.7° compared to the unloaded, neutral position for the intact spine (Fig. 4). The maximum rotation resulting from resections performed only between L4 and L5 was predicted to be 1° for a bilateral hemifacetectomy. However, it was twice as high for a two-level laminectomy (2°). When calculating for 30° flexion and allowing for muscle forces, the intersegmental angle between L4 and L5 changed by 7° for the intact functional unit. It increased to 10.3°/10.4° for a bilateral laminectomy at one or two levels.

Fig. 4.

Intersegmental rotation in the sagittal plane between L4 and L5 for the loading situations of standing (top) and forward bending (bottom) and different degrees of decompression. Left bars represent values for an intact disc, right bars those for a degenerated disc. Intersegmental rotation signifies extension if negative and flexion if positive

Assuming a degenerated disc considerably reduces intersegmental rotation and its changes, especially for forward bending (Fig. 4).

Stresses and strains in the annulus fibrosus

Maximum stresses in the annulus of the L4/5 intervertebral disc are higher after bilateral and two-level laminectomy than in the intact spine. This was the case for standing as well as for forward bending (Fig. 5). Stresses are even higher in a degenerated disc. In the L3/4 disc they are barely affected by the extent of resection or the condition of the L4/5 disc during standing. They are a slightly lower than in intact bone for a two-level laminectomy and forward bending.

Fig. 5.

Maximum von Mises equivalent stresses in the L3/4 (left two bars of each group) and L4/5 (right two bars) intervertebral discs for the loading situations of standing (top) and forward bending (bottom) and for different degrees of decompression

Strains in the L3/4 disc remained nearly unchanged regardless of the extent of resection and the condition of the L4/5 disc. Strains in the L4/5 disc increased with the extent of resection. The maximum strain during standing was 70% higher after a two-level laminectomy than in the intact spine. It was 58% higher for forward bending. Degenerated discs have to withstand lower strains than intact ones.

Differences in shapes and stresses between an intact and a degenerated disc are shown in Fig. 6 for standing and in Fig. 7 for forward bending. The concavity of the annulus at the inner region is less pronounced for degenerated discs than for intact ones. This is due to the absence of the nucleus incompressibility in the degenerated disc. Degenerated discs have higher maximum stresses and larger highly loaded areas. The highest peak stresses are found in the most posterior part of the annulus during standing and on the ventral side during forward bending. A laminectomy has a stronger influence on the amount of stresses and deformations in a disc than on their distribution.

Fig. 6.

Stress distribution in the left half of the L4/5 annulus and its shape for the loading situation of standing, top lateral view. A Intact spine and intact disc; B intact spine and degenerated disc; C laminectomy and intact disc; D laminectomy and degenerated disc. The greatest differences in shape between intact and degenerated discs are at the border to the nucleus

Fig. 7.

Stress distribution in the left half of the L4/5 annulus and its shape for the loading situation of forward bending, bottom lateral view. A Intact spine and intact disc; B intact spine and degenerated disc; C laminectomy and intact disc; D laminectomy and degenerated disc. The greatest differences in shape between intact and degenerated discs are seen at the border to the nucleus

Forces in the facet joints and intradiscal pressure

The forces between the L3 and L4 facet joints are barely affected by the extent of resection. They are zero for flexion and about 50 N each for standing.

Intradiscal pressure increase in the intact L3/4 nucleus was about 0.75 MPa for standing and 1.5 MPa for forward bending. It is independent of the extent of resection and the condition of the L4/5 disc for standing, but decreases slightly for forward bending when a bilateral two-level laminectomy is performed. A posterior resection has hardly any effect on pressure in the intact L4/5 disc for standing or forward bending.

Discussion

Different extents of resection of posterior vertebral and ligamentous parts were studied for their influence on the mechanical behaviour of the lumbosacral spine using the finite element method. Physiological loading situations were used for the first time to study the influence of different decompression procedures on the biomechanical behaviour of the lumbar spine.

Several simplifications and assumptions were necessary even for this fine-meshed model. There is insufficient knowledge of the material properties, especially those of the intervertebral discs and ligaments. Intervertebral discs show different degrees of degeneration in vivo. Here, beside intact discs, only one state of degeneration was modelled. Degenerated discs were assumed at the level where the decompression procedure was performed. Healthy discs were always assumed at the other levels. This is not necessarily the case in a patient. The facet joints vary in geometry, gap width, and orientation. These parameters were not varied in the present study. Only the two situations of standing and upper-body flexion were investigated for physiological loading. The effect of resecting posterior parts may differ for other physiological loading situations. Our model was validated using intersegmental rotations experimentally determined by Quint et al. [16]. This parameter showed a high degree of conformity for most loading situations. However, the computer model delivers additional results, which are difficult or even impossible to acquire experimentally. Therefore, most of the other parameters cannot be validated. Thus, many results of a finite element analysis only indicate trends and do not necessarily represent the correct absolute values.

The intradiscal pressures calculated for pure moment loads were in good agreement with values previously measured in vitro [17, 18]. For these nonphysiological loading situations, however, the intradiscal pressure was much lower than that measured in vivo [23, 24], since no axial preload was applied in these studies. The calculated intradiscal pressures were similar to the in vivo values for the physiological loading situations of standing and forward bending.

A facetectomy already influences the mechanical behaviour of the lumbosacral spine during loading in axial rotation with a pure moment. This is in agreement with the experimental findings of Kato et al. [10]. Resecting additional parts does not further increase the intersegmental rotation. A comparable trend is probably found in vivo. The preload caused by the upper body weight and the muscle forces should have a similar effect as a follower load [15], which has only a minor influence on intersegmental rotation [17, 18]. An increase of intersegmental rotation caused by a facetectomy is accompanied by higher stresses in the annulus and a higher intradiscal pressure.

During lateral bending and extension, the parameters studied were only slightly affected by the different extents of resection. This is in agreement with the findings of Abumi et al. [1]. For flexion, intersegmental rotation was predicted to markedly increase only after bilateral laminectomy. This is in agreement with the experimental findings of Quint et al. [16], but in contrast to those of Abumi et al. [1], who found a marked increase even after facetectomy. However, the supra- and interspinous ligaments were additionally transected in their study.

When calculating intersegmental rotation, different degrees of posterior resection evidenced the same trends for the physiological load simulating forward bending and for a pure flexion moment. However, different trends were found for standing and forward bending.

A laminectomy, even when performed at two levels, has only a negligible effect on the intersegmental rotations, stresses, strains, intradiscal pressures and forces in the facet joints of the segments above. Thus, our biomechanical results suggest that the simulated surgical procedures do not lead to secondary effects in the adjacent region.

Resection of posterior bony or ligamentous parts has a stronger influence on the amount of stresses in a disc than on their distribution. When the L4/5 disc is degenerated, the annulus shows a decrease of intersegmental rotation angles and maximum strains and an increase of maximum von Mises stresses. A degenerated disc is stiffer and thus more stressed. The lack of nucleus incompressibility increases the load that has to be carried by the annulus.

Conclusions

A left or bilateral hemifacetectomy increases intersegmental rotation and thus decreases spinal stability only for the loading situation of axial rotation. There were only minor differences between a bilateral hemifacetectomy and a hemilaminectomy. Patients should avoid excessive axial rotation after undergoing a facetectomy or laminectomy. For the studied loading situations, the difference in intersegmental rotation and thus spinal stability between a hemilaminectomy and a bilateral laminectomy is only remarkable for flexion and forward bending. Thus patients submitted to a laminectomy should strengthen their stabilizing trunk muscles and avoid excessive forward bending. Disc degeneration results in smaller intersegmental rotations and higher stresses at the respective level. Decompression procedures affect the biomechanical parameters studied less markedly in degenerated than in intact discs. Resection of bony or ligamentous posterior elements has only a minor effect on the biomechanical behaviour of the adjacent region.