Dynamic stiffness and damping of human intervertebral disc using axial oscillatory displacement under a free mass system

Abstract

The aim of this study was to analyse the dynamic response of the human intervertebral disc to vibration in a physiologically relevant frequency spectrum. Eight lumbar intervertebral discs were harvested. After preparation, each sample was subjected to a pre-loading and then dynamic compression (from 5 to 30 Hz). The dynamic compression was applied using an experimental set-up comprising a free weight loading from above and a driving oscillatory displacement from below (closest to the in vivo loading). A viscoelastic model enabled the calculation of stiffness and damping from the transfer function. From 5 Hz to 30 Hz the stiffness values are between 0.19 and 3.66 (MN/m) and the damping values between 32 and 2094 (Ns/m). The mean resonant frequency was found at 8.7 Hz. These dynamic characteristics of the intervertebral disc could be used in a three-dimensional finite elements model of the human body to study its response to vibration in the driving position.

Introduction

Pathologies affecting the spine are becoming ever more common today. They are linked to lifestyle and in particular to the widespread operation of automobiles [3, 18, 24], heavy industrial machinery and buses, and to the effort involved in lifting [9]. Many authors have studied back complaints, and have foregrounded the influence of vibrations [7] as a source of these complaints. To improve vehicle seats and to filter vibrations better [24], it is planned to design biomechanical models of the human body. To achieve these models, it is necessary to know the mechanical properties of the different structures of the human body, and we have focused first on the intervertebral disc. Most studies of the dynamic behaviour of the intervertebral disc have focused on the physiological loading of daily life and have considered creep [13], cyclic loading [2, 6, 14, 15, 16, 17], fatigue with a frequency around 1 Hz [1, 19] or impact tests [22]. The goal of this study is to characterise the dynamic stiffness and damping of human intervertebral discs subjected to vibration from 5 to 30 Hz in a sitting position in a car. For this study, in order to improve biofidelity, a free weight loading was used on the upper part of the specimen and a driving, oscillatory displacement was applied at the bottom (transmittance), whereas most authors [11, 12, 23] have chosen a fixed upper part (impedance). In this preliminary study, a simple Voigt model was chosen for its simplicity in leading to the calculation of dynamic stiffness and damping. Mean resonant frequency and static compressive stiffness were worked out in order to compare the protocol to previous studies.

Materials and methods

Specimen preparation

Eight human intervertebral discs (Table 1) were harvested within 36 h post mortem, frozen at −20 °C in vacuum-sealed plastic bags and, 12 h before testing, slowly thawed at 4 °C in a refrigerator [1, 20]. They were kept moist during preparation in saline-soaked gauze. It is now established that freezing (−20 °C) of human discs does not significantly modify their static, creep or dynamic behaviour [5, 8, 23]. The intervertebral discs (Fig. 1) were prepared by cutting posterior elements and muscular and ligamentous structures from them [4, 15, 17]. The inferior semivertebral body was embedded in polyurethane resin.

Table 1.

Details and Galante classification of specimens

Specimen	1	2	3	4	5	6	7	8
Sex	M	M	F	M	F	M	M	F
Age (years)	63	50	69	50	70	50	72	67
Disc level	L1-L2	L2-L3	L1-L2	L1-L2	L1-L2	L3-L4	L1-L2	L1-L2
Height (mm)	9.5	9.5	7.5	9	6.5	10	5	7
Disc surface (mm2)	1470	1442	1156	1389	979	1519	1322	1225
Disc grade	II	II	III	II	III	III	IV	III

Fig. 1.

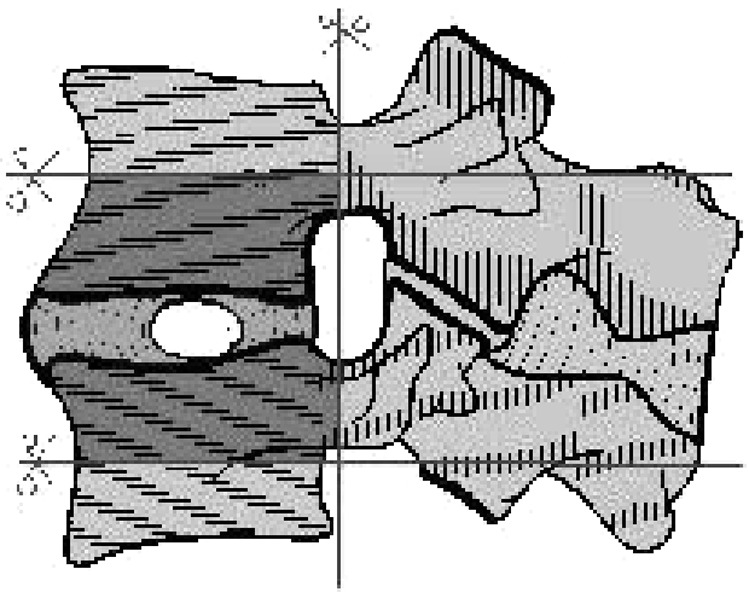
Mode of preparation of specimens for compression tests

Prior to testing, weight and small and large axis measurements (so as to calculate the cross-sectional area by approximation of the ellipsis) were recorded.

Mechanical testing

Some parameters affect disc behaviour. The main one is that fluid flow causes variations in volume [2, 7, 21] and in the mechanical properties of the disc [23]. Maintaining hydration during the experiments is therefore important [1, 3, 16, 24].

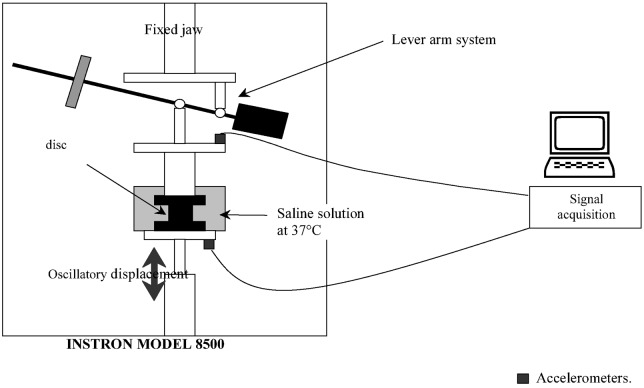
Before the mechanical test each specimen was placed in a bath in physiological saline solution at 37 °C for 30 min. The loading was then applied using an experimental set-up comprising a free weight loading from above (400 N) and a driving oscillatory displacement from below (closest to the in vivo loading) (Fig. 2). A free mass was applied to the specimens by a lever arm device fixed under the upper platen of the machine. In the specific case of small displacement, the loading system is reduced to a single mass on the vertical axis. The special alignment device provides only dynamic axial loads without any shearing forces. The test consists of (1) a pre-loading and (2) a dynamic compression (from 5 to 30 Hz).

Fig. 2.

Dynamic compression device. A free mass was applied to the specimens by the lever arm device fixed under the upper platen of the machine. In the specific case of small displacement, the loading system is reduced to a single mass on the vertical axis. The special alignment device provides only dynamic axial loads without any shearing forces. The loading was applied using the lever arm and a driving oscillatory displacement from below (closest to the in vivo loading)

Pre-loading

To precondition the specimen [11], static pre-loading at 400 N for 15 min was applied from above, followed by an oscillatory displacement of 0.3 mm amplitude by the lower actuator (while keeping the same 400 N upper load) for 1 min at 5 Hz. The 400 N load corresponds to the body above this segment [18].

Dynamic test

The dynamic compression was applied using the experimental set-up comprising a free weight loading from above (400 N) and a driving oscillatory displacement (dependent on frequency) from below. The program for sinusoidal sweeping frequency was defined thus: from 5 to 30 Hz every 5 Hz for 5 s. After 30 Hz a second test was done at 5 Hz (5 s) to check the mechanical properties of the disc. The displacement of the hydraulic actuator was varied for each frequency in order to achieve the desired acceleration magnitude at the lower input (0.5 m.s⁻² RMS). Two accelerometers (lower input and higher output, model 2635, Bruel and Kjaer) enabled the measurement of transmissibility (Fig. 2). Gain and phase were then calculated using Labview software (sampling rate: 0.001 s) (Fig. 3).

Fig. 3.

Typical raw data: gain versus frequency

A control procedure was carried out using a standard material with similar and well-known material properties: polyvinylsiloxane. The samples were placed on the experimental set-up to establish its reliability. There was no machine resonance and no influence of the length of the upper arm or of the bath on the mechanical data.

Stiffness and damping computing

A simple Voigt model was used to approximate the disc behaviour. The use of the dynamic equation of movement enabled the computation of axial dynamic stiffness (S) and damping (D) based on the acquisition of the input and output accelerations. This acquisition enabled the definition of transmissibility with the gain G and the phase ϕ.

The stiffness and damping are defined by:

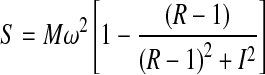1

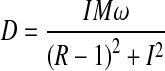2

with M the free mass applied to the specimen, ω=2×π×f (f=frequency), R=G cos ϕ, and I=G sin ϕ.

Resonant frequency

The resonant frequency was determined from the gain versus frequency acquisition (Fig. 3).

After the dynamic test each specimen was observed and weighed, and the height was measured with pins and a vernier caliper.

Static axial stiffness

Moreover, after the dynamic test a static compression evaluation was performed on the specimens using a universal testing machine (Instron model 5500, UK). The test conditions were the same as those for the dynamic test (i.e. a saline bath maintained at 37 °C). The compression was conducted up to 400 N (800 N/min). Two different values of the stiffness were computed from the curves, from the initial slope (less than 0.5 mm) and from the major slope (above 1.5 mm). The calculation used by Markolf [20] including the tangent of the curve at the maximum load was also performed.

After mechanical tests each specimen was sectioned, photographed, and graded using Galante’s scale [3] by two surgeons.

Results

No modification of weight or height was found before and after the dynamic test. No influence on stiffness and damping was observed in regard to the 5 Hz loading performed at the beginning and end of the dynamic test. These results showed that this specific test procedure induces no mechanical modification of the discs (Table 2).

Table 2.

Dynamic axial stiffness and damping values for human lumbar intervertebral discs

Frequency (Hz)	Stiffness (MN/m)		Damping (Ns/m)
	Mean	Standard deviation	Mean	Standard deviation
5	0.25	0.08	2567	2663
10	0.19	0.01	237	49
15	0.64	0.04	101	35
20	1.34	0.09	32	18
25	2.24	0.21	1875	603
30	3.66	0.37	229	59

The values for both dynamic parameters are given in Table 2 for the frequencies ranging from 5 to 30 Hz. The axial dynamic stiffness increases from 10 Hz to 30 Hz. The damping is lowered between 10 to 20 Hz.

A mean resonant frequency at 8.7 Hz (range: 8–10.4 Hz) was obtained for these intervertebral disc specimens (without posterior element).

The static stiffness (tangent at 400 N) varied from 0.6 to 0.9 MN/m (Table 3).

Table 3.

Static axial stiffness from the literature for lumbar intervertebral discs

Reference	Static axial stiffness, MN/m			Maximum load, N
	Range and mean (standard deviation)
Asano et al. [2]	0–0.5 mm 0.49 (0.04)	0.5–1 mm 0.73 (0.06)	1–1.5 mm 1.18 (0.09)	1500
Brown et al. [4]	0.1–1.5 (initial slope)			450–900
	2.1–3.6 (major slope)
Markolf [20]	1.23–3.32 (tangent at max. load)			220–670
Present study	0.05 (0.02) (initial slope, less than 0.5 mm)			400
	0.64 (0.1) (major slope, more than 1.5 mm)
	0.60–0.94 (tangent at max. load)

Discussion

The mechanical response of the intervertebral disc to different loading situations is one of the keys to understanding and predicting its behaviour. The axial load situation was evaluated in this study because the vibration inputs experienced by workers are primarily axial [11].

The large variation in damping coefficients may be linked to the degeneration grades (II to IV on Galante’s scale). However, the limited number of specimens tested did not allow determination of the possible role of disc degeneration in the segmental response in vibration.

Resonant frequency

In vivo studies have demonstrated that the resonant frequency of the body is 4–6 Hz [11]. The value found in the current study (8.7 Hz) using excised intervertebral discs without a posterior arch should be compared to the simulation performed by Kasra et al. [11] on a three-dimensional model of the L2–L3 disc vertebra unit. They found, with an upper mass of 40 kg and using free-vibration analysis, a resonant frequency of 6.1 Hz.

Comparison of static and dynamic axial stiffness: present study versus previous studies

According to the study of Markolf [20] ,the lumbar discs showed a non-linear load-deflection curve in the static experiment. The static axial stiffness was compared to the values of previous studies (Table 3). Results depend on the load applied and the stiffness computation. In respect of the tangent of the curve at the maximum load [20], a lower value was obtained for the current specimens. This difference is due to different maximum loads (Table 3) and may be related to the age of the subjects (age range was 21–55 years in Markolf’s study [20] versus 50–72 years in the present study).

For dynamic axial stiffness the values obtained are in the same range as the static ones. The static experiments showed that the values of this parameter are highly dependent on the displacement imposed on the specimen and are also dependent on the time [21]. The results must be analysed in the light of these findings. The set-up used enabled characterization of the dynamic axial stiffness according to the displacement and the frequency applied to the specimen.

According to Smeathers et al. [23] (in the range 0.01–10 Hz) the intervertebral discs get stiffer and less hysteretic as frequency increases. This is confirmed by the observation of the present results in the same frequency range. An increase in stiffness as a function of frequency was also noted by Kaigle et al. [10].

The experiment set-up can explain different values in comparison to other dynamic studies [11, 23], as well as the preparation of the specimens and the choice of the viscoelastic model [6].

These dynamic characteristics of the intervertebral disc could be used in a 3D finite elements model of the human body to study its response to vibration in the driving position.

Conclusions

The goal of this study was to estimate the dynamic axial stiffness and damping of human lumbar intervertebral discs in the range of frequencies transmitted by a car seat. In order to reproduce the in vivo conditions, a free mass system was developed to define the previous parameters and the resonant frequency. Due to the viscoelastic properties of the intervertebral disc the values are highly dependent on the load and displacement applied to the specimens. Considering this point, the results are in accordance with previous studies. A comparison was also conducted for static axial stiffness. Finally, this methodology can be applied to other soft tissues such as muscle or fat tissue.