Biomechanical simulations of the spine deformation process in adolescent idiopathic scoliosis from different pathogenesis hypotheses

Abstract

It is generally recognized that progressive adolescent idiopathic scoliosis (AIS) evolves within a self-sustaining biomechanical process involving asymmetrical growth modulation of vertebrae due to altered spinal load distribution. A biomechanical finite element model of normal thoracic and lumbar spine integrating vertebral growth was used to simulate the progression of spinal deformities over 24 months. Five pathogenesis hypotheses of AIS were represented, using an initial geometrical eccentricity (gravity line imbalance of 3 mm or 2° rotation) at the thoracic apex to trigger the self-sustaining deformation process. For each simulation, regional (thoracic Cobb angle, kyphosis) and local scoliotic descriptors (axial rotation and wedging of the thoracic apical vertebra) were evaluated at each growth cycle. The simulated AIS pathogeneses resulted in the development of different scoliotic deformities. Imbalance of 3 mm in the frontal plane, combined or not with the sagittal plane, resulted in the closest representation of typical scoliotic deformities, with the thoracic Cobb angle progressing up to 39° (26° when a sagittal offset was added). The apical vertebral rotation increased by 7° towards the convexity of the curve, while the apical wedging increased to 8.5° (7.3° with the sagittal eccentricity) and this deformity evolved towards the vertebral frontal plane. A sole eccentricity in the sagittal plane generated a non-significant frontal plane deformity. Simulations involving an initial rotational shift (2°) in the transverse plane globally produced relatively small and non-typical scoliotic deformations. Overall, the thoracic segment predominantly was sensitive to imbalances in the frontal plane, although unidirectional geometrical eccentricities in different planes produced three-dimensional deformities at the regional and vertebral levels, and their deformities did not cumulate when combined. These results support the hypothesis of a prime lesion involving the precarious balance in the frontal plane, which could concomitantly be associated with a hypokyphotic component. They also suggest that coupling mechanisms are involved in the deformation process.

Introduction

Adolescent idiopathic scoliosis (AIS) is a complex three-dimensional (3D) anomaly of the spine involving lateral deviations in the frontal plane, modifications of the sagittal profile, spinal torsion and transverse plane deformations [16, 21, 23]. There is still no generally accepted scientific theory for its etiology [7, 16, 21, 23]. The pathogenesis of AIS is not clearly defined regarding either how structural deformities develop or in which sequence they appear.

Some researchers argue that the initial lesion originates from a primary rotational deformity, with secondary development of frontal curvatures and modification of sagittal profiles in response to this instability [6, 16, 21, 24]. Deane and Duthie [10] measured a relative lengthening of the anterior thoracic and lumbar spine in scoliotic specimens and suggested a primary instability in the sagittal equilibrium. Similarly, Sommerville [27] suggested that the deformity consists of a structural lordosis consequent to a failure of growth of the posterior elements. Other theories state that the deformity results from a reduction of the thoracic kyphosis in a fixed structural lordotic area, which under the influence of transverse or coronal plane asymmetry, rotates to the side and gives rise to a lateral curvature [12, 18]. White [39] observed the presence of a slight physiological thoracic curve, thus he associated the prime scoliotic lesion with the precarious coronal balance of the spine and consequent asymmetrical loading of vertebrae, which might rotate into the convexity of the curve. Following onset of the initial deformity, it is generally recognized that progressive scoliosis evolves within a self-sustaining biomechanical cycle involving asymmetrical loading of the spine, alteration of vertebral growth (“growth modulation”), development of scoliotic deformities and so on [6, 16, 22].

AIS essentially develops during adolescent growth spurt [14, 38]. Growing bones react to loads applied on their cartilaginous growth plates, with perpendicular loading of the plates modifying the rate of longitudinal epiphyseal growth according to the Hueter-Volkmann principle. This principle states that increased pressure on the plate retards growth (Hueter), and conversely reduced pressure accelerates growth (Volkmann) [1, 31]. For asymmetrically loaded vertebrae, endplates initially parallel in the frontal plane become wedged in 3D while the vertebrae are rotating in space [4, 22, 28]. Torsion or shear forces, which are parallel to the plates, essentially alter the direction of growth, with cartilaginous columns leaning under the forces [1, 19].

In a previous study, we developed a biomechanical model of the spine that incorporates vertebral growth, and we simulated the self-sustaining progression of vertebral and spinal scoliotic deformities in response to a slight imbalance in the frontal plane [36]. The objective of this paper is to investigate the deformation process that could result from different pathogenesis hypotheses. Simulations will be compared to previous studies and clinical observations.

Materials and methods

Biomechanical model of bone growth modulation

The biomechanical model used in this study was presented in detail in a previous paper [36], and is here summarized. The local bone x-axis is defined as the direction perpendicular to the growth plates. The local y- and z-axes refer to directions parallel to the growth plates. The resultant growth includes a baseline growth along x only, and a growth modulation component. Longitudinal growth over a given period (δG_x) is expressed in terms of growth strain increments (in mm/mm). Based on the work of Stokes et al. [29], corresponding deformation increments δε_i due to growth modulation are defined by the expression δε_i=β_i σ_i δG_x, and include three direction components (i=x,y,z). They depend on the baseline growth (δG_x), on a functional biomechanical stimulus represented by internal stresses σ_i and on a parameter β_i simulating the sensitivity of the bone tissue to that stimulus. In the case of beam elements, which are used to model the vertebral bodies, the deformation increments due to growth modulation δε_i can be simulated by applying equivalent internal forces δF_Mi based on the bone mechanical properties E_i, defined as the modulus of elasticity (i=x) or shear modulus (i=y,z):

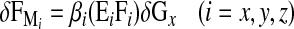where δF_Mi, β_i, E_i, and F_i are respectively in N, MPa^–1, MPa and N. Force increments due to growth modulation can be evaluated for internal forces ΔF_i or variations of internal forces DF_i, which are directly calculated from simulations of the finite element model in response to a specified loading condition. In this study, longitudinal growth and resultant growth modulation are modeled on the vertebral body only. This simplification is justified because posterior parts of the vertebra have essentially completed their longitudinal growth before the first decade [37, 41], while the vertebral body pursues its longitudinal growth during puberty [38], when progression of AIS is most at risk. Growth of intervertebral discs was not considered, based on an in-house study on 20 patients (mean age: 11.8±2.6 years old) over a growth period of 2.6±1.0 years, which showed a mean growth of less than 0.3 mm/year. Modulation of the discs was indirectly taken into account, as the intervertebral discs will deform to minimize the energy of deformation of the global spine.

Finite element model of thoracic and lumbar spine

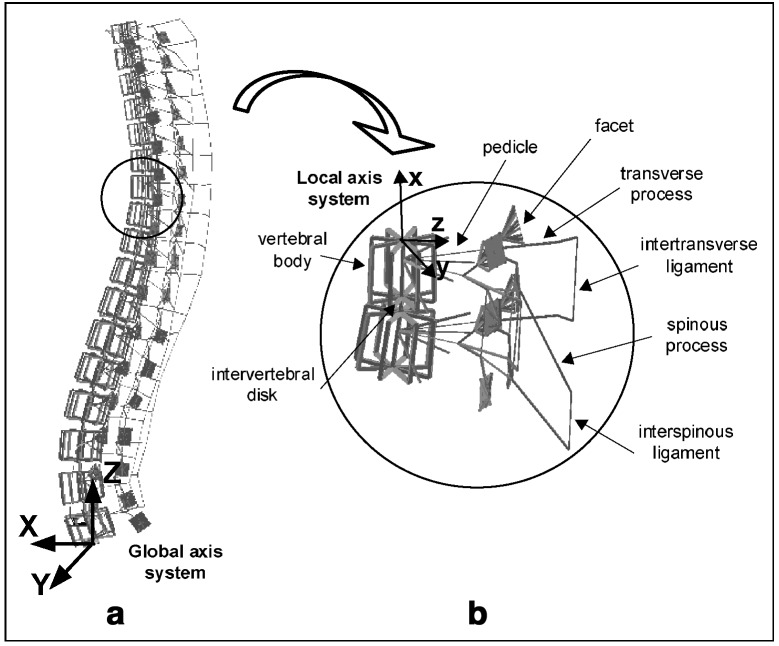
A personalized geometric model is obtained from a 3D reconstruction of spinal structures using a multiview radiographic technique [2, 8]. This model is used to generate the biomechanical finite element model, which represents estimates of the structural behavior of the vertebrae, intervertebral discs, facet joints and ligaments (Fig. 1). Mechanical properties of the finite element model were obtained from experimental studies [2, 11]. Each vertebral body (26 elements in total) is modeled by ten beam elements interconnected within a rigid crossbar system (16 beam elements). Two contiguous elements are centered in the vertebral body and the remaining eight distributed along the vertebral edge in order to enable a representative distribution of variable internal forces within the vertebral body (Fig.1). The osseo-ligamentous part of the model was assessed in previous studies [2, 11]. In this model, the global axis system is defined by three mutually perpendicular axes corresponding to the anterior (X), left (Y) and upward (Z) directions.

Fig. 1.

Finite element model: (a) thoracic and lumbar spine; (b) vertebral motion segment

Integration of growth and growth modulation into the finite element model

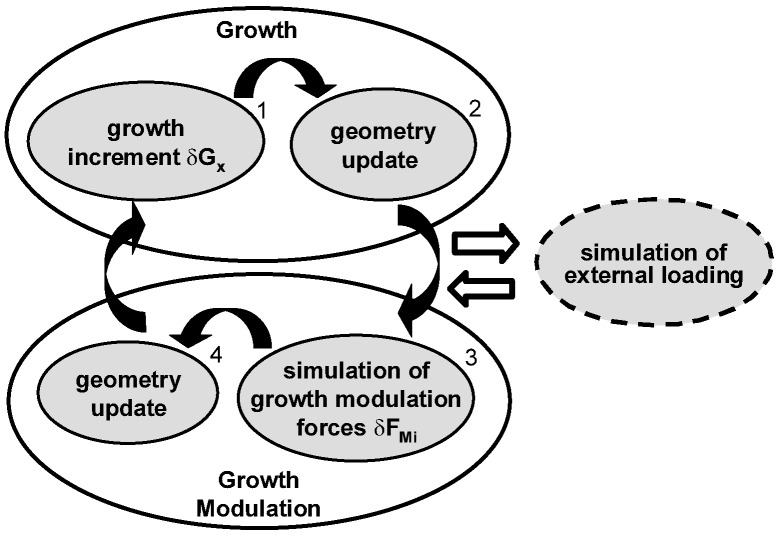
Simulation of vertebral growth and growth modulation is implemented separately in an iterative procedure (Fig. 2). Vertebral growth includes application of a growth increment ΔG_x (step 1), followed by an update of the spine geometry by relocation of model nodes (step 2). Monthly lengthening values ΔG_x are adapted from published rates of 0.8 and 1.1 mm/year respectively for the thoracic and lumbar vertebrae [13, 33].

Fig. 2.

Biomechanical iterative procedure successively simulating growth, asymmetrical loading of the spine and corresponding growth modulation

The procedure of growth modulation uses as input the output from an external loading step. The corresponding growth modulation simulation consists of a modeling artifice used to perform the geometry change due to growth modulation. It is isolated by resetting stresses and strains to zero before and after numerical resolution. In this study, it is assumed that growth modulation will result from a modification or shift from the normal loading evaluated on a reference spine, with the latter remaining constant throughout the simulation process. Loads applied on spinal configurations were based on the experimental fact that longitudinal bone growth is essentially affected by static continuous loading as compared to dynamic intermittent loading involved in motions [15, 40]. Spinal loads incorporated gravity and the corresponding stabilizing vertical action of muscles acting on vertebrae. It is then assumed that the principal component of the resultant loads on the vertebral bodies lies close to the gravity direction. Gravity loads of each vertebral level were derived from the work of Schultz and co-workers [25]. These gravitational loads were amplified based on the equations of Nachemson [20] in order to integrate the muscular component for a subject in an upright standing position. This approach of estimation of spinal and muscle loads was preferred, since resulting combined gravity and muscle forces are obtained from measurements of intradiscal pressures, which are closely related to vertebral growth plates activity. These forces (Table 1) were applied on superior vertebral endplate centers along global Z-axis and remained constant throughout all growth cycles. Internal stress states σ and σ’ respectively generated on the reference and altered (scoliotic) configurations were used to compute the differential stress state Δσ=σ’-σ. The altered profile was updated at each cycle due to cumulative growth effects. For all simulations, boundary conditions of the model included all degrees of freedom fixed at L5 and forward and lateral flexions as well as vertical translation permitted at T1. These approximate the real balancing of the trunk but represent reasonably well the conditions at T1 and L5. Sensitivity studies showed that the model response was not significantly altered when constrained by other plausible boundary conditions.

Table 1.

Numerical description of combined gravitational and muscular loading applied along global Z-axis for an approximated subject body mass of 45 kg: cumulative mass percentages (%) for each level i (based on Schultz et al. [25]); cumulative Mass_i on vertebral level i; Ptot_i=(15+2.1*Mass_i), formula for resultant cumulative mass on the corresponding intervertebral disk for a subject in upright standing position (from Nachemson [20]); Δ(Ptot_i)=Ptot_i–Ptot_i−1; Δ(Force_i)=Δ(Ptot_i)*g, with g=9.81 m/s²

Vertebral level i	% of total mass for each level i	Massi	Ptoti	Δ(Ptoti)	Δ(Forcei)
		(Kg)	(Kg)	(Kg)	(N)
1 (T1)	14.0	6.3	28.2	28.2	276.9
2 (T2)	16.6	7.5	30.7	2.5	24.1
3 (T3)	19.2	8.6	33.1	2.5	24.1
4 (T4)	21.8	9.8	35.6	2.5	24.1
5 (T5)	24.4	11.0	38.1	2.5	24.1
6 (T6)	27.0	12.2	40.5	2.5	24.1
7 (T7)	29.6	13.3	43.0	2.5	24.1
8 (T8)	32.2	14.5	45.4	2.5	24.1
9 (T9)	34.8	15.7	47.9	2.5	24.1
10 (T10)	37.4	16.8	50.3	2.5	24.1
11 (T11)	40.0	18.0	52.8	2.5	24.1
12 (T12)	42.6	19.2	55.3	2.5	24.1
13 (L1)	45.2	20.3	57.7	2.5	24.1
14 (L2)	47.8	21.5	60.2	2.5	24.1
15 (L3)	50.4	22.7	62.6	2.5	24.1
16 (L4)	53.0	23.9	65.1	2.5	24.1
17 (L5)	55.6	25.0	67.5	2.5	24.1

Numerical solution of the external loading provides internal forces F_i in beam elements composing the vertebral bodies. These forces are used to calculate the modulating forces (step 3), which are subsequently applied on corresponding elements of the vertebral bodies to simulate growth modulation. The model is solved numerically and the spinal geometry is updated according to the resulting deformed shape (step 4). The method of solution considers geometric non-linearity due to large displacements and strains as well as non-linearity due to status change at the contact of facet joints. The stresses are then reset to zero as part of the modeling artifice used to simulate growth modulation. This cycle is repeated for the number of growth increments desired.

Qualitative evaluation of the model

From a phenomenological point of view, the model responds in a coherent manner. The developed model of growth modulation could adequately represent the Hueter-Volkmann principle along bone x-axis, with forces simulating reduced and accelerated growth respectively in regions of increased and decreased pressure [36]. Growth modulation components in directions parallel to the endplates (along bone local y- and z-axes) resulted in shear forces altering the direction of bone growth (i.e., altering space orientation of the longitudinal x-axis of the beam elements) in a similar way to experimental observations.

Simulations

This model was used to simulate the progression of spinal deformities representing five different pathogenesis hypotheses of AIS. The geometry of a non-pathologic female subject without spinal deformity was chosen as the reference spinal configuration. The initial altered profile used to trigger the deformation process was obtained by imposing on the reference configuration a geometrical eccentricity representing the corresponding initiating hypothesis. The tested eccentricities included 3 mm linear shifts in the frontal (PA) [39] or in the sagittal (Lat) [27] plane (equivalent to a Cobb angle of 2°), 2° rotational shift in the transverse plane (Rot) [6, 16, 21, 24] and combinations Lat-PA and Lat-Rot [12, 18]. The initial altered profile was generated only for the first step, by simulating imposed eccentricities in the global axis system at the eighth thoracic vertebra, which was assumed to be the apical vertebra of the (future) scoliotic curve. When required, displacement constraints were simultaneously applied along other directions. For instance, a sole eccentricity in the frontal plane (PA) was combined with constraints in the sagittal plane (Lat), and vice-versa. The resulting deformed shape could include modifications in other planes than the plane(s) of eccentricities, due to the slightly asymmetrical reference configuration as well as coupling mechanisms. A body mass of 45 kg was used in the calculation of spinal loads. Growth modulation effects were simulated along bone x-axis only (β_x=0.6 MPa^–1, β_y=β_z=0) for 24 cycles or months. The value of the sensitivity factor β_x was based on a physiologic rationale limiting the amplitude of growth modulation within a cycle by the magnitude of the integrated growth increment, and was obtained empirically from the model. Growth modulation along y and z was neglected, based on the fact that important forces are experimentally required to generate modifications of bone geometry [1, 19], suggesting that the effects of δFMy and δFMz would be secondary compared to the contribution of δFMx.

At each iteration, scoliotic descriptors were evaluated analytically on the updated spinal configuration. Two regional descriptors were used to characterize the spinal curvatures of the thoracic segment: the Cobb angle in the frontal plane (Cobb) and the kyphosis curvature (k_t) [17]. Three local descriptors were calculated at the thoracic apical vertebra, generally the most deformed vertebra:

1. The maximum 3D wedging angle (ω)

2. The angular orientation (θ_ω) of the line joining the maximum and minimum heights of the vertebral body with respect to the sagittal plane of the vertebra [4]

3. The axial rotation (θ_z) calculated using an analytical method adapted from Stokes [30], which is negative for clockwise rotation and positive for counterclockwise rotation for the vertebra viewed from above [17]

Results

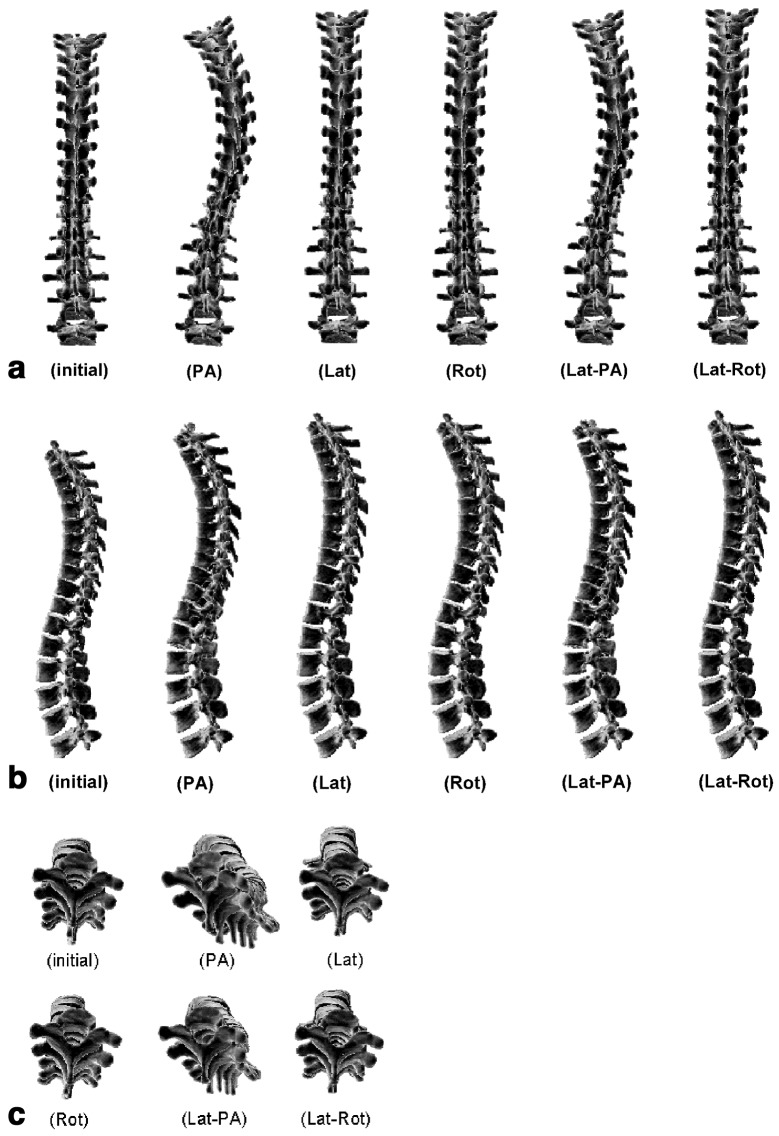
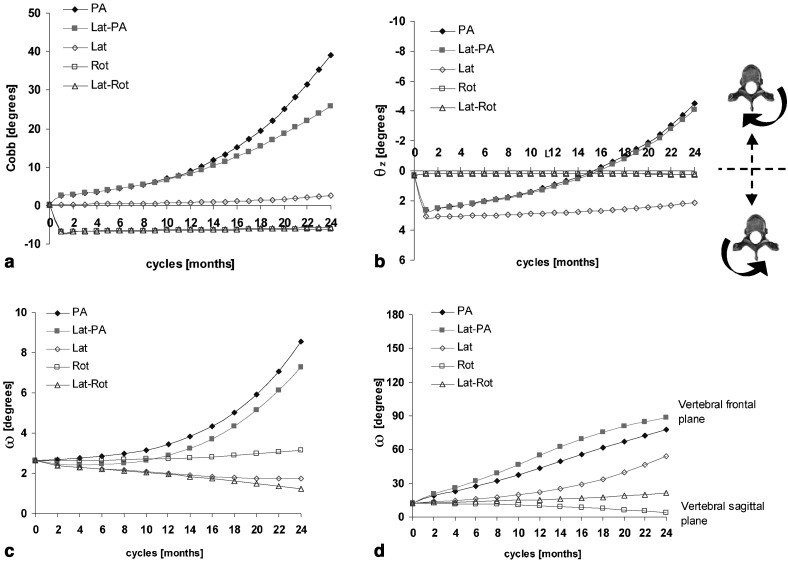
Frontal, sagittal and transverse spinal views of the reference and resultant configurations at the 24th month are presented for the five pathogenesis hypotheses (Fig. 3). For cases involving a frontal eccentricity (PA), a visible amplification of the thoracic scoliotic curve appeared in the coronal plane, with a non-linear increase of the Cobb angle up to 39° (Fig. 4a). The Cobb angle reached 26° when combined with the sagittal eccentricity (Lat-PA) (Fig. 4a). No visible deformation was observed in the frontal plane when a sole sagittal eccentricity (Lat) was simulated, with a very slight 2° increase of the Cobb angle over 24 months (Fig. 4a). Cases integrating a rotational shift in the transverse plane (Rot and Lat-Rot) both indicated a stable left thoracic curve of 6° originating from the generation of the initial altered profile (Fig. 4a). Table 2 summarizes scoliotic descriptors for the reference spinal configuration and the five resultant simulated configurations. In addition, a typical scoliotic profile representing mean values and standard deviations of scoliotic descriptors evaluated for 25 progressive thoracic scolioses are shown for comparison (in-house clinical study).

Fig. 3.

Reference and resulting configurations at the 24th month for five pathogenesis hypotheses in: (a) frontal spinal view; (b) sagittal spinal view; (c) transverse spinal view

Fig. 4.

Monthly evolution of scoliotic descriptors for five pathogenesis hypotheses: (a) Cobb angle; (b) vertebral axial rotation (θ_z); (c) maximum wedging angle (ω); and (d) its angular orientation with respect to the sagittal plane of the vertebra (θ_ω)

Table 2.

Scoliotic descriptors for the initial spinal configuration, for a typical progressive scoliotic profile (mean and standard deviation for 25 subjects) as well as for the simulated configurations for the five pathogenesis hypotheses of adolescent idiopathic scoliosis (PA: linear shift in the frontal plane; Lat: linear shift in the sagittal plane; Rot: rotational shift in the transverse plane; Lat-PA, Lat-Rot: combined shifts). Values are presented for the thoracic Cobb angle in the frontal plane (Cobb), kyphosis curvature (k_t), maximum 3D wedging angle (ω), angular orientation of the line joining the maximum and minimum heights of the vertebral body with respect to the sagittal plane of the vertebra (θ_ω), and axial rotation (θ_z). All values are in degrees

	Thoracic segment		Thoracic apex
	Cobb	kt	ω	θω	θz
Reference	0	35	2.6	12	0.3
Average scoliotic profile	37±6	28±10	6.9±2.9	76±26	−10.9±7.8
PA	39	35	8.5	78	−4.5
Lat-PA	26	27	7.3	89	−4.1
Lat	3	27	1.8	54	2.1
Rot	−6	36	3.2	4	0.3
Lat-Rot	−6	35	1.2	22	0.3

For eccentricities not involving a sagittal component (PA, Rot), the kyphosis was stable (35°) over the 24 cycles. This was similar for the combined eccentricity in the sagittal and transverse planes (Lat-Rot) (Table 2). When a sole sagittal shift was imposed in the sagittal plane (Lat) or when it was combined with a frontal offset (Lat-PA), the kyphosis decreased approximately 7° between the first and last cycles.

Vertebral axial rotations were generated in the transverse plane when eccentricities were simulated in the frontal plane (PA, Lat-PA), with θ_z progressing by approximately 7° clockwise in both cases (Fig. 4b; Table 2). No vertebral apical rotation developed when a sole rotational shift was imposed in the transverse plane (Rot) or combined with a sagittal offset (Lat-Rot) (Fig. 4b). In the case of a linear shift in the sagittal plane (Lat), an initial vertebral axial rotation of 3° counterclockwise appeared at the first cycle due to the initial altered profile, and remained quite stable thereafter (Fig. 4b).

Eccentricities in the frontal plane (PA) showed increasing wedging angle ω at the thoracic apical vertebra, progressing non-linearly from 2.6° to 8.5° (PA) and 7.3° (Lat-PA) at the 24th month (Fig. 4c) (Table 2). The corresponding angular orientation θ_ω evolved from 12° to about 80°, indicating that the maximum vertebral wedging was shifted from the sagittal plane towards the frontal plane of the vertebra (Fig. 4d). Apical wedging ω resulting from a rotational shift in the transverse plane (Rot) was little modified (Fig. 4c), with its angular orientation evolving 9° towards the vertebral sagittal plane (Fig. 4d). When a sole linear shift was imposed in the sagittal plane (Lat) or combined with a rotational offset (Lat-Rot), wedging angle ω of the thoracic apical vertebra showed a slightly decreasing trend, from 2.6° to 1.8° and 1.2° respectively (Fig. 4c), with corresponding θ_ω evolving non-linearly towards the vertebral frontal plane of 41° (Lat) and 10° (Lat-Rot) (Fig. 4d). Initial non-zero values for vertebral rotation and wedging angle are associated with the initial geometry of the subject and with generation of the initial altered spinal profile required to trigger the process.

Discussion and conclusion

A biomechanical model of the spine integrating vertebral growth modulation allowed the simulation of five different pathogenesis hypotheses of AIS adapted from the literature. It was found that there is no unique simulated AIS pathogenesis that results in the development of scoliotic deformities. The eccentricities involving the frontal plane combined or not with a sagittal offset generate the closest representation of scoliotic deformities. These observations support the pathogenesis hypotheses of a prime scoliotic lesion in the precarious coronal balance, as proposed by White [39], and of a reduced thoracic kyphosis under the influence of a coronal plane asymmetry, as presented by Dickson et al. and Millner [12, 18]. These results suggest that the thoracic segment is more sensitive to imbalances in the frontal plane when submitted to the self-sustaining progression of deformities, and that the sagittal equilibrium is much more stable.

As reported in several studies, wedging of the thoracic apex increases with curve severity [22, 34] and the thoracic apical rotation progresses clockwise towards the curve convexity with scoliosis progression [9, 34]. A sole shift in the PA plane did not alter the sagittal plane, while the sagittal component indeed contributed to the reduction of the thoracic kyphosis.

Simulations involving a rotational shift in the transverse plane globally produced small and non-typical scoliotic deformations, which suggests that this is not a primary factor in the initiation of scoliosis. The growth modulation process modeled along bone x-axis only can explain the relatively stable response over cycles. While a rotational shift is expected to mainly generate shear forces in the transverse plane, growth modulation effects only act in the direction perpendicular to the plates.

Unidirectional eccentricities in different planes produced 3D deformities at the regional and vertebral levels. These deformities did not accumulate when eccentricities were combined, suggesting that coupling mechanisms as well as non-linearities are involved in the deformation process. When a sole frontal imbalance is simulated, the thoracic apical vertebra shifts laterally and becomes wedged while concomitantly rotating clockwise towards the convexity of the thoracic curve. This “deformation coupling mechanism” operates in the opposite direction to the motion coupling observed in non-pathologic thoracic spines [39] and implies that a spinal alteration in one plane may generate complex deformities in 3D.

The modeling approach consists of a phenomenological representation of a biological process. Certain parameters require a more detailed characterization before this model can provide a predictive representation of scoliosis, for which patient-specific validation could be conducted. Refinement of this modeling approach should include integration of the rib cage, muscle actions and abdominal pressure, which may modify the relative stiffnesses of spinal segments. The coupling mechanisms attributed to costo-vertebral joints would potentially modify the development of deformities [3]. Experimental studies are required to better define the loads affecting vertebral structures. A mechano-biological definition of growth-plates behavior is also needed to develop a more physiologic model of growth modulation. In this study, the concept of vertebral growth modulation assumes a linear relationship centered on zero between the growth alteration and the stress or internal forces. Some authors suggest a neutral zone in the neighborhood of physiological bone loading, which prevents the growth plates from responding to load modifications below or above a certain threshold [15, 26]. This can explain why certain curves will evolve and others not. Neglecting growth of posterior elements could also represent certain limitations of the developed modeling approach in cases simulating very severe scoliotic progression or involving an extended growth period. Nevertheless, the present study investigated relatively mild scoliosis severities and involved simulations of progressive scoliosis on a limited growth period (24 months).

The initial scoliotic instability was modeled by a geometrical eccentricity from a reference configuration. It could also be initiated by forces originating from an asymmetry of muscular activity associated with postural instability or by asymmetrical growth, for instance of ribs or vertebral bodies. Stokes and Laible [29] developed a finite element model of the spine submitted to an 11% asymmetry in rib length and integrating growth modulation, to study developmental mechanisms of scoliosis. A small thoracic scoliosis curvature (≈3°) convex toward the side of the longer ribs was obtained, but the scoliotic pattern of axial rotation did not always develop. The authors suggested that missing components may be muscles or asymmetric growth modulation of vertebral bodies. Different biomechanical models of the spine have also tested the AIS pathogenesis concept of asymmetrical vertebral body growth, where the anterior part of the vertebral body grows faster compared to its posterior region [5, 32]. However, they do not integrate the self-sustaining deforming process of growth modulation consequent to the altered distribution of spinal loads due to the asymmetrical growth. In lieu of obtained results, it would be anticipated that the cumulative effects of asymmetrical growth and growth modulation on vertebral bodies could generate non-negligible progressive scoliotic deformities.

The biomechanical model allowed relative comparisons of different scoliotic pathogeneses and supported hypotheses of a prime lesion involving the frontal plane, potentially combined with the sagittal plane, which in turn generated 3D deformities. In a longitudinal study on progressive scoliosis [35], considerable variability was found in the evolution of some scoliotic descriptors such as axial rotation and kyphotic profile of the subject. It is suggested that the “secondary effects” of a lateral (or transverse) imbalance could be associated with this variability. They could physiologically represent individual characteristics such as the initial precariousness of the subject’s lateral profile and their muscular capacity, as well as the complex coupling involved in normal motions and scoliotic deformities, which overlap from a normal to a pathologic state. Moreover, the developed modeling approach agrees with the observed natural history of scoliosis, where identical initial spinal configurations could result in progressive or non-progressive deformities, depending on the values of the sensitivity factors β_i.

For the first time, a biomechanical finite element model of the thoracic and lumbar spine incorporated vertebral growth modulation and could reproduce in a representative manner the development of spinal curvatures and of intrinsic alterations of vertebrae associated with scoliosis. In the long term, this modeling tool may be useful to improve our understanding of the complex mechanisms involved in scoliotic progression.