Measurement of the volume growth rate of single budding yeast with the MOSFET-based microfluidic Coulter counter

Abstract

We report on measurements of the volume growth rate of ten individual budding yeast cells using a recently developed MOSFET-based microfluidic Coulter counter. The MOSFET-based microfluidic Coulter counter is very sensitive, provides signals that are immune from the baseline drift, and can work with cell culture media of complex composition. These desirable features allow us to directly measure the volume growth rate of single cells of Saccharomyces cerevisiae LYH3865 strain budding yeast in YNB culture media over a whole cell cycle. Results indicate that all budding yeast follow a sigmoid volume growth profile with reduced growth rates at the initial stage before the bud emerges and the final stage after the daughter gets mature. Analysis of the data indicates that even though all piecewise linear, Gomperitz, and Hill’s function models can fit the global growth profile equally well, the data strongly support local exponential growth phenomenon. Accurate volume growth measurements are important for applications in systems biology where quantitative parameters are required for modeling and simulation.

1. Introduction

Bioassays are typically performed on ensembles of cells. The assay results can depend crucially on the state of cells relative to one another. If the cells in an ensemble have a multimodal distribution with respect to some variable, then measurements that depend on that variable are confounded by averaging. The cell cycle has been shown to provide an example that is of importance when studying regulatory networks in systems biology.¹ One solution is to prepare a population of cells that maintain cell cycle synchrony. A synchronous population has a unimodal population density that moves through the cell cycle as a soliton and is periodic in time.² Because of the inherent asymmetry involved in the division of budding yeast, prepared population synchrony decays very rapidly.^3–5 However, simulations have shown that a continuous volume filtration strategy can extend prepared synchrony by an order of magnitude. The calculation of the design parameters and the volume filtration cutoffs require accurate models of individual yeast growth rates as a function of the cell cycle.⁶

Budding yeast is a well studied eukaryotic model organism, which are useful in the study of basic biological process^7–9 as well as complex human diseases and have found widespread applications in bioprocess and industry. Currently, budding yeast are at the centre of several large scale systems biology and bioinformatics efforts aiming at extending the understanding of cell cycle progression, integration of genetic regulation, aging effects and physiological adaptation.

The volume growth of yeast has been studied for decades. Measurements of individual live cells by microscopy have revealed a sigmoid growth curve.^9,10 Despite these measurements, controversy remains regarding the precise functional representation of the growth curve. Among the possible volume growth models, polynomial and exponential remain as contenders.

Although the volume growth rate of individual budding yeast cells can be determined by microscopy, this method requires geometric assumptions of the yeast cell that may not be strictly valid.^11,12 More complex optical methods, such as those providing high quality z-stacks,¹³ allow for accurate cell volume measurements. However, these techniques are extremely data intensive and very expensive. Recently new techniques to monitor cell size, such as the suspended microchannel resonator (SMR),¹⁴ have been developed. However, their applications to monitor live cell volume growth rate have not been demonstrated.

One convenient device that gives direct results of the cell volume is the Coulter counter, which has been widely used for clinical purposes and for bioprocess research.^15,16 In a Coulter counter, a small aperture connects two fluid chambers and a baseline ionic current is induced by an electric bias across the aperture. When a non-conducting particle enters the aperture, it displaces a volume of electrolyte equivalent to its own volume, giving rise to a transiently increased resistance of the sensing aperture. This transient increase of resistance results in a decrease of the ionic current or an increase of the voltage drop across the sensing aperture. If the size of the particle is much smaller than that of the aperture, the amplitude of the current or voltage modulation is proportional to the volume ratio of the particle to the sensing aperture, which gives the particle size directly.¹⁷ However, commercial Coulter counters have a few weaknesses in cell volume measurements. For example, commercial Coulter counters require that cells be suspended in a dielectric contrast fluid such as Isoton. These fluids lack the nutrients required for cell growth and cannot match the osmolarity of all cell mediums. Differences in osmolarity will lead to swelling or even rupture of the cells, drastically affecting the volume measurement. Another constraint of the commercial Coulter counter is that it only makes one-time detection because of the unswitchable delivery routine, which prohibits successive volume measurements for single cells. There is one report of constructing a pressure control system to reverse the pressure and deliver particles back and forth through the sensing aperture of a Coulter counter. However, the system requires a complex pressure control circuit and a pressure regulation system.¹⁸

Recognizing the drawbacks of commercial Coulter counters, researchers have developed on-chip Coulter counters for various applications. Compared with commercial Coulter counters, on-chip Coulter counters can have advantages such as compact and portable, low volume of reagents, reduced cost for each device, and possible integration with other functional devices.^19,20 One important recent development of on-chip Coulter counters is the fabrication of nanoscale apertures to detect nanoparticles such as DNA molecules.^21–24 All these on-chip Coulter counters follow the traditional delivery routine and the sensing objects only pass through the sensing channel once. To date, on-chip Coulter counters have not been used to measure the volume growth of single cells.

Very recently, Hua and Pennell reported an on-chip device that can trap a cell in a small sensing channel and measure the swelling of cells in response to the osmolarity change by monitoring the impedance of the sensing channel.²⁵ The device is very effective for monitoring large volume change in a short period. However, it is well-known that in microfluidic circuits, the channel impedance drifts over time because of changes in the media due to evaporation and electrochemical reactions at the electrodes, which are especially true for live cell culture media due to their complex components. In fact, baseline signal drift can be seen in Hua and Pennell’s experiment and therefore, it still remains to be demonstrated for their reported technique to measure relatively smaller volume change over a long time.

In this paper, we report volume growth rate measurements of individual budding yeast cells with a recently developed MOS-FET-based microfluidic Coulter counter.²⁶ Taking advantage of the enhanced sensitivity of the MOSFET-based Coulter counter and the flexibility to move yeast cells back and forth through the sensing aperture, we were able to measure the volume growth rate of ten individual budding yeast cells. It is worth noting that since the technique measures the impedance pulse, the baseline impedance drift over time is not important. The measurement was performed with the YNB buffer, a traditional yeast culture medium, allowing cell growth in a physiologically relevant environment. The measurement results were analyzed and compared with existing mathematical models for cell growth rate.

2. Experimental methods

2.1 The baby machine and single yeast cells

Saccharomyces cerevisiae LYH3865 strain budding yeast¹ was cultured in YNB media containing 2% glucose and 0.2% glutamine in this study. A baby machine was used to produce populations of newborn daughter yeast cells.²⁷ The baby machine consists of a Millipore nitrocellulose porous membrane coated with poly-d-lysine. The membrane was supported by a stainless steel mesh sandwiched between two plastic funnels approximately 1 inch in diameter. A 2 mL active yeast culture was loaded onto the porous membrane and the yeast cells were adhered to the coated poly-d-lysine. The baby machine was then inverted and warm media were perfused through the porous membrane at a rate of 1 mL s⁻¹. As the yeast cells reproduce, the mothers stayed attached to the membrane while the daughters dropped and were collected in the media. The baby machine effluent was then diluted appropriately to contain about 100 cells mL⁻¹, and placed in an incubator for two hours. Typically, when yeast cells are introduced into fresh media they experience a lag phase, during which the yeast condition their media and then resume growth.²⁸ During the incubation step the diameter of the daughters may expand slightly, and finally reaches an average of 3.5 µm in diameter. The volume growth during the incubation period is slow and follows the trend as we measured before the bud emerges. Therefore, measurement starting from the end of the 2 hour incubation period still captures all essential volume growth characteristics that are of interest without losing important information.

2.2 Volume measurement with the MOSFET-based microfluidic Coulter counter

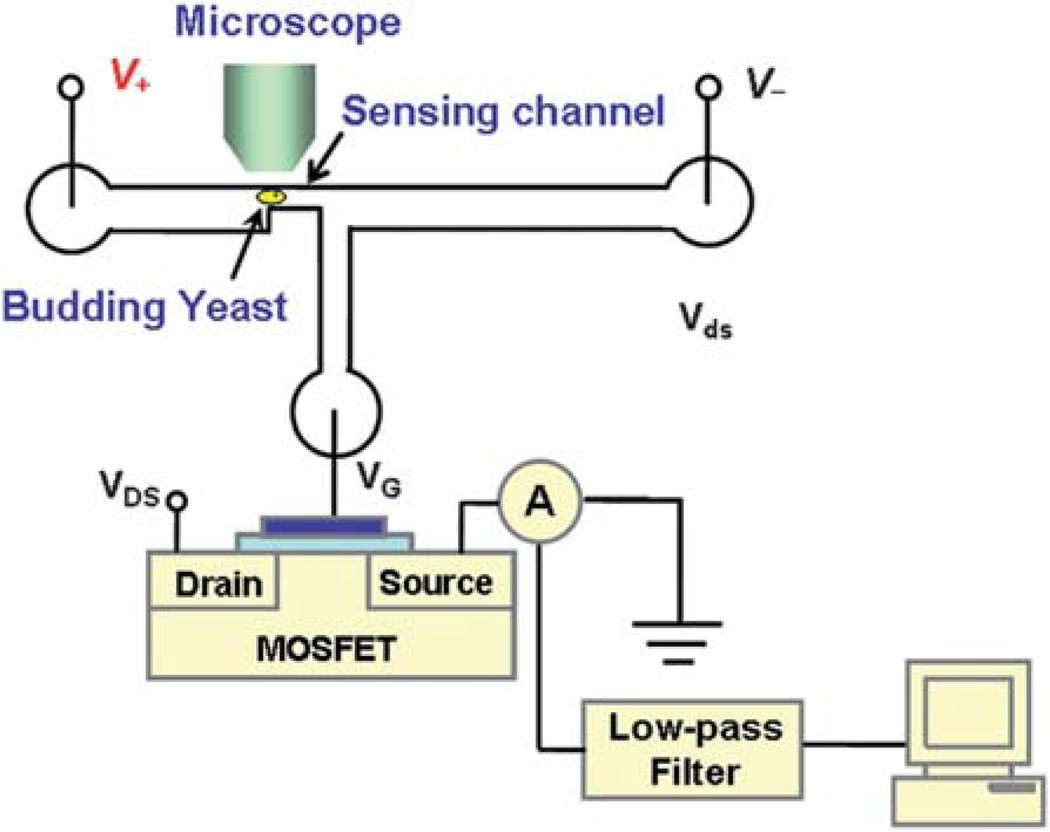
The volume measurement was performed with a recently developed MOSFET-based microfluidic Coulter counter.^26,29 As shown in Fig. 1, the device consists of a three-terminal PDMS microfluidic circuit bonded to a glass substrate. The horizontal fluidic circuit is composed of two large microchannels sandwiching a small sensing channel (15 µm × 15 µm cross-section and 50 µm long). A vertical microchannel connects the gate of a MOSFET (2N7000 N-channel FET, Fairchild Semiconductor Co.) to the exit of the sensing channel to detect the electric potential there, whose change is related to the resistance modulation of the sensing channel upon the translocation of a single yeast cell.

Fig. 1.

Schematic of the measurement setup of the MOSFET-based microfluidic Coulter counter (not to scale). The fluidic and MOSFET circuits are commonly grounded.

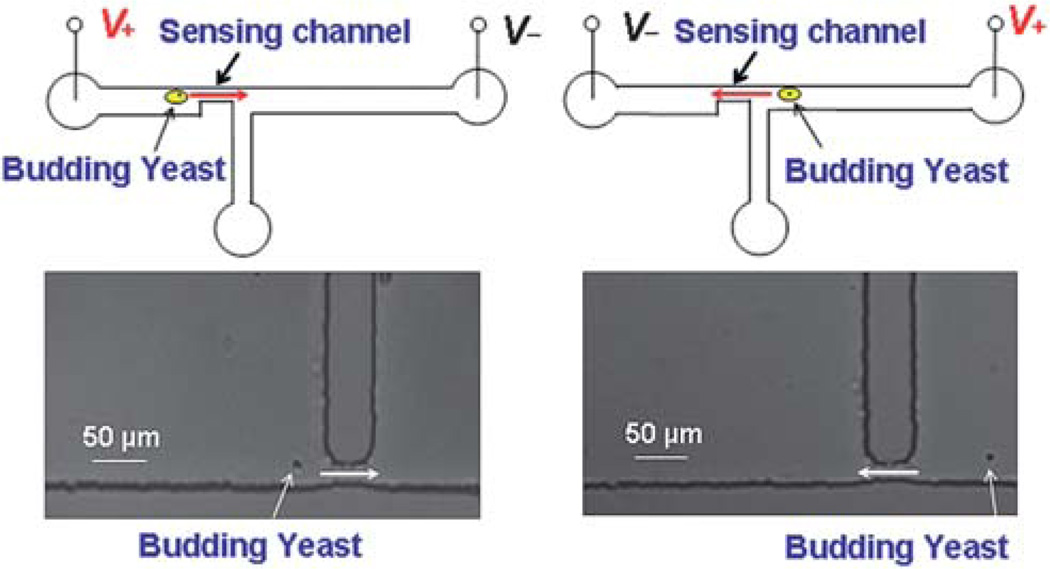
In the experiments, YNB media was first loaded into the three wells of the microfluidic device. The device temperature, monitored with a thermocouple (800004, Sper Scientific) every 15 min, was held constant at 29 ± 1 °C by radiation from a lamp. A small portion of daughter cells from the incubator was then loaded to the device and one cell was selected and moved back and forth through the sensing channel for volume growth rate measurements over ~2.5 hours. The motion of the cell was realized by electroosmotic flow induced by an electric bias applied across the horizontal channel, as shown in Fig. 2. The PDMS–glass microchannel has a negative zeta potential, which will lead to electroosmotic flow under the applied electric bias. If the electric field is reversed, the direction of the flow is also altered. In this manner, the selected cell can be moved back and forth by switching the polarity of the applied electric bias. Each time the yeast was translocated through the sensing channel from the upstream to the downstream, the MOSFET drain current modulation was recorded. The resistance modulation of the sensing channel from the translocation of the yeast cell leads to a modulation of the MOSFET’s gate potential, and hence, a pulse of the MOSFET drain current.

Fig. 2.

Schematic and microscopic images of a single yeast cell moved back and forth through the sensing channel by switching the applied electrical voltage. (Left panel) The yeast moves from the upstream to the downstream channel. (Right panel) The yeast moves back from the downstream to the upstream channel.

Theoretical analysis of the drain current modulation while the MOSFET is operating in the sub-threshold regime is given by eqn (1):²⁹

$$\frac{\mathrm{\Delta }{I}_{\mathrm{D}}}{I_{\mathrm{D}}}\approx (\frac{q}{\mathit{\text{kT}}}-\frac{1}{2V_{\mathrm{G}}})(V_{\mathrm{G}}-V_{-})\left(\frac{R}{R_{\mathrm{t}}}\right)\frac{\mathrm{\Delta }R}{R},$$ (1)

where I_D and ΔI_D are the MOSFET drain current and its modulation, respectively; q, k, and T are the elementary electronic charge, the Boltzmann constant, and temperature, respectively; V_G and V₋ are the MOSFET gate potential and the potential applied to the downstream well, respectively; R, ΔR, and R_t are the resistance of the sensing channel, its modulation, and the total resistance of the three horizontal channels, respectively. Based on eqn (1), the percentage modulation of the MOSFET drain current can be 30–50 times larger than the percentage modulation of the resistance. This amplified percentage modulation leads to a pulse easily detectable from baseline, which enhances the sensitivity of the device to extract smaller resistance modulation.

Under a DC electric field, the intact cell membrane of yeast cells would block ion transport, and hence, the cells behave like a good insulator.^30,31 If the yeast cell is regarded as a sphere and non-conductive relative to the highly conductive culture media, the resistance modulation to the baseline resistance can be written as:²⁹

$$\frac{\mathrm{\Delta }R}{R}=\frac{1}{4}\frac{\pi d^3}{\mathit{\text{LWD}}},$$ (2)

where d is the yeast cell diameter, L, W and D are the length, width and depth of the sensing channel, respectively. The above equation indicates that the resistance modulation of the sensing channel is directly proportional to the volume ratio of the cell to the sensing channel. Note that this expression is accurate only if the diameter of the sphere is much smaller than the size of the sensing aperture. In our case, because of the enhanced sensitivity, we can use relatively large channel to detect small cells, and the cross-sectional area ratio of the yeast cell to the sensing channel is less than 0.085. It has been shown that the upper limit of the cross-sectional area ratio for a linear response is about 0.16,²⁹ which is still much larger than that for the largest yeast cell in our measurements.

It is worth noting that the shape of a budding yeast cell is not strictly spherical, but can be described more appropriately as an ellipsoid. However, this can only lead to very small error. For example, it has been shown that compared to a sphere of the same volume, an ellipsoid of revolution with an axial ratio of 4 to 1 would give rise to a pulse difference of merely 3%.³² Given the fact that budding yeast usually have a much less axial ratio than 4 : 1, the error from non-spherical geometry will be minimal. A budded yeast cell presents a lopsided peanut shape, which is neither spherical nor elliptical. Fortunately, both our previous study and results in the literature show that for two microparticles of the same size stick together translocated through the sensing aperture of a Coulter counter, the resulted pulse amplitude would be doubled. This indicates that even for a lopsided peanut shape particle, the resistance modulation is still approximately proportional to that of the volume ratio, as long as the cross-sectional area of the particle is much smaller than that of the sensing aperture,²⁹ which is exactly the case in our measurements.

2.3 The effect of the baseline MOSFET drain current drift

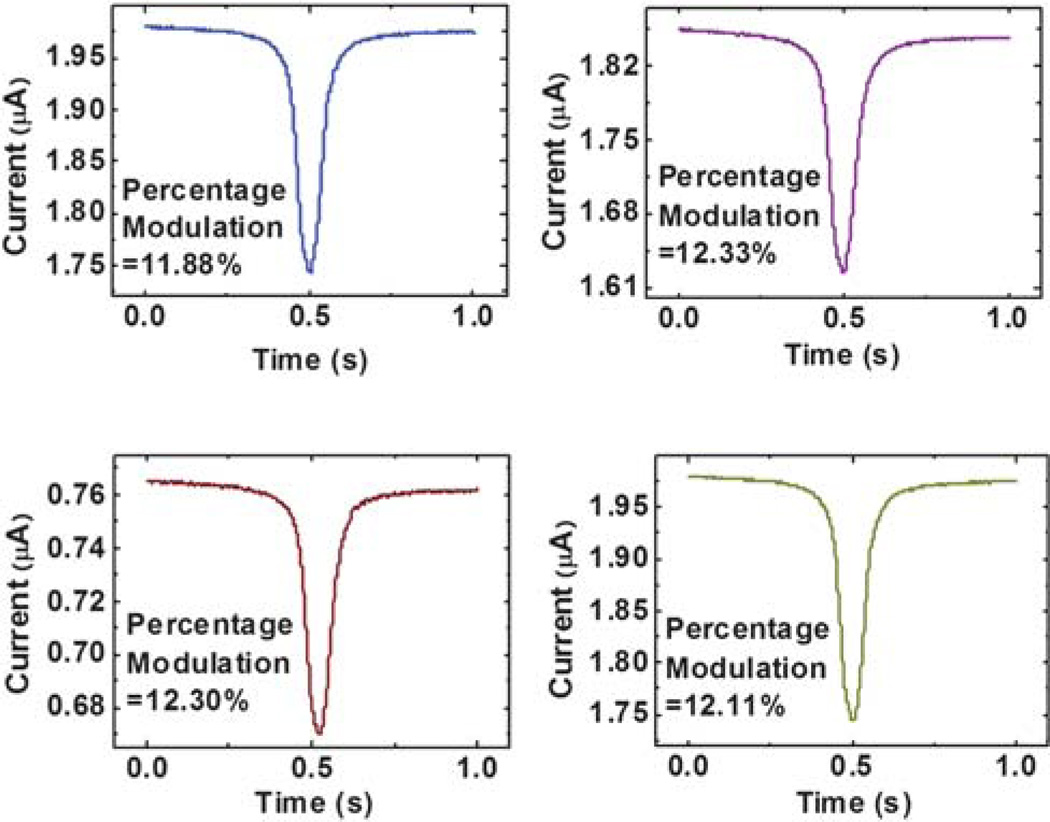
Eqn (1) and (2) indicate that the percentage modulation of the MOSFET drain current is linearly proportional to the volume ratio of the sensing objects to the sensing channel, as experimentally confirmed using polystyrene beads.²⁹ One more problem in the experiment is that the baseline MOSFET drain current could drift over time in the experiment, even though all the potentials supplied to the fluidic circuit and the MOSFET are kept constant. Fortunately, eqn (1) indicates that the percentage modulation of the MOSFET drain current is not a function of the baseline drain current if the MOSFET is working in its sub-threshold regime and V_G and V₋ are held constant. To prove this, we conducted a characterization run in which we moved the same polystyrene bead back and forth through the sensing channel 10 times during a period of a little over an hour and recorded the corresponding MOSFET drain current modulation. The characterization results show that indeed, the percentage modulation of the MOSFET drain current is not a function of the baseline MOSFET drain current, as shown in Fig. 3. The average percentage modulation of the MOSFET drain current is 12.17% with a standard deviation of 0.22%, considering the measurement uncertainty, the measured modulation can be regarded as the same. To extract the drain current modulation from the drifting baseline MOSFET drain current, a linear fit of the MOSFET drain current was first constructed over a short time period including the modulation event and the modulation was traced and extracted using a MATLAB 7.0.4 (MATLAB®) code.

Fig. 3.

Calibration results of the MOSFET drain current modulation as the same 4.84 µm in diameter polystyrene bead moves back and forth through the sensing channel.

2.4 Calibration of the size measurement with the microfluidic Coulter counter

To remove the measurement error from possible slight geometrical variations of the sensing microchannel because of various factors in the fabrication process, after each measurement of the budding yeast growth rate, the performance of each device was calibrated with more than a hundred of 4.84 µm in diameter polystyrene beads (PS05N, Bangs Laboratories, Inc.). The mean diameter of a total of 100 microbeads was taken as 4.84 µm, according to the quoted size of the microbeads from the manufacturer. The standard deviation for 100 microbeads as measured with the MOSFET-based microfluidic Coulter counter ranged from 0.2 µm to 0.3 µm, which was less than half of the quoted value (0.59 µm) from the manufacturer. To verify the size of the microbead used, we examined a total of 102 microbeads using an SEM. The mean diameter of the microbeads was determined to be 4.80 µm, in very good agreement with the quoted value (4.84 µm) from the manufacturer. The standard deviation of the 102 microbeads was calculated as σ = 0.15 µm, which is also much less than the quoted value (0.59 µm). The volume of the measured yeast cell was then calculated based on the percentage modulation of the MOSFET drain current from the translocation of the polystyrene beads. We believe that this calibration process could help to remove the systematic error of the volume growth measurement.

2.5 Measurement uncertainty

Several factors can contribute to the measurement uncertainty. The major factor contributing to the measurement uncertainty is from the calibration of the microfluidic Coulter counter with the 100 microbeads. Taking manufacture specified standard deviation of 0.59 µm, the uncertainty of the mean size of the 100 beads is then $0.59\times 2/\sqrt{100}=0.118$ µm.³³ This corresponds to a volume uncertainty of 0.118 × 3/4.84 = 7.31% with respect to the manufacture specified mean size of 4.84 µm, and therefore, leads to the same uncertainty in the calculated yeast cell volume. This uncertainty source is from the calibration process because of the non-uniformity of the polystyrene beads. It only leads to a systematic error in the measurement results but does not affect the trend of the yeast growth curve, which is one major consideration of the current research. More accurate measurements with less uncertainty can be achieved by using beads of more uniform size distribution for calibration. Another uncertainty source is the data extraction from the linear fit of the drifting baseline MOSFET drain current. The ten repetitive measurements of the same polystyrene bead present a standard deviation of 0.22%. Following the standard uncertainty analysis approach,³³ within 95% confidence, the uncertainty from this source is 2.262 times the standard deviation, which leads to an uncertainty of 0.498%. In addition, as indicated in the literature and discussed above, for Coulter counters, the uncertainty from the non-spherical geometry only leads to a deviation of about 3%. The standard uncertainty combining these uncertainties can then be calculated as $\sqrt{{(7.31\%)}^2+{(0.489\%)}^2+{(3\%)}^2}=7.92\%$.

2.6 Effects of the electric field

A complete understanding of the effects of the electric field on cell growth is not achieved yet but it is known that the external electric field affects cell growth because it can generate stress on the cell membrane, reorganize the membrane components, and even kill the cell.^34,35 The interaction between the applied electric field and cells occurs through both direct electric field interaction and induced Joule heating effect.³⁶ The imposed transmembrane potential induced by an external DC electric field across the membrane of a spherical cell in suspension can be approximated as:³⁷

$$|\mathrm{\Delta }U|=1.5|E|R,$$ (3)

where |E| denotes the external electric field and R is the cell radius.

Beside the imposed transmembrane potential, cells generally maintain a negative endogenous transmembrane potential due to the existing electric field at the cell membrane. For fungi such as budding yeast, the endogenous potential ranges from −120 to −250 mV.³⁸

In our measurement, the maximum electric field is inside the small sensing channel as 122.6 V cm⁻¹, whereas the minimum electric field of 2.3 V cm⁻¹ is within the upstream microchannel. If the yeast is assumed to be a sphere with a diameter of 4 µm, the highest imposed transmembrane potential is only 36.77 mV while the cell traverses the sensing channel. In addition, the yeast translocates the sensing channel within a time period of 0.2 s. The relatively low imposed transmembrane potential and the short time period for the yeast to experience this potential help to reduce the effects of the electric field on the cell growth.

As to the Joule heating effect, because the electric field is only applied for about 1 minute every 15 to 20 minutes, conservative estimation yields a maximum temperature rise of 0.2 °C in the sensing channel, following the discussion in literature.^39,40 Since this temperature rise is smaller than the natural temperature variation 1 °C for cells,³⁶ we believe that neglecting it will not cause any significant error in the experiment.

3. Results and discussions

3.1 Experimental results

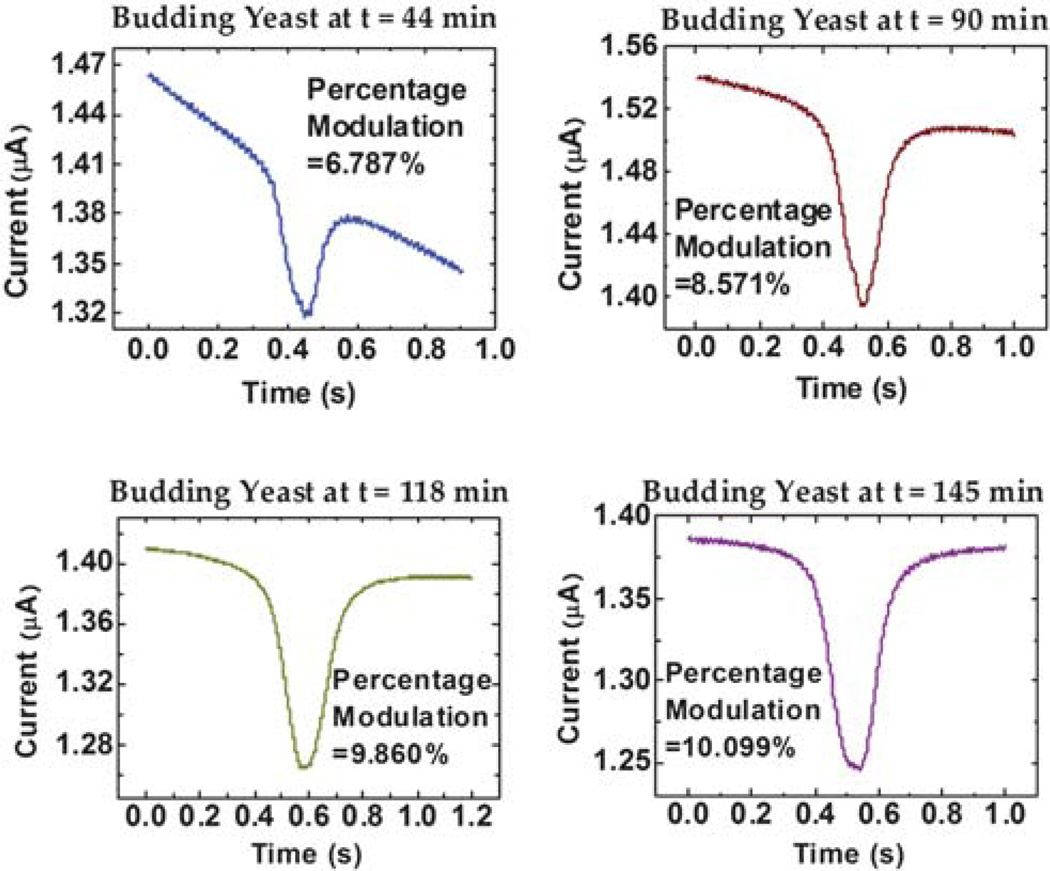
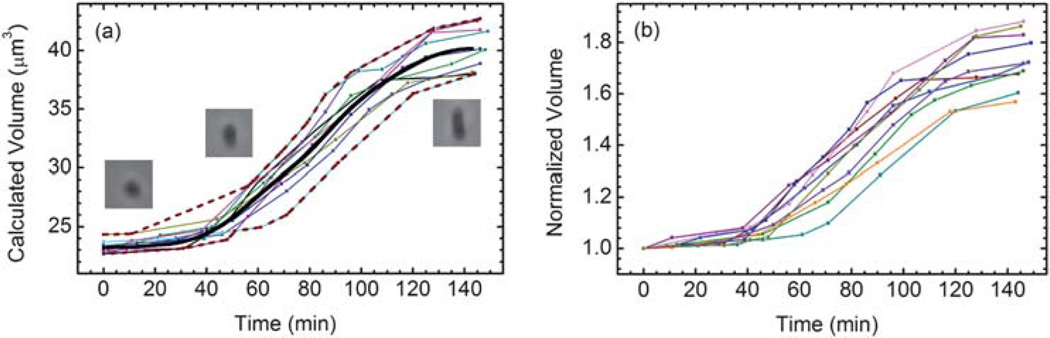
Fig. 4 shows the recorded MOSFET drain current as a function of time when a budding yeast cell was translocated through the sensing channel at different time points. Each translocation event corresponds to one MOSFET drain current modulation and the percentage modulation of the MOSFET drain current increases over time, because of the increasing yeast cell volume as the cell grows. Fig. 5a plots the volume growth profile of ten different individual budding yeast cells, whose volumes increase from 22.7–24.3 µm³ to 37.9–42.7 µm³. The initial volume dispersion may be attributed to a combination of measurement uncertainty and inherent population variation. The volume of daughters eluted from the baby machine, even very uniform, is not the same.²⁷ This volume difference can be slightly amplified in the incubator, even though ideally the yeast cell will not grow during the two hours before they adapt to the suitable condition.

Fig. 4.

Drain current modulation of the MOSFET measured for a single yeast cell at different times.

Fig. 5.

(a) The absolute volume growth over time for 10 different daughter yeast cells. The volume growth data are seen to be bounded by the dashed red curves, computed as the pointwise minimum and maximum value of the ten linearly interpolated curves. (b) The normalized volume growth curves with respect to the initial volume of each yeast cell.

Fig. 5a depicts the volume growth curves for ten individual budding yeast cells. Four curves are composed of 9 data points and the rest six curves are composed of 10 data points. The time at which the first measurement is conducted inside the microfluidic device is defined as t = 0. The average interval time step between each measurement is around 15 min. This interval was selected based on two considerations: (1) to minimize the effects of the electric field; and (2) to take one measurement while the cell volume growth is not exceeding 10%. A simple formula based on an exponential upper bound was used to compute the time step. For instance, if the growth rate is assumed to be 0.62% per minute,⁴¹ then sampling every h minutes h < 1000/6.2 × ln (1.1) ≈ 15 min will suffice.

All ten measured growth curves display a sigmoid shape characterized by an increase in slope where budding occurs, followed by a decrease in slope when the budded daughter cell becomes mature. The data are seen to lie within an envelope that is bounded by two sigmoid curves computed from the family of interpolants and shown as the dashed red lines in Fig. 5a. The solid black curve at the center represents the pointwise average over the 10 interpolants of the data. The maximum root mean square deviation of the data from the mean curve is 1.38 µm³. The small residual is a further indication, beyond visual inspection, that the mean curve well describes the central tendency of the data. The mean curve exhibits the sigmoid shape, which compares well with published literature.^9,10

The percentage growth of the yeast cell volume can be better perceived in a normalized growth rate, where the volume of each yeast cell is normalized with respect to its initial volume, as shown in Fig. 5b. It can be seen that the total volume of the mother cell and its daughter can increase by 56% to 88%, which indicates that the volume of the mother and daughter pair does not double prior to segregation at the end of mitosis. This phenomenon is attributed to the observation that the daughter cell is smaller at division than the mother.⁶ The magnitude of the size difference depends on the yeast strain, the growth environments and the replicative age of the mother. The larger the mother daughter size disparity the faster an initially synchronous culture will dephase. Quantitative data of the type shown in Fig. 5b will help us to more accurately parameterize models of yeast population growth and division.⁴¹

3.2 Data analysis

In this section we provide an analysis of the measured data to investigate biophysical aspects of the yeast growth. An aspect of the analysis is to quantify the variation of the data and to determine the features that appear systematic. One way to accomplish this is to compute a mean curve and a bounding envelope, and to analyze the individual measurements in relationship to these. Further we use the mean curve and its derivative to examine local and global models of growth. The volume measurements from different experiments were made at non-corresponding time points, with non-uniform spacing within an experiment. Data analysis in such a situation is best performed using interpolation. All calculations were performed in the Mathematica environment (Wolfram Research Inc.). The measured data were linearly interpolated and the pointwise min and max were computed to produce the upper and lower boundary curves. The effect of interpolation order has been checked by also performing third order interpolation and we found essentially no effects on the appearance of the mean curve or important derived quantities such as the RMSD.

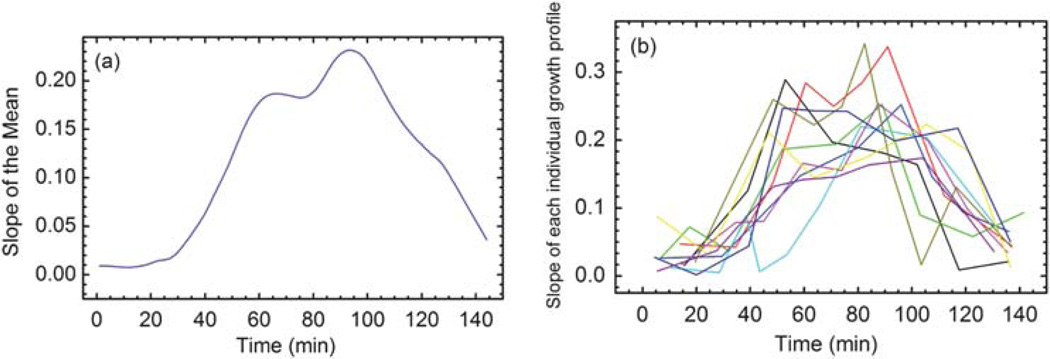
An essential tool to analyze the properties of the data is the derivative of the mean curve shown in Fig. 6a. The derivative provides a natural way to decompose the growth into several phases. Fig. 6a indicates that the qualitative behavior of the derivative of the mean curve recapitulates the features of each individual curve (as shown in Fig. 6b) without introducing distortion. The essential qualitative behavior is that the slope(s) rise to a maximum and then decline, while always remaining positive, as is to be expected of growth phenomena. The mean curve begins with a 30–40 minute period of near linear growth, with a rate of ~0.01 µm³ min⁻¹. The derivative is seen to be multimodal with a brief shelf starting at 60 minutes that interrupts a 20–30 minute period of exponential like growth. The shelf then rises to the global maximum at 95 minutes. After this the derivative is in decline, nearly returning to its original value of 0.01 µm³ min⁻¹. The links between yeast growth and metabolism are still incompletely understood. Many metabolic shifts and effects are known in yeast, too numerous to review or to comprehensively cite.^42,43 We draw attention to one well known metabolic shift that impacts growth rate and is an interesting phenomenon that could be studied with the technique described in this paper. The diauxic shift is the transition from growth on fermentable sugars such as glucose to that on non-fermentable carbon sources such as ethanol, lactate, acetate and others, that become available or have accumulated in the media during prior metabolic activity.^44,45 This phenomenon is commonly associated with a bisigmoid growth curve where the growth rate slows and then increases again. Often this behavior is attributed as a clever strategy on the part of yeast to outcompete other species which are less alcohol tolerant by rapidly consuming the high chemical potential carbon sources. Similar metabolic behaviors that result in changes in growth rate, such as the acetate switch, are well known in the bacterial world.⁴⁶ Several of the individual derivative curves, shown in Fig. 6b, at least four of the ten, display multimodality, providing evidence that this feature is realized, perhaps in a subpopulation. However, the derivative data are noisy and we have small sample. We therefore conclude that the shelf in the derivative of the mean curve is an interesting and perhaps spurious feature revealed by the analysis that requires further measurements for confirmation.

Fig. 6.

(a) The slope of the growth curve calculated as the derivative of the mean curve with respect to time. (b) The slope of each individual growth profile. The slopes confirm that the mean curve captures the features of each individual curve.

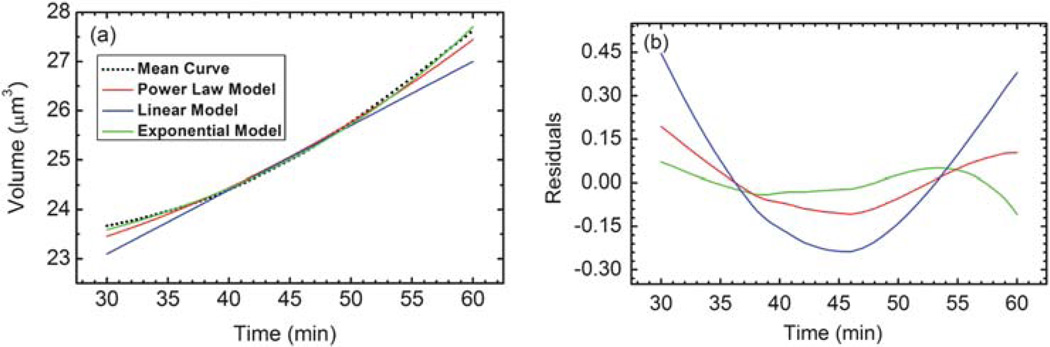
Now we turn to analyzing mathematical descriptions or models of the mean growth curve. The data from 30 minutes to 60 minutes are best fit by an exponential model, as shown in Fig. 7. Three growth models are considered. In Fig. 7a, the green curve depicts the best fit exponential model of the form ae^ct + b, the blue curve depicts the best fit linear model of the form at + b, while the red curve represents a power law model of the form at^c + b. While the linear model has one fewer parameter, it is clear from the mean curve and its derivative, that the growth data display non-zero curvature. While the power law model fits the data qualitatively, the residuals in Fig. 7b show that the exponential fit is a better representation. The residuals also reveal that the time window in which the yeast are growing near-exponentially lies within the time interval from 37–54 minutes. The best fit parameters of the three models are shown in Table 1. These parameters can be used to accurately estimate the growth rate within this portion of the growth curve.

Fig. 7.

(a) The best fit models of three different functions for the local volume growth between 30 and 60 minutes. (b) The residuals of the three best fits.

Table 1.

Best fit parameters and RMSD determined for the three different models against the mean curve data between t = 30 min and t = 60 min

Parameter	aect + b	at + b	atc + b
a	0.43	0.13	0.00068
b	22.03	19.20	22.33
c	0.043		2.18
RMSD	0.036	0.20	0.083

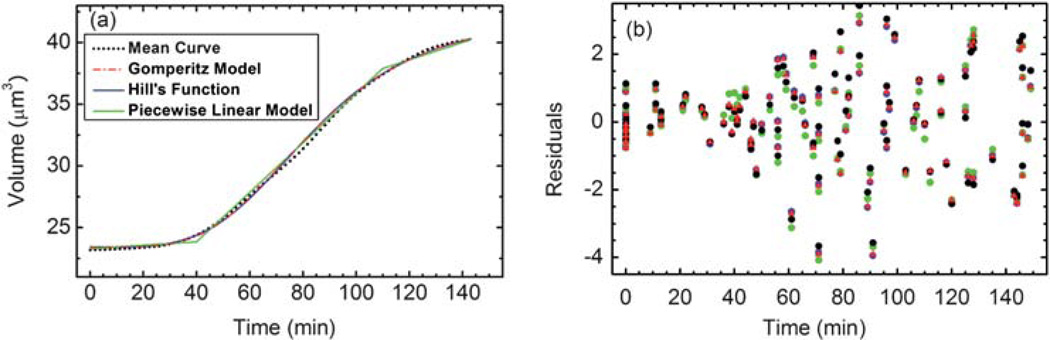
Globally the growth data support several sigmoid models nearly equally well: a piecewise linear (PL) model with three segments,

$$\text{PL}(t)=\{\begin{array}{cc}\hfill a(t-40)+b\hfill & \hfill \text{for }0\le t<40\hfill \\ \hfill (d-b)(t-40)/70+b\hfill & \hfill \text{for }40\le t<110\hfill \\ \hfill c(t-110)+d\hfill & \hfill \text{for }t\ge 100\hfill \end{array},$$ (4)

a Gomperitz growth model, a + b exp (−exp (−ct + d)), and a Hill’s function, a + (bt^d/(t^d + c^d)), all fit the data with nearly the same root mean square deviation (RMSD) as the mean curve, as shown in Fig. 8 and summarized in Table 2.

Fig. 8.

(a) Three different models for the global volume growth versus the mean experimental growth curve. (b) The residuals of the three different models in the corresponding colors.

Table 2.

Best fit parameters determined for the three models for the global growth

Parameter	Hill	Gomperitz	PL
a	23.4171	23.4366	0.0138779
b	19.001	18.4648	23.8511
c	84.2354	0.0342305	0.0706643
d	3.92566	2.47842	37.9011

4. Summary

In this paper, we report on the measurements of the volume growth of individual budding yeast with a MOSFET-based microfluidic Coulter counter. The enhanced sensitivity and the ability of using YNB media in the device allow for direct measurements of the volume growth rate of individual live yeast cells with a high resolution.

Measurement results of ten individual budding yeast cells indicate a sigmoid volume growth profile with reduced growth rates (0.01 µm³ min⁻¹) at the initial and the final stage of the cell cycle. The maximum growth rate in the fast growth phase is more than an order of magnitude larger, around 0.25 µm³ min⁻¹. Detailed analysis of the growth curve strongly suggests an exponential growth phenomenon and we conclude that the local exponential growth is a genuine feature of volume growth. However, the global growth curve can be described equally well by a piecewise linear model and nonlinear growth models.

The simple and convenient volume growth measurement technique and the ability to use live-cell culture media in the measurements provide the possibility to measure yeast cell volume growth under different relevant physiological conditions to study the effects of different factors on yeast cell cycle.