A Stretching Device for High Resolution Live-Cell Imaging

Abstract

Several custom-built and commercially available devices are available to investigate cellular responses to substrate strain. However, analysis of structural dynamics by microscopy in living cells during stretch is not readily feasible. We describe a novel stretch device optimized for high-resolution live-cell imaging. The unit assembles onto standard inverted microscopes and applies constant magnitude or cyclic stretch at physiological magnitudes to cultured cells on elastic membranes. Interchangeable modular indenters enable delivery of equibiaxial and uniaxial stretch profiles. Strain analysis performed by tracking fluorescent microspheres adhered onto the substrate demonstrated reproducible application of stretch profiles. In endothelial cells transiently expressing EGFP-vimentin and paxillin-DsRed2 and subjected to constant magnitude equibiaxial stretch, the 2-D strain tensor demonstrated efficient transmission through the extracellular matrix and focal adhesions. Decreased transmission to the intermediate filament network was measured, and a heterogeneous spatial distribution of maximum stretch magnitude revealed discrete sites of strain focusing. Spatial correlation of vimentin and paxillin displacement vectors provided an estimate of the extent of mechanical coupling between the structures. Interestingly, switching the spatial profile of substrate strain reveals that actin-mediated edge ruffling is not desensitized to repeated mechano-stimulation. These initial observations show that the stretch device is compatible with live-cell microscopy and is a novel tool for measuring dynamic structural remodeling under mechanical strain.

INTRODUCTION

Mechanical stresses such as tension, compression, and shear play important roles in regulating cell growth and function. In the vasculature, hemodynamic stimuli consisting of fluid shear stress and cyclic circumferential strain from pulsatile blood flow regulate smooth muscle and endothelial cell migration, proliferation, and protein expression.^{8, 19} In early development, mechanical tension may impact cell fate decisions during embryogenesis and control morphogenetic movements during convergent extension.^{17, 26} The lung, bone, and skeletal muscle are other systems in which physical cues are critical for cell development and function (reviewed in ²²). Disruption of normal mechanical loading contributes to a wide range of pathological conditions, including hypertension, atherosclerosis, and osteoporosis. During mechanical strain, resultant forces are transmitted from the basement membrane to cells via receptors that connect the extracellular matrix to the cytoskeleton. Since many cellular components experience tension, a variety of mechanotransducers have been proposed, including integrins, focal adhesion proteins, and the cytoskeleton.^{9, 26} However, mechanisms by which cells transduce external physical cues into biochemical communication remain elusive.

Accumulating evidence from studies using total internal reflection fluorescence microscopy suggests the existence of a molecular clutch between focal adhesion components and the actin cytoskeleton at the leading edge of migrating cells.^{3, 13} In endothelial cells exposed to a step increase in hemodynamic shear stress, strain focusing in the intermediate filament network occurs within minutes near locations consistent with cytoskeletal interaction with focal adhesion sites or intercellular junctions.¹¹ Redistribution of intracellular stress is accompanied by increased actin edge ruffling,⁵ decreased centripetal remodeling of stress fibers, and the formation of new focal complexes.²¹ These data demonstrate that rapid force transmission through the cytoskeleton to discrete locations of the cell serves to initiate biochemical signaling, but the involvement of force transmission through molecular clutches associated with cell-substrate adhesion sites would be more clearly demonstrated by directly measuring dynamic structural remodeling events in response to mechanical stretch of the substrate.

A major hurdle to performing such measurements is the difficulty to perform high-resolution imaging while applying stretch. Although several custom-built^{1, 4, 6, 15, 18, 20, 24, 27, 28} and commercially available (e.g. Flexcell International) devices have been developed to apply substrate stretch to cells in vitro, few existing designs are optimized for high-resolution live-cell microscopy. Existing devices compatible with continuous visualization of cells are capable of only limited image resolution and thus only provide measurements of orientation and shape at the cellular length scale. For optical measurements at higher spatial resolution, investigators have largely relied on imaging fixed cells, which provides snapshots of structural adaptation but does not allow measurements of spatiotemporal dynamics. Additional limitations of existing stretch devices include: (1) too large or mechanically complex for assembly onto a microscope stage without interfering with the optics; (2) only compatible with upright microscopes and limited numerical aperture; (3) designed for a specific spatial strain profile (i.e. separate devices are required to apply biaxial and uniaxial strain); and (4) manually operated or otherwise not designed for cyclic stretch.

To address these limitations, we designed a new stretch device optimized for high-resolution live-cell imaging during the application of arbitrary spatiotemporal strain profiles. The unit mounts onto the stage of standard inverted microscopes. Modular indenters enable delivery of equibiaxial and uniaxial strain to cultured cells on elastic membranes at magnitudes up to 14%, spanning the physiological range. Spatial heterogeneity of strain associated with vacuum suction is avoided, and a spatially uniform strain field can be achieved. Additionally, the elastic membrane effectively remains stationary during stretch so that cells can be observed continuously. Analysis of the imposed strain field performed by tracking fluorescent microspheres adhered onto the substrate confirmed that equibiaxial and uniaxial strain were uniform at locations across the viewable area of the membrane. The intracellular strain fields computed from displacements of focal adhesions and intermediate filaments indicate mechanical coupling of focal adhesions and the cytoskeleton in aortic endothelial cells. Furthermore, switching the spatial profile of substrate strain reveals that actin-mediated edge ruffling is not desensitized to repeated mechano-stimulation, unlike the response to fluid shear stress.

MATERIALS AND METHODS

Device Design

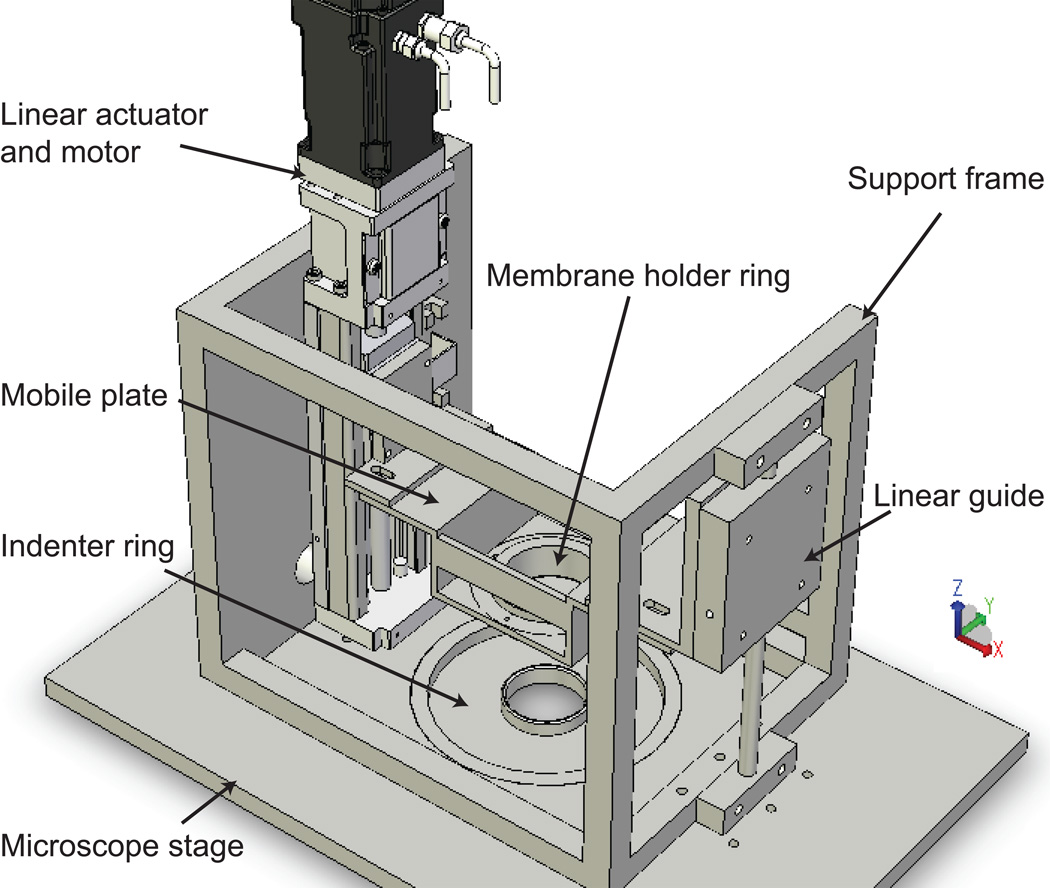
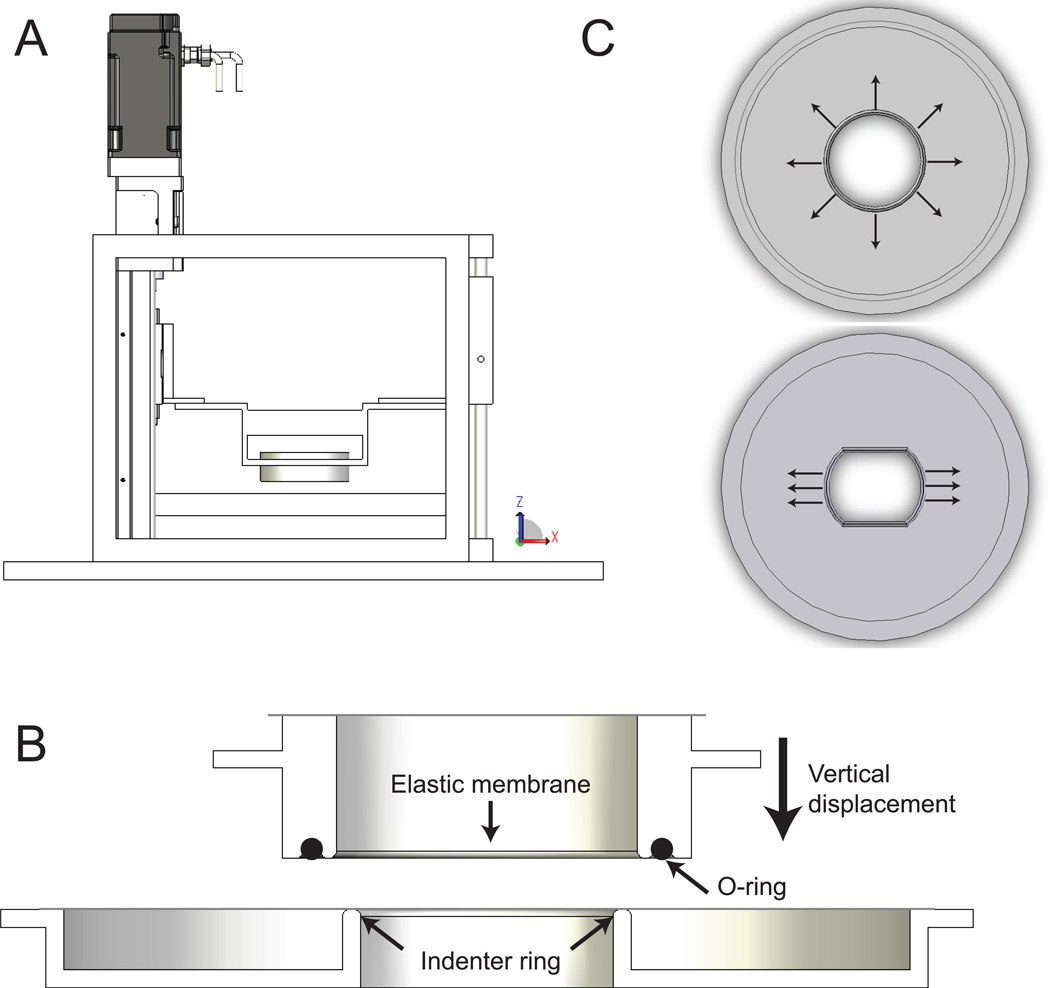
The stretch device (Figures 1 and 2 A) was developed for high-resolution imaging of living cells and tissues during constant magnitude and cyclic stretch. The principle of stretching is based on indenter designs described elsewhere.^{14, 18, 25, 27} The membrane holder ring (MHR) is a hollow cylinder with a flange and a circular groove on the bottom. A silicon O-ring (2-029, McMaster-Carr, Elmhurst, IL) is used to secure a transparent silicon elastic membrane (0.25 mm-thick, Specialty Manufacturing Inc., Saginaw, MI) in the bottom circular groove. The MHR–elastic membrane culture vessel fits into a conventional 6-cm cell culture dish (11.2 cm² working area), and the flange allows easy transfer of cells from the incubator to the stretch device. Screw positions on the flange connect the MHR with the mobile plate (MP). The MP is connected to a linear actuator (URS2602A, Danaher Motion, Washington, DC) on one end and a linear guide (1BA06BH0, Danaher Motion) on the other via its two arms. Vertical displacement of the MP is driven by a servomotor (AKM-13C, Danaher Motion) coupled to the linear actuator and controlled by a programmable encoder (S20260-CNS, Danaher Motion), which enables programming of arbitrary temporal waveforms of motion. Ball bearings in the linear guide prevent horizontal movement of the MP. The modular indenter ring (IR) serves as a microscope stage insert. Since the diameter of the IR is smaller than that of the MHR, the membrane is stretched over the IR as the MP and the MHR are lowered (Figure 2 B). The shape of the indenter specifies whether the spatial strain profile is equibiaxial or uniaxial (Figure 2 C).

Figure 1.

Cell stretcher schematic. The elastic membrane with cultured cells is assembled in the membrane holder ring. The membrane holder ring is fixed to the mobile plate. Vertical motion of the mobile plate is driven by the motor along the linear actuator. The membrane is stretched over the indenter ring, which serves as the microscope stage insert. The linear guide restricts horizontal movement of the mobile plate. Spatial and temporal strain profiles are controlled by the shape of the indenter ring and a programmable encoder, respectively.

Figure 2.

(A) Side view of the cell stretcher. (B) Cross-sectional view of the membrane holder ring (MHR) and the indenter ring (IR). The elastic membrane is secured in the circular groove at the bottom of the MHR using a silicon O-ring. At the home position the membrane is flush with the indenter ring. Vertical displacement of the MHR driven by the motor stretches the membrane over the indenter ring. The vertical position of the membrane remains stationary during stretch. (C) Modular indenter designs allow easy switching between equibiaxial (top) and uniaxial (bottom) strain profiles.

Continuous observation of cells cultured on the elastic membrane is possible since the focal distance remains effectively constant during the stretch process and the recessed stage insert enables access of objective lens to its full working distance. The microscope stage position in the z-direction is adjusted to account for minor changes in membrane thickness as a function of stretch amplitude. Focus shifts are linear with respect to stroke amplitude and constant as a function of number of stretch cycles, thereby allowing preprogramming of the stage position to “autofocus” during repeated stretching. The MP arm lengths can be slightly adjusted in both x- and y- directions over a ~1 mm range to ensure that the MHR and IR are concentric. An alignment ring that fits securely between the inner diameter of the MHR and the outer diameter of the IR was fabricated to aid this process. The device frame (Figure 1) provides structural support for the linear actuator and the linear guide and is mounted onto the microscope stage. The MHR and IRs were machined from 316L stainless steel and electropolished to a pharmaceutical-grade finish (Flow Products, Kenosha, WI), and other machined components were constructed from aluminum. The microscope stage and stretch device were enclosed in an Okolab microscope cage incubator (Warner Instruments, Hamden, CT) and maintained at 37 °C and 5% CO₂. The cell culture microenvironment was maintained at pH 7.4 by equilibration with 5% CO₂ at 100% relative humidity using a custom culture dish lid.

Calibration

Fluorescent microspheres (0.5 µm, Polysciences, Inc, Warrington, PA) adhered onto the elastic membrane served as fiducial markers for homogenous finite strain analysis. The membrane was assembled into the MHR, secured with a silicon O-ring, and subjected to five different levels of stretch to construct a calibration curve relating the motor stroke amplitude (1–3 motor revolutions; vertical displacements ranging from 2.25–6.76 mm) to the resulting 2-D Lagrangian strain magnitude. Images were acquired for each constant magnitude stretch–relaxation cycle, and marker coordinates (on average 40 µm apart) were determined in each image.

Delaunay triangulation was used to find the smallest set of triangles connecting all the markers in an image, which provided maximum spatial resolution for estimating the strain field. In order to maximize the sensitivity to detect strain magnitude, triangles that deviated significantly from a regular (equilateral) shape were rejected using the following algorithm, which was adapted from a built-in algorithm in SALOME (www.salome-platform.org). The aspect ratio quality Q_κ for triangle element κ was computed as Q_κ = α h_maxs_κ/Δ_κ, where h_max is the length of the longest edge, s_κ is the semiperimeter, and Δ_κ is the area. The normalization factor α was chosen so that Q_κ = 1 when κ is an equilateral triangle. For a 2-D, 3-node element with vertices A, B, and C, $\alpha =\sqrt{3}/6,h_{\text{max}}=\text{max}(\overline{\mathit{\text{AB}}},\overline{\mathit{\text{BC}}},\overline{\mathit{\text{AC}}}),s_{\kappa }=(\overline{\mathit{\text{AB}}}+\overline{\mathit{\text{BC}}}+\overline{\mathit{\text{AC}}})/2,\text{ and }{\mathrm{\Delta }}_{\kappa }=\sqrt{s_{\kappa }(s_{\kappa }-\overline{\mathit{\text{AB}}})(s_{\kappa }-\overline{\mathit{\text{BC}}})(s_{\kappa }-\overline{\mathit{\text{AC}}})}$. In this study, the threshold for Q_κ was set at 2.

The Lagrangian strain tensor E_ij for each local triangle element was computed based on the change in segment lengths before and after deformation as described previously.¹¹ The components of E_ij were computed by solving the equation ds² − ds₀² = 2E_ijda_ida_j, where ds and ds₀ are the deformed and undeformed distances between adjacent vertices, respectively, and da_i is the projected initial distance onto the i^th axis. Einstein’s summation convention for repeated indices is implied. In order to compute the mean strain magnitude across an image, strain components from triangle elements were weighted by the area Δ_κ. To verify strain field uniformity over large regions of the substrate, strain tensors were compared in fields of view located at varying radial distances from the center of the elastic membrane. At least 10 independent experiments were performed for each spatial strain profile, and each measurement was an average of three repeated stretch cycles. Strain relaxation and hysteresis in repeated cycles were not observed, indicating that the substrate underwent elastic deformation.

Cell Culture and Image Acquisition

Bovine aortic endothelial cells were maintained in Dulbecco’s Modified Eagle Medium (DMEM, Gibco, Gaithersburg, MD) supplemented with 10% heat-inactivated newborn calf serum (HyClone, Logan, UT), 2.92 mg/ml L-glutamine (Gibco), 50 u/ml penicillin (Gibco), and 50 µg/ml streptomycin (Gibco) using established techniques.¹⁰ Cells were transiently transfected with plasmid DNA encoding enhanced green fluorescent protein (EGFP)-vimentin (pEGFP-hVIM-Myc; a gift from R. D. Goldman, Northwestern University), paxillin-DsRed2 (a gift from A. F. Horwitz, University of Virginia), and pEGFP-actin (Clontech, Mountain View, CA) using a liposome-mediated method according to manufacturer’s recommendations (Lipofectin, Invitrogen, Carlsbad, CA). After 24 h, transfected cells were seeded on a sterilized elastic membrane coated for 2 h with 15 µg/ml fibronectin (Sigma-Aldrich, St. Louis, MO) and assembled in the MHR. Fluorescent microspheres (0.1 µm, Molecular Probes, Eugene, OR) that were pre-adhered by drying on the elastic membrane prior to fibronectin coating were used to measure the imposed substrate strain. Image stacks with 8–10 optical sections spaced 300 nm apart were acquired before and 3 min after application of constant magnitude equibiaxial stretch (3 motor revolutions; vertical displacement of 6.76 mm) through a 40X/0.75 NA objective lens (Olympus America, Center Valley, PA) using a DeltaVision RT Restoration Microscope (Applied Precision, Issaquah, WA) and a cooled CCD camera (MicroMax, Princeton Instruments, Trenton, NJ). For cyclic stretch experiments, the indenter motion was sinusoidal, and time-lapse images of endothelial cells expressing EGFP-actin were acquired every 3 min. The motor was held at the stretched position for ~30 s during acquisition of multi-wavelength 3-D image stacks (4 optical sections spaced 300 nm apart). The motion profile was immediately restarted after image acquisition. To switch between equibiaxial and uniaxial stretch profiles, the MP was raised, the indenter was replaced, and cyclic stretch was restarted within 2 min. Because the MHR was not removed, it remained concentric with the new indenter, and the field of view remained unchanged. Since the IR consisted of a narrow ridge (so surface area of contact between the IR and the elastic substrate was minimized) and was polished to pharmaceutical processing grade (to minimize friction), the strain rate of elastic substrate was faster than detectable under image acquisition protocols used in this study. As a result, temporal changes in substrate strain were considered to be the same as those programmed into the motor. Images were deconvolved in softWoRx software (Applied Precision) using a constrained iterative algorithm and an experimentally measured point spread function.¹²

Computation of Cytoplasmic Strain Field

Optical sections close to the elastic membrane with vimentin intermediate filaments or paxillin-containing adhesion sites in focus were selected for analysis. Vimentin optical sections were located on average 600 nm above paxillin sections. To compute the projected 2-D intracellular deformation field as described by the Lagrangian strain tensor, 10–30 corresponding landmark positions were tracked before and after constant magnitude equibiaxial stretch. In cells expressing EGFP-vimentin and paxillin-dsRed2, cytoskeletal positions where three or more filaments intersect and individual adhesion sites were chosen as vertex points, respectively. Delaunay triangulation was used to connect adjacent vertices, and E_ij was computed from the shape change of triangle meshes as described above. To determine the magnitudes and directions for the principal components of strain in each mesh element, the eigenvectors of E_ij were computed. The eigenvalues (E_I, E_II), which are the principal values of strain oriented along the principal axes determined by the unit eigenvectors, were expressed as the principal stretch ratios (λ_I, λ_II) as computed from E_i = 1/2(λ_i² − 1). The principal stretch ratios represent the maximum and minimum stretch along axes oriented such that the shear component in the strain field is zero. Computations were carried out using MATLAB (MathWorks, Natick, MA). A total of five cells from three separate experiments were analyzed.

Statistical Analysis

Data are presented as mean ± standard deviation unless otherwise specified. The Student’s t-test was used to determine statistical significance between groups. Differences were considered statistically significant when p<0.05.

Results

Application of Uniform Equibiaxial or Uniaxial Strain

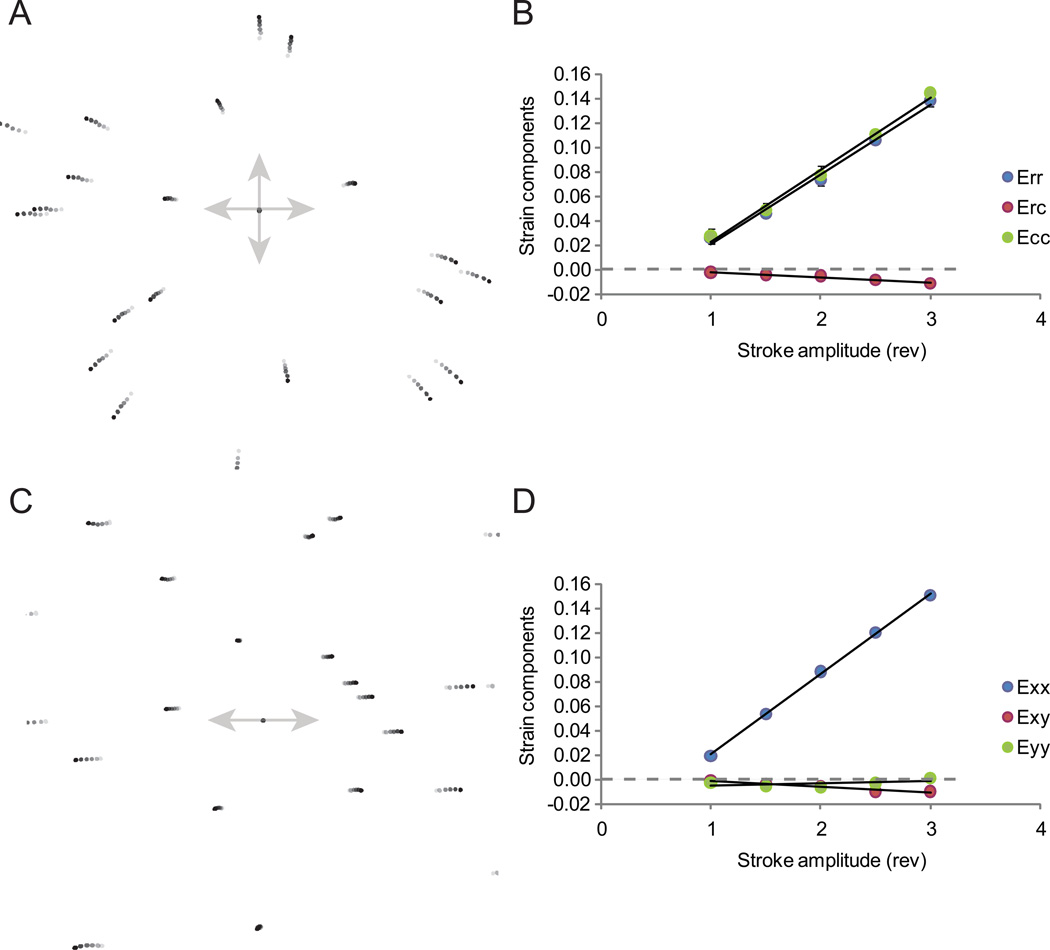
Fluorescent microspheres adhered onto the elastic membrane served as markers for homogenous finite strain analysis. Membranes were stretched to five motor stroke amplitudes (1, 1.5, 2, 2.5, and 3 motor revolutions) in random order to avoid biasing, and the three components of the 2-D strain tensor were measured. Overlay images of representative fluorescent markers demonstrated that marker displacements followed linear trajectories with respect to stroke amplitude when substrates were subjected to either equibiaxial (Figure 3 A) or uniaxial (Figure 3 C) strain. During equibiaxial strain, marker trajectories were oriented in radial directions relative to the center of the substrate, whereas during uniaxial strain, markers followed paths oriented parallel to the strain axis. Using polar (r, c) coordinates for equibiaxial strain and Cartesian (x, y) coordinates for uniaxial strain, the relationship between E_ij and motor stroke amplitude from independent experiments was determined using a linear curve fit (R² > 0.99) (Figure 3 B, D). Small variations in E_ij for repeated stretch cycles indicate that the measurements were reproducible at all stroke amplitudes.

Figure 3.

Calibration of substrate strain using fluorescent microspheres as fiducial marks. (A, C) Overlay image of fluorescent microspheres subjected to different levels of (A) equibiaxial and (C) uniaxial stretch. Markers aligned at substrate center. Gray level indicates motor stroke amplitude: 0 (lightest, zero stretch) to 3 motor revolutions (darkest, maximum stretch). (B, D) Representative calibration curves for (B) equibiaxial and (D) uniaxial stretch. The relationship between E_ij and stroke amplitude was determined using a linear curve fit.

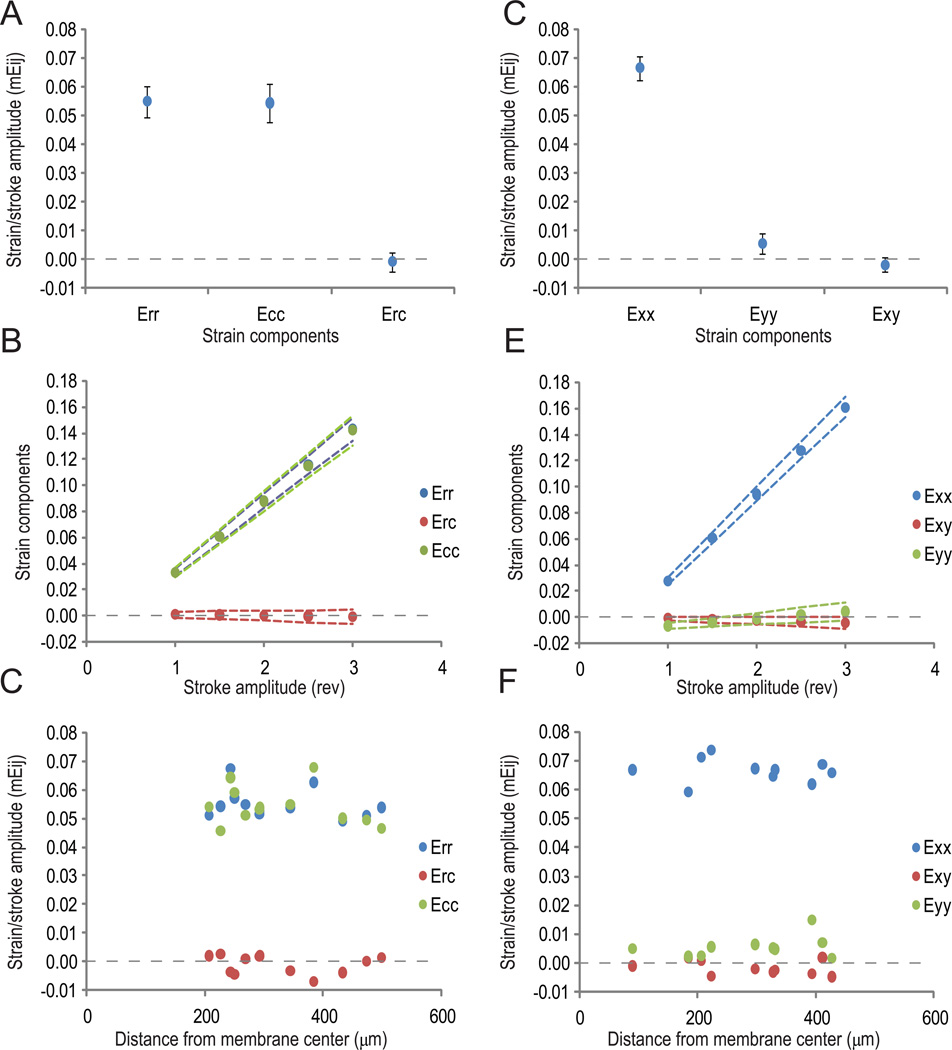
To validate the strain field across experiments, the slopes (m_Eij, in units of strain/motor revolution) of independent calibration curves were compared (Figure 4). Using the equibiaxial indenter, mean slopes m_Err (0.055±0.005) and m_Ecc (0.054±0.007) were not significantly different from each other (Figure 4 A), and m_Erc (−0.001±0.003) was not significantly different from zero (n=12). Moreover, m_Erc values were not significantly different from zero for all levels of stretch. Figure 4 B shows the three mean components of _Eij and their respective 95% confidence intervals. The confidence intervals for m_Eij demonstrate that the predicted strain magnitude for a given motor home position was accurate to ±1% for the largest stroke amplitude (corresponding to an error of ±8%). The motor home position was defined to be where the elastic substrate just made contact with the indenter. The home position was estimated manually with a precision of ~1 mm. Since the calibration curves extrapolate to zero strain magnitude at a motor stroke amplitude of 0.40 motor revolutions (0.9 mm), either the uncertainty in the x-intercept results from uncertainty in estimating the point of contact, or the the calibration curves may become nonlinear as the strain magnitude approaches zero. Using the uniaxial indenter, mean slopes parallel (m_Exx) and perpendicular (m_Eyy) to the strain axis were 0.067±0.004 and 0.006±0.004, respectively (Figure 4 D), thus resulting in true uniaxial strain (n=10). The corresponding operation curve is shown in Figure 4 E, with the x-intercepts set to the average motor home position. The 95% confidence interval for m_Exx demonstrates that strain magnitude prediction for a given motor home position was accurate to ±1% for the largest stroke amplitude (corresponding to an error of ±5%). Although m_Eyy was nonzero, the measured strain magnitudes were small, ranging from −0.6% to 0.4% for the given stroke amplitudes.

Figure 4.

(A, D) Mean strain/stroke ratios (m_Eij) of the three components of the strain tensor for (A) equibiaxial and (D) uniaxial stretch. (B, E) Operation curves for (B) equibiaxial and (E) uniaxial stretch, showing the three mean components of E_ij and their respective 95% confidence intervals (dotted lines). (C, F) Mean strain/stroke ratios measured at different positions on the membrane for (C) equibiaxial and (F) uniaxial stretch.

Using a 40X/0.75 NA objective lens, the effective imaging area for equibiaxial strain had a radius of approximately 600 µm. For uniaxial strain, the effective imaging area had semi-major and semi-minor axes of approximately 600 µm and 300 µm, respectively. To confirm strain field uniformity, we tested whether m_Eij for the normal components were correlated with radial distance r from the membrane center. Using the equibiaxial indenter (Figure 4 C), the correlation coefficients (ρ(m_Err, r) = −0.26 and ρ(m_Ecc, r) = −0.25) were not statistically significant, suggesting that a linear correlation between the variables did not exist. Similarly, using the uniaxial indenter (Figure 4 F), the correlation coefficients (ρ(m_Exx, r) = −0.13 and ρ(m_Eyy, r) = 0.35) were not statistically significant. Taken together, these data confirm that the stretch device applies uniform equibiaxial and uniaxial stretch to the membrane. Sinusoidal motion profiles to achieve cyclic stretching at 1 Hz over the same range of stroke amplitudes were programmed using the encoder and verified using a digital software oscilloscope.

Cytoskeleton and Focal Adhesion Strain Analysis

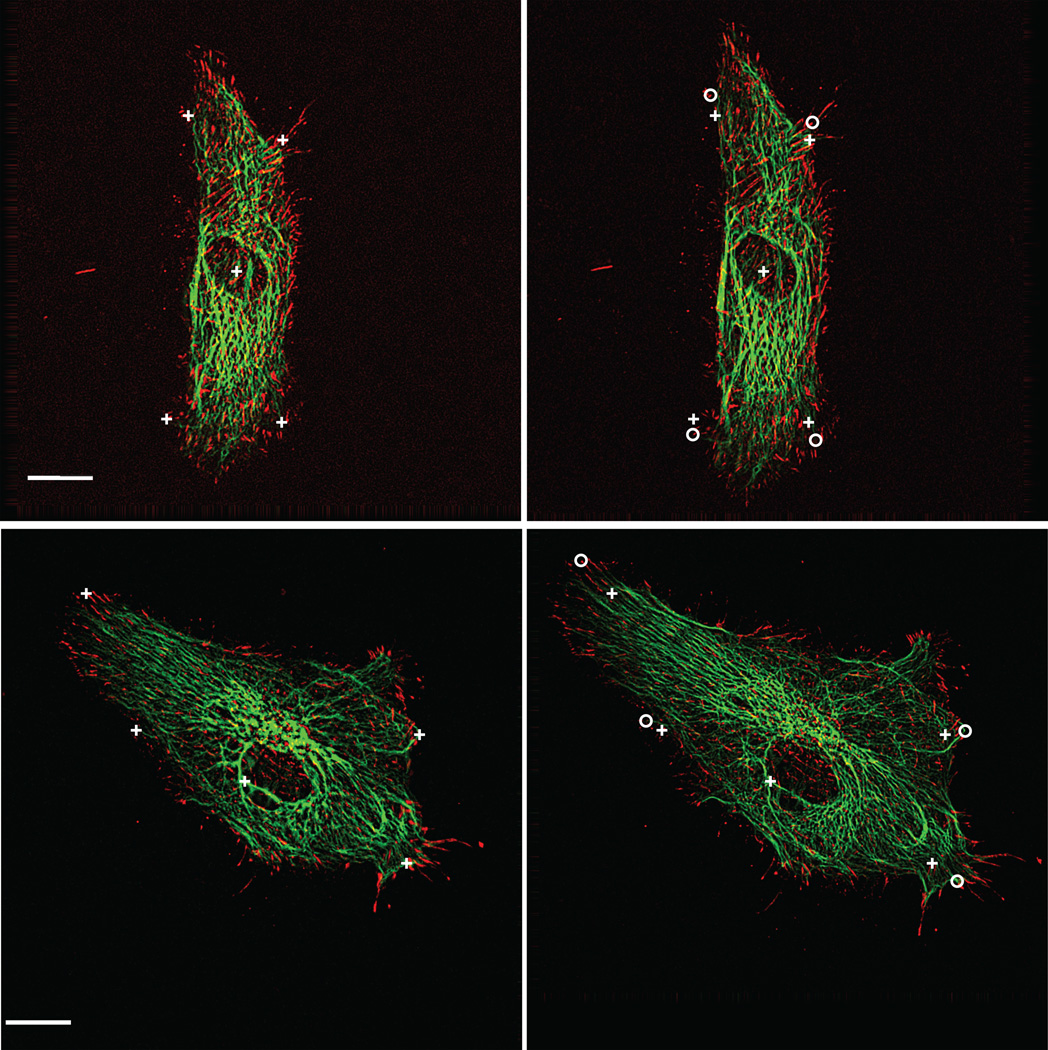
To examine the relative deformation fields of the cytoskeleton and focal adhesions in response to substrate strain, bovine aortic endothelial cells were cotransfected with EGFP-vimentin and paxillin-DsRed2. Figure 5 shows representative image pairs of two cells acquired before (Figure 5 A, C) and 3 min after (Figure 5 B, D) 14% equibiaxial substrate strain. Image pairs were registered using a reference fiducial (center cross), and markers at cell edges before (crosses) and after (circles) substrate stretch show the local magnitude and direction of displacement. Labeling of the intermediate filaments (IF) and the focal adhesions (FA) enabled direct estimation of the strain field, which represented relative displacement among the fields of filament intersections and FA positions, respectively. For each cell, 10–30 of these landmark positions were tracked before and after equibiaxial stretch of the substrate. Delaunay triangulation was used to connect adjacent vertices, and E_ij was computed from the shape change of triangle meshes.

Figure 5.

Bovine aortic endothelial cells transiently expressing EGFP-vimentin (green) and paxillin-DsRed2 (red). Image pairs were acquired before and 3 min after application of 14% constant magnitude equibiaxial stretch. Adjacent cells in confluent monolayer are not expressing fluorescently labeled proteins. Markers at cell edges before (crosses) and after (circles) stretch show the extent of deformation. Center cross denotes reference fiducial used for image registration. Scale bar, 10 µm.

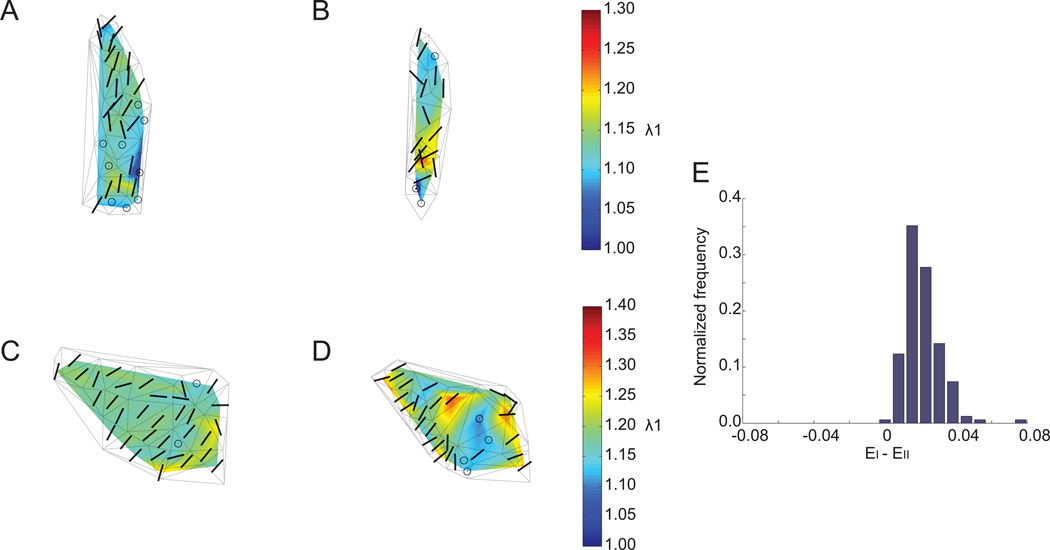
Mechanical stretch of the substrate induced significant regional deformation of both FAs and IFs, as indicated by the principal stretch ratio λ_I computed for the two cells shown in Figure 5. The distribution of the maximum stretch ratio magnitude (λ_I) computed from the paxillin-containing adhesions in response to 14% constant magnitude equibiaxial substrate stretch varied smoothly and closely matched the expected magnitude of substrate stretch (Figure 6 A, C, color scale). In contrast, the spatial distribution of λ_I in the vimentin network revealed spatial heterogeneity and strain focusing (localized peaks) consistent with that measured in cells subjected to shear stress (Figure 6 B, D, color scale).¹¹

Figure 6.

(A–D) Magnitude (color scale) and orientation (bars, circles) of principal stretch ratio λ_I computed from the (A, C) FA and (B, D) IF for the two cells in Fig. 5. Circles represent regions in which an eigenplane represents principal stretch. Delaunay triangulations of vertices are superimposed for spatial reference. (E) Normalized histogram of E_I − E_II computed from adhered microspheres subjected to 14% constant magnitude equibiaxial stretch. For FA and IF strain analysis, E_I − E_II that fell within the 95% confidence interval of this distribution were considered zero.

In order to estimate the principal axes of strain, the eigenvectors of E_ij were computed. To determine whether unique principal axes existed, we first determined the error associated with image analysis. Assuming equibiaxial stretch of fixed fiducial marks on the substrate, the difference between principal eigenvalues (E_I − E_II) should be zero; a non-zero value represents measurement errors associated with image analysis. E_I − E_II was computed from the equibiaxial stretch calibration data using adhered microspheres, first for all triangle elements (vertices had mean separation distance of 40 µm) and then for triangles with perimeters comparable to that of the FA and IF landmarks in cells (mean separation distance of 13 µm). Comparison of the two groups revealed the variance and mean of E_I − E_II were not statistically different, suggesting that measurement error was not dependent on triangle mesh size at this length scale. Figure 6 E shows a normalized histogram of E_I − E_II computed from all triangles. The distribution was fitted with a Gaussian function (R² = 0.97) with a mean and standard deviation of 0.019±0.012 (n=162 triangles). For the analysis of cellular strain, E_I − E_II values that fell within the 95% confidence interval of this distribution were considered to be not significantly different from zero. In these cases, a unique set of principal axes does not exist, and an eigenplane represents principal stretch.

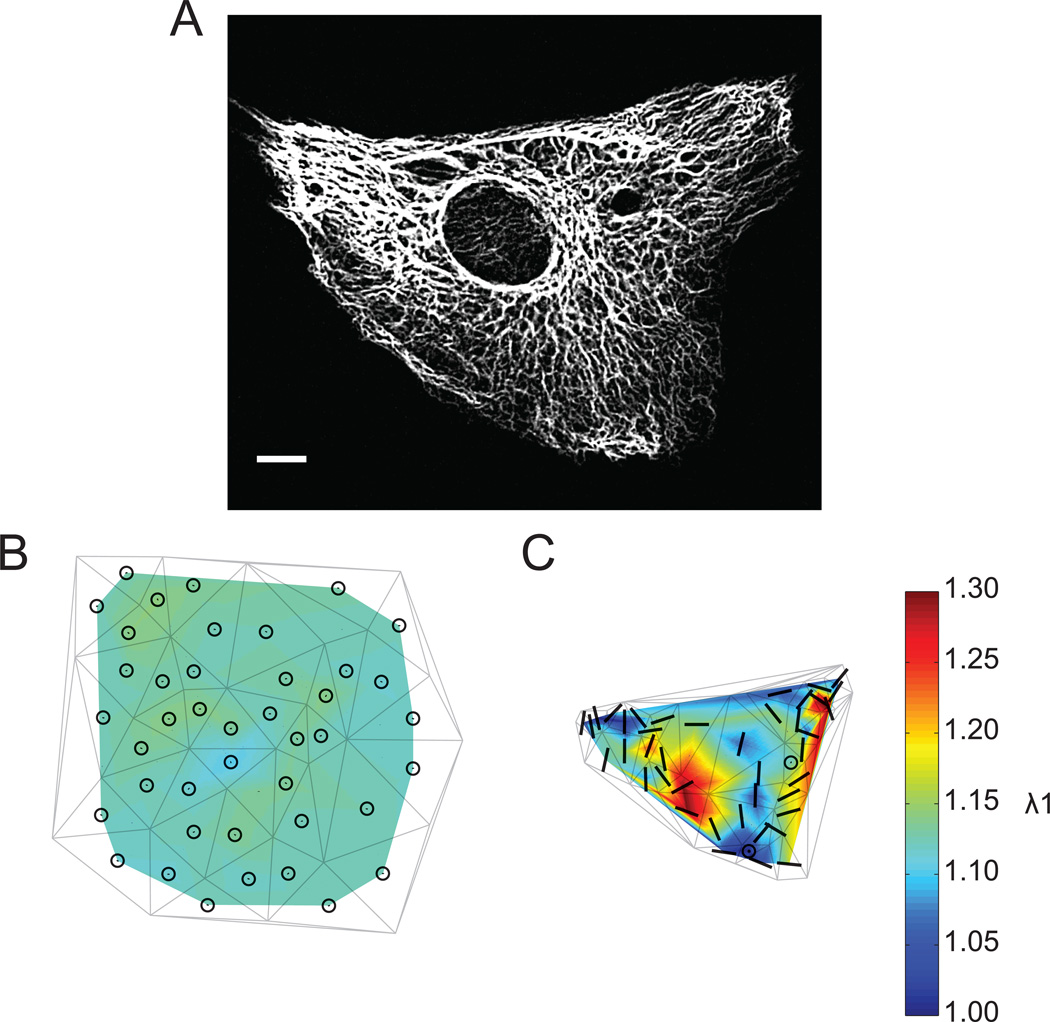
Applying this error analysis approach and plotting the eigenvector directions in FA and IF triangle meshes indicated that the first principal axes of stretch were regionally correlated and varied with cell morphology (Figure 6 A–D, bars/circles). In elongated cells the principal axes were oriented along the major axis of cell shape (Figure 6 A, B). Alignment with cell shape was not observed in cells with higher degrees of spreading (Figure 6 C, D). Strain directions in these cells were likely dependent on local cytoskeletal architecture. To validate further the statistical analysis of principal stretch orientations in cells subjected to equibiaxial substrate stretch, strain maps measured using the IF network and the underlying substrate (using adhered microspheres on the elastic membrane) were directly compared (Figure 7). Figure 7 A shows a cell expressing EGFP-vimentin following 12% constant magnitude equibiaxial substrate strain. Strain magnitude measured from fluorescent microspheres as fiducial marks on the substrate was spatially uniform (Figure 7 B, color scale), and an eigenplane represented principal stretch everywhere in the region where the cell was located (Figure 7 B, circles). In contrast, the magnitude and orientation of the first principal stretch ratio computed from IF intersections exhibited strain focusing (Figure 7 C, color scale) and regionally correlated principal axes (Figure 7 C, bars).

Figure 7.

(A) Representative endothelial cell expressing EGFP-vimentin. Scale bar, 20 µm. (B, C) Magnitude (color scale) and orientation (bars, circles) of principal stretch ratio λ_I computed from markers (B) on the membrane and (C) in the IF network after 12% constant magnitude equibiaxial stretch. Circles indicate regions in which an eigenplane represents principal stretch. Delaunay triangulations of vertices are superimposed for spatial reference.

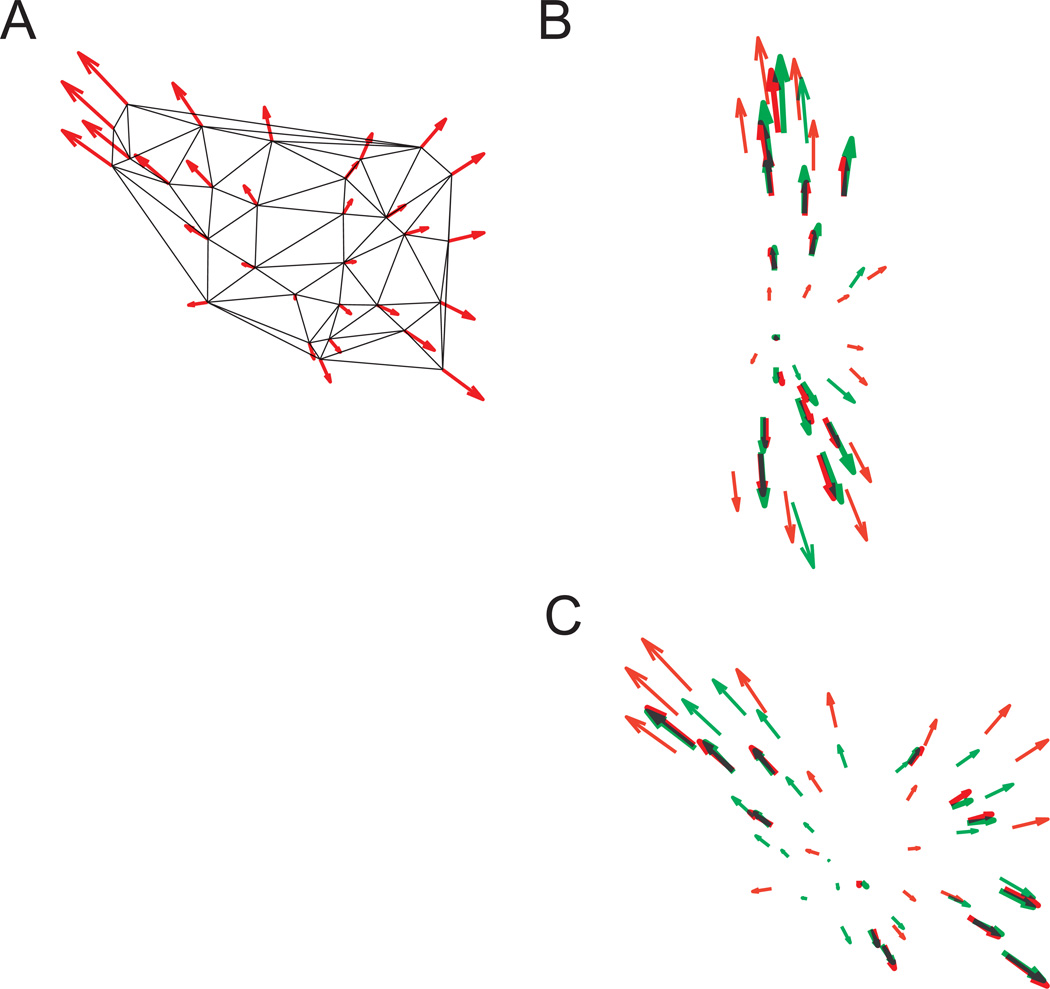
We next estimated the extent of mechanical coupling between paxillin and vimentin using relative displacement maps. For equibiaxial stretch, structural deformation indicated by subcellular FA or IF landmarks occurred in the radial direction away from an arbitrary center in a manner consistent with calibration data (Figure 8). FA and IF vertices in close proximity (separation distance ≤ 2.5 µm) were paired, and the degrees of correlation in the direction and magnitude of their displacement vectors were computed. Direction coupling score was computed as DCS cos(θ), where θ is the angle between the paired vectors. Magnitude coupling score was computed relative to paxillin as $\mathit{\text{MCS}}=\overline{|u_{\mathit{\text{vim}}}|}/\overline{|u_{\mathit{\text{pax}}}|}$. If the displacement vectors are identical, then DCS = 1 and MCS =1. A high degree of directional coupling between the FA and IF deformation fields existed (DCS = 0.95 ± 0.13, n = 53 vector pairs from five cells). Although a high degree of magnitude coupling was also observed (MCS = 0.93 ± 0.34), a larger degree of heterogeneity existed, which may have contributed to the spatial variations in the principal axis of stretch. These data represent quantitative measurements of connectivity at a subcellular length scale during application of substrate strain.

Figure 8.

(A) Relative displacement of FA vertices induced by substrate stretch. Cells were aligned at a center landmark. Arrow length and orientation indicate magnitude and direction of the corresponding vertex. (B, C) Relative displacement maps for the two cells in Fig. 5 subjected to 14% constant magnitude equibiaxial stretch. Red and green arrows represent FA and IF vectors, respectively. Bold arrows indicate paired vectors in close proximity.

Dynamics of Strain-Induced Actin Ruffling during Changes in Cyclic Strain Profiles

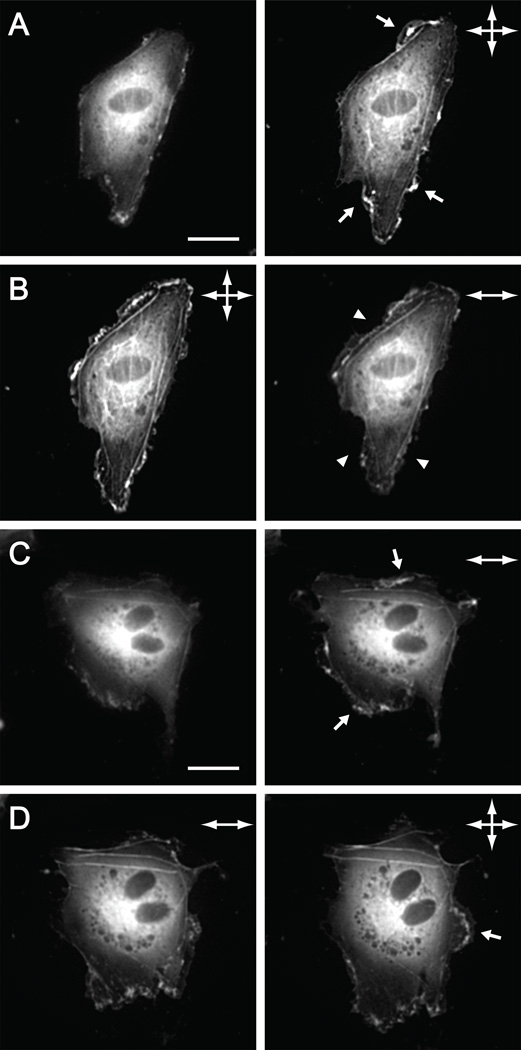
Actin-mediated lamellipodia extensions and edge ruffles represent one of the fastest structural responses to onset of fluid shear stress.⁵ To determine whether onset of substrate stretch induces rapid changes in actin edge activity, confluent ECs expressing EGFP-actin were subjected to either cyclic uniaxial or cyclic equibiaxial substrate stretch (12%, 1 Hz) for 15 min, a timescale that corresponds to maximal edge activity under shear stress.⁵ Onset of either cyclic equibiaxial or cyclic uniaxial stretch enhanced existing ruffling activity within 3 min (Figure 9 A, C). The rapid non-directional increase in edge ruffling supports the hypothesis that this initial response does not contribute to establishing directionality.

Figure 9.

Bovine aortic endothelial cells transiently expressing EGFP-actin and subjected to different substrate stretch regimes. (A) Images acquired before and 3 min after onset of cyclic equibiaxial substrate stretch (12%, 1 Hz). (B) After 15 min equibiaxial substrate stretch, images were acquired before and 3 min after switching to cyclic uniaxial substrate stretch (12%, 1 Hz). (C) Images acquired before and 3 min after onset of cyclic uniaxial substrate stretch. (D) After 15 min uniaxial substrate stretch, images were acquired before and 3 min after switching to cyclic equibiaxial substrate stretch. Arrows and arrowheads indicate regions of enhanced and suppressed lamellipodium formation and edge ruffling, respectively. Scale bars, 20 µm.

In order to determine the effect of a change in substrate strain profile on actin edge activity, the cyclic stretch profile was changed either from uniaxial to equibiaxial or from equibiaxial to uniaxial, and cells were stretched for an additional 15 min. Edge activity was regionally suppressed within 3 min when the stretch profile was changed from equibiaxial to uniaxial (Figure 9 B), whereas a change from uniaxial to equibiaxial stretch triggered a new burst of edge ruffling in regions where the activity was previously low (Figure 9 D). These experiments using multiple indenters show different actin-mediated edge responses based on a change in mechanical stimulus.

Discussion

The stretch device presented here was designed for high-resolution imaging of cells and tissues subjected to custom spatiotemporal strain profiles. The small footprint of the apparatus allows easy assembly onto the stage of standard inverted microscopes without interference with the optics. The recessed stage insert/indenter ring allows access to the full working distance of common objective lenses. In addition to retaining the advantages of existing indenter devices (including no compressive loading, vacuum suction, or vertical movement of the membrane), the current design improves upon some of the common limitations. Some stretch devices are capable of either uniaxial or equibiaxial stretch but are not designed for cyclic stretch profiles. Others perform cyclic stretch but are limited to one spatial strain profile (e.g. either equibiaxial or uniaxial). Here, the spatiotemporal strain profile may be customized spatially by changing indenter rings or temporally via the programmable encoder, eliminating the need for separate devices. In particular, the ability to change the applied spatial strain profile during experiments may be useful for identifying mechanically-induced polarity cues and for determining whether preconditioning modifies cell responses to strain.

Devices exist that allow continuous low-resolution visualization of cells during substrate stretch to determine cell shape,¹⁵ to track exogenous markers on cell surfaces,² or to measure [Ca²⁺]_i at the length scale of individual cells.⁷ However, high-resolution imaging of intracellular structural dynamics during stretch is not readily feasible. One major challenge is to account for stretch-induced horizontal movements in xy and focus changes in z which become more pronounced at higher magnifications and at higher stretch magnitudes.¹⁵ Using our device, movements in xyz are relatively consistent between stretch cycles and are linear with respect to the stretch magnitude. This feature enabled easy compensation for these effects by moving the microscope stage relative to the objective lens. Importantly, this approach allows imaging of targets away from the center of the elastic membrane. Consistent movements in xyz (errors of <100 µm in xy and <10 µm in z) are in part due to the use of an encoder-controlled servomotor whose motion profiles were verified by comparing the motor position feedback to the position command.

The calibration results confirmed that the stretch device applies uniform equibiaxial and uniaxial strain to the elastic membrane. The 95% confidence intervals of the E_ij vs. stroke amplitude operation curve showed that strain magnitudes for a given home position were reproducible with an error of ±8%. As proof of principle, endothelial cells were subjected to 14% constant magnitude equibiaxial stretch. Mean strain components averaged across the entire cell indicated a strongly correlated strain field computed from relative displacements of the adhesion sites, suggesting that these can be used to estimate reliably the applied strain magnitude in the absence of fiducial markers. However, the strain field computed from landmarks on the vimentin cytoskeleton was less well correlated with substrate strain, which may reflect rapid cytoskeletal remodeling in response to increased tension. Initial observations suggest that cell morphology and local cytoskeletal architecture play an important role in regulating force transmission, consistent with previous observations in vascular smooth muscle cells.² Alignment of the principal axes of strain along the major axis of cell shape was evident in elongated cells. In less elongated cells with a higher degree of spreading, strain directions computed from the IF cytoskeleton remained regionally correlated, but they were no longer oriented towards a major axis based on cell shape. Strain focusing was observed at discrete locations in the IF network, whereas the spatial distribution of strain was more uniform when computed from the positions of the FAs.

Onset of fluid shear stress induces rapid formation of lamellipodia and edge ruffles. In subconfluent endothelial cells, for example, edge ruffling and area expansion occurs within minutes after onset of steady unidirectional shear stress.^{5, 21} These initial transient responses peak after 12–15 min and then subside. Directional ruffling and planar cell polarity develops on a longer time scale (>30 min). However, direct, localized applications of force to the cell surface have demonstrated rapid, local activation of Rac GTPase, which is associated with actin-mediated ruffling.²³ Furthermore, in vascular smooth muscle cells, unidirectional substrate stretch causes increased lamellipodium extension at the ends of the cells and decreased extension along the stretched sides of cells.¹⁶ Based on these reports, it was not clear whether a nondirectional or directional response should occur in endothelial cells subjected to uniaxial substrate strain. Here, actin-mediated edge ruffling was enhanced by onset of either equibiaxial or uniaxial cyclic substrate strain, consistent with the response that was previously observed in response to onset of shear stress.^{5, 21}

Switching between spatial strain profiles with minimal delay during an experiment revealed new details about the sensitivity of actin ruffling dynamics to changes in mechanical stimuli. After 15 min of cyclic uniaxial strain, a time scale consistent with maximum actin ruffling in shear stress experiments,⁵ switching to cyclic equibiaxial strain at the same peak-to-peak linear strain magnitude induced a second burst of actin edge ruffles. Since 12% equibiaxial strain produces 25% area strain, we hypothesize that this behavior represents a response to increasing the area strain in the cell. Thus, desensitization of actin ruffling to a second, increased dose of strain does not appear to occur as it does after increasing the magnitude of shear stress.⁵ In a similar fashion, switching from equibiaxial to uniaxial strain resulted in decreased activity of actin structural dynamics, consistent with the hypothesis that actin dynamics are suppressed in response to decreased intracellular tension after releasing substrate strain. Overall, we hypothesize that distinct integrating signals in response to shear stress or substrate strain, perhaps involving integrin–extracellular matrix adhesions, confer differential sensitivities to subsequent changes in external mechanical stimulation profiles. Our strain device enables investigation of these as yet unsolved mechanisms.

Our results show that the stretch device is compatible with the use of endogenous structural markers that provide precise mapping of mechanical interactions within the cell. In addition to measurements of FA/IF morphodynamics and strain fields, correlation of relative displacement vectors provides readouts of mechanical coupling during stretch. Together, these measurements may be used to test hypotheses on connectivity and force transmission. One future goal is to implement real-time image acquisition schemes during cyclic stretch. The linear encoder can be programmed to send TTL marker pulses to trigger image acquisition at specific motor positions. To image the steady state component, images are acquired at a set motor position (e.g. unstretched or stretched). To determine the adaptive changes over time, images are acquired asynchronously over several stretch cycles and reconstructed to reveal real-time information during one cycle. Since light scattering properties of the membrane changes upon stretching, point spread functions measured at multiple stroke amplitudes are required for optimal image reconstruction. Both acquisition schemes may reveal new information on structural dynamics during stretch.

In summary, we report a versatile, novel stretch device designed for high-resolution live-cell microscopy. This device enables quantitative measurements of structural dynamics in cells and tissues subjected to mechanical stretch, as demonstrated using endothelial cells expressing fluorescently-labeled focal adhesions and cytoskeleton. Results obtained using this device may elucidate molecular mechanisms in stretch-mediated mechanotransduction, and facilitate comparison of dynamic structural remodeling in response to mechanical forces of different spatiotemporal signatures (e.g. strain vs. shear stress; equibiaxial vs. uniaxial strain).

ABBREVIATIONS

EGFP

enhanced green fluorescent protein

FA

focal adhesion

IF

intermediate filament

IR

indenter ring

MHR

membrane holder ring

MP

moving plate