Mapping cardiac surface mechanics with structured light imaging

Abstract

Cardiovascular disease often manifests as a combination of pathological electrical and structural heart remodeling. The relationship between mechanics and electrophysiology is crucial to our understanding of mechanisms of cardiac arrhythmias and the treatment of cardiac disease. While several technologies exist for describing whole heart electrophysiology, studies of cardiac mechanics are often limited to rhythmic patterns or small sections of tissue. Here, we present a comprehensive system based on ultrafast three-dimensional (3-D) structured light imaging to map surface dynamics of whole heart cardiac motion. Additionally, we introduce a novel nonrigid motion-tracking algorithm based on an isometry-maximizing optimization framework that forms correspondences between consecutive 3-D frames without the use of any fiducial markers. By combining our 3-D imaging system with nonrigid surface registration, we are able to measure cardiac surface mechanics at unprecedented spatial and temporal resolution. In conclusion, we demonstrate accurate cardiac deformation at over 200,000 surface points of a rabbit heart recorded at 200 frames/s and validate our results on highly contrasting heart motions during normal sinus rhythm, ventricular pacing, and ventricular fibrillation.

excitation and contraction in the heart are highly coupled physiological events. Depolarization of cardiac myocytes leads to influx of calcium and subsequent contraction of the muscle (34a). In healthy tissue, contraction follows electrical excitation by a few milliseconds, producing an electromechanical wave that propagates across cardiac tissue. During disease, abnormal mechanical function is involved in the development and maintenance of cardiac arrhythmias, and vice versa (37). Thus the ability to dynamically assess electrical activity and mechanical deformation of the entire cardiac surface would greatly aid in the development and evaluation of new electromechanical models and therapies for cardiac disease. Currently, there is a need for acquisition methods that provide high-resolution four-dimensional (4-D) [three-dimensional (3-D) surface + time] data of cardiac mechanics for understanding complex interactions between excitation and contraction during rhythmic and arrhythmic cardiac events. While several techniques exist for whole heart electrical mapping [e.g., optical mapping of voltage-sensitive dyes and electrocardiographic imaging (ECGI)], similar instruments are not available for similar whole heart mechanical mapping in 4-D space.

Over the past century, cardiac mechanics have been studied using a wide variety of tools. Before the 1930s, investigators used mechanical recorders (e.g., surface kymograph, myograph, cardiometer, intraventricular pressure recorder, etc.) to provided valuable information on bulk cardiac motion (41, 43). However, data were limited to one or a sparse number of locations. During the 1930s, advances in cinematography (42, 43) and the Roentgen Kymograph (32) provided imaging techniques that increased spatial resolution of mechanical measurements in cardiac tissues. Nevertheless, many of these methods were limited to fiducial markers added to the myocardial surface, reducing the resolution of mechanical measurements (9, 24, 43). Presently, tagged magnetic resonance imaging (MRI) and tissue-Doppler speckle tracking represent the most popular techniques for mechanical evaluation of cardiac deformation. Although both methods provide high-spatial resolution in four dimensions, whole heart imaging with MRI or ultrasound is presently limited to rhythmic patterns because of scanning, decreasing temporal resolution to 15–20 ms, and making imaging of noncyclic arrhythmias impossible (27, 28).

To compare mechanical contraction with electrical excitation, mechanical mapping techniques must be able to measure whole heart cardiac deformation with similar resolution to that of electrical mapping techniques used to record transmembrane potential (e.g., microelectrodes and optical mapping of voltage-sensitive dyes) and surface electrograms (e.g., electrode arrays). Mapping resolution for these systems is defined both temporally and spatially. Temporally, action potentials and electrograms contain spectral information between 0 and 100 Hz, with the highest frequency components occurring in the action potential upstroke (26) or the QRS complex (7), respectively. Therefore, according to the Nyquist sampling theorem, temporal sampling typically occurs at >200 Hz for high-fidelity reconstruction of action potentials and electrograms in electrical mapping systems. Spatially, the length constant provides a measure of the extent of an action potential across tissue. Length constants in healthy myocardium are reported at 940 μm along cardiac fibers and 340 μm across cardiac fibers (35). Whereas most electrogram mapping systems, such as contact electroanatonic mapping (CARTO) (3) and ECGI (39), are not capable of these resolutions, transmembrane potential mapping systems like optical mapping of voltage-sensitive dyes have demonstrated spatial resolutions of ∼1 mm (2).

High-resolution mechanical mapping with the resolution of electrical mapping is not possible with current technological approaches. Structured light-based 3-D imaging is a relatively new technique for physiological experimentation; however, it may offer a unique optical solution for dual measurement of electrophysiology and mechanics. Structured light imaging has gained much popularity in a wide range of areas, including realistic human performance capture, precision shape measurement for industrial production control, and entertainment (e.g., the Microsoft Kinect, the first consumer-grade structured light application). Methodologically, structured light imaging is similar to stereo-based imaging with two cameras, except that one camera is replaced with a projector (31). With the use of the projector, structured patterns or fringe patterns are projected onto an object of interest. As the patterns strike the object, the 3-D surface distorts the fringes. A camera then acquires the distorted fringe patterns, which are digitally combined to triangulate surface depths and reconstruct the object in 3-D space. Because structured light relies on actively projected patterns and not inherent surface texture, it is not limited by texture or shape like stereo-based methods.

To our knowledge, structured light imaging has never been applied to measure epicardial deformation of a beating heart. Here, we present a novel application of our high-speed structured light imaging system (30) for high-resolution 3-D mechanical mapping of epicardial deformation in a beating rabbit heart. This system is capable of achieving frame rates up to 667 frames/s with in-plane spatial resolution (X, Y) of 87 μm and depth resolution (Z) of 10 μm. In addition, we adopted a highly robust nonrigid surface-matching algorithm (19, 21) to track dense surface motion across 3-D surfaces through time. Our tracking approach is purely geometric and therefore does not require fiducial markers. By combining our structured light imaging system with a fiducial-free, motion-tracking algorithm, we are able to image and describe 3-D cardiac mechanics (i.e., strain, curvature, displacement, etc.) at resolutions and frame rates not previously achievable with other techniques. The following study will present a brief description of our structured light imaging system, a validation of our markerless tracking algorithm, and a demonstration of mechanical mapping in rhythmic and arrhythmic beating hearts.

METHODS

Tissue preparation.

We imaged Langendorff-perfused hearts (n = 4) isolated from New Zealand white rabbits. All studies were approved by the Institutional Animal Care and Use Committee of Washington University in St. Louis. While this ex vivo model does not completely capture in vivo cardiac mechanics because of unloading during removal, it still provides a means to validate our system on a dynamically deforming heart. Each heart was removed via a midsternal thoracotamy and immediately perfused with oxygenated (95% O₂-5% CO₂) Tyrode solution at a constant pressure of 60 ± 5 mmHg and temperature of 37°C. Once cannulated, hearts were placed in a custom superfusion chamber with an optical window for structured light imaging. Ag/AgCl pellet electrodes were placed near the atrioventricular groove to record ECG measurements during experimentation. The structured light imaging system was synchronized with ECG recordings via an external function generator. Following sinus rhythm (SR) recordings, a custom bipolar electrode was placed near the left ventricular apex of the heart to stimulate different contractile rates. Hearts were imaged at ∼17 unique pacing cycles lengths (CLs), ranging from 300 to 143 ms. We also studied ventricular fibrillation (VF) induced by burst pacing in the setting of global ischemia.

Ultrafast 3-D imaging using structured light.

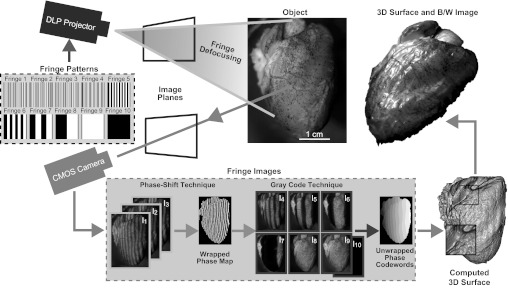
A complete description and validation of our structured light system has been previously presented (40). Figure 1 shows the general framework of our 3-D imaging system. Briefly, binary fringe patterns (fringe 1–10) are projected sequentially at 2,000 frames/s from a properly defocused digital light processing video projector (LightCommander, LogicPD, Eden Prairie, MN) onto an object to produce sinusoidal fringe patterns. Defocusing binary patterns, instead of generating sinusoidal fringe patterns in the projector hardware, is an essential technique to achieving high frame rates with structured light (18). Two types of fringe patterns are projected onto the heart: 120° phase-shifted patterns (fringe 1–3) with a resolution of 36 pixels/fringe and binary patterns for spatial phase unwrapping (fringe 4–10). Distorted fringes are acquired with a synchronized high-speed complementary metal oxide semiconductor (CMOS) camera (Phantom V9.1, Vision Research, Wayne, NJ) and digitized into fringe images (I1–I10). As demonstrated in Fig. 1, phase-shifted fringe images (I1–I3) are encoded in a three-step, phase-shifting algorithm to create a wrapped phase map of the object. Simply, each phase-shifted fringe image (I1–I3) can be described as

$$I_k\left(x,y\right)=I\prime \left(x,y\right)+I″\left(x,y\right)\cos \left[\mathrm{\Phi }\left(x,y\right)-2k\pi /3\right]$$ 1

where I_k denotes the intensity of the kth fringe image, I′ the average intensity, I″ the intensity modulation or amplitude of the sinusoidal fringe, Φ is the phase and corresponds to the position within a sinusoidal fringe pattern relative to the initial crest, and k = 1, 2, or 3 for I₁, I₂, or I₃, respectively. From these three equations, the exact phase can be solved for as

$$\mathrm{\Phi }\left(x,y\right)=\arctan \left[\sqrt{3}\left(I_1-I_2\right)/\left(2I_3-I_1-I_2\right)\right]$$ 2

The phase values obtained from this equation range from −π to +π with 2π discontinuities when solved for using the four-quadrant arctangent function. Together, they constitute the wrapped phase map that is ultimately used to create the 3-D frame, as shown in Fig. 1. For object depth to be reconstructed, 2π discontinuities must be removed and a continuous phase map must be generated through an additional step called spatial phase unwrapping (13). To this end, we employ a combination of gray code pattern and phase shifting to assist in phase unwrapping and removal of depth discontinuities using fringe images I4–I10 (47). Once the phase is unwrapped, depth can be properly reconstructed with a phase-to-height calibration method previously described (45, 46). For our experiments, camera resolution was set to 576 × 576 pixels (87 μm/pixel on the heart surface), exposure time was set to 490 μs, and camera frame rate was set to 2,000 frames/s to limit data size. Because 10 fringe images are used to construct a single 3-D frame, shape acquisition occurred at 200 frames/s. While 200 frames/s is significantly less than the 667 frames/s maximum reported in our previous studies (17, 40), it was sufficient for capturing motion of the beating rabbit heart.

Fig. 1.

Setup of structured light imaging system. A digital light processing (DLP) projector sequentially projects 10 binary, fringe patterns onto an object. Binary fringe patterns are defocused to produce sinusoidal fringes. A computer-controlled complementary metal oxide semiconductor (CMOS) camera simultaneously captures fringe images (I1–I10). Sinusoidal fringe images I1–I3 are combined to produce a wrapped phase map of the object. Fringe images I4–I10 are then used to unwrap phase discontinuities to produce an unwrapped phase map that can be mapped to depth with a phase-to-height conversion algorithm. Each 3-dimensional (3-D) surface is then wrapped with a black and white (B/W) image of the object to capture both 3-D geometry and texture.

Tracking nonrigid motion in the beating heart.

Our proposed imaging system captures dense 3-D surface geometries at high frame rates, but the analysis of surface mechanics (such as space curves, velocities, and strain) is not immediately possible due to the lack of interframe correspondences. Here, we adapt the multiframe geometric registration approach of Li et al. (19, 21) that uses a state-of-the-art deformation model for estimating dense correspondences between consecutive 3-D scans.

Traditionally, these temporal correspondences are established either by tracking sparse markers attached to the subject or by using more sophisticated vision-based methods that densely estimate the scene flow relying purely on surface texture (6, 10, 22). While the former approach achieves reliable position measurements, its resolution is limited by marker density. On the other hand, vision-based tracking techniques consider the full image resolution of the sensor but rely heavily on discriminating color textures and linear response of the surface reflection. The texture of a heart is somewhat limited for these methods, exhibiting few, sparse landmarks such as fat, vasculature, tissue color variations, and surface specularities. Correlating texture information between consecutive frames is therefore susceptible to the accumulation of errors (drift) as shown in results, but more importantly regions poor in color variations are impossible to track for extended periods.

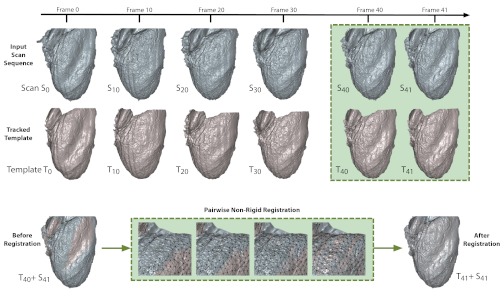
Our method does not use texture information at all but extracts accurate correspondences exclusively from the high frame-rate depth scans using a template-based nonrigid 3-D registration algorithm (Fig. 2). The idea consists of computing optimal deformations that warp a template T_i (set to the initial scan S₀ = T₀) to all subsequent scans S_i (with i = 1…n) such that their geometric shapes are aligned. Hence, all tracked template meshes T_i are geometrically aligned with the shapes of S_i and have compatible mesh vertices and the same edge connectivity as S₀. Not only are point-to-point correspondences between scans unknown in the beginning, but also the acquisition coverage is only partial (i.e., we only record from a single view). We must therefore also determine the regions of overlap between consecutive scans and provide an accurate description of surface deformation in incomplete regions to obtain full interframe correspondences. Since we do not make any assumption about heart shape and motion, we introduce a deformation model that is as general as possible but also avoids unnatural distortions (such as local shearing and scaling). Our deformation model is described by a rigidity-maximizing regularization energy, and the rest pose of the heart, T₀, is defined as its zero energy state. Promoting local rigidity is essential for producing natural deformations and maximizing geometric similarity when matching continuously deforming scans (20, 21).

Fig. 2.

Markerless motion tracking algorithm. For a given input sequence of 3-D scans (blue), a template (T₀) is created for the first frame of the scan (S₀) to remove noise along edges and fill holes in the 3-D surface. During surface registration, template surfaces (red) are matched to subsequent input scans using a pairwise nonrigid registration optimization technique. Once optimization is complete, a new template is produced that aligns with the input scan. This process is repeated sequentially through all frames of interest.

Correspondences between the current frame template, T_i, and the next scan, S_i+1, are found by an iterative algorithm known as nonrigid iterative closest point (ICP). Nonrigid ICP begins with 1) estimating the closest point on S_i+1 for every vertex in T_i. Next, 2) we prune away those correspondences that lie on the boundary of the target mesh and those with largely incompatible surface normals (i.e., if the angle between them is above 20°). As a final step, 3) we compute an optimal deformation using the local rigidity maximizing deformation model to bring T_i to alignment with S_i+1, yielding the aligned source mesh T_i+1. Notice that steps 1 and 2 only provide rough correspondences and overlapping regions that serve as an initialization for the continuous optimization in step 3. Correspondence positions are further refined during the deformation process. All three steps are repeated until a deformation energy defined in step 3 falls below a threshold or when a total number of iterations have been reached. Each pairwise registration converges in <100 iterations of nonrigid ICP (i.e., several seconds of computation). Moreover, our deformation model is general in that any heart shape or imaging viewpoint can be modeled and tracked. We use the same optimization parameters as described in the template-based tracking framework by Li et al. (19). This method defines its regularization energy on a coarser, uniformly subsampled deformation graph (using ∼12,000 nodes in contrast to 200,000 scanned points) and progressively reduces stiffness to avoid local minima during the optimization. In this way, the linear weights between the energy terms are automatically adjusted, and no manual assistance is required. Our nonrigid tracking code is fully implemented in C++ and uses an efficient sparse linear solver based on Cholesky factorization for the Gauss-Newton steps (c.f., http://www.cise.ufl.edu/research/sparse/SuiteSparse/). The tracking experiments were conducted on a 2.2-GHz quad core Intel Core i7 machine with 8 GB RAM.

Algorithmic validation.

To validate the reliability and robustness of our markerless motion-tracking algorithm, we used traditional fiducial markers to identify tracking inaccuracies. Verhoeff's elastin stain (5% alcoholic hematoxylin, 10% ferric chloride, and Verhoeff's iodine in a ratio of 5:2:2) was applied to each heart with a nasal sprayer to create a discrete pattern of dots on the surface of the heart. As shown in Fig. 1, the Verhoeff's stain produced >100 high-contrast markers ∼1 mm in diameter that did not bleed or fade significantly when the heart was submerged in Tyrode solution.

Following data acquisition, 10 fiducial markers were selected within the texture images of the structured light data in areas of varying curvature and displacement on the right ventricular (RV) epicardium. The points were then manually tracked through two consecutive cardiac cycles, as determined by a simultaneously recorded cardiac ECG. We selected the RV for validation because it displayed the greatest nonrigid body motion in our unloaded preparation. This process was applied for n = 3 hearts during SR and ventricular pacing at CLs of 200 and 143 ms. Manual tracking served as our ground truth and was compared with our markerless surface-matching algorithm described above. For comparative purposes, we also used a traditional texture correlation algorithm, previously described (17), to track motion at each of the 10 labeled points. All errors were defined by Euclidian distance between manually tracked and algorithmically predicted trajectories.

RESULTS

By combining structured light imaging with nonrigid surface registration, we are able to track and describe complex deformations of the heart at 200 frames/s with an in-plane spatial resolution of 87 μm and depth resolution of 10 μm (supplemental movie 1). For a rabbit heart specifically, our system can track motion at more than 200,000 points on the epicaridium during rhythmic and arrhythmic contractions. High spatiotemporal motion tracking allows for mechanical mapping of displacements, strain, etc., without the use of spatial interpolation or gating to rhythmic cardiac events. For these mechanical metrics to be meaningful, however, motion tracking must be reliable over multiple cycles and robust to different physiological conditions.

Algorithmic reliability.

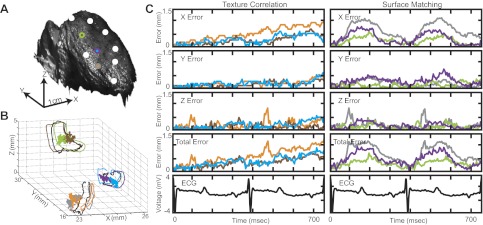
Figure 3 demonstrates tracking errors from a representative heart during SR. To illustrate algorithmic reliability, we isolated 3 of the 10 tracked points on the anterior surface of the RV (bicolor circles in Fig. 3A). For each point, three 3-D trajectories are displayed in Fig. 3B for one cardiac cycle based on the three tracking methods employed: manual tracking (black), texture correlation (brown, blue, orange), and markerless surface matching (green, purple, gray). Errors for algorithmically predicted trajectories were calculated per frame and plotted at the corresponding 3-D trajectory centroid in the same color as its respective trajectory (Fig. 3B). In-plane error (X, Y), out-of plane error (Z), and total absolute error per frame are displayed in Fig. 3C for each point over two cardiac cycles. As shown in Fig. 3B, cardiac displacements form loops in 3-D space during SR. Errors produced by texture correlation and surface matching are clustered near the centroid (zero error) for each 3-D loop and are independent of loop size. When employing texture correlation (Fig. 3C, left), we observed propagation of error for all tracked points (10 of 10) over the two cardiac cycles in all examined hearts (3 of 3). Total error for texture correlation increased from 0 to 1.27 (orange), 0.85 (blue), and 0.52 (brown) mm over the two cycles (Fig. 3C, left). For markerless surface matching, error profiles are cyclical over the two cardiac cycles with total error oscillating between 0 and maximum values of 1.23 (gray), 0.97 (purple), and 0.72 (green) mm (Fig. 3C, right).

Fig. 3.

Validation of markerless motion tracking algorithm during sinus rhythm (SR). A: anterior surface of the right ventricle (RV) labeled with 10 points (7 white and 3 bicolored). B: 3-D trajectories of bicolored points. For each bicolored point, 3 trajectories are plotted based on the 3 tracking methods employed: manual tracking (black), texture correlation (brown, orange, blue), and surface matching (gray, purple, green). Colored dots at the centroid of each trajectory represent Euclidian error for each motion-tracking algorithm. C: absolute error in X, Y, and Z directions and total error for each bicolored point over 2 cardiac cycles.

Algorithmic robustness.

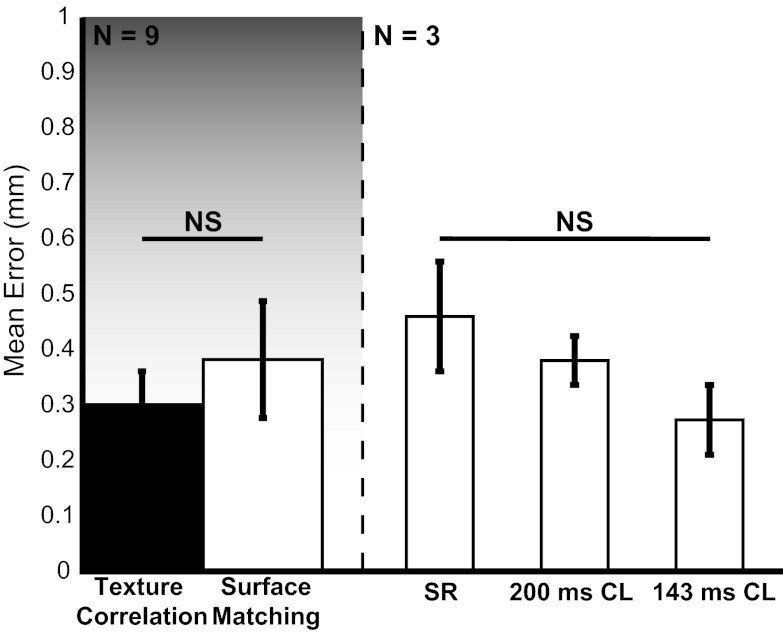
To examine the robustness of our tracking algorithm to different physiological conditions, we measured mean error over one cardiac cycle for all tracked points (n = 10) in all examined hearts (n = 3) during three pacing conditions: SR, pacing at CL = 200 ms, and pacing at CL = 143 ms. Mean error was calculated by averaging error per tracked point for each heart (n = 3) and each pacing condition (n = 3) yielding nine different error scores. Error scores were grouped by tracking method (left) and pacing rate (right) to analyze variability (Fig. 4). A single cardiac cycle was used in this analysis to remove algorithmic bias introduced by error propagation in the texture correlation method. All error bars represent standard error calculated on the mean composite error score. Significance between groups was determined by the Mann-Whitney U-test (α = 0.05) because of nonnormality. Overall, a nonsignificant difference in mean error was observed between texture correlation (0.29 ± 0.06 mm) and surface matching (0.37 ± 0.10 mm). Additionally, both methods display mean errors below 0.5 mm, <5% of the apex-base distance. During experimentation, we observed a decrease in overall cardiac displacement with increased pacing rate. We hypothesize that a decrease in pacing-induced global displacement decreases interframe variations in the data, reducing tracking error. As shown in Fig. 4, tracking error produced by surface matching displays a nonsignificant (P > 0.05) decreasing trend with increasing pacing rate: 0.46 ± 0.10 mm for SR, 0.38 ± 0.04 mm for CL = 200 ms, and 0.27 ± 0.06 mm for CL = 143 ms. Although the results are not statistically significant, this trend suggests a correlation between tracking error and global displacement.

Fig. 4.

Validation of markerless motion tracking algorithm for n = 3 hearts for SR, 200 ms cycle length (CL) ventricular pacing, and 143 ms ventricular pacing. Left: comparison of mean error for markerless surface matching (white) to traditional texture correlation (black). Right: comparison of mean error for markerless surface matching during SR, 200 ms CL ventricular pacing, and 143 ms ventricular pacing. Error bars represent standard deviation of the mean. Significance between groups is calculated with the Mann-Whitney U-test. P < 0.05 considered significant; NS, not significant.

Surface mechanics of the beating heart.

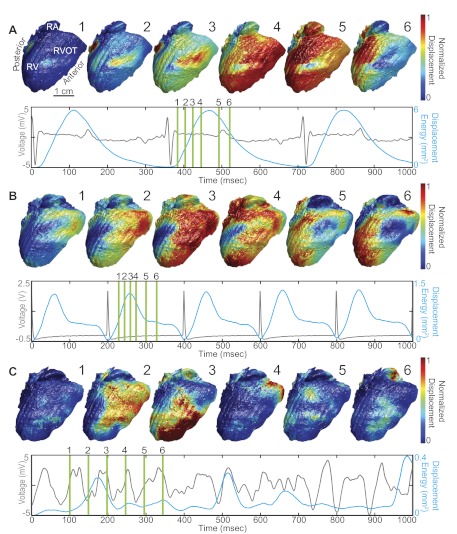
Because of the accuracy and precision of our system, we can provide detailed evaluations of cardiac surface mechanics. Here, we demonstrate our system's ability to calculate surface displacement during rhythmic and arrhythmic contractile patterns. Displacement was calculated as the Euclidian norm between a pixel in a particular frame and its respective location at end diastole determined by a simultaneously recorded cardiac ECG. Figure 5, A–C, depicts three different analyses of cardiac displacement during SR (A), ventricular pacing at CL = 200 ms (B), and VF (C). For each case, displacement is normalized between 0 (blue) and 1 (red) and mapped to the deforming epicardial surface to create movies of cardiac displacement (supplemental movies 2–4). Six frames from each movie are displayed in Fig. 5 to highlight variations in displacement patterns observed for each of the three cases. To provide a macroscopic measure of tissue displacement, we spatially integrated squared displacements on the surface of the heart before normalization and divided by the number of surface pixels. This metric, referred to as displacement energy, was interpolated to 2 kHz to match the sampling rate of the ECG. Paired ECG (gray) and displacement energy (blue) data are displayed for each respective case in Fig. 5.

Fig. 5.

Analysis of motion in the beating rabbit heart for SR (A), apical pacing (CL = 200 ms; B), and ventricular fibrillation (C). For each case, sequences of 6 normalized displacement maps are displayed. Location of sequence frames is indicated by green bars on a simultaneously recorded ECG (gray). Displacement energy (blue), a measure of total tissue displacement, is overlaid on each respective ECG.

Analysis of displacement reveals three different patterns of motion during SR, ventricular pacing, and VF. For SR (Fig. 5A, 1–6), contraction begins midway up the anterior paraseptal RV (1 and 2) and initially spreads toward the anterior aspect of the interventricular septum (3). The displacement wave then wraps around the initialization point and spread toward the posterior aspect of the heart (4). During this process, displacement transfers from the RV to the right atrium (5). SR displacement energy displays close correlation with the cardiac ECG. Peak displacement energy is achieved ∼100 ms following ventricular excitation (as determined by the R wave of the ECG), which corresponds to the end systolic phase. Mechanical relaxation (diastole) coincides with the T wave of the ECG, a marker of cardiac repolarization. When ventricular pacing is applied near the apex (Fig. 5B, 1–6), we observed a different mechanical displacement pattern compared with SR. Displacement first appears near the RV outflow track in the anterior RV (1 and 2). Similar to the pattern observed during SR, the paced displacement wave initially propagates over the surface from the anterior to posterior RV (3). During the diastolic interval, however, the displacement wave splits into inferior and superior waves-wrapping around a large area of the RV posterior wall (4). The inferior and superior displacement waves eventually rejoin (5) before displacing the remaining RV posterior wall (6). This complex pattern of mechanical displacement during relaxation manifests as a plateau in the displacement energy curve. During VF (Fig. 5C), we observed a classic example of fibrillatory mechanical and electrical activity. Instead of displaying a regular contractile pattern, the heart quivers irregularly. Although a few strong displacement peaks are observed in the displacement energy trace, displacement peaks are not 1:1 with electrical activity. Additionally, each major displacement peak during VF is the result of a unique displacement pattern (supplemental movie 4).

As mentioned previously, we observed greater displacement during SR rather than during rapid pacing. When validating our motion tracking algorithms, tracking of SR data displayed greater mean error compared with pacing data, presumably because of greater displacements in the SR data. The observation of greater displacement during SR is clearly confirmed by the displacement energy signals displayed in Fig. 5. Peak displacement energy is largest during SR at 5.0 mm² and decreases to 1.3 mm² during apical pacing and 0.4 mm² during VF.

DISCUSSION

In this study, we present the first step in the development of a system to measure whole heart excitation-contraction coupling. Here, we demonstrate whole heart optical mapping of regional epicardial mechanics with structured light imaging and nonrigid surface registration. Our system has several benefits over current well-established techniques for studies of cardiac mechanics. First, the in-plane spatial resolution of our structured light system is 87 μm and the depth resolution is 10 μm. Post surface registration, we measured a mean tracking error of 0.37 ± 0.10 mm and a maximum error for all hearts of 1.23 mm. These errors were found to be cyclical and nonpropagating, an important advantage over texture-based tracking methods. While tracking error reduces the resolution of our system, our method still maintains comparable resolution to MRI and video-based techniques. In published work with 4-D MRI, Prinzen et al. (27) demonstrated a spatial resolution of 1.25 × 3 × 6 mm for measuring strain and producing mechanical activation patterns in paced canine hearts. More recently, Gaudette et al. (11) presented a technique for two-dimensional (2-D) computer-aided speckle interferometry (CASI) at a spatial resolution of 50 μm/pixel for regional epicardial displacement tracking in Langendorff-perfused rabbit hearts. Unlike 2-D techniques such as speckle tracking, structured light imaging accounts for out-of-plane motion and surface curvature. Second, we are able to accurately measure and track cardiac surface motion without relying on fiducial markers or implanted sensors that limit spatial resolution and potentially damage the myocardium in techniques such as biplane radiography (25), sonomicrometry (38), and other video-based techniques (12). Third, our system measures dynamic deformation of the heart in real time. Thus it is able to measure mechanical deformation in 4-D during both rhythmic and arrhythmic conditions. Other technologies are currently limited to rhythmic patterns or lower dimensional data. Finally, our system is able to capture whole heart 3-D deformation at frame rates up to 667 frames/s. This frame rate is an order of magnitude large than current technology, such as 4-D MRI and 4-D echocardiography, where temporal sampling is reduced to 15–20 ms (∼50–60 frames/s) because of scanning (28, 34, 44).

Although our current data are limited to ex vivo measurements of unloaded rabbit hearts, parallels to well-established physiological phenomena of excitation-contraction coupling are immediately evident in this study. First, our data exhibit anatomical correlation to published electrical data. As shown in Fig. 5A, we observed earliest epicardial displacement of the cardiac surface during SR in the RV anterior-paraseptal region, a pattern common to all hearts in our study. This location of earliest epicardial displacement coincides with the location of initial epicardial depolarization, as documented in rabbits (30) and in humans (29). Second, our data display close temporal coupling with electrical recordings in working and impaired myocardium. In Fig. 5, A and B, maximum displacement energy is reached following the QRS complex of the ECG (Fig. 5A) or the ventricular pacing artifact (Fig. 5B), markers of mechanical systole. Additionally, relaxation coincides with the ECG T wave, an indicator of mechanical diastole. Conversely, mechanical analysis of VF (Fig. 5C) clearly shows dissociation of electrical and mechanical activity. In a recent study of long-duration VF, Kong et al. (16) demonstrated desynchronization of intramural recordings of calcium transients and membrane voltage as well as prolongation of calcium transients during VF and global ischemia. Dissociation of mechanical and electrical recordings observed in our ischemia-induced VF model may also result from impaired calcium handling aiding in arrhythmia promotion. Further studies are necessary to investigate this hypothesis.

Presently, no existing technology has the ability to simultaneously measure excitation and contraction in the whole heart. As a result, mechanics and electrophysiology are often studied separately. In basic research, fluorescent imaging of voltage-sensitive dyes is one of the most common techniques for measuring whole heart electrophysiology (8). This technique has enabled ex vivo analysis of arrhythmias, therapeutic interventions, and basic physiology with high-spatial (350–2,000 μm/pixel) and temporal (> 500 frames/s) resolution in animal and human tissues. Despite its diagnostic advantages, fluorescence imaging techniques are limited to mechanically arrested hearts because of significant motion artifacts introduced by contraction. Recently, Bourgeois et al. (4) and Seo et al. (33) demonstrated the feasibility of 2-D motion tracking applied to beating pig and rabbit hearts for motion artifact correction in optical imaging and strain measurement at a sparse collection of fiducial markers. If meaningful analysis of excitation-contraction coupling is to be performed with optical techniques, however, mechanical mapping must have comparable resolution to optical mapping techniques. As demonstrated here, we propose that this can be achieved with structured light imaging. Multiplexing structured light with fluorescence imaging of beating hearts in a single camera system may provide a means to digitally correct motion artifact in fluorescence data on a pixel-by-pixel basis. This system could be extended to image multiple fluorescent dyes to sense intracellular calcium, potassium, sodium, various metabolites, etc. Multimodal data from such a system would aid in the development of novel computational models of whole heart electromechanical coupling for both health and disease. Where current analyses (36) are limited to rhythmic data, our method could provide arrhythmic data necessary for understanding complex systemic interactions during atrial and ventricular fibrillation. From such models, accurate measures of tissues properties can be extracted and used for furthering our knowledge of cardiac disease and developing novel therapies.

Limitations.

We acknowledge several limitations in our study. First, displacement and strain patterns were measured on passive, unloaded myocardium, which will likely be different from loaded myocardium. Future studies will focus on working heart and in vivo models for more accurate analysis of physiological contraction. Second, our current structured light system is limited to a single camera viewpoint and only measures 3-D surfaces, not volumes. With the use of multiple synchronized cameras and projectors, it is possible to capture a panoramic image of the heart as done previously in electrical mapping systems (5, 14, 23, 30). Because of the large size of our data (over 7 GB for a 200 frame sequence), the tracking method presented herein has a high computational cost (up to a minute per frame on a 2.2-GHz Intel Core i7 processor depending on the level of deformation). However, our ability to recover the shape and motion of any heart would allow us to build a complete database covering the entire space of possible deformations (1) as a precomputation step. Parallel matching and statistical model reduction techniques could significantly boost the convergence rate of our nonrigid alignment technique and potentially offer a real-time solution. Finally, while our measurement error (87 μm in-plane and 10 μm depth) is small compared with other well-established technologies, tracking error produced during registration reduces system resolution. One way to improve tracking accuracy is to increase the measurement resolution of our system with different optics to maximize the available pixels used on our current CMOS chip. Using texture information in conjunction with 3-D geometry in a new tracking algorithm may improve tracking accuracy. Nevertheless, tracking errors produced by our system are comparable with those in previous studies on excitation or contraction with other measurement modalities. Therefore, we are confident our system has sufficient resolution for accurate analysis of combined excitation-contraction coupling.

GRANTS

This study was supported by National Heart, Lung, and Blood Institute Grants HL-067322, HL-108617, and HL-085369 and National Science Foundation Grant CMMI-1150711.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

J.I.L., S.Z., H.L., and I.R.E., conception and design of research; J.I.L. and S.Z. performed experiments; J.I.L., S.Z., H.L., and C.C.S. analyzed data; J.I.L., S.Z., H.L., C.C.S., and I.R.E. interpreted results of experiments; J.I.L., H.L., and C.C.S. prepared figures; J.I.L., S.Z., H.L., and I.R.E. drafted manuscript; J.I.L., S.Z., H.L., C.C.S., and I.R.E. edited and revised manuscript; J.I.L., S.Z., H.L., and I.R.E. approved final version of manuscript.