Use of Alternative Time Scales in Cox Proportional Hazard Models: Implications for Time-Varying Environmental Exposures

Abstract

Issues surrounding choice of time scales in Cox proportional hazard regression models have received limited attention in the literature. Although the choice between time on study and ‘attained’ age time scales has been examined, the calendar time scale may be of interest when modeling health effects of environmental exposures with noteworthy secular trends such as ambient particulate matter air pollution in large epidemiological cohort studies. The authors use simulation studies to examine performance (bias, mean squared error, coverage probabilities, and power) of models using all three time scales when the primary exposure of interest depends on calendar time. Results show that performance of models fit to the calendar time scale varies inversely with the strength of the linear association between the time-varying primary exposure and calendar time. Although models fit to attained age and time on study that do not adjust for calendar time were relatively robust, the authors conclude that care should be exercised when using time scales that are highly correlated with exposures of interest.

INTRODUCTION

Issues surrounding the choice of time scales in Cox proportional hazard regression models have received some attention in the literature [1-6]. In most of these studies, the choice has been between time on study (e.g., time since randomization/enrollment) or ‘attained’ age. Historically, the Cox model was developed for clinical studies in which a sample of individuals was followed from a well-defined starting point (e.g. diagnosis of a disease; day of randomization) until the end point of interest occurred, the individual was lost-to-follow-up, or the study ended. Thus, time on study was the natural choice of time scale for these analyses. With the increase in large scale cohort studies that follow individuals over time for the occurrence of one or many different types of events, interest in the use of alternative time scales has grown. Such interest has primarily focused on use of an attained age scale where the primary time variable in the Cox model is defined by study participants’ age at entry into the study and age at which they experience an event or their follow-up is censored. Use of the attained age scale provides the most flexible control for age effects while avoiding the need to include an effect of age (or some parameterization of it) that satisfies the proportional hazard assumption underlying the Cox model. It also provides a relatively meaningful basis on which to examine how risk varies over time.

Increasing interest in the effects of environmental exposures on health outcomes [7-9] raises the possibility of a third time scale for consideration, in particular, calendar time. In analyses of exposures that are correlated with calendar time, it presents several potential advantages over the use of the time on study or attained age scale. For example, Shih et al [10] evaluated the effects of mean ambient particulate matter air pollution concentrations < 2.5 μm (PM_2.5) and < 10 μm (PM₁₀) in aerodynamic diameter on risk of venous thromboembolism using data from the Women's Health Initiative hormone therapy trials. In this study, spatially interpolated, geocoded address-specific mean ambient PM_2.5 and PM₁₀ concentrations [11] were available over follow-up for each woman at every venous thromboembolic event for which they were at risk. The authors modeled these concentrations as a time-varying exposure in Cox models fit over calendar time such that event-specific risk sets had comparable exposure information, i.e., within a risk set, exposures were drawn from the same calendar period, a condition that may not be satisfied in analyses on the attained age or time on study scales.

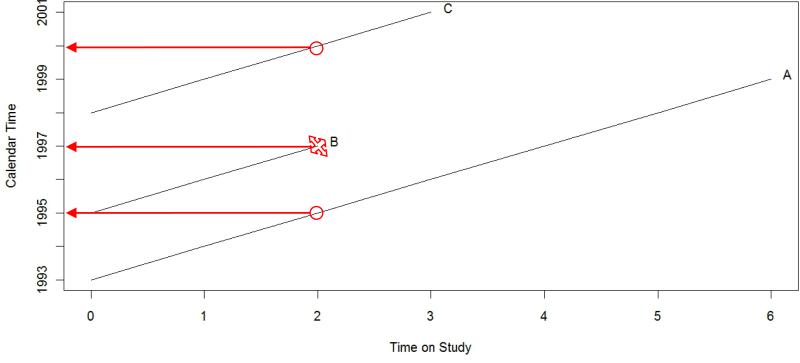
Figure 1 illustrates the concerns that may arise when fitting a Cox model to the traditional time on study scale when interest in assessing the effect of a time-varying exposure such as PM_2.5 and PM₁₀ is paramount. The figure graphs the follow-up times for time on study versus calendar time for three hypothetical study participants, A, B and C. Participant A enrolled in 1993 and was followed for 6 years; participant B enrolled in 1995 and was followed for 2 years; and participant C enrolled in 1998 and was followed for 3 years. Participant B is assumed to have an event while participants A and C are right-censored. When analyzing the effect of a time-varying exposure on the hazard function, a model fit to the time on study scale would compare exposure information for all participants, A, B and C, at participant B's event time as a function of follow-up time since A and C would be considered to be part of participant B's “at-risk” set. However, as denoted by the red arrows, this means that the exposure information for the primary time-varying covariate of interest originates in different calendar years: participant A's data from 1995; participant B's from 1997; and participant C's from 2000.

Figure 1.

Plots the follow-up times versus calendar time for three hypothetical study participants, A, B and C. Participant B is assumed to have an event and the red arrows denote the calendar year from which time-varying exposure information would be pulled when fitting a Cox model to the time on study scale.

Pulling exposure measurements from different calendar years as shown in Figure 1 might not be a concern if interest lies in estimating the effect of time-varying exposures without temporal trends such as blood pressure or cell phone usage. However, with the large number of temporally variable environmental exposures that may be associated with disease risk [12-15], true associations could be obscured when there is inadequate control for these secular trends. For example, it is well known that PM₁₀ concentrations declined in the U.S. between 1980 to 2008 which covers the time period illustrated in Figure 1 [12]. Other examples of calendar time-dependent exposures exist inside and outside the field of environmental epidemiology. For instance, since the removal of lead from gasoline and other consumer products beginning in the 1970s, there have been marked declines both in ambient lead exposure and blood lead concentrations among the U.S. population [16-17]. Similar to exposures to PM_2.5 and PM₁₀, ignoring these temporal declines in the context of Cox models of lead's health effects on an attained age or time on study scale could yield inappropriate comparisons. Similarly, proportion of U.S. households with wireless-only phone service nearly doubled between 2007 and 2010 [14], which could affect the failure rate of land-line-based telephone health survey contacts or introduce bias in studies of health effects because health status and service utilization varies by household telephone status [14].

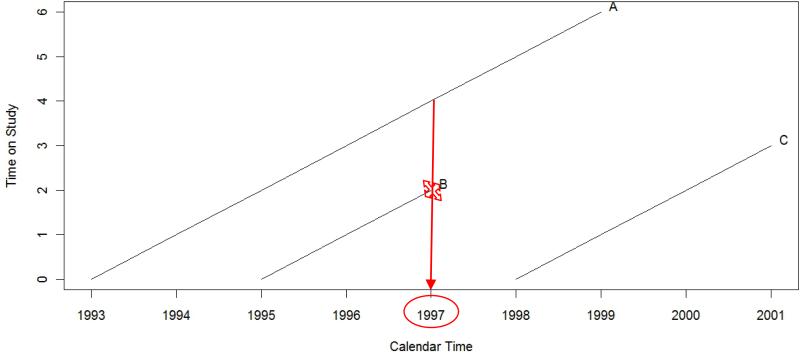
Figure 2 illustrates how a Cox model fit to the calendar time scale would be able to ensure that environmental exposure measures are pulled from the same calendar time point. In Figure 2, the follow-up times for the same three hypothetical study participants from Figure 1 are shown, but the axes are reversed so that the primary time scale for the analysis is calendar time. Participant B's event now occurs on a specific date in 1997 and now only participant A remains in the “at-risk” set for this particular event. Conveniently, when analyzing the data on the calendar time scale, exposure information for participants A and B will now all come from the same calendar time point, potentially ensuring comparability. Nonetheless, the pulling of exposures from the same year does not guarantee unbiased estimation of the true association between a time-varying environmental exposure and the outcome. In cases where there is an association between the time-varying exposure of interest and calendar time but no association between calendar time and the outcome, controlling for calendar time as either the time scale of interest or as a covariate might very likely dilute the true association. Moreover, it is also possible that as a surrogate for cumulative exposure to the environmental measure, use of calendar time as the primary time scale for analysis may confound estimation of the true, but unknown, health effects of the environmental exposure [18].

Figure 2.

While the findings in the literature discuss choice of attained age versus time on study, to date, there has been no evaluation of the use of calendar time in settings with (calendar) time-varying environmental exposures. For example, when considering use of a time on study versus attained age scale, some have argued that the attained age scale is preferable in both clinical and epidemiologic studies since the effect of age on an individual's hazard is generally much larger than the effect of time on study and because age effects often fail to satisfy the proportional hazard assumption. Korn et al [1] suggest that use of the attained age time scale with stratification by birth cohort is the most appropriate approach in cohort studies. The authors indicate that use of this model is equivalent to a model using time on study as the primary time scale when the effect of age on the hazard function for an event is exponential; otherwise inferences may differ. Thiebaut and Benichou [2] describe the degree of bias in time on study analyses with various types of age adjustments for data generated under an attained age model, confirming the suggestions of Korn et al [1] through simulations while Commenges, Leteineur, and Joly [5] use a simulation study to show how typical parametric modeling of age on the time on study scale (i.e, via stratification or using five-year indicator variables) may lead to biased results. Cheung, Gao, and Knoo [3] utilize a relative survival analysis approach to argue heuristically that use of attained age as the time scale in a Cox analysis of age at diagnosis of cancer and mortality is the most appropriate.

The aim of this paper is to provide insight into the modeling of time-varying environmental exposures such as PM_2.5 and PM₁₀, the values of which may vary over calendar time. Specifically, this paper aims to establish the conditions under which variation with calendar time will not bias inferences drawn from Cox models. We use simulation studies to examine how performance (bias, mean squared error, coverage probabilities, and power) of models fit to all three time scale are affected when the primary exposure depends on calendar time.

METHODS

Simulated data

The design of the simulation was based in part on the design of the Women's Health Initiative hormone therapy trials (WHI HT) [19]. Data was generated for a sample of 1000 study participants. Calendar time was represented to begin at year 0 and was generated uniformly between 0 and 6 calendar years for each study participant. Age at enrollment was also generated uniformly between the ages of 50 and 79. To generate time-varying values of the environmental exposure, we let P_ij denote the i^th woman's j^th value of the environmental variable and let cy_ij denote the corresponding calendar year of the j^th observation for the i^th woman. We let j range from 0 to 9 so that each woman had a total of 10 years of data generated for the time-varying environmental exposure assuming that the value of P_ij is constant between calendar year j and j+1. Datasets were generated under two different assumptions (scenarios) about the relationship between P_ij and cy_ij. In both, the underlying distribution for values of P_ij were based on observed distributions for PM₁₀ in the U.S. between 1980 and 2008 [12].

Scenario 1: Assumes environmental exposure is uncorrelated with calendar year

Annual values of the time-varying exposure, P_ij, were generated for individual i and follow-up year j independently of and with little variation within individuals over calendar year. Specifically, it was assumed that:

$$P_{i0}\sim N(30,5)$$

and

$$P_{ij}\sim N(P_{i,j=1},1,5)\text{where}j=1,\dots ,9.$$

Scenario 2: Assumes environmental exposure has a linear association with calendar year

Annual values of the environmental exposure were generated such that they were linearly dependent on calendar year. Specifically, it was assumed that:

$$P_{i0}\sim N(30-{{\beta }_1}^{\ast }c{y}_{i0},5)$$

and

$$P_{ij}\sim N(P_{i,j-1}-{\beta }_1,1,5)\text{where}j=1,\dots ,9.$$

where cy_i0 represents the calendar year that subject i was enrolled. Simulations were done across a range of values for β₁ (namely β₁ was set equal to 1, 2, ...,10); β₁ represents the average annual linear decrease that occurs for the environmental variable.

Generation of event times utilized permutational algorithms with a rejection sampler (PAR), an approach that has been shown to appropriately handle time-varying covariates when performing simulation studies of the Cox model [20]. Specifically, PAR is used to generate event times conditional on age and time-varying values of P_ij using the following steps:

1. Generate N survival times T_i for i = 1, . . . ,N from a generic distribution. A Weibull distribution with shape parameter equal to 0.5 and scale parameter 66 was selected to yield a reasonable distribution of event times over a follow-up of 10 years.

2. Generate N censoring times C_i for i = 1, . . . ,N from a generic distribution. A uniform distribution between 5 and 10 years was selected to reasonably reflect follow-up times in the WHI CT and to yield a censoring rate of 66%.

3. Define $t_i^{\ast }=\min (T_i,C_i)$ and δ_i = 1(T_i < C_i) i = 1,...,N, then sort the N survival status pairs ($t_i^{\ast },{\delta }_i$) so that $t_i^{\ast }<t_{i+1}^{\ast }$.

4. Using the covariate values generated above for age at enrollment and the time-varying environmental exposure, P_ij, create N individual matrices of covariate values, denoted by X_s for s=1, . . . , N. Each matrix had 10 rows, each of which represented a one-year follow-up time, and 3 columns which contained age at enrollment (not time-varying), age at enrollment squared (not time-varying), and the values P_sj for j = 0,...,9. Define X_s(t) as the vector of covariate values at time t (t = 1, . . . ,10) for subject s (s=1, . . . , N).

5. Starting from the earliest observed time, $t_1^{\ast }$, randomly assign each consecutive survival status pair ($t_i^{\ast },{\delta }_i$) to a vector of current covariate values X_s(t) using the following rules:

   1. If δ_i = 1 (i.e, $t_i^{\ast }$ is an event), use a rejection sampler to assign the covariate vector. First, define R_i as the risk set for $t_i^{\ast }$ such that it contains the individual covariate matrices that have not yet been selected and randomly sample X_s($t_i^{\ast }$) from the individuals in R_i. Draw U from a uniform distribution between 0 and 1. Compute the hazard ratio associated with the covariate vector X_s($t_i^{\ast }$), namely $h\left(X_s\left(t_i^{\ast }\right)\right)=\exp \left({\gamma }^{\prime }{X}_s\left(t_i^{\ast }\right)\right)$. If $U<h\left(X_s\left(t_i^{\ast }\right)\right)∕c_{t_i^{\ast }}$ where $c_{t_i^{\ast }}=\max \left(\exp \left({\gamma }^{\prime }{x}_v\left(t_i^{\ast }\right)\right)\right)$ for v ⊂ R_i then assign ${\mathrm{X}}_{\mathrm{s}}\left(t_i^{\ast }\right)$ with event time $t_i^{\ast }$; otherwise repeat this step.
   2. If δ_i = 0, assign a subject who is censored at time $t_i^{\ast }$ by simple random sampling from the risk set R_i with equal probability 1/size(R_i).

The underlying Cox model that is used in these calculations assumes

$${\lambda }_i\left(t\right)={\lambda }_0{\left(t\right)}^{\ast }\exp ({{\gamma }_1}^{\ast }ag{e}_i+{{\gamma }_2}^{\ast }ag{e}_i^2+{{\gamma }_3}^{\ast }{P}_{ij})fort\subset [j,j+1]$$

where j = 0,1,...,9 and age_i denotes age at enrollment for the i^th woman. For all simulations, γ₁ = ln(1.17) and γ₂ = ln(0.999) to allow for a reasonable effect of age on the hazard. A range of values for γ₃ were considered, corresponding to hazard ratios of 1.1, 1.2, 1.3, 1.4, and 2 for a 10 unit increase in the environmental exposure, P_ij. In all scenarios, 100 simulations were performed.

Models used to estimate the effect of the environmental exposure

A total of five Cox models are reported on herein. The details of these models (time scale + control variables used) are shown in Table 1. Results from an additional 25 models are available as Supplementary Material. All models include time-varying values of the environmental exposure, denoted by P(m) in Table 1 to highlight the fact that the value of the environmental exposure is selected relative to the time scale over which the model is being fit (m = t denotes the time on study scale, = a denotes the attained age scale, and = cy denotes the calendar year scale). Additionally, all models fit to the time on study and calendar time scales control for age at enrollment and age squared while the models fit to the attained age scale all control for birth cohort (categorized into 5-year increments) as a stratification variable in the Cox model. The analytic data sets used to fit models on each of the three time scales were appropriately manipulated so that each woman had a total number of rows corresponding to the number of events for which that woman was at risk for the outcome. Each row contained the woman's exposure information for each event and start and stop time syntax was utilized in R's coxph() command.

Table 1.

Results assuming environmental exposure is uncorrelated with calendar time.

Model	Time Scale	Controls	Abs.Bias	MSE	Coverage	Power
HR for 10-unit change in P = 1.1
T1	Time on study	agei+agei2+P(t)	0.0095	0.00026	0.94	0.18
T2	Time on study	agei+agei2+cy(t)+P(t)	0.0095	0.00026	0.94	0.17
A1	Attained age	birth.cohorti +P(a)	0.0095	0.00026	0.93	0.16
A2	Attained age	birth.cohorti + cy(a) +P(a)	0.0094	0.00026	0.93	0.16
C1	Calendar time	agei+agei2+P(cy)	0.0092	0.00025	0.94	0.17
HR for 10-unit change in P = 1.2
Tl	Time on study	agei+agei2+P(t)	0.0087	0.00024	0.97	0.32
T2	Time on study	agei+agei2+cy(t)+P(t)	0.0087	0.00024	0.97	0.32
A1	Attained age	birth.cohorti +P(a)	0.0083	0.00023	0.96	0.33
A2	Attained age	birth.cohorti + cy(a) +P(a)	0.0084	0.00024	0.96	0.30
C1	Calendar time	agei+agei2+P(cy)	0.0088	0.00024	0.96	0.33
HR for 10-unit change in P = 1.3
T1	Time on study	agei+agei2+P(t)	0.0085	0.00023	0.94	0.67
T2	Time on study	agei+agei2+cy(t)+P(t)	0.0085	0.00023	0.95	0.67
A1	Attained age	birth.cohorti +P(a)	0.0086	0.00023	0.94	0.70
A2	Attained age	birth.cohorti + cy(a) +P(a)	0.0087	0.00024	0.95	0.65
C1	Calendar time	agei+agei2+P(cy)	0.0088	0.00023	0.94	0.67
HR for 10-unit change in P = 1.4
T1	Time on study	agei+agei2+P(t)	0.0084	0.00024	0.96	0.90
T2	Time on study	agei+agei2+cy(t)+P(t)	0.0084	0.00024	0.96	0.91
A1	Attained age	birth.cohorti +P(a)	0.0085	0.00024	0.94	0.90
A2	Attained age	birth.cohorti + cy(a) +P(a)	0.0087	0.00024	0.94	0.90
C1	Calendar time	agei+agei2+P(cy)	0.0088	0.00024	0.93	0.90
HR for 10-unit change in P = 2
T1	Time on study	agei+agei2+P(t)	0.0085	0.00023	0.94	1.00
T2	Time on study	agei+agei2+cy(t)+P(t)	0.0087	0.00024	0.95	1.00
A1	Attained age	birth.cohorti +P(a)	0.0089	0.00024	0.93	1.00
A2	Attained age	birth.cohorti + cy(a) +P(a)	0.0088	0.00024	0.94	1.00
C1	Calendar time	agei+agei2+P(cy)	0.0084	0.00024	0.93	1.00

Notes: P(m) and cy(m) denote that the time-varying values of the environmental exposure and calendar year variables, respectively, are selected relative to the time scale over which the model is being fit. MSE = Mean Squared Error.

Evaluating performance of models

The following metrics were used to evaluate the performance of each model over the 100 simulations performed.

Absolute bias

Mean absolute difference between γ₃ and ${\widehat{\gamma }}_3$ for each model.

Mean squared error (MSE)

Mean of the mean squared error for each model (e.g., mean of ${\left({\gamma }_3\text{-}{\widehat{\gamma }}_3\right)}^2+\mathrm{var}\left({\widehat{\gamma }}_3\right)$).

Coverage probability

Percentage of times the 95% confidence interval for ${\widehat{\gamma }}_3$ contained the true value.

Power

Percentage of time the 95% confidence interval for ${\widehat{\gamma }}_3$ did not contain 0.

RESULTS

When environmental exposure is uncorrelated with calendar time

Table 1 shows the results from our simulation study under Scenario 1 for a range of values of γ₃. For each value of γ₃, performance of the models across time scales is indistinguishable: mean absolute bias and mean square error are extremely low (less than 0.0095 and 0.00027, respectively), coverage probabilities hover near 95%, and power is similar, with power increasing as γ₃ increases.

When environmental exposure has a linear association with calendar year

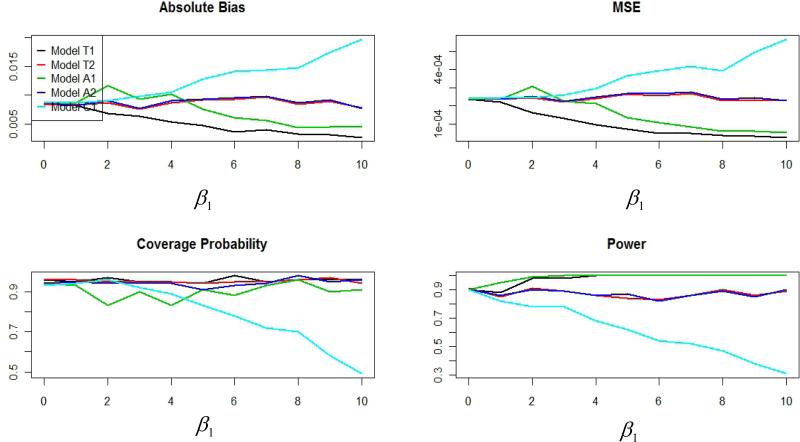
Figure 3 plot absolute bias, MSE, coverage probabilities, and power for each of the five models as a function of function of β₁ (e.g, the average annual linear decrease in the environmental variable) when γ₃ = ln(1.4)/10. As shown, the performance of the calendar time scale model (C1) is the most sensitive to increasing values of β₁. The performance of model C1 decreases as β₁ increases, with particularly poor performance for values of β₁ greater than three (or about 0.60 of the standard deviation in the baseline distribution of P_ij). Additionally, the time on study and age models which control for calendar time (T2 and A2, respectively) perform worse than those that do not (T1 and A1, respectively). In fact, the performance of models T1 and A1 steadily improves as β₁ increases while the performance of models T2 and A2 remains relatively stable as β₁ increases.

Figure 3.

Plots of absolute bias, MSE, coverage probabilities, and power as a function of β₁ when γ₃ = ln(1.4)/10, corresponding to a hazard ratio of 1.4 per 10-unit increase in the environmental exposure.

DISCUSSION

The aim of this paper was to provide insight into Cox modeling of time-varying exposures such as ambient particulate matter concentrations (PM_2.5 and PM₁₀). To this end, we used simulation studies to examine how performance from models fit to three different time scales (time on study, attained age, and calendar time) were affected when the primary exposure linearly depended on calendar time. In the case when environmental exposures are uncorrelated with calendar time, the models considered are shown to be almost indistinguishable. Conversely, when there is a linear correlation, our results show that it is not the linear dependence itself that is problematic when fitting a Cox model. Instead, decreased performance is driven by the attempt to control for the dependence between the time-varying environmental exposure and calendar year, either by using calendar time as a covariate or as the time scale of analysis.

The model fit on the calendar time scale was generally the most sensitive to increasing the linear association between the environmental exposure and calendar time. The performance of this model varied inversely with the strength of the linear association, as more of the risk associated with variability in the environmental exposure is attributed to differences in calendar time.

It is important to put these findings into context. We considered values for the average annual decrease in the environmental exposure that ranged from 1 to 10 (or 0.1 to 1 standard deviation of the baseline variance in the simulated values of the environmental exposure). Such increases are quite extreme for a measure like PM₁₀ with data from the Environmental Protection Agency (EPA) showing an average annual decrease in exposure concentrations of only β₁ = 0.33 μg/m³ between 1980 and 2008 [12]. Nonetheless, declines in other environmental exposures may be more problematic. For example, the average annual decline of lead in ambient air was approximately 0.023 μg/m³ between 1990 and 2000 [12], a value corresponding to β₁ = 2 (or 0.40 of the standard deviation in the baseline distribution of the environmental exposure).

Controlling for calendar time as a covariate when fitting models to the time on study and attained age scales decreased performance in cases where the linear association between the environmental exposure and calendar time was high (again greater than three). This is expected because multivariable regression models tend to be unstable when two highly correlated variables are included.

Increasing interest in the effects of exposures to particulate matter in ambient air on the survival time scale piqued our interest in understanding whether fitting environmental exposure models over the calendar year time scale may be useful. Results presented herein suggest that this is not necessarily the case. Indeed, exposures originating in disparate years (as illustrated in Figure 1) do not appear to be problematic for the time on study and attained age time scales. However, trying to control for calendar time using a linear covariate or modeling on the calendar time scale can decrease model performance if the linear correlation between the exposure and calendar time is high.