Analysis of Parasite and Other Skewed Counts

Abstract

Objective

To review methods for the statistical analysis of parasite and other skewed count data.

Methods

Statistical methods for skewed count data are described and compared, with reference to those used over a ten year period of Tropical Medicine and International Health. Two parasitological datasets are used for illustration.

Results

Ninety papers were identified, 89 with descriptive and 60 with inferential analysis. A lack of clarity is noted in identifying measures of location, in particular the Williams and geometric mean. The different measures are compared, emphasizing the legitimacy of the arithmetic mean for skewed data. In the published papers, the t test and related methods were often used on untransformed data, which is likely to be invalid. Several approaches to inferential analysis are described, emphasizing 1) non-parametric methods, while noting that they are not simply comparisons of medians, and 2) generalized linear modelling, in particular with the negative binomial distribution. Additional methods, such as the bootstrap, with potential for greater use are described.

Conclusions

Clarity is recommended when describing transformations and measures of location. It is suggested that non-parametric methods and generalized linear models are likely to be sufficient for most analyses.

82, 83, 84... 87

weevils today, Mr. Victor.

That’s above average, but the trend is down.

In a wartime detention camp, a boy counts the vermin in his food rations (from the film Empire of the Sun, based on the autobiographical novel by JG Ballard).

Introduction

Counting items such as parasites results in non-negative integer data: 0, 1, 2, etc. The aim of this paper is to review methods for statistical analysis of such data in medical research. The focus will be on parasite counts although most of the same methods are applicable to other count data such as numbers of insects, plaques or disease episodes.

Descriptive analysis of such data usually includes summary numbers which aim to convey average values of the data. In statistics these are called ‘measures of location’. For count data even these simple measures prove problematic. This is because the data are often skewed: their ‘long tail’ (Mumpower and McClelland 2002) means that a small proportion of people can, for example, harbour a large proportion of the parasites. In basic statistics it is often taught that such skewness precludes the use of the arithmetic mean because it is ‘overly’ influenced by the high values (Kirkwood and Sterne 2003). A possible alternative is to analyse the logarithms of the data instead of the original values. However, for count data, this is only feasible in the absence of zeros, because the logarithm of zero is not a finite number. This has led to controversy over what measures of location are appropriate, and to basic terms such as ‘geometric mean’ being used inconsistently.

Much of this controversy results from a reliance on statistical methods which use the normal (Gaussian) distribution, whose symmetry usually precludes a good fit to count data. However, this dependence is now largely outdated, due to the availability of approaches based on skewed distributions such as the negative binomial (Anderson and May 1991).

The current paper aims to review the statistical methods currently being used for such data, and describe their advantages and disadvantages. It will concentrate on the most common kinds of analyses, leaving aside more specialized ones such as spatial patterns, repeatability and reproducibility. Descriptive methods will be addressed first, then inferential methods, the latter being those which compare counts between groups or correlate them with other variables.

Methods and Results

Descriptive methods

Measures of location: median and means

Location is “the notion of central or ‘typical value’ in a sample distribution” (Everitt 1995). The most commonly measures of location are the median, and various types of mean. The median is the middle value of the sorted data. If the number of values is even, then there are two middle values, and the convention is to define the median as the value half way between them. The median is zero if more than half of the values are zero.

By default ‘the mean’ usually refers to the arithmetic mean — the sum of the values divided by n, the number of values — although there are other types of mean which may be useful for count data. In particular, the geometric mean is obtained by multiplying together all the data values, then taking the nth root (Borowski and Borwein 1989, Everitt 1995). The geometric mean is always less than the arithmetic mean, unless all values in the dataset are identical, in which case the two are equal(Borowski and Borwein 1989). The geometric mean is zero whenever any of the individual values is zero. This makes it rather meaningless for datasets with zeros, e.g. uninfected people.

The geometric mean is related to logarithmic transformation of the data. If there are no zero values, then the geometric mean equals the exponential of the mean of the log-values. Any exponent can be used, but it must equal the logarithm base, e.g. 10 to the power of the mean of the log₁₀-values. This suggests the following modification of the geometric mean to accommodate zero values: add 1 to all the data values, then take the geometric mean, then subtract 1 again. This is known as the Williams mean (Williams 1937). There are also other types of mean. For example, the square mean root is the square of the mean of the square root-transformed data. This measure has applications in meta-analysis(Bushman and Wang 1995) and in assessing the agreement of counts between observers or methods(Alexander et al. 2007). Other powers can also be used: in general these are called power means or algebraic means(Bonferroni 1950).

Confusion between geometric and Williams means

In the medical research literature, the Williams mean is sometimes called the geometric mean, as in the onchocerciasis community microfilarial load (CMFL) (Remme et al. 1986). Nevertheless, the two are not equal. One disadvantage of the Williams mean is its dependence on the choice of units. For example, if skin snips weigh 2mg, the CMFL per snip is not double the CMFL per mg, although both units are used in the literature(Marshall et al. 1986) (Remme et al. 1986). This scale dependence can be avoided by adding and subtracting a value with units e.g. 1/mg rather than a dimensionless 1(Alexander et al. 2005).

The geometric mean is not a clever way to estimate the arithmetic mean

Fulford explains that the Williams mean (he calls it the geometric mean) should not be used to estimate the arithmetic mean (Fulford 1994). Similarly, Dobson et al (Dobson et al. 2009) define helminth vaccine efficacy as a fold reduction in arithmetic mean egg count, then show that this is not well estimated by a ratio of Williams means. The points made by these papers are valid although may seem rather tautological. The different types of mean differ mathematically so it should not be a surprise that one of them cannot properly estimate another. Their values are no more commensurable than, for example, weight-for-height and weight-for-age in nutrition.

Choice of measure of location: arithmetic versus geometric mean

Compared to the arithmetic mean, the geometric mean is said to be ‘not overly influenced by the very large values in a skewed distribution’(Kirkwood and Sterne 2003). How much is ‘overly’? We can try to answer this question objectively by going back to whichever health outcomes motivated the study.

A clear-cut example would be noise pollution. Human perception of sound is approximately logarithmic in that orders of magnitude change in sound pressure (measured in Pascals) are perceived as approximately uniform increments on a linear scale. This is known as Weber’s law(Wojtczak and Viemeister 2008) and is why sound volumes are expressed in decibels (log-ratio of pressure over baseline). Hence, averaging is more aligned with human perception if done on the logarithmic scale: geometric mean of Pascals or arithmetic mean of decibels(Olayinka and Abdullahi 2009). This reasoning is independent of the statistical distribution of the data: even if the decibel values were skewed, their arithmetic mean would still be more relevant than the geometric mean.

The choice of measure of location may not always be so straightforward. If we consider malaria parasite density, then we could imagine either the arithmetic or the geometric mean having more interest, depending on the purpose of the study. If the intensity of transmission is of interest, it may be reasonable to assume that this is proportional to parasite density, in which case the arithmetic mean would be relevant. This would correspond to the use of the annual transmission potential (ATP) in filarial diseases, which is based on the arithmetic mean number of filariae per mosquito(Bockarie et al. 1996). If, by contrast, the objective of the study relates to number of clinical cases, the geometric mean may be more appropriate because the relation of parasite density to the probability of being a case (as opposed to asymptomatic) is non-linear, the slope reducing at higher densities(Smith et al. 1994). In this case, we would need to exclude non-parasitaemic people from the calculation of the geometric mean, although this is not problematic for this purpose because, by definition, they cannot have malaria.

In other situations another measure of location, such as the median, may be preferable. The general point is to ‘deconstruct’ the problem(Hand 1994) so that the choice of measure is subordinated to the study’s objectives, with purely statistical concerns — for example achieving a normal distribution — being secondary.

Measures of dispersion

The most commonly used measures of dispersion are probably the standard deviation, range, and interquartile range. The standard deviation is the square root of the variance, which is the average squared deviation from the mean. More specifically, the standard deviation equals $\sqrt[]{{\Sigma }_i{(x_i-\stackrel{‒}{x})}^2∕(n-1)}$ where ${\Sigma }_i$ means the sum over the data values x_i , and $\stackrel{‒}{x}$ is the sample mean. The range is the interval between the minimum and maximum values in the data. This tends to increase with larger sample sizes. Percentiles are values below which a certain percentage of the data lie, after they have been sorted into ascending order. The median, for example, is the 50^th percentile. The interquartile range is the interval between the 25^th and 75^th percentiles: this interval contains the middle half of the data.

Since the distributions of count data are usually asymmetric, using the standard deviation for error bars, or in ± notation about the mean, are not usually helpful. This is because they will often imply negative values whereas, of course, for count data the lowest possible value is zero. For example, looking at the mean and standard deviation of the hookworm egg counts in Table 1, quoting ‘126 ± 322’ would be rather meaningless. The interquartile range would be one preferable option. Similarly, error bars based on standard deviations are likely to go below zero, as in, for example, the figure showing schistosomiasis faecal eggs per gram by age in one of the papers in the review described below(Seto et al. 2007). Again, plotting the interquartile range, or superimposing box and whisker plots(Kirkwood and Sterne 2003), would be better options.

Table 1.

Descriptive statistics of example datasets.

	Hookworm eggs	Plasmodium falciparum asexual blood stages
Sample size (male:female)	1237 (603:634)	477 (247:230)
Mean age in years (range)	26 (0-95)	4.9 (1-10)
Mass or volume of each sample	two Kato-Katz faecal slides, totalling approximately 1/12g	1 high power field of a thick blood film, approximately 0.001-0.0025 μL (Warrell and Gilles 2002)
Percent positive	76	100a
Mean	126	139
Median	22	74
Geometric mean	0b	59
Williams mean	18	61
Range	0 – 4,803	1 - 4,941
Inter-quartile range	1 – 103	23 – 181
Standard deviation	322	266
Reference	Cundhill et al (2011)	(Dunyo et al. 2006)

^aA positive malaria slide was an entry criterion for the study.

^bThe geometric mean is necessarily zero because the dataset contains zero values (i.e. negative people).

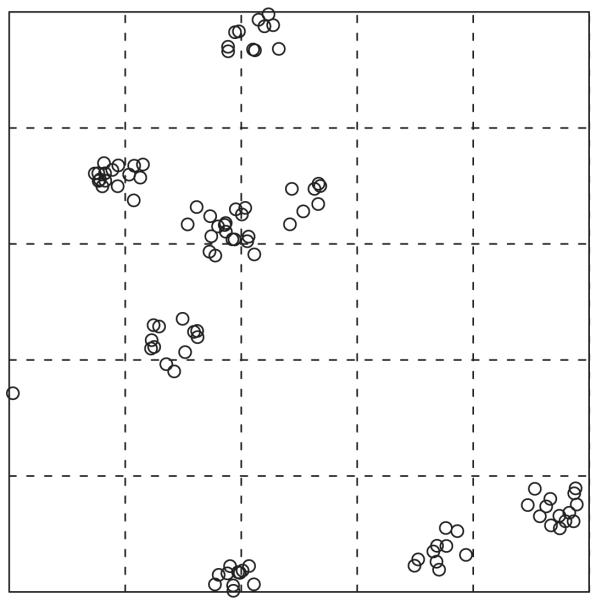
For count data, the greatest utility of the standard deviation or variance may be to assess how homogeneous a distribution the data have. The Poisson distribution results from homogeneous processes, which are the simplest models for count data. The mean and variance of the Poisson distribution are equal whereas, if the variance of data is considerably greater than the mean, there is said to be overdispersion (Elliott 1977, Mwangi et al. 2008). The variance of the negative binomial distribution, for example, equals μ + μ²/k, where μ is the mean and k is a positive-valued parameter. For small values of k the variance is much greater than the mean, reflecting a high degree of overdispersion. Such distributions are sometimes also called ‘contagious’ — even if no infectious disease is involved — because they reflect clustering in the data(Elliott 1977). These two situations — homogeneity and overdispersion — are illustrated in Figure 1. It is also possible for the variance to be less than the mean. This occurs when distances between events tend to be similar, with both smaller and larger distances being rare. This is rare in practice but would be the case, for example, for spatial events on an even grid.

Figure 1.

Simulated spatial data showing homogeneous and clustered processes in the left and right panels, respectively. The dashed lines divide each area into a 5×5 grid. For the homogenous process, the variance and mean of the 25 counts are similar: 3.8 and 4.0 respectively, consistent with a Poisson distribution. For the clustered process, the variance is much larger than the mean: 19.3 versus 3.8, indicating overdispersion. Although these data are spatial, the same principle applies to counts per person, for example. The data were generated using the ‘rpoispp’ and ‘rMatClust’ functions of the ‘spatstat’ package in the R software.

Example datasets

Hookworm eggs

These are baseline data from a longitudinal study of hookworm in Minas Gerais state, Brazil(Cundill et al. 2011). Table 1 shows summary statistics for the total egg count from two Kato-Katz thick smears, each pair being prepared from a single stool sample. Those with missing data on age, sex, or either egg count have been excluded.

Plasmodium falciparum asexual blood stages

Children participating in a trial of anti-malarial drugs had a thick blood film read microscopically(Dunyo et al. 2006). The parasite counts from a single high power field are shown in Table 1.

Literature review

Statistical methods used for parasite count data were reviewed over ten years of Tropical Medicine and International Health. The following search was done in the PubMed online database:

(parasit* OR malaria* OR helmint* OR filar*) AND (count* OR intensit* OR densit*) AND trop med int health

For the years 2001-2010 (volumes 6-15), the search returned 156 papers. They were retained in the review if they were found to include either i) descriptive analysis of parasite count data, or ii) inferential analysis in which count data constituted an outcome variable. Papers using correlation coefficients — which do not distinguish between outcome and explanatory variables — were also included under the second category. Of the 156 papers, 90 were found to include such analyses: 89 descriptive and 60 inferential.

Methods for descriptive and inferential analysis are shown in Table 2 and Table 3. The former includes measures of location, of which the geometric mean was the most commonly used (51% of papers). In some papers, the Williams mean was calculated but presented as the geometric mean. It’s likely that there were other instances of this which could not be unambiguously identified from the text. In other words, the Williams mean category (13%) was difficult, in practice, to separate from the geometric mean. The arithmetic mean was also commonly used (35%) and the median less so (7%).

Table 2.

Descriptive measures of location for parasite count data used in 89 papers in Tropical Medicine and International Health, 2001-2010.

Descriptive measure of location	Number of papers (%)a
Arithmetic mean	31 (35)
Geometric meanb, or arithmetic mean of logarithms
zeros absent	25 (28)
zeros present	7 (8)
unclear whether zeros present or not	13 (15)
Williams mean or similarb,c	12 (13)
Median	6 (7)
Prevalence by category of infection intensity	20 (22)
Otherd	1 (1)

^aThe percentages add to more than 100 because some papers used more than one measure.

^bThe term ‘geometric mean’ is sometimes used in these papers to refer to the Williams mean. Unambiguous examples of this, e.g. evidenced by an equation in the paper, are included under ‘Williams mean or similar’. However, it is likely that more of the ‘geometric means’ are, in fact, Williams means, especially where the data included zeros.

^cWilliams mean = (geometric mean of (x+δ)- δ, when δ=1. Here, ‘similar’ measures include those which: used values of δ other than 1; added 1 without then subtracting it; or took the mean of log(x+1) without then exponentiating.

^dThe arithmetic mean restricted to parasite-positive individuals.

Table 3.

Inferential statistical methods used for parasite count data in 60 papers in Tropical Medicine and International Health, 2001-2010.

Inferential Method	Number of papers (%)a
Distribution-based:
Normal (Gaussian)b
on untransformed data	6 (10)
after transformation of the data: logarithmic	9 (15)
other	8 (13)
unclear what, if any, transformation was used	9 (15)
Negative binomial	6 (10)
Poisson with allowance for overdispersion	1 (2)
Non-parametric	14 (23)
Otherc	8 (13)
Unclear	7 (12)

^aThe percentages add to more than 100 because some papers used more than one method.

^bIncluding t test, analysis of variance (ANOVA), and ordinary least squares regression.

^cComprising: ratios of parasite densities as response variable (2); χ² test for trend on infection categories (1); normal distribution-based analysis of village-level indices (1); inference on overlap of confidence intervals (1); Wagstaff index of aggregation of parasites among people (1); logistic regression of high versus low parasite intensity (1); review citing previous analysis (1).

Inferential analysis

t test and related methods

The t test compares means between two samples. Although it assumes that the samples are drawn from normal distributions with equal means, the results are surprisingly robust to departure from these assumptions (Heeren and d’Agostino 1987). Nevertheless, it is liable to break down when ‘skew is severe or when population variances and sample sizes both differ’(Stonehouse and Forrester 1998, Boneau 1960). At least one of these two circumstances is likely to pertain with count data. Skewness has already been mentioned, while a difference in means implies a difference in variances if the data are actually drawn from, for example, a Poisson or negative binomial distribution. Hence the t test cannot be recommended for untransformed parasite data. The same caveats apply to regression and analysis of variance, because these are all mathematically similar. Nevertheless, such analyses were done on untransformed data in at least 10% of the papers in the literature review (Table 3).

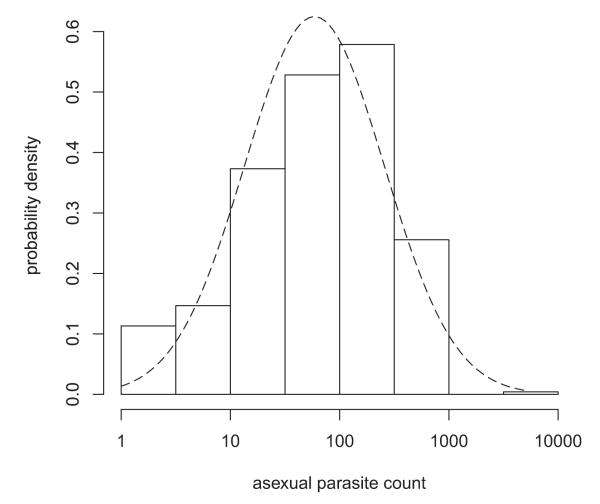
The performance of these methods may be improved by first transforming the data. In particular, if there are no zeros in the data, then a logarithmic transformation may suffice. Moreover, the t test and related techniques will then yield ratios of geometric means and so can easily be interpreted. Such methods were used in at least 15% of the papers in Table 3. As noted above, their robustness means that the normal distribution does not need to be a perfect fit for the results to be reliable. Figure 2 shows a histogram of malaria parasite densities from Dunyo et al. (2006) on a log scale. The shape is similar to that of the superimposed fitted normal curve, suggesting that the t test and related methods are likely to be applicable to the log-transformed data.

Figure 2.

Histogram, on a log scale, of numbers of Plasmodium falciparum asexual blood stages on one high power field of a thick blood film in a clinical trial (Dunyo et al. 2006). The dashed line is the fitted normal distribution.

The logarithmic transformation is not applicable, however, in the presence of zeros. Various other options are available although, in most cases, they lack the same ease of interpretation. One option is to add 1, or another value, before taking logarithms. Table 2 shows that at least 13% of papers in the literature review used a transformation other than the simple logarithmic, while in 15% it was not clear what, if any, transformation was used. For negative binomial distributions, the value k/2 can be added instead of 1 before taking logarithms, or an inverse hyperbolic sine transformation can be used (Beall 1942, Anscombe 1948, Laubscher 1961, Elliott 1977). Apart from the basic logarithmic transformation, these have at least two disadvantages. With few exceptions, the results cannot be interpreted as easily, and the transformation ‘cannot remove the clump’ of zeros, if present, and so the data will not be normalized(Hallstrom 2010). In general, if zeros are present, then other techniques, in particular generalized linear models (see below), are likely to be preferable to normal-theory methods on transformed data(O’Hara and Kotze 2010).

Non-parametric methods

These methods generally use the ranks of the data rather than the original values. This means that, for example, a single data value much greater than the others will not greatly affect the results as it would for a t test. One of the simplest non-parametric methods is the Mann-Whitney test, which compares data from two independent samples. In the literature review, non-parametric methods were used in 23% of those papers which used any inferential method (Table 3). Nevertheless, they do have some disadvantages:

If the sample size is low, and the distribution of the data is close to normal, then they are likely to have considerably lower power than parametric methods such as the t test(Bland 1995). In these — rather limited — circumstances, a parametric method is likely to be preferable.

Contrary to common conception they cannot, in general, be interpreted as comparisons of medians(Hart 2001). For example, the Mann-Whitney test (also known as the Wilcoxon test) assesses whether two distribution functions are unequal for at least one value (Conover 1980). The test can only be interpreted as a comparison of medians if the samples are drawn from populations whose distributions have the same shape, i.e., when represented graphically, they can be laid exactly on top of each other simply by shifting one along the horizontal axis by an amount Δ: a ‘shift alternative’(Bauer 1972). This is unlikely to apply to count data but, if it were, it’s likely that a t test would have applicable in the first place (Bland 1995). When software provides a confidence interval, it’s not necessarily for the difference in medians.

They are not generally capable of complex analyses, in particular those with multiple explanatory (predictor) variables.

Overall, non-parametric methods are suitable for simple analyses of skewed count data, although are not as foolproof as they may appear.

Generalized linear models

We have seen techniques which assume that the distribution of the data is normal (Gaussian) and others which do not depend on it having any particular form. Another option is to find a distribution which does fit the data adequately: this is done in generalized linear modelling. This can be thought of a kind of regression in which:

The distribution of the data is not necessarily normal. For count data the Poisson or negative binomial, for example, may be suitable.

We model a function of the mean, not necessarily the mean itself. This function is called the link function and, for present purposes, is likely to be the logarithm. It is conventional here for statistical packages to use the natural (base e) logarithms

Parasite counts are usually overdispersed relative to Poisson, requiring a distribution such as the negative binomial which can accommodate this. If a Poisson distribution is used regardless, the results can be misleading (Barker and Cadwell 2008). However, it is possible to use the ‘sandwich’ estimator (e.g. with the ‘vce(robust)’ option in STATA) or ‘quasi-likelihood’ models, both of which effectively multiply the standard errors by a factor estimated from the data (White 1980, Sileshi 2006, Noe et al. 2010), but which do not fully characterize a specific distribution for the data.

Once the distribution has been chosen, a generalized linear model is fitted by maximizing the likelihood — i.e. the probability of the data, considered as a function of the model parameters (Everitt 1995) — over possible values of the regression coefficients. A couple of points are worth stressing.

First, it is the fitted mean, not the data, which is transformed in this approach. Hence, a logarithmic link function models the logarithm of the arithmetic mean, not the geometric mean as with an ordinary regression on the log-transformed data.

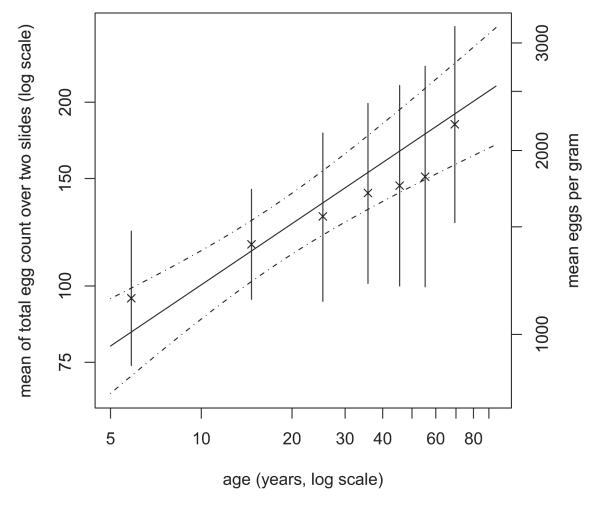
Secondly, the data must have values which are feasible for the chosen distribution. In the case of the Poisson or negative binomial distributions, for example, which apply to whole-number (integer) data, then, we must model the actual counts. If we have, for example, a set of parasite counts based on varying numbers of replicates, e.g. Kato-Katz slides, we should not input the average values to the GLM, since these are not necessarily whole numbers. Rather, the log number of replicates should be included as an offset in the model. This is an explanatory variable with its regression coefficient constrained to equal 1. In the example of multiple slides per person, if there is a single explanatory variable x with coefficient β, then we model the log mean count per person as log_e(μ)=α+ βx + log_e(n), so log_e(μ/n) = α+ βx. We can then obtain exp(β) as the ratio of the average count per slide, even though we specified the total count as the response variable. Similarly, when analysing the incidence of events when the follow-up time varies between people, using log-time as an offset enables the analysis to yield rate ratios. Figure 3 shows mean hookworm egg count fitted as a function of age. As with other regression models, different forms of dependence can be included (e.g. polynomial), as can multiple explanatory variables.

Figure 3.

Negative binomial regression of faecal egg count on age, the sloped solid line showing the fitted values. The × symbols are the means by age group, with vertical solid lines showing the 95% confidence intervals. Although age groups are shown, the fitted model uses the exact age for each person. The curved dashed lines are the pointwise 95% confidence intervals based on the whole dataset.

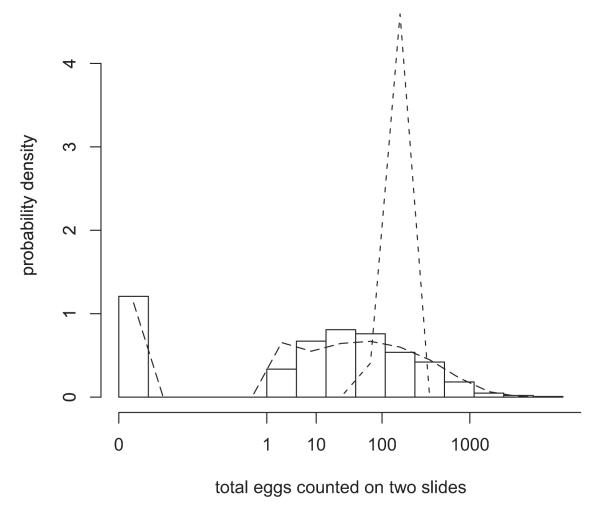
O’Hara & Kotze compared GLMs with transformation-based methods and found that the latter perform poorly — in terms of bias and sampling error — unless dispersion is small and the mean counts large(O’Hara and Kotze 2010). Goodness of fit measures for generalized linear models, and negative binomial regression in particular, include checking that the residual deviance is similar to the residual degrees of freedom (Hilbe 2007), and plotting the residuals against fitted values to check that they have random scatter with constant variance (McCullagh and Nelder 1983). Chi-squared tests can also be done to compare the numbers in various categories of the outcome variable with those expected under the given distribution. However, it should be borne in mind that, with a large sample size, a departure from the assumed distribution may be large enough to be detected by the goodness-of-fit test, but too small to affect materially the results of the main analysis. The present author tends to rely on visual assessment of the overall distribution as shown in Figure 4.

Figure 4.

Histogram of numbers of hookworm eggs counted on two Kato-Katz slides per person in the baseline survey of a prospective study in Brazil. The axis labels show the original values although the scale has been eighth-root transformed. The dashed line is the fitted negative binomial distribution and the dotted line the fitted Poisson.

Other distributions for skewed data include versions of the Poisson and negative binomial in which the proportion of zeros is defined by additional parameters. These are called zero-inflated distributions. The zero-inflated negative binomial may be a better fit than the negative binomial in some cases(Walker et al. 2009). If zeros were not recorded in the dataset then a zero-truncated distribution may be suitable, while if counting stopped at a maximum value — for example no more than 500 Ascaris eggs were counted per slide by Cundill et al (2011) — then censored distributions are available(Hilbe 2007). There are yet other distributions which have been little (Grenfell et al. 1990, Shoukri et al. 2004) (Hoshino 2005), if at all, (Dobbie 2001, Massé and Theodorescu 2005, Shmueli et al. 2005) used for parasite data.

Other methods with potential for greater use

There are several statistical methods which have not been described above but which have scope for greater use with count data. The bootstrap was notable by its absence in the articles reviewed. This approach is based on re-sampling the data and observing the sampling variation in any outcome of choice, such as a difference or ratio in medians or means(Efron and Tibshirani 1993). For simple comparisons this would seem to have some advantages over non-parametric methods. However, it is not recommended for small sample sizes because the discreteness of the sampling distribution may make the inference unreliable.

The median or other percentile of the counts can be modelled as a function of explanatory variables using quantile regression(Yu et al. 2003). Transformation of the counts may be advisable but, since the usual functions maintain rank order (they are monotonic), this will not affect the interpretation of the results.

In many cases the negative (zero) instances may warrant different treatment, whether for purely statistical reasons or due to clinical or scientific distinctions between them and the positive group. There is a well-developed literature on models which treat these two groups distinctly within a single overall analysis. These may be referred to as two-part, mixture, or bivarate models(Moulton et al. 2002, Lachenbruch 2002, Hallstrom 2010). When the proportion of zeros is modelled as a function of covariates, then zero-inflated distributions are in this category. The results for the zero and non-zero parts of the model can be presented separately or, depending on the kind of model, it may be possible to synthesize them to report the overall mean(Burton et al. 2003).

Finally, when no single parameter, such as the median or mean, is found to be an adequate summary of the data(Montresor 2007), infection intensity classes (eg negative, mild, moderate, heavy) can be analysed as ordered categories (Agresti 1999).

Discussion

The statistical challenges of count data result not so much from extreme skewness per se as from its combination with zero values. If there are no zero values then analysis of log-transformed data by common methods such as the t test may be applicable, yielding results in terms of geometric means. However, when zeros are present, the log transformation is not readily applicable, and the geometric mean is zero, complicating the choice of measure of location for count data.

The Williams mean is an attempt to retrieve the geometric mean by applying it to the counts plus one, then subtracting one again. This approach is commonly used in analysis of parasite counts, although more for expediency than for clinical or biological relevance. Moreover, since it is sometimes misleadingly called the geometric mean, it is often difficult to decide from the text of a paper what was actually done.

There is some resistance to using the arithmetic mean as a measure of location, given that basic statistics teaching usually brands it unsuitable for skewed data. Nevertheless, in some circumstances the mean is the most relevant outcome measure. In health economics, for example, the mean cost per patient is proportional to the total cost, and for that reason it is more relevant than other measures such as the median(Barber and Thompson 2000). This should not, and need not, be trumped by concerns over difficulty of analysis. Similarly, in parasitology, the arithmetic mean per person may be of interest because, for example, the total community burden in terms of parasite numbers is proportional to the arithmetic mean. Methods are available which model the arithmetic mean while accommodating skewness in the data. The median can also be used, although will be zero if the prevalence is less than 50%. Non-parametric methods are commonly said to assess differences between medians, although this is not generally the case. It is possible to do sample size calculations and statistical analysis in terms of arithmetic means via suitable distributions such as the negative binomial (Alexander et al. 2011).

Choosing the most relevant measure of location will affect how any further analysis is done. Given the powerful statistical software now readily available, it should be possible to choose a method not solely on statistical considerations — finding one whose assumptions are justified — but based on how closely it responds to the original research question (Hand 1994).

The current paper emphasizes generalized linear models (GLMs), in particular with the negative binomial distribution. Fuller explications of GLMs are available elsewhere (Gardner et al. 1995, Wilson and Grenfell 1997, Coxe et al. 2009, McElduff et al. 2010). The negative binomial often provides a good fit to parasite data(Anderson and May 1991) although other distributions may be better for particular datasets(Walker et al. 2009). One review of analysis methods for entomological data recommended negative binomial and quasi-likelihood approaches (Sileshi 2006), while another of aquatic organisms favoured the latter(Noe et al. 2010). One concern with the negative binomial is that, empirically, the dispersion parameter (k) is often found to increase with the mean(Alexander et al. 2011), yet basic models assume it to be constant. On the other hand, a simulation study has found likelihood-based analysis to be robust to this(Aban et al. 2008). There are also alternative parameterizations of the negative binomial with different variance-mean dependence (Hilbe 2007). GLM techniques for taking account of clustering can also be used in cohort studies with multiple disease episodes or repeated measures per person, although the issue of time dependence is likely to arise and this is beyond the scope of the current paper.

When describing any numerical information there is a trade-off to be made between the conciseness of any summary measure and the information it conveys. For parasite data, the case has been made for summarizing intensity in the form of categories rather than any single value(Montresor 2007). This is indeed more informative, but less concise. For some purposes, such as clinical trials, a single measure per arm — such as a mean — is likely to be preferred. If categories are used in clinical trials, they will probably be further summarized into a single measure, such as the proportion with heavy infection.