Weak Anti-localization and Quantum Oscillations of Surface States in Topological Insulator Bi₂Se₂Te

Abstract

Topological insulators, a new quantum state of matter, create exciting opportunities for studying topological quantum physics and for exploring spintronic applications due to their gapless helical metallic surface states. Here, we report the observation of weak anti-localization and quantum oscillations originated from surface states in Bi₂Se₂Te crystals. Angle-resolved photoemission spectroscopy measurements on cleaved Bi₂Se₂Te crystals show a well-defined linear dispersion without intersection of the conduction band. The measured weak anti-localization effect agrees well with the Hikami-Larkin-Nagaoka model and the extracted phase coherent length shows a power-law dependence with temperature (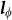∼T^−0.44), indicating the presence of the surface states. More importantly, the analysis of a Landau-level fan diagram of Shubnikov-de Hass oscillations yields a finite Berry phase of ∼0.42π, suggesting the Dirac nature of the surface states. Our results demonstrate that Bi₂Se₂Te can serve as a suitable topological insulator candidate for achieving intrinsic quantum transport of surface Dirac fermions.

As a new class of quantum matter, topological insulators (TIs) with time-reversal-symmetry protected helical surface states¹,²,³,⁴ induced by a strong spin-orbit coupling⁵,⁶,⁷ have been identified as promising materials for exploiting exciting physics such as Majorana fermions⁸, monopole magnets⁹, and a superconducting proximity effect⁸,¹⁰, as well as developing potential applications in quantum computing¹¹. Bi-based chalcogenides are confirmed as prototypical TIs due to their simple surface Dirac cone and relatively large bulk energy gap⁷. To probe the exotic spin-locked Dirac fermions and control the helical surface states, substantial effort has been made in both improving material performance by electrostatic gating¹²,¹³,¹⁴,¹⁵, substitutional doping¹⁶,¹⁷,¹⁸,¹⁹,²⁰, and stoichiometric component engineering²¹,²²,²³,²⁴ in ternary tetradymite compounds²⁵, and in developing sensitive techniques for revealing surface helical features, such as angle-resolved photoemission spectroscopy (ARPES)²⁶,²⁷,²⁸,²⁹,³⁰, scanning tunneling microscopy³¹,³²,³³, low-temperature transport¹²,¹⁹,³⁴,³⁵,³⁶, and optical polarization³⁷. However, the dominant bulk conduction arising from naturally occurring crystal imperfections and residual carrier doping has greatly hindered the detection of Dirac fermions by means of weak anti-localization effect¹³ and quantum oscillations³⁴ at low temperatures. Recently, Bi₂Te₂Se (BTS), with a ternary tetradymite structure, has shown a low carrier concentration of ∼10¹⁶ cm⁻³ and a large bulk resistivity of ∼6 Ω cm due to the ordered occupation of Te/Se in the quintuple-layer unit¹⁴,³⁸. In contrast, Bi₂Se₂Te (BST) has rarely been investigated although theoretical calculations predict that both BTS and BST with ordered or partially disordered atomic structures are stable topological insulators²⁵.

In this work, we report weak anti-localization (WAL) and Shubnikov-de Haas (SdH) oscillations originating from the BST surface states. The WAL effect is only sensitive to the perpendicular component of the magnetic field and can be well described by the Hikami-Larkin-Nagaoka model where the temperature dependence of the phase coherent length shows a power-law behavior of ∼T^−0.44. SdH oscillations also reveal a well defined 2D Fermi surface in the BST crystal which survives up to ∼7 K. The finite Berry phase of 0.42π extracted from the SdH oscillations elucidates the Dirac nature of surface states. More importantly, the surface conductance contributes up to ∼57% of the total conductance, indicative of dominant surface transport.

Results

Structural characterizations of BST crystal

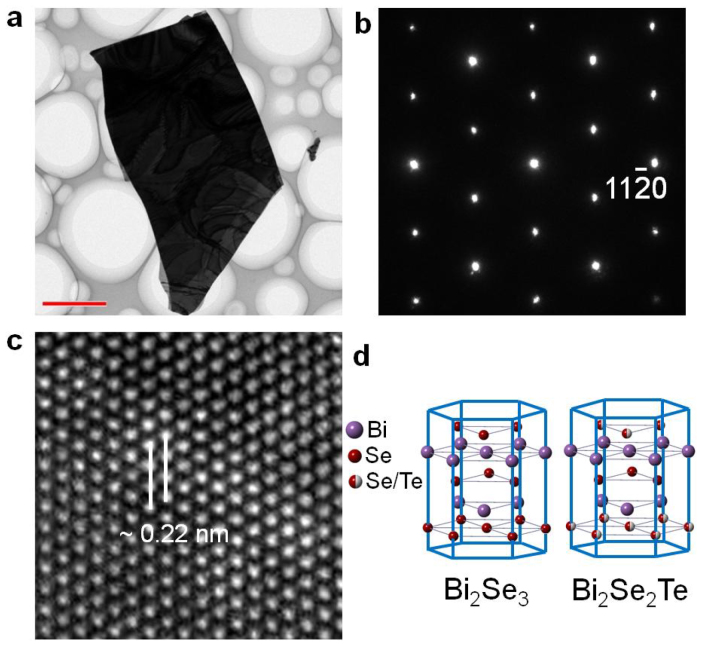
A high-quality single crystal of BST with a small concentration gradient was produced via the Bridgman technique. Elemental concentration profiles along the ingot were obtained by using wavelength dispersive micro-analysis. The results show that the compositions of Bi, Se, and Te in the crystal have a small variation along the growth direction of the ingot (less than 3%), confirming the high quality (Supplementary Fig. S1). Transmission electron microscopy (TEM) was performed to determine the structural characteristics. Flakes of the BST were obtained by mechanical exfoliation of cleaved crystals. A low magnification TEM image is shown in Fig. 1a, revealing sizes of several to tens micrometers in width/length for the exfoliated flakes. Sharp selected-area electron diffraction pattern indicated a perfect single crystalline rhombohedral phase of BST (Fig. 1b). The atomic plane spacings in high-resolution TEM images were determined to be 0.22 nm, as marked by a pair of parallel lines in Fig. 1c, which is consistent with the d-spacings of the 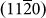planes in BST (Supplementary Table S1). The powder X-ray diffraction (XRD) pattern shows deviations from that of ordered skippenite structure (Supplementary Fig. S2)³⁹, which may suggest a disordered occupation of Te/Se on outer quintuple layers²⁵ (Fig. 1d). Unlike the central-layer substitution in BTS¹⁴,⁴⁰, the partially disordered BST structure resulting from random Te substitutions of Se atoms in outer quintuple layers is a very low-energy structure and thus conforms to Hume-Rothery solid-solution rules²⁵. Furthermore, the powder XRD refinement experiments confirm such a disordered occupation of Te/Se on the outermost quintuple layers and present the non-stoichiometric formula of Bi₂Se_1.88Te_1.12 for our BST crystal (Supplementary Table S1). This is in a good agreement with previous XRD experiments on a solid solution of Bi₂Te_3−xSe_x⁴¹. In fact, the carrier concentration in Bi₂Te_3−xSe_x is extremely sensitive to the value of x. The non-stoichiometric BST with a low x can greatly reduce the residual carrier concentration in the bulk⁴⁰ and thus benefits the surface-dominated transport, as to be discussed later.

Figure 1. Structural characterization of cleaved flakes from Bi₂Se₂Te (BST) crystal.

(a) Low-magnification TEM image, (b) Selected area electron diffraction pattern, (c) High-resolution TEM (HRTEM) image of a BST flake on a holey carbon grid, respectively. The sharp SAED pattern in (b) indicates the high-quality single crystal. The HRTEM image in (c) reveals a perfect crystalline structure and the spacing between the 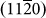atomic planes is resolved to be 0.22 nm (marked by a pair of parallel lines). (d) Layered crystal structure of Bi₂Se₃ and Bi₂Se₂Te, showing the disordered occupation of Se/Te atoms in outer quintuple layers. Scale bars in (a) is 2 μm.

Electronic structure of BST crystal

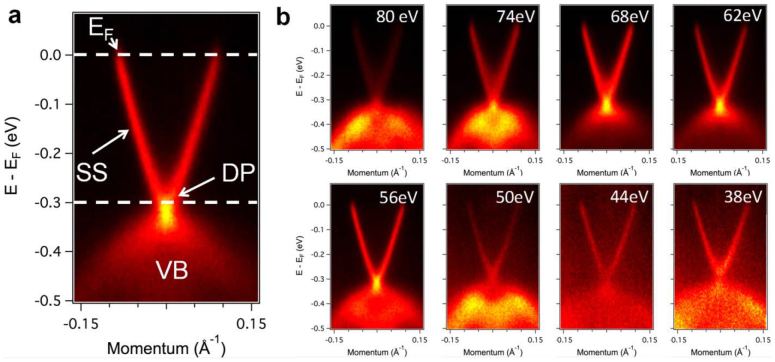
To verify the characteristics of the surface states of the BST crystal, high–resolution ARPES experiments were performed under different photon energies. Fig. 2a shows the ARPES intensity around the center of the surface Brillouin zone. A familiar “V” shaped surface state with linear dispersion was clearly resolved, indicating the presence of Dirac fermions. The Fermi level is located ∼0.3 eV above the Dirac point, which is lower than the reported value of 0.425 eV⁴², probably because of the reduced carrier density in the bulk giving rise to a lower position of Fermi level relative to the Dirac point (Fig. 2a). Furthermore, the ARPES measurements under a series of photon excitation energies show that the Fermi level intersects only the Dirac cone with an absence of the conduction band in the band structure (Fig. 2b), which is favorable in the course of searching for an ideal TI candidate²⁴,⁴⁰,⁴³. It is also revealed that the “V” shaped dispersion of surface states is stationary with varied photon energy unlike the “M” shaped dispersion of the VB (Fig. 2b), showing the robustness of the surface states with photon energy²⁴. The Dirac cone intersects the Fermi level at a momentum of 0.07 Å⁻¹, yielding a Fermi velocity of 6.4×10⁵ m/s by momentum distribution curve fitting (Supplementary Fig. S3), which is reasonably close to the reported value⁴².

Figure 2. Angle-resolved photoemission spectroscopy (ARPES) of Bi₂Se₂Te (BST) crystal.

(a) Measured band structure curve of BST along the Γ point taken at a photon energy of 60 eV. A single Dirac cone was clearly resolved and no conduction band was observed. The Dirac point (DP) is located ∼0.3 eV away from the Fermi level. (b) Photo-energy-dependent band structure curves of BST at different excitation photon energies of 80, 74, 68, 62, 56, 50, 46, and 38 eV, respectively.

Temperature-dependent longitudinal and Hall resistances of BST crystal

Hall bar devices with standard six-terminal geometry were fabricated for transport measurements. The temperature dependence of the longitudinal resistance of the BST crystal is shown in Fig. 3a. The longitudinal resistance R_xx increases roughly two orders of magnitude upon cooling from room temperature, indicating a non-metallic behavior¹⁴,³⁸,⁴⁰,⁴³. The Arrhenius plot of R_xx (lower inset of Fig. 3a) exhibits thermal activation behavior in a temperature range from 300 K down to 120 K. By using R_xx∼ 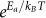, where E_a is the activation energy and k_B is the Boltzmann constant, an activation energy of about 100 meV is extracted. This value is four times larger than the 23 meV of BTS¹⁴ but remains the same order of magnitude to that of Sn-doped BTS²⁰. A reasonable fit to the three-dimensional (3D) variable-range hopping model (VRH, G_xx∼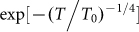¹⁴,⁴⁴,⁴⁵, suggests that the transport property is dominated by 3D VRH behavior from 100 to 20 K (red solid line in Fig. 3b), while the deviation from the fit at low temperatures (< 20 K) signifies a parallel metallic conduction from the surface states, although no apparent saturation was observed for R_xx at low temperatures (upper inset of Fig. 3a). This behavior can be further supported by the observation of the weak anti-localization effect and Shubnikov-de Hass (SdH) oscillations (discussed later). The temperature-dependent low-field (near B = 0 T) Hall coefficient (Fig. 3c) R_H shows a sign transition from positive to negative upon cooling from 300 to 1.9 K, representing a charge carrier switch from holes to electrons in the BST crystal similar to previously reported results in the BTS system¹⁴,⁴⁰. The inset in Fig. 3c displays magnetic field-dependent Hall resistance at 1.9 K, showing little difference of R_H between low-fields and high-fields. Above ∼100 K, the Hall coefficient R_H has a thermal activation behavior, suggesting that the Fermi level is far from the conduction band and is located inside the bulk band gap²⁰. The low-field R_H of −10.9 Ω T⁻¹ at 1.9 K provides an estimated electron concentration of 1.4×10¹⁶ cm⁻³, in the same order of magnitude as that of BTS¹⁴,⁴⁰. The Hall mobility can be determined to be 264 cm²V⁻¹s⁻¹. It is believed that the low mobility of bulk carriers may enhance the surface state contribution due to the suppression of bulk carrier interference with quantum oscillations¹⁴,²²,⁴⁰. In our case, such a low carrier concentration and bulk carrier mobility may help to detect the surface transport in the BST crystal.

Figure 3. Electrical transport of Bi₂Se₂Te (BST) crystal under zero magnetic field.

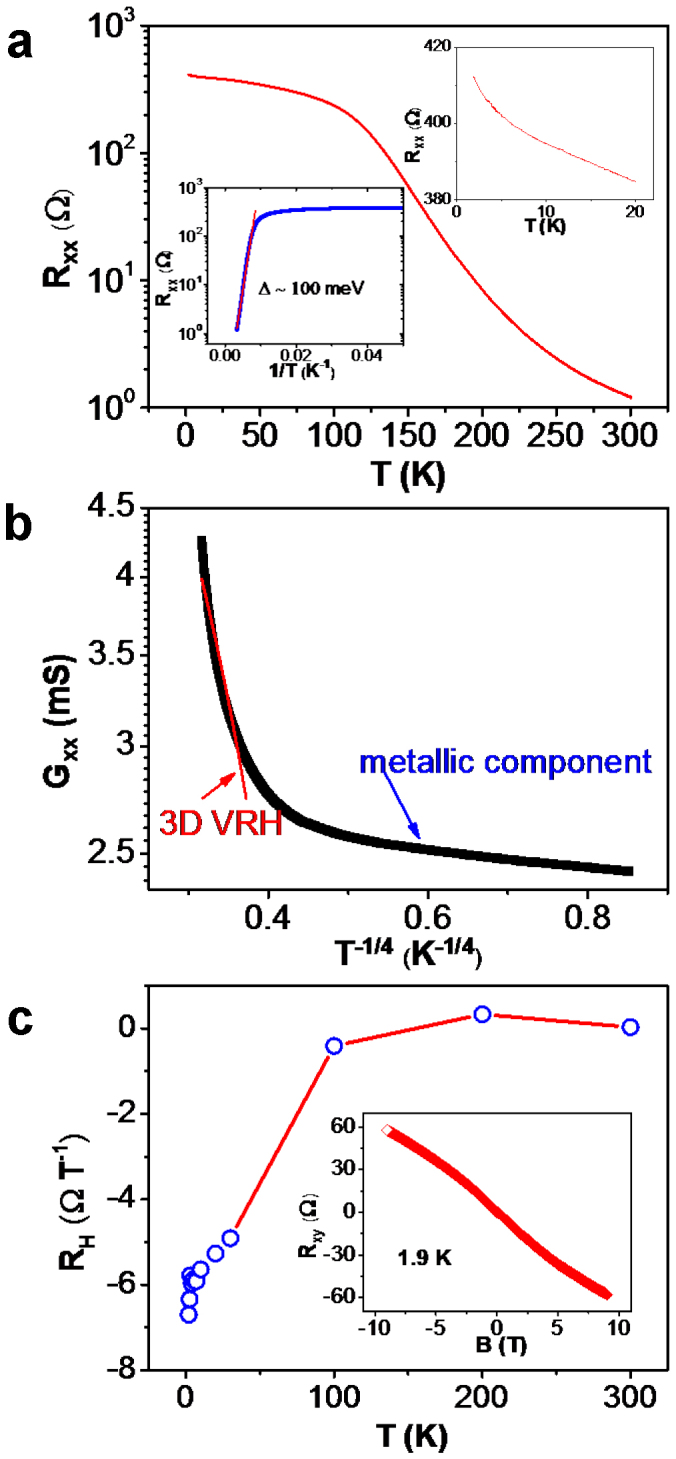
(a) Temperature-dependence of longitudinal resistance R_xx. Lower inset shows the Arrhenius plot of R_xx∼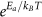, which yields an activation energy of 100 meV in the temperature range of 120-300 K. Upper inset plots the R_xx at temperature lower than 20 K and no apparent saturation was observed. (b) A plot of longitudinal conductance G_xx vs T^−1/4. Solid line (red) is the data fit to the 3D variable range hopping (VRH): G_xx∼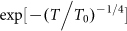; deviation from the fit at low temperature signifies the parallel metallic conduction. (c) Temperature-dependence of the low-field R_H. Inset shows the R_xy curve at 1.9 K. The dominant charge carriers are electrons.

Weak anti-localization (WAL) effect in BST crystal

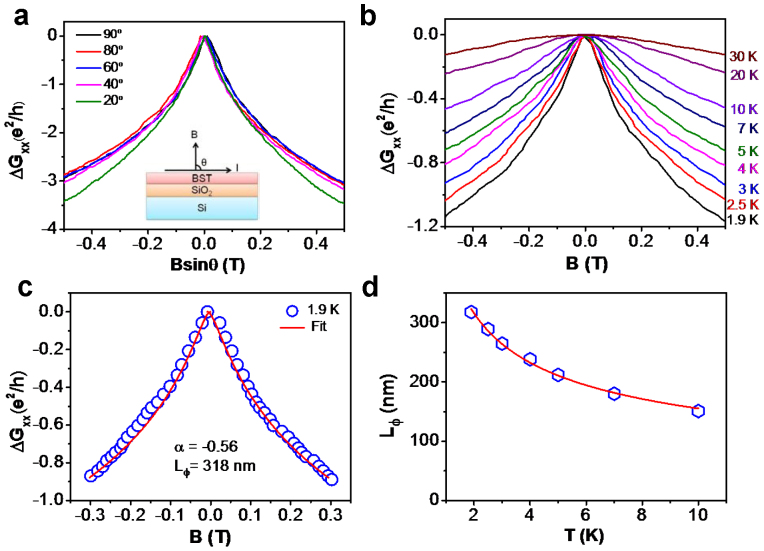
As a quantum correction to classical magnetoresistance, the WAL effect is a signature of topological surface states originating from the Berry's phase which is associated with the helical states¹³,¹⁵,⁴⁶. The sheet magnetoresistance at different tilt angles (θ) reveals the features of the WAL effect - the presence of sharp cusps at zero magnetic field¹³,¹⁸,²²,⁴⁷,⁴⁸,⁴⁹ (Supplementary Fig. S4a). However, the existence of cusp features of magnetoresistance at θ = 0 gives a hint to a partial 3D contribution of bulk spin-orbit coupling, which was also observed in Bi₂(Se_xTe_1−x)₃ nanoribbons (Supplementary Fig. S4a)²². The WAL induced by 2D surface states is characterized by a sole dependence on the perpendicular component of the applied magnetic field, Bsinθ, of the magnetoresistance¹⁸,²². Therefore, to extract the pure 2D surface state contribution, we can subtract the 3D WAL contribution from the magnetoconductance at other angles, i.e. 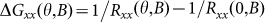. Fig. 4a shows traces of the sheet magnetoconductance as a function of Bsinθ. ΔG_xx(θ, B) displays cusp-like maxima at B = 0 at each tilt angle and all traces follow the same curve at low magnetic fields (≤ 0.1 T) but they deviate from each other at higher magnetic fields, which confirms the 2D nature of WAL effect¹⁸,²². The temperature-dependent of ΔG_xx is shown in Fig. 4b, revealing the sharp negative cusps characteristic of WAL. Similar to previous observations¹⁸,²²,⁴⁸, as the temperature increases, the cusps are broadened and finally disappear owing to the decrease in the phase coherent length at higher temperatures (Fig. 4d). The WAL can persist up to 10 K.

Figure 4. Weak anti-localization (WAL) effect in BST crystal.

(a) The change of sheet magnetoconductance plotted in the perpendicular magnetic field component of the magnetic field, Bsinθ, at 1.9 K. The only perpendicular component dependent features indicate that WAL is induced by 2D surface electrons. (b) The change of sheet magnetoconductance (ΔG_xx) in perpendicular magnetic fields (θ = 90°) at temperatures ranging from 1.9 to 30 K. It shows the WAL features (sharp cusps at around zero magnetic field) persistent until 10 K. (c) Trace of sheet magnetoconductance's change at 1.9 K, the solid lines (red) are fits of 2D localization theory, where α is -0.56, and 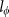is 318 nm, confirming the 2D nature of WAL. (d) Temperature dependence of phase coherent length L_φ obtained by fitting ΔG_xx to 2D localization theory. The solid line (red) shows the power law dependence of temperature as 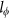∼T^−0.44.

The quantum correction to the 2D magnetoconduction can be described by the Hikami-Larkin-Nagaoka (HLN) model⁵⁰. In a strong spin-orbit interaction and a low mobility regime, i.e. 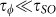and 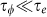, the conduction correction is given by 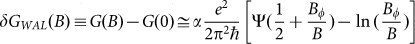, where 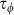is dephasing time, 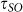(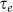) is spin-orbit (elastic) scattering time, α is a WAL coefficient, e is the electronic charge, 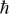is the reduced Planck's constant, Ψ is the digamma function, and 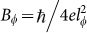is a magnetic field characterized by coherence length 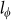( 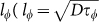, D is diffusion constant). For the topological surface states the WAL should give α a value of −0.5¹³,¹⁸,²²,⁴⁸,⁴⁹. Fitting ΔG_xx at 1.9 K with the HLN equation yields α = −0.56 and 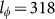nm (Fig. 4c), confirming the 2D nature of WAL. The obtained coherence length as a function of temperature is shown in Fig. 4d. The coherence length decreases from 318 to 150 nm as the temperature increases from 1.9 to 10 K and this monotonous reduction of coherence length was also observed in other TI systems²²,⁴⁸. A power law fit of 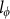with temperature gives a relationship of 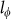∼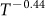(Fig. 4d). Theoretically, for 2D systems the power law dependence of coherence length is 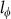∼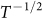, while for 3D system the power law dependence changes to be 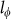∼ 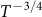(ref. 51). Hence, the temperature-dependent behavior of coherence length further proves that the WAL at low magnetic fields originated from the 2D surface states.

Quantum oscillations in BST crystal

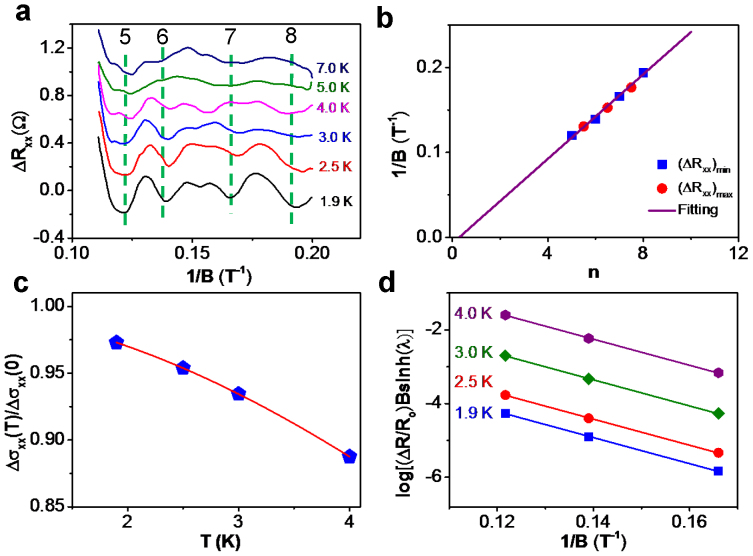
Quantum oscillations such as SdH oscillations and Aharonov-Bohm (A-B) interference have been identified as convincing tools for characterizing surface states in topological insulators¹²,¹⁹,³⁴,³⁵,⁵². Compared with extensive exploration of SdH oscillations in Bi₂Te₂Se (BTS)¹⁴,³⁸ and in Sn-doped BTS crystal²⁰, surface transport properties were rarely investigated in its “sister” tetradymite structure-Bi₂Se₂Te (BST) crystal although theoretical calculations predicted it to be an excellent TI candidate²⁵. In this regard, we carried out low-temperature magnetotransport measurements to provide experimental evidence for the surface state dominated transport in BST crystal. The magnetic field is perpendicular to both the current flow and the surface of the BST nanoflake. The magnetic-field dependent longitudinal resistance R_xx shows traces of SdH oscillations in our raw data (Supplementary Fig. S5a). After a direct subtraction of the smooth background (Supplementary Fig. S5a), the oscillatory part of R_xx (ΔR_xx) displays periodic peaks (maxima) and valleys (minima) with 1/B (Fig. 5a), revealing the evident existence of a well-defined Fermi surface¹²,³⁴,⁵³. The SdH oscillations survive up to 7 K (Fig. 5a). A single oscillation frequency can be extracted from fast Fourier transform (FFT) spectra (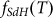∼44.9 T, Supplementary Fig. S6). For a 2D system, the SdH oscillation frequency is directly related to the cross section A_F of the Fermi surface in momentum space via the Onsager relation: 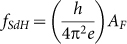, where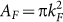, k_F is the Fermi vector, e is the electron charge, and h is Planck constant. The 2D surface carrier density n_2D is related to k_F by 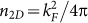. By substituting f_SdH, the Fermi vector k_F can be determined to be 0.037 Å⁻¹, corresponding to a 2D carrier density of 1.1×10¹² cm⁻². If the SdH oscillations come from the bulk state, the period of SdH oscillations must be related to a 3D Fermi sphere with a radius of 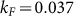Å⁻¹ in momentum space and give a carrier density of 7.45×10¹⁸ cm⁻³, which is completely inconsistent with the Hall value of 1.4×10¹⁶ cm⁻³. Thus, the SdH oscillations are originated from 2D surface states. In Fig. 5b, we plot the 1/B values corresponding to the maxima (red closed circles) and the minima (blue closed rectangles) of ΔR_xx versus Landau level index n by assigning the index in the regime of Ref.19. Linear fitting of the data yields a finite intercept of 0.29 (corresponding to a Berry phase of 0.42π), highlighting the topological surface states as the origin of the SdH oscillations. The discrepancy of the extrapolated values with the expected value of 0.5 from the massless Dirac fermions were reported by several groups¹⁴,¹⁹,²⁰,³⁴,³⁸ and the possible origin of this discrepancy is attributed to the Zeeman coupling of the spin to the magnetic field¹⁹,⁴⁹, in which a 2D quantum limit was achieved under a high magnetic field (∼60 T)¹⁹. Another possible explanation of the discrepancy is attributed to the deviation of dispersion relation from an ideal linear dispersion for Dirac fermions³⁶,⁵⁴. In the present study, the magnetoresistance measurement was performed at a much lower magnetic field (9 T), therefore we believe that this discrepancy arises from the non-ideal linear dispersion in the energy bands⁵⁴, which is also shown in the ARPES spectrum of BST (Fig. 2). In addition, the fitting of 1/B (minima and maxima of ΔR_xx) with Landau filling level n can also give a value of k_F = 0.036 Å⁻¹, which is in a good agreement with the aforementioned SdH calculations.

Figure 5. SdH oscillations in BST crystal.

(a) Shubnikuv-de Hass oscillations at different temperatures. The green dashed lines mark the SdH dips at Laudau filling factors of 5, 6, 7, and 8. (b) Landau-level fan diagram for SdH oscillations in ΔR_xx. Linear fitting of the periodic maxima and minima as a function of the Landau level index n gives a nonzero intersects of 0.29, corresponding to a nonzero Berry's phase of 0.42π. (c) Temperature dependence of the normalized conductivity amplitude Δσ_xx(T)/Δσ_xx(0). The solid line (red) is best fit to λ(T)/sinh(λ(T)). A magnetic field of 7.6 T was used to extract the cyclotron effective mass: ∼0.111m₀. (d) Dingle plots of log [(ΔR/R₀)Bsinh(λ)] versus 1/B at four different temperatures. Transport lifetime τ, mean free path 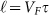, and mobility μ can be extracted from the best fit to log [(ΔR/R₀)Bsinh(λ)].

The temperature-dependent amplitude of Δσ_xx of the SdH oscillations can be described by 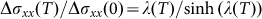, where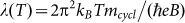, m_cyclis the cyclotron mass, 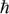is the reduced Planck's constant, and k_B is Boltzmann's constant. By performing the best fit of the conductivity oscillation amplitude to the 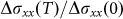equation, m_cyclis extracted to be ∼0.111 m_e (m_eis the free electron mass), as shown in Fig. 5c. The Fermi level is described by 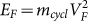and V_Fis related to k_F by 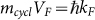, where V_F is the Fermi velocity¹²,³⁴,⁵⁵. This yields a Fermi level of ∼95 meV above the Dirac point and a Fermi velocity of 3.9×10⁵ m s⁻¹, which are smaller than those from the ARPES results. Previous reports on Bi₂Se₃ suggests that for samples with low carrier concentration (∼10¹⁷ cm⁻³), discrepancies emerge for the position of the Fermi level inferred from ARPES and from transport experiments⁵⁵. Surface charge accumulation induced band-bending is responsible for the discrepancy¹⁹,⁵⁵, while the lower Fermi velocity (3.9×10⁵ m s⁻¹) obtained from SdH oscillations compared with that of ARPES (6.4×10⁵ m s⁻¹) is probably due to the deviations of surface states from the linear dispersion when going away from the Dirac point⁴².

The transport lifetime of the surface states (τ) can be estimated by utilizing the Dingle plot¹²,¹⁹,³⁴,⁵². Since 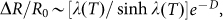, where 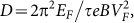, the lifetime τ can be derived from the slope in Dingle plot by 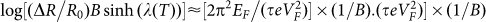(Fig. 4d). The fit in Fig. 4d gives a transport lifetime of ∼3.5×10⁻¹³ s, corresponding to a mean free path 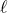of ∼136 nm (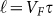). The surface mobility 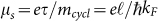can be estimated as ∼5593 cm² V⁻¹ s⁻¹, which is more than twenty times larger than the Hall mobility of 264 cm² V⁻¹ s⁻¹ from the bulk (see Table 1). According to these calculated results, the surface contribution to the total conduction can be estimated as ∼57% (see Table 2), which suggests dominant surface transport in BST crystal.

Table 1. Estimated parameters from the SdH oscillations at T = 1.9 K.

fSdH(T)	N2D(1012 cm−2)	mcycl(m0)	kF(Å−1)	VF(105 ms−1)	EF (meV)	τ (10−13 s)	ℓ (nm)	μ (cm2V−1s−1)
44.9	1.1	0.111	0.037	3.9	~95	3.53	~136	~5593

Table 2. Estimated surface conduction contribution with zero magnetic field at T = 1.9 K.

G (surface) (mS)	R (total) (Ω)	Rsheet (total) (ΩW−1)	Gsheet (total) (mS)	G (surface)/ Gsheet (total)
1.97	412.7	289.3	3.46	~57%

Discussion

In summary, ARPES experiments provide direct evidence of topological surface states in the BST crystal. The high binding energy of the Dirac point probably originates from the Se vacancies created by Se out-diffusion⁵⁶ during the pre-annealing process prior to ARPES measurements. In addition, the non-stoichiometric form of BST (Bi₂Se_1.88Te_1.12) can be considered as excessive substitution of Se atoms in outmost quintuple layers of Bi₂Se₃ by Te atoms, which effectively compensates the Se vacancies and lift up the position of the conduction band minimum, leading to the absence of the conduction band in full photon energy-dependent ARPES measurement (Fig. 2)²⁵,⁴⁰,⁴². Both the WAL effect and SdH oscillations have unambiguously shown dominate surface transport in the BST crystal. Theoretical calculations predict that introducing Te into the central layer of Bi₂Se₃ to form the ordered BST structure may make it a superior TI material that behaves like Bi₂Se₃ with a well-defined Dirac cone located inside the bulk band gap²⁵. However, finding effective ways of introducing Te into the central layer remains a challenge. Doping BST further with compensation elements, like Sb²⁴ and Sn²⁰, may provide an alternative way for tuning the relative position of Fermi level and Dirac point, making the BST crystal an ideal platform for exploring exotic quantum physical phenomena and device applications.

Methods

Sample preparation and characterization

High-quality single crystalline Bi₂Se₂Te (BST) with a small concentration gradient was obtained by the Bridgman technique. Proper ratios of high purity metals of bismuth (99.999%), selenium (99.999%) and tellurium (99.999%) were sealed in a quartz tube and melted into an ingot in an induction furnace to homogenize the composition. The ingot was then sealed in a quartz tube with a larger diameter and loaded into a Bridgman furnace. A crystal was obtained by withdrawing the quartz tube at 1 mm/hr after being heated to 800°C and kept at a constant temperature. Concentration profiles along the ingot were obtained by using electron probe micro-analysis which was performed in a JEOL JAMP-7830F Auger Microprobe. (Supplementary information). Thin flakes of BST with typical sizes of several micrometers in length/width were mechanically exfoliated from bulk crystals and transferred onto holey carbon copper grids for TEM characterizations, which were performed with a FEI Tecnai F20 TEM operating at 200 KV and equipped with an energy-dispersive spectroscopy detector.

Angle-resolved photoemission spectroscopy experiments

High-resolution ARPES experiments were performed on beam line 12.0.1 of the Advance Light Source at Lawrence Berkeley National Laboratory. The data were recorded with a VG-Scienta SES100 electron analyzer at low temperature (< 50 K) at photon energies ranging from 30 to 80 eV. The typical energy and momentum resolution was 20–30 meV and 1% of the surface Brillouin zone (BZ), respectively. Samples were cleaved in situ and were measured under a vacuum level better than 5×10⁻¹¹ Torr.

Transport properties of BST

For transport measurements, Ohmic contacts were made by using room-temperature cured silver paste. The sample used for Hall measurements and SdH studies was 0.5 mm wide and 0.05 mm thick and the voltage contact distance is 0.6 mm. The longitudinal resistance R_xx and the transverse resistance R_xy were measured simultaneously by a standard six-probe method in a Quantum Design physical properties measurement system (PPMS-9T) which has a capability of sweeping the magnetic field between ± 9 T at temperatures down to 1.9 K.

Author Contributions

F. X. conceived the idea and supervised the overall research. L. Bao and L. H. designed and performed the experiments. L. H. fabricated the devices and carried out low-temperature transport measurements. T. R. and T. L. synthesized the Bi₂Se₂Te crystal. Z. C. and J. Z. performed the structural analysis. P. Z. and A. V. carried out the ARPES measurements. N. M. and L. H contributed to the analysis. L. Bao, N. M. and F. X., wrote the paper with helps from all other co-authors. L. Bao and L. H. contributed equally to this work.

Supplementary Material

Supplementary Information

Supplementary Information

Reprints and permission information is available online at http://npg.nature.com/reprintsandpermission.