A Clique-Based Method Using Dynamic Programming for Computing Edit Distance Between Unordered Trees

Abstract

Many kinds of tree-structured data, such as RNA secondary structures, have become available due to the progress of techniques in the field of molecular biology. To analyze the tree-structured data, various measures for computing the similarity between them have been developed and applied. Among them, tree edit distance is one of the most widely used measures. However, the tree edit distance problem for unordered trees is NP-hard. Therefore, it is required to develop efficient algorithms for the problem. Recently, a practical method called clique-based algorithm has been proposed, but it is not fast for large trees.

This article presents an improved clique-based method for the tree edit distance problem for unordered trees. The improved method is obtained by introducing a dynamic programming scheme and heuristic techniques to the previous clique-based method. To evaluate the efficiency of the improved method, we applied the method to comparison of real tree structured data such as glycan structures. For large tree-structures, the improved method is much faster than the previous method. In particular, for hard instances, the improved method achieved more than 100 times speed-up.

1. Introduction

Tree-structured data, such as RNA secondary structures (Jiang et al., 2002; Zaki et al., 2005), phylogenetic trees (Horesh et al., 2006), glycans (Aoki et al., 2004), and vascular trees (Yu et al., 2007), often appear in computational biology. Consequently, various techniques have been developed and applied to analysis of these tree-structured data. Among them, comparison of tree-structured data is important because it can be used to search for similar objects. The tree edit distance is one of the most widely used measures for comparison of tree-structured data (Bille, 2005). In this measure, the distance between two trees is measured by the minimum cost sequence of edit operations that transforms one tree into another tree, where an edit operation is either a deletion of a node, an insertion of a node, or a substitution of a node label. For the tree edit distance problem for ordered trees, Tai (1979) developed an O(n⁶) time algorithm, where n is the number of nodes in a larger input tree. After several improvements, Demaine et al. developed an O(n³) time algorithm and showed that this bound is optimal under some computation strategy (Demaine et al., 2009).

The tree edit distance between ordered trees is useful if the ordering among children has important meanings. However, it is preferable to regard input trees as unordered trees in some applications (Aoki et al., 2004; Horesh et al., 2006). Unfortunately, Zhang et al. (1992) proved that the tree edit distance problem for unordered trees is NP-hard. In order to cope with this hardness, Akutsu et al. (2011a) developed a fixed parameter algorithm that works in O(2.62^k · poly(n)) time, where k is the maximum allowed edit distance. Although their algorithm might be useful for comparison of very similar trees (i.e., where k is small), it is not useful for comparison of non similar trees. Horesh et al. (2006) developed an A* algorithm. Although their algorithm works efficiently for comparison of moderate size unlabeled trees under the unit cost distance (i.e., the cost of each edit operation is 1), it is unclear whether it can be efficiently applied to labeled trees or general cost cases.

Fukagawa et al. (2011) recently proposed a practical method for computing the tree edit distance between unordered trees using algorithms for computing the maximum clique (Tomita et al., 2010, 2011). In this method, an instance of the tree edit distance is directly transformed into an instance of the maximum vertex weighted clique problem, and then an existing clique solver (Nakamura and Tomita, 2005) is applied. Although similar reductions have been proposed for variants of the tree edit distance problem (Pelillo et al., 1999; Torsello and Hancock, 2003) and other problems (Ogawa, 1986), to the best of our knowledge, it was the first method that exactly solves the proper tree edit distance problem for unordered trees using the maximum clique. The method was applied to comparison and search of similar glycan structures and shown to be efficient for moderate-size tree structures (Fukagawa et al., 2011). However, it was not fast enough if large glycan or tree structures were given.

Therefore, in the preliminary version of this paper (Akutsu et al., 2011b), we improved the method of Fukagawa et al. (2011) and developed a dynamic programming (DP)-based algorithm that repeatedly solves instances of the maximum vertex weighted clique problem as subproblems. Due to this improvement, sparser graphs are generated and thus maximum clique instances can be solved more efficiently in many cases. Although multiple clique instances must be solved in the improved method, it is expected that speed-up due to sparsity is more beneficial if input trees are large. Furthermore, by using the feature of DP, we introduced heuristic techniques that do not violate the optimality of the solution. When it was applied to comparison of large glycan structures, our improved method showed speed-up in most cases. However, there are still cases in which it takes a long CPU time (user time). In particular, it takes a very long CPU time if there are many leaves. In such a case, constructed graphs would contain many vertices and edges, and thus, a clique algorithm would not work efficiently.

In this full version, we augment this DP-based approach by introducing new heuristic techniques to further reduce the computation time without violating the optimality of the solution, especially for trees with many leaves or many isomorphic subtrees. Furthermore, in order to use maximum clique algorithms in place of maximum vertex weighted clique algorithms, we develop a new clique-based method for computing the unordered tree edit distance in which the maximum vertex weighted clique problem is transformed into the maximum clique problem.

We compare the improved clique-based method and the maximum clique-based method with the previous maximum vertex weighted clique-based method (Fukagawa et al., 2011) using glycan data obtained from the Kyoto Encyclopedia of Genes and Genomes (KEGG) database (Kanehisa et al., 2010) and Weblogs data CSLOGS, opened to the public¹ (Zaki et al., 2005). The results suggest that the improved clique-based method is much faster than the maximum clique-based method and previous clique-based method (Fukagawa et al., 2011) in most cases of comparison of large tree-structured data. In particular, when many leaves or isomorphic subtrees exist, our improved method shows significant speed-up.

2. Tree Edit Distance

Before presenting the method, we briefly review tree edit distance and edit distance mapping for rooted, labeled, and unordered trees (Bille, 2005; Zhang et al., 1992).

Let T be a rooted, unordered tree where each node v has a label ℓ(v) over an alphabet Σ. r(T), V(T), and E(T) denote the root, the set of nodes, and the set of edges of T, respectively. For a node 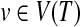, des(v) and T(v) denote the set of descendants of v (not including v) and the subtree induced by v and its descendants, respectively. In this paper, n denotes the number of nodes in a larger input tree, that is, n = max{|V(T₁)|,|V(T₂)|}) where T₁ and T₂ are input trees.

An edit operation on a tree T is either a deletion, an insertion, or a substitution, each of which is defined by the following (Fig. 1):

• • Deletion: Delete a nonroot node v in T with parent u, making the children of v become children of u. The children are inserted in the place of v into the set of the children of u.

• • Insertion: Inverse of the deletion; insert a node v as a child of u in T, making v the parent of some of the children of u.

• • Substitution: Change the label of a node v in T.

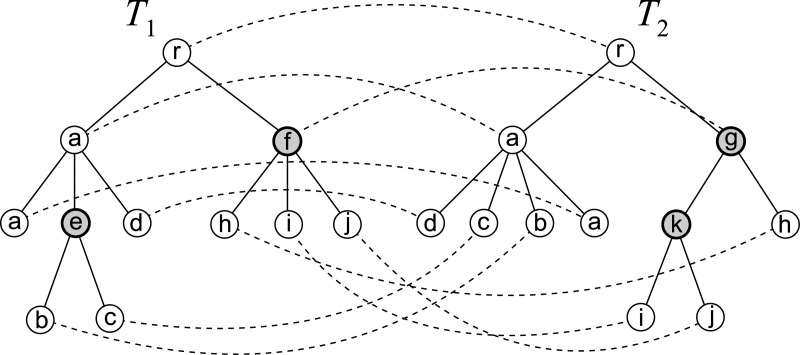
Fig. 1.

Example of tree edit operations and edit distance mapping for unordered trees. T₂ is obtained from T₁ by deletion of node labeled e, insertion of node labeled k, and substitution of node labeled f with node labeled g, in which a tree can contain nodes with the same label. The corresponding mapping M is shown with dashed curves.

For each edit operation, the cost is defined as follows.

• • γ(a, ε): cost of deleting a node labeled with a.

• • γ(ε, a): cost of inserting a node labeled with a.

• • γ(a, b): cost of substituting a node with label a to label b.

The edit distance dist(T₁, T₂) between two unordered trees T₁ and T₂ is the cost of the minimum cost sequence of edit operations that transforms T₁ to T₂, where we adopt the following standard assumption so that dist(T₁, T₂) becomes a distance metric (Bille, 2005; Zhang et al., 1992):

• • γ(a, b) ≥ 0 for any ,

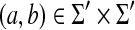• • γ(a, a) = 0 for any ,

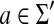• • γ(a, b) = γ(b, a) for any ,

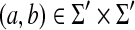• • γ(a, c) ≤ γ(a, b) + γ(b, c) for any ,

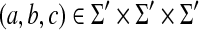where Σ′ = Σ ∪ {ε}.

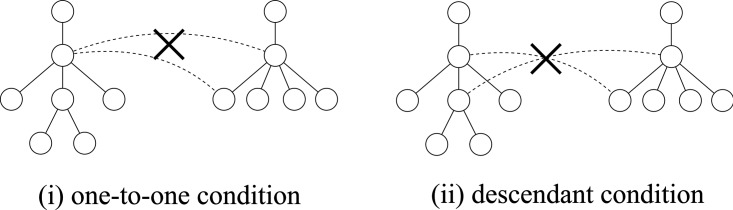
There is a close relationship between the edit distance and the edit distance mapping (or just mapping) (Bille, 2005; Zhang et al., 1992). M ⊆ V(T₁) × V(T₂) is called a mapping if the following conditions are satisfied for any two pairs (u₁, v₁), 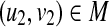(Fig. 2):

• (i) u₁ = u₂ iff v₁ = v₂,

• (ii) .

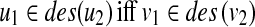Fig. 2.

Example of the condition of the edit distance mapping. The left and right figures correspond to conditions (i) and (ii) for the edit distance mapping, respectively, where (i) stands for one-to-one condition, and (ii) stands for descendant condition.

Let I₁ and I₂ be the sets of nodes in V(T₁) and V(T₂) not appearing in M, respectively. Then, the following equality holds (Bille, 2005; Zhang et al., 1992):

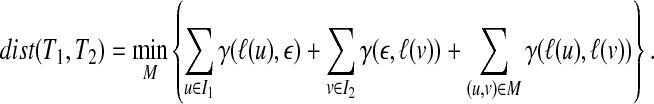Here, we introduce a score function f (u, v) for 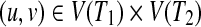defined by

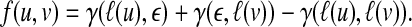Then, we can see that f (u, v) = f (v, u) ≥ 0 holds. It should also be noted that under the unit cost model (i.e., γ(a, b) = 1 for all a ≠ b), f (u, v) = 2 holds if ℓ(u) = ℓ(v), and f (u, v) = 1 holds otherwise. Let score(M) be the score of a mapping M defined by

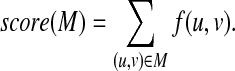Let M_OPT be the mapping with the maximum score. Then, the following property holds (Akutsu et al., 2011a):

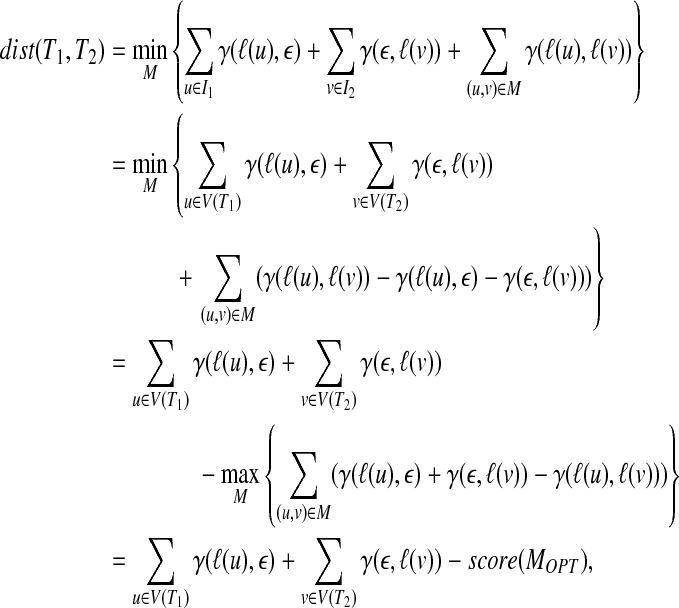(1)

assuming that the root of T₁ corresponds to the root of T₂ in M_OPT, where this assumption can be removed if we add dummy nodes as new roots. It is to be noted that the first and second terms in the right-hand side of the last equality are invariant with a mapping. Therefore, this equality means that the tree edit distance can be obtained by computing a mapping with the maximum score.

3. Method

3.1. Maximum vertex weighted clique

Let G = (V, E) be an undirected graph. A subgraph G′ = (V′, E′) of G = (V, E) is called a clique if it is a complete subgraph (i.e., 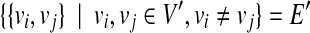). The maximum clique problem is to find a clique with the maximum number of vertices in a given undirected graph G = (V, E). Although the maximum clique problem is NP-hard, several practical algorithms have been developed (Tomita et al., 2010, 2011). In this article, we use a variant of the maximum clique problem called the maximum vertex weighted clique problem. In this variant, each vertex v has a weight w(v) and the problem is to find a clique G′ = (V′, E′), which maximizes 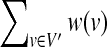(Fig. 3).

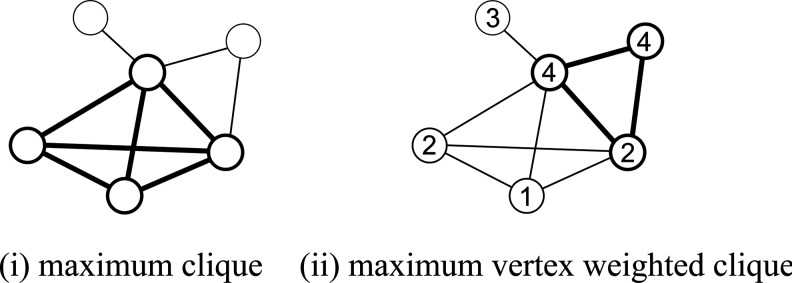
Fig. 3.

Example of the maximum clique and the maximum vertex weighted clique. The size of the maximum clique of the left graph is 4, while the weight of the maximum vertex weighted clique of the right graph is 10.

3.2. Algorithm MWCQ and MCS

Nakamura and Tomita developed a practically efficient algorithm called MWCQ for the maximum vertex weighted clique problem (Nakamura and Tomita, 2005). After preliminary experiments on maximum vertex weighted clique algorithms (Nakamura and Tomita, 2005), we employ MWCQ as a solver for the maximum vertex weighted clique problem. Here, we briefly review MWCQ.

The underlining algorithm of MWCQ is a very simple and fast branch-and-bound depth-first-search algorithm MCQ for finding a maximum clique of an unweighted graph (Tomita and Seki, 2003; Tomita et al., 2011). MCQ employs greedy approximate coloring to obtain an upper bound of the size of a maximum clique. The size of a maximum clique in an unweighted graph is bounded above by the number of approximate color classes (the total number of disjoint sets of independent set). This relation contributes to an effective bounding condition.

For a vertex weighted graph, the maximum weight of a clique in a graph is bounded above by the summation of the maximum weight in each approximate color class (independent set). Then we have a simple algorithm MWCQ for finding a maximum vertex weighted clique by introducing the above new bounding condition into MCQ, instead of the previous one together with appropriate ordering of vertices as in MCQ.

Furthermore, Tomita et al. (2010) proposed a new branch-and-bound algorithm MCS for the maximum clique problem. In MCS, new approximate coloring is introduced along with other new techniques, which makes MCS much faster than MCQ for most instances. In order to use MCS, to be shown below, we develop a method that does not use a maximum vertex weighted clique algorithm but instead uses a maximum clique algorithm.

3.3. Previous method

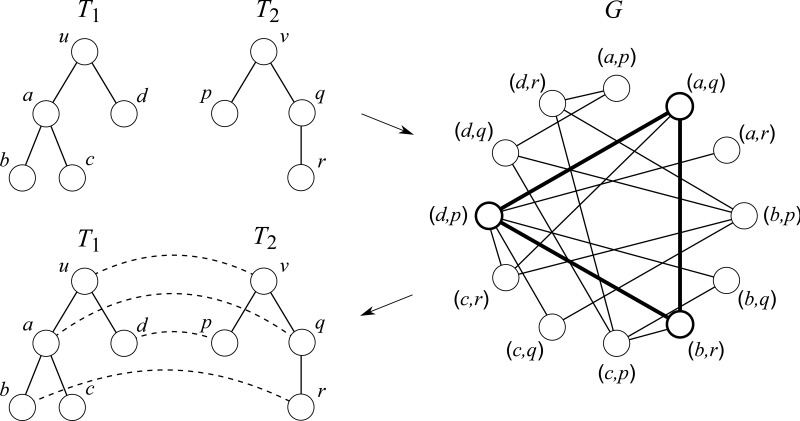
Before presenting our improved clique-based method, we briefly review the previous clique-based method (Fukagawa et al., 2011) (Fig. 4), which is referred to as CliqueEdit in this paper.

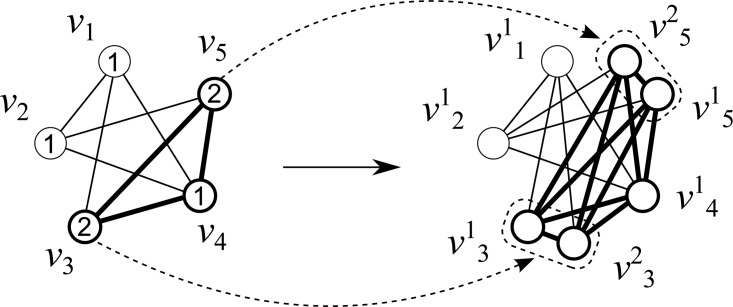
Fig. 4.

Example of a reduction in the previous method, CliqueEdit. A maximum clique is shown with bold lines in graph G, and the corresponding mapping is shown by dashed lines in the bottom left side.

CliqueEdit is based on a simple reduction from the tree edit distance problem for unordered trees to the maximum vertex weighted clique problem. Based on Equation (1), for calculating the tree edit distance, it is enough to find a mapping M maximizing 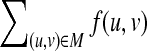. In order to find such a mapping, an undirected graph G = (V, E) is constructed from two input trees T₁ and T₂ by

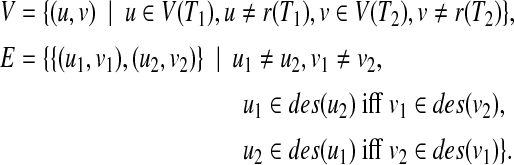Then, we can see that there is a one-to-one correspondence between the set of cliques and the set of mappings [i.e., (u, v) in a clique corresponds to (u, v) in a mapping M]. By assigning a weight w(x) = f (u, v) to each vertex 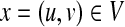, an optimal mapping M_OPT corresponds to a maximum vertex weighted clique. Therefore, the tree edit distance problem can be solved by computing a maximum vertex weighted clique.

3.4. Reduction from the maximum vertex weighted clique problem to the maximum clique problem

In order to use MCS (Tomita et al., 2010) instead of MWCQ (Nakamura and Tomita, 2005), we develop a simple method that transforms the maximum vertex weighted clique problem into the maximum clique problem.

Let G = (V, E) be a weighted graph such that 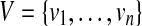and each vertex v_i has a weight w(v_i). From G = (V, E), we construct an unweighted graph 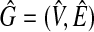by (Fig. 5)

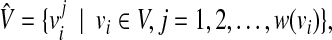(2)

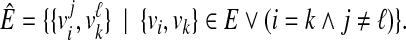(3)

Fig. 5.

Example of transformation of a vertex weighted graph into an unweighted graph; v₃ and v₅ are duplicated.

Proposition 1

The weight of the maximum vertex weighted clique of G = (V, E) is equal to the size of the maximum clique of .

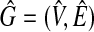Proof. Suppose that there exists a clique G_c = (V_c, E_c) with the weight W and the size m in G, where

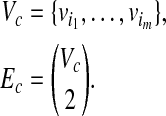In this case, there also exists a clique 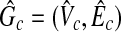in 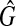, where

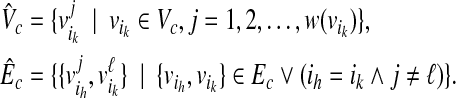Since 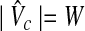and 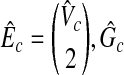is a clique with the size W. Hence, if there exists a clique with the weight W in G, there exists a clique with the size W in 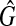, so that if G has the maximum vertex weighted clique with the weight W, 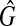has the maximum clique with the size W.

Conversely, we assume that there exists a clique 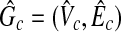with the size W in 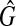, where

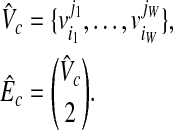Here, 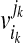is a copy of v_ik and i_h = i_k can hold. From the way to construct 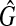[see Eq. (2) and (3)], there also exists at least one clique 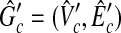with the size W′(≥W) in 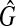, where

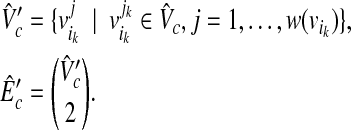In this case, there also exists a clique G_c = (V_c, E_c) in G, where

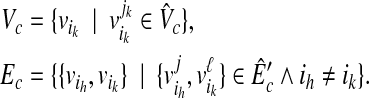Since the weight of G_c is equal to W′ and 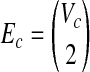, G_c is a clique with the weight W′. Hence, if there exists a clique with the size W in 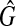, there exists a clique with the size W′(≥W) in 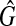, so that there exist a clique with the weight W′ in G. Thus, if 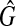has the maximum clique with the size W, G has the maximum vertex weighted clique with the weight W. Therefore, the weight of the maximum vertex weighted clique of G is equal to the size of the maximum clique of .  ■

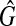The method of combining this transformation with CliqueEdit is called UwCliqueEdit. Since a vertex with weight w is transformed into w vertices, this method can only be applied to graphs with small integer vertex weights. However, if we consider the unit cost edit distance, each vertex in G = (V, E) has weights 1 or 2. Therefore, this method can be applied to computation of the unit cost tree edit distance.

3.5. Improved method

In order to improve CliqueEdit, we combine a dynamic programming (DP) approach employed in (Akutsu et al., 2011a) with the clique-based approach. We call the resulting method DpCliqueEdit.

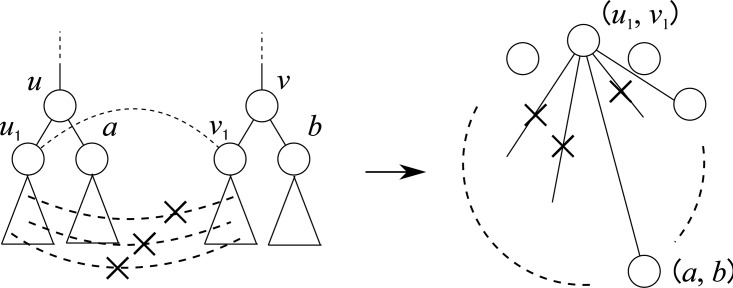
Let 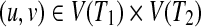. We define W[u, v] as the score of an optimal mapping between T₁(u) and T₂(v), where the root of T₁(u) need not correspond to the root of T₂(v). We compute W[u, v] in a bottom-up way (i.e., from leaves to roots) using DP. Suppose that W[u′, v′] are already computed for all 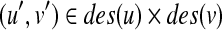. Then, we construct an undirected vertex weighted graph G_{(u, v)} = (V_{(u, v)}, E_{(u, v)}) by

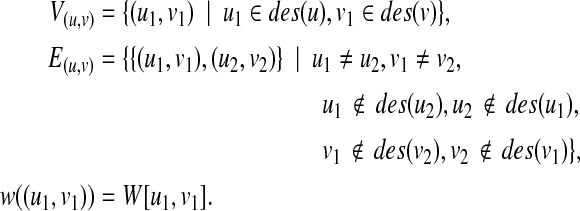Let W_max be the weight of the maximum vertex weighted clique for G_{(u, v)}. Then, we calculate W[u, v] by²

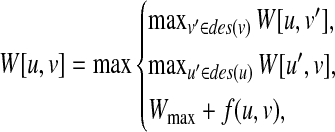where W[u, v] is initialized by

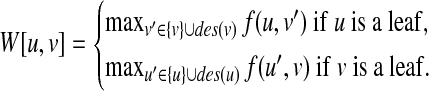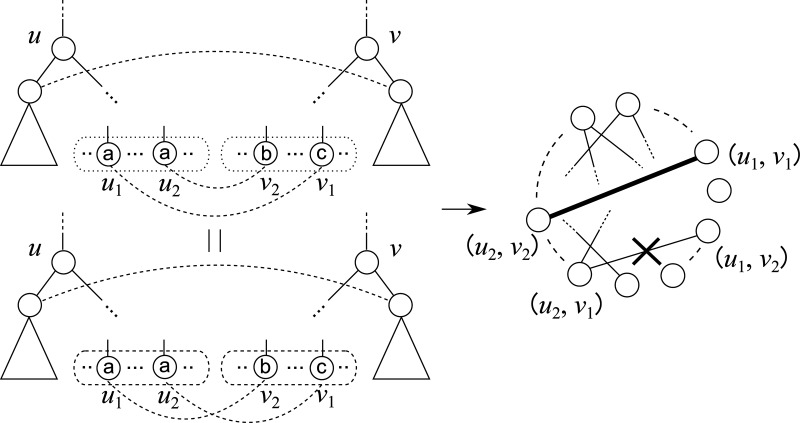
Different from the reduction in CliqueEdit, edges are not created in DpCliqueEdit if there is a descendant–ancestor relation between u₁ and u₂ (or between v₁ and v₂; Fig. 6). Therefore, it is expected that graphs constructed in DpCliqueEdit are much sparser than those in CliqueEdit, though DpCliqueEdit must solve many clique instances. Since sparseness of the graph greatly affects the efficiency of clique finding, it is also expected that DpCliqueEdit is faster than CliqueEdit if nonsmall trees are given. It is to be noted that transformation to maximum clique cannot be applied to this case because W[u, v] might take a large value even for the unit cost case.

Fig. 6.

Difference between the reductions in CliqueEdit and DpCliqueEdit. In computation of W[u, v] in DpCliqueEdit, vertex (u₁, v₁) in G_{(u, v)} is not connected to any one of the vertices corresponding to pairs of descendants of u₁ and v₁.

3.6. Heuristics

In addition to the use of dynamic programming, we introduce some heuristic techniques to reduce the computation time without violating the optimality of the solution.

An important observation is that

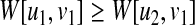(4)

always holds if u₂ is a descendant of u₁. Based on it, we introduce the following two heuristic techniques.

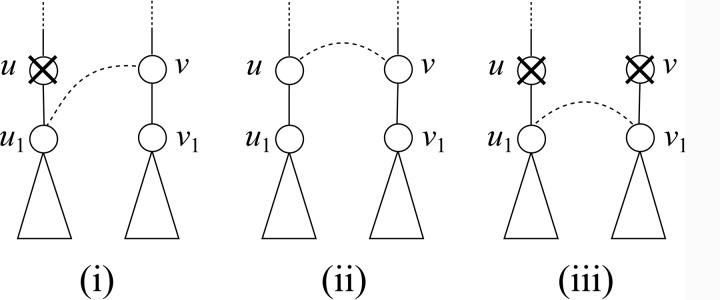
(1) Each of u and v has only one child.

In this case, we need not construct G_{(u, v)}. Instead, we can compute W[u, v] simply by taking the maximum of

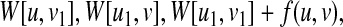where u₁ and v₁ are the children of u and v, respectively (Fig. 7).

Fig. 7.

Example of heuristic technique (1); (i), (ii), and (iii) denote the cases (i) ∼ (iii) in the proof of Proposition 2.

Proposition 2

If each of 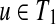and 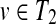has only one child, W[u, v] can be computed by W[u, v] = max{W[u, v₁],W[u₁, v],W[u₁, v₁] + f (u, v)}, where u₁ and v₁ are the children of u and v, respectively.

Proof. We consider the following three cases.

• (i) In the case that u (resp. v) is deleted and v (resp. u) is not deleted, from the assumption and Equation (4), since 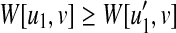for all 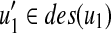(resp. 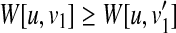for all 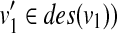, W[u, v] = W[u₁, v] (resp. W[u, v] = W[u, v₁]) holds.

• (ii) In the case that u corresponds to v, since each of u and v has only one child, W_max = W[u₁, v₁], where W_max is the weight of the maximum vertex weighted clique for G_{(u, v)}. Hence, W[u, v] = W_max + f (u, v) = W[u₁, v₁] + f (u, v).

• (iii) In the case that both u and v are deleted, W[u, v] = W[u₁, v₁] apparently. Now, the score of this case is smaller than or equal to that of case (ii), because f (u, v) ≥ 0.

Therefore, we can calculate W[u, v] by▪

  ■

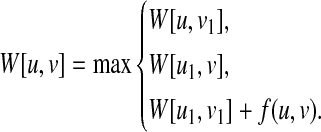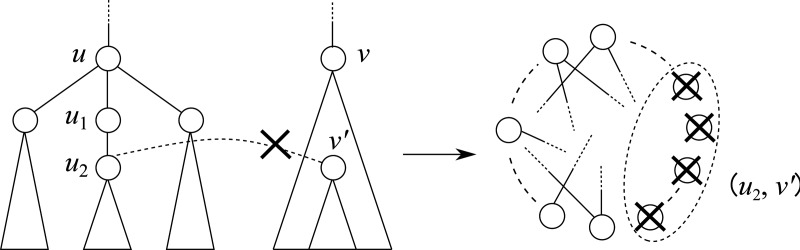
(2) 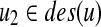(resp. 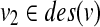) does not have a sibling.

In this case, we need not generate a vertex (u₂, v′) for any v′ (resp. (u′, v₂) for any u′) in the construction of G_{(u, v)} because any mapping between T₁(u₂) and T₂(v) can be included in some mapping between T₁(u₁) and T₂(v) where u₁ is the parent of u₂ (Fig. 8).

Fig. 8.

Example of heuristic technique (2); a vertex (u₂, v′) is not necessary for any v′ in the construction of G_{(u, v)}.

Proposition 3

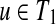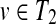Suppose that and . If 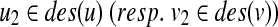does not have a sibling, W[u, v] can be computed without generating a vertex (u₂, v′) for any v′ (resp. (u′, v₂) for any u′) in the construction of G_{(u, v)}, where ).

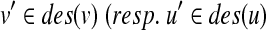Proof. Consider a mapping between T₁(u) and T₂(v). A weighted graph G_{(u, v)} is constructed from T₁(u) and T₂(v). Besides, let G_c2 = (V _c2, E_c2) be a clique including 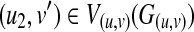. Here, because any mapping between T₁(u₂) and T₂(v) can be included in some mapping between T₁(u₁) and T₂(v), there also exists a clique G_c1 = (V_c1, E_c1), including 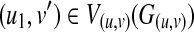, where u₁ is the parent of u₂ and V_c2(G_c2)\{(u₂,v′)} = V_c1(G_c1)\{(u₁,v′)}. Furthermore, W[u₁, v′] ≥ W[u₂, v′]. Let w(G_c1) and w(G_c2) be the weights of the G_c1 and G_c2, respectively. Then, the following inequality holds:

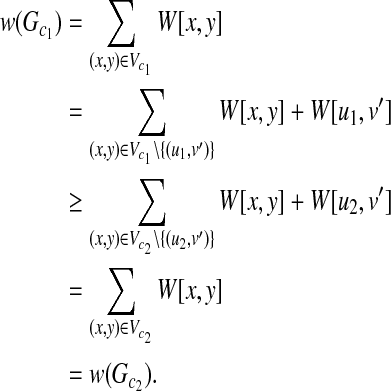Hence, the score of G_c2 is smaller than or equal to that of G_c1. Therefore, we need not generate a vertex (u₂, v′) for any v′ in the construction of G_{(u, v)}.  ■

Although DpCliqueEdit with heuristic techniques (1) and (2) is much faster than CliqueEdit (Akutsu et al., 2011b) in most cases, it takes a very long CPU time in some cases, especially if there are many leaves. In such a case, constructed graphs would contain many vertices and edges, and thus a clique algorithm does not work efficiently. In order to cope with such difficult cases, we introduce other heuristic techniques as follows. The efficiency of MWCQ is much affected by the number of edges in G_{(u, v)}. Due to the definition of E_{(u, v)} described in Section 3.5, if u₁, v₁, u₂, v₂ are leaves, there is always an edge between (u₁, v₁) and (u₂, v₂). Therefore, if there are many leaves in T₁ and T₂, G_{(u, v)} has many edges and then MWCQ takes much longer computation time. Since more than half of nodes are leaves even in binary trees, some heuristic techniques handling leaves are necessary for further speed-up.

(3) u₁, u₂, v₁, and v₂ (u₁ ≠ u₂, v₁ ≠ v₂) are leaves, and ℓ(u₁) = ℓ(u₂) or ℓ(v₁) = ℓ(v₂).

In this case, we need not create an edge {(u₁, v₂), (u₂, v₁)} for any u₁, u₂, v₁, and v₂ in the construction of G_{(u, v),} because the score of a mapping including two pairs (u₁, v₂), (u₂, v₁) is equal to that of a mapping including two pairs (u₁, v₁), (u₂, v₂). Therefore, we have only to create an edge {(u₁, v₁), (u₂, v₂)} without creating an edge {(u₁, v₂), (u₂, v₁)} (Fig. 9).

Fig. 9.

Example of heuristic technique (3); u₁, u₂, v₁, and v₂ are leaves and ℓ(u₁) = ℓ(u₂). In this case, we need not create {(u₁, v₂), (u₂, v₁)}.

Proposition 4

Suppose that u₁, 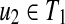, and v₁, 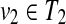. If u₁, u₂, v₁, and v₂ (u₁ ≠ u₂, v₁ ≠ v₂) are leaves, and ℓ(u₁) = ℓ(u₂) or ℓ(v₁) = ℓ(v₂), W[u,v] can be computed without creating an edge {(u₁, v₂), (u₂, v₁)} for any u₁, u₂, v₁, and v₂ in the construction of G_{(u, v)}.

Proof. If there exists a mapping M that includes two pairs (u₁, v₁), (u₂, v₂) between T₁ and T₂, it is implied that there also exists a mapping M′ that includes two pairs (u₁, v₂), (u₂, v₁) instead of (u₁, v₁), (u₂, v₂) between T₁ and T₂. Now, the following equality holds:

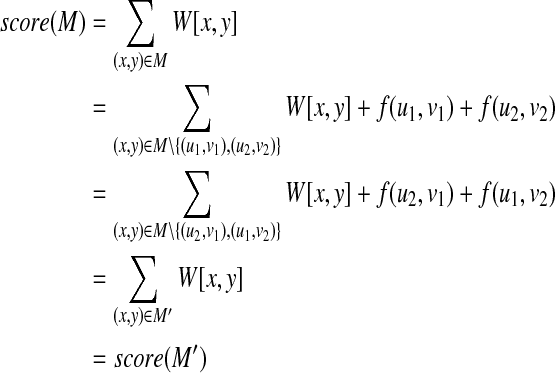Hence, the score of a mapping including two pairs (u₁, v₂), (u₂, v₁) is equal to that of a mapping including two pairs (u₁, v₁), (u₂, v₂). Therefore, we have only to create an edge {(u₁, v₁), (u₂, v₂)} without creating an edge {(u₁, v₂), (u₂, v₁)}.  ■

(4) u₁, u₂, v₁, and v₂ (u₁ ≠ u₂, v₁ ≠ v₂) are leaves, and all labels of them are different.

In this case, we need not create an edge {(u₁, v₂), (u₂, v₁)} for any u₁, u₂, v₁, and v₂ in the construction of G_{(u, v)} for the same reason as in case (3).

Proposition 5

Suppose that u₁, 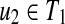and v₁, 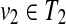. If u₁, u₂, v₁, and v₂ (u₁ ≠ u₂, v₁ ≠ v₂) are leaves, and ℓ(u₁),ℓ(u₂),ℓ(v₁), and ℓ(v₂) are different, W[u, v] can be computed without creating an edge {(u₁, v₂), (u₂, v₁)} for any u₁, u₂, v₁, and v₂ in the construction of G_{(u, v)}.

Proposition 5 can be proved in the same way as the proof of Proposition 4, so we omit the proof of Proposition 5.

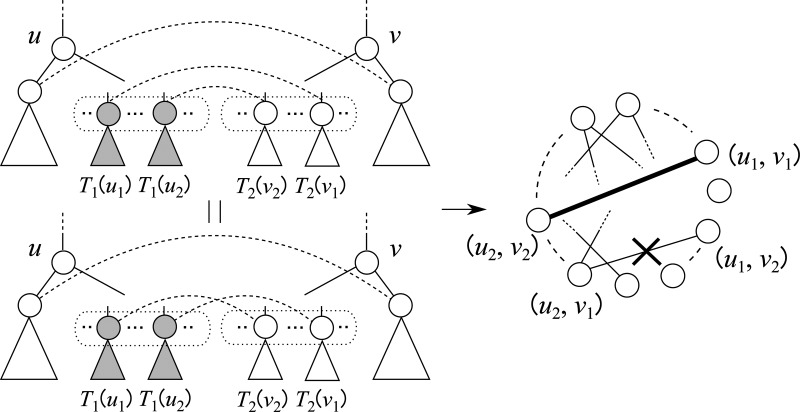
The idea of (3) focusing on the same labeled leaves is extended to the isomorphic subtrees. If T₁ and T₂ are isomorphic including label information, we write T₁ ≈ T₂.

(5) T₁(u₁) ≈ T₁(u₂) (u₁ ≠ u₂) or T₂(v₁) ≈ T₂(v₂) (v₁ ≠ v₂).

In this case, we need not create an edge {(u₁, v₂), (u₂, v₁)} for any u₁, u₂, v₁, and v₂ in the construction of G_{(u, v)} because of the following reason. When T₁(u₁) ≈ T₁(u₂) or T₂(v₁) ≈ T₂(v₂), the score of mapping {(T₁(u₁), T₂(v₂)), (T₁(u₂),T₂(v₁))} is equal to that of mapping {(T₁(u₁), T₂(v₁)), (T₁(u₂), T₂(v₂))}. Therefore, we have only to create an edge {(u₁, v₁), (u₂, v₂)} without creating an edge {(u₁, v₂), (u₂, v₁)} (Fig. 10).

Fig. 10.

Example of heuristic technique (4); T₁(u₁) and T₁(u₂) are isomorphic including label information. In this case, we need not create {(u₁, v₂), (u₂, v₁)}.

Proposition 6

Suppose that u₁, 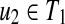and v₁, 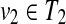. If T₁(u₁) ≈ T₁(u₂) (u₁ ≠ u₂) or T₂(v₁) ≈ T₂(v₂) (v₁ ≠ v₂), W[u, v] can be computed without creating an edge {(u₁, v₂), (u₂, v₁)} for any u₁, u₂, v₁, and v₂ in the construction of G_{(u, v)}.

Proof. If there exists a mapping M that includes two pairs (u₁, v₁), (u₂, v₂) between T₁ and T₂, it is implied that there also exists a mapping M′ that includes two pairs (u₁, v₂), (u₂, v₁) instead of (u₁, v₁), (u₂, v₂) between T₁ and T₂. Moreover, from the assumption, the score of mapping {(T₁(u₁), T₂(v₂)), (T₁(u₂), T₂(v₁))} is equal to that of mapping {(T₁(u₁), T₂(v₁)), (T₁(u₂), T₂(v₂))}, that is, W[u₁, v₁] = W[u₂, v₁] and W[u₂, v₂] = W[u₁, v₂]. Now, the following equality holds,

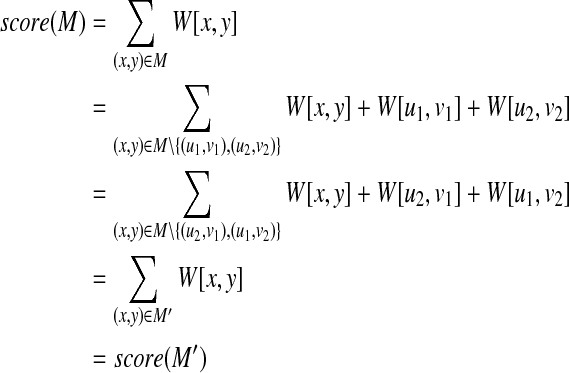Thus, the score of a mapping including two pairs (u₁, v₂), (u₂, v₁) is equal to that of a mapping including two pairs (u₁, v₁), (u₂, v₂). Therefore, we have only to create an edge {(u₁, v₁), (u₂, v₂)} without creating an edge {(u₁, v₂), (u₂, v₁)}.  ■

It is expensive to determine whether two graphs are isomorphic or not, but we can solve the problem easier when the two graphs are trees. Though various algorithms are invented for the problem, we employ an algorithm introduced in Matoušek and Nešetřil (1998). The algorithm transforms the tree isomorphism problem into the comparison of simple numerical sequences.

From the Propositions 2∼6, we have the following theorem.

Theorem 1

DpCliqueEdit with the heuristic (1)∼(5) computes dist(T₁, T₂) without violating the optimality of the solution.

It should be noted that we can use the heuristic techniques only if DP is introduced to the clique-based approach.

4. Experimental Results

To evaluate the efficiency of the improved method and heuristic techniques, we applied CliqueEdit, UwCliqueEdit, and DpCliqueEdit to comparison of real tree-structured data. As the tree-structured data, we employed glycan structures that were obtained from KEGG/Glycan database (Kanehisa et al., 2010) and CSLOGS dataset, which consists of Weblogs files (Zaki et al., 2005).

It is to be noted that, as far as we know, no other publicly available program exists for precisely computing the unordered tree edit distance, and thus we only compared these methods. From the result given in Horesh et al. (2006), it is considered that CliqueEdit has similar efficiency (Fukagawa et al., 2011) to the A*-algorithm for unordered tree edit distance (Horesh et al., 2006).

We implemented CliqueEdit, UwCliqueEdit, and DpCliqueEdit using C++ language and compared UwCliqueEdit and DpCliqueEdit with CliqueEdit, the previous method. In the implementations of CliqueEdit and DpCliqueEdit, MWCQ (Nakamura and Tomita, 2005) was used as a maximum vertex weighted clique algorithm, while in that of UwCliqueEdit, MCS (Tomita et al., 2010) was used as a maximum clique algorithm. DpCliqueEdit-A, DpCliqueEdit-B, DpCliqueEdit-C, DpCliqueEdit-D, and DpCliqueEdit-E represent DpCliqueEdit without heuristics, with heuristics (1)(2), with heuristics (1)(2)(3), with heuristics (1)(2)(3)(5), and with all heuristics, respectively. The preliminary version of DpCliqueEdit in Akutsu et al. (2011b) is equivalent to DpCliqueEdit-B. We performed computational experiments using a PC with 2.66 GHz Intel Core i7 CPU and 3.88 GB RAM, running under the Mac OS X operating system. In this article, we focus only on the computational efficiency and do not conduct computational experiments for evaluating the performance (i.e., accuracy of comparison) of CliqueEdit, UwCliqueEdit, and DpCliqueEdit. Because these methods compute the same distances, the performance of CliqueEdit was already evaluated in the previous work (Fukagawa et al., 2011), and the tree edit distance is the most established distance measure for trees (Bille, 2005).

For evaluation of the methods, we used the standard weighting scheme (i.e., f (u,v) = 2 for ℓ(u) = ℓ(v), f (u,v) = 1 for ℓ(u) ≠ ℓ(v)) corresponding to the unit cost edit distance.

4.1. Glycan structures

As in our previous work (Fukagawa et al., 2011), we randomly selected 100 pairs of glycan structures with a specified range of the total number of nodes (i.e., the sum of the numbers of nodes in T₁ and T₂) and measured the average CPU time per pair. Unbalanced cases in which the size of one structure was smaller than one-third of the other structure were excluded. For each of the ranges in 60∼79, we took the average over 20 pairs because there were not enough number of pairs, whereas we could use 19 pairs among 20 pairs for the range of 70∼74 because there was a hard case for which DpCliqueEdit-A could not output a solution within 60 minutes. For the ranges of 80∼84, 85∼89, and 90∼94, only 9, 5, and 4 pairs were available, respectively. We could use only 4 pairs among 5 pairs for the range of 85∼89 and 2 pairs among 4 pairs for the range of 90∼94, because there were hard cases for which DpCliqueEdit-A could not output a solution within 60 minutes.

The result of the computational experiment is shown in Table 1. From this table, it is seen that DpCliqueEdit-B, DpCliqueEdit-C, DpCliqueEdit-D, and DpCliqueEdit-E are much faster than CliqueEdit, UwCliqueEdit, and DpCliqueEdit-A for nonsmall glycan structures. In particular, DpCliqueEdit-D is the fastest for comparison of large glycan structures. Although UwCliqueEdit is faster than CliqueEdit in most cases, it is not fast for comparison of large glycan structures, because it constructs larger and denser graph Ĝ as G becomes larger, and thus MCS does not work efficiently. Besides, DpCliqueEdit-A is not fast despite the fact that DpCliqueEdit-B∼DpCliqueEdit-E are faster than the other methods. This is because DpCliqueEdit repeatedly solves instances of the maximum vertex weighted clique problem as subproblems, so that it takes a long CPU time if the heuristic techniques are not introduced. Since the heuristic techniques proposed in this article cannot be used without using DP, DP needs to be introduced in order to reduce the computation time. Although CliqueEdit and UwCliqueEdit are faster than DpCliqueEdit-B∼DpCliqueEdit-E for small glycan structures, comparison of large glycan structures is more crucial because it takes a large amount of time.

Table 1.

CPU Time for Comparing Glycans

Total # nodes	Clique Edit	UwClique Edit	DpClique Edit-A	DpClique Edit-B	DpClique Edit-C	DpClique Edit-D	DpClique Edit-E
30∼34	0.002	0.003	0.013	0.006	0.006	0.006	0.009
35∼39	0.004	0.007	0.027	0.011	0.011	0.012	0.017
40∼44	0.056	0.035	0.107	0.026	0.019	0.021	0.029
45∼49	0.064	0.036	0.126	0.031	0.030	0.031	0.040
50∼54	0.078	0.049	0.228	0.039	0.037	0.039	0.051
55∼59	1.987	0.433	8.968	0.108	0.088	0.086	0.096
60∼64	2.746	4.949	1.780	0.167	0.163	0.149	0.177
65∼69	64.290	9.303	39.460	0.381	0.364	0.328	0.357
70∼74	58.690	0.099	1.337	0.545	0.436	0.463	0.501
75∼79	2.441	0.918	4.051	0.953	0.752	0.754	0.781
80∼84	7.150	6.570	44.630	2.516	2.268	1.620	1.653
85∼89	237.700	28.030	21.110	3.205	3.205	2.413	2.490
90∼94	303.200	1211.000	1710.000	38.810	26.300	8.165	9.475

Average CPU time (user time, sec.) per glycan pair is shown for each case. Boldface indicates the best results for each case.

Table 2 shows the results on pairs of trees (i.e., hard cases) for which some of the examined methods could not compute the distance within 60 minutes. From this table, though there is no great difference between DpCliqueEdit-B∼DpCliqueEdit-E except for the range of 90∼94 in Table 1, we find that DpCliqueEdit-D and DpCliqueEdit-E are much faster than the other methods in hard cases. This implies that DpCliqueEdit-D and DpCliqueEdit-E utilize the existence of the same labeled leaves, different labeled leaves, and isomorphic subtrees, and thus need much shorter time for MWCQ. It takes a long CPU time for DpCliqueEdit-A to output a solution in most cases. This is because it costs a lot of CPU time to construct G_{(u, v)} and solve the maximum vertex weighted clique problem repeatedly. It is also seen that there are some instances in which UwCliqueEdit can solve within 60 minutes, whereas CliqueEdit or DpCliqueEdit-B cannot solve within 60 minutes. However, UwCliqueEdit is not faster than CliqueEdit and DpCliqueEdit-B for comparison of large glycan structures.

Table 2.

CPU Time for Comparing Glycans for Each Hard Case

Glycan pair	Total # nodes	Clique Edit	UwClique Edit	DpClique Edit-A	DpClique Edit-B	DpClique Edit-C	DpClique Edit-D	DpClique Edit-E
{G04520, G04682}	35	693.400	-	223.900	225.800	0.020	0.020	0.020
{G04520, G05248}	36	1124.000	-	284.500	285.900	0.020	0.020	0.020
{G03769, G04682}	71	-	491.400	-	-	10.910	0.490	0.520
{G03769, G04520}	72	-	59.080	-	-	11.800	0.420	0.450
{G03769, G05248}	72	-	17.380	-	-	56.500	0.600	0.630
{G03769, G05297}	72	-	17.590	-	-	56.560	0.600	0.630
{G03655, G03769}	88	108.600	277.400	-	300.700	31.170	5.610	6.430
{G03769, G04206}	91	844.100	1397.000	-	5.870	5.250	5.830	5.120
{G03769, G11847}	91	132.100	911.500	-	108.400	82.880	28.120	22.200

Average CPU time (sec.) per glycan pair is shown for each case. CPU time (sec.) per glycan pair is shown for each hard case. “-” denotes that the program could not output a solution within 60 minutes ( = 3600 seconds). Boldface indicates the best results for each case.

From the results of these computational experiments, we can conclude that DpCliqueEdit-D and DpCliqueEdit-E are more useful than the other proposed clique-based methods. Using heuristics (3) and (5), DpCliqueEdit-D and DpCliqueEdit-E are much faster than DpCliqueEdit-B (i.e., the preliminary version of DpCliqueEdit in Akutsu et al., 2011b).

4.2. CSLOGS Dataset

As in the comparison of glycan structures, we randomly selected 100 pairs of Weblogs data with a specified range of the total number of nodes (i.e., the sum of the numbers of nodes in T₁ and T₂) and measured the average CPU time per pair. Different from comparison of the glycan structures, we randomly selected trees from CSLOGS and created two subdatasets called SUBLOGS3 and SUBLOGS5 in this article. Each sub-dataset has 15,000 trees whose sizes are restricted to smaller than or equal to 80, where the maximum number of children of each node is limited to smaller than or equal to 3 and 5 in SUBLOGS3 and SUBLOGS5, respectively. The percentage of the number of trees in which the maximum number of children of each node are restricted to 3 and 5 is about 65% and 81% of the total number of them in CSLOGS. Unbalanced cases mentioned in Section 4.1 were excluded.

The results of the computational experiments we performed with SUBLOGS3 and SUBLOGS5 are shown in Table 3 and Table 4, respectively. From Table 3, it is seen that UwCliqueEdit is the fastest for small trees. However, as the total number of nodes of input trees becomes larger, it takes longer CPU time for UwCliqueEdit to solve the problem, and there are hard cases for which UwCliqueEdit could not output a solution within 60 minutes. For nonsmall trees, although most methods could not solve the problem in 60 minutes in some cases, DpCliqueEdit-E could solve it in 60 minutes for all cases we selected in this experiment. Similarly, from Table 4, we find that UwCliqueEdit is faster than any other method for small trees, and DpCliqueEdit-E is the fastest for nonsmall trees.

Table 3.

CPU Time for Comparing Weblogs Data Obtained from SUBLOGS3 Dataset

Total # nodes	Clique Edit	UwClique Edit	DpClique Edit-A	DpClique Edit-B	DpClique Edit-C	DpClique Edit-D	DpClique Edit-E
30∼34	0.003	0.003	0.010	0.007	0.007	0.007	0.008
35∼39	0.009	0.009	0.024	0.018	0.017	0.018	0.018
40∼44	0.061	0.023	0.068	0.038	0.032	0.031	0.033
45∼49	0.218	0.100	0.155	0.059	0.053	0.051	0.050
50∼54	2.928	0.129	0.370	0.222	0.119	0.117	0.095
55∼59	2.189	0.809	2.965	0.210	0.173	0.182	0.167
60∼64	-	39.940	-	20.450	0.542	1.904	0.297
65∼69	-	17.380	-	-	2.230	1.106	0.662
70∼74	-	-	-	-	3.589	1.423	1.024
75∼79	-	-	-	-	-	1.895	1.566
80∼84	-	-	-	-	-	-	2.625
85∼89	-	-	-	-	-	46.920	10.550
90∼94	-	-	-	-	-	-	50.570
95∼99	-	-	-	-	-	-	64.980

Average CPU time (sec.) per Weblogs pair is shown for each case. The maximum number of children of each node is limited to smaller than or equal to 3. “-” denotes that there is at least one hard case for which the program could not output a solution within 60 minutes (= 3600 seconds). Boldface indicates the best results for each case.

Table 4.

CPU Time for Comparing Weblogs Data Obtained from SUBLOGS5 Dataset

Total # nodes	Clique Edit	UwClique Edit	DpClique Edit-A	DpClique Edit-B	DpClique Edit-C	DpClique Edit-D	DpClique Edit-E
30∼34	0.010	0.005	0.029	0.011	0.010	0.011	0.008
35∼39	0.244	0.034	0.357	0.114	0.027	0.025	0.016
40∼44	44.090	4.067	41.000	4.630	2.890	1.913	0.028
45∼49	35.380	7.310	19.140	3.075	1.079	0.994	0.101
50∼54	-	-	-	-	-	-	0.141
55∼59	-	53.750	-	-	12.580	12.260	0.423
60∼64	-	-	-	-	-	-	17.240
65∼69	-	-	-	-	-	-	10.850

Average CPU time (sec.) per Weblogs pair is shown for each case. The maximum number of children of each node is limited to smaller than or equal to 5. “-” denotes that there is at least one hard case for which the program could not output a solution within 60 minutes ( = 3600 seconds). Boldface indicates the best results for each case.

Although there is no great difference between DpCliqueEdit-D and DpCliqueEdit-E for comparison of glycan structures, DpCliqueEdit-E is the most useful for comparison of trees. In CSLOGS, there are 13,361 unique Web pages (Zaki et al., 2005), and each Web page is assigned to each node as a label so that there are many leaves with different labels. Therefore, heuristic (4) works efficiently.

5. Conclusion

In this paper, we proposed an improved clique-based method by introducing DP and several heuristic techniques for computing the tree edit distance between rooted, unordered trees. DP and the heuristic techniques are very useful and the improved method is much faster than the previous method in most cases of comparison of real tree-structured data. In particular, for hard instances of comparison of glycan structures, the improved method achieved more than 100 times speed-up. Although the improved method is not faster for comparison of small glycans, it is not crucial because comparison of large glycan structures takes much longer CPU time than that of small glycans. In comparison of Weblogs data, it takes a long CPU time to compute the edit distance between trees when there exist some nodes with many children. However, most biological data, such as glycans, RNA secondary structures, and vascular trees, might have few internal nodes with many children.

Although the improved method is much faster than the previous method, there are still cases for which it takes a long CPU time. In particular, it takes a long CPU time if there are long subtrees (i.e., there are many nodes but few leaves) because heuristics (1)(2) proposed in this article can reduce the computation time only if there are nodes with one child in the long subtrees, and heuristics (3)(4)(5) cannot well contribute to reduction of the number of edges in such cases. Thus, the maximum vertex weighted clique algorithm does not work efficiently. How to cope with such cases is left for future work.

Moreover, in order to achieve further speed-up, we should develop an improved algorithm for the maximum vertex weighted clique problem because an improvement of the efficiency of clique-finding directly leads to an improvement in the efficiency of our proposed algorithm. In particular, a maximum vertex weighted clique solver specialized for properties of weighted graphs generated by the clique-based algorithm might be useful for the tree edit distance problem. How to develop such an algorithm is also left as future work.

In addition to the future work mentioned above, some modifications are needed for application to analysis of tree-structured data used in computational biology. Although we have used the unit cost edit distance in computational experiments, more suitable cost functions should be used for analysis of biological and other objects. Development of cost functions suitable to individual applications is also left for future work.

Acknowledgments

This work was partially supported by research collaboration projects by National Institute for Informatics and Institute for Chemical Research, Kyoto University. The work of TA was partially supported by MEXT Grant-in-Aid No.22240009. The work of DF and AT was partly supported by MEXT Grant-in-Aid No.18049069. The work of ET was partially supported by MEXT Grant-in-Aid No.22500009.

Disclosure Statement

No competing financial interests exist.