Abstract
Reaction pathway of (−)-cocaine hydrolysis catalyzed by our recently discovered most efficient cocaine hydrolase, which is the A199S/F227A/S287G/A328W/Y332G mutant of human butyrylcholinesterase (BChE), and the corresponding free energy profile have been studied by performing first-principles pseudobond quantum mechanical/molecular mechanical (QM/MM)-free energy (FE) calculations. Based on the QM/MM-FE results, the catalytic hydrolysis process consists of four major reaction steps, including the nucleophilic attack on carbonyl carbon of (−)-cocaine benzoyl ester by hydroxyl group of S198, dissociation of (−)-cocaine benzoyl ester, nucleophilic attack on carbonyl carbon of (−)-cocaine benzoyl ester by water, and finally the dissociation between (−)-cocaine benzoyl group and S198 of the enzyme. The second reaction step is rate-determining. The calculated free energy barrier associated with the transition state for the rate-determining step is ~15.0 kcal/mol, which is in excellent agreement with the experimentally-derived activation free energy of ~14.7 kcal/mol. The mechanistic insights obtained from the present study will be valuable for rational design of more active cocaine hydrolase against (−)-cocaine. In particular, future efforts aiming at further increasing the catalytic activity of the enzyme against (−)-cocaine should focus on stabilization of the transition state for the second reaction step in which the benzoyl ester of (−)-cocaine dissociates.
Introduction
Cocaine is recognized as the most reinforcing drug of abuse.1–3 It directly affects the brain and produces a number of toxic effects at high dose. Despite intensive efforts toward education, cocaine abuse continues to be a serious public health problem.4 Recent surveys in the United States show that cocaine was the first on the list of the causes of the illicit-drug-related emergency department visits.5 This widely abused drug produces potent stimulation in both central nervous system (CNS) and cardiovascular system. The potent stimulation is followed by depression.6 The common effects of overdosed cocaine include respiratory depression, cardiac arrhythmia, and acute hypertension. The disastrous medical and social consequences of cocaine addiction have made a high priority the development of an anti-cocaine medication.7–8 Unfortunately, there is no FDA-approved medication specific for cocaine overdose or addiction, and the search for an effective and safe treatment continues.9–13
There are two enantiomers of cocaine. One is the naturally occurring (−)-cocaine which is biologically active. The other is the unnatural (+)-cocaine which is biologically inactive. The classic CNS-receptor antagonist approach has failed to yield an anti-cocaine therapeutic agent against (−)-cocaine, due to the difficulties inherent in blocking a blocker. Nevertheless, we have developed a proof of principle for a peripheral blocker to accelerate (−)-cocaine metabolism in the circulation.5,7,12–18 Butyrylcholinesterase (BChE) is the principal enzyme catalyzing the hydrolysis of (−)-cocaine into its biologically inactive metabolites in human plasma16 and, thus, the BChE-catalyzed hydrolysis of (−)-cocaine is the cocaine-metabolizing pathway most suitable for amplification in the development of an anti-cocaine medication. However, the catalytic efficiency of wild-type BChE against (−)-cocaine is rather low (kcat = 4.1 ± 0.4 min−1, KM = 4.5 ± 0.3 μM).19
To understand the fundamental reaction mechanism for BChE-catalyzed hydrolysis of (−)-cocaine, we have carried out extensive computational studies on wild-type BChE interacting with (−)-cocaine4,16,20–22 in comparison with available experimental kinetic data. Experimental kinetic analysis23 revealed that the rate-determining step for wild-type BChE-catalyzed hydrolysis of (−)-cocaine is the formation of the enzyme-substrate complex, rather than any step of the chemical reaction process. As a result, the catalytic rate constant for wild-type BChE-catalyzed hydrolysis of (−)-cocaine is independent of the pH of the reaction solution. According to our computational results,4,16,21 (−)-cocaine first slides down the substrate-binding gorge of BChE to bind to W82 and stands vertically in the gorge between D70 and W82 (non-prereactive enzyme-substrate complex) and then rotates to a position in the catalytic site within a favorable distance for nucleophilic attack and hydrolysis by S198 (prereactive enzyme-substrate complex). Based on the free energy profiles determined by using the potential of mean force (PMF) approach,4,21,24 the highest free energy barrier for the pre-chemical reaction process is associated with the (−)-cocaine rotation in the BChE active site from the non-prereactive complex to the prereactive complex.21 There is no significant free energy barrier for non-prereactive enzyme-substrate binding process.4 In light of the mechanistic insights, we have successfully designed and discovered a set of BChE mutants with significantly improved catalytic efficiency against (−)-cocaine.10,12–13,18,22,25–27 Within all cocaine-metabolizing enzymes reported in literature so far, the most efficient one is the A199S/F227A/S287G/A328W/Y332G mutant of human BChE.13 It has been shown that this BChE mutant has a ~2000-fold improved catalytic efficiency13 against (−)-cocaine compared to the wild-type. Thus, this BChE mutant has been recognized as a true cocaine hydrolase.28 The pretreatment with this BChE mutant (using a dose of 0.01 mg per mouse, i.v.) can fully protect mice from the acute toxicity of a lethal dose of cocaine (180 mg/kg, i.p.), good for cocaine overdose treatment.13 It is interesting for anti-cocaine medication development to further improve the catalytic activity of this enzyme against (−)-cocaine in order to minimize the dose required for the practical anti-cocaine medication. The lower the enzyme dose required, the less expensive the practical medication. In order to further improve the catalytic activity against (−)-cocaine, one first needs to understand the detailed reaction mechanism of (−)-cocaine hydrolysis catalyzed by the cocaine hydrolase.
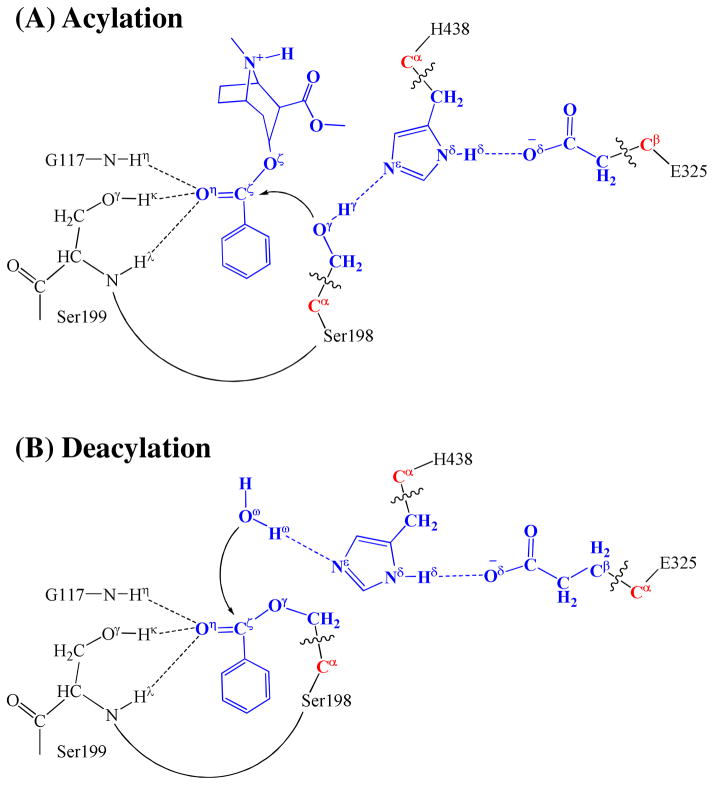
Recently, the first-principles quantum mechanical methods, in particular the combined quantum mechanical/molecular mechanical (QM/MM) methods, have been widely applied in drug design and have been proven valuable in studying mechanistic aspects for a wide range of biomolecular systems related to drug design.29–34 However, it should be pointed out that, within all computational studies on BChE-catalyzed hydrolysis of (−)- cocaine reported so far, only wild-type BChE has been subjected to the QM/MM reaction-coordinate calculations on the entire chemical reaction process.16,20 There has been no complete reaction-coordinate calculation on any BChE mutant against (−)- cocaine, although it has been known that the rate-determining step is no longer the (−)- cocaine rotation in the active site of the enzyme.4,21 One of the chemical reaction steps must be rate-determining for the cocaine hydrolase against (−)-cocaine. In the present study, we have carried out extensive computational studies using first-principles pseudobond quantum mechanical/molecular mechanical-free energy (QM/MM-FE) approach,35–38 which has been demonstrated to be a powerful tool in simulating a variety of enzymes,13,39–51 to uncover the detailed mechanism for (−)-cocaine hydrolysis catalyzed by the A199S/F227A/S287G/A328W/Y332G mutant. Based on the detailed mechanistic insights obtained from our recent computational studies on the mechanisms for hydrolyses of (−)-cocaine and other carboxylic esters catalyzed by wild-type BChE and cocaine esterase (CocE),12–13,18,20,22,52–56 (−)-cocaine hydrolysis in the A199S/F227A/S287G/A328W/Y332G mutant might undergo a very similar pathway as that in wild-type BChE,16 which consists of two major stages. The first stage is likely acylation, leading to covalent bond formation between (−)-cocaine and the enzyme and the departure of ecgonine methyl ester group from the benzoyl ester group of (−)-cocaine. The second stage is likely deacylation, resulting in the dissociation of the (−)-cocaine benzoyl ester from the enzyme, in which a water molecule acts as the nucleophile and the free state of enzyme is restored afterwards.
Further, on the basis of our initial computational exploration of a possible reaction pathway for (−)-cocaine hydrolysis catalyzed by the A199S/F227A/S287G/A328W/Y332G mutant, in the present study, we proposed a working hypothesis for the more detailed reaction pathway of (−)-cocaine hydrolysis by this BChE mutant (Scheme 1). The computational results clearly reveal the detailed reaction pathway and the corresponding free energy profile for (−)-cocaine hydrolysis catalyzed by the A199S/F227A/S287G/A328W/Y332G mutant. Based on the free energy profile, the rate-determining reaction step has been identified. In addition, the roles of essential residues forming the catalytic triad and oxyanion hole are discussed below based on the QM/MM-optimized geometries of key states of the system during the catalytic reaction process.
Scheme 1.
Proposed catalytic mechanism for the hydrolysis of (−)-cocaine catalyzed by the A199S/F227A/S287G/A328W/Y332G mutant of BChE.
Results and Discussion
Fundamental Reaction Pathway
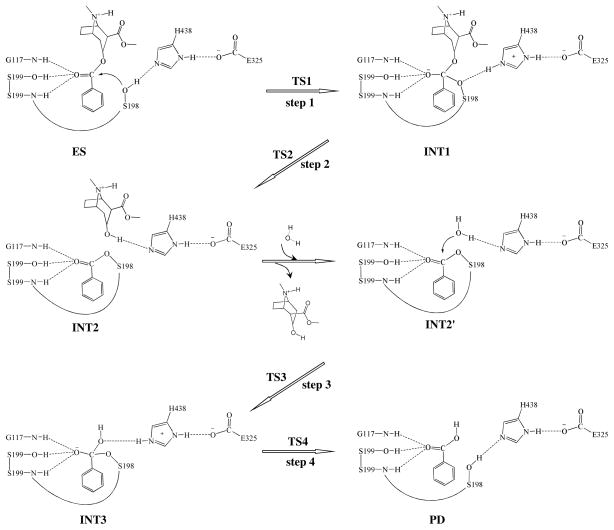
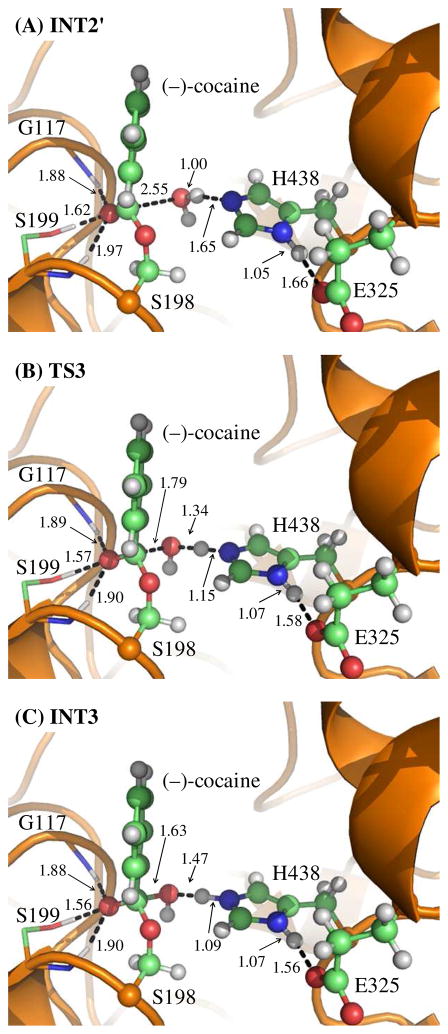
Our QM/MM reaction coordinate calculations at the B3LYP/6-31G*:AMBER level revealed that the (−)-cocaine hydrolysis catalyzed by the cocaine hydrolase (the A199S/F227A/S287G/A328W/Y332G mutant of BChE) can be described in four major reaction steps. The first reaction step is the nucleophilic attack on the carbonyl carbon (Cζ) of (−)-cocaine benzoyl ester by Oγ atom in S198 side chain. The second reaction step is the dissociation between benzoyl ester and ecgonine methyl ester of (−)-cocaine. The third reaction step is the nucleophilic attack on the carbonyl carbon (Cζ) of (−)-cocaine benzoyl ester by a water molecule. The final reaction step is the dissociation between (−)- cocaine benzoyl group and S198 of the enzyme. The QM/MM-optimized geometries of the reactant, intermediates, and transition states are shown in Figures 1 to 4. The values of 10 key internuclear distances reflecting the geometrical changes are also given in Tables 1 and 2 for the acylation and deacylation stages, respectively. Below we discuss each of these reaction steps in detail.
Figure 1.
Key states for the reaction step 1, the nucleophilic attack by Oγ atom of S198 side chain. The geometries were optimized at the QM/MM(B3LYP/6-31G*:AMBER) level. The non-polar hydrogen atoms in oxyanion hole are not shown for clarity. The key distances in the figure are in angstroms. Carbon, oxygen, nitrogen, and hydrogen atoms are colored in green, red, blue, and white, respectively. The backbone of the protein is rendered as a cartoon and colored in orange. The QM atoms are represented as ball and stick, and the surrounding residues rendered as stick. The figures below are represented using the same method.
Figure 4.
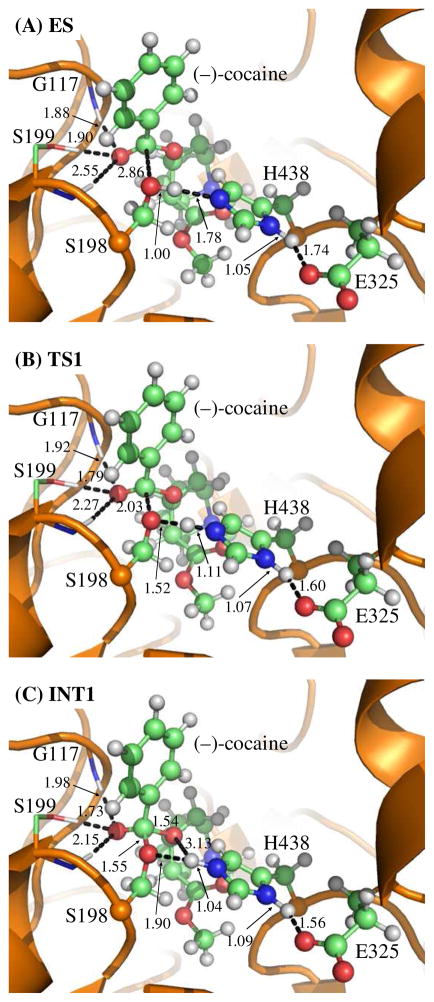
Key states for step 4, the dissociation of (−)-cocaine benzoyl group from S198 of the enzyme. The geometries were optimized at the QM/MM(B3LYP/6-31G*:AMBER) level.
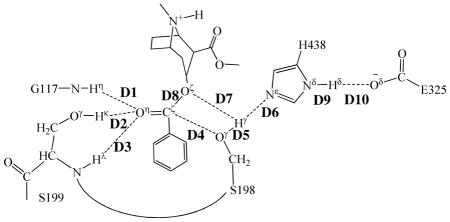
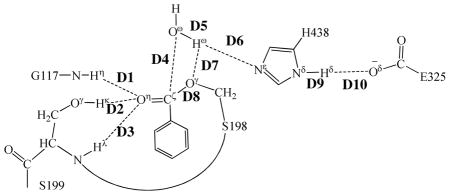
Table 1.
Key internuclear distances (D1 to D10, in angstrom) in the QM/MM-optimized geometries of the key states of the acylation stage.
| |||||||
|---|---|---|---|---|---|---|---|
| ES | TS1 | INT1 | TS2 | INT1′ | TS2′ | INT2 | |
| D1 | 1.88 | 1.92 | 1.98 | 1.97 | 2.00 | 2.02 | 1.99 |
| D2 | 1.90 | 1.79 | 1.73 | 1.72 | 1.70 | 1.68 | 1.69 |
| D3 | 2.55 | 2.27 | 2.15 | 2.03 | 1.98 | 1.97 | 1.98 |
| D4 | 2.86 | 2.03 | 1.55 | 1.39 | 1.37 | 1.35 | 1.33 |
| D5 | 1.00 | 1.52 | 1.90 | 2.24 | 2.23 | 2.37 | 2.94 |
| D6 | 1.78 | 1.11 | 1.04 | 1.02 | 1.02 | 1.18 | 2.73 |
| D7 | 3.69 | 3.09 | 3.13 | 3.31 | 3.31 | 1.33 | 0.97 |
| D8 | 1.36 | 1.42 | 1.54 | 2.09 | 2.30 | 2.39 | 2.64 |
| D9 | 1.05 | 1.07 | 1.09 | 1.08 | 1.08 | 1.07 | 1.05 |
| D10 | 1.74 | 1.60 | 1.56 | 1.59 | 1.59 | 1.67 | 1.71 |
Table 2.
Key internuclear distances (D1 to D10, in angstrom) in the QM/MM-optimized geometries of the key states of the deacylation stage
| |||||
|---|---|---|---|---|---|
| INT2′ | TS3 | INT3 | TS4 | PD | |
| D1 | 1.88 | 1.89 | 1.88 | 1.80 | 1.81 |
| D2 | 1.62 | 1.57 | 1.56 | 1.64 | 1.68 |
| D3 | 1.97 | 1.90 | 1.90 | 1.99 | 2.09 |
| D4 | 2.55 | 1.79 | 1.63 | 1.40 | 1.35 |
| D5 | 1.00 | 1.34 | 1.47 | 2.41 | 2.80 |
| D6 | 1.65 | 1.15 | 1.09 | 1.26 | 1.72 |
| D7 | 2.77 | 2.58 | 2.53 | 1.24 | 1.00 |
| D8 | 1.34 | 1.42 | 1.46 | 1.95 | 2.50 |
| D9 | 1.05 | 1.07 | 1.07 | 1.06 | 1.05 |
| D10 | 1.66 | 1.58 | 1.56 | 1.62 | 1.69 |
Step 1: Nucleophilic attack on the Cζ atom by Oγ atom of S198
The nucleophilic attack process proceeds as the serine hydroxyl oxygen, i.e. Oγ atom of S198, gradually approaches the Cζ atom of (−)-cocaine benzoyl ester. Meanwhile, the serine hydroxyl hydrogen, i.e. Hγ atom of S198, gradually moves towards the nitrogen (Nε) atom of H438 side chain. Since this reaction step involves the breaking of Oγ–Hγ bond and the formation of both Cζ–Oγ and Nε–Hγ bonds as shown in Scheme 1, the distance between Oγ and Hγ (RO γ –Hγ), the distance between Cζ and Oγ (RCζ–Oγ), and the distance between Nε and Hγ (RNε–Hγ) reflect the nature of chemical reaction step 1. Therefore, the reaction coordinate for the current reaction step was set as ROγ–Hγ – RCζ–Oγ – RNε–Hγ. As shown in the QM/MM-optimized geometries (Figure 1), while the Oγ atom of S198 gradually approaches the Cζ atom, the geometry of reactant (ES), in which the Cζ atom is sp2 hybridized and is in a planar geometry with its three bonding atoms, gradually changes into a tetrahedral geometry centering on the sp3 hybridized Cζ atom in an intermediate (INT1) through a transition state (TS1).
Step 2: Dissociation of (−)-cocaine benzoyl ester
In this reaction step, the ecgonine group of (−)-cocaine gradually departs from the (−)-cocaine benzoyl ester group in which the benzoyl ester bond Cζ–Oζ is broken. Meanwhile, the proton (Hγ) attached to Nε atom of H438 side chain transfers to the benzoyl ester oxygen (Oζ) of (−)-cocaine. The changes of the distances of RCζ–Oζ, ROζ–Hγ, and RNε–Hγ reflect the nature of the dissociation process. Thus, the reaction coordinate for reaction step 2 was chosen as RCζ–Oζ + RNε–Hγ – ROζ–Hγ.
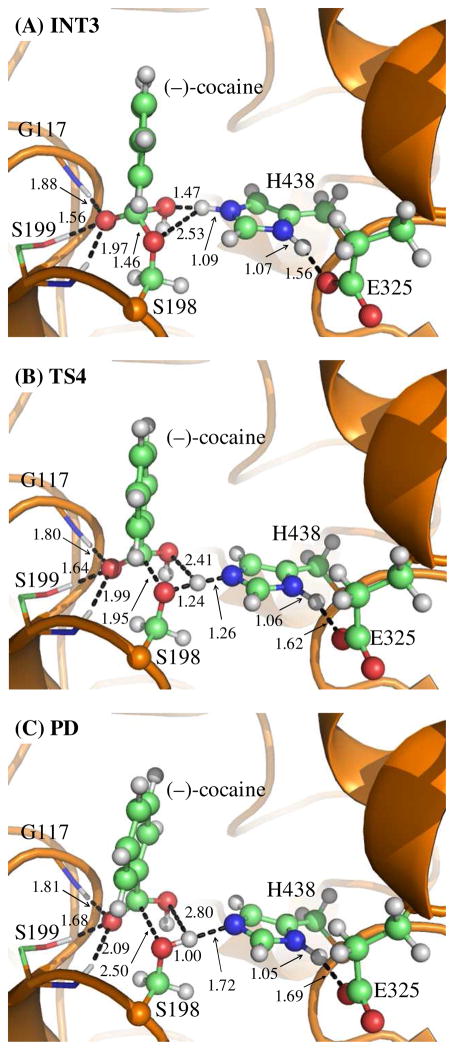
Contrary to what we purposed in Scheme 1 where only one transition state is hypothesized for reaction step 2, two transition states were found in the current reaction step. This observation is similar to that in CocE-catalyzed (−)-cocaine hydrolysis where two transition states were characterized in the dissociation of (−)-cocaine benzoyl ester.51 The two transition states here are denoted by TS2 and TS2′, respectively. The intermediate between the two transition states is labeled as INT1′. The QM/MMoptimized geometries of the intermediates and transition states of current reaction step are given in Figure 2. In the geometry of INT1 (Figure 1C) where the serine hydroxyl proton (Hγ) has been transferred to Nε atom of H438 in the reaction step 1, the distance (ROγ–Hγ) between Oγ atom of S198 and Hγ atom of H438 side chain is 1.90 Å, indicating a strong hydrogen bond of Nε–Hγ···Oγ between S198 hydroxyl oxygen and H438 side chain. However, the distance (ROζ–Hγ) between Hγ and the leaving ester oxygen (Oζ) to which Hγ is about to be transferred is 3.13 Å, indicating a very weak interaction between Hγ and Oζ atoms and an unfavorable environment for proton transfer from Nε atom of H438 to the leaving ester oxygen (Oζ) atom. In the sub-step of changing from INT1 to INT1′, the major structural change is the gradual breaking of the covalent bond Cζ–Oζ (RCζ–Oζ is 1.54 Å in INT1, 2.09 Å in TS2, and 2.30 Å in INT1′). During this process, ROζ–Hγ does not decrease, but slightly increase from 3.13 Å in INT1 to 3.31 Å in TS2 and remains this distance until reaching INT1′. The changes of ROζ–Hγ indicate that H438, one of the catalytic-triad residues, does not facilitate the breaking of covalent bond Cζ–Oζ in the sub-step of changing from INT1 to INT1′. However, in the sub-step of changing from INT1′ to INT2, the Hγ atom is gradually transferred to the leaving ester oxygen (Oζ) from the H438 side chain as the covalent bond Cζ–Oζ is continuously breaking (RCζ–Oζ is 2.30 Å in INT1′, 2.39 Å in TS2′, and 2.64 Å in INT2), suggesting that H438 begins to facilitate the breaking of covalent bond Cζ–Oζ in the sub-step of changing from INT1′ to INT2. Clearly, the proton transfer in the reaction step 2 proceeds not simultaneously with, but almost after, the breaking of Cζ–Oζ covalent bond, and H438 facilitates this covalent bond breaking only in the sub-step associated with TS2′.
Figure 2.
Key states except INT1 for reaction step 2, the dissociation of (−)-cocaine benzoyl ester. The geometries were optimized at the QM/MM(B3LYP/6-31G*:AMBER) level. The structure of INT1 is given in Figure 1C.
Step 3: Nucleophilic attack on Cζ atom by a water molecule
The ecgonine methyl ester was removed from the above-discussed QM/MM-optimized geometry of INT2 to construct the initial structure of INT2′ for the reaction coordinate calculations on the deacylation stage. The current nucleophilic process proceeds in a similar way as in the reaction step 1, which involves the breaking of Oω–Hω bond and the formation of both Cζ–Oω and Nε–Hω bonds. Thus the distances ROω–Hω, RCζ–Oω, and RNε–Hω were chosen to establish the reaction coordinate as ROω–Hω – RCζ–Oω – RNε–Hω for the current reaction step. In proceeding from INT2′ to INT3 through the transition state TS3 (Figure 3), the nucleophilic water gradually approaches Cζ atom with a spontaneous proton (Hω) transfer from Oω atom of the nucleophilic water to Nε atom of H438 side chain. The QM/MMoptimized geometry of INT3 shows that the nucleophilic attack process is completed with a water molecule dissociating into hydroxide ion attaching to Cζ atom and a proton (Hω) attaching to Nε atom.
Figure 3.
Key states for reaction step 3, the nucleophilic attack on the benzoyl carbonyl carbon atom by a water molecule. The geometries were optimized at the QM/MM(B3LYP/6-31G*:AMBER) level.
Step 4: Dissociation between (−)-cocaine benzoyl group and S198
The proton transfer between Nε atom of H438 side chain and Oγ atom of S198 side chain and the breaking of covalent bond Cζ–Oγ are involved in the dissociation of benzoyl-enzyme. The changes of the distances RCζ–Oγ, ROγ–Hω, and RNε–Hω reflect the nature of reaction step 4. Thus, the reaction coordinate for current reaction step was expressed as RCζ–Oγ + RNε–Hω – ROγ–Hω. Reaction step 4 is similar to reaction step 2, the dissociation of benzoyl ester. In both reaction steps, one type of C–O covalent bond is broken and one proton is transferred from Nε atom of H438 to the oxygen atom of broken C–O covalent bond. There are differences between the reaction steps 2 and 4. One difference is that the proton transfer in current reaction step proceeds spontaneously as C–O bond is gradually broken while that in reaction step 2 does not proceed spontaneously. As shown in Figure 4, while Cζ–Oγ covalent bond gradually breaks, the distance between Oγ atom and Hω atom becomes closer and closer, illustrating a spontaneous proton transfer from Nε atom of H438 side chain to Oγ atom of S198. The other difference is that, since the proton is spontaneously transferred while Cζ–Oγ covalent bond gradually breaks, the H438 facilitates the breaking of Cζ–Oγ covalent bond throughout the current reaction step, whereas in reaction step 2 the H438 facilitates the breaking of Cζ–Oζ covalent bond only in the sub-step associated with TS2′.
Energetics
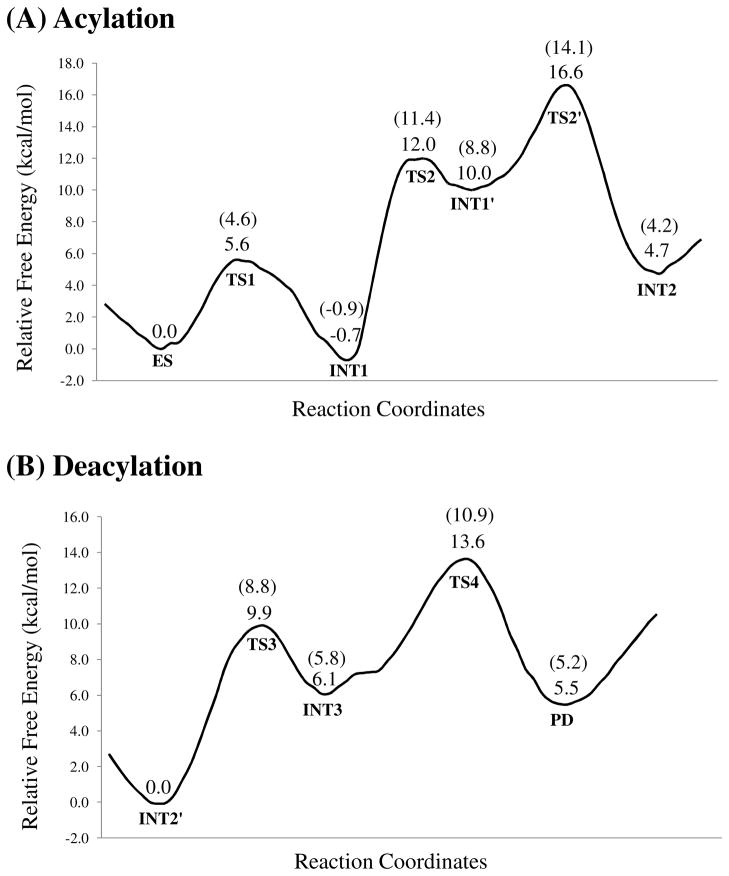
Using the QM/MM-optimized geometries at the QM/MM(B3LYP/6-31G*:AMBER) level, we carried out QM/MM single-point energy calculations at the QM/MM(MP2/6-31+G*:AMBER) level for each geometry along the minimum-energy path for both acylation and deacylation stages. For each geometry along the minimum-energy path, the ESP charges determined in the QM part of the QM/MM single-point energy calculation were used in subsequent FEP simulations for estimating the free energy changes along the reaction path. Depicted in Figure 5 is the energy profile determined by the QM/MM-FE calculations excluding the zero-point and thermal corrections for the QM subsystem. The values given in the parentheses are the corresponding relative free energies with the zero-point and thermal corrections for the QM subsystem. The relative free energy was taken as the average of the “forward” and “backward” perturbation results in which the difference between the “forward” and “backward” perturbation results was 0.9 kcal/mol (suggesting an error of ±0.5 kcal/mol) for the calculated overall free energy barrier of the acylation stage and 0.2 kcal/mol (suggesting an error of ±0.1 kcal/mol) for the calculated overall free energy barrier of the deacylation stage. The differences between the “forward” and the “backward” perturbations are reasonably small, suggesting that the FEP calculations converged well in terms of the number of the FEP windows used.
Figure 5.
Free energy profile determined by performing the QM/MM-FE calculations at the MP2/6-31+G*:AMBER level excluding the zero-point and thermal corrections for the QM subsystem. The values in parenthesis are relative free energies including zero-point and thermal corrections for the QM subsystem.
As clearly shown in Figure 5A, there are three transition states in the acylation stage. Technically, there are a total of five reaction steps for the entire hydrolysis reaction, instead of the four reaction steps hypothesized in Scheme 1. Nevertheless, in order to clearly describe the hydrolysis mechanism, we still keep the notation used in Scheme 1. This means that the reaction step 2, which is the dissociation of (−)-cocaine benzoyl ester, consists of two sub-steps associated with TS2 and TS2′. The free energy barriers with zero-point and thermal corrections for the QM subsystem of the two sub-steps associated with the TS2 and TS2′ are ~12.3 and ~5.3 kcal/mol, respectively. The free energy of TS2′ is higher than that of TS2. Therefore, the overall free energy barrier of the entire reaction step 2, i.e. the free energy change from the INT1 to TS2′, is ~15.0 kcal/mol which is higher than the corresponding energy barrier for reaction step 1 (~4.5 kcal/mol). As a result, the reaction step 2 is rate-determining for the acylation stage. In deacylation stage, the free energy barriers with zero-point and thermal corrections for the QM subsystem of reaction steps 3 and 4 are ~8.8 and ~5.1 kcal/mol, respectively. The free energy of TS4 is higher than that of TS3 and, therefore, the free energy change (~10.9 kcal/mol) from INT2′ to TS4 is the overall free energy barrier for the deacylation stage. Obviously, the reaction step 2 in the acylation stage, where the free energy barrier is ~15.0 kcal/mol, is rate-determining for the whole (−)-cocaine hydrolysis catalyzed by the A199S/F227A/S287G/A328W/Y332G mutant of human BChE. The calculated free energy barrier of ~15.0 kcal/mol is in excellent agreement with the activation free energy of 14.7 kcal/mol derived from the experimental rate constant (kcat = 5700 min−1)13 by using the conventional transition state theory (CTST).12,57–58 Based on the mechnaistic insights, future computational design aiming at further improving the catalytic activity of the cocaine hydrolase against (−)-cocaine should focus on the stabilization of the transition state (TS2′) for the second reaction step.
The Role of catalytic triad and oxyanion hole
According to the mechanism described by the pseudobond first-principles QM/MM-FE calculations, the catalytic triad and oxyanion hole are the most essential factors in the (−)- cocaine hydrolysis. The first residue in catalytic triad, S198, acts as a nucleophile in reaction step 1 and then forms a covalent bond with carbonyl carbon (Cζ) atom of (−)- cocaine benzoyl ester until the end of hydrolysis reaction. The second residue in catalytic triad, H438, serves as a general base accepting the proton from nucleophile to facilitate the two nucleophilic attack processes, i.e. reaction steps 1 and 3. The proton is then transferred to the leaving group by H438 in the two dissociation processes, i.e. reaction steps 2 and 4. H438 facilitates either the formation or breaking of the C–O covalent bond in each reaction step. As seen from Figures 2 to 5, H438 is in turn stabilized by E325 via a strong hydrogen bond of Nδ–Hδ···Oδ between their side chains throughout the entire hydrolysis process. Note that in the reaction step 2, which is rate-determining, H438 does not facilitate the breaking of Cζ–Oζ covalent bond in the very beginning, but starts to stabilize the negatively charged Oζ atom only in the sub-step associated with TS2′. An effort aiming at releasing the facilitation function of H438 at the very beginning of the breaking of Cζ–Oζ covalent bond is thus very promising in stabilizing TS2′ and decreasing the rate-determining energy barrier.
The oxyanion hole consists of the backbone amides of S199 and G117 and the hydroxyl group of S199. Based on the QM/MM reaction coordinate calculations, the carbonyl oxygen (Oη) of (−)-cocaine forms three hydrogen bonds with the oxyanion hole throughout the hydrolysis reaction. One is the hydrogen bond of N–Hη···Oη with the backbone NH group (Hη) of G117; the second is the hydrogen bond of Oγ–Hκ···Oη with hydroxyl hydrogen (Hκ) of S199 side chain; the third is the hydrogen bond of N–Hλ···Oη with the backbone NH group (Hλ) of S199. As shown in Figure 1A, there are two strong (N–Hη···Oη and Oγ–Hκ···Oη) and one weak (N–Hλ···Oη) hydrogen bonds in the structure of ES. The N–Hλ···Oη is weak in ES with the Hλ···Oη distance of ~2.6 Å and then becomes strong with the Hλ···Oη distance of ~2.0 Å in the subsequent states of the hydrolysis reaction. The other two hydrogen bonds N–Hη···Oη and Oγ–Hκ···Oη are steadily strong throughout the hydrolysis reaction, with the Hη···Oη and Hκ···Oη distances being ~1.9 Å and ~1.6 Å, respectively. Therefore, all these three hydrogen bonds stabilize the negative charge of carbonyl oxygen (Oη) developing during the hydrolysis reaction.
Methods
Structure Preparation
The starting model of the system was based on our previously reported molecular dynamics (MD) simulation performed on the first transition state (TS1) for the A199S/F227A/S287G/A328W/Y332G mutant of BChE with (−)-cocaine.13 In the MD simulation, the system was solvated in a rectangular box of TIP3P water molecules with a minimum solute-wall distance of 10 Å. It was gradually heated from T = 10 K to T = 298.15 K in 30 ps before running the MD simulation at T = 298.15 K for ~2 ns. The time step used for the MD simulation was 2 fs. The SHAKE algorithm was used to fix all covalent bonds containing hydrogen atoms. The particle mesh Ewald (PME) method was used to treat long-range electrostatic interactions. In the present study, a snapshot close to the average structure from the MD simulation was used to prepare the initial structure for the QM/MM calculations. Since the ecgonine group of (−)-cocaine leaves the system after the acylation stage, the structure of INT2′ was constructed by removing the ecgonine group of (−)-cocaine out of the QM/MM-optimized INT2 structure. The constructed INT2′ was also solvated in a rectangular box of TIP3P water molecules with a minimum solute-wall distance of 10 Å, and was then equilibrated by performing a ~ 2 ns MD simulation with the same procedure mentioned above. A snapshot close to the average structure from this MD simulation was selected to prepare the initial structure of INT2′ for the QM/MM reaction-coordinate calculations. Since we are interested in the reaction center, the water molecules beyond 50 Å of the carbonyl carbon (Cζ) of (−)-cocaine benzoyl ester were removed in the preparation of initial reaction systems. Prior to the QM/MM geometry optimizations, the initial reaction systems were energy-minimized with the MM method by using the revised AMBER8 program,51 where the convergence criterion is the root-mean-square deviation (RMSD) of the energy gradient being smaller than 0.1 kcal·mol−1·Å−1.
QM/MM-FE Simulation
All of the QM/MM calculations were performed by using the pseudobond QM/MM method35–36 implemented recently in a revised version13 of Gaussian0359 and AMBER860 programs. The QM/MM interface was treated by the pseudobond approach, where a seven-valence-electron atom with an effective core potential is constructed to replace the boundary atom of the environment part and to form a pseudobond with the boundary atom of the active part. In QM/MM calculations, all atoms of (−)-cocaine and the side chains of S198, H438, and E325 were considered as the QM atoms, whereas the other atoms were regarded as MM atoms (Figure 6). The QM/MM calculations were performed with an iterative minimization procedure37 at the B3LYP/6-31G*:AMBER level, i.e. the QM calculations were carried out at the B3LYP/6-31G* level, whereas the MM calculations were carried out by using the AMBER force field implemented in the AMBER8 program.60 For QM subsystem, the convergence criterion for geometry optimizations follows the original Gaussian0359 defaults; for MM subsystem, the geometry optimization convergence criterion is the RMSD of the energy gradient less than 0.1 kcal·mol−1·Å−1. An iterative restrained optimization procedure37 was then repeatedly applied to different points along the reaction coordinate, resulting in a minimum-energy path. Full QM/MM geometry-optimizations at the B3LYP/6-31G*:AMBER level followed by vibrational frequency analyses were performed to characterize the reactant, intermediates, and transition states. The contribution of the QM subsystem fluctuation to the free energy change was then calculated with obtained frequencies using the harmonic approximation. In addition, single-point energy calculations were carried out at the QM/MM(MP2/6-31+G*:AMBER) level for each geometry along the minimum-energy path.
Figure 6.
Division of the QM/MM systems for simulating the (−)-cocaine hydrolysis catalyzed by the A199S/F227A/S287G/A328W/Y332G mutant of BChE. Atoms in blue are treated by QM method. Three boundary carbon atoms (Cα or Cβ, colored in red) are treated with the improved pseudobond parameters.35 All other atoms belong to the MM subsystem.
The free energy changes associated with the QM-MM interaction were then determined by the free energy perturbation (FEP) method37,61 using a revised version51 of the AMBER8 program. The FEP calculations enabled us to more reasonably determine the relative free energy changes due to the QM-MM interaction. In FEP calculations, sampling of the MM subsystem was carried out with the QM subsystem frozen at different states along the reaction path.37 Technically, the final (relative) free energy determined by the QM/MM-FE calculations is the QM part of the QM/MM energy (excluding the Columbic interaction energy between the point charges of the MM atoms and the ESP charges of the QM atoms) plus the relative free energy change determined by the FEP calculations. In FEP calculations, the time step used was 2 fs, and bond lengths involving hydrogen atoms were constrained. In sampling of MM subsystem by MD simulations, the temperature was maintained at 298.15 K. Each window of the FEP calculation consisted of 50 ps of equilibration and 300 ps of sampling. The choice of the 300 ps sampling for each window was based on the observation that there was no noticeable difference between the FEP results obtained from the 300 ps sampling and those from the 500 ps sampling for the rate-determining step of the enzymatic reaction process. Both the forward and backward reaction directions were subjected to the FEP calculations. The final relative free energies were taken as the average of the “forward” and “backward” perturbation results.
The MD simulations and QM/MM-FE calculations were performed on a supercomputer (e.g. IBM X-series Cluster with 340 nodes or 1,360 processors) at University of Kentucky Center for Computational Sciences. The other less-time-consuming modeling and computations were carried out on SGI Fuel workstations and a 34-processor IBM x335 Linux cluster in our own lab.
Conclusion
The (−)-cocaine hydrolysis catalyzed by the cocaine hydrolase (i.e. the A199S/F227A/S287G/A328W/Y332G mutant of human BChE) has been studied by using first-principles QM/MM-FE approach. The detailed reaction pathway has been elucidated. First, a nucleophilic attack on carbonyl carbon (Cζ) of (−)-cocaine benzoyl ester is carried out by hydroxyl oxygen (Oγ) of S198. This process is facilitated by H438 through proton (Hγ) transfer from S198 hydroxyl to Nε atom of H438 side chain, which increases the nucleophilicity of the S198 hydroxyl. H438 is in turn stabilized by another hydrogen bond with E325. The S198 nucleophile attacks the electron-deficient Cζ atom forming a tetrahedral intermediate, in which the carbonyl oxygen (Oη) of (−)-cocaine with developing negative charge is stabilized through three hydrogen bonds formed with the oxyanion hole. Then H438 transfers the proton (Hγ) to the ester oxygen (Oζ) of leaving ecgonine group, completing the acylation stage. Starting from the acylated enzyme, a water molecule which is activated by H438 initiates the deacylation stage. The reaction steps similar to those in the acylation stage are repeated in the deacylation stage in terms of the covalent bond formation and breaking, and the benzoic acid is released while the original enzyme form is restored to its free state. The second reaction step of the entire reaction process, where the benzoyl ester dissociates, is found to be rate-determining. The calculated free energy barrier is ~15.0 kcal/mol and is in excellent agreement with the experimentally derived activation free energy of ~14.7 kcal/mol.
The QM/MM-optimized geometries indicate that oxyanion hole stabilizes the negative charge of the carbonyl oxygen developing during the hydrolysis reaction by providing three hydrogen bonds from backbone amides of S199 and G117 and the hydroxyl group of S199. The hydrogen bond with hydroxyl group of S199 is further confirmed to have important contribution in stabilizing the transition state for the rate-determining step.
The elucidated reaction mechanism provides details of the hydrolysis reaction, especially the rate-determining step and the nature of the transition states. In light of new mechanistic insights obtained in the present investigation, future efforts aiming at further increasing catalytic activity of the cocaine hydrolase against (−)-cocaine should focus on the reaction step 2, i.e. the dissociation of the benzoyl ester. Note that H438 does not facilitate the breaking of Cζ–Oζ covalent bond in the very beginning of the reaction step 2. An effort of releasing the facilitation function of H438 on the breaking of Cζ–Oζ covalent bond immediately when Cζ–Oζ covalent bond starts to break is thus very likely to further improve the catalytic activity of the cocaine hydrolase against (−)-cocaine. Thus, the new mechanistic insights obtained from the present computational study will be value for future rational design of more efficient cocaine hydrolase to be used in the treatment of cocaine overdose and abuse.
Acknowledgments
This work was supported in part by NIH (grants R01 DA013930 and R01 DA025100). Liu worked in Zhan’s laboratory for this project as a visiting scientist under the NIH funding support. The entire research was performed at the University of Kentucky. The authors acknowledge the Center for Computational Sciences (CCS) at University of Kentucky for supercomputing time on IBM X-series Cluster with 340 nodes or 1,360 processors.
References
- 1.Mendelson JH, Mello NK. N Engl J Med. 1996;334:965–972. doi: 10.1056/NEJM199604113341507. [DOI] [PubMed] [Google Scholar]
- 2.Paula S, Tabet MR, Farr CD, Norman AB, Ball WJ. J Med Chem. 2003;47:133–142. doi: 10.1021/jm030351z. [DOI] [PubMed] [Google Scholar]
- 3.Singh S. Chem Rev. 2000;100:925–1024. doi: 10.1021/cr9700538. [DOI] [PubMed] [Google Scholar]
- 4.Huang X, Zheng F, Zhan CG. J Phys Chem B. 2011;115:11254–11260. doi: 10.1021/jp2047807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Meijler MM, Kaufmann GF, Qi L, Mee JM, Coyle AR, Moss JA, Wirsching P, Matsushita M, Janda KD. J Am Chem Soc. 2005;127:2477–2484. doi: 10.1021/ja043935e. [DOI] [PubMed] [Google Scholar]
- 6.Sparenborg S, Vocci F, Zukin S. Drug Alcohol Depend. 1997;48:149–51. doi: 10.1016/s0376-8716(97)00072-0. [DOI] [PubMed] [Google Scholar]
- 7.Gorelick DA. Drug Alcohol Depend. 1997;48:159–65. doi: 10.1016/s0376-8716(97)00119-1. [DOI] [PubMed] [Google Scholar]
- 8.Gorelick DA, Gardner EL, Xi ZX. Drugs. 2004;64:1547–73. doi: 10.2165/00003495-200464140-00004. [DOI] [PubMed] [Google Scholar]
- 9.Dickerson TJ, Janda KD. Recent Advances for the Treatment of Cocaine Abuse: Central Nervous System Immunopharmacotherapy. Drug Addiction. 2008:217–229. doi: 10.1208/aapsj070359. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- 10.Gao D, Cho H, Yang W, Pan Y, Yang G, Tai HH, Zhan CG. Angew Chem Int Ed. 2006;45:653–657. doi: 10.1002/anie.200503025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Vocci FJ, Acri J, Elkashef A. Am J Psychiat. 2005;162:1432–1440. doi: 10.1176/appi.ajp.162.8.1432. [DOI] [PubMed] [Google Scholar]
- 12.Pan Y, Gao D, Yang W, Cho H, Yang G, Tai HH, Zhan CG. Proc Nat Acad Sci USA. 2005;102:16656–16661. doi: 10.1073/pnas.0507332102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Zheng F, Yang W, Ko MC, Liu J, Cho H, Gao D, Tong M, Tai HH, Woods JH, Zhan CG. J Am Chem Soc. 2008;130:12148–12155. doi: 10.1021/ja803646t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Landry DW, Zhao K, Yang GX, Glickman M, Georgiadis TM. Science. 1993;259:1899–1901. doi: 10.1126/science.8456315. [DOI] [PubMed] [Google Scholar]
- 15.Mets B, Winger G, Cabrera C, Seo S, Jamdar S, Yang G, Zhao K, Briscoe RJ, Almonte R, Woods JH, Landry DW. Proc Nat Acad Sci USA. 1998;95:10176–10181. doi: 10.1073/pnas.95.17.10176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zhan CG, Zheng F, Landry DW. J Am Chem Soc. 2003;125:2462–74. doi: 10.1021/ja020850+. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Rogers CJ, Mee JM, Kaufmann GF, Dickerson TJ, Janda KD. J Am Chem Soc. 2005;127:10016–10017. doi: 10.1021/ja053086a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Pan YM, Gao DQ, Yang WC, Cho H, Zhan CG. J Am Chem Soc. 2007;129:13537–13543. doi: 10.1021/ja073724k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Sun H, Pang YP, Lockridge O, Brimijoin S. Mol Pharmacol. 2002;62:220–224. doi: 10.1124/mol.62.2.220. [DOI] [PubMed] [Google Scholar]
- 20.Zhan CG, Gao DQ. Biophys J. 2005;89:3863–3872. doi: 10.1529/biophysj.105.070276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Huang X, Pan Y, Zheng F, Zhan CG. J Phys Chem B. 2010;114:13545–13554. doi: 10.1021/jp106539w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hamza A, Cho H, Tai HH, Zhan CG. J Phys Chem B. 2005;109:4776–4782. doi: 10.1021/jp0447136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Sun H, El Yazal J, Lockridge O, Schopfer LM, Brimijoin S, Pang YP. J Biol Chem. 2001;276:9330–9336. doi: 10.1074/jbc.M006676200. [DOI] [PubMed] [Google Scholar]
- 24.Huang X, Gao D, Zhan CG. Org Biomol Chem. 2011;9:4138–4143. doi: 10.1039/c0ob00972e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Yang W, Pan Y, Zheng F, Cho H, Tai HH, Zhan CG. Biophys J. 2009;96:1931–1938. doi: 10.1016/j.bpj.2008.11.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Yang WC, Xue L, Fang L, Chen X, Zhan CG. Chem Biol Interact. 2010;187:148–152. doi: 10.1016/j.cbi.2010.01.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Zheng F, Yang WC, Xue L, Hou SR, Liu JJ, Zhan CG. Biochemistry. 2010;49:9113–9119. doi: 10.1021/bi1011628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Gao Y, Orson FM, Kinsey B, Kosten T, Brimijoin S. Chem Biol Interact. 2010;187:421–424. doi: 10.1016/j.cbi.2010.02.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Adrian JM. Drug Discovery Today. 2005;10:1393–1402. doi: 10.1016/S1359-6446(05)03611-1. [DOI] [PubMed] [Google Scholar]
- 30.Cavalli A, Carloni P, Recanatini M. Chem Rev. 2006;106:3497–3519. doi: 10.1021/cr050579p. [DOI] [PubMed] [Google Scholar]
- 31.Menikarachchi LC, Gascon JA. Curr Top Med Chem. 2010;10:46–54. doi: 10.2174/156802610790232297. [DOI] [PubMed] [Google Scholar]
- 32.Raha K, Peters MB, Wang B, Yu N, WollaCott AM, Westerhoff LM, Merz KM. Drug Discovery Today. 2007;12:725–731. doi: 10.1016/j.drudis.2007.07.006. [DOI] [PubMed] [Google Scholar]
- 33.Zhou T, Huang DZ, Caflisch A. Curr Top Med Chem. 2010;10:33–45. doi: 10.2174/156802610790232242. [DOI] [PubMed] [Google Scholar]
- 34.De Vivo M. Front Biosci. 2011;16:1619–1633. doi: 10.2741/3809. [DOI] [PubMed] [Google Scholar]
- 35.Zhang YK. J Chem Phys. 2005;122:024114. doi: 10.1063/1.1834899. [DOI] [PubMed] [Google Scholar]
- 36.Zhang YK, Lee TS, Yang WT. J Chem Phys. 1999;110:46–54. [Google Scholar]
- 37.Zhang YK, Liu HY, Yang WT. J Chem Phys. 2000;112:3483–3492. [Google Scholar]
- 38.Zhang YK. Theor Chem Acc. 2006;116:43–50. [Google Scholar]
- 39.Hu P, Zhang YK. J Am Chem Soc. 2006;128:1272–1278. doi: 10.1021/ja056153+. [DOI] [PubMed] [Google Scholar]
- 40.Liu H, Zhang Y, Yang W. J Am Chem Soc. 2000;122:6560–6570. [Google Scholar]
- 41.Zhang Y, Kua J, McCammon JA. J Am Chem Soc. 2002;124:10572–10577. doi: 10.1021/ja020243m. [DOI] [PubMed] [Google Scholar]
- 42.Cisneros GA, Liu H, Zhang Y, Yang W. J Am Chem Soc. 2003;125:10384–10393. doi: 10.1021/ja029672a. [DOI] [PubMed] [Google Scholar]
- 43.Zhang Y, Kua J, McCammon JA. J Phys Chem B. 2003;107:4459–4463. [Google Scholar]
- 44.Cheng Y, Zhang Y, McCammon JA. J Am Chem Soc. 2005;127:1553–1562. doi: 10.1021/ja0464084. [DOI] [PubMed] [Google Scholar]
- 45.Corminboeuf C, Hu P, Tuckerman ME, Zhang Y. J Am Chem Soc. 2006;128:4530–4531. doi: 10.1021/ja0600882. [DOI] [PubMed] [Google Scholar]
- 46.Wang L, Yu X, Hu P, Broyde S, Zhang Y. J Am Chem Soc. 2007;129:4731–4737. doi: 10.1021/ja068821c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Wang S, Hu P, Zhang Y. J Phys Chem B. 2007;111:3758–3764. doi: 10.1021/jp067147i. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Xiao C, Zhang Y. J Phys Chem B. 2007;111:6229–6235. doi: 10.1021/jp068657f. [DOI] [PubMed] [Google Scholar]
- 49.Hu P, Wang S, Zhang Y. J Am Chem Soc. 2008;130:3806–3813. doi: 10.1021/ja075896n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Cheng Y, Zhang Y, McCammon JA. Protein Sci. 2006;15:672–683. doi: 10.1110/ps.051852306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Liu J, Hamza A, Zhan CG. J Am Chem Soc. 2009;131:11964–75. doi: 10.1021/ja903990p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Gao DQ, Zhan CG. J Phys Chem B. 2005;109:23070–23076. doi: 10.1021/jp053736x. [DOI] [PubMed] [Google Scholar]
- 53.Zheng F, Zhan CG. Org Biomol Chem. 2008;6:836–843. doi: 10.1039/b716268e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Gao DQ, Zhan CG. Proteins. 2006;62:99–110. doi: 10.1002/prot.20713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Zheng F, Zhan CG. J Comput Aid Mol Des. 2008;22:661–671. doi: 10.1007/s10822-007-9144-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Zhan CG. Expert Rev Clin Pharmacol. 2009;2:1–4. doi: 10.1586/17512433.2.1.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Truhlar DG, Garrett BC. Annu Rev Phys Chem. 1984;35:159–189. [Google Scholar]
- 58.Alvarez-Idaboy JR, Galano A, Bravo-Perez G, Ruiz ME. J Am Chem Soc. 2001;123:8387–8395. doi: 10.1021/ja010693z. [DOI] [PubMed] [Google Scholar]
- 59.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Montgomery JJA, Vreven T, Kudin KN, Burant JC, Millam JM, Iyengar SS, Tomasi J, Barone V, Mennucci B, Cossi M, Scalmani G, Rega N, Petersson GA, Nakatsuji H, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Klene M, Li X, Knox JE, Hratchian HP, Cross JB, Bakken V, Adamo C, Jaramillo J, Gomperts R, Stratmann RE, Yazyev O, Austin AJ, Cammi R, Pomelli C, Ochterski JW, Ayala PY, Morokuma K, Voth GA, Salvador P, Dannenberg JJ, Zakrzewski VG, Dapprich S, Daniels AD, Strain MC, Farkas O, Malick DK, Rabuck AD, Raghavachari K, Foresman JB, Ortiz JV, Cui Q, Baboul AG, Clifford S, Cioslowski J, Stefanov BB, Liu G, Liashenko A, Piskorz P, Komaromi I, Martin RL, Fox DJ, Keith T, Al-Laham MA, Peng CY, Nanayakkara A, Challacombe M, Gill PMW, Johnson B, Chen W, Wong MW, Gonzalez C, Pople JA. Gaussian 03, Revision C.02. Gaussian, Inc; Wallingford CT: 2004. [Google Scholar]
- 60.Case DA, Darden TA, Cheatham TEI, Simmerling CL, Wang J, Duke RE, Luo R, Merz KM, Wang B, Pearlman DA, Crowley M, Brozell S, Tsui V, Gohlke H, Mongan J, Hornak V, Cui G, Beroza P, Schafmeister C, Caldwell JW, Ross WS, Kollman PA. AMBER 8. University of California; San Francisco: 2004. [Google Scholar]
- 61.Zhang Y, Liu H, Yang W. Ab initio qm/mm and free energy calculationsof enzyme reactions. In: Schlick T, Gan HH, editors. Computational Methods for Macromolecular Modeling-Challenges and Applications. Springer-Verlag; New York: 2002. pp. 332–354. [Google Scholar]