Processing and analysis of cardiac optical mapping data obtained with potentiometric dyes

Abstract

Optical mapping has become an increasingly important tool to study cardiac electrophysiology in the past 20 years. Multiple methods are used to process and analyze cardiac optical mapping data, and no consensus currently exists regarding the optimum methods. The specific methods chosen to process optical mapping data are important because inappropriate data processing can affect the content of the data and thus alter the conclusions of the studies. Details of the different steps in processing optical imaging data, including image segmentation, spatial filtering, temporal filtering, and baseline drift removal, are provided in this review. We also provide descriptions of the common analyses performed on data obtained from cardiac optical imaging, including activation mapping, action potential duration mapping, repolarization mapping, conduction velocity measurements, and optical action potential upstroke analysis. Optical mapping is often used to study complex arrhythmias, and we also discuss dominant frequency analysis and phase mapping techniques used for the analysis of cardiac fibrillation.

this review article is part of a collection on Electrophysiology and Excitation-Contraction Coupling. Other articles appearing in this collection, as well as a full archive of all Review collections, can be found online at http://ajpheart.physiology.org/.

Introduction

Optical imaging with voltage-sensitive dyes has become a fundamental tool for electrophysiological mapping of the heart (10, 11, 40). With its high spatiotemporal resolution, cardiac optical mapping has helped to enhance our understanding of complex arrhythmias (16), as well as our knowledge of electrophysiological remodeling in disease states (14, 25). Optical mapping studies have also been useful in the development and evaluation of therapeutic strategies for the treatment of cardiovascular disease (2).

The principles and techniques of cardiac optical mapping have been extensively reviewed (11, 17, 23). However, despite the recent proliferation of optical mapping laboratories and the increasing use of this technique, there is a deficiency in the literature about the standard methods for processing and analyzing cardiac optical mapping data. This is surprising since the methods chosen to process these data can affect and alter the content of the data (32) and ultimately the conclusions of the studies.

Here, following a brief overview of cardiac optical mapping, we will systematically review and describe the methods used to process optical mapping data. This review will focus exclusively on transmembrane voltage data. Analysis of multiparametric optical imaging data, combining voltage mapping with calcium or metabolic imaging, are outside the scope of this current review. We will describe important steps in data processing such as image segmentation, spatial and temporal filtering, and drift removal. Furthermore, we will highlight how inappropriate data processing can distort optical signals leading to misinterpretation of its physiological significance. Finally, this review will discuss the methods used to create standard electrophysiology maps [activation, action potential duration (APD), and conduction velocity (CV)] and to analyze complex arrhythmias. These methods will be illustrated using our freely available MATLAB-based analysis software (efimov.wustl.edu).

Principles of Cardiac Optical Mapping

Fluorescence recordings of potentiometric dyes was first demonstrated by Salzberg et al. (41) on neurons in 1973 and by Salama and Morad (40) in cardiac tissue in 1976. Optical mapping studies are based on the principle that voltage-sensitive dyes alter their emission spectra in response to changes in transmembrane voltage (8). As a result, when appropriately filtered, changes in the quantity of emitted fluorescent light are proportional to changes in transmembrane voltage, thus allowing for a noninvasive assessment of transmembrane voltage changes. Currently, 4-(2-(6-(dibutylamino)-2-naphthalenyl)ethenyl)-1-(3-sulfopropyl)-pyridinium (di-4-ANEPPS), developed by the Loew laboratory (13), is the most widely used potentiometric dye because of its rapid response time and low cytotoxicity.

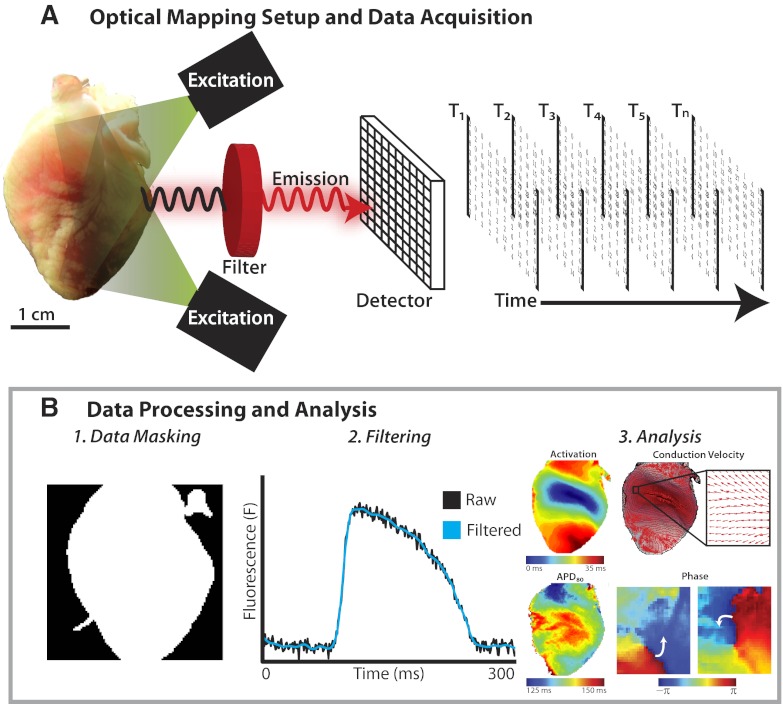
During a typical optical mapping experiment, the heart is perfused ex vivo and stained with a voltage-sensitive dye, which binds to the outer layer of cell bilayer membranes of cardiomyocytes. As shown in Fig. 1A, left, the dye is then excited by a light source with the appropriate excitation wavelength, which corresponds to the dye's absorption spectrum. When the dye returns to its ground state from its excited state, it emits photons of a wavelength longer than that of the excitation light. The system of optics then filters the emitted photons and focuses the light onto a photodetector, which quantifies the amount of emitted fluorescent light for each of its multiple pixels. Data are then acquired at a set sampling frequency, in the form of a series of matrixes of fluorescence intensity, as shown in Fig. 1A, right. For the remainder of this article, we will focus on how these raw data are appropriately processed and analyzed. For more information on the principles of optical mapping and the experimental set-ups, the reader is directed to multiple excellent and comprehensive reviews on the subject available in the literature (11, 12, 17).

Fig. 1.

Overview of cardiac optical mapping. A: experimental setup and data acquisition. The heart stained with a voltage-sensitive dye emits fluorescent light when excited by the excitation light. The emitted fluorescent light is filtered and detected, and the data stored as a series of matrixes of fluorescent intensity at different time points. B: data processing and analysis. Following acquisition, the raw data undergo processing, including data masking (1), digital filtering (2), and drift removal. The processed optical signals are then used for electrophysiological analyses (3).

Signal Processing of Optical Signals

Despite advances in camera systems and voltage-sensitive dyes, recording optical action potentials (OAPs) with high signal-to-noise ratios (SNRs) remain a challenge because of the low fractional change of fluorescence of voltage-sensitive dyes and the high acquisition rates needed for high-fidelity signal reconstruction (32). As a result, raw optical data often contain high-frequency noise (>100 Hz) that hampers immediate analysis of optical data. To overcome these complications, several digital signal processing techniques can be employed to remove high-frequency noise and improve data quality. Here we will review several standard techniques and demonstrate efficient methods for signal processing in current practice.

Digital data format.

There is a multitude of optical mapping systems that are currently available, all of which output data in similar formats. For the purpose of this review, we will illustrate the processing of optical imaging data using a representative data set recorded from the MiCAM ULTIMA (SciMedia, Costa Mesa, CA) imaging system. This system uses a 100 × 100 pixel complementary metal oxide semiconductor (CMOS) camera that can achieve acquisition rates of up to 10,000 frames/s. Data from this system are saved as a series of 100 × 100 matrixes, each acquired at a specific time point, as shown in Fig. 1A. Each pixel represents a measure of fluorescent intensity collected from a specific location on the tissue preparation at a specific time. Background fluorescence is automatically removed per pixel to allow for better visualization of fluorescence changes produced by membrane voltage changes and inverted to correspond with action potentials measured by microelectrode systems. Additionally, the MiCAM ULTIMA system provides a background image of the preparation by averaging fluorescence intensity of the first four frames. This background image provides a spatial connection between the tissue preparation and OAPs.

Data obtained from other optical imaging systems [CMOS, charge-coupled device (CCD), or photodiode array] will vary depending on array size and sampling rate. All analysis and processing methods described herein are universal and can be applied to all camera systems. All data presented were collected from Langendorff-perfused rabbit hearts (New Zealand white, 7 to 8 mo old, 3–5 kg) as previously described (26). Data were sampled at 1 kHz and analyzed using a custom MATLAB (2011B, Mathworks, Natick, MA) graphical user interface available from efimov.wustl.edu by request. All experiments were approved by the Institutional Animal Care and Use Committee of Washington University in St. Louis.

Data masking.

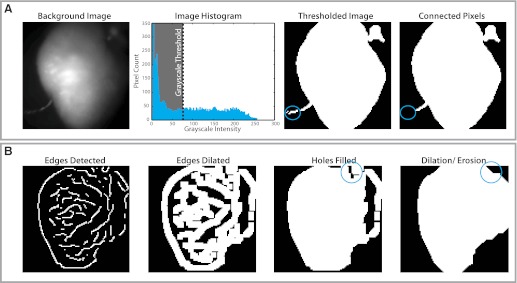
Depending on the tissue preparation, each fluorescent frame will contain a combination of pixels on the preparation (i.e., foreground pixels) and outside the preparation (i.e., background pixels). While pixels on tissue contain important optical information, background pixels contain noise that can skew data analysis and should be systematically rejected. Background pixels can be easily segmented from foreground data by creating a binary mask of 1 s (included pixels) and 0 s (excluded pixels) and applying the mask to each frame in the sequence. Binary masks are typically created manually or algorithmically. Manual segmentation, the simplest and most common technique, requires a user to define tissue background borders. Conversely, automatic segmentation involves applying a thresholding (Fig. 2A) or edge detection (Fig. 2B) algorithm to determine tissue boundaries. In thresholding routines, the background imaged is first converted into a 256-bit grayscale image. A grayscale threshold is next selected and applied to the image. All pixels greater than or equal to the threshold criteria are labeled with 1 s (white) and are included for processing. All pixels below the threshold are labeled with 0 s (black) and rejected. This process creates a binary image that highlights areas of interest for further processing. Background objects with pixels above the threshold will also be included. As shown in Fig. 2A, pixels over a pacing electrode (circled blue) are identified with the foreground pixels. These undesirable pixels can be easily removed through a connected component analysis where the largest area of connected foreground components are identified and isolated. Image thresholding is a rudimentary technique for image segmentation that may be inappropriate in poor lighting or fields of view that include pieces of instrumentation.

Fig. 2.

Data masking. Pixels over myocardial tissue (foreground) are segmented from the pixels in the background, which are removed. A: thresholding method for data masking. The background image is converted into a 256-bit grayscale image, and a grayscale threshold is selected and applied. Pixels above the threshold (white) are retained, and those below threshold (black) are rejected. Nonmyocardial pixels in the thresholded image (in this example, a stimulating electrode, blue circle) are removed using a connected component analysis. B: edge-detection algorithms for data masking. Edges are detected using specific algorithms, and these edges are then dilated to create an enclosed object. Enclosed regions (blue circle) are then filled with a flood algorithm, and further dilation or erosion is performed as required.

Alternatively, edge detection algorithms can be applied as demonstrated in Fig. 2B. Briefly, object edges are detected using a two-dimensional differentiation operator (e.g., Sobel filters, Canny filters, Prewitt filters, etc.) (1, 33, 46, 49). Detected edges are then dilated by a desired pixel thickness to create an enclosed object. Enclosed regions or holes are filled with a flood algorithm. If gaps in the binary mask still exist, dilation and/or erosion algorithms can be applied to add or remove pixels, respectively. Automatic image segmentation is not always perfect, though it is an excellent method to quickly eliminate the majority of noisy background pixels before manual segmentation.

Digital filtering.

Once the pixels of interest have been isolated from background pixels, digital filtering is routinely applied to improve SNR of the optical data. Despite the widespread use of digital filters in optical mapping studies, no consensus technique(s) exists for creating or applying filters to optical data. Thus a wide variety of filters are used to remove noise from OAPs. In this section, we will cover popular spatial and temporal digital filtering techniques.

SPATIAL FILTERING.

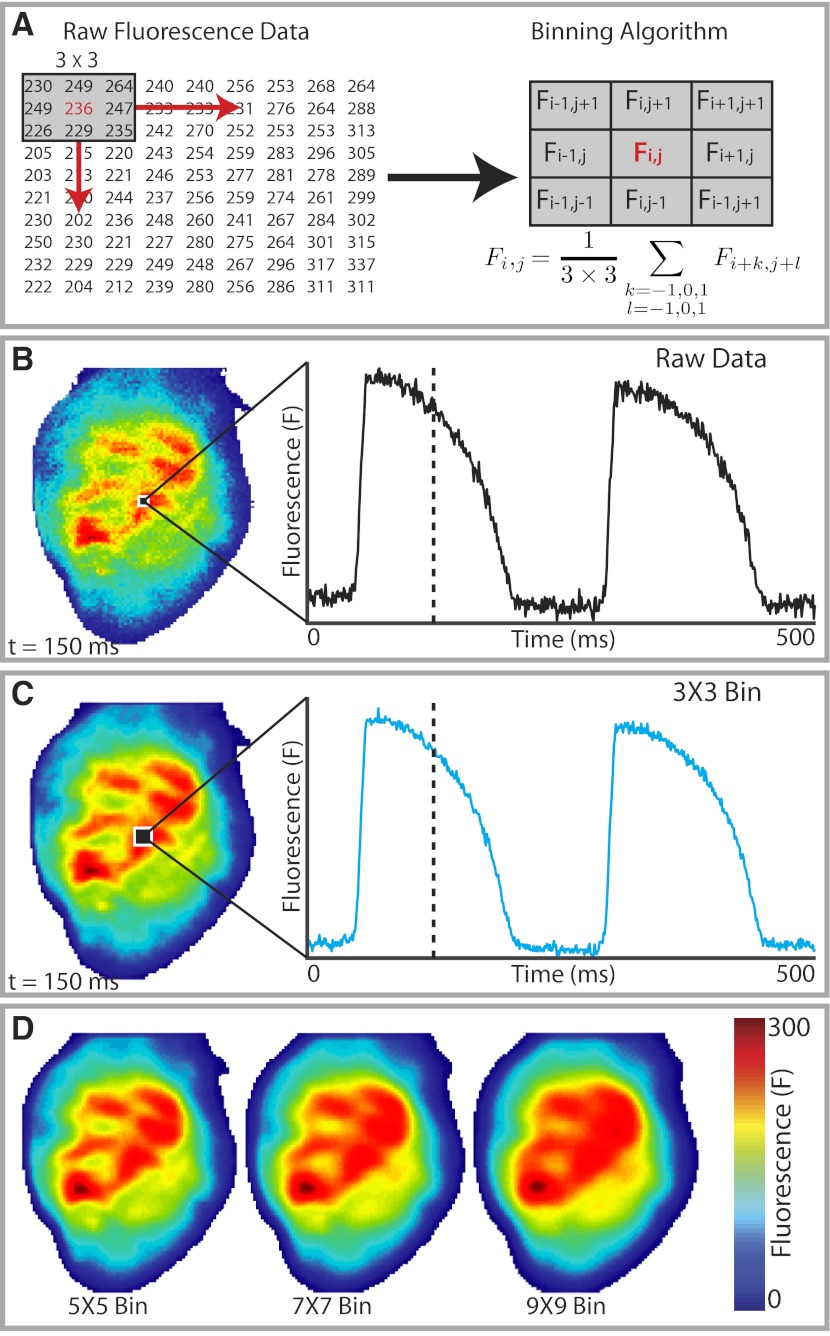
Spatial filtering of pixels, also known as binning, is one of the most straightforward methods used for postacquisition high-frequency noise reduction. In typical binning algorithms, each fluorescent pixel (F_i,j) is averaged with its neighboring pixels as defined by a desired convolution bin or kernel. Figure 3, A–C, demonstrates binning with a 3 × 3 uniform bin. For this particular kernel, neighboring pixels and each center pixel are averaged over each frame equally (Fig. 3A). Although the SNR of the raw data is quite high (Fig. 3B), 3 × 3 binning results in moderate reduction of the remaining high-frequency noise (Fig. 3C). For noisy data, larger bin sizes (e.g., 5 × 5, 7 × 7, etc.) can be employed for greater improvements to SNR. As bin size increases, spatial broadening can produce distortion to signals and must be considered if analyses of activation time, CV, or arrhythmia cycle length are to be accurately performed. The distortion created by spatial broadening can also smooth out important features of the OAP, and caution should be applied when using larger bin sizes. Figure 3D demonstrates spatial broadening in optical signals for 5 × 5, 7 × 7, and 9 × 9 uniform bins. One method to minimize the effect of spatial broadening during binning is with Gaussian kernels, which place greater weight on pixels closer to the center pixel as described by a Gaussian curve.

Fig. 3.

Spatial filtering (binning). A: example of 3 × 3 binning. The fluorescence intensity of each pixel (F_i,j) is averaged with its 8 immediate neighbors to obtain its filtered or binned value. This operation is done for all the pixels in the matrix. B: fluorescence intensity map and the optical action potential (AP) from a single pixel for raw unfiltered data. C: fluorescence intensity map and optical AP (OAP) following 3 × 3 binning. Binning has removed some of the high-frequency noise from the OAP but creates spatial broadening, where a spatial averaging effect is seen on the binned fluorescent intensity map. D: increasing spatial broadening effect with greater bin sizes.

TEMPORAL FILTERING.

Temporal filtering, applied on a pixel-by-pixel basis, offers numerous versatile strategies for noise reduction by removing portions of a signal spectrum contributing to noise (44). These strategies are not exclusive to optical mapping data and can be applied universally to other experimental data. Before significant improvements to digital signal processors and internal memory in personal computers, time-domain moving average filters were quite popular for filtering of optical data due to their simple design and ease of implementation and remain widely used in the optical mapping community (20, 24, 45). This convolution-based filtering strategy involves creating a kernel or window of appropriate length to average time variant signals. Similar to binning algorithms, window size and window shape can be adjusted to alter the amount of high-frequency attenuation. Moving average filters can be in the form of a simple moving average where an unweighted mean is used, or in the form of a weighted moving average, where different weights are assigned to data at different positions of the sample window.

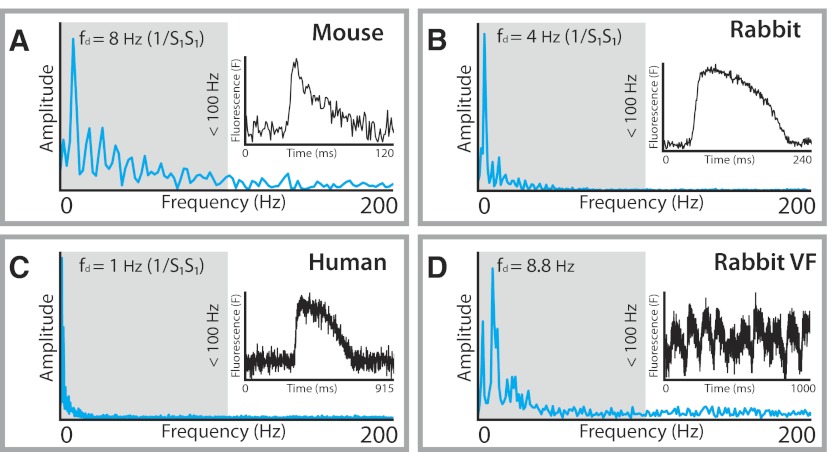
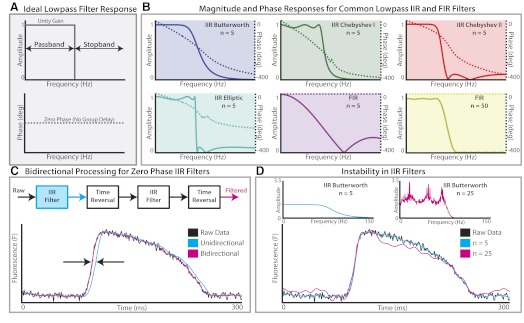
Today, modern digital filter design typically begins in the frequency domain. By taking the Fourier transform of a signal of interest, dominant frequencies in a time-variant signal can be identified. The dominant frequency spectrum of optical data is below 100 Hz, as shown in Fig. 4, which displays Tukey-windowed power spectra from four common research models used in optical mapping studies: mouse (Fig. 4A), rabbit (Fig. 4B), human (Fig. 4C), and rabbit polymorphic ventricular fibrillation (VF, Fig. 4D). For each species, frequency components near zero are characteristic of the plateau phase and repolarization of the OAP while the upstroke of the OAP is primarily composed of components of higher frequency. Thus an ideal temporal filter for optical data is a low-pass filter that passes frequencies 0–100 Hz and attenuates frequencies above 100 Hz (Fig. 5A). Moreover, the filter should possess a zero phase response so as not to impart time-domain delays, referred to as group delay, to frequencies in the passband. This ideal brickwall filter is of infinite order and therefore not physically realizable for real world applications. As a result, brickwall filters must be digitally approximated by optimized microprocessors designed for fast digital signal processing. These approximations can be divided into two classes of filters: infinite impulse response (IIR) and finite impulse response (FIR) filters. For researchers performing optical mapping studies, an understanding of the minute details of IIR and FIR filters is not critical to successful implementation of temporal filters. Both types of filters can be applied for successful filtering. However, a few basics concepts are important when designing and applying appropriate FIR and IIR filters for optical data.

Fig. 4.

Power spectra for representative OAPs from 3 experimental species. The spectra for mouse (A), rabbit (B), and human (C) OAPs during a regular paced rhythm are shown. The dominant frequencies (f_d) for each of these examples correspond to the pacing frequency (the reciprocal of the pacing cycle length). The power spectrum for an example of rabbit ventricular fibrillation (VF; D) is also shown. All the major frequency peaks are below 100 Hz, suggesting that low-pass filters that attenuate frequencies above 100 Hz are suitable for processing optical mapping data.

Fig. 5.

Overview of temporal filters. A: ideal lowpass filter (“brickwall” filter) is a filter that attenuates all frequencies in the stopband and passes all frequencies in the passband with no phase delay. B: magnitude (solid lines) and phase (dashed lines) responses for 6 common lowpass infinite impulse response (IIR) and finite inpulse response (FIR) filters (n denotes the order of the filter). Of these 6 examples, the 50th-order FIR filter is closest in its magnitude and phase response to the ideal filter shown in A. C: because IIR filters impart a nonuniform phase delay as shown in the phase responses in B, bidirectional filtering is required to produce zero phase delay. D: instability in higher-order IIR filters. The magnitude responses for a 5th- and 25th-order Butterworth filter are shown (top). The instability of the 25th-order filter creates a rippling effect on the OAP plateau, which may be mistaken for afterdepolarizations.

Robust filter design begins with an understanding of the characteristic trade-offs in each class of filter. Figure 5B depicts four common IIR filters (Butterworth, Chebyshev type 1, Chebyshev type 2, and Elliptic) and two FIR filters. The main advantage of IIR filters over FIR filters is their ability to meet a set of design criteria with much lower order than FIR filters, making them more computationally efficient for real-time applications. As demonstrated in Fig. 5B, a 50th-order FIR filter is necessary to match the performance of a 5th-order Butterworth IIR filter. Within the class of IIR filters, important nuances between filters are apparent. Butterworth filters have a maximally flat passband but slow roll-off during the transition from passband to stop band. Chebyshev type-1 and type-2 filters typically display a faster roll-off than Butterworth filters but contain ripple in the pass- or stop band, respectively. If a sharp transition between pass- and stop bands is required, IIR elliptic filters are the best option but must be tested carefully for distortion because of ripple in both pass- and stop bands. While IIR filters are able to achieve sharper filter characteristics at lower orders, FIR filters can have a linear phase response. As a result, linear-phase FIR filters impart a uniform phase delay to all frequencies in the passband that can be easily calculated and subtracted to create a zero-phase filter.

As mentioned previously, zero-phase filtering is ultimately desired in an ideal filter so raw and filtered data align temporally. For FIR filters with a constant phase response over the entire frequency spectrum, phase delay can be removed by shifting the filtered signal a constant amount. For IIR filters, bidirectional processing must be employed to cancel phase effects. During this process, a raw signal is passed both forward and in reverse through a filter, thus cancelling the phase shift at all frequencies. Figure 5C provides a simple example of unidirectional and bidirectional processing with a Chebyshev type-2 IIR filter. Unidirectional filtering with the IIR filter clearly produces phase lag to the filtered signal (blue), which will advance the time of activation and repolarization. Once bidirectional processing is applied, phase lag between filtered and raw signals is removed. While this process is typically applied to create zero-phase IIR filters, bidirectional processing can also be applied to FIR filters.

Another important consideration when choosing between FIR and IIR filters is stability. FIR filters are inherently stable because the output does not depend on previous outputs from the filter. IIR filters, conversely, depend on feedback from the filter output, which could make the output grow without bound. Thus IIR filters can have issues with stability, especially as filter order is increased for sharper roll-offs. An example of instability in IIR filters is demonstrated in Fig. 5D for a Butterworth filter of order 5 and order 25. When both filters are applied bidirectionally, the 25th-order Butterworth filter clearly distorts the OAP shape, which could lead to a physiological misinterpretation of the data. Comparing the magnitude response for both filters shows a likely cause of distortion to the filtered signal. While the passband of the 5th-order filter has a maximally flat unity gain, significant ripple is observed in the passband of the 25th-order filter. This high-order IIR filter may not affect the analysis of activation time or CV; however, it may lead to inconsistent calculations of APD and thus its use should be avoided.

ALTERATION OF DATA CONTENT BY INAPPROPRIATE FILTERING.

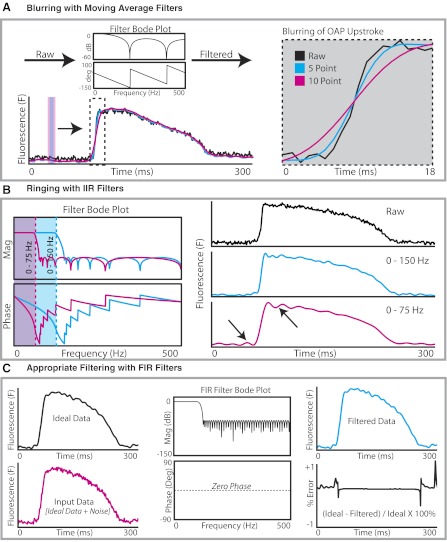
Depending on filter design and the application technique, it is well known that filter-induced artifacts can easily produce distortion in optical signals. These artifacts can occur when data are overfiltered in an attempt to remove noise from poor quality data. Figure 6 displays two well-established scenarios of inappropriate filtering with moving average filters (Fig. 6A) and IIR filters (Fig. 6B) as well as an example of successful filtering with an FIR filter (Fig. 6C). Researchers involved in the field of cardiac optical mapping need to be alert to the possibility of filtered-induced artifacts when interpreting their data.

Fig. 6.

Examples of overfiltering and appropriate filtering. A: blurring effect of moving average filters. Inset: the greater the number of time points averaged using the moving average filter, the greater the blurring effect on OAP upstroke. The moving average filter prolonged the rise time of the OAP, decreased maximum first derivative of the fluorescent signal (dF/dt_max), and can alter activation times. B: ringing with IIR filters. Reducing the passband frequency from 150 Hz (blue) to 75 Hz (red) creates a ringing effect, most prominent immediately before and after the OAP upstroke (arrows). These fluctuations resulting from overfiltering should not be mistaken for early or delayed afterdepolarizations. Mag, magnitude. C: appropriate filtering and filter testing. Windowed, uniform white noise (150–400 Hz) superimposed onto an ideal OAP (black) is to create an OAP with high-frequency noise (red). This result is then filtered to remove the high-frequency noise to produce the filtered OAP (blue). The amount of error created by the filter is calculated by quantifying the difference between the filtered OAP and the original ideal OAP.

As shown in Fig. 6A, when the number of time points averaged using a moving-average filter is increased in an effort to better attenuate high-frequency noise, a noticeable reduction in OAP upstroke velocity is observed in OAPs. Such filtering will affect the results of the values of maximum first derivative of the fluorescence signal (dF/dt_max) and the rise time of the OAP. Another effect of altering the upstroke of the OAP is the alteration of activation times. From our experience, if there is a significant blurring effect from moving-average filters, activation times across the experimental preparation can be altered nonuniformly. This blurring has the undesired effect of producing activation maps that are different when using filtered data compared with raw unfiltered data. Consequently, these nonuniform alterations in activation times will also affect local CV calculations. Subtle shifts in activation times as a result of inappropriate filtering also become important when mapping of transmembrane voltage is combined with mapping of calcium transients. Dual voltage and calcium optical mapping has been used to identify instances where the calcium transient preceded the action potential, as evidence of triggered activity (22). In such cases, subtle changes in activation times of several milliseconds resulting from inappropriate filtering may affect whether calcium precedes voltage or vice versa for a particular pixel.

Another undesired effect that can arise from inappropriate filtering or overfiltering is the effect of ringing with IIR filters (Fig. 6B). Ringing is said to occur when a nonoscillating input produces an oscillating output once the data are filtered and is referred to mathematically as the Gibbs phenomenon. Ringing can be produced when the passband is narrowed to filter out higher-frequency components. As shown in Fig. 6B, when the passband frequency is reduced from 150 to 75 Hz while the filter order remains unchanged, the filtered data demonstrate oscillations and bumps before and after the OAP upstroke, as shown by arrowheads. It is important to recognize ringing when analyzing optical imaging data. Failure to recognize ringing may lead to these bumps and oscillations being wrongly attributed to biological phenomena such as early afterdepolarizations (if occurring on the OAP plateau) or delayed afterdepolarizations triggering an action potential (if occurring before an OAP upstroke).

One approach to prevent inappropriate filtering leading to an alteration in the content of the data is to test the performance of the filter and to measure the amount of error generated by the filter, as shown in Fig. 6C. In this example, windowed, uniform white noise (150–400 Hz) is superimposed onto an idealized OAP and then filtered using an FIR filter (0–100-Hz passband, 50th order). The filtered OAP is then compared with the original idealized OAP, and the differences are computed as the error produced by the filter. This example shows appropriate filtering with an FIR filter as the filtered data faithfully matches the initial idealized OAP with minimal error (Fig. 6C, bottom right).

Ensemble averaging.

For analyzing rhythmic data, ensemble averaging can be an effective tool for eliminating stochastic noise. During ensemble averaging, optical signals are divided into individual repeated segments or single OAPs. OAPs are then averaged together to create a mean OAP. Although this technique is beneficial for rhythmic data, it cannot be employed for analysis of noncyclical pacing protocols or arrhythmic data. It is also unsuitable if there are beat-to-beat variations during regular pacing, such as during APD alternans. Mironov et al. (32) recently showed that efficient spatial and temporal filtering is comparable with the ensemble averaging of 100 OAPs.

Drift correction and normalization.

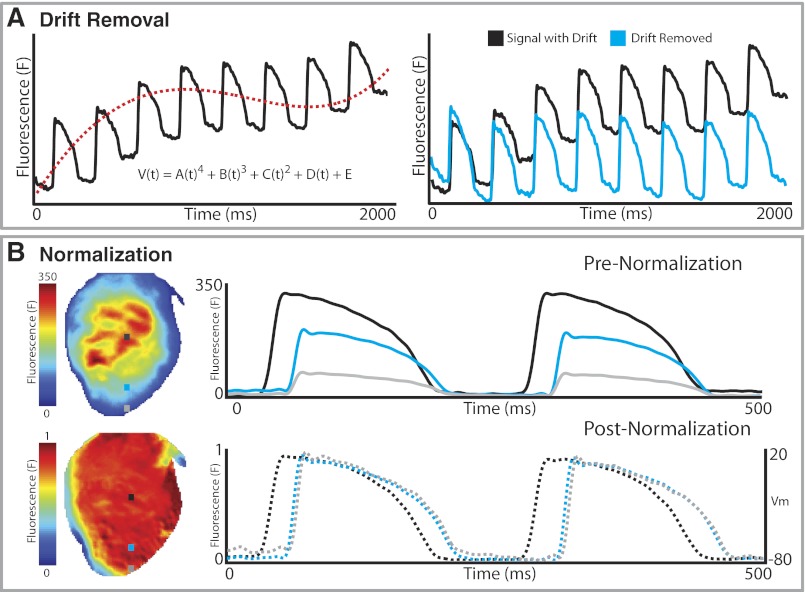
Drift of baseline in optical recordings due to photo bleaching or motion is a well-known concern. Drift is characterized by low-frequency content and can display either linear or nonlinear behavior as shown in Fig. 7A. Removing drift becomes difficult when signals display varying nonlinear drift on a file-by-file or pixel-by-pixel basis. However, drift ought to be removed and a constant baseline level achieved if analyses of activation time, CV, and APD are to be accurately calculated. There are several common ways to remove drift from optical signals; two of the simplest are high-pass filtering and polynomial fitting to the original signal. Caution needs to be taken when applying high-pass filters with passbands > 0.5 Hz because of the low-frequency content contained in the plateau phase of cardiac action potentials. As seen in Fig. 7A, polynomial fitting can be applied to subtract drift from a signal. In this example, a fourth-order polynomial (red dash line) was fit to the optical signal (black) and subtracted from the signal to yield a steady baseline (cyan).

Fig. 7.

Drift removal and normalization. A: background drift from the raw data (black) is removed by fitting a polynomial equation to the background drift (a 4th-order polynomial in this example, dashed red line), and subtracting that from the raw signal to remove drift (cyan). B: OAPs from all the pixels are normalized to the same amplitude so that peak fluorescence (F = 1) corresponds to a depolarized membrane potential and baseline fluorescence (F = 0) corresponds to the resting membrane potential (V_m).

Once drift has been removed from optical recordings, the data can be normalized. Fluorescence intensity will often vary across a preparation for various reasons (e.g., nonuniform illumination of a preparation, unequal dye loading, tissue thickness, etc.) as demonstrated in Fig. 7B, top. To better visualize patterns of excitation and repolarization, each pixel can be normalized from 0 (minimum fluorescence) to 1 (maximum fluorescence). As seen in Fig. 7B, bottom, after normalization the OAPs near the edge of the preparation have the same magnitude as the signal from the center of the preparation. Once this process is complete, optical signals can be mapped to the voltage domain for correspondence to microelectrode data.

Analysis of Optical Imaging Data

Following the above steps to filter and process the raw optical signals, the resultant conditioned optical signals can then used for analyses to investigate activation and repolarization properties of myocardial tissue. In this section, conventional methods for generating activation maps and APD maps, calculating local conduction velocities, and for arrhythmia analysis are described.

Activation maps.

One advantage of optical mapping over other experimental electrophysiological techniques, such as multielectrode arrays, is the ability to simultaneously record OAPs from a large number of sites, for example up to 10,000 pixels, thus allowing the generation of extremely high-resolution (∼350 μm/pixel) activation maps from the rabbit heart.

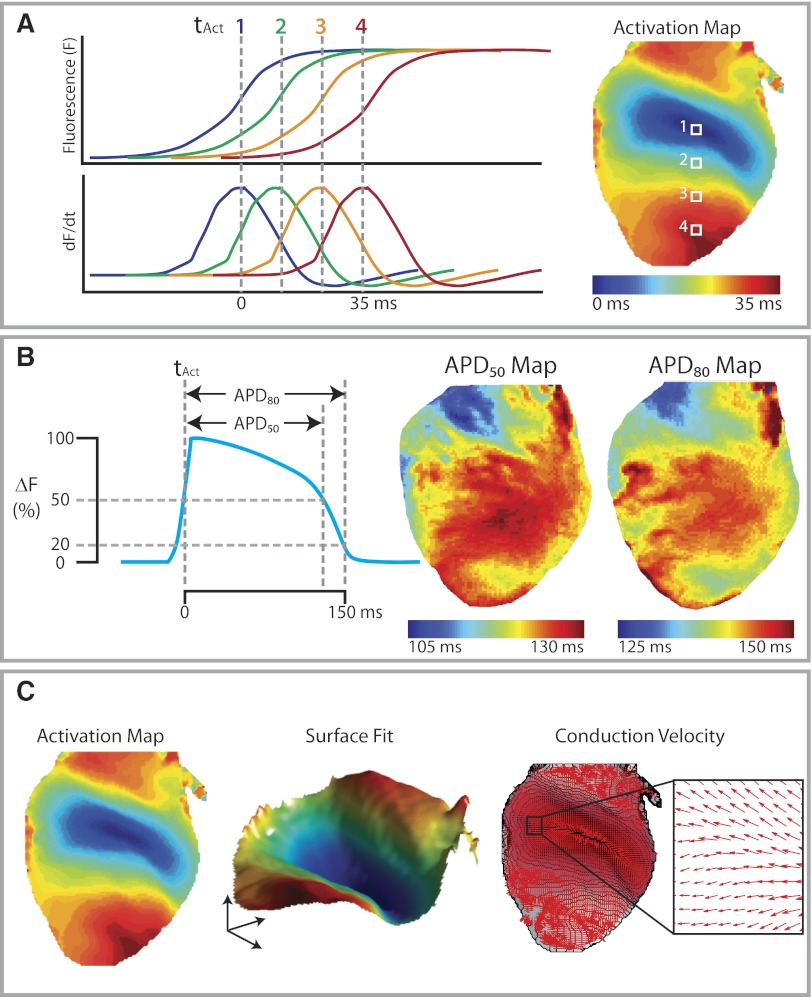
The first step in the creation of activation maps is to assign each pixel its activation time. Figure 8A shows an example of optical mapping data from a rabbit heart that was paced near the base of the ventricles. The OAP upstrokes and the corresponding dF/dt traces for four pixels along the base-apex axis are depicted to illustrate how the activation times are assigned for these pixels. By convention, the activation time is defined as the time of dF/dt_max, which corresponds to the steepest segment of the OAP upstroke (11). The activation map, usually shown as an isochronal map, can then be generated once all pixels have been assigned their activation times (Fig. 8A, right). It has to be noted that, unlike for single cell microelectrode recordings, the activation time for an optical mapping pixel represents the averaged activation times for all the cells within that pixel.

Fig. 8.

Analysis of optical mapping data. A: activation mapping. The OAP upstrokes and their corresponding dF/dt traces for 4 points on a rabbit heart. Each point is assigned an activation time (t_act) based on the time of dF/dt_max to generate the isochronal activation map. B: Action potential duration (APD) measurements. APD₅₀ is measured from t_act to time of 50% repolarization, whereas APD₈₀ is measured to 80% repolarization. APD maps demonstrating regional heterogeneities are shown (right). C: conduction velocity analysis. Data are taken from the activation map (left) to fit onto a smoothed surface (middle). The surface was smoothed with a 5 × 5 Gaussian kernel. Local conduction vectors are then calculated from the smoothed activation surface with the magnitudes of local conduction velocity represented by the length of the arrows and the directions of activation represented by the directions of the arrows.

In practice, user input is required to select a time window that encompasses the activation times of all the pixels for a single action potential propagation. This is easily done when the heart is in sinus rhythm or a paced rhythm, where the activation impulses propagate periodically across the myocardium, separated by periods of electrical inactivity. Selecting activation time windows becomes more difficult when the heart is in a reentrant rhythm or fibrillation, where the myocardium is being continuously activated. Because each activation map can only depict the activation pattern of a single impulse, multiple sequential activation maps are often needed to show activation sequences in reentrant tachycardias such as ventricular tachycardia (31).

APD maps.

Another advantage of optical mapping of transmembrane voltage over electrode array recordings is the ability to study the repolarization of myocardial tissue. Because changes in fluorescence intensity are proportional to changes in transmembrane voltage, values for APDs can be calculated from the optical signal (10). As with the activation times, the values of APDs obtained from optical signals are for a cluster of cells within each pixel, as opposed to a single cell.

The definitions of optical APDs are similar to those used to calculate APDs from gold-standard microelectrode recordings. As shown in Fig. 8B, left, the APD₈₀ is defined as the duration between the activation time and the time of 80% repolarization (i.e., when the inverted fractional change in fluorescence is at 20% of its peak). Similarly, APD₅₀ is defined as the duration between the activation time and the time of 50% repolarization. The use of different measures of APDs allows a description of not only the duration of the OAP but also the shape. Maps of APDs (Fig. 8B, middle and right) can be generated to show any apical-basal or endocardial-epicardial gradients in APDs or spatial heterogeneities in APDs, which are thought to be important in arrhythmogenesis (3, 10). The dispersion of APDs can also be calculated based on the variation of APD values within an area of interest. The standard deviation and the range of APD values (difference between 95 and 5% of APD distribution) are two commonly used measures of APD dispersion (7).

CV maps.

Optical mapping data can also be used to generate local conduction vectors, which then allow for the quantification of local conduction velocities as well as providing a description of the direction of activation of the myocardium. A general description of how local CV vectors are calculated is provided below, and more specific details can be found in the original references (4, 39) and in a detailed review on imaging electrical wave propagation and conduction (34).

One method of calculating local CV vectors is to compare activation times between the pixel of interest with that of its immediate neighbors, where greater differences in activation times represent faster local CVs, and smaller differences inactivation times represent slower CVs. Practically, this is done by calculating gradient vectors of activation for each pixel (39). The horizontal component of the gradient vector for a pixel is calculated from the activation time delay between its two adjacent neighbors in the horizontal direction divided by the distance between the two neighbors. The vertical component of the gradient vector is similarly calculated using its neighbors in the vertical direction. The local gradient vector is the resultant of the vertical and horizontal components. Local CV vectors are vectors with the opposite orientations as the gradient vectors, and with magnitudes equal to the reciprocal of the gradient vectors. This method has the advantage of being able to detect heterogeneities in local conduction velocities and directions as the CVs are calculated using true activation times. However, it cannot compute local CVs from data where neighboring pixels have the same activation times, such as when the sampling frequency is low.

Another method for calculating CVs is to fit a surface to activation time data as shown in Fig. 8C, middle. Polynomial surface fitting or local kernel smooth routines can be used to fit a surface to the activation data (4). Local velocity vectors are then computed from the gradient of the fitted surface. This method has the advantage of being able to deal with missing data points, noisy data, and multiple neighboring pixels that have the same activation time. Polynomial surface fitting methods are best suited to uniform activation patterns that can be described by polynomial equations. When significant regional heterogeneities in CV and direction of activation exist, kernel surface smoothing may provide superior results.

Another consideration was derived from our experience with panoramic imaging (27). Conduction is recorded over a curved surface, which should be considered when calculating velocity, because “flattening” the field of view alters actual CV. However, such improvement requires panoramic imaging instrumentation, which has not yet received widespread application (19, 27, 38).

Repolarization maps.

Optical mapping data can also be analyzed to create repolarization maps to assess the direction of repolarization. The method of creating of repolarization maps is similar to that of activation maps, except each pixel is assigned a repolarization time instead of an activation time to create the isochronal maps. The repolarization time may be defined as the maximum second derivative (d²F/dt²) of the optical signal at the end of the OAP (11), or the time of 90% repolarization (11, 35). Under certain conditions, repolarization alternans due to APD alternans may be out of phase in different parts of the heart surface (37). The occurrence of such spatially discordant alternans can be clearly depicted using a series of repolarization maps, showing different repolarization patterns for consecutive beats. In such cases, ensemble averaging must be avoided since this will alter repolarization maps, and individual beats must be depicted with separate repolarization maps since they will vary from beat to beat.

OAP upstroke analysis.

Analyses of the OAP upstroke can also be performed to provide information about membrane excitability and local CV. Two common analyses of the OAP upstroke include the rise time and the maximum first derivative value of the OAP upstroke (dF/dt_max) (9). The rise time, which reflects the time taken by the OAP upstroke can be measured between time between takeoff (maximum value of d²F/dt²) and the peak of the action potential (9) or between 10 and 90% of the OAP upstroke (35). In addition, it has been shown that the morphology of OAP can also provide information about the subsurface orientation of the propagation wavefront (18, 21).

Arrhythmia analysis and phase mapping.

Another key advantage of optical mapping is the ability to study activation during complex cardiac arrhythmias such as atrial fibrillation (AF) and VF. Because of the complex and irregular activation patterns that occur in AF and VF, specific analyses such as phase mapping are required for these arrhythmias.

Phase mapping is an analysis technique used to depict the spatiotemporal changes in activation during cardiac fibrillation (15, 16). Phase is a variable that describes the progression through the action potential in a specific region of myocardium through a cycle between −π and +π. Phase mapping is useful in fibrillation because of the spatiotemporal variation in activation periods (i.e., the time taken to cycle between −π and +π varies between different locations and between different time points for the same location).

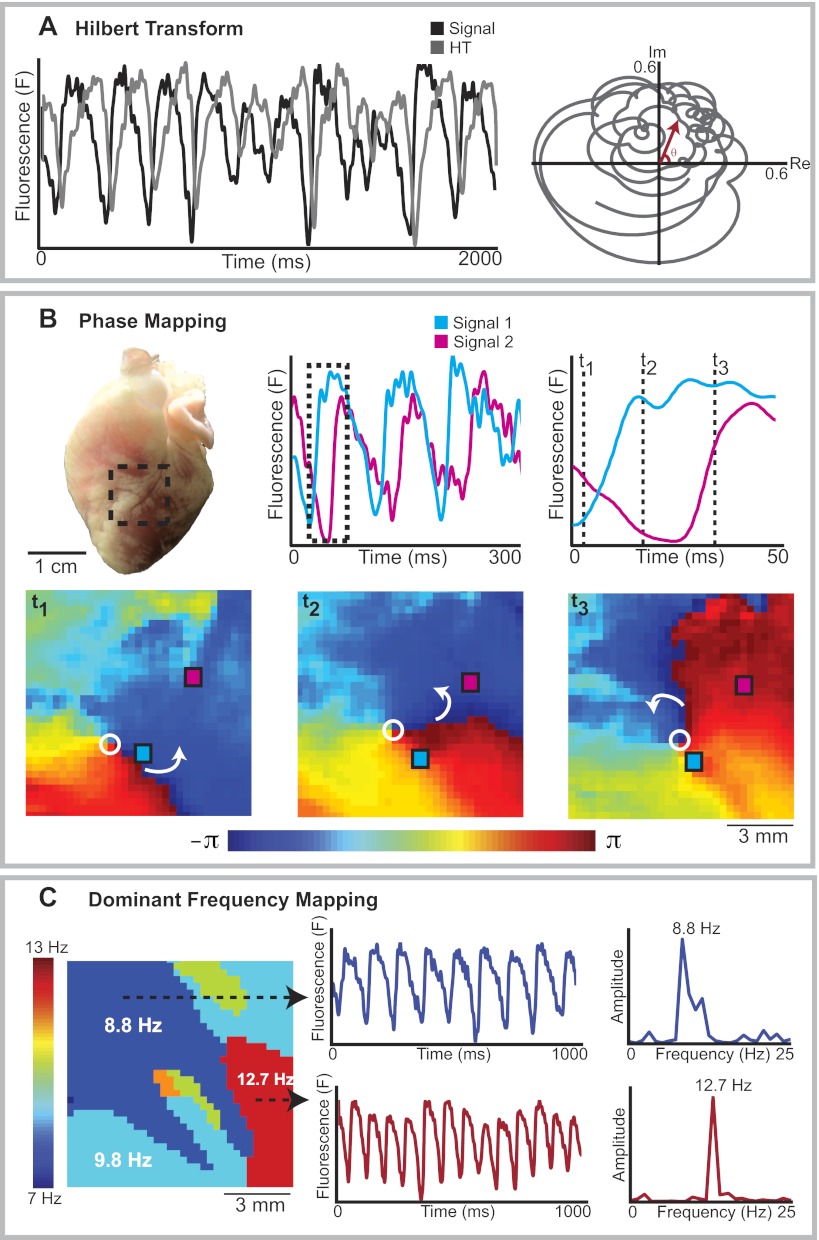
To create a phase map, each optical mapping pixel has to be assigned an instantaneous phase value (between −π and +π) for that given time point. The instantaneous phase can be computed by first performing a Hilbert transform (HT) (6), as shown in Fig. 9A, left, where the optical signal for an optical mapping pixel is shown in black and the corresponding HT signal shown in gray. The relationship between the optical signal and the HT signal over time can then be shown on a phase space plot (Fig. 9A, right) where optical signal values are represented on the real axis and the HT values on the imaginary axis. The instantaneous phase at any time point is the angle θ on this phase space plot. The methodological details of calculating instantaneous phase are beyond the scope of this review and can be found elsewhere in significant depth (43).

Fig. 9.

Arrhythmia analysis. A: Hilbert transform (HT). To calculate instantaneous phase, an HT is first performed. A, left: optical transmembrane voltage signal (black) and its corresponding HT signal (gray). The HT values are then plotted against the optical signal values on the imaginary (Im) and real (Re) axes of a phase space plot respectively (right) and the instantaneous phase at a given time point is the angle θ. B: phase mapping. B, top: OAP recordings from 2 locations on a rabbit heart in VF (red and blue). B, bottom: corresponding phase maps, showing the instantaneous phase for all the pixels within the region of interest, at 3 time points. These sequential phase maps show rotation around a phase singularity (open circle), with the white arrows showing the direction of rotation. C: dominant frequency (DF) mapping. A DF map during rabbit VF is shown (left). Distinct areas with different dominant frequencies are present. The transmembrane voltage traces (middle) and power spectra (right) from a region with highest DF (12.7 Hz, red) and a second region with lower DF (8.8 Hz, blue) are shown.

Once the instantaneous phase values have been calculated, a series of phase maps can be generated as shown in the example in Fig. 9B, which shows the changes in phase during rabbit VF. Phase maps are useful because they can show points of phase singularities around which the reentrant activation waves rotate. The points of phase singularity are denoted with an open circle in example in Fig. 9B. The study of these phase singularities has helped to provide important insights into the formation and termination of rotors that sustain fibrillation (30, 42).

Dominant frequency analysis.

Spectral and dominant frequency analyses have become increasingly popular in arrhythmia research, predominantly in studies of complex arrhythmias such as AF (47, 48). Areas of dominant frequency are of interest because they have been shown to correspond to locations of AF drivers (28, 29). A recent study demonstrated that dominant frequency values obtained by optical mapping correlate well to those from electrogram recordings (5). Dominant frequency analysis is performed by carrying out a Fourier transform to represent the signals in the frequency domain by decomposing the signal to a sum of weighted sinusoidal functions (36). An example of dominant frequency analysis during rabbit VF is shown in Fig. 9C, where the optical signals (Fig. 9C, middle) undergo a Fourier transform to generate the power spectra of those signals (Fig. 9C, right). The dominant frequency (the frequency with the highest power) for each pixel can then be represented on a dominant frequency map (Fig. 9C, left) to display distinct areas with different dominant frequencies.

Recommendations for Processing Optical Mapping Data

As illustrated above, there are multiple ways to process optical mapping data, and the selection of the specific methods to process these data can potentially alter the content of the data and the conclusions of the studies. We accept that there is not a single optimal way to process optical mapping data, and the methods used should be governed in part by the nature of the experiments. We also acknowledge that different laboratories will have their preferred methods for processing these data, which have been validated and proven effective. However, for researchers new to cardiac optical mapping, we will endeavor to make some general recommendations on how these data should be processed, based on our own experience. Table 1 lists the specifics on our recommendations on how to process optical mapping data. We also provide a MATLAB-based optical mapping analysis package with test data for interested researchers at efimov.wustl.edu.

Table 1.

Recommendations for processing and analyzing cardiac optical imaging data

	Recommendations
Data masking	Grayscale thresholding + connected component analysis
Spatial filtering	3 × 3 uniform binning
Temporal filtering	FIR filter, 50th order
	Passband 0-100 Hz
	Zero phase filter
Ensemble averaging	Not recommended unless low SNR despite spatial and temporal filtering
Drift removal	Linear or polynomial fitting to remove drift
Activation mapping	dF/dtmax for activation time (tact)
APD calculations	APD80: duration between tact and 80% repolarization
	APD50: duration between tact and 50% repolarization
Local CV calculation	Calculate from local gradients of activation from tact
	(with kernel smoothing of tact surface)
Repolarization mapping	d2F/dtmax2 for repolarization times
OAP upstroke analysis	Rise time and dF/dtmax analyses
Phase mapping	Hilbert transform to calculate instantaneous phase

FIR, finite impulse filter; SNR, signal-to-noise ratio; dF/dt_max, maximum first derivative of the fluorescent signal; APD, action potential (AP) duration; CV, conduction velocity; d²F/dt_max², maximum second derivative of the optical signal at the end of the optical AP (OAP).

Conclusions

The use of optical mapping in basic, and translational cardiac research has increased exponentially in recent years. There are numerous ways to process and analyze raw optical mapping data, and the methods selected to process these data can affect their ultimate content and the conclusions drawn from the experiments. A basic understanding of the methods to process optical mapping data, including the advantages and disadvantages of each method and their potential pitfalls, is essential to any researcher involved in cardiac optical mapping studies.

GRANTS

This research was supported by National Institutes of Health Grants R01-HL-085369, R01-HL-067322, R01-HL-082729, R01-EB-008999, R21-HL-108617, R21-HL-112278, and T32-HL-007275. F. S. Ng was supported by a British Heart Foundation Travel Fellowship FS/11/69/29017 and by a UK National Institute for Health research clinical lectureship.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

J.I.L., F.S.N., and I.R.E. conception and design of research; J.I.L. and M.S.S. performed experiments; J.I.L., F.S.N., and M.S.S. analyzed data; J.I.L., F.S.N., R.M.A., and I.R.E. interpreted results of experiments; J.I.L., F.S.N., and M.S.S. prepared figures; J.I.L., F.S.N., and M.S.S. drafted manuscript; J.I.L., F.S.N., R.M.A., and I.R.E. edited and revised manuscript; J.I.L., F.S.N., and I.R.E. approved final version of manuscript.