Comparison of Kinetic Models for Analysis of Pyruvate-to-Lactate Exchange by Hyperpolarized ¹³C NMR

Abstract

The activity of specific enzyme-catalyzed reactions may be detected in vivo by ¹³C NMR of hyperpolarized (HP) substrates. The signal from HP substrates and products, acquired over time, have been fit to a number of different mathematical models to determine fluxes, but these models have not been critically compared. In this study, two-pool and three-pool first-order models were constructed to measure flux through lactate dehydrogenase in isolated glioblastoma cells by NMR detection of lactate and pyruvate following addition of hyperpolarized [1-¹³C]pyruvate. Mass spectrometry (MS) was used to independently monitor ¹³C enrichment in intra- and extracellular lactate. Six models were evaluated using time dependent pyruvate C2 and lactate C1 HP NMR data acquired by use of selective excitation pulses plus ¹³C enrichment data from intracellular and extracellular lactate measured by MS. A three-pool bi-directional model provided the most accurate description of pyruvate metabolism in these cells. With computed values for the T₁ of pyruvate and lactate as well as the effect of pulsing, the initial flux through lactate dehydrogenase (LDH) was well-determined by both the two-pool bidirectional and unidirectional models when only HP data was available. The three-pool model was necessary to fit the combined data from both MS and HP, but the simpler two-pool exchange model was sufficient to determine the ¹³C lactate concentration when the lactate appearance was measured only by HP.

Introduction

Metabolism of ¹³C-enriched substrates, monitored as a function of time by NMR, may be analyzed using suitable mathematical models to determine fluxes through specific enzyme-catalyzed reactions in intact tissues and in vivo (1,2). Although the ability to image fluxes through specific reactions would have considerable clinical utility, methods based on conventional ¹³C NMR are limited by poor spatial resolution and the requirement for many hours of data acquisition. The recent introduction of a fast dissolution Dynamic Nuclear Polarization (DNP) technique that increases NMR signal >10,000-fold (3) offers the potential of detecting ¹³C-enriched products with a temporal resolution of a few seconds and acquisition of a complete kinetic data set within a few minutes. The clinical potential of this method is widely recognized and studies of cancer have been the focus of most early studies (4). In tumor cells, for example, excess conversion of pyruvate to lactate occurs as the result of hypoxia or of intrinsic metabolic reprogramming during malignant transformation (5), and therefore may serve as a useful biomarker of malignancy in vivo (6–13) and in cultured cells (12,14–17). Recently, flux from hyperpolarized (HP) ¹³C-pyruvate to HP ¹³C-lactate was reported based on the observed time-intensity curve of HP ¹³C-lactate (4,11–21). These measurements have the potential to distinguish healthy vs. diseased tissue and have been used to monitor treatment response in cancer (4,13,16–20).

The mathematical models used for analysis of HP kinetic data must differ significantly from those described previously for analysis of chemical or enzyme kinetics because factors other than simple flux affect the appearance of HP nuclei in an end-product such as lactate. First, the T₁ of the various metabolites will influence the appearance of HP [1-¹³C]lactate. Even if fluxes are identical, a long T₁ of [1-¹³C]pyruvate or [1-¹³C]lactate favors the appearance of HP [1-¹³C]lactate signal compared to a shorter T₁. Second, the flip angle and repetition rates for observing the HP pyruvate and lactate signals will influence the time-intensity curve of HP [1-¹³C]lactate. The T₁ of lactate and pyruvate measured in aqueous solution may not be relevant in an intracellular environment where binding to enzymes and increased viscosity may shorten T₁. This combination of unknown T₁ decay rate constants, relatively short duration of observation, the effects of acquisition conditions, and unknown pool sizes of the relevant metabolites present challenges in measuring fluxes from dynamic HP data sets. The delivery of pyruvate to the region of interest adds an additional complication in vivo.

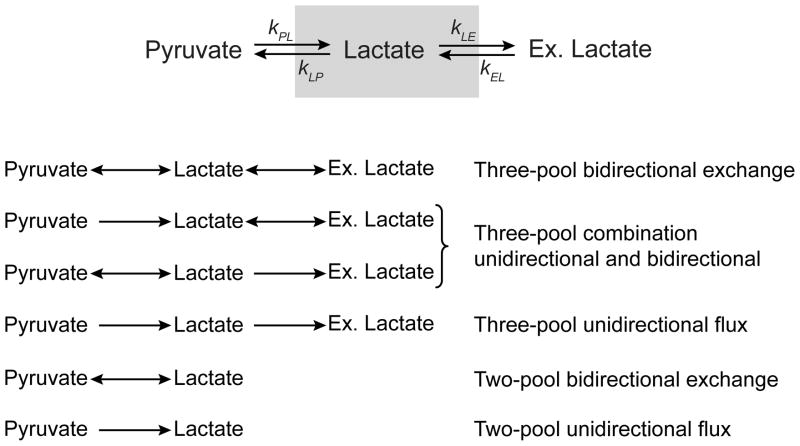
A simple model for detection of ¹³C-enriched lactate after administration of labeled pyruvate is to consider three pools: intracellular pyruvate, intracellular lactate, and extracellular lactate. Even this three-pool model becomes rather complex once the effects of T₁ and radiofrequency (RF) excitation are included. The accuracy of rate constants determined by fitting an HP data set to a lactate appearance curve will be improved if the number of unknowns is minimized or constrained. One approach taken previously was to assume that the back reaction, HP [1-¹³C]lactate to HP [1-¹³C]pyruvate, is negligible (15,17,19,20). This assumption, which is equivalent to the Michaelis-Menten kinetics model, may be appropriate if lactate rapidly exits the cytosol and no longer has access to lactate dehydrogenase. Another simplifying assumption is that the mass of lactate does not change over the time of HP observations. Over the ~2 minute time period in which HP experiments are carried out, this is a reasonable assumption. Information about the decay of HP [1-¹³C]pyruvate signal would also be useful but detection of this signal is complicated by its high intensity; even a tip angle as small as 1° can overflow the receiver and smaller tip angles mean lower signal from the metabolites of interest. The accuracy of flux measurements determined by fitting an HP data set assuming two pools (pyruvate and lactate) or three pools (pyruvate and intracellular lactate and extracellular lactate), or assuming unidirectional versus bi-directional exchange has not been investigated.

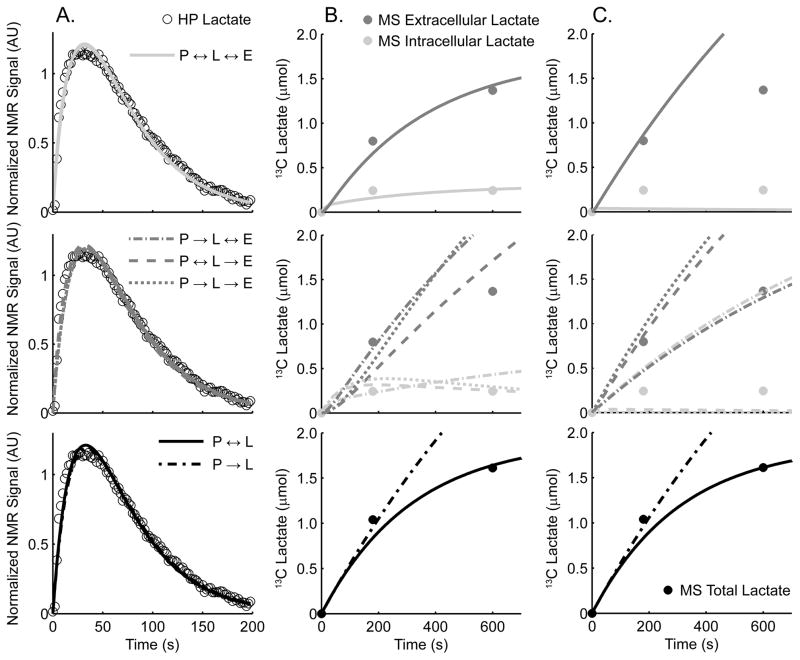
In this study, six kinetic models, summarized in Figure 1, were constructed and assessed. HP and mass spectrometric (MS) data were acquired from a convenient model system, a glioblastoma cell line. In this case, unlike in vivo or in perfused cells, the model does not need to include the delivery of pyruvate as a function of time since the cells are delivered to the hyperpolarized solution by a nearly instantaneous bolus. Three of the kinetic models allowed bi-directional flux between pyruvate and intracellular lactate, between intracellular lactate and extracellular lactate, or bi-directional flux among all three compartments. A fourth model incorporated unidirectional flux from pyruvate to intracellular lactate to extracellular lactate. A fifth model assumed a two-pool bidirectional exchange as applied earlier (4,11–14,16,18,21–23). The sixth model allowed only forward flux, pyruvate to lactate, as described in other reports (15,17,19,20). The most flexible model, three compartments with bi-directional fluxes, was fit simultaneously to both the MS and HP data sets to determine T₁ values for pyruvate and lactate. Using a large sample of randomized initial conditions, each of the six models was then used for fitting the HP data alone or the MS and HP data simultaneously. Only the two-pool bidirectional exchange or three-pool bidirectional exchange models were capable of providing results compatible with MS data and only the two-pool model accurately predicted the MS curve when the MS data is not provided as part of the fitting. Nevertheless, the initial rate of conversion of pyruvate to lactate could be estimated by all six models even when fitting only the HP data to the models. There was little difference in fluxes returned by fitting to either the unidirectional or bidirectional two-pool models.

Figure 1. Two and Three Pool Models.

The six models used to fit the kinetic data are shown. The definition of rate constants are: k_ij is the rate of transfer from pool i to pool j and P stands for pyruvate, L for lactate (total or intracellular), and E is for Extracellular lactate. Total pyruvate is in exchange with lactate such that it is converted instantly upon entering the cytosol. k_LP, k_LE, and k_EL can be set to zero in different combinations to create the various models.

Experimental

Shaped Pulses

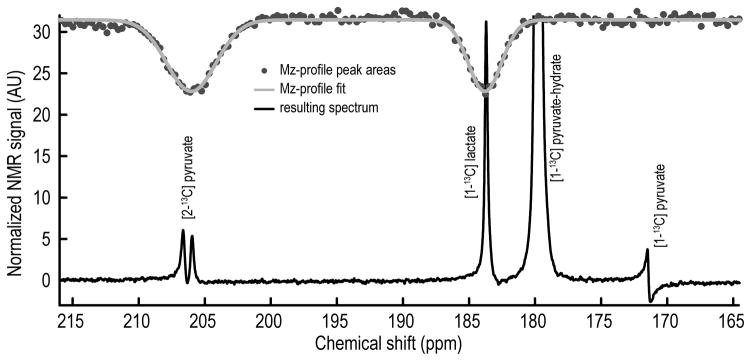
Selective pulses were created with VNMRJ PBox software (Agilent). Two Gaussian shapes were combined with frequency offsets set to pyruvate C2 (205.8 ppm) and lactate C1 (183.4 ppm) referenced to pyruvate C1 (171.1 ppm) with bandwidths of 500 Hz and 350 Hz, respectively. To test the efficiency of this double-Gaussian selective-excitation pulse, a frequency profile was collected using a concentrated sample of [1,6-¹³C₂]glucose (any enriched sample could be used). A series of spectra were collected by applying the double-Gaussian selective pulse at variable center frequencies followed by a single readout 90°-nonselective excitation. A plot of ¹³C magnetization versus center frequency verified the shape of the double-Gaussian excitation profile. The curve at the top of Figure 2 shows the resulting double-Gaussian z-magnetization profile collected using the glucose standard along with a fit of these data to the double-Gaussian function shown below.

Figure 2. Excitation Profile and Cell Suspension Spectrum.

This ¹³C NMR spectrum, the sum of 30 free induction decays, was acquired by application of a double-Gaussian selective pulse. The excitation angle experienced by lactate C1 (183.4 ppm) and pyruvate C2 (205.8 ppm) was ~18 degrees. Pyruvate C1 (171.1 ppm) with an approximate flip angle of <0.05° and pyruvate-hydrate C1 (179.5 ppm) with an approximate flip angle of 6.8° were also visible. The complete pulse Mz-profile across the spectrum is shown as a gray line.

$$\text{Signal}=A\left[exp\left(\frac{-{(x-b_1)}^2}{2{c_1}^2}\right)+exp\left(\frac{-{(x-b_2)}^2}{2{c_2}^2}\right)\right]+d$$ [1]

The single ¹³C spectrum shown in Figure 2 shows the results of application of this double-Gaussian excitation profile on a cell sample exposed to hyperpolarized [1-¹³C]pyruvate (discussed below).

Cell Preparation and Mass Spectrometry

SF188-derived glioblastoma cells overexpressing human Bcl-xL were grown as described previously (24). For HP experiments, cells were disengaged from the culture dish using 0.05% Trypsin/EDTA and rinsed once with PBS. Cells were resuspended at 1.25 ×10⁸ cells per mL Dulbecco’s Modified Eagle Medium (DMEM) containing L-glutamine (4 mM), NaHCO₃ (42.5 mM), HEPES (25 mM), dialyzed fetal calf serum (10% v/v) and Penicillin/Streptomycin. For MS analysis, 1 ×10⁷ cells were resuspended in 60 μl of the same medium with 6 mM Na-[3-¹³C]-pyruvate added for a concentration of 1×10⁸ cells/ml in 100 μl, and incubated at 37° C for 0, 3, and 10 minutes. After the culture period, both the medium and cell pellet were immediately frozen at −80° C. Cell pellets were reconstituted in 1 mL of 50% methanol spiked with 10.4 nmol isotopic lactate standard (Sodium L-[¹³C₃]-Lactate, Cambridge Isotope Labs), subjected to three freeze-thaw cycles and centrifuged to remove debris. For analysis of the culture medium, an aliquot of 25 μl was combined with 10.4 nmol of Sodium L-[¹³C₃]-Lactate and metabolites were extracted with sequential addition of 1 mL each of methanol, chloroform and water and recovery of the aqueous phase. Metabolites from both the intracellular and extracellular pools were evaporated and derivatized with 100 μl Tri-Sil reagent (Pierce), then analyzed for total lactate abundance and ¹³C enrichment as described previously (25).

Hyperpolarization and NMR Spectroscopy

Hyperpolarized pyruvate was prepared using 8.6 μL of neat [1-¹³C₁]pyruvic acid with 15 mM OX63 radical in an Oxford HyperSense DNP system (Oxford Instruments Molecular Biotools Ltd, Oxfordshire, UK). Microwave irradiation at 94.125 GHz with a power of 100 mW was applied for approximately 2 hours at 1.4 K. Rapid dissolution of the frozen sample was performed with 4 mL of 15.3 mM sodium bicarbonate at 190° C and 10 bar. 200 μl of the HP solution was placed in a 10 mm NMR tube and centered in a Varian 10-mm broadband probe tuned to ¹³C in a 9.4 Tesla magnet. Using a syringe attached by tubing to the top of the NMR tube, 0.8 mL of the cell suspension was introduced to the HP solution at the moment acquisition began, with a 6 mM final pyruvate concentration and cell density of 1.0 ×10⁸ cells/mL.

100 serial 18° double-Gaussian pulses were applied every 2 seconds. ¹³C spectra were collected with an acquisition time of 1 s over a bandwidth of 32 kHz into 32051 points and zero-filled before apodization and Fourier transformation. FIDs were simultaneously fit to a 4-resonance model using Bayesian Analysis (26–29) with uncorrelated phase to account for phasing errors of off-resonance peaks. The area of the pyruvate C2 resonance was used as a normalization factor for all resonances in each experiment to account for small differences in polarization levels, sample handling, timing, etc. Subsequently, the area of lactate C1 was additionally normalized in each experiment to account for any differences in cell number. The rate of signal decay due to RF depolarization by application of the selective double-Gaussian pulse was determined in a separate experiment without cells. An aliquot of pyruvic acid was hyperpolarized and dissolved into 4 mL of 160 mM sodium bicarbonate. 1 mL of the resulting solution was placed in a 10 mm NMR tube. First, the T₁ of pyruvate C1 was determined by applying fifteen 1° excitations over a period of ~30 s and this was followed by fifteen selective double-Gaussian excitations. The true T₁ of pyruvate C1 was evaluated from the first block of data and this was fixed in fitting the second block of data to evaluate the rate of pyruvate C1 decay solely due to RF depolarization during the double-Gaussian pulses.

Our objective was to use the natural-abundance pyruvate C2 signal as an indirect measure of the C1 signal so that destruction of polarization in C1 by application of RF observation pulses could be minimized. This was accomplished as follows. Given that all three carbons of pyruvate experience the same metabolism in the conversion of pyruvate to lactate, the decay curves of pyruvate C2 and C1 should be proportional to each other except for small differences in T₁ and applied pulse angles. Since the pyruvate C1 signal was not always visible from one experiment to another (it received on average an observation pulse estimated at <0.05°) while pyruvate C2 was always visible (it experienced an 18° pulse), we evaluated the decay rate constants for the two signals in those experiments where both signals were detected. Those decay rates (the rate of signal loss by all mechanism combined), when fitted to an exponential decay function, were estimated with a 95% confidence of fitting to be 0.0207 ± 0.0027 s⁻¹ and 0.0304 ± 0.0014 s⁻¹ for pyruvate C1 and C2, respectively. Data for C1 could then be estimated from the C2 time-course even when C1 was not detected using the relationship C1= 100*exp((τ₂−τ₁)t)C2 = 100*exp(0.00973t)C2. Both the lactate C1 and calculated pyruvate C1 HP curves were then fit to various metabolic models.

Modeling

Previous attempts at modeling pyruvate metabolite kinetics assume a set of first-order differential equations that describe the time dependent fate of each detected signal (4,11–13,15,17,18). Since these equations are first-order, they can be combined into a single differential equation using matrix notation:

$$\frac{d}{dt}\left[\begin{array}{c}\mathit{Pyr}\\ \mathit{Lac}\\ \mathit{ExLac}\end{array}\right]=\left[\begin{array}{ccc}-k_{PL}-{\rho }_P& k_{LP}& 0\\ k_{PL}& -k_{LE}-k_{LP}-{\rho }_L& k_{EL}\\ 0& k_{LE}& -k_{EL}-{\rho }_L\end{array}\right]\left[\begin{array}{c}\mathit{Pyr}\\ \mathit{Lac}\\ \mathit{ExLac}\end{array}\right]$$ [2]

where ρ_i = 1/T_1i for HP data, and ρ_i = 0 for MS. P is [1-¹³C₁]pyruvate, L represents intracellular [1-¹³C₁]lactate or total [1-¹³C₁]lactate, and E is extracellular [1-¹³C₁]lactate. Desired k_ij values can be set to zero to create each of the different models described in Figure 1. For example, all ks are set to zero except for k_PL to create the unidirectional two-pool model. This equation can be reduced by substitution to a simple differential equation dx/dt = Dx that has an exact solution x(t) = exp(D(t − t₀))x₀. This is the same solution as seen in the modified Bloch formulations (4,11–14,16–18). A delivery term accounting for time-dependent appearance of pyruvate was not needed in this experiment, but such a term could easily be added if necessary and the matrix equation would then take the form used by Spielman, et al. (19). A fourth pool, separating intracellular and extracellular pyruvate, could be included; however this only adds additional variables and does not benefit the determination of flux from pyruvate to lactate, which is the primary value under investigation in the literature. Since we were primarily interested in the total ¹³C transfer from pyruvate to lactate, rather than defining whether pyruvate transport or LDH activity was rate limiting, the extracellular and intracellular pyruvate pools were included as a single pool. Simulations using the four pool model did not produce significantly better fits of the data.

Fits were calculated by minimizing the sum of squares of the error using a program written in MATLAB (MathWorks). The program is a converging iterative method that is highly dependent upon the initial values given. For this reason, 1000 sets of uncorrelated initial values were used to avoid inclusion of fitting results derived from local minima detected by the fitting routine. The model solves this equation for each TR applying RF depolarization at each time-point to HP lactate only since pyruvate C1 experiences a minute excitation. Since the NMR cannot distinguish between intracellular and extracellular lactate, the sum of the two modeled lactate pools was used to fit the HP data set in the three-pool models. The RF depolarization rate was set based on the signal loss measured in a non-metabolic experiment with this frequency-selective double-Gaussian pulse.

The three-pool bi-directional exchange model was fit simultaneously to the HP and MS data sets with limited ranges of T₁ for lactate (20–35 s) and pyruvate (42–53 s). The allowed T₁ value ranges were determined by inversion recovery experiments in suspension medium. First, 1000 sets of randomized initial conditions for all ks were used to fit this model with the average values of both the HP (n=3) and MS (n=4) data sets. A histogram was constructed using the resultant error values. Utilizing this plot, the results corresponding to larger error values, which represent local minima, can be excluded. The best fits determined by histogram analysis of the resulting error values were then used to determine the pyruvate and lactate T₁ values.

The parameter ρ_i represents the decay of magnetization; for lactate this is the combined effect of the decay of both the intracellular and extracellular pools. The pyruvate decay includes all effects not caused by direct saturation or kinetics including T₁ relaxation, saturation of the hydrate signal (6.8°) and any possible magnetization transfer from the pyruvate C2 (which is present only at natural abundance). Both of these effects are likely negligible, however the model has the capability of accounting for them with in the ρ_i term since we are not interested in determining the “true” T₁ relaxation rates. The resulting ρ_i values were then set in the fitting program to determine kinetic rate constants for all six models with or without MS data using the same 1000 sets of initial values. T₁s were determined first in order to require all models to have the same T₁ values. This offers a comparable result for flux across all models. This was important for the remaining 5 models because they cannot reproduce the MS data. Therefore these models can mistakenly use the T₁ to compensate for changes in the k parameters.

Results

NMR

The use of a Gaussian-shaped pulse to excite [1-¹³C]lactate while applying a nominal flip angle to [1-¹³C]pyruvate minimizes the amplitude of [1-¹³C]pyruvate, eliminates the need to consider the destruction of magnetization caused by pulsing on carbon 1 of pyruvate, and prolongs the availability of HP [1-¹³C]pyruvate magnetization in the system. The efficiency of the double-Gaussian frequency selection is illustrated in Figure 2. The spectrum in this case is dominated by the pyruvate-hydrate C1 resonance at 179.5 ppm while the lactate C1 resonance at 183.4 ppm and the natural abundance pyruvate C2 doublet at 205.8 ppm were also easily detected. The frequency bandwidths of the Gaussians were narrow enough that the excitations were well separated from each other while still allowing nominal excitation of pyruvate C1. [1-¹³C]Alanine was detected in this cell line (data not shown) but is not seen here due to the selectivity of the shaped pulse combined with the relatively small amount of hyperpolarized alanine present in these cells.

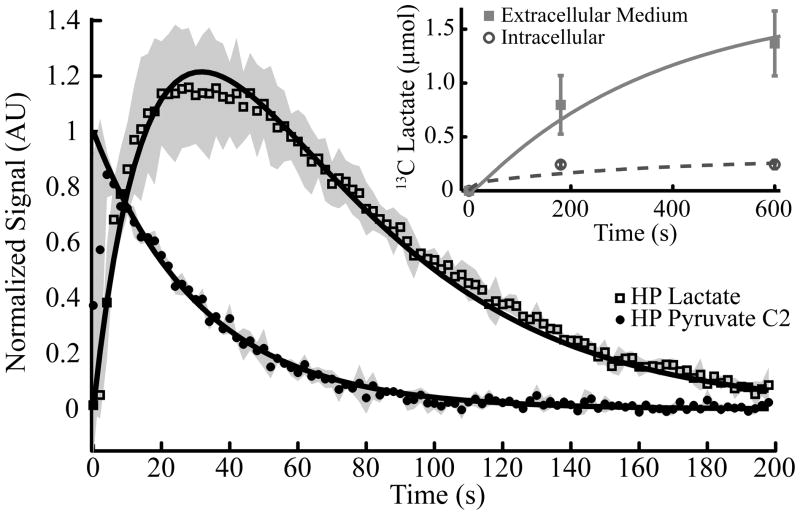
Formation of HP [1-¹³C]lactate was monitored every 2 seconds after the introduction of 6 mM HP [1-¹³C]pyruvate into the 1 mL suspension of glioblastoma cells (n=3) (see Figure 3). The HP data was then normalized to the initial value of the pyruvate C2 signal to compensate for any variations in the polarization level. Since the number of moles of pyruvate is precisely known at time = 0, this provides a direct measure of the initial signal per mole, supplying a y-axis for the NMR signal that can be translated into an actual number of moles detected given that T₁s and RF decay rates are known.

Figure 3. Lactate Kinetics in Cell Suspension.

Spectra were collected following the addition of 6 mM [1-¹³C₁]pyruvate in a cell suspension. The excitation profile was a double-Gaussian excitation designed to observe the hyperpolarized natural abundance C2 of pyruvate and the C1 of lactate. ¹³C lactate detected by MS in the medium and in the intracellular pool is shown in the inset. These data was fit simultaneously with the hyperpolarized ¹³C lactate to determine kinetic rates for a three-pool exchange model (fitted curves). Shaded areas denote the standard deviations of the lactate and pyruvate C2 data (n=3).

Mass Spectrometry

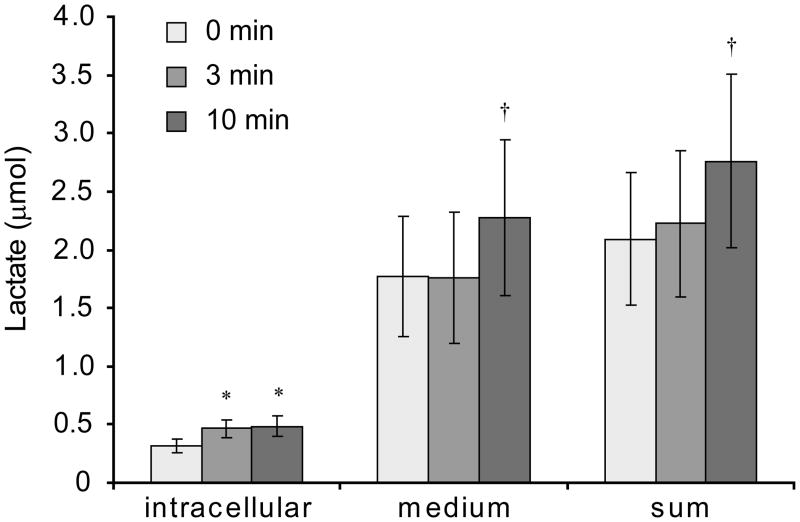
In a separate set of experiments using [3-¹³C]pyruvate exposed to cells, both intracellular and extracellular [3-¹³C]lactate and total lactate were measured by MS at 3 time points (0, 3, and 10 min). These data showed that intracellular ¹³C lactate reaches isotopic equilibrium quickly and is then exported out of the cell. The intracellular pool reaches isotopic equilibrium within the first 3 minutes with a final abundance of ¹³C lactate of 244 ± 39 nmol (mean ± 1 s.d., n=4). By the 10 minute time-point, it was apparent that the extracellular ¹³C lactate was near equilibrium as well (Figure 3, inset). The total intracellular lactate pool increased within the first 3 minutes from 319 ± 56 nmol to 486 ± 87 nmol. Importantly, despite entry of ¹³C into the lactate pool, the total abundance of lactate within the system (sum of intracellular and extracellular pools) did not change appreciably during the time of the HP experiment (Figure 4). Thus, ¹³C enrichment in the lactate pool was primarily due to exchanges between pyruvate and lactate and not net synthesis of lactate. This is in agreement with previous reports (11–13).

Figure 4. Lactate Pool Sizes.

Pool sizes for lactate intracellular, extracellular, and total lactate. The intracellular lactate pool does increase significantly within the first three minutes (* p < 0.005) but the total lactate does not increase until later at the 600 s time-point († p < 0.01). p values based on the student t-test.

Modeling

Both the HP and MS data sets were fit simultaneously to a three-pool bi-directional exchange model (Model 1, Figure 1) beginning with 1000 randomly generated initial k values and constrained ranges for the T₁ values of pyruvate and lactate. The resulting fits reported a T₁ value of 48.03 s for pyruvate C1 (ρ_P = 0.021 s⁻¹) and a T₁ of 28.41 s for lactate C1 (ρ_L = 0.035 s⁻¹). All six models were fit again after fixing these T₁ values using the average values of the HP (n=3) and MS (n=4) data sets. The resulting apparent rate constants for the three-pool bi-directional exchange model were: k_PL = 1.11 × 10⁻³ s⁻¹, k_LP = 0.015 s⁻¹, k_LE = 0.06 s⁻¹, and k_EL = 0.01 s⁻¹ corresponding to an initial flux rate of 241 μmol/billion cells/hr into the lactate pool. The fitted curves are shown in Figure 3.

Figure 5 shows the results of fitting the HP and MS curves simultaneously (A and B) or fitting the HP alone (A and C) for the six different kinetic models. Here, the T₁ value for pyruvate C1 and lactate C1 were fixed to the values determined earlier. Interestingly, all six models were able to provide good fits to the HP lactate signal with or without the MS data (A). When both the MS lactate and HP lactate were used to determine the kinetics (B) only the three-pool bi-directional model and the two-pool bi-directional model were able to produce good fits to the MS data. The remaining models resulted in indistinguishable HP fits but could not fit the MS data. However, when the HP data was fit without the MS information (C), the calculated ¹³C lactate time-courses were inconsistent with the MS data for all of the three-compartment models. Similarly, the unidirectional two compartment model, pyruvate → lactate, resulted in a curve that was incompatible with the measured MS data. Finally, the two-pool bi-directional was the only model to result in a curve that was compatible with the MS observations.

Figure 5. Comparing Model Results.

Fitting results corresponding with Table 1. Column A contains the resulting HP fits for the corresponding MS plots in B and C. Fits for the MS lactate data (B) and curves generated by fitting HP data only (C) with MS data displayed for reference are also shown. The first row plots the results for the three-pool bidirectional model, while the remaining three-pool models (each containing at least one unidirectional component) are shown in the second row. The third row displays the results of the two-pool models, both the bidirectional model and the unidirectional model (the two most commonly used models in the HP literature).

Although only the two-compartment bi-directional model provided data consistent with MS results acquired over 10 minutes, only the three-pool bi-directional model is capable of matching the MS data completely where the intracellular and extracellular pools of ¹³C lactate are discernible. However, all 6 models provided similar initial flux values, summarized in Table 1. Initial flux rates of ¹³C from pyruvate to lactate at time = 0 are shown in units of μmol/billion cells/hr. There is a slight underestimation for the two two-pool models compared to the full three-pool bidirectional model that best fits both the full MS and HP data sets. Since MS or other alternative methods of measuring ¹³C lactate concentration as a function of time are unavailable for HP pyruvate experiments in vivo, it is important that the results of fitting HP only agree well with those that included the MS data. Both the two-pool bidirectional model and the two-pool unidirectional model provide nearly identical results whether determined by HP and MS or HP only as well as resulting in similar initial flux values as each other, with the unidirectional model resulting in a slightly lower value than the bidirectional model result. The three-pool bidirectional model, which best fits the MS data, does not reproduce the results when fitting HP data only. In fact, the back reaction k_EL was minimized and all k values had nearly the same result as those from the third model: P ↔ L → E. Additionally, the other two three-pool models did not have converging values for k_EL and k_LE.

Table 1. Flux from Pyruvate to Lactate.

Initial flux values for pyruvate to lactate for the six different models of Figure 1 fit (n=3) with and without MS data. The flux is calculated by multiplying the k_PL rate constant by the initial pyruvate concentration. Three-pool models were fit with the two pool lactate MS data while two-pool models were fit with the total lactate pool. These values correspond to the curves shown in Figure 5.

Model	P → L (t0) (μmol/billion cells/hr)
	Fitting MS and HP	Fitting HP only
P ↔ L ↔ E	253 ± 81	293 ± 119*
P → L ↔ E	208 ± 32	210 ± 32**
P ↔ L → E	241 ± 61	293 ± 119
P → L → E	208 ± 31	210 ± 32**
P ↔ L	221 ± 41	224 ± 54
P → L	208 ± 32	210 ± 32

^*k_LE minimized resulting in model identical to P ↔ L → E

^**k_EL and k_LE did not converge

Using the same methods with the HP data alone, both of the two-pool models were explored further to determine the impact of the variables on the determined flux. Data was fit to the HP lactate curve without including any information from pyruvate, to simulate a lack of knowledge of the pyruvate that can occur with more complicated systems. The lactate HP data was fit again, this time utilizing the initial signal of the pyruvate time course which serves as a normalization and measure of the concentration-to-signal ratio. Then, adding the HP pyruvate time course back into the fitting, the models were explored when T₁s and RF depolarization are fit simultaneously, RF depolarization is ignored, and when a large RF depolarization rate is fixed. All of these results are displayed in Table 2. In addition to table 2, the models were fit with intentionally incorrect parameter values. Using large and small RF depolarization rates as well as a large T₁ for lactate (T_1L = T_1P = 48 s). In this case where the pyruvate time course is known and its relation to concentration is not complicated, the model cannot fit the data except in the case of a large T₁ and a large RF depolarization rate resulting in a flux of 223.7 μmol/billion cells/hr for the bidirectional model, but still cannot fit the data with the forward model.

Table 2. Fitted Results for Two-pool Models Under Various Conditions.

Both of the two-pool models were fit to the HP lactate curve with and without the pyruvate HP data. The first set was done without pyruvate; secondly, the initial value of the pyruvate decay was included as a normalization factor. The third set was done with the pyruvate time-course included as well as the initial value and then the last set was done by excluding the decay due to pulsing. All of these models fit the lactate curve well. Flux is the initial flux from pyruvate into lactate at time t = 0 in μmol/billion cells/hr.

	Two-pool Bidirectional (P ↔ L)				Two-pool Unidirectional (P → L)
	flux	T1L (s)	pw	T1P (s)	flux	T1L (s)	pw	T1P (s)
HP Lactate Fit
No Pyruvate	989	43	9.0°	57	6356	54	3.4°	51
Lactate & Pyr (t=0)	242	45	9.3°	59	236	32	16.8°	60
HP Lactate and Pyruvate Fit
With RF signal decay	223	294	1.2°	46	217	37	10.4°	48
Ignore decay	223	179	-	47	219	25	-	48
Large decay (18°)	216	224	-	48	214	64	-	48

Discussion

With the increase in NMR sensitivity provided by DNP, ¹³C NMR has become a promising modality to non-invasively measure metabolic fluxes through individual enzymatic catalyzed steps. However, measurement of these fluxes in vivo with hyperpolarized ¹³C NMR is not straightforward. We used a simplified metabolic model of glioblastoma cells in a suspension to evaluate the reliability of six different approaches for measuring kinetic parameters. The detection of both [1-¹³C]lactate and natural abundance [2-¹³C]pyruvate with a high signal-to-noise ratio was enabled by use of a selective double-Gaussian excitation pulse. This method had the advantage of markedly attenuating the HP [1-¹³C]pyruvate signal and preserving polarization in the pyruvate pool for an extended period. Although high quality time-intensity data for both HP [1-¹³C]lactate and HP [2-¹³C]pyruvate could be obtained in this system, a number of issues arise when attempting to fit these data to kinetic models.

Previous studies have used the signal from C1 of pyruvate to determine the relation between pyruvate signal and concentration (12,17,18). This information is essential for measuring flux in absolute units and for direct comparison between experiments, but this approach has the disadvantage that acquisition of the C1 signal depletes polarization. Observation of the pyruvate C2 signal also allows an absolute measure of the initial pyruvate signal but it has the advantage of preserving polarization in the C1 of pyruvate for exchange into the lactate pool. A second advantage of the double-Gaussian pulse is that the shallow flip angle associated with the pyruvate C1 resonance means that the signal decay in pyruvate C1 was due essentially entirely to T₁ and kinetic exchange without depletion due to RF pulses. While this approach is useful in vitro where the pyruvate C1 signal is significantly higher than the lactate C1 signal, it may not be the best approach in vivo since the pyruvate and lactate signals are usually comparable in intensity. Instead of using the C2 in this case, it might be advantageous to utilize selective pulsing to excite the pyruvate C1 with a smaller tip angle than the lactate in order to preserve more of the polarization while still being able to detect it directly. Indeed, Vigneron and co-workers have demonstrated the utility of this approach in a mouse model of prostate cancer (30).

In preliminary experiments with simulated data sets, the interaction between T₁ of the lactate pool and signal destruction due to RF pulses was investigated. After n pulses, the NMR signal is described by the equation S (n)= M₀ cos⁽ⁿ⁻¹⁾ θ sin θ exp(−(n−1)TR/T₁) (31), where TR is the repetition time. This can be rewritten in terms of time such that the equation becomes:

$$\begin{array}{l}S(t)=tan(\theta )M_{0}cos{(\theta )}^{t/TR}{e}^{-t/T_1}\\ =tan(\theta )M_0{e}^{-(a+b)t}\end{array}$$ [3]

where a is 1/T₁ and b = −log(cos θ)/TR. This equation indicates that signal decay due to flip angle and T₁ are indistinguishable, and that both factors will interact in the fitting. Some previous studies have ignored RF depolarization due to minimal excitation angles (4,12,13,15), while some have taken this decay into account (17,19). In this experiment, a 1 mL volume was used to reduce errors associated with RF depolarization in sample outside of the active coil region (32). We then directly measured the decay due to RF depolarization in the same volume in the absence of metabolism to be sure this parameter was accurate and then it was included in the model.

In some reports of exchange modeling, the T₁s were assumed fixed or the same for all metabolites due to the large number of parameters (4,11–13,17,21). In the current study, a complete set of HP data plus MS data was used to fit the most flexible model, three-compartment bi-directional exchange, to determine the T₁s of pyruvate and lactate. This was done for ease in comparing across the different models, but is not necessary when determining the initial flux rate of a given model. RF depolarization and T₁ relaxation rates can be fit simultaneously for the two different two-pool models and still output the same flux value (Table 2). There is a strong correlation between the resulting T₁s and RF depolarization rate due to the relationship described above. This also means that the choice of T₁ and RF depolarization rate can influence the ability to fit the model. For example, when both values are set incorrectly or if the pulse angle is set too high such that the fitted T₁ cannot compensate for this faster decay of signal, the model will be unable to fit the data well.

In this experiment, which does not have a pyruvate input function, the shape of the HP pyruvate curve seems to dictate the flux value. If the lactate HP time-course is fit alone, neither of the two-pool models can accurately determine the flux value (Table 2). This might indicate that unknowns associated with the delivery of the pyruvate might result in incorrect flux measurements if the T₁s and RF depolarization are not well known.

As shown in Figure 5C where MS data were not included in fitting, four of the six models produced implausible results for lactate enrichment, even though all six models fit the HP data set. This led to an important clarification: all models containing a unidirectional flux were capable of fitting experimental data when only HP data are considered. However the presence of a unidirectional flux was not consistent with the observed approach to equilibrium in the MS data. One important measurement from this data is the flux from pyruvate to lactate. While the flux values for ¹³C labeling change over time with the changing concentration of the label, the initial flux of ¹³C from [1-¹³C]pyruvate into [1-¹³C]lactate reflects the absolute flux in one direction upon the introduction of pyruvate to the cells. These values are listed in the first column of Table 1. When the MS data is included in the fit, these values are approximately the same regardless of the model used (column one). None of the results are significantly different from the full bidirectional model results (student t-test).

Although the three-pool bi-directional exchange model appeared to be the most accurate based on the MS data, both of the two-pool models result in an accurate estimate of initial flux value with or without inclusion of the MS data (Table 1). These are the models most commonly chosen in HP flux measurement experiments in the literature (4,11–20). The resulting initial flux rates for these three models are not significantly different and have an average value of 222 ± 52 μmol/billion cells/hr. This consistency among the three models suggests that other groups investigating isolated cells in suspension would have arrived at the same results regardless of the model chosen (4,12,16–18). Whether the results are correct or not depends upon the accuracy in determining decay rates due to pulsing and relaxation. Lactate labeling inside the cell and export of labeled lactate into the extracellular space both occur rapidly in this system and reach equilibrium within 3 minutes, or approximately within the time course of the ¹³C NMR observations. In this model system, when pyruvate is the major carbon source, transfer of ¹³C between pyruvate and lactate detected by HP NMR is the result of bi-directional equilibrium exchanges among these pools rather than net lactate formation.

Conversion of pyruvate to lactate is a classical hallmark of tumor metabolism and is positively influenced by many of the tumorigenic mutations that promote the malignant transformation of human cells (5). Exchanges between pyruvate and lactate are catalyzed by lactate dehydrogenase (LDH), which is highly expressed in malignant cells (33). Thus the precise measurement of LDH flux in tumors is a major goal for advanced metabolic imaging in cancer. The robustness of the approach presented here is underscored by the observation that the measured LDH flux, 253 ± 81 μmol/billion cells/hr for a full bidirectional exchange model, is close to the rate of ¹³C lactate formation in these same cells measured by conventional NMR, 370 μmol/billion cells/hr (34). The modest reduction in LDH flux here and the lack of net lactate formation are likely due to the absence of glucose in the medium as HP experiments performed in the presence of glucose result in increased lactate signal (data not shown). Ongoing glycolysis would tend to lower the cellular NAD+/NADH ratio, favoring the net formation of lactate. The pyruvate/lactate ratio in various compartments is commonly used as a surrogate for the cytoplasmic NAD⁺/NADH ratio (35). We suggest that the method described here, including the key element of quantification of pyruvate abundance, could be adapted to provide an estimation of the cytoplasmic NAD⁺/NADH ratio in tumor cells in culture and in vivo.

Although the capacity of each model to fit HP data sets was indistinguishable, the additional information provided by MS demonstrated that the three-pool exchange model captures the kinetics of conversion of pyruvate to intracellular lactate and eventual export to extracellular lactate in these glioblastoma cells. Nevertheless the choice of model made little difference in determining the initial flux of pyruvate into lactate, at least in these experiments, where delivery of hyperpolarized material is precisely controlled. Analysis of data from isolated perfused tissues or from in vivo exams is further complicated by the changing concentration of the delivered hyperpolarized molecule. As shown in the first two rows of Table 2, a HP z-axis provided by the pyruvate signal at t = 0 provides enough information to accurately determine the flux value when only lactate data is provided. Therefore, a measure or model of the pyruvate concentration during its delivery in these more complex systems should be sufficient to extract accurate flux data.

Abbreviations

DNP

Dynamic Nuclear Polarization

HP

Hyperpolarized

LDH

lactate dehydrogenase

MS

Mass Spectrometry

RF

radiofrequency