Enhanced Phase Synchronization of Blood Flow Oscillations between Heated and Adjacent Non-heated Sacral Skin

Abstract

The study of skin microcirculation may be used to assess risk for pressure ulcers. It is observed that local heating not only causes an increase in blood flow of the heated skin but also in the adjacent non-heated skin. The underlying physiological mechanism of this indirect vasodilation of the non-heated skin remains unclear. We hypothesized that blood flow oscillations (BFO) in the adjacent non-heated skin area synchronize with BFO in the heated skin, thus inducing a vasodilatory response. We investigated BFO in the heated and adjacent non-heated skin (12.1±1.2 cm distance) on the sacrum in 12 healthy participants. The ensemble empirical mode decomposition (EEMD) was used to decompose blood flow signals into a set of intrinsic mode functions (IMFs), and the IMFs with power spectra over the frequency range of 0.0095–0.02 Hz, 0.02–0.05 Hz, and 0.05–0.15 Hz were chosen as the characteristic components corresponding to metabolic, neurogenic, and myogenic regulations, respectively. Then, the instantaneous phase of the characteristic components was calculated using the Hilbert transform. From the time series of phase difference between a pair of characteristic components, the epochs of phase synchronization were detected. The results showed that myogenic and neurogenic BFO exhibit self-phase synchronization during the slower vasodilation of the heated skin. In the non-heated skin, the degree of synchronization of BFO is associated with the changes in blood flow.

1 Introduction

The study of skin microcirculation may be used to assess risk for pressure ulcers and effectiveness of preventive intervention [11, 12, 14, 15, 21]. A basic function of skin microcirculation is to regulate blood flow to meet the metabolic demands of local cells and to regulate skin temperature through a dynamic control of vascular resistance and blood flow redistribution [34, 35]. Pathological conditions (eg. spinal cord injury and aging) cause an impairment of vasodilatory response [12, 24, 26]. Recent studies have shown the promise that skin blood flow may be used to assess comparative effectiveness of preventive interventions, including wheelchair tilt and recline usage and alternating pressure support surfaces [14, 15]. Through relative changes in skin perfusion, proper wheelchair tilt and recline angles can be determined for reducing skin ischemia, thus preventing superficial pressure ulcers. Skin blood flow oscillations (BFO) provide another means to examine the underlying physiological regulations and pathological changes in people with various neurological diseases. BFO exhibits five characteristic frequencies, including metabolic (0.0095–0.02 Hz), neurogenic (0.02–0.05 Hz), myogenic (0.05–0.15 Hz), respiratory (0.15–0.4 Hz), and cardiac (0.4–2.0 Hz) origins [11, 12]. In addition to frequency components of BFO, the complexity of BFO also provides useful information to quantify microvascular dysfunction. Liao and Jan demonstrated that a decrease in complexity of skin BFO is associated with impaired vasodilation in people with SCI [21]. The exact role of skin blood flow in the pressure ulcer development remains to be determined.

Local heating causes a biphasic increase in skin blood flow, including the first peak induced by sensory axon reflex and the second peak induced by endothelial nitric oxide [23]. We observed that local heating not only causes an increase in skin blood flow in the heated skin but also in the non-heated skin (ie. no change in skin temperate). An example of this non-heating induced vasodilation was shown in Fig. 1. The phenomenon may be critical in understanding the role of microvascular network in regulating skin blood flow. This indirect vasodilation may be attributed to the interaction of BFO [40, 42]. The heart and respiratory oscillations have been found to be synchronized [37, 40, 42]. Stefanovska et al. [44] demonstrated that BFO generated by cardiac and respiratory systems are strongly self-synchronized (spatially synchronized between oscillations of the same physiological origin) throughout the entire network. The authors suggested that myogenic oscillations at best are only weakly self-synchronized [40, 44].

Fig. 1.

Influence of local heating on blood flow in the adjacent non-heated sacral skin area (distance to the heated skin area about 10 cm). (a) After a 10-min pre-heating period, a heating probe was used to heat the sacral skin to 42°C in 2 minutes and to maintain that temperature for 50 min, inducing a biphasic vasodilation in the heated skin area. (b) At a sacral skin site 10 cm distance to the heated skin, skin blood flow also shows an increasing trend.

To investigate self-synchronization of BFO during local heating, a number of issues need to be addressed. First, myogenic, neurogenic, and metabolic oscillations cannot be selectively measured and thus have to be extracted from blood flow signals. Second, because blood flow in the heated skin is much higher than in the surrounding area (Fig. 1), synchronization measures that quantify interrelation between amplitudes, e.g. coherence function, may not be suitable. On the other hand, these oscillators at different sites of the network may be weakly self-synchronized. Since weak couplings typically affect the phases while the amplitudes may remain uncorrelated [29], considering phase synchronization may be a good choice. Third, the instantaneous phase of a signal can be defined from the Hilbert transform [33] or wavelet transform [48]. In wavelet approach, one needs to choose the center frequency and the frequency width of the wavelet, which adjust the frequency range of interest. Unfortunately, the characteristic frequencies of BFO are not constant but vary with time even without external stimulation [42, 43, 45]. The Hilbert transform is free of parameters. However, it requires a narrow-band power spectrum of the signal [31]. In previous studies signals to be analyzed were usually band-pass filtered [17, 28]. However, it has been found that band-pass filtering can lead to spurious detection of phase synchronization [49, 51]. An alternative approach is the empirical mode decomposition (EMD) [8] or the ensemble EMD (EEMD) [50]. These two techniques were designed to extract intrinsic modes from nonlinear and non-stationary data. Each mode admits well-behaved Hilbert transform and is related to a specific physiologic process [8]. Finally, because phase synchronization may occur only in some time intervals, indices characterizing the overall degree of phase synchronization [18, 31] may be less suitable. Recently, techniques for detecting epochs of phase synchronization have been proposed [1, 16]. However, these techniques involve the choice of a number of parameters, which may be a challenge in practical applications. In this study, we used the concept of phase synchronization to investigate the relationship of BFO between heated skin and non-heated sacral skin. We hypothesized that BFO in the non-heated skin synchronize with BFO in the heated skin, thus inducing a vasodilatory response.

2 Methods

2.1 Participants

Twelve healthy participants (age 25.3±5.4 yrs (mean ± standard deviation), 5 males and 7 females, body mass index 23.2±2.4 kg/m²) were recruited into this study. The exclusion criteria included any diagnosed cardiopulmonary diseases, smoking history, or use of any medication that may affect cardiopulmonary function. This study was approved by the University Institutional Review Board. Informed consent was obtained from each participant prior to any testing.

2.2 Procedures

The experimental protocol included a 10-min pre-heating period, a 50-min heating period, and a 10-min recovery period. While research participants were in a prone position, a combined probe of heating and laser Doppler flowmetry (LDF) (Probe 415-242 & PF5010, Perimed AB) was used to heat the sacral skin to 42°C in 2 minutes and to maintain that temperature for 50 min. The specific location on the sacrum is the midpoint between right posterior superior iliac spine (PSIS) and spinal processes. The other LDF probe was placed on the left sacrum at the same horizontal level with the distance between two LDF probes at 12.1±1.2 cm. LDF used in this study utilizes a 780 nm laser light with a separation of 0.25 mm between emitting and receiving probes. This configuration leads to a measurement depth on the order of 0.5–1 mm for the human skin [9]. The sampling rate of LDF blood flow signals was 32 Hz. The LDF is a well accepted tool to assess microcirculation, and a comparison of skin perfusion measured between LDF and radioisotropic clearance techniques (the most accurate measurement of skin perfusion) yields a linear relationship with correlation coefficients up to 0.98 [27].

2.3 Extraction of the characteristic components of BFO

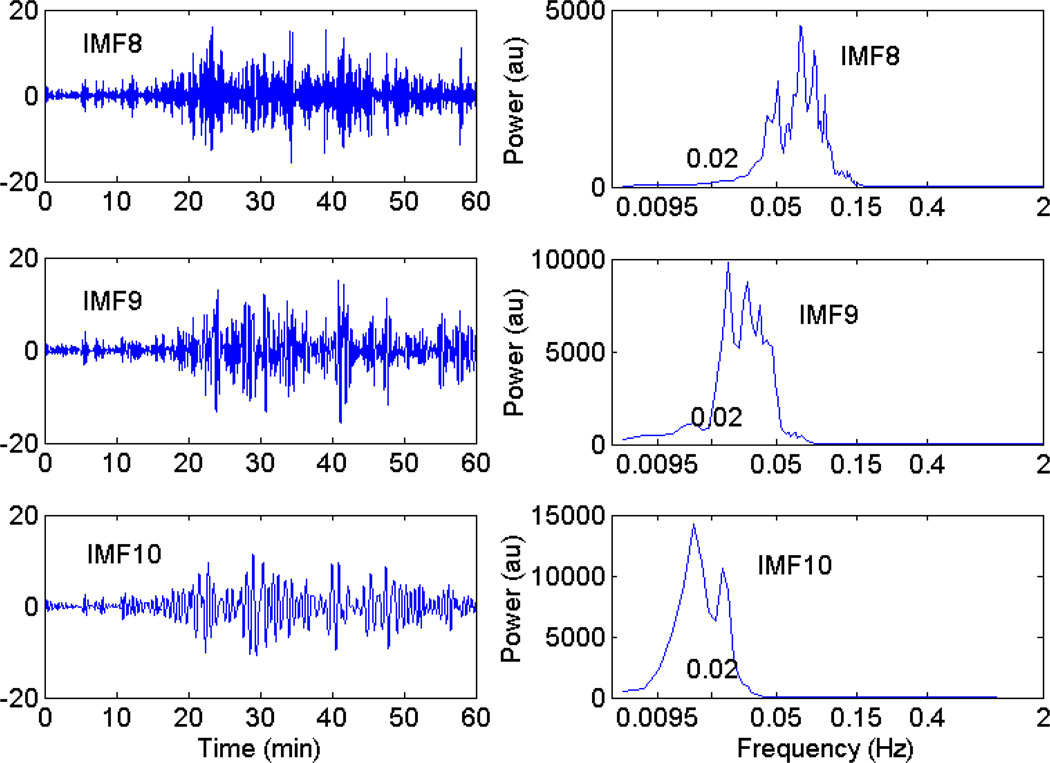
We used the EEMD method [50] to extract the characteristic components of BFO. This technique is based on the assumption that any complicated data set consists of a finite and often small number of ‘intrinsic mode functions’ (IMFs) that admit well-behaved Hilbert transforms [8]. Moreover, each IMF can be related to a specific underlying process [8]. Fig. 2 shows the obtained IMFs from the blood flow signal shown in Fig. 1a and their power spectra. By visually inspecting the power spectra of the IMFs, one can easily choose an IMF as metabolic, neurogenic or myogenic component of BFO. According to this principle, the eighth IMF (IMF8), ninth IMF (IMF9), and tenth IMF (IMF10) were respectively chosen as myogenic, neurogenic, and metabolic component of BFO for all data sets of this study.

Fig. 2.

Intrinsic mode functions (IMFs) extracted from the blood flow signal shown in Figure 1a during 1–60 min (left panel) and their power spectra (right panel). Only the eighth IMF (IMF8), the ninth IMF (IMF9), and the tenth IMF (IMF10) are calculated and shown in the left panel. By visually inspecting the power spectra of the IMFs, IMF8, IMF9 and IMF10 were respectively chosen as myogenic, neurogenic, and metabolic component (right panel).

2.4 Instantaneous phase

From a characteristic component of BFO, x(t), the Hilbert transform can be used to construct an analytic signal, z_x(t) = x(t) + ix̃(t) = A(t)e^iØ(t), where x̃(t) is the Hilbert transform of x(t), defined as [33]

$$\tilde{x}(t)=\frac{1}{\pi }p.v.{\displaystyle \int \frac{x(\tau )}{t-\tau }d\tau }$$ (1)

where p.v. denotes the Cauchy principal value. The instantaneous phase is given by

$$Ø(t)=\mathit{\text{arctan}}\frac{\tilde{x}(t)}{x(t)}$$ (2)

It should be noted that this method can only be applied when the signal x(t) has a narrow frequency band.

2.5 Detection of epochs of phase synchronization

For a pair of characteristic components of BFO, we considered the instantaneous phase difference

$$\mathrm{\Delta }Ø={Ø}_1-{Ø}_2$$ (3)

where Ø₁ and Ø₂ are the unwrapped instantaneous phases of the components. The presence of 1:1 phase synchronization is defined by the condition |ΔØ| < const [47]. In this case the phase difference ΔØ fluctuates around a horizontal plateau. To detect the epochs of phase synchronization, we adopted the algorithm proposed by Karavaev et al. [16]. This algorithm consists of linear approximation of the series of instantaneous phase difference in a moving window using the least squares approach. As illustrated in Fig. 3a, for each time moment t, we calculate the slope of the linear regression line, α, in the window [t − τ/2, t + τ/2], and thus obtaining a time series consisting of such slopes (Fig. 3b). Intuitively, in a region of phase synchronization the phase difference fluctuates around a horizontal plateau, resulting in small values of |α|. Therefore, an epoch was considered as a synchronization epoch if |α| is smaller than a threshold δ for all time moments in the epoch and the duration of the epoch exceeds T seconds.

Fig. 3.

Detection of epochs of phase synchronization. (a) The time series of instantaneous phase difference between a pair of characteristic components of blood flow oscillations (hear only a 10-min segment is shown). At each time moment t, the slope of the linear regression line, α, in the window [t − τ/2, t + τ/2] is calculated. It should be noted that α is not defined for the initial and final regions of the time series of phase difference with the duration of τ/2. (b) The time series of α. An epoch is considered as a synchronization epoch if |α| is smaller than a threshold δ for all time moments in the epoch and its duration exceeds T seconds.

The detected epochs of phase synchronization depend on the parameters τ, δ, and T (Fig. 3). Karavaev et al. [16] proposed that choosing these parameters should be guided by the concept that the automatically detected epochs should be similar to those identified by visual inspection. The authors recommended the following parameters: τ is close to the characteristic period of oscillations, T is about one to two characteristic periods, and δ is about 0.005–0.01. However, we found that the parameter δ is dependent on the number of data points in one characteristic period of oscillations.

2.6 Simulation study on coupled model systems

To test the reliability of the above algorithm and investigate the dependence of the parameters τ, δ, and T on the number of data points in one characteristic period of oscillations, we considered two coupled Rössler systems [36]

$$\begin{array}{c}{\dot{x}}_{1,2}=-{\omega }_{1,2}{y}_{1,2}-z_{1,2}+C(x_{2,1}-x_{1,2})\hfill \\ {\dot{y}}_{1,2=}{\omega }_{1,2}{x}_{1,2}+0.15y_{1,2}\hfill \\ {\dot{z}}_{1,2}=0.2+z_{1,2}(x_{1,2}-10)\hfill \end{array}$$ (4)

where the parameters ω_1,2=1±Δω control the frequency mismatch and the parameter C controls the strength of coupling [33]. We used ω_1,2=1±0.1 and C from 0 to 0.5 with a step of 0.01. The Rössler system has a narrow frequency band [18], and the instantaneous phase can be defined through the Hilbert transform [33]. The blood flow signals to be analyzed had a duration of 60 min and were recorded with a 32 Hz sampling rate. To decrease the time spent on surrogate tests, we re-sampled the characteristic components to 8 Hz. Thus, under the assumptions that myogenic, neurogenic, and metabolic BFO have a characteristic frequency of 0.1 Hz, 0.04 Hz, and 0.01 Hz [42, 43], they have approximate 80 points, 200 points, and 800 points per cycle, respectively. Therefore, we integrated Eq. 4 using a Runge-Kutta 4th order scheme with a step of 0.01 sec and a time span of 60 min, yielding a time series with approximately 680 points per cycle. Then the time series was sub-sampled by a factor of 3 to yield a time series with approximately 230 points per cycle, and sub-sampled by a factor of 8 to yield a time series with approximately 80 points per cycle. The degree of phase synchronization was quantified by the percentage of phase synchronization, defined as [1, 17]

$$s=\frac{{\displaystyle {\sum }_{k=1}^n{d}_k}}{l}\times 100\%$$ (5)

where n is the number of epochs of phase synchronization, d_k is the duration of the kth epoch, and l is the entire duration of time. Fig. 4 shows the phase difference between x₁ and x₂ (Eq. 4) and the values of s for different coupling strengths C. The parameters are as follows. For the time series with approximately 80 points per cycle, τ=6 sec, δ=0.015, T=8 sec; for the time series with approximately 230 points per cycle, τ=15 sec, δ=0.008, T=20 sec; and for the time series with approximately 680 points per cycle, τ=45 sec, δ=0.002, T=60 sec. The simulation results showed that, when using appropriate parameters τ, δ, and T, s monotonously increases with C, indicating that the algorithm described in section 2.4 can reliably quantify the degree of phase synchronization. Also, the results indicated that the parameters should be chosen according to the number of data points in one cycle.

Fig. 4.

Results of simulation study on two coupled Rössler systems. (a), (c), and (e) Phase difference of the coupled systems (x₁ and x₂ in Eq. 4) with approximately 680 points per cycle (a), 230 points per cycle (c), and 80 points per cycle (e) for different strengths of coupling. (b), (d), and (f) Percentage of phase synchronization versus the strength of coupling.

2.7 Estimation of the statistical significance level of results

Because spurious phase synchronization can be detected even in the case of completely uncorrelated phases [33], we assessed the statistical significance of obtained results using surrogate time series [38]. For each of a pair of IMFs that represent myogenic, neurogenic, or metabolic BFO, we generated a surrogate time series by performing a Fourier transform on the IMF, preserving the amplitudes of the Fourier transform but randomizing the phases, and performing an inverse Fourier transform. Then, we s calculated value using the same procedure performed on the original data. We repeated this process (2000 times in this study) and obtained a probability distribution of s, P(s). As illustrated in Fig. 5, for a result s′ calculated from blood flow data, its significance level p is defined as the ratio of the area under P(s) corresponding to s ≥ s' to the entire area under P(s) [17]. Particularly, If s′ is smaller (lager) than all values of s calculated from surrogate data, p=1 (p=0). When p<0.05, s′ was considered to be statistically significant. The 5% significance level s_0.05 (95% confidence level) is defined as the s value when the ratio equals to 0.05 (Fig. 5).

Fig. 5.

Estimation of the statistical significance level of results. Suppose that the percentage of phase synchronization of blood flow oscillations is s′, and that the probability distribution of s, constructed from surrogate time series, is P(s). The significance level of s′ is defined as the ratio of the area under P(s) corresponding to s ≥ s′ (the shadow part) to the entire area under P(s). The 5% significance level s_0.05 (95% confidence level) is the s value when the ratio equals to 0.05. In this example, P(s) was constructed from 2000 pairs surrogate time series.

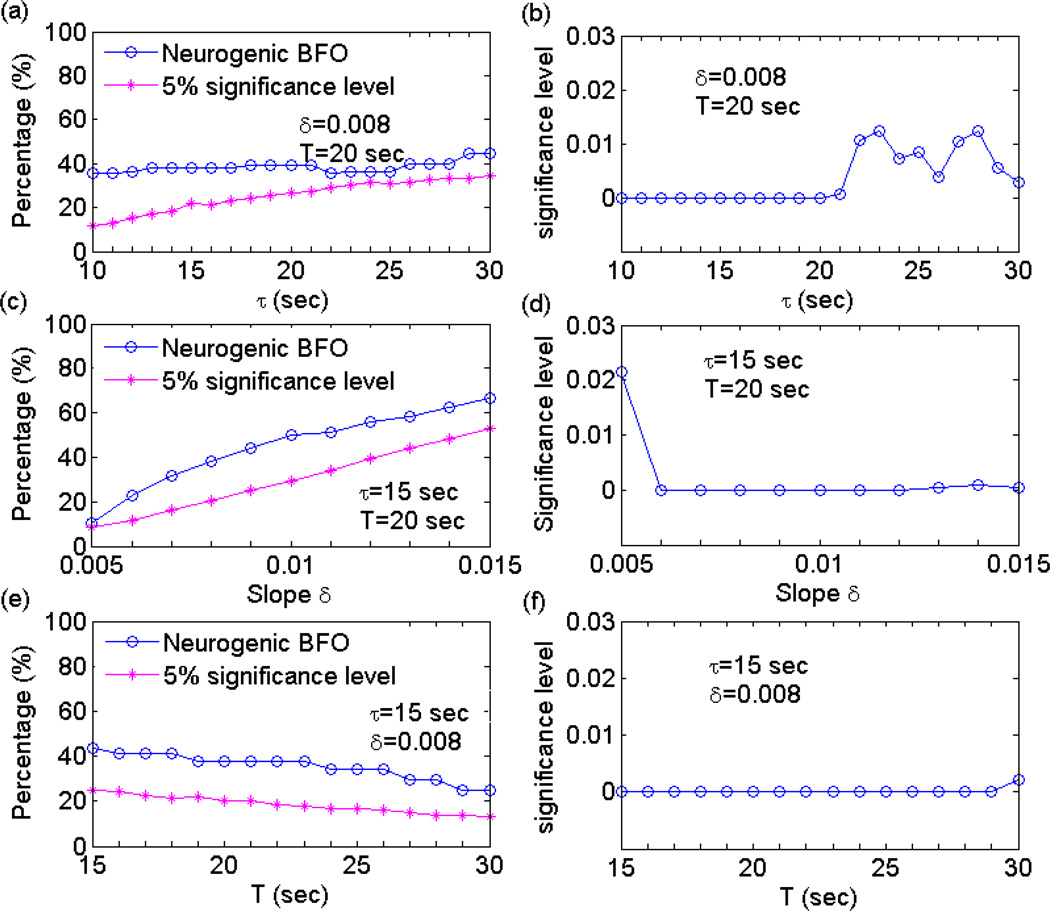
To examine whether the parameters τ, δ, and T used in section 2.5 are suitable for blood flow data, we calculated s and its significance level for myogenic BFO and neurogenic BFO for wide ranges of the parameters. One of them was varied while the other two were kept constant. Fig. 6 shows an example of the results for myogenic BFO and Fig. 7 shows an example for neurogenic BFO. The results showed that for certain ranges of the parameters, s calculated from blood flow data shows similar changes as compared to s_0.05 (obtained from surrogate data) (left panels in Fig. 6 & 7) and thus its p value remains stable (left panels in Fig. 6 & 7). This means that the parameters τ, δ, and T used in section 2.5 are appropriate for blood flow data.

Fig. 6.

An example of percentage of phase synchronization of myogenic blood flow oscillations and its significance level for varying parameters. From the myogenic components extracted from the blood flow signals shown in Figure 1a, b during 1–60 min, 2000 pairs of phase randomized time series were generated. One parameter was varied while the other two parameters were kept constant. was calculated for the myogenic components and for surrogate time series during 51–60 min. (a), (b) τ varied from 2 sec to 12 sec while δ and T were respectively 0.015 and 8 sec. (c), (d) δ varied from 0.01 to 0.02 while τ and T were respectively 6 sec and 8 sec. (e), (f) T varied from 4 sec to 16 sec while τ and δ were respectively 6 sec and 0.015.

Fig. 7.

An example of percentage of phase synchronization of neurogenic BFO and its significance level for varying parameters. From the neurogenic components extracted from the blood flow signals shown in Figure 1a, b during 1–60 min, 2000 pairs of phase randomized time series were generated. One parameter was varied while the other two parameters were kept constant. The parameter s was calculated for the neurogenic components and for surrogate time series during 51–60 min. (a), (b) τ varied from 10 sec to 30 sec while δ and T were respectively 0.008 and 20 sec. (c), (d) δ varied from 0.005 to 0.015 while τ and T were respectively 15 sec and 20 sec. (e), (f) T varied from 15 sec to 30 sec while τ and δ were respectively 15 sec and 0.008.

2.8 Application to blood flow data

The sustained local heating induced a biphasic blood flow response (Fig. 1a). The first peak is mediated by sensory axon reflex mechanism and the second peak is mediated by endothelial nitric oxide mechanism [7]. Thus, in different stages of local heating, BFO may exhibit different degrees of self-synchronization. We performed the following steps:

1. Extract myogenic, neurogenic, and metabolic component of BFO from skin blood flow signals (1–60 min) using the EEMD method and then re-sample them to 8 Hz.

2. For a pair of characteristic components of BFO, calculate their instantaneous phase using the Hilbert transform. Then apply the algorithm described in section 2.4 to the time series of phase difference to detect all epochs of phase synchronization, using the following parameters: for myogenic BFO, τ=6 sec, δ=0.015, T=8 sec, for neurogenic BFO, τ=15 sec, δ=0.008, T=20 sec, and for metabolic BFO, τ=45 sec, δ=0.002, T=60 sec.

3. Calculate the percentage of phase synchronization, s, in the following time intervals: 1–10 min, 11–20 min, 21–30 min, 31–40 min, 41–50 min, and 51–60 min.

4. For a pair of myogenic, neurogenic, or metabolic components of BFO, generate 2000 pairs of phase randomized time series. Then calculate s in each of the above time intervals and obtain a probability distribution of s, P(s).

5. Calculate the significance level p of s obtained in step (iii) based on P(s) obtained in step (iv).

3 Results

Fig. 8 shows the normalized skin blood flow (normalized to the mean of blood flow during 1–10 min) in the non-heated skin and values for myogenic and neurogenic BFO. Blood flow in the non-heated skin showed a sustained increase during 11–50 min (Fig. 8a). The percentage of phase synchronization, both for myogenic and neurogenic BFO, took larger values during 1–10 min, followed by a decrease during 11–20 min, then increased and maintained larger values (Fig. 8b and 8c).

Fig. 8.

(a) Normalized skin blood flow (normalized to the mean of blood flow during 1–10 min) in the non-heated skin. Values are means ± SE. (b) Percentage of phase synchronization of myogenic blood flow oscillations. (c) Percentage of phase synchronization of neurogenic blood flow oscillations.

Fig. 9 shows the statistical significance levels of the results shown in Fig. 8b and 8c. At baseline, significance level for both myogenic and neurogenic BFO was lower than 0.05 in most of the research participants (Fig. 9a), suggesting the existence of self-phase synchronization. On the contrary, during 11–20 min, the period of rapid vasodilation of the heated skin, significance level was higher than 0.05 in most subjects (Fig. 9b). Then it showed a decrease, particularly for myogenic BFO during 41–50 min (Fig. 9e) and neurogenic BFO during 51–60 min (Fig. 9f).

Fig. 9.

Statistical significance levels of the results shown in Figure 8b and 8c. For each pair of myogenic or neurogenic components of blood flow oscillations, 2000 pairs of surrogate time series were generated. The statistical significance level of during 1–10 min (a), 11–20 min (b), 21–30 min (c), 31–40 min (d), 41–50 min (e), and 51–60 min (f) was calculated using the method described in section 2.7. To show the significance levels in a logarithmic scale, the value of zero was set to 10⁻⁴.

For metabolic BFO, we did not observe self-phase synchronization. In most of the subjects s value for real data was similar to that for surrogate data, and the significance level was higher than 0.05.

4 Discussion

We have used the concept of phase synchronization to quantify interactions between BFO in the heated and non-heated skin. The results indicated that myogenic and neurogenic BFO exhibit self-synchronization during the slower vasodilation of the heated skin. Moreover, the degree of synchronization is associated with the changes in blood flow in the non-heated skin.

The approach used in this study is based on the assumption that BFO at around 0.1, 0.04, and 0.01 Hz are respectively attributed to the myogenic, neurogenic, and metabolic activities [42, 43]. To the best of our knowledge, although it was suggested that myogenic BFO may be weakly spatially synchronized [44], no study has reported the existence of self-synchronization of myogenic and neurogenic BFO. A possible reason is that the instantaneous frequencies of these oscillations cannot be measured and tracing the phases of low-frequency oscillations with time is extremely difficult [46]. Indeed, a major problem in the analysis of physiological signals is the presence of nonstationarity, which makes traditional approaches, e.g. Fourier transform based approaches, unreliable [22]. In this study, the instantaneous phase of myogenic, neurogenic, and metabolic oscillations was derived by means of the EEMD and Hilbert transform. Unlike the Fourier transform, Hilbert transform does not assume that signals are composed of superimposed sinusoidal oscillations with constant amplitude and frequency. Thus, instantaneous phases derived from Hilbert transform are more suitable for assessing the relationship between complex oscillations [5]. In order to obtain meaningful instantaneous phases, Hilbert transform requires that an oscillatory signal should be symmetric with respect to the local zero mean and should have the same number of zero crossings and extreme [8]. The IMFs obtained from the EEMD satisfy this requirement. The EEMD has been demonstrated to be able to serve as a blind time-variant filter to extract the embedded nonstationary oscillations adaptively [22, 50]. In this study, each of the blood flow signals was decomposed into 16 IMFs and the eighth IMF (IMF8), ninth IMF (IMF9), and tenth IMF (IMF10) were respectively chosen as myogenic, neurogenic, and metabolic component (Fig. 2). As shown in Fig. 2, the instantaneous frequencies of the three IMFs are not necessarily confined to the range 0.05–0.15 Hz, 0.02–0.05 Hz, and 0.0095–0.02 Hz, respectively. This is probably an inherent feature of the EEMD method differing from band-pass filters. Band-pass filters may not be suitable for our purpose because the characteristic frequencies of BFO can vary with time [42, 43], the extremely low frequencies of the characteristic components, e.g. metabolic component, make it difficult to design an appropriate band-pass filter, and band-pass filtering can lead to a spurious increase in the degree of phase synchronization [49, 51].

An important issue is the validation of the existence of phase synchronization. As synchronization is a process of adjustment of rhythms due to interaction, one can find short epochs where phases seem to be locked due to an occasional coincidence of frequencies [32]. A natural way to address this problem is to use the surrogate data technique [32, 38]. In the case of testing for phase synchronization, a commonly used approach to construct surrogates is to preserve the amplitudes of the Fourier transform of the original signal but randomize the Fourier phases. In this case, the corresponding null hypothesis is that the putative synchronization between the underlying systems can be explained by linear Gaussian stochastic processes observed through a nonlinear measure. However, the concept of phase synchronization assumes the mutual adaption of self-sustained oscillators, i.e. nonlinear deterministic system. Nevertheless, Rosenblum et al. [32] suggested that some empirical methods can be used in particular experiments. We also employed more sophisticated methods to generate surrogate data, e.g. surrogate data that preserve the probability distribution of the original data or preserve the linear cross-correlation between the original data. The obtained results were similar to those shown in Fig. 9.

We noted that the probability distribution of s, P(s), constructed from surrogate data, depends on properties of the original data. This means that for different subjects, a value of s may not necessarily indicate the same degree of phase synchronization. On the other hand, for a pair of characteristic components of BFO, P(s) may be different among the six time intervals (1–10 min to 51–60 min) when the number of surrogate time series is relatively small. In our case, P(s) was constructed from 2000 pairs of surrogate time series and was slightly different among the time intervals. Therefore, we calculated value for blood flow data and surrogate data in the same time intervals (Fig. 9).

Another important issue is choosing appropriate parameters for the algorithm for detecting epochs of phase synchronization. The suitability of the chosen parameters was verified by the simulation study on coupled Rössler systems (Fig. 4) and surrogate tests (Fig. 6 and 7). Although the dynamics of the coupled model systems may be different from that of BFO, they provide a controlled setting for investigating the dependence of the parameters on the number of data points in one period. On the other hand, the results of surrogate tests showed that although s changes with the parameters, for certain ranges of the parameters, value for blood flow data and that for surrogate data show similar changes (Fig. 6 and 7). This means that our judgment about the presence of synchronization is valid for certain ranges of the parameters.

The presence of self-synchronization of myogenic BFO during local heating is probably associated with skin vasomotion. Skin vasomotion is the rhythmic variation of arteriolar diameter resulting from smooth muscle dilation and constriction [30, 34], which depend on complex interplay between vasodilator and vasoconstrictor stimuli such as metabolic stress, neurotransmitters, circulating hormones, and blood pressure [30, 35]. Vasomotion has been found to be particularly prominent under metabolic stress [30]. When there is a local metabolic demand in tissue, an ideal vascular response should be coordinated changes over multiple vascular segments [30]. Any change in the diameter of one vascular segment can lead to diameter changes in other segments in the network due to changes in the distribution of blood flow and pressure [39]. In such coordinating responses, the myogenic response is thought to be a potential mechanism [30]. Previous in vivo studies have revealed a high degree of synchronization between adjacent vessels in microvascular networks [30]. BFO result from the motion of the blood cells and their interaction with the vessel wall and have been demonstrated to be dependent on arteriolar diameter oscillations [19]. Because the slower vasodilation (31–60 min) is known to be primarily mediated by local generation of nitric oxide [4], we speculate that self-synchronization of myogenic BFO may be a consequence of synchronized vasomotion due to the elevated metabolic demand in the heated skin. Our results also indicated that myogenic BFO present self-synchronization during the pre-heating period (1–10 min). We hypothesized that it may be from spontaneous activity of vascular smooth muscle cells, because vasomotion has been observed in isolated arterioles in the absence of endothelium [6] and spontaneous activity of vascular smooth muscle cells has been suggested to be a mechanism contributing to this particular aspect of microvascular function [34]. We did not observe synchronization during the rapid vasodilation (11–20 min), probably because of the dominance of the activity of local sensory nerves [4], which may disturb the rhythm of myogenic oscillations.

Self-synchronization of neurogenic BFO is probably associated with sympathetic nerve activity. The neurogenic process is controlled by the autonomous nervous system, which provides synchronization of the function of the entire system [2, 42]. It has been demonstrated that sympathetic nerve activity influences skin BFO with frequencies of 0.02–0.05 Hz [2, 41]. Sympathetic nerves are continuously active so that all innervated blood vessels are under some degree of continuous contraction and relaxation, providing one of the fundamental mechanisms for the control of blood flow and pressure [2, 41]. Thus, the observed self-synchronization of neurogenic BFO may be a reflection of the sympathetic innervation of vessels. We did not observe self-synchronization during the stage of rapid vasodilation (11–20 min) probably because in this stage neurogenic BFO are a superposition with a dominant component associated with local activity of sensory nerves. Future studies may validate our findings in people with spinal cord injury [2].

Our results also indicated that self-synchronization of BFO is associated with the changes in blood flow in the non-heated skin. As shown in Fig.10a and 10b, the normalized skin blood flow is positively correlated with the degree of self-synchronization of myogenic and particularly neurogenic oscillations. This observation is consistent with the results of our previous study [12], in which we observed an increase in the power of neurogenic component response to local heating. Our results are inconsistent with the results of the study by Minson et al. [23]. They did not observe differences in blood flow in response to local heating between two protocols, with antebrachial cutaneous nerve block and without block. They thus suggested that sympathetic cutaneous nerves do not contribute to the slower vasodilation. A later study by this group suggested that an unknown vasodilator is present and mediates a portion of the slower vasodilation [25]. Our results suggest that the neurogenic control mechanism is involved in the slower vasodilation. However, studies are needed to further explore the connection between sympathovagal control and BFO within the 0.02–0.05 Hz frequency band. On the other hand, self-synchronization of myogenic BFO is associated with changes in wavelet amplitude of this component (Fig. 10c), but we did not observe such association for neurogenic oscillations (Fig. 10d). This implies that self-synchronization of myogenic BFO enhances the intensity of myogenic activity in the non-heated skin.

Fig. 10.

Percentage of phase synchronization versus normalized blood flow (normalized to the mean blood flow during 1–10 min) and normalized wavelet amplitude (normalized to the wavelet amplitude during 1–10 min) in the non-heated skin. A wavelet amplitude refers to the norm of a wavelet coefficient, which is defined as $w(s,t)={\displaystyle {\int }_{-\infty }^{\infty }\frac{1}{\sqrt{s}}\psi \left(\frac{u-t}{s}\right)}f(u)\mathit{\text{du}}$, where ψ(u) is the mother wavelet function and f(u) is the original signal. Here the Morlet wavelet ψ(u) = π^−1/4e^iw₀ue^−u2/2 with ω₀=2π was used. Because a value of s does not necessarily mean the same degree of synchronization for different subjects, each value shown in the figure is a mean value of the 12 subjects. (a) and (c) Myogenic blood flow oscillations. (b) and (d) Neurogenic blood flow oscillations.

Our long-term goal is to develop non-invasive tools for detecting risk for pressure ulcers in various pathological populations. In our previous studies, we have confirmed that wavelet analysis of BFO can be used to study blood flow regulatory mechanisms [10–12]. The method has a great potential to study the effect of neurological injury (eg. spinal cord injury, peripheral neuropathy) on microvascular dysfunction and its influences on the risk for ischemic injury and subsequent pressure ulcers. We also demonstrated that nonlinear properties of skin BFO are associated with vasodilatory function [20, 21]. By assessing the nonlinear property of blood flow oscillations, the clinicians may better understand the effect of various risk factors of pressure ulcer on causing soft tissue ischemia. In this study, we demonstrated that self-synchronization of BFO is associated with the regulation of skin blood flow. Skin blood flow in a single vessel depends on the conductance not only of itself but also of all vessels to which it is connected [30]. To increase blood flow to a specific microvascular bed, coordinated changes in multiple vessel segments may be necessary. Therefore, the microvascular system may be regarded as a network of dynamic elements, and BFO at one site should be regarded as a result of the network dynamically interacting to optimize distribution of blood flow in the microvascular bed. To understand the dynamics of BFO in such a network and characterize normal and/or impaired microcirculation function, we probably should consider not only BFO at one site, but also the relationship between BFO in the network. This study demonstrates the feasibility of quantifying interactions between BFO in a microvascular network using the concept of phase synchronization. However, our results were obtained from healthy young subjects. In real-life situations, subjects may be elderly and/or suffer from diseases that affects the vasodilatory mechanisms [13, 24, 26], or they take medications that affects these mechanisms. These conditions may attenuate the phase synchronization of the microvascular network. In these cases, myogenic BFO may exhibit a lower degree of synchronization. Further studies need to explore the role of self-synchronization of BFO in the regulation of blood flow in pathological conditions.

There were limitations in this study. The self-phase synchronization of BFO was assessed in the condition of local heating induced vasodilation. Whether our findings can be applied to pressure induced vasodilation or reactive hyperemia remains unknown. However, we have demonstrated the feasibility of our approach for studying the relationship of BFO in different skin sites. In this study, we recruited male and female participants into this study. Although gender may have an influence on skin blood flow response to local heating [3], we did not observe a significant difference in skin blood flow between males and females in either the pre-heating period or the heating period in this study.

Our results demonstrated that myogenic and neurogenic BFO exhibit self-synchronization during local heating, which is associated with the changes in blood flow in the non-heated skin. Our findings suggest that self-synchronization of BFO plays a role in the regulation of skin blood flow.

Abbreviations

BFO

Blood Flow Oscillations

EEMD

Ensemble Empirical Mode Decomposition

IMF

Intrinsic Mode Functions