Estimation of Mediation Effects for Zero-inflated Regression Models

Abstract

The goal of mediation analysis is to identify and explicate the mechanism that underlies a relationship between a risk factor and an outcome via an intermediate variable (mediator). In this paper, we consider the estimation of mediation effects in zero-inflated (ZI) models intended to accommodate `extra' zeros in count data. Focusing on the ZI negative binomial (ZINB) models, we provide a mediation formula approach to estimate the (overall) mediation effect in the standard two-stage mediation framework under a key sequential ignorability assumption. We also consider a novel decomposition of the overall mediation effect for the ZI context using a three-stage mediation model. Estimation of the components of the overall mediation effect requires an assumption involving the joint distribution of two counterfactuals. Simulation study results demonstrate low bias of mediation effect estimators and close-to-nominal coverage probability (CP) of confidence intervals. We also modify the mediation formula method by replacing `exact' integration with a Monte Carlo integration method. The method is applied to a cohort study of dental caries in very low birth weight adolescents. For overall mediation effect estimation, sensitivity analysis was conducted to quantify the degree to which key assumption must be violated to reverse the original conclusion.

1. INTRODUCTION

The target of many empirical studies in the social, behavioral and health sciences is the causal mediation (or indirect) effect, which measures the extent to which the effect of the exposure on the outcome is mediated through some particular pathway. The examination of mediation is important because identification of the extent to which change in one or more mediating variables account for an observed exposure effect may shed light on the theoretical basis of the same exposure effect, and therefore provide the target for future preventative studies.

The most commonly used method of mediation analysis has been proposed by Baron and Kenny within the framework of linear structural equation modeling (LSEM) [1] and involves series of linear regression models. The mediation effect is quantified by difference in coefficient [2] or product of coefficient approach [3] where both the dependent variables and mediators are continuous and normal-based models are assumed. For linear models using ordinary least squares and where there is no missing data, the estimators from the two methods are identical [4]. One major limitation of the LSEM framework is that the methods developed are not generalizable to nonlinear models. Both binary outcome [5, 6] and binary mediator [7] contexts were studied recently using logistic regression models. Imai et al. provided a general approach to causal mediation analysis that accommodated linear and nonlinear, parametric and nonparametric models, continuous, discrete or binary mediators, and various types of outcome variables [8]. Sensitivity analysis in a commonly used model was also developed [8, 9]. Imai et al.'s mediation analysis is based on what Pearl [10] refers to as the `mediation formula'. In this approach, the mean potential outcome is computed by integrating (or summing) over the probability density distribution of the mediators. The key assumption made by the mediation formula approach is that of `sequential ignorability'. This assumption consists of no unmeasured confounding as well as the requirement that no mediator-outcome confounder be affected by exposure [11]. Although the definition of the above mediation effect was mostly confined to two-stage mediation, approaches for multiple-stage mediation analysis were also proposed [12, 13]. Albert and Nelson [13] extended the standard two-stage mediation analysis to allow for multiple stages of mediation involving mixed types of variables. In this approach, the overall exposure effect can be broken down into path-specific effects using the potential outcomes framework and a generalized mediation formula under some identifiability assumptions.

A common problem encountered in medical, public health and social science studies is the presence of a high number of zeros, a problem known as zero inflation (ZI). For example, the distribution of the decayed, missing and filled teeth index (DMFT), a count response variable from an ongoing longitudinal study which compares very low birth weight (VLBW) adolescents with full-term adolescents, contains a large number of zeros [14]. Zero-inflated data are often analyzed via a two-component mixture models combining a point mass at zero with a proper count distribution (Poisson and negative binomial regression model for unbounded data, binomial and beta-binomial for bounded data) [15, 16]. ZI models assume an initial process to determine membership into one of two latent populations, generally referred to the `susceptible' and `non-susceptible' populations. The approach for ZI models uses two regression models, one (logit or probit regression) modeling the susceptible probability, and the other (log linear regression for Poisson/NB, logistic regression for binomial or beta-binomial) modeling the mean for the susceptible population. Explanatory variables are allowed to have a different impact for the two processes [17], and the two models are fit simultaneously using maximum likelihood estimation. Generally, separate exposure effects are estimated for the susceptible probability and susceptible population mean respectively [18, 19], though inference for the overall mean for the ZI model was also considered [20, 21]. Previously, we proposed an `average predicted value' (APV) method to assess an overall mean exposure effect in the context of ZI regression models, which allows covariate-adjusted estimation of flexible functions of exposure group means [22].

Previous research in relevant applications such as dental caries (for example, [22]), has demonstrated the potential for considerable improvement in fit and consequent inferences using ZINB in place of standard regression models. This advantage can be expected to carry over into mediation analysis, which has been of increasing interest as dental and other researchers seek to describe and uncover mechanisms explaining observed treatment or exposure effects [23]. Unfortunately, available methods for mediation analysis, which typically rely on standard regression models, are not suitable for zero-inflated count outcomes. Furthermore, the two-component structure of the ZI models is not utilized in standard methods, and an approach to mediation analysis that considers the separate contribution of these two components would also be of interest.

In the present paper, we focus on mediation analysis for ZI models, particularly, the ZINB model. For estimation of the overall mediation effect, we apply the mediation formula within the standard two-stage framework. In addition, a further exploration of causal mechanisms for zero-inflated responses is possible by decomposing the indirect effect into two paths: one through a latent variable representing the subpopulation (`susceptible' or `non-susceptible'), the other going directly from the mediator to the final outcome variable. We introduce a three-stage mediation framework and additional identifying assumptions to estimate the effects corresponding to these pathways.

The rest of the paper is organized as follows. Section 2 describes ZINB model. In Section 3, we define the natural indirect effect, natural direct effect, total causal effect and decomposition of the overall mediation effect in the ZINB model. Section 4 presents a mediation formula approach to estimate the overall mediation effect under given identifying assumptions and also discuss computation using a Monte Carlo integration method as an alternative to `exact' integration. Section 5 presents the method to estimate the decomposition of the overall mediation effect with mediation formula. Simulation studies are used in Section 6 to examine the statistical properties of the proposed methods. Section 7 describes the application of the proposed method to the dental data and presents a sensitivity analysis. Discussion and suggestions for further research are presented in Section 8.

2. STATISTICAL MODELS

We consider models for a count outcome y based on the zero-inflated negative binomial (ZINB) model. In this model, two latent subpopulations can be defined, a susceptible population with responses distributed as negative binomial (mean λ) and a non-susceptible group with responses fixed at zero. The mixture probability, denoted as ψ, is the probability of being in the susceptible population. The negative binomial distribution has mass function given by

$$nb(y;\lambda ,\varphi )=\frac{\Gamma (y+1∕\varphi )}{y!\Gamma (1∕\varphi )}{\left(\frac{1}{1+\varphi \lambda }\right)}^{1∕\varphi }\times {\left(\frac{1}{1∕\varphi +\lambda }\right)}^y$$ (1)

Where ϕ is the dispersion parameter, and mean and variance is λ and λ(1 + ϕλ).

The ZINB model has a probability density function given by

$$P(y;\psi ,\lambda ,\varphi )=\{\begin{array}{cc}(1-\psi )+\psi nb(y;\lambda ,\varphi )\hfill & \text{for}y=0\hfill \\ \psi nb(y;\lambda ,\varphi )\hfill & \text{for}y>0\hfill \end{array}\phantom{\}}$$ (2)

with mean and variance given by ψλ and ψλ(1 + λ(1 − ψ + ϕ)).

As ϕ approaches zero, the ZINB model approaches the zero-inflated Poisson (ZIP) model. The negative binomial mean (λ) and the non-zero probability (ψ) may be modeled with a logistic regression model and a log-linear regression model, i.e. logit(ψ) = α′x and ln(λ) = β′x. Because the count responses for all subjects are assumed to be independent, the log-likelihood of the ZINB model are defined by summing the log of the expressions in equation (2) over all the subjects. The resulting log-likelihood is then maximized simultaneously to estimate all parameters in the model. In the present paper, estimation (maximization) was implemented using the adaptive Gaussian quadrature algorithm in the SAS PROC NLMIXED procedure.

3. DEFINING OVERALL AND DECOMPOSITION OF MEDIATION EFFECTS

3.1 Defining causal mediation effects

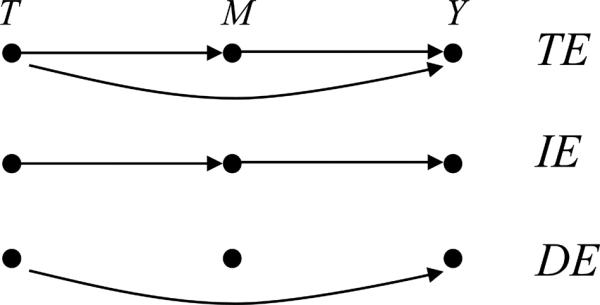
Consider the general casual model including a binary exposure or treatment indicator (T), a mediator (M) and an outcome (Y), where T may affect Y directly and/or T may affect M, which then affects Y (consider here as a ZI count outcome). Figure 1 shows the path diagram. To define the causal mediation effects, we use the potential outcomes framework. Under the standard two-stage mediation model, the causal mediation effect under exposure t is defined as

$$IE\left(t\right)\equiv E\left\{Y(t,M\left(1\right))\right\}-E\left\{Y(t,M\left(0\right))\right\}$$ (3)

Here, Y(t, M(t′)) denotes the counterfactual value that Y would attain if T was set to t, and M set to the counterfactual value that would be observed if T was set to t′. IE(t) is called the natural indirect effect, and represents the difference between two mean potential outcomes that would result under exposure status t, but where the mediator takes values that would result under the two different exposure statuses. Similarly, we can define the natural direct effect and the total causal effect in the potential outcomes framework as

$$DE\left(t\right)\equiv E\left\{Y(1,M\left(t\right))\right\}-E\left\{Y(0,M\left(t\right))\right\}$$ (4)

$$TE\equiv E\left\{Y(1,M\left(1\right))\right\}-E\left\{Y(0,M\left(0\right))\right\}$$ (5)

It is easy to derive the important relationship TE = IE(t) + DE(1- t); in words, the total causal effect is equal to the sum of the natural indirect effect under one exposure status and the natural direct effect under the other exposure status, which was shown before [9, 10]. In this paper, we consider t = 1 only and denote IE(1) as IE and DE(0) as DE; for t = 0, the method will be similar.

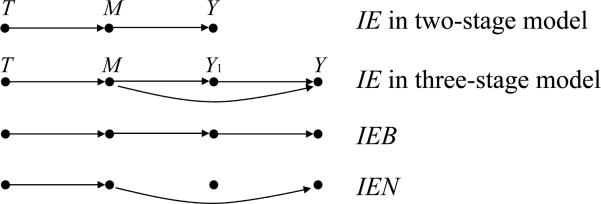
Figure 1.

Path diagram for a mediation model in two-stage framework. T = exposure or treatment, M = mediator, Y = outcome; TE = total casual effect, IE = natural indirect effect, DE = natural direct effect.

3.2 Defining decomposition of overall natural indirect effect

In ZI models, it is possible to further dissect the total natural indirect effect. We do this by introducing a latent variable Y₁ indicating whether or not the subject is susceptible. Thus, our approach conceives of `susceptibility' as manipulable, rather than a fixed trait. Incorporating this latent variable, which we refer to as the `susceptibility indicator', we obtain an extended causal model involving, in causal order, the variables (T, M, Y₁, Y), and thus three stages of mediation (Figure 2). This model allows us to partition the overall total natural indirect effect into two paths, through or not through Y₁. We will follow the notation used by Albert and Nelson [13] in their three-stage mediation framework. In our ZI model, the potential outcome of Y given manipulation D, with corresponding exposure indicator variables d = (d₀, d₁, d₂, d_1,2), can be written as Y(d₀, M(d₁), Y₁(d₂, M(d_1,2))), where Y₁(d₂, M(d_1,2)) is the potential outcome for Y₁, were exposure set to d₂, and M set to the value it would take were exposure set to d_1,2.

Figure 2.

Path diagram for decomposition of overall mediation effect in three-stage framework. Y₁ = susceptible group indicator; IEB = natural indirect effect through susceptible group indicator (Y₁), IEN = natural indirect effect not through Y₁. T, M, Y, and IE are shown as Figure 1.

The total natural indirect effect can be broken into two path-specific effects, one path effect (denoted `IEB', meaning Indirect Effect by affecting Binary component of ZINB model) is through the susceptibility indicator Y<sub>1</sub>; the other is the direct effect of M on Y (denoted as `IEN', meaning Indirect Effect by affecting NB component of ZINB model directly), that is, the part of the mediation effect not through Y₁ (Figure 2). IEB and IEN are each defined as the difference between two mean potential outcomes as follows,

$$IEB\equiv E\left\{Y(1,M\left(0\right),Y_1(1,M\left(1\right)))\right\}-E\left\{Y(1,M\left(0\right),Y_1(1,M\left(0\right)))\right\}$$ (6)

$$IEN\equiv E\left\{Y(1,M\left(1\right),Y_1(1,M\left(1\right)))\right\}-E\left\{Y(1,M\left(0\right),Y_1(1,M\left(1\right)))\right\}$$ (7)

Note that the sum of IEB and IEN is equal to IE. An alternative decomposition of the overall mediation effect (where IEB is defined as difference in the means of Y(1, M(1), Y₁(1, M(1)))) and Y(1, M(1), Y₁(1, M(0)))), and IEN is defined as the difference the means of Y(1, M(1), Y₁(1, M(0)))) and Y(1, M(0), Y₁(1, M(0))))) can be handled similarly and thus is not discussed here.

4. ANALYSIS OF OVERALL MEDIATION EFFECT FOR ZERO-INFLATED MODEL

4.1 Mediation formula (causal model) approach

4.1.1 Identification of causal mediation effects

We present identification results for the (overall) indirect and direct effects, defined by (3) and (4) using the potential outcomes framework described above. Under the two-stage mediation model, the causal effects are identified nonparametrically (thus, under our ZINB as well) under sequential ignorability. We use the following version of this assumption (following Imai et al. [9]): Assumption 1 (Sequential Ignorability)

$$\{Y(t^{\prime },m),M\left(t\right)\}⫫T\mid W=w$$ (8)

$$Y(t^{\prime },m)⫫M\left(t\right)\mid W=w,T=t$$ (9)

Thus, the exposure or treatment is first assumed to be ignorable given the baseline covariates, and then the mediator variable is assumed to be ignorable given observed values of exposure status and the baseline covariates.

4.1.2. Estimation of overall mediation effect for the ZINB model

Under assumption 1, the natural indirect effect, natural direct effect and total causal effect can be calculated respectively as:

$$IE=\int \int E\{Y\mid M=m,T=1,W=w\}(d{F}_{M\mid T=1,W=w}\left(m\right)-d{F}_{M\mid T=0,W=w}\left(m\right))d{F}_W\left(w\right)$$ (10)

$$DE=\int \int (E\{Y\mid M=m,T=1,W=w\}-E\{Y\mid M=m,T=0,W=w\})d{F}_{M\mid T=0,W=w}\left(m\right)d{F}_W\left(w\right)$$ (11)

$$TE=\int \int (E\{Y\mid M=m,T=1,W=w\}d{F}_{M\mid T=1,W=w}\left(m\right)-E\{Y\mid M=m,T=0,W=w\}d{F}_{M\mid T=0,W=w}\left(m\right))d{F}_W\left(w\right)$$ (12)

Proofs of above equations were shown by Imai et al. [9] and Shpitser and VanderWeele [24]. Summation should be used in place of integration in the case of discrete mediators and/or discrete covariates.

Integrations can be approximated using Monte Carlo integration, which averages the integrand over randomly generated realizations of the assumed distribution of the mediator [25]. Suppose that m₁ … m_n and m₁' … m_n' are randomly generated from the assumed distribution of M(0) and M(1) respectively. Formulae (10) can then be approximated by the following expressions, and formula (11) can be expressed in similar way:

$$IE\approx \frac{1}{N}\sum _{j=1}^N\left(\frac{1}{n}\sum _{i=1}^{n}E\{Y\mid M={m_i}^{\prime },T=1,W=w_j\}-\frac{1}{n}\sum _{i=1}^{n}E\{Y\mid M=m_i,T=1,W=w_j\}\right)$$ (13)

To carry out estimation of the direct and indirect effects in (10) and (11) we need a model for the regression of Y on M, T, and W. For the present application of interest, we will consider the following zero-inflated model. The model for Y, allowing the mediator (M) to affect both the susceptibility indicator (Y₁) and the response Y given susceptible is given as:

$$\text{logit}\left(\psi \right)={\alpha }_0+{\alpha }_{1}t+{\alpha }_{2}m+{\alpha }^{\prime }\mathit{w}\text{ln}\left(\lambda \right)={\beta }_0+{\beta }_{1}t+{\beta }_{2}m+{\beta }^{\prime }\mathit{w}$$ (14)

For the mediator, we consider appropriate regression models for the binary and continuous mediator cases (allowing the mediator to depend on the exposure variable and baseline covariates (W)); specifically, we use the following regression models for a binary and continuous mediator, respectively,

$$\text{logit}\left(m\right)={\gamma }_0+{\gamma }_{1}x+{\gamma }^{\prime }\mathit{w}m={\gamma }_0+{\gamma }_{1}x+{\gamma }^{\prime }\mathit{w}+\epsilon ,\text{where}\epsilon ~\mathrm{N}(0,{\sigma }^2)$$ (15)

4.2 Sensitivity analysis

For the identified overall mediation effect in our potential outcomes framework, the quantity cannot be given a causal interpretation without the particular assumption sets (8) and (9). Assumption (8) is satisfied in randomized treatment study or cohort study, where randomization probabilities may be a function of baseline covariates, w. Assumption (9) may not hold if there exists unmeasured confounding for the mediator-outcome relationship. We examine the effect of violation of assumption (9) on estimation of the overall indirect and direct effects. To calculate the necessary joint distribution (possibly involving both continuous and discrete variables) we use the approach of Albert and Nelson [13] which applies the Gaussian copula [26].

We propose a sensitivity analysis based on a general model for the joint probability of Y(t',m) and M(t). The count outcome Y has K + 1 possible values (0, 1, 2, …K), where K is the assumed upper limit for Y. P_Y(t′,m)(y) = P{Y(t', m) ≤ y} and P_M(t)(m) = P{M(t) ≤ m} will denote the cumulative distribution functions of Y and M. We suppose that there are, corresponding to Y(t', m) and M(t), latent variables, denoted as Y*(t', m) and M*(t) respectively, which are marginally distributed as standard normal and satisfy the relationship Y*(t', m) = Φ⁻¹{P_Y(t′,m)(y)} and M*(t) = Φ⁻¹{P_M(t)}, where Φ is the standard normal distribution function. In addition, Y*(t', m) and M*(t) are assumed bivariate normally distributed with correlation ρ, for all t, t' and m. In order to properly handle the discrete nature of the distributions of Y, we propose a Monte Carlo approach similar to that used by Albert and Nelson [13] to compute the conditional distributions P{Y(t', m_i) = j, j = 1, 2, …, K | M(t) = m_i} for possible values of m_i. Specifically, we use the following algorithm:

• (1)Sample a mediator m_i ~ f_M(t) (m), i = 1, 2, …, n.
• (2)For a continuous m_i, get U₁ = Φ⁻¹{P_M(t)(m_i)}. For a binary m_i, if m_i = 0 then draw a uniform variate u₁ from the interval [0, P_M(t)(0)], if m_i = 1 then draw a uniform variate u₁ from the interval (P_M(t) (0), 1], let U₁ = Φ⁻¹{u₁}.
• (3)Draw a variate U₂ ~ N (ρU₁, 1 - ρ²), let u₂ = Φ(U₂).
• (4)Let C_ji = 1 if u₂∈ (P_y(t′,mi)(j-1), P_Y(t′,mi)(j)], and C_ji = 0, otherwise, for j = 1, 2, …, K (with the subscript i indicating the conditioning on m_i).
• (5)Repeat steps 2 – 4 with independent draws a large number of (say R) times obtaining C_jir in the rth replicate for r = 1, 2, 3, …, R.
• (6)Following the R replications for each m_i, we estimate the conditional probability $P\{Y(t\prime ,m_i)=j\mid M\left(t\right)=m_i\}\text{as}\frac{{\sum }_r{C}_{jir}}{R}\text{for}j,j=1,2,\dots ,K$.
• (7)Repeat steps 1 – 6 n times, we can obtain an estimate of E{Y(t', M(t))} as $\frac{1}{n}{\sum }_{i=1}^n\left({\sum }_{j=1}^{K}jP\{Y(t\prime m_i,)=jM\mid \left(t\right)=m_i\}\right)$.

Therefore, supposing that the correlation ρ between Y*(t', m) and M*(t) is given, the overall natural indirect effect is identified and given by

$$IE=\frac{1}{n}\left\{\sum _{i=1}^n\left(\sum _{j=1}^{K}jP\{Y(1,{m_i}^{\prime })=j\mid M\left(1\right)={m_i}^{\prime }\}\right)-\sum _{i=1}^n\left(\sum _{j=1}^{K}jP\{Y(1,m_i)=j\mid M\left(0\right)=m_i\}\right)\right\}$$ (16)

where m_i and $m_i^{\prime }$ are randomly generated from the assumed distribution of M(0) and M(1) as shown before. These estimates can be recomputed using the above algorithm over varying values for ρ to provide a sensitivity analysis.

5. DECOMPOSITION OF THE CAUSAL EFFECT FOR ZERO-INFLATED MODEL

5.1 Identifying decomposition path effects

To identify the path effects of the decomposed overall indirect effect ((6) and (7) given in Section 3.2), we extend the preceding sequential ignorability assumption to the three-stage causal model case. The three-stage sequential ignorability assumption is given as Assumption 2:

$$\{Y(t^{″},m^{\prime },y_1),Y_1(t^{\prime },m),M\left(t\right)\}⫫T\mid W=w$$ (17)

$$\{Y(t^{″},m^{\prime },y_1),Y_1(t^{\prime },m)\}⫫M\left(t\right)\mid W=w,T=t$$ (18)

$$Y(t^{\prime },m^{\prime },y_1)⫫Y_1(t,m)\mid W=w,T=t,M=m$$ (19)

Thus, each intermediate variable in the model is assumed to be ignorable (that is independent of subsequent potential outcomes) given all preceding variables in the causal model.

5.2 Estimation of decomposition of overall mediation effect for the ZINB model

To demonstrate identifiability of the decomposition path effects, we will examine identification of the relevant potential outcome means (of the general form E(Y(d₀, M(d₁), Y₁(d₂, M(d_1,2))))) given baseline covariate w under sequential ignorability (Assumption 2). Under Assumption 2 it can be shown (See Appendix A) that,

$$E\left\{Y(d_0,M\left(d_1\right),Y_1(d_2,M\left(d_{1,2}\right)))\right\}=\int \int E\{Y\mid T=d_0,M=m,Y_1=1\}E\{Y_1\mid T=d_2,M=m^{\prime }\}{d}^2{F}_{M\left(d_1\right),M\left(d_{1,2}\right)}(m,m^{\prime })$$ (20)

As before, integration will be interpreted as summation in the case of a discrete mediator. Note that in general the expectations and distribution in (20) will be conditional on baseline covariates w; however, this conditioning is left out of the expression, and those below, for brevity. When d₁ and d_1,2 are unequal (thus, equal to 1 and 0 or vice versa), expression (20) shows that we require the joint distribution of M(1) and M(0) in order to estimate E(Y(d₀, M(d₁), Y₁(d₂, M(d_1,2)))). As seen in equations (6) and (7), both IEB and IEN involve an expected potential outcome in which d₁ does not equal d_1,2 – namely, (E{Y(1, M(0), Y₁(1, M(1)))}); d₁ equals d_1,2 in the other potential outcomes (E{Y(1, M(0), Y₁(1, M(0)))} and E{Y(1, M(1), Y₁(1, M(1)))}). Generally the joint distribution of M(1) and M(0) is unknown and cannot be estimated because both of these outcomes cannot be observed for the same subject. For identifiability we need to make an untestable assumption regarding the joint distribution of these two potential outcomes. For instance, in the continuous mediator case, we may assume that M(1) and M(0) are bivariate normally distributed with specified correlation coefficient τ. Under this assumption in addition to Assumption 2, the expected potential outcome E(Y(d₀, M(d₁), Y₁(d₂, M(d_1,2)))) when d₁ ≠ d_1,2 can be identified and computed using formula (20). The nonidentifiability of some pathway effects in three (or more) stage mediation is also mentioned by Avin et al. [27] and Albert and Nelson [13]. When d₁ equals d_1,2, E(Y(d₀, M(d₁), Y₁(d₂, M(d₁)))) can be estimated by

$$E\left\{Y(d_0,M\left(d_1\right),Y_1(d_2,M\left(d_1\right)))\right\}=\int E\{Y\mid T=d_0,M=m,Y_1=1\}E\{Y_1\mid T=d_2,M=m\}d{F}_{M\left(d_1\right)}\left(m\right)$$ (21)

A proof of formulae (20) and (21) under assumptions (17) – (19) is given in Appendix A.

Similar expressions using Monte Carlo integration can be used to estimate the components of the overall mediation effect (that is, IEB and IEN).

6. SIMULATION STUDY

In this section, simulation study was used to examine the natural indirect estimator from mediation formula approach for a binary as well as a continuous mediator. In addition, we want to assess the effect of the correlation (τ) between the (assumed bivariate normal) counterfactuals M(1) and M(0) on the estimation of the mediation effects through susceptibility indicator Y₁ (IEB), and not through Y₁ (IEN).

6.1 Estimation of overall mediation effects (IE)

In our first simulation study, we studied the mediation effect (IE) assuming a ZINB model with different types of mediators. The logistic regression model for the susceptible probability and log-linear model for the susceptible population mean both include a binary exposure indicator (T = 1 if exposed, 0, otherwise), a common categorical covariate, W (constrained so that each exposure group had a 50% frequency of w = 1) and a mediator variable, M (either binary or continuous). The model is thus given as (14) and (15) for ZI outcome and mediator respectively. The other parameter that needs to be specified is the negative binomial dispersion parameter ϕ, and we chose 0.5 for all our simulation scenarios.

We considered nine scenarios which are distinguished in the magnitude of the natural indirect effect IE (corresponding to parameter α₂, β₂ and γ₁) and direct effect DE (corresponding to parameter α₁ and β₁) for each set. In the continuous mediator scenario, two standard deviation values for the mediator were considered, small σ (equal to 0.5) and large σ (equal to 2.5). For each of above scenarios and type of mediators, 1000 simulated datasets were generated with sample sizes of 200 (100 per exposure group) and 1000 (500 per exposure group).

The true natural indirect effect is defined by the function on the right hand side of (10), with true coefficients in place of the estimates. For each generated dataset, the mediation formula approach was used to calculate the estimated IE, and 95% confidence intervals were constructed by taking 1000 bootstrap samples. From the simulations, we calculated the average estimate of IE; the average percent error (PE = 100 × (Average Estimated IE − True IE)/true IE) of IE, a measure of relative bias; the SD of estimated IE; the average estimated SE of estimated IE; the coverage probability (CP, percent of simulated datasets for which 95% confidence interval for IE covered the true value).

The simulation results are given in Table 1 with total sample size 200 and 1000 respectively. For binary mediator, we see that the mediation formula approach produces a small bias in its estimation of IE, and the average PE is less than 2.1% for all scenarios with sample size 200. The coverage probabilities of 95% confidence intervals deviate from the nominal level for four of nine scenarios by around 3%. When the sample size per group is increased to 500, the mediation formula approach also shows very low bias (less than 2%) and the coverage probability improves compared with the smaller sample size scenarios. For the continuous mediator variables case, the proposed approach provides relative biases of less than 9% for all scenarios with n = 100 per group, and less than 6% for all scenarios with n = 500 per group for both small and large mediator SD scenarios. Bootstrap 95% confidence intervals are conservative for zero-IE scenarios with small mediator SD (around 99%), but are good for all scenarios (within 2% of nominal level) when the mediator SD increases from 0.5 to 2.5.

Table 1.

Simulation statistics for the natural indirect effect of binary and continuous mediators using mediation formula approach on data generated from ZINB/logit-log model.

				Sample Size
				100					500
Mediator a	Sigma b	True DE Est	True IE Est	Ave Est IE	Ave PE (%)	SD of Est IE	AVE SE	CP (%)	Ave Est IE	Ave PE (%)	SD of Est IE	AVE SE	CP (%)
B	NA	−0.766	0.000	−0.001	-	0.044	0.048	98.0	−0.001	-	0.017	0.018	94.2
		−0.888	−0.263	−0.265	0.61	0.117	0.121	94.3	−0.264	0.38	0.050	0.051	95.1
		−1.243	−0.753	−0.755	0.29	0.268	0.262	93.1	−0.753	0.02	0.111	0.111	95.2
		−0.265	0.000	−0.001	-	0.059	0.066	97.8	0.000	-	0.024	0.025	95.4
		−0.308	−0.241	−0.242	0.34	0.126	0.131	95.1	−0.240	−0.53	0.056	0.055	95.2
		−0.319	−0.773	−0.773	0.04	0.270	0.256	91.8	−0.771	−0.32	0.112	0.109	94.7
		0.000	0.000	−0.002	-	0.065	0.075	97.7	0.000	-	0.027	0.028	95.5
		0.000	−0.276	−0.277	0.14	0.145	0.149	95.3	−0.272	−1.49	0.062	0.062	93.7
		0.000	−0.710	−0.725	2.02	0.245	0.249	95.0	−0.707	−0.55	0.105	0.105	95.1
C	0.5	−0.690	0.000	−0.001	.	0.023	0.036	99.6	0.000	.	0.006	0.008	99.3
		−0.789	−0.197	−0.207	5.31	0.205	0.218	95.1	−0.201	2.05	0.093	0.089	92.9
		−1.194	−0.734	−0.775	5.47	0.394	0.384	92.7	−0.736	0.17	0.159	0.157	94.0
		−0.240	0.000	−0.001	-	0.032	0.048	99.9	0.000	-	0.010	0.011	98.3
		−0.274	−0.280	−0.304	8.38	0.280	0.292	93.9	−0.278	−0.68	0.116	0.119	95.9
		−0.340	−0.720	−0.748	3.93	0.398	0.410	93.2	−0.720	0.01	0.161	0.164	96.3
		0.000	0.000	−0.000	-	0.027	0.047	100.0	0.000	-	0.006	0.009	99.7
		0.000	−0.148	−0.150	0.87	0.282	0.282	93.6	−0.157	5.93	0.118	0.118	94.5
		0.000	−0.642	−0.668	4.07	0.365	0.389	95.3	−0.650	1.17	0.166	0.158	94.0
C	2.5	−0.777	0.000	0.000	.	0.069	0.077	96.1	−0.001	.	0.032	0.031	93.5
		−0.817	−0.234	−0.238	1.97	0.158	0.157	94.5	−0.235	0.50	0.063	0.067	96.0
		−1.074	−0.749	−0.721	−3.84	0.497	0.515	95.1	−0.748	−0.19	0.225	0.222	94.5
		−0.269	0.000	0.001	-	0.095	0.100	95.6	0.002	-	0.040	0.041	95.0
		−0.280	−0.250	−0.245	−1.71	0.191	0.196	93.8	−0.252	1.02	0.086	0.084	94.2
		−0.383	−0.798	−0.788	−1.22	0.606	0.645	94.9	−0.810	1.55	0.267	0.277	94.6
		0.000	0.000	−0.001	-	0.111	0.111	94.6	−0.000	-	0.044	0.046	95.6
		0.000	−0.227	−0.209	−8.08	0.207	0.217	94.8	−0.222	−2.03	0.095	0.093	95.1
		0.000	−0.726	−0.753	3.70	0.579	0.595	95.0	−0.732	0.77	0.240	0.251	94.9

^aB = binary mediator; C = continuous mediator

^bstandard deviation of continuous mediator

6.2 Estimation of decomposed mediation effects (IEB and IEN)

For the estimation of decomposed mediation effects, we assumed that M(1) and M(0) are bivariate normally distributed with correlation coefficient τ. We considered 6 scenarios in each set, all with large natural indirect effect (IE), but different magnitudes of the natural direct effect (DE) and natural indirect effects through susceptible probability (IEB). In each scenario, the potential outcome means for the true IEB and IEN, was computed using `exact' integration formula (20) and (21) with true coefficients, and for the calculation of estimated IEB and IEN, the Monte Carlo integration method with 10,000 Monte Carlo samples (draws from the joint distribution of M(1) and M(0) with specified correlation coefficient τ) was used. Three sets of IEB and IEN were calculated corresponding to three assumed τ values (0.0, 0.4 and 0.9). Simulation results for IEB estimator with n = 100 per group are given in Table 3. The true IEB magnitude decreases but the true IE stays constant as the specified correlation coefficient τ between M(1) and M(0) increases. Not surprisingly, the IEB estimator assuming the correct τ produces lowest bias than IEB estimators assuming the wrong τs. When calculating the IEB estimator with mis-specified τ, scenarios with similar magnitude of IEB and IEN (scenario 2 and 5 in each set) always produce much higher bias compared with scenarios in which either IEB or IEN predominates. When sample size increases to 500 per group or considering estimator of the proportion accounted for by IEB (calculated by $\frac{IEB}{IE}\times 100$), the results are similar and not shown.

Table 3.

Estimated causal effects of interest based on the mediation formula approach from three different ZINB models using VLBW Study Data (exposure = VLBW, mediator = AvgOHI, outcome = DMFT).

	Full Model*	Reduced Model A*	Reduced Model B*
Mediation IE	0.03 (−0.14, 0.19)	0.02 (−0.11, 0.15)	0
Through Y1 (IEB)	0.01 (−0.18, 0.27)#	0.02 (−0.11, 0.15)	0
Not through Y1 (IEN)	0.02 (−0.21, 0.12)#	0	0
Direct DE	−0.70 (−1.47, 0.07)	−0.72 (−1.53, 0.05)	−0.69 (−1.54, 0.06)
Total TE	−0.67 (−1.45, 0.10)	−0.69 (−1.52, 0.08)	−0.69 (−1.54, 0.06)

Monte Carlo integration with 10,000 samples was used for estimation of IEB and IEN.

^*: In the full model, potential mediator AvgOHI is included in both components of ZINB model, and in reduced model A, AvgOHI is only included in the binary component of ZINB, and in reduced model B, AvgOHI is not included in the ZINB model.

^#: Requires assumed correlation (τ) between counterfactual values for the mediator; here we assume τ = 0.4.

7. APPLICATION

Our motivating example comes from a cohort study investigating the effect of VLBW (possibly with bronchopulmonary dysplasia) on dental caries in adolescence [14]. The study involved 224 infants (139 VLBW, 85 normal term), and the dental outcomes (including enamel defects, oral health behavior, and dental caries) were assessed at around age 14. The exposure variable is the binary variable referred to as “birth group”, namely, VLBW (birth group = 1) and normal term (birth group = 0). The outcome considered in this example is the DMFT (decayed, missing, and filled teeth) count. We also considered, in separate models, the potential mediator: average “Oral Hygiene Index” (AvgOHI), a bounded continuous variable. The primary study found that the VLBW group had a lower mean DMFT than the normal term group, which may be explained by the facts that VLBW children might be receiving more extensive dental care. We wanted to test this hypothesis and explore whether the effect of VLBW on DMFT is explained by its effect on AvgOHI using the proposed methods discussed above.

The dental dataset with complete model variables gave us a final sample size of 203 subjects which are used for our analysis. We note that the observed average DMFT (SD) was 2.42 (2.94) for the normal term group (n = 78) and 1.67 (2.74) for VLBW group (n = 125). The models (14) and (15) in which mediator AvgOHI was included in both binary and NB components of ZINB model were fitted using maximum likelihood estimation. Three baseline covariates (SES, race and sex) were included in all three models, so that parameters were α′ = (α₃, α₄, α₅), β′ = (β₃, β₄, β₅), and γ′ = (γ₃, γ₄, γ₅). Estimates of IEB, IEN, IE, DE, and TE, using mediation formula approaches are provided in Table 3 (column full model). The result indicates that DE predominates in the TE and nearly zero estimated mediation effect through AvgOHI was identified. When the birth group changes from normal term to VLBW, the mean DMFT decreases an estimated 0.67 (total causal effect). This decrease can be decomposed into an estimate change of 0.03 (−0.14, 0.19) attributable to the AvgOHI and an estimated change of −0.70 (−1.47, 0.07) attributable to other (unknown) pathways. With respect to the decomposition of the overall indirect effect, under the assumption of a moderate correlation (τ = 0.4) between the two mediator counterfactuals, the natural indirect effect can be broken into path effects through susceptibility indicator Y₁ (estimated IEB = 0.01 (−0.18, 0.27)) and directly (estimated IEN = 0.02 (−0.21, 0.12)). As the correlation coefficient τ varies from 0 to 1, IEB and IEN estimates are contained in the bounded interval [−0.01, 0.06] and [−0.03, 0.04] respectively. Note that 95% CIs for the decomposed indirect effect estimators above at any value of τ all cover 0 indicating no significant decomposed path effects.

For comparison, we also considered two reduced ZINB models, one (model A) dropping the potential mediator AvgOHI, from the NB component (β₂ = 0), and the other (model B) dropping AvgOHI from both components of the ZINB model (α₂, β₂ = 0) (Table 3). According to the Akaike information criterion (AIC, goodness-of-fit criterion), the original (full) model and model A are superior to model B (AIC_Full = 732.4, AIC_{Model A} = 731.2 and AIC_{Model B} = 737.8). The overall indirect (mediation) effect estimate (of VLBW on DMFT through AvgOHI) for reduced model A (0.02) is similar with that for full model (0.03). Note that for the former model, the mediation effect is entirely through the susceptibility indicator, as only this submodel involves the mediator. Reduced model B is not applicable for estimation of the mediation effect since the mediator is not included at all in the ZINB model.

In summary, no significant indirect effects of VLBW on DMFT through AvgOHI, either overall or via decomposed paths through susceptibility or the susceptible group NB mean, were detected. It appears that other mediators besides OHI will be needed to explain the advantageous effect of VLBW on dental caries.

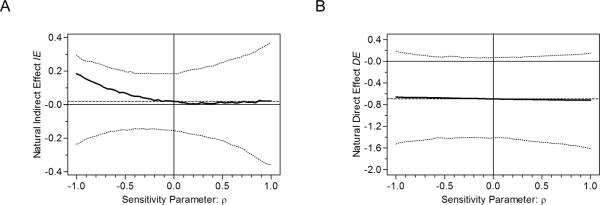
In a sensitivity analysis, we examined the effect on DE and IE estimates of varying the assumed counterfactual correlation coefficient ρ (between (Y | m, t′) and (M | t)) from −1 to 1 in increments of 0.04. The change in IE and DE estimates over ρ is shown in Figure 3. The plots indicate that the IE estimate is a minimum at ρ = 0.24 (Fig 3A) and DE decreases as ρ increases (Fig 3B), however, the range for each estimator was consistent with the original conclusion indicating nonsignificant DE and IE effects (95% CIs cover 0). Thus, we find that mediation formula estimates of the direct and indirect effects in the dental data are fairly robust to possible violations of the no M-Y confounding assumption (9).

Figure 3.

Sensitivity analysis for dental data involving the continuous mediator `AvgOHI'. Panels A and B show estimated IE and DE for varying correlation ρ between (Y | m, t′) and (M | t) for AvgOHI. The solid line represents the estimated indirect and direct effect. The areas between dotted lines represent the 95% confidence intervals for the natural indirect and natural direct effects at each value of ρ.

8. DISCUSSION

In this article, we studied mediation analysis for ZI models using a mediation formula approach. A three-stage path framework was introduced due to the special two-component structure of the ZI model allowing us to further decompose the natural indirect effect, a decomposition which is not possible in mediation analysis based on standard linear regression models. The method described in this paper has been implemented in a SAS macro which is available for downloading from the webpage http://epbiwww.case.edu/index.php/people/faculty/53-albert. One limitation of this approach is that it depends on a parametric model specification; different model choices may produce different estimated mediation effects.

We addressed mediation analysis using the potential outcomes framework, where true causal effects are defined as differences in potential outcome means. The mediation formula calculates potential outcome means by integrating or summing over the mediator probability distribution space. Integration was carried out using the `QUAD' function in SAS/IML, which uses an adaptive (Romberg-type) numerical integration technique. For some complex situations (for example, involving double integrals), this function may fail due to slow convergence or strong oscillation. We overcome this problem by approximating the integral calculation with Monte Carlo integration techniques, a version of which was used by Imai et al. [8]. In the continuous mediator case, more Monte Carlo samples are needed to achieve a good approximation of the mediator distribution and thus less deviation from estimates using the mediation formula with `exact' integration when facing higher mediator variance.

The three-stage path framework used for ZINB model mediation analysis allows us to further decompose the natural indirect effect under additional assumptions. Estimation of the decomposed effects (namely, through or not through the susceptibility indicator) involves the joint distribution of counterfactuals (namely, M(1) and M(0)). This problem, which only occurs when there are more than two stages of mediation, was also mentioned by Avin et al. [27] and Albert and Nelson [13]. The simple identifying assumption that the counterfactuals are independent may not be scientifically plausible. In simulation studies, we examined the effect of varying a counterfactual correlation coefficient (under a bivariate normal model for M(1) and M(0)) on the estimation of IEB and IEN. An interesting finding is that when either IEB or IEN predominates, estimation of IEB is robust to mis-specification of the correlation coefficient (τ). However, in the case where IEB and IEN are of similar magnitude, the IEB estimator can be substantially biased if a wrong τ is chosen. Although the joint distribution for these two counterfactuals is nonidentifiable, it may be reasonable in many applications to assume a positive correlation between M(1) and M(0). For example, we assume a moderate correlation (τ = 0.4) between M(1) and M(0) in the estimation of IEB and IEN in our VLBW study example. Alternatively, it may be sensible in a given application to present bounds for these effects over a plausible range for τ.

We developed a sensitivity analysis to assess the impact of violation of key sequential ignorability assumption on the overall mediation effect estimates. While the method of Imai et al. [8, 9] used the correlation between the model errors as their sensitivity parameter, our approach uses a correlation coefficient ρ between latent variables underlying the mediator and outcome adjusted for mediator. Consequently, our approach is more general and may accommodate additional types of mediator/outcome variables. Nonzero ρ implies that there exists an omitted variable that affect both mediator and outcome variables. The magnitude of ρ is a measure of the overall strength of the association between the omitted variable and the two response variables (mediator and outcome). A researcher who finds ρ difficult to interpret or specify may simply make use of bounds for the estimator of interest by considering ρ over a plausible range, or even over the entire range, [−1, 1] as done in the above data example.

In conclusion, we have proposed a mediation formula approach for mediation analysis of ZI models which allows estimation of direct and indirect effects, as well as a further decomposition of the indirect effect through consideration of the latent susceptibility indicator. Further work is needed to study multiple mediators in ZI models.

Table 2.

Simulation statistics for the natural indirect effect decomposition with mediation formula approach for continuous mediator on data generated from ZINB/logit-log model, standard deviation of mediator and dispersion parameters are all 0.5, n = 100 per group.

True τ (M(1), M(0))	True DE	True IE	True IEB	Est IE	Est IEB τ (M(1), M(0)) = 0.0		Est IEB τ (M(1), M(0)) = 0.4		Est IEB τ (M(1), M(0)) = 0.9
					Bias	CP (%)	Bias	CP (%)	Bias	CP (%)
0.0	−0.113	−0.780	−0.057	−0.843	−0.010	94.6	−0.007	94.6	−0.004	94.8
	−0.092	−0.828	−0.533	−0.826	0.009	94.3	0.040	93.5	0.079	91.8
	−0.117	−0.775	−0.742	−0.768	0.007	94.6	0.010	95.1	0.014	95.3
	−1.371	−0.741	−0.053	−0.784	−0.007	94.0	−0.005	93.9	−0.002	93.9
	−1.171	−0.817	−0.530	−0.839	−0.006	94.0	0.028	93.6	0.072	91.8
	−0.857	−0.761	−0.735	−0.766	0.010	94.7	0.016	94.6	0.022	94.2
0.4	−0.113	−0.780	−0.052	−0.830	−0.022	93.7	−0.019	93.9	−0.016	93.9
	−0.092	−0.828	−0.501	−0.842	−0.034	95.2	−0.003	95.3	0.038	94.6
	−0.117	−0.775	−0.738	−0.789	0.003	95.3	0.008	95.3	0.014	95.3
	−1.371	−0.741	−0.047	−0.777	0.005	94.2	0.005	94.4	0.005	94.2
	−1.171	−0.817	−0.495	−0.836	−0.041	95.1	−0.007	94.7	0.037	94.1
	−0.857	−0.761	−0.731	−0.752	0.006	93.9	0.009	94.1	0.012	93.5
0.9	−0.113	−0.780	−0.046	−0.825	0.005	95.7	0.005	95.7	0.006	95.6
	−0.092	−0.828	−0.460	−0.822	−0.057	95.3	−0.027	95.4	0.012	95.0
	−0.117	−0.775	−0.733	−0.789	−0.011	95.7	−0.006	95.6	−0.001	95.2
	−1.371	−0.741	−0.040	−0.800	−0.035	94.7	−0.031	94.6	−0.025	94.6
	−1.171	−0.817	−0.452	−0.837	−0.089	95.0	−0.054	95.6	−0.010	95.4
	−0.857	−0.761	−0.726	−0.760	−0.003	94.9	0.001	95.0	0.006	94.9

APPENDIX A: PROOF OF FORMULA (20) AND (21)

First, note that expressions for the mean of Y(d₀, M(d₁), Y₁(d₂, M(d_1,2))) in general involve the potential outcomes of M and Y₁, the latter being random variables (representing endogenous variables in the causal model [13]). Therefore, obtaining the marginal mean of the potential outcome Y(d₀, M(d₁), Y₁(d₂, M(d_1,2))) requires integrating over M and Y₁ as follows,

$$\begin{array}{c}\hfill E\left\{Y(d_0,M\left(d_1\right),Y_1(d_2,M\left(d_{1,2}\right)))\right\}=\sum _{y_1=0,1}\int E\{Y(d_0,m,y_1)\mid M\left(d_1\right)=m,Y_1(d_2,M\left(d_{1,2}\right))=y_1\}\hfill \\ \hfill P\{Y_1(d_2,M\left(d_{1,2}\right))=y_1\mid M\left(d_1\right)=m\}d{F}_{M\left(d_1\right)}\left(m\right)\hfill \\ \hfill =\int E\{Y(d_0,m,1)\mid M\left(d_1\right)=m,Y_1(d_2,M\left(d_{1,2}\right))=1\}P\{Y_1(d_2,M\left(d_{1,2}\right))=1\mid M\left(d_1\right)=m\}d{F}_{M\left(d_1\right)}\left(m\right)\hfill \end{array}$$

The second equation follows from the fact that when y₁ = 0 (the subject belongs to the non-susceptible group), E{Y(d₀, m, 0) | M(d₁) = m, Y₁(d₂, M(d_1,2)) = 0} = 0. We can therefore express E(Y(d₀, M(d₁), Y₁(d₂, M(d_1,2)))), as a function of E{Y(d₀, m, 1) | M(d₁) = m, Y₁(d₂, M(d_1,2)) = 1} and P{Y₁(d₂, M(d_1,2)) = 1 | M(d₁) = m}. The former term is identifiable which is shown,

$$\begin{array}{cc}\hfill & E\{Y(d_0,m,1)\mid M\left(d_1\right)=m,Y_1(d_2,M\left(d_{1,2}\right))=1\}\hfill \\ \hfill & =E\{Y(d_0,m,1)\mid M\left(d_1\right)=m,(Y_1(d_2,m^{\prime })\mid M\left(d_{1,2}\right)=m^{\prime })=1\}Definition\hfill \\ \hfill & =E\{Y(d_0,m,1)\mid M\left(d_1\right)=m,(Y_1(d_2,m^{\prime })\mid T=d_{1,2},M\left(d_{1,2}\right)=m^{\prime })=1\}\left(17\right)\hfill \\ \hfill & =E\{Y(d_0,m,1)\mid M\left(d_1\right)=m,(Y_1(d_2,m^{\prime })\mid T=d_{1,2})=1\}\left(18\right)\hfill \\ \hfill & =E\{Y(d_0,m,1)\mid M\left(d_1\right)=m,(Y_1(d_2,m^{\prime })\mid T=d_2)=1\}\left(17\right)\hfill \\ \hfill & =E\{Y(d_0,m,1)\mid M\left(d_1\right)=m,(Y_1(d_2,m^{\prime })\mid T=d_2,M\left(d_2\right)=m^{\prime })=1\}\left(18\right)\hfill \\ \hfill & =E\{Y(d_0,m,1)\mid M\left(d_1\right)=m,Y_1(d_2,M\left(d_2\right))=1\}Consistency\hfill \\ \hfill & =E\{Y(d_0,m,1)\mid T=d_1,M\left(d_1\right)=m,Y_1(d_2,M\left(d_2\right))=1\}\left(17\right)\hfill \\ \hfill & =E\{Y(d_0,m,1)\mid T=d_1,Y_1(d_2,M\left(d_2\right))=1\}\left(18\right)\hfill \\ \hfill & =E\{Y(d_0,m,1)\mid T=d_2,Y_1(d_2,M\left(d_2\right))=1\}\left(17\right)\hfill \\ \hfill & =E\{Y(d_0,m,1)\mid T=d_2,M\left(d_2\right)=m,Y_1(d_2,M\left(d_2\right))=1\}\left(18\right)\hfill \\ \hfill & =E\{Y(d_0,m,1)\mid T=d_2,M\left(d_2\right)=m\}\left(19\right)\hfill \\ \hfill & =E\{Y(d_0,m,1)\mid T=d_2\}\left(18\right)\hfill \\ \hfill & =E\{Y(d_0,m,1)\mid T=d_0\}\left(17\right)\hfill \\ \hfill & =E\{Y(d_0,m,1)\mid T=d_0,M\left(d_0\right)=m\}\left(18\right)\hfill \\ \hfill & =E\{Y(d_0,m,1)\mid T=d_0,M\left(d_0\right)=m,Y_1(d_0,M\left(d_0\right))=1\}\left(19\right)\hfill \\ \hfill & =E\{Y\mid T=d_0,M=m,Y_1=1\}Consistency\hfill \end{array}$$

For formula (20), under the condition d₁ ≠ d_1,2,

$$\begin{array}{cc}\hfill & P\{Y_1(d_2,M\left(d_{1,2}\right))=1\mid M\left(d_1\right)=m\}=E\{Y_1(d_2,M\left(d_{1,2}\right))\mid M\left(d_1\right)=m\}Definition\hfill \\ \hfill & =\int E\{Y_1(d_2,m^{\prime })\mid M\left(d_{1,2}\right)=m^{\prime },M\left(d_1\right)=m\}d{F}_{M\left(d_{1,2}\right)\mid M\left(d_1\right)=m}\left(m^{\prime }\right)Definition\hfill \\ \hfill & =\int E\{Y_1(d_2,m^{\prime })\mid T=d_1,M\left(d_{1,2}\right)=m^{\prime },M\left(d_1\right)=m\}d{F}_{M\left(d_{1,2}\right)\mid M\left(d_1\right)=m}\left(m^{\prime }\right)\left(17\right)\hfill \\ \hfill & =\int E\{Y_1(d_2,m^{\prime })\mid T=d_1,M\left(d_{1,2}\right)=m^{\prime }\}d{F}_{M\left(d_{1,2}\right)\mid M\left(d_1\right)=m}\left(m^{\prime }\right)\left(18\right)\hfill \\ \hfill & =\int E\{Y_1(d_2,m^{\prime })\mid T=d_{1,2},M\left(d_{1,2}\right)=m^{\prime }\}d{F}_{M\left(d_{1,2}\right)\mid M\left(d_1\right)=m}\left(m^{\prime }\right)\left(17\right)\hfill \\ \hfill & =\int E\{Y_1(d_2,m^{\prime })\mid T=d_{1,2}\}d{F}_{M\left(d_{1,2}\right)\mid M\left(d_1\right)=m}\left(m^{\prime }\right)\left(18\right)\hfill \\ \hfill & =\int E\{Y_1(d_2,m^{\prime })\mid T=d_2\}d{F}_{M\left(d_{1,2}\right)\mid M\left(d_1\right)=m}\left(m^{\prime }\right)\left(17\right)\hfill \\ \hfill & =\int E\{Y_1(d_2,m^{\prime })\mid T=d_2,M\left(d_2\right)=m^{\prime }\}d{F}_{M\left(d_{1,2}\right)\mid M\left(d_1\right)=m}\left(m^{\prime }\right)\left(18\right)\hfill \\ \hfill & =\int E\{Y_1\mid T=d_{2,M=m^{\prime }}\}d{F}_{M\left(d_{1,2}\right)\mid M\left(d_1\right)=m}\left(m^{\prime }\right)Consistency\hfill \end{array}$$

Then we have,

$$\begin{array}{cc}\hfill & E\left\{Y(d_0,M\left(d_1\right),Y_1(d_2,M\left(d_{1,2}\right)))\right\}\hfill \\ \hfill & =\int \int E\{Y\mid T=d_0,M=m,Y_1=1\}E\{Y_1\mid T=d_2,M=m^{\prime }\}d{F}_{M\left(d_{1,2}\right)\mid M\left(d_1\right)=m}\left(m^{\prime }\right)d{F}_{M\left(d_1\right)}\left(m\right)\hfill \\ \hfill & =\int \int E\{Y\mid T=d_0,M=m,Y_1=1\}E\{Y_1\mid T=d_2,M=m^{\prime }\}{d}^2{F}_{M\left(d_1\right),M\left(d_{1,2}\right)}(m,m^{\prime })\hfill \end{array}$$

Therefore when d₁ ≠ d_1,2, formula (20) holds.

For formula (21), under the condition d₁ = d_1,2,

$$\begin{array}{cc}\hfill & P\{Y_1(d_2,M\left(d_{1,2}\right))=1\mid M\left(d_1\right)=m\}\hfill \\ \hfill & =P\{Y_1(d_2,M\left(d_1\right))=1\mid M\left(d_1\right)=m\}Condition{d}_1=d_{1,2}\hfill \\ \hfill & =E\{Y_1(d_2,m)\mid M\left(d_1\right)=m\}Definition\hfill \\ \hfill & =E\{Y_1(d_2,m)\mid T=d_1,M\left(d_1\right)=m\}\left(17\right)\hfill \\ \hfill & =E\{Y_1(d_2,m)\mid T=d_1\}\left(18\right)\hfill \\ \hfill & =E\{Y_1(d_2,m)\mid T=d_2\}\left(17\right)\hfill \\ \hfill & =E\{Y_1(d_2,m)\mid T=d_2,M\left(d_2\right)=m\}\left(18\right)\hfill \\ \hfill & =E\{Y_1\mid T=d_2,M=m\}Consistency\hfill \end{array}$$

This gives:

$$\begin{array}{cc}\hfill & E\left\{Y(d_0,M\left(d_1\right),Y_1(d_2,M\left(d_1\right)))\right\}\hfill \\ \hfill & =\int E\{Y\mid T=d_0,M=m,Y_1=1\}E\{Y_1\mid T=d_2,M=m\}d{F}_{M\left(d_1\right)}\left(m\right)\hfill \end{array}$$

So formula (21) also holds.