Basic biostatistics for post-graduate students

Abstract

Statistical methods are important to draw valid conclusions from the obtained data. This article provides background information related to fundamental methods and techniques in biostatistics for the use of postgraduate students. Main focus is given to types of data, measurement of central variations and basic tests, which are useful for analysis of different types of observations. Few parameters like normal distribution, calculation of sample size, level of significance, null hypothesis, indices of variability, and different test are explained in detail by giving suitable examples. Using these guidelines, we are confident enough that postgraduate students will be able to classify distribution of data along with application of proper test. Information is also given regarding various free software programs and websites useful for calculations of statistics. Thus, postgraduate students will be benefitted in both ways whether they opt for academics or for industry.

Introduction

Statistics is basically a way of thinking about data that are variable. This article deals with basic biostatistical concepts and their application to enable postgraduate medical and allied science students to analyze and interpret their study data and to critically interpret published literature. Acquiring such skills currently forms an integral part of their postgraduate training. It has been commonly seen that most postgraduate students have an inherent apprehension and prefer staying away from biostatistics, except for memorizing some information that helps them through their postgraduate examination. Self-motivation for effective learning and application of statistics is lacking.

Statistics implies both, data and statistical methods. It can be considered as an art as well as science. Statistics can neither prove not disprove anything. It is just a tool. Statistics without scientific application has no roots. Thus, statistics may be defined as the discipline concerned with the treatment of numerical data derived from group of individuals. These individuals may be human beings, animals, or other organisms. Biostatistics is a branch of statistics applied to biological or medical sciences. Biostatistics covers applications and contributions not only from health, medicines and, nutrition but also from fields such as genetics, biology, epidemiology, and many others.[1] Biostatistics mainly consists of various steps like generation of hypothesis, collection of data, and application of statistical analysis. To begin with, readers should know about the data obtained during the experiment, its distribution, and its analysis to draw a valid conclusion from the experiment.

Statistical method has two major branches mainly descriptive and inferential. Descriptive statistics explain the distribution of population measurements by providing types of data, estimates of central tendency (mean, mode and median), and measures of variability (standard deviation, correlation coefficient), whereas inferential statistics is used to express the level of certainty about estimates and includes hypothesis testing, standard error of mean, and confidence interval.

Types of Data

Observations recorded during research constitute data. There are three types of data i.e. nominal, ordinal, and interval data. Statistical methods for analysis mainly depend on type of data. Generally, data show picture of the variability and central tendency. Therefore, it is very important to understand the types of data.

1) Nominal data: This is synonymous with categorical data where data is simply assigned “names” or categories based on the presence or absence of certain attributes/characteristics without any ranking between the categories.[2] For example, patients are categorized by gender as males or females; by religion as Hindu, Muslim, or Christian. It also includes binominal data, which refers to two possible outcomes. For example, outcome of cancer may be death or survival, drug therapy with drug ‘X’ will show improvement or no improvement at all.

2) Ordinal data: It is also called as ordered, categorical, or graded data. Generally, this type of data is expressed as scores or ranks. There is a natural order among categories, and they can be ranked or arranged in order.[2] For example, pain may be classified as mild, moderate, and severe. Since there is an order between the three grades of pain, this type of data is called as ordinal. To indicate the intensity of pain, it may also be expressed as scores (mild = 1, moderate = 2, severe = 3). Hence, data can be arranged in an order and rank.

3) Interval data: This type of data is characterized by an equal and definite interval between two measurements. For example, weight is expressed as 20, 21, 22, 23, 24 kg. The interval between 20 and 21 is same as that between 23 and 24. Interval type of data can be either continuous or discrete. A continuous variable can take any value within a given range. For example: hemoglobin (Hb) level may be taken as 11.3, 12.6, 13.4 gm % while a discrete variable is usually assigned integer values i.e. does not have fractional values. For example, blood pressure values are generally discrete variables or number of cigarettes smoked per day by a person.

Sometimes, certain data may be converted from one form to another form to reduce skewness and make it to follow the normal distribution. For example, drug doses are converted to their log values and plotted in dose response curve to obtain a straight line so that analysis becomes easy.[3] Data can be transformed by taking the logarithm, square root, or reciprocal. Logarithmic conversion is the most common data transformation used in medical research.

Measures of Central Tendencies

Mean, median, and mode are the three measures of central tendencies. Mean is the common measure of central tendency, most widely used in calculations of averages. It is least affected by sampling fluctuations. The mean of a number of individual values (X) is always nearer the true value of the individual value itself. Mean shows less variation than that of individual values, hence they give confidence in using them. It is calculated by adding up the individual values (Σx) and dividing the sum by number of items (n). Suppose height of 7 children's is 60, 70, 80, 90, 90, 100, and 110 cms. Addition of height of 7 children is 600 cm, so mean(X) = Σx/n=600/7=85.71.

Median is an average, which is obtained by getting middle values of a set of data arranged or ordered from lowest to the highest (or vice versa). In this process, 50% of the population has the value smaller than and 50% of samples have the value larger than median. It is used for scores and ranks. Median is a better indicator of central value when one or more of the lowest or the highest observations are wide apart or are not evenly distributed. Median in case of even number of observations is taken arbitrary as an average of two middle values, and in case of odd number, the central value forms the median. In above example, median would be 90. Mode is the most frequent value, or it is the point of maximum concentration. Most fashionable number, which occurred repeatedly, contributes mode in a distribution of quantitative data . In above example, mode is 90. Mode is used when the values are widely varying and is rarely used in medical studies. For skewed distribution or samples where there is wide variation, mode, and median are useful.

Even after calculating the mean, it is necessary to have some index of variability among the data. Range or the lowest and the highest values can be given, but this is not very useful if one of these extreme values is far off from the rest. At the same time, it does not tell how the observations are scattered around the mean. Therefore, following indices of variability play a key role in biostatistics.

Standard Deviation

In addition to the mean, the degree of variability of responses has to be indicated since the same mean may be obtained from different sets of values. Standard deviation (SD) describes the variability of the observation about the mean.[4] To describe the scatter of the population, most useful measure of variability is SD. Summary measures of variability of individuals (mean, median, and mode) are further needed to be tested for reliability of statistics based on samples from population variability of individual.

To calculate the SD, we need its square called variance. Variance is the average square deviation around the mean and is calculated by Variance = Σ(x-x-) 2/n OR Σ(x-x-) 2/n-1, now SD = √variance. SD helps us to predict how far the given value is away from the mean, and therefore, we can predict the coverage of values. SD is more appropriate only if data are normally distributed. If individual observations are clustered around sample mean (M) and are scattered evenly around it, the SD helps to calculate a range that will include a given percentage of observation. For example, if N ≥ 30, the range M ± 2(SD) will include 95% of observation and the range M ± 3(SD) will include 99% of observation. If observations are widely dispersed, central values are less representative of data, hence variance is taken. While reporting mean and SD, better way of representation is ‘mean (SD)’ rather than ‘mean ± SD’ to minimize confusion with confidence interval.[5,6]

Correlation Coefficient

Correlation is relationship between two variables. It is used to measure the degree of linear relationship between two continuous variables.[7] It is represented by ‘r’. In Chi-square test, we do not get the degree of association, but we can know whether they are dependent or independent of each other. Correlation may be due to some direct relationship between two variables. This also may be due to some inherent factors common to both variables. The correlation is expressed in terms of coefficient. The correlation coefficient values are always between -1 and +1. If the variables are not correlated, then correlation coefficient is zero. The maximum value of 1 is obtained if there is a straight line in scatter plot and considered as perfect positive correlation. The association is positive if the values of x-axis and y-axis tend to be high or low together. On the contrary, the association is negative i.e. -1 if the high y axis values tends to go with low values of x axis and considered as perfect negative correlation. Larger the correlation coefficient, stronger is the association. A weak correlation may be statistically significant if the numbers of observation are large. Correlation between the two variables does not necessarily suggest the cause and effect relationship. It indicates the strength of association for any data in comparable terms as for example, correlation between height and weight, age and height, weight loss and poverty, parity and birth weight, socioeconomic status and hemoglobin. While performing these tests, it requires x and y variables to be normally distributed. It is generally used to form hypothesis and to suggest areas of future research.

Types of Distribution

Though this universe is full of uncertainty and variability, a large set of experimental/biological observations always tend towards a normal distribution. This unique behavior of data is the key to entire inferential statistics. There are two types of distribution.

1) Gaussian /normal distribution

If data is symmetrically distributed on both sides of mean and form a bell-shaped curve in frequency distribution plot, the distribution of data is called normal or Gaussian. The noted statistician professor Gauss developed this, and therefore, it was named after him. The normal curve describes the ideal distribution of continuous values i.e. heart rate, blood sugar level and Hb % level. Whether our data is normally distributed or not, can be checked by putting our raw data of study directly into computer software and applying distribution test. Statistical treatment of data can generate a number of useful measurements, the most important of which are mean and standard deviation of mean. In an ideal Gaussian distribution, the values lying between the points 1 SD below and 1 SD above the mean value (i.e. ± 1 SD) will include 68.27% of all values. The range, mean ± 2 SD includes approximately 95% of values distributed about this mean, excluding 2.5% above and 2.5% below the range [Figure 1]. In ideal distribution of the values; the mean, mode, and median are equal within population under study.[8] Even if distribution in original population is far from normal, the distribution of sample averages tend to become normal as size of sample increases. This is the single most important reason for the curve of normal distribution. Various methods of analysis are available to make assumptions about normality, including ‘t’ test and analysis of variance (ANOVA). In normal distribution, skew is zero. If the difference (mean–median) is positive, the curve is positively skewed and if it is (mean–median) negative, the curve is negatively skewed, and therefore, measure of central tendency differs [Figure 1]

Figure 1.

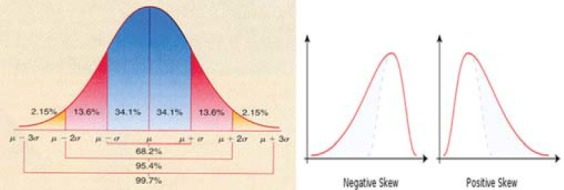
Diagram showing normal distribution curve with negative and positive skew μ = Mean, σ = Standard deviation

2) Non-Gaussian (non-normal) distribution

If the data is skewed on one side, then the distribution is non-normal. It may be binominal distribution or Poisson distribution. In binominal distribution, event can have only one of two possible outcomes such as yes/no, positive/negative, survival/death, and smokers/non-smokers. When distribution of data is non-Gaussian, different test like Wilcoxon, Mann-Whitney, Kruskal-Wallis, and Friedman test can be applied depending on nature of data.

Standard Error of Mean

Since we study some points or events (sample) to draw conclusions about all patients or population and use the sample mean (M) as an estimate of the population mean (M¹), we need to know how far M can vary from M¹ if repeated samples of size N are taken. A measure of this variability is provided by Standard error of mean (SEM), which is calculated as (SEM = SD/√n). SEM is always less than SD. What SD is to the sample, the SEM is to the population mean.

Applications of Standard Error of Mean:

Applications of SEM include:

• 1)To determine whether a sample is drawn from same population or not when it's mean is known.
• 2)To work out the limits of desired confidence within which the population mean should lie. For example, take fasting blood sugar of 200 lawyers. Suppose mean is 90 mg% and SD = 8 mg%. With 95% confidence limits, fasting blood sugar of lawyer's would be; n = 200, SD = 8; hence SEM = SD/√n=8/√200=8/14.14=0.56. Hence,

  Mean fasting blood sugar + 2 SEM = 90 + (2 × 0.56) = 91.12 while

  Mean fasting blood sugar - 2 SEM = 90 - (2 × 0.56) = 88.88

  So, confidence limits of fasting blood sugar of lawyer's population are 88.88 to 91.12 mg %. If mean fasting blood sugar of another lawyer is 80, we can say that, he is not from the same population.

Confidence Interval (CI) OR (Fiducial limits)

Confidence limits are two extremes of a measurement within which 95% observations would lie. These describe the limits within which 95% of the mean values if determined in similar experiments are likely to fall. The value of ‘t’ corresponding to a probability of 0.05 for the appropriate degree of freedom is read from the table of distribution. By multiplying this value with the standard error, the 95% confidence limits for the mean are obtained as per formula below.

Lower confidence limit = mean - (t_0.05 × SEM)

Upper confidence limit = mean + (t_0.05 × SEM)

If n > 30, the interval M ± 2(SEM) will include M with a probability of 95% and the interval M ± 2.8(SEM) will include M with probability of 99%. These intervals are, therefore, called the 95% and 99% confidence intervals, respectively.[9] The important difference between the ‘p’ value and confidence interval is that confidence interval represents clinical significance, whereas ‘p’ value indicates statistical significance. Therefore, in many clinical studies, confidence interval is preferred instead of ‘p’ value,[4] and some journals specifically ask for these values.

Various medical journals use mean and SEM to describe variability within the sample. The SEM is a measure of precision for estimated population mean, whereas SD is a measure of data variability around mean of a sample of population. Hence, SEM is not a descriptive statistics and should not be used as such.[10] Correct use of SEM would be only to indicate precision of estimated mean of population.

Null Hypothesis

The primary object of statistical analysis is to find out whether the effect produced by a compound under study is genuine and is not due to chance. Hence, the analysis usually attaches a test of statistical significance. First step in such a test is to state the null hypothesis. In null hypothesis (statistical hypothesis), we make assumption that there exist no differences between the two groups. Alternative hypothesis (research hypothesis) states that there is a difference between two groups. For example, a new drug ‘A’ is claimed to have analgesic activity and we want to test it with the placebo. In this study, the null hypothesis would be ‘drug A is not better than the placebo.’ Alternative hypothesis would be ‘there is a difference between new drug ‘A’ and placebo.’ When the null hypothesis is accepted, the difference between the two groups is not significant. It means, both samples were drawn from single population, and the difference obtained between two groups was due to chance. If alternative hypothesis is proved i.e. null hypothesis is rejected, then the difference between two groups is statistically significant. A difference between drug ‘A’ and placebo group, which would have arisen by chance is less than five percent of the cases, that is less than 1 in 20 times is considered as statistically significant (P < 0.05). In any experimental procedure, there is possibility of occurring two errors.

1) Type I Error (False positive)

This is also known as α error. It is the probability of finding a difference; when no such difference actually exists, which results in the acceptance of an inactive compound as an active compound. Such an error, which is not unusual, may be tolerated because in subsequent trials, the compound will reveal itself as inactive and thus finally rejected.[11] For example, we proved in our trial that new drug ‘A’ has an analgesic action and accepted as an analgesic. If we commit type I error in this experiment, then subsequent trial on this compound will automatically reject our claim that drug ‘A’ is having analgesic action and later on drug ‘A’ will be thrown out of market. Type I error is actually fixed in advance by choice of the level of significance employed in test.[12] It may be noted that type I error can be made small by changing the level of significance and by increasing the size of sample.

2) Type II Error (False negative)

This is also called as β error. It is the probability of inability to detect the difference when it actually exists, thus resulting in the rejection of an active compound as an inactive. This error is more serious than type I error because once we labeled the compound as inactive, there is possibility that nobody will try it again. Thus, an active compound will be lost.[11] This type of error can be minimized by taking larger sample and by employing sufficient dose of the compound under trial. For example, we claim that drug ‘A’ is not having analgesic activity after suitable trial. Therefore, drug ‘A’ will not be tried by any other researcher for its analgesic activity and thus drug ‘A’, in spite of having analgesic activity, will be lost just because of our type II error. Hence, researcher should be very careful while reporting type II error.

Level of Significance

If the probability (P) of an event or outcome is high, we say it is not rare or not uncommon. But, if the P is low, we say it is rare or uncommon. In biostatistics, a rare event or outcome is called significant, whereas a non-rare event is called non-significant. The ‘P’ value at which we regard an event or outcomes as enough to be regarded as significant is called the significance level.[2] In medical research, most commonly P value less than 0.05 or 5% is considered as significant level . However, on justifiable grounds, we may adopt a different standard like P < 0.01 or 1%. Whenever possible, it is better to give actual P values instead of P < 0.05.[13] Even if we have found the true value or population value from sample, we cannot be confident as we are dealing with a part of population only; howsoever big the sample may be. We would be wrong in 5% cases only if we place the population value within 95% confidence limits. Significant or insignificant indicates whether a value is likely or unlikely to occur by chance. ‘P’ indicates probability of relative frequency of occurrence of the difference by chance.

Outliers

Sometimes, when we analyze the data, one value is very extreme from the others. Such value is referred as outliers. This could be due to two reasons. Firstly, the value obtained may be due to chance; in that case, we should keep that value in final analysis as the value is from the same distribution. Secondly, it may be due to mistake. Causes may be listed as typographical or measurement errors. In such cases, these values should be deleted, to avoid invalid results.

One-tailed and Two-tailed Test

When comparing two groups of continuous data, the null hypothesis is that there is no real difference between the groups (A and B). The alternative hypothesis is that there is a real difference between the groups. This difference could be in either direction e.g. A > B or A < B. When there is some sure way to know in advance that the difference could only be in one direction e.g. A > B and when a good ground considers only one possibility, the test is called one-tailed test. Whenever we consider both the possibilities, the test of significance is known as a two-tailed test. For example, when we know that English boys are taller than Indian boys, the result will lie at one end that is one tail distribution, hence one tail test is used. When we are not absolutely sure of the direction of difference, which is usual, it is always better to use two-tailed test.[14] For example, a new drug ‘X’ is supposed to have an antihypertensive activity, and we want to compare it with atenolol. In this case, as we don’t know exact direction of effect of drug ‘X’, so one should prefer two-tailed test. When you want to know the action of particular drug is different from that of another, but the direction is not specific, always use two-tailed test. At present, most of the journals use two-sided P values as a standard norm in biomedical research.[15]

Importance of Sample Size Determination

Sample is a fraction of the universe. Studying the universe is the best parameter. But, when it is possible to achieve the same result by taking fraction of the universe, a sample is taken. Applying this, we are saving time, manpower, cost, and at the same time, increasing efficiency. Hence, an adequate sample size is of prime importance in biomedical studies. If sample size is too small, it will not give us valid results, and validity in such a case is questionable, and therefore, whole study will be a waste. Furthermore, large sample requires more cost and manpower. It is a misuse of money to enroll more subjects than required. A good small sample is much better than a bad large sample. Hence, appropriate sample size will be ethical to produce precise results.

Factors Influencing Sample Size Include

• 1)Prevalence of particular event or characteristics- If the prevalence is high, small sample can be taken and vice versa. If prevalence is not known, then it can be obtained by a pilot study.
• 2)Probability level considered for accuracy of estimate- If we need more safeguard about conclusions on data, we need a larger sample. Hence, the size of sample would be larger when the safeguard is 99% than when it is only 95%. If only a small difference is expected and if we need to detect even that small difference, then we need a large sample.
• 3)Availability of money, material, and manpower.
• 4)Time bound study curtails the sample size as routinely observed with dissertation work in post graduate courses.

Sample Size Determination and Variance Estimate

To calculate sample size, the formula requires the knowledge of standard deviation or variance, but the population variance is unknown. Therefore, standard deviation has to be estimated. Frequently used sources for estimation of standard deviation are:

1. A pilot[16] or preliminary sample may be drawn from the population, and the variance computed from the sample may be used as an estimate of standard deviation. Observations used in pilot sample may be counted as a part of the final sample.[17]

2. Estimates of standard deviation may be accessible from the previous or similar studies,[17] but sometimes, they may not be correct.

Calculation of Sample Size

Calculation of sample size plays a key role while doing any research. Before calculation of sample size, following five points are to be considered very carefully. First of all, we have to assess the minimum expected difference between the groups. Then, we have to find out standard deviation of variables. Different methods for determination of standard deviation have already been discussed previously. Now, set the level of significance (alpha level, generally set at P < 0.05) and Power of study (1-beta = 80%). After deciding all these parameters, we have to select the formula from computer programs to obtain the sample size. Various softwares are available free of cost for calculation of sample size and power of study. Lastly, appropriate allowances are given for non-compliance and dropouts, and this will be the final sample size for each group in study. We will work on two examples to understand sample size calculation.

• a)The mean (SD) diastolic blood pressure of hypertensive patient after enalapril therapy is found to be 88(8). It is claimed that telmisartan is better than enalapril, and a trial is to be conducted to find out the truth. By our convenience, suppose we take minimum expected difference between the two groups is 6 at significance level of 0.05 with 80% power. Results will be analyzed by unpaired ‘t’ test. In this case, minimum expected difference is 6, SD is 8 from previous study, alpha level is 0.05, and power of study is 80%. After putting all these values in computer program, sample size comes out to be 29. If we take allowance to non-compliance and dropout to be 4, then final sample size for each group would be 33.
• b)The mean hemoglobin (SD) of newborn is observed to be 10.5 (1.4) in pregnant mother of low socioeconomic group. It was decided to carry out a study to decide whether iron and folic acid supplementation would increase hemoglobin level of newborn. There will be two groups, one with supplementation and other without supplementation. Minimum difference expected between the two groups is taken as 1.0 with 0.05 level of significance and power as 90%. In this example, SD is 1.4 with minimum difference 1.0. After keeping these values in computer-based formula, sample size comes out to be 42 and with allowance of 10%, final sample size would be 46 in each group.

Power of Study

It is a probability that study will reveal a difference between the groups if the difference actually exists. A more powerful study is required to pick up the higher chances of existing differences. Power is calculated by subtracting the beta error from 1. Hence, power is (1-Beta). Power of study is very important while calculation of sample size. Power of study can be calculated after completion of study called as posteriori power calculation. This is very important to know whether study had enough power to pick up the difference if it existed. Any study to be scientifically sound should have at least 80% power. If power of study is less than 80% and the difference between groups is not significant, then we can say that difference between groups could not be detected, rather than no difference between the groups. In this case, power of study is too low to pick up the exiting difference. It means probability of missing the difference is high and hence the study could have missed to detect the difference. If we increase the power of study, then sample size also increases. It is always better to decide power of study at initial level of research.

How to Choose an Appropriate Statistical Test

There are number of tests in biostatistics, but choice mainly depends on characteristics and type of analysis of data. Sometimes, we need to find out the difference between means or medians or association between the variables. Number of groups used in a study may vary; therefore, study design also varies. Hence, in such situation, we will have to make the decision which is more precise while selecting the appropriate test. Inappropriate test will lead to invalid conclusions. Statistical tests can be divided into parametric and non-parametric tests. If variables follow normal distribution, data can be subjected to parametric test, and for non-Gaussian distribution, we should apply non-parametric test. Statistical test should be decided at the start of the study. Following are the different parametric test used in analysis of various types of data.

1) Student's ‘t’ Test

Mr. W. S. Gosset, a civil service statistician, introduced ‘t’ distribution of small samples and published his work under the pseudonym ‘Student.’ This is one of the most widely used tests in pharmacological investigations, involving the use of small samples. The ‘t’ test is always applied for analysis when the number of sample is 30 or less. It is usually applicable for graded data like blood sugar level, body weight, height etc. If sample size is more than 30, ‘Z’ test is applied. There are two types of ‘t’ test, paired and unpaired.

When to apply paired and unpaired

• a)When comparison has to be made between two measurements in the same subjects after two consecutive treatments, paired ‘t’ test is used. For example, when we want to compare effect of drug A (i.e. decrease blood sugar) before start of treatment (baseline) and after 1 month of treatment with drug A.
• b)When comparison is made between two measurements in two different groups, unpaired ‘t’ test is used. For example, when we compare the effects of drug A and B (i.e. mean change in blood sugar) after one month from baseline in both groups, unpaired ‘t’ test’ is applicable.

2) ANOVA

When we want to compare two sets of unpaired or paired data, the student's ‘t’ test is applied. However, when there are 3 or more sets of data to analyze, we need the help of well-designed and multi-talented method called as analysis of variance (ANOVA). This test compares multiple groups at one time.[18] In ANOVA, we draw assumption that each sample is randomly drawn from the normal population, and also they have same variance as that of population. There are two types of ANOVA.

A) One way ANOVA

It compares three or more unmatched groups when the data are categorized in one way. For example, we may compare a control group with three different doses of aspirin in rats. Here, there are four unmatched group of rats. Therefore, we should apply one way ANOVA. We should choose repeated measures ANOVA test when the trial uses matched subjects. For example, effect of supplementation of vitamin C in each subject before, during, and after the treatment. Matching should not be based on the variable you are com paring. For example, if you are comparing blood pressures in two groups, it is better to match based on age or other variables, but it should not be to match based on blood pressure. The term repeated measures applies strictly when you give treatments repeatedly to one subjects. ANOVA works well even if the distribution is only approximately Gaussian. Therefore, these tests are used routinely in many field of science. The P value is calculated from the ANOVA table.

B) Two way ANOVA

Also called two factors ANOVA, determines how a response is affected by two factors. For example, you might measure a response to three different drugs in both men and women. This is a complicated test. Therefore, we think that for postgraduates, this test may not be so useful.

Importance of post hoc test

Post tests are the modification of ‘t’ test. They account for multiple comparisons, as well as for the fact that the comparison are interrelated. ANOVA only directs whether there is significant difference between the various groups or not. If the results are significant, ANOVA does not tell us at what point the difference between various groups subsist. But, post test is capable to pinpoint the exact difference between the different groups of comparison. Therefore, post tests are very useful as far as statistics is concerned. There are five types of post- hoc test namely; Dunnett's, Turkey, Newman-Keuls, Bonferroni, and test for linear trend between mean and column number.[18]

How to select a post test?

• I)Select Dunnett's post-hoc test if one column represents control group and we wish to compare all other columns to that control column but not to each other.
• II)Select the test for linear trend if the columns are arranged in a natural order (i.e. dose or time) and we want to test whether there is a trend so that values increases (or decreases) as you move from left to right across the columns.
• III)Select Bonferroni, Turkey's, or Newman's test if we want to compare all pairs of columns.

Following are the non-parametric tests used for analysis of different types of data.

1) Chi-square test

The Chi-square test is a non-parametric test of proportions. This test is not based on any assumption or distribution of any variable. This test, though different, follows a specific distribution known as Chi-square distribution, which is very useful in research. It is most commonly used when data are in frequencies such as number of responses in two or more categories. This test involves the calculations of a quantity called Chi-square (x²) from Greek letter ‘Chi’(x) and pronounced as ‘Kye.’ It was developed by Karl Pearson.

Applications

• a)Test of proportion: This test is used to find the significance of difference in two or more than two proportions.
• b)Test of association: The test of association between two events in binomial or multinomial samples is the most important application of the test in statistical methods. It measures the probabilities of association between two discrete attributes. Two events can often be studied for their association such as smoking and cancer, treatment and outcome of disease, level of cholesterol and coronary heart disease. In these cases, there are two possibilities, either they influence or affect each other or they do not. In other words, you can say that they are dependent or independent of each other. Thus, the test measures the probability (P) or relative frequency of association due to chance and also if two events are associated or dependent on each other. Varieties used are generally dichotomous e.g. improved / not improved. If data are not in that format, investigator can transform data into dichotomous data by specifying above and below limit. Multinomial sample is also useful to find out association between two discrete attributes. For example, to test the association between numbers of cigarettes equal to 10, 11- 20, 21-30, and more than 30 smoked per day and the incidence of lung cancer. Since, the table presents joint occurrence of two sets of events, the treatment and outcome of disease, it is called contingency table (Con- together, tangle- to touch).

How to prepare 2 × 2 table

When there are only two samples, each divided into two classes, it is called as four cell or 2 × 2 contingency table. In contingency table, we need to enter the actual number of subjects in each category. We cannot enter fractions or percentage or mean. Most contingency tables have two rows (two groups) and two columns (two possible outcomes). The top row usually represents exposure to a risk factor or treatment, and bottom row is mainly for control. The outcome is entered as column on the right side with the positive outcome as the first column and the negative outcome as the second column. A particular subject or patient can be only in one column but not in both. The following table explains it in more detail:

Even if sample size is small (< 30), this test is used by using Yates correction, but frequency in each cell should not be less than 5.[19] Though, Chi-square test tells an association between two events or characters, it does not measure the strength of association. This is the limitation of this test. It only indicates the probability (P) of occurrence of association by chance. Yate's correction is not applicable to tables larger than 2 X 2. When total number of items in 2 X 2 table is less than 40 or number in any cell is less than 5, Fischer's test is more reliable than the Chi-square test.[20]

2) Wilcoxon-Matched-Pairs Signed-Ranks Test

This is a non-parametric test. This test is used when data are not normally distributed in a paired design. It is also called Wilcoxon-Matched Pair test. It analyses only the difference between the paired measurements for each subject. If P value is small, we can reject the idea that the difference is coincidence and conclude that the populations have different medians.

3) Mann-Whitney test

It is a Student's ‘t’ test performed on ranks. For large numbers, it is almost as sensitive as Student's ‘t’ test. For small numbers with unknown distribution, this test is more sensitive than Student's ‘t’ test. This test is generally used when two unpaired groups are to be compared and the scale is ordinal (i.e. ranks and scores), which are not normally distributed.

4) Friedman test

This is a non-parametric test, which compares three or more paired groups. In this, we have to rank the values in each row from low to high. The goal of using a matched test is to control experimental variability between subjects, thus increasing the power of the test.

5) Kruskal-Wallis test

It is a non-parametric test, which compares three or more unpaired groups. Non-parametric tests are less powerful than parametric tests. Generally, P values tend to be higher, making it harder to detect real differences. Therefore, first of all, try to transform the data. Sometimes, simple transformation will convert non-Gaussian data to a Gaussian distribution. Non-parametric test is considered only if outcome variable is in rank or scale with only a few categories [Table 1]. In this case, population is far from Gaussian or one or few values are off scale, too high, or too low to measure.

Table 1.

Summary of statistical tests applied for different types of data

Common problems faced by researcher in any trial and how to address them

Whenever any researcher thinks of any experimental or clinical trial, number of queries arises before him/her. To explain some common difficulties, we will take one example and try to solve it. Suppose, we want to perform a clinical trial on effect of supplementation of vitamin C on blood glucose level in patients of type II diabetes mellitus on metformin. Two groups of patients will be involved. One group will receive vitamin C and other placebo.

a) How much should be the sample size?

In such trial, first problem is to find out the sample size. As discussed earlier, sample size can be calculated if we have S.D, minimum expected difference, alpha level, and power of study. S.D. can be taken from the previous study. If the previous study report is not reliable, you can do pilot study on few patients and from that you will get S.D. Minimum expected difference can be decided by investigator, so that the difference would be clinically important. In this case, Vitamin C being an antioxidant, we will take difference between the two groups in blood sugar level to be 15. Minimum level of significance may be taken as 0.05 or with reliable ground we can increase it, and lastly, power of study is taken as 80% or you may increase power of study up to 95%, but in both the situations, sample size will be increased accordingly. After putting all the values in computer software program, we will get sample size for each group.

b) Which test should I apply?

After calculating sample size, next question is to apply suitable statistical test. We can apply parametric or non-parametric test. If data are normally distributed, we should use parametric test otherwise apply non-parametric test. In this trial, we are measuring blood sugar level in both groups after 0, 6, 12 weeks, and if data are normally distributed, then we can apply repeated measure ANOVA in both the groups followed by Turkey's post-hoc test if we want to compare all pairs of column with each other and Dunnet's post-hoc for comparing 0 with 6 or 12 weeks observations only. If we want to see whether supplementation of vitamin C has any effect on blood glucose level as compared to placebo, then we will have to consider change from baseline i.e. from 0 to 12 weeks in both groups and apply unpaired ‘t’ with two-tailed test as directions of result is non-specific. If we are comparing effects only after 12 weeks, then paired ‘t’ test can be applied for intra-group comparison and unpaired ‘t’ test for inter-group comparison. If we want to find out any difference between basic demographic data regarding gender ratio in each group, we will have to apply Chi-square test.

c) Is there any correlation between the variable?

To see whether there is any correlation between age and blood sugar level or gender and blood sugar level, we will apply Spearman or Pearson correlation coefficient test, depending on Gaussian or non-Gaussian distribution of data. If you answer all these questions before start of the trial, it becomes painless to conduct research efficiently.

Softwares for Biostatistics

Statistical computations are now made very feasible owing to availability of computers and suitable software programs. Now a days, computers are mostly used for performing various statistical tests as it is very tedious to perform it manually. Commonly used software's are MS Office Excel, Graph Pad Prism, SPSS, NCSS, Instant, Dataplot, Sigmastat, Graph Pad Instat, Sysstat, Genstat, MINITAB, SAS, STATA, and Sigma Graph Pad. Free website for statistical softwares are www.statistics.com, http://biostat.mc.vanderbilt.edu/wiki/Main/PowerSampleSize.

Statistical methods are necessary to draw valid conclusion from the data. The postgraduate students should be aware of different types of data, measures of central tendencies, and different tests commonly used in biostatistics, so that they would be able to apply these tests and analyze the data themselves. This article provides a background information, and an attempt is made to highlight the basic principles of statistical techniques and methods for the use of postgraduate students.