Automatic and robust calibration of optical detector arrays for biomedical diffuse optical spectroscopy

Abstract

The design and testing of a new, fully automated, calibration approach is described. The process was used to calibrate an image-guided diffuse optical spectroscopy system with 16 photomultiplier tubes (PMTs), but can be extended to any large array of optical detectors and associated imaging geometry. The design goals were accomplished by developing a routine for robust automated calibration of the multi-detector array within 45 minutes. Our process was able to characterize individual detectors to a median norm of the residuals of 0.03 V for amplitude and 4.4 degrees in phase and achieved less than 5% variation between all the detectors at the 95% confidence interval for equivalent measurements. Repeatability of the calibrated data from the imaging system was found to be within 0.05 V for amplitude and 0.2 degrees for phase, and was used to evaluate tissue-simulating phantoms in two separate imaging geometries. Spectroscopic imaging of total hemoglobin concentration was recovered to within 5% of the true value in both cases. Future work will focus on streamlining the technology for use in a clinical setting with expectations of achieving accurate quantification of suspicious lesions in the breast.

1. Introduction

Image-guided optical spectroscopy is a non-invasive complement to dynamic contrast enhanced MR imaging (DCE-MRI) of breast that produces functional maps of tissue physiology, and could be used to inform decisions about magnetic resonance (MR)-guided biopsy. In previous studies, a frequency domain optical imaging system was developed to collect amplitude and phase data concurrently with the patient’s DCE-MRI exam [1,2]. Standardization and calibration of new and existing imaging systems is a challenge that must be tackled before larger clinical trials are possible [3]. Currently, near infrared spectroscopy (NIRS) systems exploit detectors that have variable gain settings, and require careful calibration in order to ensure the data is robust between scans and from day to day. Previously, calibration of these systems has been a difficult and time-consuming process [4–6], which was adequate during development, but not sufficient for day-to-day use. To improve on calibration design, a methodology to characterize and calibrate a large array of optical detectors automatically was developed. The automation simplifies standardization and quality control between scans, and is expected to lead to more accurate quantification of the relevant tissues of interest when the system is transported to other sites.

Every imaging modality requires standardization and packaging before clinical use. For example, x-ray computed tomography is calibrated based on phantoms standardized to Houndsfield (or CT) units, and tested routinely for quality assurance (QA) [7–9]. Detectors in PET [10–12], x-ray mammography [13–16], ultrasound [17–19], and MRI [20–23] must be similarly calibrated and then tested regularly to normalize variations in detector responsivity. Each system has its own procedure depending on the type of detector, but the goal of calibration remains the same: every pixel, detector, or coil element must produce the same measurement response for equivalent inputs, across as wide of a signal dynamic range as possible. These calibration procedures are especially important for imaging systems that rely on relative measurements since no absolute reference is available for comparison [23,24], and care must be exercised to ensure data reliability over time.

Since optical imaging and NIRS are typically based on relative measurements [25] that are captured with an array of detectors, meaningful data collection requires instruments that are well-calibrated. For example, a Diffuse Optical Tomography (DOT) system at the University of Pennsylvania uses continuous wave measurements that are recorded with a CCD camera which must be characterized and adjusted for dark current noise before imaging can be performed. These signals are adjusted to match data collected in the frequency domain that are measured by avalanche photodiodes (APD) [4]. At Dartmouth, a breast imaging system involving 16 photomultiplier tube (PMT) detectors is used to monitor neoadjuvant chemotherapy, which requires consistency between longitudinal imaging sessions. It is calibrated by measuring the amplitude and phase at every gain setting, and scaling the offsets and slopes to provide a linear response over a dynamic range that is restricted for each gain level [26,27]. A frequency domain photon migration (FDPM) system was developed at the University of California—Irvine, and is now part of a multi-center clinical trial having a goal of evaluating performance across different institutions [28–31]. Prior to initiating this trial, effort to characterize the instrument’s amplitude and phase responses, and standardize them between replicated instruments was required [32,33]. These instruments, as well as others, are working their way towards clinical implementation, and similarly to the UCI system, will need to have standardized calibration methods in place.

In the optical imaging studies reported here, instrumentation and methods for automated calibration are outlined, which can be extended to large arrays of optical detectors. The process incorporates motorized filter wheels to vary laser intensity over a large dynamic range, and is coupled with acquisition and post-processing software to fully characterize and calibrate the responsivity of PMTs for MR-guided optical breast spectroscopy. This procedure is essentially independent of detector type and data collection geometry [34]. Standardization is a critical prerequisite for emerging imaging modalities to have clinical impact, and accessibility is important as the emphasis shifts from engineering design to routine clinical use. Repeatability and performance of the imaging system after calibration is presented in terms of tissue simulating breast phantoms. This report also considers design and test results in tissue-simulating breast phantoms representing different data collection geometries.

2. Methods and materials

2.1. Instrumentation

The MR-NIRS system in this study [1] has six intensity modulated laser diodes with wavelengths spanning 660 nm to 850 nm, which are used to illuminate the breast from 16 sequential source positions. During each individual source illumination, the remaining 15 fibers detect transmitted light with photomultiplier tubes (PMTs) (Hamamatsu, 9305-03). The amplitude and phase of the detected light are separated by a lock-in detection method. The imaging system is housed in the MR console room and 12 m fiber bundles with 4 mm working optical diameters are passed through a custom penetration panel in the wall to enter the MR scanner room. These fibers are coupled into a custom breast MR coil (Phillips) for simultaneous MR and optical imaging of patients or phantoms. More details on the imaging instrumentation can be found in a previous publication [1].

Additional instrumentation has now been implemented to automate calibration. Specifically, every gain setting of the PMTs must be measured through the same phantom without altering the setup in order to compare amplitudes and phases across gain settings. Thus, the laser source is coupled to a pair of motorized filter wheels (Thorlabs, Newton, NJ) with 36 settings ranging from 0 to 4 optical density as shown in Fig. 1 . These filter wheels use collimating lenses and a light-tight coupling sleeve to deliver power as high as possible to the calibration phantom through an 800 micron source fiber. The filter wheels can be adjusted through LABVIEW software to produce the desired attenuation or generate the desired signal strength at the detector. The source fiber is coupled to the circular calibration phantom using a holder that was designed specifically for the geometry with Solidworks software (Solidworks Corp, Waltham MA) and fabricated using a 3D printer (Stratasys, Inc., Eden Prairie MN) depositing ABS plastic. This device holds up to 16 fibers equally spaced around the perimeter of the phantom and couples a centrally located SMA source fiber. The additional instrumentation was characterized prior to calibration so that software corrections can be applied after data is collected. Each gain setting of a PMT provides approximately one decade of linear response between its noise floor and saturation. Because PMTs exhibit good SNR and repeatable measurements over more than their range of linear response to measured signal strengths, measurement standard deviation is not an appropriate indicator of linearity, and the PMT’s must be characterized prior to calibration.

Fig. 1.

(a) Outline of calibration process used with the MRI-guided diffuse optical spectroscopy. (b) Diffuse optical spectroscopy system rack. (c) Calibration imaging geometry with a source fiber in the center for light delivery. (d) Motorized OD filter wheels used to automatically vary the incident laser intensity applied to the phantom and received by the detector array. (e) Example phantoms in the parallel plate geometry. (f) Reconstructed 3D image volume. (g) Cross-section of imaged total hemoglobin estimates that are within 5% of the true value.

2.2. Individual PMT characterization

The calibration set up uses a phantom with a central SMA source and 15 detector fibers arranged in a circular geometry with equal path lengths between each source and each detector (Fig. 1(c)). A 785 nm frequency modulated laser is maximally attenuated to a source strength of approximately 10 μW. An initial measurement is performed to check each PMT and gain setting for being either saturated or below the noise floor. Each PMT measures the signal ten times at each acceptable gain setting before lowering the filter attenuation to the next setting. The system characterizes all detectors in parallel and steps through 36 filter settings in approximately 20 minutes. The amplitude should scale linearly with input power with a slope of unity, and while gain levels change the offset and slope, the linear response regions are the ones which can be calibrated. The phase shift should be constant with input intensity, and so calibration for the phase shift offset and slight slope effects is also needed across the different gain levels.

Collected data is sorted by gain setting and detector number and plotted versus relative source strength as shown in Fig. 2 . Input laser power is assumed to be 10 mW and is adjusted based on the filter configurations. Data outside the linear range is discarded with the exception of the lowest gain setting, which establishes the lower end of the linear region. Amplitude data is then collected and a first order trend line is fit to the data using MATLAB’s robustfit.m algorithm.

Fig. 2.

Intra-PMT calibration. (a) Amplitude recorded over a large range of input intensities and a region of linearity is selected. (b) Same as (a) for phase. (c) Calibrated amplitude for each individual detector at every gain setting after slopes and offsets are fit to the data in (a). (d) Same as (c) for phase.

This algorithm removes outliers and is more reliable in the presence of faulty data. While the data extremes are usually not problematic, the fitting is performed automatically and is less likely to require inspection (using robustfit.m relative to polyfit.m in MatLab). Amplitude data yields a slope and an offset for each PMT and gain setting for a total of 15 × 9 slopes and 15 × 9 offsets. Similar processing occurs for the phase data. Past results suggest that phase data typically has a slightly smaller range of linearity relative to its amplitude counterparts [1,35]. Therefore, data censored during the amplitude processing should similarly not be used in the phase calibration. Within the linear range, phase response is expected to be flat, independently of source strength, and is fit with a 0th order approximation to yield phase offsets for each PMT and associated gain setting. Once all of the slopes and offsets have been tabulated, subtracting them from the uncalibrated data yields the calibrated response as indicated in Fig. 2.

2.3. Inter-PMT calibration

Once the PMTs are characterized and calibrated individually, the next step is to calibrate the detectors. In the past, this process has relied on a rotary stage optical switch that paired optical fibers and PMTs for each measurement that was made possible by the rotational symmetry of the imaging geometry. Here, to eliminate the assumption of rotational symmetry in the detector array, we accounted for each PMT-detector fiber combination separately through a second step that expanded the calibration file for each source position.

During characterization of the PMTs, an amplitude slope and offset, as well as a phase offset were calculated. The offsets vary based on individual fibers coupling to the detectors as well as the fibers, themselves, whereas the amplitude slopes are intrinsic to the detectors and are unaffected by the differences in fibers or their coupling to the detectors. As a result, calculation of the amplitude slope is only necessary for each of the 15 PMTs, rather than for each PMT at each source position. Using the same experimental setup (circular phantom and central light source), the PMTs were set to the highest gain setting and the source attenuation was lowered until the light levels fell within the linear range of the detectors. Data from each of 240 fiber-PMT combinations were measured and saved. The system automatically cycles through each of the gain settings in this fashion. The calibration factors are then updated so that each fiber-PMT combination (240 combinations) at each gain setting yields the same measurement. Figure 3 shows aggregated data collected for each combination before calibration, after intra-PMT calibration, and after inter-PMT calibration. As long as the detector array measurements are repeatable, these calibration factors remain applicable for different phantoms, and in arbitrary imaging geometries.

Fig. 3.

Inter-PMT calibration. (a) Amplitude. (b) Phase. Box plots show the standard deviation of each gain setting at three stages of calibration. Intra-PMT calibration reduces the standard deviation significantly, but after inter-PMT calibration each source–detector pair is equivalent.

2.4. Verification and analysis

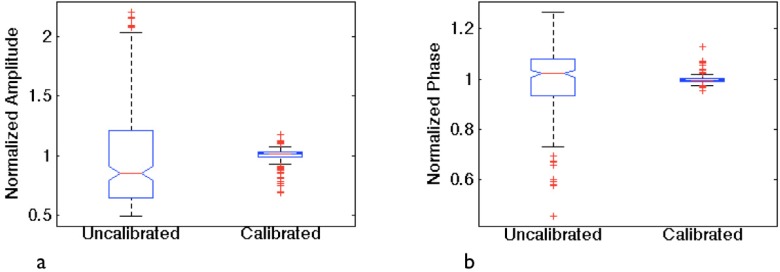
After automated calibration is complete, the data collection and processing was verified. Specifically, with a central laser source, data from all 240 PMT-fiber combinations was collected using different gain settings. Gain settings were selected prior to imaging and filter wheels were automatically adjusted to collect data within the proper range. Since the measurement path lengths were identical, a perfect calibration would yield a flat response in both amplitude and phase. Figure 4 shows results where uncalibrated test data was extremely noisy compared to calibrated data, which closely resembled a flat line and consistent detector response. The complete process from start to finish required approximately 45 minutes.

Fig. 4.

Central source testing. Box plots show the normalized standard deviation of 240 identical path length measurements before and after calibration. (a) Amplitude. (b) Phase.

2.5. Phantom image reconstruction

Phantom images are processed and reconstructed with the open source software platform, NIRFAST [36]. Briefly, the difference between measured data and a diffusion-based model of light propagation through the medium [36–38] is minimized to yield the optical properties. The lossy diffusion equation has been well studied in tissue and is an acceptable approximation in regions where scattering (μ_s′) dominates over absorption (μ_a), and source–detector separation is greater than one scattering distance [39]. Model data is calculated using the frequency domain diffusion equation (Eq. (1),

$$-\nabla ·D\nabla \Phi (r,\omega )+({\mu }_a+\frac{i\omega }{c})\Phi (r,\omega )=S(r,\omega )$$ (1)

discretized on finite elements. Here, a source S with frequency ω describes light fluence Φ through the turbid media. We also employ a modified Tikhonov regularization routine with regularization parameter, λ, using a Levenberg-Marquardt iterative update which stabilizes the estimation process by reducing the effects of noise on the image reconstruction, and eliminating improbable solutions [2]. The image formation algorithm (Eq. (2) is non-linear and solved with a Newton-type minimization method for Δc within the matrix equation [40]:

$$(J^{T}J+\lambda I)\Delta c=J^T\Delta \delta$$, (2)

which optimizes the estimation of the physiological parameters c, which includes oxygenated and deoxygenated hemoglobin concentrations, water fraction, scatter amplitude, and scatter power [41,42]. Here, J is the Jacobian matrix, I is the Identity matrix, and δ is the model-data misfit. Selection of λ is highly influential on the solutions [43] and it is chosen based on inherent system noise and fiber coupling errors, which are difficult to quantify in general because they can be case-specific [44].

2.6. Phantom imaging

Two sets of phantom experiments were conducted to demonstrate that data collected from media with different geometries and optical properties can be calibrated and reconstructed effectively. Phantoms were constructed in two different imaging geometries from Phosphate Buffered Saline (PBS), type 1 Agarose, 1% Intralipid, and whole porcine blood to match the optical properties of normal breast tissue [45]. Homogeneous reference and inclusion phantoms were formed for both geometries. The phantoms in the pentagonal geometry had a hemoglobin concentration of 15 μM, and one had a cylindrical inclusion with 1.5× hemoglobin contrast and 0.5 ml gadolinium MR contrast. The parallel plate phantoms had a hemoglobin concentration of 25 μM and an inclusion of 1.5×. Co-registration between optical and MR images of these phantoms was based on MR fiducial markers placed in the plane of the optical fibers and MR images acquired in a coronal orientation.

3. Results

3.1. Automated calibration

The hardware and software used in the automated calibration process was evaluated by performing calibration several times repeatedly. During these characterizations, PMTs typically exhibited a linear response over four orders of magnitude for amplitude and nearly the same for phase, although this range was larger when the imaging geometry involved path length variations. Using this data (Fig. 2(c-d)), we fit first order approximations to the amplitude and phase for each PMT with a median norm of the residuals of 0.03 V for amplitude and 4.4 degrees for phase between all the detectors. Similarly, we observed improvement in the data after calibration of each fiber-PMT combination at each gain setting (Fig. 3). After intra-PMT calibration (where the detectors are calibrated to themselves), the average standard deviation in amplitude was 0.07 V and 2 degrees in phase. After applying the final step of the calibration process where the detectors were calibrated to each other, the average standard deviation is reduced to less than 1 × 10⁻² for both amplitude and phase.

After automatic calibration was performed, light was collected from a central source fiber through each fiber-PMT combination. Here, we validated that each fiber-PMT combination produced the same result when the system selected the appropriate gain setting for each measurement. For measurements of the same path length through a homogeneous phantom, the sensitivity of the detectors were sufficiently different that gains varied by as many as three settings during the collection of a complete data set. Representative data from this test is shown in Fig. 4, where calibrated amplitude and phase are normalized to their means and plotted against uncalibrated amplitude and phase. The data represents a flat response with the 25th and 75th percentile falling within 3% of the median for amplitude and within 1% for phase.

3.2. System repeatability

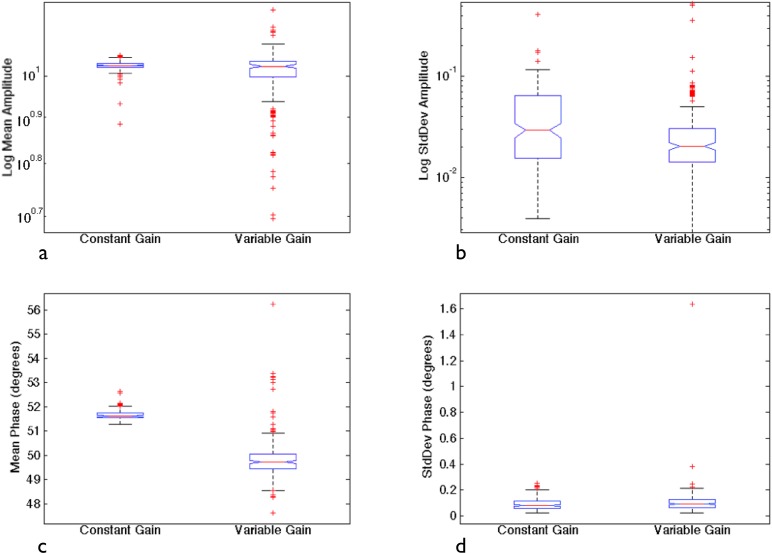
The effectiveness of the calibration method is best understood in terms of the repeatability of the resulting imaging system measurements. We examined repeatability by measuring the same phantom five times over the course of one week, turning the system off in between each data set, and recording the data with both a constant gain setting and variable gain settings. Figure 5 shows the mean recovered amplitudes and phases from these data sets as well as the standard deviations of each measurement for amplitude and phase. The standard deviations for amplitude were typically below 0.05 V for both cases. In phase, the standard deviations were typically below 0.2 degrees. The variable gain case tended to vary more than the constant gain setting, likely due to bias error from the coupling between the fiber optics and the tissue phantom. These data suggest that while the measurement system is very repeatable, error can still result from differences in fiber couplings between calibration and imaging experiments.

Fig. 5.

System repeatability evaluated from five calibrated data sets: (a) Mean amplitude, (b) Standard deviation in amplitude, (c) Mean phase, (d) Standard deviation in phase. Data sets were collected with both constant and variable gains. Each box shows the median of each averaged data set while the spread represents the associated variability.

Figure 6 presents data acquired from a highly attenuating 86 mm diameter homogeneous circular phantom with properties similar to an optically dense breast. The data recorded here is filtered to fall within the detectors’ linear response range, although data closest to the noise floor exhibits more variation.

Fig. 6.

Uncalibrated, calibrated, and modeled data using a normal source, variable gain settings, and circular geometry. These measurements are equivalent to the patient imaging geometry and show agreement with the model data. (a) Amplitude. (b) Phase.

3.3. Parallel plate geometry phantoms

The phantoms imaged in the parallel plate geometry were formed from Type 1 Agarose with a known 1.5:1 contrast of whole blood between the background and the 2 cm diameter inclusion (Fig. 7 ). A homogeneous phantom that matched the background properties was measured and used for calibration. Both phantoms were measured in one coronal plane through the inclusion and a standard T1W MRI sequence was acquired in the same cross-section. The exact locations of the optical fibers with respect to the phantoms were determined from the coronal MR images.

Fig. 7.

Phantom study in the parallel plate geometry. (a) 3D representation of combined maximum intensity projection MR image and 3D rendering of optical solution of HbT. (b) Coronal plane of optical imaging. (c) Quantitative hemoglobin overlaid. (d) Oxygen saturation. (e) Actual phantom cut in half. (f) Water fraction. (g) Scatter amplitude. (h) Scatter power. Color bars reflect the values of the two regions in each case.

MRI images were processed using NIRFAST software to yield phantom-specific meshes that were coregistered with the optical data for modeling. These data sets were processed and reconstructed with NIRFAST on a three-dimensional finite element mesh consisting of 22,720 nodes and a region-based hard prior approach. Recovered contrast was 1.43×, 4.5% different from the true value of 1.5×. Absolute optical images of reconstructed HbT are also shown in Fig. 7. Other recovered optical chromophores and scattering effects, specifically, oxygen saturation, water content, and scattering amplitude and power are also presented. We report an oxygen saturation of 65.6% and a water content of 62.0% in the background, both of which were higher in the inclusion. These images present false contrasts in the scattering parameters of 0.79× for scatter amplitude and 1.49× for scatter power, likely due to the higher noise in the phase signal.

3.4. Pentagonal geometry phantoms

The phantoms imaged in the pentagonal geometry were also constructed from Type 1 Agarose with a known 1.5:1 contrast of whole blood between the background and the 2 cm diameter inclusion (Fig. 7). Again, the inclusion and homogeneous reference phantoms were imaged coronally through the inclusion both optically and with a standard T1W MRI sequence.

Similarly to the parallel-plate geometry phantom experiment, MRI images were processed to yield phantom-specific meshes and data was reconstructed on a three-dimensional finite element mesh consisting of 15,016 nodes and a region-based hard prior approach. In the pentagonal phantoms, we were able to recover similarly accurate hemoglobin concentrations to the parallel plate geometry of 1.47×, 2% different from the true value of 1.5×. Absolute optical images of reconstructed HbT and other chromophores are shown in Fig. 8 . The oxygen saturation was 95% and 99% in the background and inclusion, respectively. Background water content was 93% though very low in the inclusion. As in the parallel plate geometry, these phantoms also presented false contrasts in scattering parameters of 2.06× for scatter amplitude and 0.67× for scatter power.

Fig. 8.

Phantom study using the pentagonal geometry. (a) 3D representation of combined maximum intensity projection MR image and 3D rendering of optical solution of HbT (Media 1 ^{(1.4MB, MOV)} ). (b) Coronal plane of optical imaging. (c) Quantitative hemoglobin overlayed, (d) Oxygen saturation, (e) Actual phantom cut in half . (f) water fraction, (g) scatter amplitude, (h) scatter power. Color bars reflects the values of the two regions in each case.

4. Discussion

4.1. Device development

The goal of data calibration is to ensure that every measurement through a homogeneous medium of equal path length is the same. Here, a robust, automatic way to calibrate an array of detectors is of practical importance, especially as experimental imaging system progress towards clinical evaluation and gain acceptance. Ideally, the type of detector and imaging geometry would not be factors—the method would be effective in any configuration. The approach we have developed is able to calibrate automatically an array of 16 PMTs, operating over a dynamic range of more than 5 orders of magnitude. Repeated experiments are consistent and the calibrated data represents a much more predicable response relative to the uncalibrated data. We found that the results from the individual PMT calibration were very favorable and minimized the error in the data to within the levels of system repeatability.

As shown in Fig. 2, each PMT has a linear range that must be used for calibration. Data must also be collected from this same range for the calibration factors to remain valid. In some cases, when the path lengths are very short, the detectors can be saturated and those data points must be eliminated. Similarly, long path lengths can prevent enough light from reaching the detectors, and also must be censored because they are too noisy. Since our detector array’s dynamic range is large, measurement of data within the linear range for every setting through the same phantom is difficult, especially for phase, which is known to have a smaller range [1,26]. Nonetheless, almost all of the measurements are made reliably, and the test data shown in Fig. 4 demonstrates that we are able to collect a uniform response from all detectors when the light signal propagates over a constant path length.

Despite these results, innate error in the calibration and bias error in the patient-fiber coupling can introduce measurement effects that cannot be corrected through calibration. The patient-fiber interface is especially important in this regard because imaging the breast with NIRS can be highly dependent on the fiber coupling [46]. Thus, measurement of a homogeneous reference phantom with each patient exam is recommended [47]. These measurements are also useful for identifying imperfections in calibration since the same flaws occur in both reference and patient data, and can be corrected before image reconstruction. Figure 6 uses a circular geometry to demonstrate the need for a reference phantom when uncalibrated data is found to be noisy. Calibration improves this data almost to identical parabolas, one for each source position, but imperfections can still be observed. The phase data especially reveals instances where a detector fiber appears to have had poor coupling and the signal seems to jump periodically. The use of a reference phantom could serve to correct this jump and yield a more accurate image reconstruction from the measurement data [48,49].

4.2. Phantom interpretation

Though phantoms are an incomplete representation of tissue, they are the best way to validate the performance of imaging hardware and algorithms, and are necessary for calibration procedures. We used two phantom experiments to evaluate the effectiveness of our calibration scheme over a range of optical properties and imaging geometries. Each used whole blood as an absorber with background concentrations covering the range of hemoglobin concentration found in healthy human breasts [35]. One percent (1%) Intralipid was added to create scattering consistent with human tissue. We considered a parallel plate geometry (Fig. 7) where the optical fibers were in the same 2D plane as well as a pentagonal geometry (Fig. 8) where the fibers were spread across the volume, and reconstructed all images in 3D. Since controlling all of the optical properties of phantoms is challenging, if not impossible [49,50], one option is to use whole blood and evaluate changes in HbT in an inclusion relative to the background as reported here.

The parallel plate phantom experiments used a fiber array that was sufficiently different from the calibration geometry. Similarly to a breast biopsy geometry, the reference and inclusion phantoms were imaged with two rows of eight fibers. The HbT recovery of 20.7:29.5 μm is lower than the expected values of 25:37.5 μm for background and inclusion, respectively. However, the recovered contrast was 1.43×, and very close to the actual contrast. Oxygen saturation was very high, 99.8:65.6 relative to tissue. Since the blood was exposed to air, we would expect this high value. We found water concentration to be 100:62%. The true values are not known exactly in these agarose phantoms, but we would expect the percentages to be high since the phantom materials are water-based. We would expect both oxygen saturation and water to be homogeneous between the inclusion and background, but their variation is likely due to cross-coupling of the image reconstruction estimates between water and scattering parameters. Scattering parameters were also expected to be homogeneous, but they resulted from different mixtures where variable local heating during phantom material preparation could have played a role in scatterer size during the gel formation process.

The pentagonal phantoms yielded similar results, demonstrating the robustness of the calibration scheme across different data collection geometries. They show good HbT recovery of 12.9:18.9 μm or 1.47× versus the correct concentrations of 15:22.5 μm or 1.5×. Oxygen saturation was consistently high between region, agreeing with past results and expectations [34,48]. Water fraction was found to be 93% in the background, but very low in the inclusion, likely a cross-coupling effect with scattering parameter estimates, which also vary more than we would expect [45]. Though the scattering and water images are noisier, we are confident in our ability to recover HbT after the new calibration.

Water estimate coupling may also be amplified in these experiments because Agarose phantoms have approximately twice the water content expected in breast tissue, and our ability to recover water is limited by the PMTs’ sensitivity to wavelengths above 850 nm. Longer wavelengths are known to improve water quantification [45,50]. Work is currently ongoing to incorporate additional wavelengths to mitigate these effects in future work, and preliminary results with this approach do show improvement [51]. The phantom results presented here demonstrate that the calibration data collected in a circular geometry can be applied to image variation parameters expected in breast tissue.

5. Conclusions

As multi-detector NIR spectroscopy is translated into more mainstream clinical use, standardization and calibration will become more critical. Image quality and region-of-interest quantification accuracy are largely dependent on detector response. In this work, the design and testing of a new, automated, calibration system was described, used to calibrate a MR-guided diffuse optical spectroscopy system, and employed in tissue simulating phantom experiments with varying geometries. A design goal of effectively calibrating a multi-detector array automatically within a short amount of time (45 minutes) was achieved. After basic functionality was demonstrated, the effectiveness of our calibration approach was tested for performance and repeatability, and finally used to accurately recover total hemoglobin concentrations in tissue-simulating phantoms. The imaging results were similar to other studies, and these methods could be applied to any optical imaging system with a large detector array. As the approach has now been validated, future work will continue to concentrate on streamlining the technology for use in a clinical setting and achieving the most accurate quantification of suspicious lesions as possible.