Task-dependent activity of motor unit populations in feline ankle extensor muscles

SUMMARY

Understanding the functional significance of the morphological diversity of mammalian skeletal muscles is limited by technical difficulties of estimating the contribution of motor units with different properties to unconstrained motor behaviours. Recently developed wavelet and principal components analysis of intramuscular myoelectric signals has linked signals with lower and higher frequency contents to the use of slower and faster motor unit populations. In this study we estimated the relative contributions of lower and higher frequency signals of cat ankle extensors (soleus, medial and lateral gastrocnemii, plantaris) during level, downslope and upslope walking and the paw-shake response. This was done using the first two myoelectric signal principal components (PCI, PCII), explaining over 90% of the signal, and an angle θ, a function of PCI/PCII, indicating the relative contribution of slower and faster motor unit populations. Mean myoelectric frequencies in all walking conditions were lowest for slow soleus (234 Hz) and highest for fast gastrocnemii (307 and 330 Hz) muscles. Motor unit populations within and across the studied muscles that demonstrated lower myoelectric frequency (suggesting slower populations) were recruited during tasks and movement phases with lower mechanical demands on the ankle extensors – during downslope and level walking and in early walking stance and paw-shake phases. With increasing mechanical demands (upslope walking, mid-phase of paw-shake cycles), motor unit populations generating higher frequency signals (suggesting faster populations) contributed progressively more. We conclude that the myoelectric frequency contents within and between feline ankle extensors vary across studied motor behaviours, with patterns that are generally consistent with muscle fibre-type composition.

INTRODUCTION

The neuromuscular and musculoskeletal systems of many animals enable them to complete a wide range of motor tasks. Related to the different demands placed on these systems, the structure of skeletal muscles in such animals shows great diversity. For example, a variety of morphological, physiological and mechanical properties of muscle fibres have been reported in a range of skeletal muscles (e.g. Close, 1972; Pette and Staron, 1990; Gans and Gaunt, 1991). The many degrees of freedom inherent with such design diversity suggests that the central nervous system must employ a number of task-specific strategies to ensure the required net propulsive force acting on the animal and muscle power output are produced over the time course of a given movement. One of the fundamental requirements of such strategies is that an appropriate number and combination of motor unit populations be activated at any one time during the specific movement. These populations are activated within individual muscles as well as across groups of muscles that share the responsibility for task control. Current understanding of the interplay between motor unit populations within and across synergistic muscles and changes that occur in response to different task demands is limited, however, because of technical difficulties associated with measuring the activity of single motor units during unrestrained motor behaviours (Hoffer et al., 1987a; Hoffer et al., 1987b; Gorassini et al., 2000). This warrants further investigation.

The recently developed wavelet and principal components analysis of intramuscular myoelectric signals has linked lower and higher frequencies in the signal to the preferential use of slower or slower and faster motor unit populations (Wakeling et al., 2002; Wakeling and Syme, 2002; Hodson-Tole and Wakeling, 2007; Lee et al., 2011). This analysis may provide new insight into the involvement of motor unit populations with different properties within and across muscles during specific dynamic motor tasks. The recorded intramuscular myoelectric activity emanates from a range of motor unit properties including the diameter of muscle fibres and the conduction velocity and firing rate of motor neurones. Muscle fibre diameter is related, in general, to muscle fibre type as determined by histochemical, immunohistochemical and electrophoretic analyses of myosin heavy chain isoforms (Pette and Staron, 2000). Mammalian skeletal muscle fibres have been divided roughly into four main categories, one slow and three fast (Pette and Staron, 2000; Schiaffino and Reggiani, 2011). There is, however, a great deal of evidence suggesting such a rigid division of skeletal muscle fibres is too limited because of the number of different combinations of enzyme activity levels and myosin heavy chain isoforms reported in the literature (Pette and Staron, 1990; Pette and Staron, 2000; Roy et al., 2008; Schiaffino and Reggiani, 2011). The conduction velocity of muscle fibres is determined, in part, by the relative rates of membrane depolarisation and hyperpolarisation, a property that varies between muscle fibre types (Adrian and Peachey, 1965; Wallinga-De Jonge et al., 1985). As the frequency of motor unit firing is related to conduction velocity under specific conditions, there is the potential for time–frequency representations of the myoelectric signal to indicate recruitment of different fibre-type populations in response to different motor demands (von Tscharner, 2000; Wakeling et al., 2002; Hodson-Tole and Wakeling, 2007).

In the cat, it has been shown that locomotion on different inclines (from about 30 deg downslope to about 30 deg upslope) significantly changes the mechanical demands of ankle extensors as evident from changes in the ankle muscle moment (from 0.2 to 0.33 N m kg⁻¹) (Gregor et al., 2006; Kaya et al., 2003; Prilutsky et al., 2011), ankle joint power (from 0.11 to 0.55 W kg⁻¹) (Prilutsky et al., 2011) and peak medial gastrocnemius forces (from 3–20 to 22–45 N, depending on cat size) (Gregor et al., 2001; Kaya et al., 2003) as well as muscle–tendon unit length trajectories and ground reaction forces (Gregor et al., 2001; Gregor et al., 2006; Kaya et al., 2003; Maas et al., 2009; Prilutsky et al., 2011). These changes influence sensory feedback from muscle afferents such as muscle spindles (Prochazka 1999; Hoffer et al., 1989; Maas et al., 2009) and Golgi tendon organs (Prochazka, 1999; Donelan et al., 2009). It is likely that the involvement of different motor unit populations during locomotion can be altered in response to the varying mechanical demands on the muscles causing changes in sensory input (e.g. Henneman, 1985). In contrast to locomotion, the paw-shake behaviour of the cat is a rapidly cycling (~10 Hz) high-velocity movement. During this motor behaviour, activity in the soleus (SO) muscle is low in comparison to the highly activated medial (MG) and lateral (LG) gastrocnemii (Smith et al., 1980) and may be a general indication of differential contributions of slower or faster motor unit populations in this task.

The goal of this study was to determine the relative contributions of lower and higher frequency signals to intramuscular myoelectric signals, and by inference the contributions of slower and faster populations of motor units activated from cat ankle extensors (SO, MG, LG and plantaris PL) during level, downslope and upslope walking and the paw-shake response using wavelet and principal components analysis. We aimed to provide further insight into the time-varying changes in the activation of different motor unit populations within and between muscles and tasks. Data presented here have previously been published in abstract form (Hodson-Tole et al., 2008; Hodson-Tole et al., 2009).

MATERIALS AND METHODS

Subjects

Four adult female cats (Felis catus L.; mass 3.29±0.23 kg; mean ± s.e.m.) were studied in these experiments. The cat has been used in a wide range of studies of locomotor biomechanics, muscle mechanics, physiology and neural control and is, therefore, a historically well-defined animal model. Recordings of myoelectric signals from feline muscles have revealed co-ordinated patterns of activation between groups of whole muscles and how these patterns change in response to different locomotor conditions (Walmsley et al., 1978; Hodgson, 1983; Pierotti et al., 1989; Carlson-Kuhta et al., 1998; Kaya et al., 2003; Gregor et al., 2001; Gregor et al., 2006) and mechanical perturbations (Gorassini et al., 1994; Torres-Oviedo et al., 2006; Karayannidou et al., 2009). The cat model has also been used extensively in studies related to the organisation of spinal reflexes and sensory feedback, and their role in the control of locomotion (Gorassini et al., 1994; Gossard, 1996; Donelan and Pearson, 2004; Maas et al., 2007; Maas et al., 2010; Ross and Nichols, 2009).

Myoelectric data were recorded from the SO, MG, LG and PL muscles of the right hindlimbs; these muscles have rather different fibre-type composition (Table 1). Cats were group housed in a large room with a 12 h:12 h light:dark cycle and ad libitum access to food and water. Prior to surgery, each cat was trained to walk at self-selected speeds along a walkway for food reward. The walkway was enclosed with Plexiglas walls, was covered in non-slip rubber matting and could be inclined from level (0 deg) to 100% slope (45 deg). Data presented here are from 0% and ±50% slopes. Prior to surgery, locomotor kinematic and kinetic data were collected in all conditions from each cat, to provide measurements with which we could check that surgery did not influence locomotor mechanics. All surgical and experimental procedures were in agreement with the ‘Principles of laboratory animal care’ (NIH publication no.86-23, revised 1985) and were approved by the Institutional Animal Care and Use Committee of the Georgia Institute of Technology.

Table 1.

Percentage of muscle fibre populations in the cat hindlimb plantar flexors

Surgical procedures

Surgical and experimental procedures were similar to those described in detail in previous studies (Gregor et al., 2006; Maas et al., 2009; Prilutsky et al., 2011) and will, therefore, only be described briefly here.

Cats were anaesthetised using isoflurane gas. The right hindlimb and skull were shaved and scrubbed; under aseptic conditions an incision was made between the knee and ankle joint on the lateral aspect of the limb, approximately parallel to the tibia. A second incision was made in the mid-line region of the skull and two connectors were secured to the skull with screws and dental cement. Teflon-insulated multi-stranded stainless steel wires (100 μm diameter, Cooner Wire, Chatsworth, CA, USA) had previously been attached to the connectors secured to the skull and were passed through a subcutaneous tunnel to the right hindlimb. The SO, MG, LG and PL muscles in the hindlimb were identified and a pair of wires, with ~2 mm cleared of insulation, was implanted into each muscle with a 3–4 mm separation between them. In accordance with descriptions of the neuromuscular compartments within feline LG muscle (English and Letbetter, 1982a; English and Letbetter, 1982b), we recorded from the mid-belly of LG corresponding to compartments LG₂ and LG₃, which have between 17 and 24% of slow-twitch fibres (Table 1). In the other muscles, recordings were conducted from the distal portion of PL (English and Letbetter, 1982a), and mid-bellies of SO and MG. According to the literature (Table 1), PL, SO and MG have on average 26%, 100% and 25% of slow-type fibres, although muscle fibre type in PL and MG has a tendency to change from faster twitch fibres in proximal parts to slow fibres in distal part of the muscle (A. W. English, personal communication). In one cat (cat C), electrodes were not placed in the PL muscle.

The location of each electrode was verified by stimulation through the implanted wires during surgery. Each subject received post-operative analgesia and antibiotics and recovered for 10–14 days prior to data collection. All were seen to demonstrate normal behaviour prior to data collection and moved with no signs of lameness.

Data collection

Reflective markers were placed over the iliac crest, hip, knee, ankle, metatarsophalangeal joint and tip of the 5th toe of the right hindlimb. Cats walked along the walkway set at 0% or 50% slope in view of a 6-camera VICON 460 motion capture system (120 Hz, VICON, Oxford, UK). Myoelectric data (3000 Hz) were synchronously collected with kinematic data using a common trigger. Paw-shake responses were elicited by attaching a piece of adhesive tape to the plantar surface of the paw of the right hindlimb. The cat was then placed on the walkway and data were collected over the entire period the cat demonstrated a paw-shake response. During this period the cat walked along the walkway, with paw-shake cycles occurring during the swing phases of the right hindlimb.

Data analysis

Wavelet and principal components analysis of myoelectric signals

This study used non-linearly scaled wavelets for processing myoelectric signals where time resolution could be adjusted to the range appropriate for the myoelectric time events (von Tscharner, 2000). The filter bank of k wavelets represented a band-pass filter for the signal, with parameters set to ensure that the original signal intensities could be approximately reconstructed from the sum of the k wavelet-transformed signals (von Tscharner, 2000). In the present study, a filter bank of 19 wavelets, indexed by 0≤k≤18, were used to decompose the myoelectric signals from each selected trial and paw-shake cycle into their intensities (von Tscharner, 2000). To reduce confounding effects of low-frequency noise due to movement artefacts, motor unit synchronisation (Kleine et al., 2001) or firing rate modulation of motor units (Lago and Jones, 1981), further analysis on selected trials used signals resolved by wavelet domains 4≤k≤18, with a total bandwidth of 69.94–1205.20 Hz. Instances when the intensity resolved by the fifth wavelet domain, k=4, was greater than intensity resolved by the subsequent wavelet, k=5, were considered noisy and discarded from the analysis. The total intensity of the signal at a given time was calculated as the sum of the intensities of the selected k wavelets (Fig. 1). The instantaneous mean frequency (f_m) at each time point was calculated from the sum of the products of the intensity and central frequency of each wavelet, divided by the sum of intensities from all wavelets. To ensure the results reflected changes in activation of different motor unit populations, principal components analysis was applied to identify the major features of the myoelectric spectra and provide a weighting, which resolves the major characteristics of the data set, and a loading score, which defines how much of each weighting is required to approximately reconstruct the original spectra.

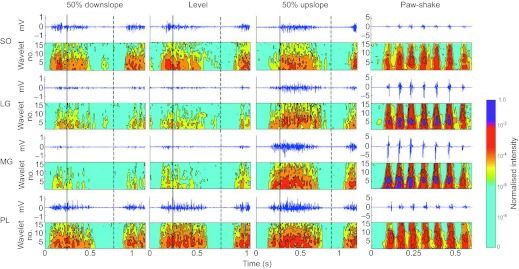
Fig. 1.

Raw myoelectric activity (mV) as a function of time and the corresponding myoelectric intensity pattern as a function of frequency (wavelet number) and time for soleus (SO), lateral gastrocnemius (LG), medial gastrocnemius (MG) and plantaris (PL) muscles during one cycle of level, upslope and downslope walking and seven cycles of paw-shake response. Solid and broken vertical lines indicate time instants of paw contact and paw-off, respectively. Note the different scale of raw myoelectric signal for paw-shake and walking conditions. Wavelet 1 corresponds to 69.94 Hz, wavelet 15 to 1205.20 Hz. Data from one representative subject.

Selection and analysis of walking data

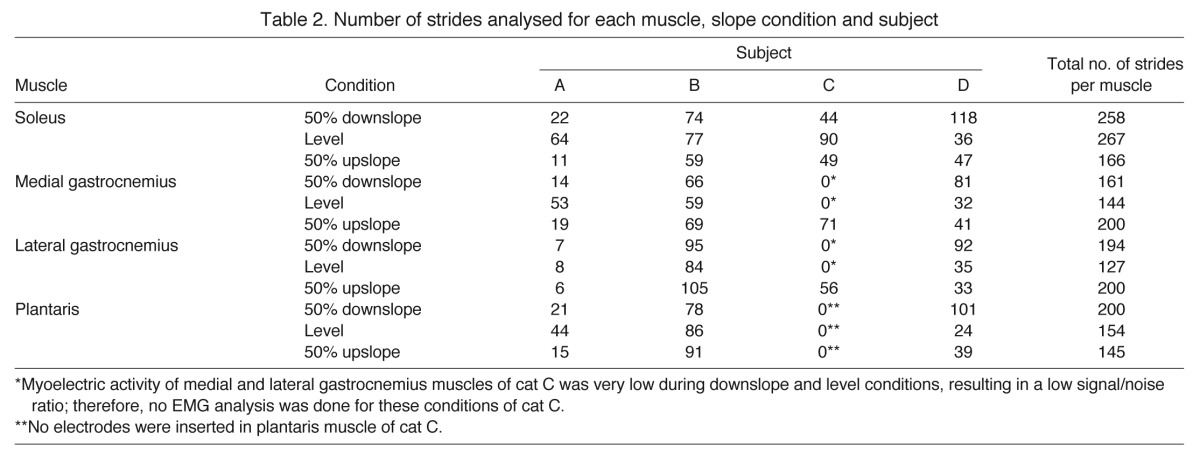
Walking trials were selected for analysis when the cat had walked at a steady, consistent speed from one end of the walkway to the other. Any trials in which paw slippage occurred were discarded. Stride duration was determined from kinematics of the paw of the right hindlimb, with the walking cycle starting with initial ground contact of the paw. To ensure that speed of walking was not a confounding variable between conditions, only strides with stance duration within the range ±150 ms of the mean stance duration calculated across the four subjects (490 ms) were selected for further analysis. A total of 1738 strides were therefore selected for analysis (Table 2).

Table 2.

Number of strides analysed for each muscle, slope condition and subject

The wavelet-transformed myoelectric signals from selected trials were partitioned into individual strides, based on timing information from the right hindlimb. Then the wavelet-transformed signals were interpolated to 100% stride duration. The maximum mean intensity from upslope walking in each cat–muscle combination was used to normalise respective spectra from all other conditions. The mean frequency spectrum for each muscle was calculated as the mean of the f_m values for each time point across each stride.

Wavelet-transformed signals from each stride were partitioned into sections of 10% stride duration. Myoelectric intensity was calculated as the sum of the intensities from the selected k wavelets, and the mean intensity spectrum calculated at each wavelet domain for each stride time window. The normalised, partitioned intensity spectra from all subjects and all muscles were compiled into a p×N [15×22160, 15 wavelets by 2216 strides × 10 (number of time windows)] matrix A. The principal components were calculated from the covariance matrix of A, with no prior subtraction of the mean data (Wakeling and Rozitis, 2004). This process will bias the first principal component to describing the mean of these data and, in turn, subsequent components will describe variance about the mean. Previous studies (Hodson-Tole and Wakeling, 2007; Hodson-Tole and Wakeling, 2008a; Hodson-Tole and Wakeling, 2008b; Lee et al., 2011) have shown that the first principal component (PCI), accounting for the most variance between the wavelets, is strongly correlated with intensity. Subtracting the mean would therefore remove an important aspect of the myoelectric signal, i.e. intensity. The second component (PCII), expressing variance relative to PCI, reveals a dichotomy between low and high frequencies (Hodson-Tole and Wakeling, 2007; Hodson-Tole and Wakeling, 2008a; Hodson-Tole and Wakeling, 2008b; Lee et al., 2011) (Fig. 2). As such our approach ensures we describe changes in signal intensity across the analysed frequency spectrum. To quantify these changes, we describe the relative frequency content of the signal by an angle θ (Eqn 1):

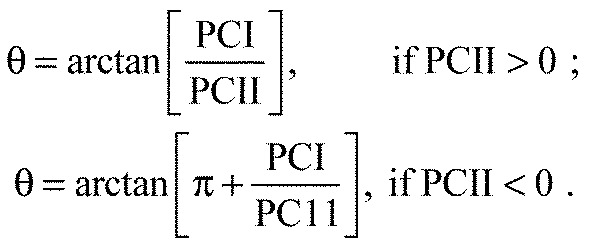(1)

As spectra were partitioned into 10 time windows, each stride was represented by 10 θ values, each representing the mean relative frequency content of the myoelectric signal from the corresponding time window (e.g. Fig. 2B).

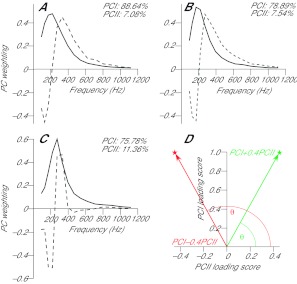
Fig. 2.

First two principal component weightings (PCI, sold line; PCII, broken line) from (A) whole stride, (B) partitioned stride and (C) paw-shake data. The amount of the original signal explained by each component is shown in the top right of each figure. Across all conditions the component weightings have very similar shapes, although for paw-shake and partitioned strides the two components explain slightly less of the original signal, indicating greater variation within the recorded signals. (D) Example of a PCI–PCII loading score vector plot, with θ calculated as the angle between the PCI–PCII loading score vector and the PCII loading score axis. The example shows how the relative amount of PCII loading score influences the θ value. Large θ values (red) indicate relatively more low-frequency signal content, small values (green) represent relatively more high-frequency signal content.

Selection and analysis of paw-shake data

Myoelectric data from paw-shake trials were wavelet transformed in the same manner described for walking data. Once transformed, paw-shake episodes were identified and the signals isolated before being split into individual shake cycles based on the myoelectric intensity. Threshold levels were calculated as 2× mean intensity of the trial (Fig. 3A). Signals from 6.7 ms before the increasing signal intensity crossed the threshold until 13.3 ms after the decreasing intensity crossed the threshold were saved as individual cycles. This ensured saved intensity spectra spanned the whole activation period for each paw-shake cycle. Trials in which four or more cycles occurred were selected for further analysis. As the paw-shake response can be divided into three distinct phases: start-up (initial 4–6 cycles), steady-state (middle 3–4 cycles) and slow-down (last 2–4 cycles) (Smith et al., 1985), individual cycles were categorised according to their position in the complete episode. Specifically, the first and last paw-shakes were identified as well as the middle cycle (Fig. 3B).

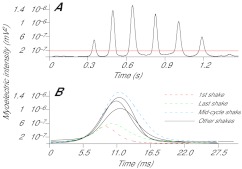
Fig. 3.

(A) Example of total myoelectric intensity as a function of time (black line) from the lateral gastrocnemius muscle of subject 2 during a paw-shake response. The red horizontal line represents the threshold value used to split the paw-shake event into individual cycles. (B) Individual cycles from the example intensity plot, with those used for analysis indicated: first shake, mid-cycle shake and last shake (see key). All other shakes are shown by black solid lines.

Across all muscles studied, a total 317 individual cycles and spectra were normalised with the same values used for walking data. Normalised spectra from all subjects and all muscles were compiled into a p×N matrix A (15×317, 15 wavelets by 317 paw-shake cycles). The principal components were calculated from the covariance matrix of A, as described above.

To enable comparison of loading scores from both walking and paw-shake data, the principal axes from the paw-shake data (ξPC_p) were rotated to match the principal axes of walking data (ξPC_s), analysed for whole strides (p×N matrix A=15×2216) (Wakeling et al., 2007). The rotation matrix R, mapping ξPC_p onto ξPC_s is given by Eqn 2:

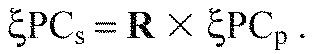(2)

The loading scores from the paw-shake data (L_p) were then rotated onto the walking data principal axes to give a set of transformed loading scores:

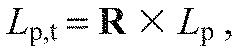(3)

which could then be plotted on the same axes as the loading scores from the walking data with θ quantifying each spectra's relative frequency contribution.

Interplay between high and low signal frequency contents during paw-shake cycles

Because of the short duration of muscle activation in the individual paw-shake cycles (~30 ms) in relation to the time resolution of the lowest frequency wavelet used (k=4, time resolution 18 ms), individual cycles were not partitioned into further time windows as had been done with walking data. Therefore, to quantify high- and low-frequency signal contents, and explore the contribution of faster and slower motor unit populations during the paw-shake response, signal analysis was optimised to high- and low-frequency bands following previous methods (Tole and Wakeling, 2007).

Two optimised wavelets were constructed on the basis that the linear combination of the principal components weightings can be used to reconstruct myoelectric intensity spectra [i(f)]:

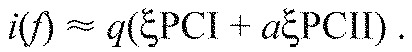(4)

Here, q scales the intensity to normalised values, a represents the relative amount of PCII to PCI loading scores and ξPCI and ξPCII are the first two principal component weightings, defined by the eigenvectors of the covariance matrix A. When satisfying the condition that reconstructed spectra must have non-negative intensities at all frequencies, there are two solutions for Eqn 4, using extreme positive (a_f) and negative (a_s) values of a. Using each of these extremes, a wavelet was constructed using least squares minimisation of a wavelet function ψ(f) to the intensity spectrum i(f), where:

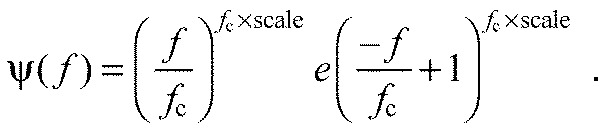(5)

f_c indicates central frequency and ‘scale’ is a scaling factor determining the width/shape of the function (von Tscharner, 2000) (see Table 3). The two defined wavelets covered high- [ψ_f(f)] and low- [ψ_s(f)] frequency domains, and were normalised to unit area of i(f) calculated from a_f and a_s, respectively. Each measured myoelectric intensity spectrum was then represented by the linear combination of the optimised wavelets ψ_f and ψ_s and their loading scores L_f and L_s, using non-negative factorisation with:

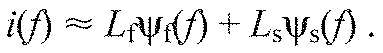(6)

Time-varying loading scores [L_f(t) and L_s(t)] were found by calculating L_f and L_s for each time point of each intensity spectrum.

Table 3.

Values for optimised slow (ψ_s) and fast (ψ_f) wavelets

Statistical analyses

General linear model, full-factorial ANOVA were used to identify statistical differences between θ values within each muscle (SPSS 16.0, Chicago, IL, USA). For partitioned walking strides, time window and condition were defined as fixed factors and subject as a random factor. For whole-stride and paw-shake data, condition was defined as a fixed factor and subject again as a random factor. When a statistical significance was identified (P≤0.05) a Bonferroni post hoc test was used to identify the location of the difference(s). The goodness-of-fit of the optimised wavelets, used to assess paw-shake data, was calculated as the coefficient of determination (r²) between the total myoelectric intensity of each paw-shake cycle and the intensity calculated for L_f(t) and L_s(t) combined and as individual factors. Data are reported as means ± s.e.m.

RESULTS

Myoelectric frequency spectra from walking data

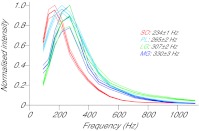
Analysis of the myoelectric frequency spectra from each of the muscles revealed significant differences in mean frequency (P=0.006), with significant differences existing between each of the muscles (P<0.001) (Fig. 4). SO had the lowest mean frequency (233.9±1.1 Hz), followed by PL (265.3±1.7), LG (307.4±2.1) and MG (330.2±3.2).

Fig. 4.

Mean intensity as a function of frequency from whole strides for soleus (red), plantaris (blue), medial gastrocnemius (purple) and lateral gastrocnemius (green), normalised to maximum value. Traces show means ± s.e.m. Mean frequency values for each muscle are shown on the right.

Comparison of whole-stride walking and paw-shake data

We found a high correlation between the intensity spectra and PCI, with r² exceeding 0.70 and attaining significance (P<0.001) for all muscle/slope combinations. PCII displayed a characteristic curve (Fig. 2) for all muscle/slope combinations with negative loadings below 174–313 Hz and positive loadings above this frequency threshold, the threshold depending on muscle and condition (Table 4).

Table 4.

Mean frequency (Hz) of intercept of PCII with y=0 for different muscles and slope conditions

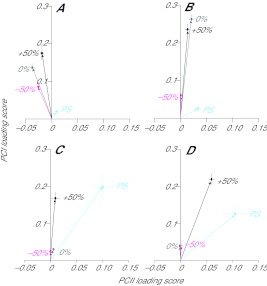
Comparison of walking and paw-shake data revealed that significant differences in angle θ occurred between conditions in the SO (P<0.001), PL (P<0.001) and MG (P=0.013) muscles, but not in the LG (P=0.051) (Fig. 5). In the SO muscle, these differences were significant between all walking conditions and paw-shake response (P≤0.001). In the PL muscle, significant differences were found between all conditions (P<0.001), except for level and upslope walking (P=0.109). In the MG muscle, significant differences existed between paw-shake data and all walking conditions (P<0.001). For all muscles, θ was greater for downslope than for upslope (Fig. 5). In all muscles, θ was always smallest for paw-shake trials, indicating that during this condition there was relatively more high-frequency content in the myoelectric signals recorded.

Fig. 5.

PCI–PCII loading score plots from whole-stride and paw-shake data collected from (A) soleus, (B) plantaris, (C) medial gastrocnemius and (D) lateral gastrocnemius. Each point represents the mean ± s.e.m. loading score value for each condition: level walking (0%, grey), downslope walking (−50%, pink), upslope walking (+50%, black) and paw-shake (PS, blue).

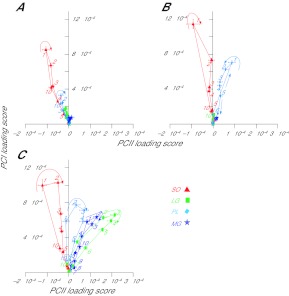
Analysis of partitioned walking strides

PCI and PCII loading scores for all partitioned walking data are shown in Fig. 6. These plots indicate the relative contribution of low and high frequency to the myoelectric signal (angle θ) for each of the 10 time bins of the walking stride. Distinct differences in the vector plots are apparent between muscles and slope conditions, indicating differences in the frequency characteristics of the myoelectric signals. Walking in downslope and level conditions was predominantly characterised by activity in SO and PL muscles (as evident from Fig. 1 and PCI loading scores in Fig. 6A,B). Upslope walking led to significant activity in all four muscles (Fig. 1, Fig. 6C). The shapes of the vector plot loops differed between muscles, and were influenced by locomotor condition. This was most apparent when comparing upslope and downslope data, where the data points changed from being spread across both quadrants of the plot (upslope, Fig. 6C) to being concentrated in the left-hand (relatively more low-frequency signal) quadrant (downslope, Fig. 6A). Vector plots for SO in level and upslope conditions (Fig. 6B,C) resulted in θ values forming loops in the left-hand quadrant, which flowed in a clockwise direction. A similar pattern of changing θ values was also found in LG and PL during upslope walking (Fig. 6C), with an increase in PCI generally having a corresponding decrease in angle θ. In all muscles, θ differed significantly between time windows (P≤0.05). Within the SO and PL muscles, θ was significantly different between conditions (P=0.034 and P=0.012, respectively), with values generally decreasing from downslope to upslope (Figs 5, 6).

Fig. 6.

PCI–PCII loading score vector plots for soleus, plantaris, medial gastrocnemius and lateral gastrocnemius from partitioned strides during walking on (A) −50% slope, (B) 0% slope and (C) +50% slope. Each point with a number represents one of 10 equal time windows into which the strides were partitioned. Arrows indicate the direction of the loops, and numbers indicate the 10% cycle time windows, with number 1 indicating the beginning of stance and number 10 indicating the end of swing. PCI loading scores correlate highly with myoelectric intensity; the angle between each PCI–PCII loading score vector and the PCII loading score axis (θ) represents the relative frequency content of the signal (see Fig. 2).

Comparison of paw-shake cycles

The paw-shake cycles were dominated by myoelectric activity in the MG and LG, with much lower activity occurring in the PL or SO muscles (Figs 1, 5). For all four muscles the PCI–PCII vector was in the upper right quadrant, indicating a predominance of myoelectric signal with higher frequency content (Fig. 5).

The two optimised wavelets explained on average 90±3% of the myoelectric intensity during the paw-shake in each of the muscles. There was no significant difference in the fit of the low-frequency wavelet (ψ_s) between the muscles (P=0.157). The fit of the high-frequency wavelet (ψ_f) differed significantly between the muscles (P<0.001), having the poorest fit in SO (r²=0.54±0.63) and the best fit in MG (r²=0.94±0.01). There were no significant differences in the fit of either ψ_s or ψ_f between the paw-shake cycles within each of the muscles (P>0.05, all cases).

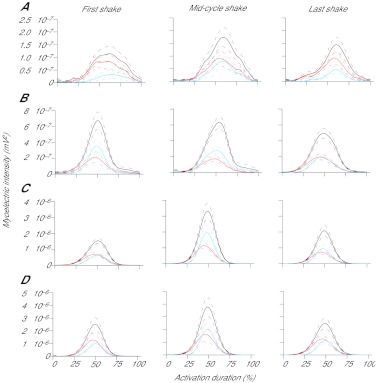
The optimised wavelets enabled the interplay between high- and low-frequency bands within the myoelectric signal to be visualised through the activation period of the paw-shake responses analysed (Fig. 7). They indicated that, in each muscle, the initial phase of each paw-shake cycle was dominated by low-frequency components [L_s(t)], with higher frequency components [L_f(t)] dominating later in the cycle, with the exception of SO. This interplay was not affected by the position of the paw-shake cycle in the whole paw-shake response (i.e. first, middle or last cycles). In MG and LG there was a trend for the mid-cycle in a paw-shake episode to have relatively more high-frequency signal than for the initial or last cycles. Significant differences in θ did not, however, occur between cycles in any of the muscles.

Fig. 7.

Total myoelectric intensity (black lines), L_s(t) (red lines) and L_f(t) (blue lines) for soleus (A), plantaris (B), lateral gastrocnemius (C) and medial gastrocnemius (D), from the first, middle and last paw-shake cycles. Solid lines in each colour represent the mean trace, with broken lines representing s.e.m. L_s(t) and L_f(t) represent the amount of the total myoelectric signal explained by the optimised low- and high-frequency wavelets, respectively. Note the different vertical axis scales between muscles.

DISCUSSION

The goal of this study was to determine relative contributions of intramuscular myoelectric signals at lower and higher frequencies from four cat ankle extensors, and by inference contributions of populations of motor units activated during level, downslope and upslope walking and paw-shake response. This study is the first to present this information during such a wide range of motor tasks, and provides a more detailed assessment of activation within these muscles than has previously been reported. We found that mean myoelectric frequencies in all walking conditions were lowest for slow SO and highest for faster LG and MG muscles (Fig. 4 and Table 1). The first two principal components of the myoelectric signal (PCI and PCII) typically explained more than 90% of signal variance. During all walking conditions, SO myoelectric signals comprised mostly low-frequency signals (angle θ, a function of the ratio PCI/PCII, was >90 deg), whereas myoelectric signals from MG, LG and PL consisted of mostly higher frequency signals (θ≤90) whose contribution increased from downslope and level walking to upslope walking and paw-shake.

It has previously been demonstrated that the relative contribution of the low- and high-frequency signal to the intramuscular myoelectric spectra is associated with a preferential use of slower or both slower and faster motor unit populations, respectively (von Tscharner, 2000; Wakeling et al., 2002; Hodson-Tole and Wakeling, 2007; Lee et al., 2011). In the following sections we consider this association and the underlying physiological mechanisms, and then analyse the obtained results in the light of the potential involvement of slower and faster motor unit populations within and between the studied ankle extensors and motor tasks.

Wavelet and principal components analysis of intramuscular myoelectric signals provides information on activation of slower and faster motor unit populations

The majority (typically around 90%) of the variance in the myoelectric signals recorded in this study was explained by the first principal component, PCI, which correlated highly with the myoelectric signal power spectral density. This was expected, as principal components analysis examines the structure of variables comprising the entire data set, in this study the 15 wavelets, and the most dominant pattern of the myoelectric signal was the power spectral density curve (see Figs 2, 4). The second principal component, PCII, although accounting for a smaller percentage of myoelectric signal variance, offered far more information regarding frequency content of the signal. PCII, for all muscles and conditions, revealed a basic division in modes of activity between low-frequency and high-frequency contents of myoelectric signals (Fig. 2). In all cases there was a negative loading below a certain frequency threshold and a positive loading above this threshold (Table 4).

The arctan of the ratio PCI/PCII, angle θ, describes the relative frequency content of the myoelectric signal (Wakeling and Rozitis, 2004; Hodson-Tole and Wakeling, 2007; Wakeling, 2009). One interpretation of the low- and high-frequency content of the intramuscular myoelectric signal (or angle θ) is that it represents the relative contribution of the population of motor units active, with larger θ values (>90 deg; low myoelectric signal frequency content) indicating greater activity in populations of slower motor units and smaller values (<90 deg; higher frequency content) indicating greater activity in populations of faster motor units (Wakeling, 2009). This interpretation is based on experimental demonstrations of a strong relationship between intramuscular myoelectric signal frequency content (and angle θ) and preferential recruitment of populations of slower or faster motor units in swimming fish (Wakeling et al., 2002), in rat muscles of different fibre composition (Kupa et al., 1995), or during activation of rat (Wakeling and Syme, 2002) and goat muscles (Lee et al., 2011) after recruitment of faster motor units was reduced by blocking nerve stimulation. The strong correlation between the frequency content of intramuscular myoelectric signals and activation of motor units with different properties has been explained by the differences in conduction velocities in muscle fibres with smaller (slow) and larger (fast) fibre diameter and the membrane properties of slow and fast muscle fibres (e.g. Kupa et al., 1995; Wakeling and Syme, 2002). Although other factors can affect the frequency content of myoelectric signals and conduction velocity – muscle length (Trontelj, 1993; Doud and Walsh, 1995), type of muscle action (eccentric or concentric) (Pasquet et al., 2006), fatigue (Dimitrova and Dimitrov, 2003) and distance between the signal source and recording electrodes (Lateva, 1988) – these factors are not expected to substantially influence the results of this study or can be accounted for. First, the mean muscle-tendon unit (Gregor et al., 2006) and muscle fascicle lengths (Maas et al., 2009) of cat SO and MG do not differ greatly between level and slope walking. Second, because these muscles operate mostly eccentrically or concentrically during stance of downslope and upslope walking, respectively, (Maas et al., 2009) and more motor units are recruited in concentric than in eccentric actions against similar loads (Pasquet et al., 2006), it is expected that during upslope walking additional faster motor units will be recruited compared with downslope and level walking and thus the myoelectric signal spectral power would shift towards higher frequencies. A significant shift in angle θ in upslope walking was observed in all muscles, except LG (which had a nearly significant shift, P=0.051; Figs 5, 6). Third, our experimental protocol assure that the animals did not experience fatigue: after each crossing of the 3 m walkway they stopped to consume food, and each walking trial was self-initiated by the animal. In addition, the analysed trials were recorded on different days. Fourth, power spectra are not expected to be distorted significantly by transduction of the myoelectric signal over a large tissue volume (e.g. Lateva, 1988) because we used implanted intramuscular electrodes with inter-electrode distances of ~3–4 mm. The association between the low- and high-frequency myoelectric signal contents and activation of slower and faster motor units has recently been challenged for myoelectric signals recorded using surface electrodes in humans (Farina, 2008a; Farina, 2008b) (but see Wakeling, 2009). However, as discussed above, most of the arguments do not apply to myoelectric signals recorded using intramuscular electrodes in an animal model.

Muscle fibre distribution in ankle extensors and patterns of motor unit involvement in different motor tasks

There was a correspondence between the mean myoelectric signal frequency of the studied muscles across all walking strides (Fig. 4) and the proportion of fibre types (Table 1): SO, composed of 100% slow fibres, had the lowest mean frequency of 234 Hz compared with PL (265 Hz and 26% of slow fibres) and LG and MG (muscles composed of less than 25% slow fibres, with mean frequencies of 307 and 330 Hz, respectively). It should be noted that the mean myoelectric frequencies from recorded muscles are expected to reflect the relative recruitment of the corresponding fibre types during walking rather than the fixed muscle fibre composition; therefore, the obtained strong correspondence between the two is striking.

The decrease in angle θ (i.e. the increase in higher frequency content of myoelectric signals) with altered walking slope conditions from downslope to level and upslope (Figs 5, 6; Table 4) was also consistent with the progressive recruitment of additional faster motor units of ankle extensors to meet the demands of increasing loads on hindlimbs, force of ankle extensors and ankle joint moment (Gregor et al., 2001; Gregor et al., 2006; Kaya et al., 2003; Maas et al., 2009; Prilutsky et al., 2011). These results suggest that during various walking conditions, motor units within and across the ankle extensors are recruited generally in accordance with their fibre-type composition. Similar conclusions were made previously based on motor unit activity recordings in humans performing nearly static, low-effort tasks (e.g. Enoka, 1995) and on results of glycogen depletion studies determining the average contribution of specific muscle fibre types to motor tasks (e.g. Armstrong and Laughlin, 1985). Advantages of the wavelet and principal components analysis are that the involvement of different fibre-type populations may be evaluated in highly dynamic, short-duration tasks (like the paw-shake response) and that this method allows for estimating changes in the relative contribution of motor unit populations with different properties during a motor task (Figs 6, 7).

For example, there was a significant difference in angle θ between time windows of walking cycles, indicating significant changes in the frequency content of myoelectric signals within strides (Fig. 6). These changes were especially apparent during upslope walking – SO, PL and LG muscles formed a clockwise loop in the PCI–PCII plane (Fig. 6C). As PCI, correlated with myoelectric signal intensity, increased from time window 10 in swing and reached its peak in time windows 2–3 in stance, generally there was a corresponding decrease in angle θ, suggesting an increasing contribution of the faster motor unit population. This pattern of changes in angle θ suggests that during upslope walking, an increase in muscle activity is dominated by recruitment of additional populations of faster motor units. In downslope and level conditions, where PCI–PCII plots for all muscles formed typically narrow loops and increased and decreased almost linearly (Fig. 6A,B), the rise and fall in muscle activity was achieved with similar frequency contents within each muscle. Reduction in the activity of SO, PL and LG within a cycle of upslope walking (from time windows 2–3 in stance to time windows 6–7 in swing) was achieved at a smaller angle θ (i.e. with higher frequency content) than those observed during an increase in muscle activity (from time window 10 in swing to time windows 2–3 in stance), which is a consequence of the clockwise loops formed by the PCI–PCII plots (Fig. 6C). Why are the wide loops formed for SO, PL and LG in upslope but not in downslope or level conditions? One possible explanation is that during stance of 50% upslope walking, the peaks of muscle fascicle shortening velocity (as measured in SO) (Maas et al., 2009) are likely to be much higher than that during level or downslope walking and even higher in comparison with early stance when muscle activity is rising and SO is lengthening. The higher the shortening velocity, the lower the force the muscle can produce at the same activation (a consequence of the force–velocity relationship) (Hill, 1938), and additional motor units need to be recruited to maintain a required force level (Bigland and Lippold, 1954; Pasquet et al., 2006). Thus, the clockwise loops in plots of PCI–PCII for SO, PL and LG could be explained by substantial differences in fascicle shortening velocities between the early and late phases of stance. Interestingly, MG, which does not demonstrate a wide loop in upslope walking (Fig. 6C), does not have big differences in shortening velocity between early and late stance [see fig. 5D of Maas et al. (Maas et al., 2009)]. Longer fascicle length values of ankle extensors in early stance of upslope walking than in late stance (Maas et al., 2009) could also contribute to lower frequency content during rising activity of these muscles (e.g. Trontelj, 1993; Doud and Walsh, 1995).

In contrast to the results presented here, reports of myoelectric signal properties from rat ankle extensor muscles found that walking up a slope (25 deg) led to an increase in the relative low-frequency signal content of the muscles studied (SO, PL and MG), indicating increased involvement of slower motor unit populations (Hodson-Tole and Wakeling, 2008a). These differences may have occurred for a number of methodological reasons, especially the anatomical differences between species studied, e.g. limb posture, relative size of individual muscles and their fibre-type proportions. It is, however, of interest that the previous study involved treadmill locomotion and did not control for differences in stance duration, as was done here, which led to significantly longer stance durations in the upslope conditions (accompanied by relatively constant fascicle strain rates) (Hodson-Tole and Wakeling, 2010). It was suggested that longer stance durations provided adequate time for activation–deactivation of slower motor units, facilitating lower metabolic cost and mechanically efficient power production in the activated units. In the data presented here, strides were only analysed if stance duration fell within a limited range of values (490±150 ms). This means that muscle force production occurred within a generally similar time frame between all slope conditions, which may have significantly influenced factors such as fascicle strain rates. Similar results have also been found in data collected from MG in humans cycling at different loads and cadences (Wakeling et al., 2006) and in rat ankle extensor muscles (Hodson-Tole and Wakeling, 2008b), where decreases in θ, indicating greater contributions of faster motor unit populations, were significantly related to increases in shortening strain rates. Therefore, activation of different motor unit populations during locomotion may not just be governed by the level of muscular force required – the time available for force production and muscle fascicle strain rate could also be crucial factors.

Relative myoelectric signal frequency content in paw-shake

Myoelectric signals collected during paw-shake had relatively more high-frequency content than any of the other motor tasks studied (Fig. 5). We interpret this result as indicating that faster motor unit populations were involved in this task in the activated muscles. This may relate, in part, to differences in the cycle duration of the motor tasks studied here. Walking trials were selected to ensure that locomotor speed was relatively consistent between conditions, resulting in a walking cadence of ~1.2 cycles s⁻¹. The paw-shake response typically occurred with a cycle frequency of ~10 Hz. Previous work has shown a correlation between faster fascicle shortening speeds and higher frequency myoelectric signal content suggestive of faster motor unit recruitment (Hodson-Tole and Wakeling, 2008b; Wakeling et al., 2006). This is expected (see above) because with increasing shortening speed the muscle contractile abilities decrease in accordance with the force–velocity relationship (Hill, 1938), and recruitment of additional motor units may be needed to maintain a desired force level (Bigland and Lippold, 1954; Pasquet et al., 2006) in addition to making faster muscle contractions more efficient as a result of shorter activation and deactivation times and higher force production at faster strain rates of newly recruited motor units. Comparison of fascicle shortening speeds reported during the paw-shake response (Prilutsky et al., 2005) and walking on different inclines (Maas et al., 2009) show that paw-shake does result in much faster fascicle shortening speeds than walking in both the SO and MG. As muscle fascicle shortening velocity influences the populations of motor units activated, it might be expected that the reduction in activity in slow-twitch SO during paw-shake (low PCI loading score, Fig. 5A) may reflect its inability to generate activity during shortening velocities seen during the movement. The fascicle shortening velocities recorded in SO during paw-shake, however, do not exceed 40% of the maximum shortening velocity reported for the muscle (Prilutsky et al., 2005). In addition, SO as well as MG develop their maximum activity and force (up to 1.5 and 16–28 N, respectively) while they are lengthening (Fowler et al., 1988; Prilutsky et al., 2005; Wakeling et al., 2002). It therefore seems unlikely that shortening velocity is a major factor in SO low activity during the paw-shake response.

The use of optimised wavelets to determine the interplay between high- and low-frequency bands during paw-shake indicates that, in all muscles, lower frequency signal components contributed almost as much to the total myoelectric activity as the faster components and were dominant in the initial part of activation during each paw-shake cycle (Fig. 7). The relatively slower motor unit populations activated early in the paw-shake cycle may act to increase the stiffness of the activated muscle and hence enhance the transmission of force generated by faster (higher threshold) motor unit populations activated later in the paw-shake cycle. Optimised wavelets also showed that the slow-twitch SO had high-frequency myoelectric signal contents during paw-shake, although their magnitude and relative contribution to the total myoelectric intensity were smaller than those of the other plantar flexors (Fig. 7A). Higher frequency components for SO can also be seen during paw-shake in Figs 1 and 5. As reported previously (e.g. McPhedran et al., 1965; Burke, 1978), homogeneously slow-twitch cat SO contains motor units with a wide range of conduction velocities of their axons, contraction times and maximum isometric tension. Taken together, these results suggest that although SO is composed entirely of slow motor units (Table 1), it can still generate higher frequency myoelectric signals.

CONCLUSION

Wavelet and principal components analysis of intramuscular myoelectric signals have previously been used in a very small number of animal species and in a limited number of motor tasks. Here, we show that the results of such analysis performed for level, downslope and upslope walking and paw-shake in the cat are in line with expectations based on known fibre-type populations within the muscles studied. Wavelet and principal components analysis enabled a more dynamic assessment of the activation of different motor unit populations in freely moving, intact animals. Our results show that the frequency content within feline ankle extensor muscles varies across motor tasks and the time course of a walking stride and paw-shake cycle, with the patterns that seem generally consistent with muscle fibre-type composition. Specifically, populations of motor units within and across studied muscles that demonstrated low-frequency myoelectric signal content (presumably relatively slow-twitch motor unit populations) were recruited during tasks and movement phases with lower mechanical demands (e.g. during downslope and level walking and in late swing/early stance of walking and the early phase of paw-shake). With increasing mechanical demands, motor unit populations with higher myoelectric frequency content (presumably faster motor units) contributed progressively more to the task. In addition, we have shown for the first time that, within muscles activated during paw-shake, high-frequency myoelectric signal components predominantly drive the activity. Motor unit populations that generate lower frequency myoelectric signals may, however, provide an important role during the initial phase of activation during paw-shake. Future work should investigate the interaction of motor unit populations between different compartments within a given muscle, and consider changes in the populations of motor units activated in response to injury and the subsequent recovery process.