Skip to main content
PMC home page
The Journal of Chemical Physics logoLink to The Journal of Chemical Physics
. 2012 Sep 24;137(12):124101. doi: 10.1063/1.4752735

Affine-response model of molecular solvation of ions: Accurate predictions of asymmetric charging free energies

Jaydeep P Bardhan 1,2, Pavel Jungwirth 3, Lee Makowski 4
PMCID: PMC3470608  PMID: 23020318

Abstract

Two mechanisms have been proposed to drive asymmetric solvent response to a solute charge: a static potential contribution similar to the liquid-vapor potential, and a steric contribution associated with a water molecule's structure and charge distribution. In this work, we use free-energy perturbation molecular-dynamics calculations in explicit water to show that these mechanisms act in complementary regimes; the large static potential (∼44 kJ/mol/e) dominates asymmetric response for deeply buried charges, and the steric contribution dominates for charges near the solute-solvent interface. Therefore, both mechanisms must be included in order to fully account for asymmetric solvation in general. Our calculations suggest that the steric contribution leads to a remarkable deviation from the popular “linear response” model in which the reaction potential changes linearly as a function of charge. In fact, the potential varies in a piecewise-linear fashion, i.e., with different proportionality constants depending on the sign of the charge. This discrepancy is significant even when the charge is completely buried, and holds for solutes larger than single atoms. Together, these mechanisms suggest that implicit-solvent models can be improved using a combination of affine response (an offset due to the static potential) and piecewise-linear response (due to the steric contribution).

INTRODUCTION

Continuum theories of molecular solvation offer significant advantages over all-atom molecular dynamics (MD) simulations in explicit solvent in terms of speed and conceptual clarity, but they rely on simplifying assumptions that can seriously compromise accuracy.1 These implicit-solvent models typically consider the solute-solvent interactions as the sum of electrostatic and non-electrostatic components, the latter including the development of a solute-shaped cavity in bulk solvent, as well as van der Waals interactions.1, 2 The electrostatic component, which often dominates for charged molecules, is an electrostatic self-energy, i.e, a free energy of charging up the solute from zero to its given charge in water.3, 4 The electrostatic component of the ion-water interactions is asymmetric with respect to the sign of the ionic charge,5, 6, 7, 8, 9, 10, 11, 12 but most Poisson-based continuum models are symmetric with respect to the sign of an introduced charge, starting with the simplest Born model,3

ΔG es =121ε water −1q2R ion , (1)

where εwater = 80 is the dielectric constant of water, and q and Rion are the ionic charge and radius, respectively. If the implicit-solvent models attempt to capture the charge sign asymmetry,6, 13, 14, 15 they do so in an effective (empirical) way, e.g., by re-parameterizing atomic radii. This simple and fast correction usually improves accuracy. However, the charge-sign symmetry of the underlying Poisson model does not allow one to fully respect the molecular origins of the asymmetric response,5, 6 which is an important drawback of such continuum solvation models.

Previous studies that focused on identifying the sources of asymmetry have discussed two mechanisms.5, 6, 7, 9, 11, 16 The first mechanism is that there exists a large electrostatic potential throughout the solute even if it is completely uncharged.7, 16 In some communities, of course, it is well known that there can be significant potential differences across liquid-vapor interfaces.16, 17, 18, 19 However, to date this term has not been incorporated explicitly as a potential in continuum Poisson models, except by Cerutti et al.16 The second mechanism is more familiar, and certainly more readily understood by intuition alone: the molecular structure of water allows the (partially positive) hydrogens to approach the solute more closely than the (partially negative) oxygen. This leads negative charges to be solvated more favorably (have more negative hydration free energies) than are positive charges of the same magnitude. This phenomenon is most clearly seen in the solvation of monatomic ions, where it is clear that the standard Born expression fails for certain approaches for defining the radii.5, 6

Using free-energy perturbation (FEP) molecular-dynamics calculations in explicit water, we demonstrate that these two sources of asymmetry are both significant, but in complementary types of problems: the static-potential contribution is the major source of asymmetry for deeply buried charges, and the water-structure contribution is dominant for charges near the solute-solvent interface. Both mechanisms must be included in order to match charging free energy curves for ions and for charges in larger solutes. Two remarkable results emerge from our analysis of water-structure asymmetry. First, asymmetric response can be significant even for charges that are completely buried, so long as they are within a few Angstroms of the solvent interface. This implies that a full accounting of asymmetric solvation cannot be attained by a universal atomic radius, or attributed to specific chemical interactions such as hydrogen bonding. The second finding was more surprising, at least to us: although asymmetric response is obviously a nonlinear phenomenon, the reaction potential induced by solvent polarization varies in a piecewise-linear fashion. That is, for positive charges, linear response holds with one proportionality constant, and for negative charges linear response holds with a different constant.

Overall, the present work is motivated by the notion that continuum hydration models can be interpreted as approximations to the generalized potential of mean force (PMF) that the solvent exerts on the solute.1 In principle, this can be obtained exactly by integrating out the solvent degrees of freedom,1 but it turns out to be more practical to focus on simple and easily computable approximations such as Poisson models. We follow the common decomposition of the PMF into two steps, a non-polar step in which one “grows” a completely uncharged form of the solute (i.e., a hydrophobic isostere) into the solvent, and second an electrostatic charging component in which the charge distribution is developed from zero to its final state. This leads us to analyze continuum electrostatic models from the perspective that they should reproduce charging free energies; consequently, FEP calculations offer a mean to understand fundamental limitations of the standard Poisson-type models at a level of detail inaccessible to experiment. As an additional advantage, the PMF interpretation allows us to set εsolute = 1, sidestepping the potentially contentious issue of selecting an effective dielectric constant to capture implicit structural relaxation.20

METHODS

In order to obtain reference data, we performed explicit solvent free-energy perturbation molecular dynamics simulations of charging of sodium and chloride ions, as well as larger quasi-spherical charged solutes constructed from van der Waals spheres arranged on a Cartesian lattice with a grid spacing of 0.5 Å, where each sphere had the same van der Waals parameters as a sodium ion. We employed the NAMD software21 with the CHARMM22 forcefield and TIP3P water.23 Simulations employed periodic boundary conditions, with enough water molecules in the unit cell to ensure that at least 10 Å of solvent separated the solute from the cell boundary. Long-range electrostatic interactions were computed using NAMD’s particle mesh Ewald (PME) implementation with interpolation order 4 and grid spacing of 1.0 Å. All simulations were conducted in the NPT ensemble at 300 K (Langevin damping coefficient of 5 ps−1) and 1.01325 bar (Nose-Hoover Langevin piston with oscillation period 200 fs, damping time 100 fs, and piston temperature 300 K).

To account for changes in the net charge of the system during the FEP calculations, we followed the suggestion of Hénin et al.24 and used the correction term described by Hummer et al.,25 though it should be noted that alternatives exist.26 Convergence was assessed by comparing the forward and backward FEP results; for the monatomic ions, all results were within 0.5 kcal/mol, and for the lattice-sphere model, all results were within 0.2 kcal/mol. Additionally the sodium and chloride calculations were repeated three times, giving a total of six charging free energies for each of the four combinations (sodium and chloride each being charged to +1e and −1e); all standard deviations were less than 0.25 kcal/mol.

Static potentials were computed by fitting each set of free-energy results over the interval −0.2e ⩽ q ⩽ +0.2e to a shifted quadratic of the form ΔG=12Lq2+φ static q. Such a fit over a small charge interval ensures an accurate estimation of the slope at the value of charge q = 0 (i.e., the static potential).

RESULTS

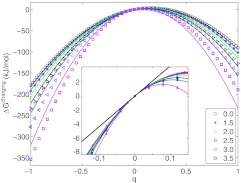
Figure 1 shows plots of the charging free energies of a single charge at different points in a sphere of radius 4 Å. Charging simulations were conducted for charges placed at lattice points along the positive x axis. In all cases, the mean static potential (i.e., the slope of the charging free energy at a zero value of charge, depicted in the inset) is practically the same, 43.5 kJ/mol/e with standard deviation of 1.3 kJ/mol/e, indicating an almost perfectly uniform static potential field in the sphere. The data in Figure 1 also reveal a marked asymmetry of the charging free energy with respect to the sign of the charge: for a solvent-exposed unit charge the asymmetry is approximately 167.4 kJ/mol, but even for a centrally placed charge, the difference in free energies amounts to 83.7 kJ/mol. Results for an affine-response model (i.e., Born-type linear response plus the static potential) are plotted as individual curves in Figure 1. The static potential depends only weakly on solute size and shape,7, 16 while the Born self-energy is inversely proportional to the solute radius; therefore, the static potential can have a substantial contribution to the charging free energy, particularly for larger, highly charged, solutes. Note that the affine-response model captures almost all of the sign asymmetry for buried charges, but not for those within a few Angstroms of the surface. Clearly, an additional mechanism contributes to the asymmetry of the charging free energy.5, 6

Figure 1.

Figure 1

Open in a new tab

Charging free energies for charges placed in a quasi-spherical solute of radius 4 Å. Symbols represent FEP results for charges placed at different lattice points (x, 0, 0), where x spans the distance from 0 to 3.5 Åfrom the center of the sphere; results for x = 0.5 and x = 1 are omitted in the main figure for clarity, but included in the inset. Curves represent affine-response models derived from quadratic fitting over the interval −0.2e ⩽ q ⩽ +0.2e. Inset shows that the slopes of the charging free energies are practically identical for all charge positions at q = 0, indicating a nearly uniform static potential (mean value of 43.5 kJ/mol/e (thick line) with a standard deviation 1.3 kJ/mol/e) throughout the solute.

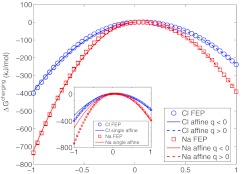
This second source asymmetry is readily seen when calculating charging free energies for the small ions sodium and chloride, for which the charging free energy is dominated by solvent polarization by the solute charge—the static potential contributes only a small amount to the overall asymmetry. Following previous studies,8 we varied the charges of sodium-like and chloride-like ions over the range of −1e ⩽ q ⩽ +1e (Figure 2). The static potentials were 46.9 kJ/mol/e for sodium and 38.1 kJ/mol/e for chloride, in agreement with previous observation of a weakly non-monotonic static potential for spherical solutes as a function of solute radius.7 The large charge-sign asymmetries for these monovalent ions (roughly 334 kJ/mol for sodium-sized ions and 167 kJ/mol for chloride-sized ions) cannot be captured by the effect of the static potential only, but are fit very well by a piecewise affine mode (Figure 2), i.e.,

ΔG=12L(−)q2+φ static q,q≤012L(+)q2+φ static q,q≥0. (2)

For sodium-sized ions, L(+) = −433.0 kJ/mol/e2 and L(−) = −677.8, and for chloride-sized ions L(+) = −274.9 and L(−) = −351.9. As expected, the difference between curvatures for positive vs. negative charges decreases in magnitude as the solute radius increases, or alternatively as the charge is moved away from the surface of a larger solute into its interior (Figure 1).

Figure 2.

Figure 2

Open in a new tab

Charging free energies for sodium and chloride. Affine-response model captures a portion of the FEP results but not over the entire range of q; piecewise response is needed to fit over the whole range. Inset: The single-coefficient response model (small symbols) reproduces the FEP results less accurately; the model parameters were determined separately over the intervals q > 0 and q < 0 but constrained to have the same static potential.

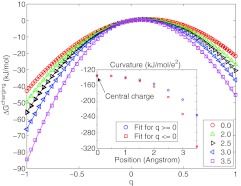
Next, we performed the same type of fits to a piecewise affine model for the lattice-model spherical solute with a radius of 4 Å, and found excellent agreement with explicit solvent FEP data (Figure 3). For a centrally placed charge the asymmetry is small (|L(+) − L(−)| ⩽ 0.85 kJ/mol/e2), but it grows steadily as the charge approaches the interface, reaching 80 kJ/mol/e2 at the surface (inset of Figure 3). This is comparable in magnitude to the difference observed for chloride-sized ions. Solvent response to deeply buried charges is thus nearly symmetric with respect to the sign of the charge; however, asymmetries are significant for charges within a few Angstroms of the surface, i.e., even when not directly solvent exposed.

Figure 3.

Figure 3

Open in a new tab

Piecewise affine response model for charging free energies for buried as well as surface charges in the 4-Å-radius lattice solute. A static potential of 43.5 kJ/mol/e was used for all fits and then the curvatures were fit separately for positive and negative values of q. (Inset) The curvatures reveal symmetric response for deeply buried charges (the center of the sphere is 0), but an increasingly asymmetric response for charges approaching the surface.

A question of some interest, particularly for generalized-Born type theories, is whether one may fit “positive” and “negative” radii to capture these discrepancies. We have found that L(+) is fit better by Born-type expressions than is L(−), and that the difference between them does not depend in a simple way on the nominal radius. For the sodium-sized ion, of radius approximately 1.6 Å, the Born-radius deviation is 0.56 Å, whereas the deviation is 0.5 Å for the chloride-sized one (radius approximately 2.1 Å). If one fits a single deviation for all the charging free energies in the larger lattice sphere solute, the deviation is about 0.4 Å; importantly, however, it is impossible to simultaneously fit one deviation that works for both the central charge and for the solvent-exposed charges. Characterizing these deviations in more detail is a subject of current work.

DISCUSSION

In this work, we have used free-energy MD calculations in explicit solvent to study two proposed explanations for the long-known phenomenon of water solvent's asymmetric response to positive and negative solute charges.5 One mechanism is the potential difference across the liquid-vapor interface,17, 18, 19 which we term a static potential because it exists in the completely uncharged solute. The other mechanism, widely discussed in the ion solvation literature,5, 6, 9 is the fact that water hydrogens can approach the solute more closely than the water oxygen.

Our calculations have employed the TIP3P model of water. Earlier studies suggest that different water models will give similar results for the static potential and the magnitude of asymmetry due to water structure. These studies9, 11 indicate that the large energetic contributions of interest will not be affected qualitatively. For instance, Mobley et al. studied polar solutes and found qualitatively similar asymmetries, with TIP3P in the middle of the range.11 Rajamani et al. used four water models (including TIP3P) and found that the average magnitude of asymmetry, approximately 225 kJ/mol, was much larger than the differences between water models, the largest being about 50 kJ/mol.9

Three key findings emerge from our results. First, we find that these two mechanisms are important in complementary types of solvation problems, and therefore both are required in any general treatment of asymmetric solvation electrostatics. Whereas the static-potential contribution is the major contributor to asymmetry for charges that are deeply buried, the steric contribution is dominant for charges near a surface. It is simple enough to adjust the atomic radii to fit a set of charging free energies, but such an approach conflates these two distinct mechanisms and therefore may bias calculations. Second, our results show that the water-structure contribution to asymmetry are relevant for buried charges as well as for solvent exposed ones. Previous studies have not analyzed the magnitude of this asymmetry for buried charges. Third, we find that where the steric contribution to asymmetry is significant, the reaction potential does not vary linearly but piecewise linearly; that is, given the charge's sign, the curvature is constant over the range 0 ⩽ |q| ⩽ 1e. This indicates that water response is piecewise-linear rather than purely linear. Combined with the static potential, we are led to suggest a piecewise-affine model for solvation.

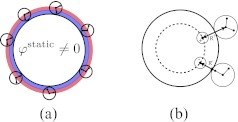
The existence of a significant non-zero electrostatic surface potential even in an uncharged solute has been known for some time.7, 16 This static potential arises from preferred orientation of water molecules at the solute-solvent interface in the absence of solute charge, with the positively charged water hydrogen coming on an average closer to the surface than the negatively charged water oxygens (Figure 4a). The charging free energy then includes additional work done against the field induced by the average solvent structure around the uncharged solute. In keeping with our view of the continuum electrostatic model as a mean to approximate to the charging free energy component of the PMF,1 we assume that the static potential depends only on the solute-solvent van der Waals interactions, e.g., Lennard-Jones parameters, and not on specific chemical details. This additional term represents a “constant” added to the potential against which the charging process does work, and leads to an extension of linear-response models to affine response. Denoting the potential in the uncharged solute by φstatic, the affine model reads is φ = Lq + φstatic instead of the standard linear response relation φ = Lq.27 Additional terms may be needed to capture the static potential inside a solute embedded in an aqueous electrolyte instead of pure water as assumed here. For physiological solutions the differences are likely to be small, because the dielectric constants at the relevant ionic strengths are not significantly different from that of pure water compared to that of the solute dielectric constant.

Figure 4.

Figure 4

Open in a new tab

Schematic representation of the two contributions to the asymmetric solvent response with respect to the solute charge. (a) Average water orientation at the surface of an uncharged solute gives rise to a non-zero static potential. It can be interpreted as a continuum density of oriented solvent dipoles at the surface. (b) Steric asymmetry in water hydrogen (smaller) and oxygen (larger) drives asymmetric response with water molecules being able to approach a negative charge more closely than a positive charge. This applies even to situations in which the charge is not directly solvent exposed.

Regardless of whether the solvent is a pure water or a dilute electrolyte, the underlying static potential field is due to charges strictly outside the solute and, therefore, must satisfy the Laplace equation exactly. Standard implicit-solvent models usually assume that the potential in the solute is zero if the solute were completely uncharged, and therefore do not include this electrostatic contribution to the PMF or solvation free energy.28 In the simplest possible affine-response model, the static potential is non-zero, but assumed constant throughout the solute. Earlier studies have shown that the static potential is remarkably constant even in real proteins with complex (non-spherical) geometries.16 Using a different water model and protocol for estimating φstatic, the authors of that study16 found a mean static potential of 40.6 kJ/mol with a standard deviation of 4.2 kJ/mol, which is very similar to the value found here.

The remarkable uniformity of the static potential in solutes with complex shapes may be rationalized using an elementary result from continuum models of electrostatic theory—a uniform dipole distribution over a surface generates a constant potential inside the solute.29 Although real water does not form a completely uniform distribution of dipoles around a non-spherical solute, the average static potential can be well modeled using such a uniform distribution (Figure 4a). As an interesting consequence, if the static potential is a constant, the solvation energy of a net-neutral group (e.g., an ion pair or salt bridge) is unchanged upon moving from linear to affine response. Also, in the limit of a spherical solute with radius going to infinity, the surface potential of the water-hydrophobic interface should be recovered.17, 18, 19 Finally, we note that extending a continuum model from linear to affine response with a constant static potential entails essentially trivial modifications to software: the overall solvation free energy for the solute changes by its net charge multiplied by the static potential.

The inclusion of the static-potential contribution improves models of asymmetry very well for deeply buried charges, but incompletely for charges near the solvent, such as ions or atoms near the surface of the solute (even completely buried ones). What is the origin of this asymmetric response? The water dipole is atomistically asymmetric due to the different sizes of oxygen and hydrogen (Figure 4b). The continuum approximation of water as a collection of point dipoles1 thus fails for charges close to the interface, within one or two diameters of a water molecule, where this size asymmetry comes into play (Figure 3). Remarkably, the charging free energy for such a charge still follows linear response, however, differently for positive vs. negative charges, i.e., one can employ a piecewise affine response model. This asymmetry seems to favor negative charges over positive ones to be situated more towards the surface of a protein,30 but a complete analysis must also account for the influence of solvent screening on charge-charge interactions. After submission of the present paper, a complementary study has been published37 which confirms our analysis of the origins of the charge asymmetry in ion hydration and demonstrates an alternative method to include asymmetry in continuum electrostatics theories.

Results from earlier studies have hinted that these two sources of asymmetry might need to be combined for a general treatment;7, 16 one of our contributions in this paper is the explicit inclusion of both mechanisms, and the characterization of their relative magnitudes in different systems. It has long been established that a non-trivial electrostatic potential, of the order of 20-45 kJ/mol/e, at the center of completely uncharged spherical molecules.7 More recently, though, it was shown that such a large and remarkably uniform potential exists also in proteins and that including it improves agreement between explicit-solvent MD and implicit-solvent Poisson models.16 Nevertheless, it was found in the same study that adding the static-potential component did not fully resolve discrepancies between implicit and explicit solvent models. Our results suggest that much of the remaining error may be due to the sign-dependent affine response for charges close to the protein surface. Older continuum-model studies of ion hydration asymmetry present an additional clue that multiple mechanisms could be needed. Many authors had suggested that different definitions of ion radii should be used for anions vs. cations, on the basis of water structure and the size of the cavity formed by ions with charges of opposite signs.5, 6 Rashin and Honig found, however, that even with these different definitions, accurate prediction of cation solvation enthalpies required an empirical increase of cationic radii of about 7%.6 This modification leads to energetic changes quite comparable in magnitude to the reduction in cation charging free energies due to the static potential.

CONCLUSION

The piecewise-affine model proposed in this study, consistently and with molecular-level justification, puts together the effects of the static potential (around the uncharged solute) and the asymmetry in cation-water and anion-water interactions. The steric origin of sign-dependent affine response suggests that polarization effects beyond the first solvation shell are important, which might be addressed with nonlocal dielectric theory.31, 32 Basilevsky and Parsons have shown that different solvent-correlation lengths should be used for cations and anions,33 though the difference they found should decrease somewhat when one accounts for the static-potential contribution. Finally, the present model may be applicable also for charging free energies of divalent ions, where a discontinuity in the derivative occurs when water molecules in the first solvation shell become maximally polarized.34 Other types of nonlinear effects,35, 36 particularly those involving specific hydrogen bonds, remain outside the scope of the present model.

ACKNOWLEDGMENTS

The authors gratefully acknowledge support from a Rush University New Investigator award and the National Institutes of Health (NIH) GM102642 (J.P.B.), The Czech Ministry of Education (Grant No. LH12001) (P.J.), and NIH (GM085648) and NSF (MCB1158340) (L.M.). P.J. also thanks the Academy of Sciences for support via the Praemium Academie Award. The authors thank R. S. Eisenberg for valuable discussions, support, and encouragement, and the Rush Medical College for hospitality.

References

  1. Roux B. and Simonson T., “Implicit solvent models,” Biophys. Chem. 78, 1–20 (1999). 10.1016/S0301-4622(98)00226-9 [DOI] [PubMed] [Google Scholar]
  2. Tomasi J., Mennucci B., and Cammi R., “Quantum mechanical continuum solvation models,” Chem. Rev. 105, 2999–3093 (2005). 10.1021/cr9904009 [DOI] [PubMed] [Google Scholar]
  3. Born M., “Volume and heat of hydration of ions,” Z. Phys. 1, 45 (1920). 10.1007/BF01881023 [DOI] [Google Scholar]
  4. Tomasi J. and Persico M., “Molecular interactions in solution: An overview of methods based on continuous descriptions of the solvent,” Chem. Rev. 94, 2027–2094 (1994). 10.1021/cr00031a013 [DOI] [Google Scholar]
  5. Latimer W. M., Pitzer K. S., and Slansky C. M., “The free energy of hydration of gaseous ions, and the absolute potential of the normal calomel electrode,” J. Chem. Phys. 7, 108–112 (1939). 10.1063/1.1750387 [DOI] [Google Scholar]
  6. Rashin A. A. and Honig B., “Reevaluation of the Born model of ion hydration,” J. Phys. Chem. 89, 5588–5593 (1985). 10.1021/j100272a006 [DOI] [Google Scholar]
  7. Ashbaugh H. S., “Convergence of molecular and macroscopic continuum descriptions of ion hydration,” J. Phys. Chem. B 104, 7235–7238 (2000). 10.1021/jp0015067 [DOI] [Google Scholar]
  8. R. M. Lynden-Bell, Rasaiah J. C., and Noworyta J. P., “Using simulation to study solvation in water,” Pure Appl. Chem. 73, 1721–1731 (2001). 10.1351/pac200173111721 [DOI] [Google Scholar]
  9. Rajamani S., Ghosh T., and Garde S., “Size dependent ion hydration, its asymmetry, and convergence to macroscopic behavior,” J. Chem. Phys. 120, 4457 (2004). 10.1063/1.1644536 [DOI] [PubMed] [Google Scholar]
  10. Fedorov M. V. and Kornyshev A. A., “Unravelling the solvent response to neutral and charged solutes,” Mol. Phys. 105, 1–16 (2007). 10.1080/00268970601110316 [DOI] [Google Scholar]
  11. Mobley D. L., A. E.BarberII, Fennell C. J., and Dill K. A., “Charge asymmetries in hydration of polar solutes,” J. Phys. Chem. B 112, 2405–2414 (2008). 10.1021/jp709958f [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Fennell C. J. and Dill K. A., “Physical modeling of aqueous solvation,” J. Stat. Phys. 145, 209 (2011). 10.1007/s10955-011-0232-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Gallicchio E., Paris K., and Levy R. M., “The AGBNP2 implicit solvation model,” J. Chem. Theory Comput. 5, 2544–2564 (2009). 10.1021/ct900234u [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Marenich A. V., Cramer C. J., and Truhlar D. G., “Universal solvation model based on the Generalized Born approximation with asymmetric descreening,” J. Chem. Theory Comput. 5, 2447–2464 (2009). 10.1021/ct900312z [DOI] [PubMed] [Google Scholar]
  15. Corbeil C. R., Sulea T., and Purisima E. O., “Rapid prediction of solvation free energy. 2. The first-shell hydration (FiSH) continuum model,” J. Chem. Theory Comput. 6, 1622–1637 (2010). 10.1021/ct9006037 [DOI] [PubMed] [Google Scholar]
  16. Cerutti D. S., Baker N. A., and McCammon J. A., “Solvent reaction field potential inside an uncharged globular protein: A bridge between implicit and explicit solvent models?” J. Chem. Phys. 127, 155101 (2007). 10.1063/1.2771171 [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Paluch M., “Electrical properties of free surface of water and aqueous solutions,” Adv. Colloid Interface Sci. 84, 27–45 (2000). 10.1016/S0001-8686(99)00014-7 [DOI] [PubMed] [Google Scholar]
  18. Harder E. and Roux B., “On the origin of the electrostatic potential difference at the liquid-vapor interface,” J. Chem. Phys. 129, 234706 (2008). 10.1063/1.3027513 [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Kathmann S. M., Kuo I-F. W., Mundy C. J., and Schenter G. K., “Understanding the surface potential of water,” J. Phys. Chem. B 115, 4369–4377 (2011). 10.1021/jp1116036 [DOI] [PubMed] [Google Scholar]
  20. Schutz C. N. and Warshel A., “What are the dielectric constants of proteins and how to validate electrostatic models?” Proteins 44, 400–417 (2001). 10.1002/prot.1106 [DOI] [PubMed] [Google Scholar]
  21. Phillips J. C., Braun R., Wang W., Gumbart J., Tajkhorshid E., Villa E., Chipot C., Skeel R. D., Kale L., and Schulten K., “Scalable molecular dynamics with NAMD,” J. Comput. Chem. 26, 1781–1802 (2005). 10.1002/jcc.20289 [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. A. D.MacKerellJr., Bashford D., Bellott M., R. L.DunbrackJr., Evanseck J. D., Field M. J., Fischer S., Gao J., Guo H., Ha S., Joseph–McCarthy D., Kuchnir L., Kuczera K., Lau F. T. K., Mattos C., Michnick S., Ngo T., Nguyen D. T., Prodhom B., W. E.ReiherIII, Roux B., Schlenkrich M., Smith J. C., Stote R., Straub J., Watanabe M., Wiorkiewicz–Kuczera J., Yin D., and Karplus M., “All-atom empirical potential for molecular modeling and dynamics studies of proteins,” J. Phys. Chem. B 102, 3586–3616 (1998). 10.1021/jp973084f [DOI] [PubMed] [Google Scholar]
  23. Jorgensen W. L., Chandrasekhar J., Madura J. D., Impey R. W., and Klein M. L., “Comparison of simple potential functions for simulating liquid water,” J. Chem. Phys. 79, 926–935 (1983). 10.1063/1.445869 [DOI] [Google Scholar]
  24. Hénin J., Harrison C., and Chipot C., “In silico alchemy: A tutorial for alchemical free-energy perturbation calculations with NAMD,” see www.ks.uiuc.edu/Training/Tutorials/namd/FEP/tutorial-FEP.pdf for the NAMD software.
  25. Hummer G., Pratt L. R., and García A. E., “Free energy of ionic hydration,” J. Phys. Chem. 100, 1206–1215 (1996). 10.1021/jp951011v [DOI] [Google Scholar]
  26. Svensson B. R. and Woodward C. E., “Widom's method for uniform and non-uniform electrolyte solutions,” Mol. Phys. 64, 247–259 (1998). 10.1080/00268978800100203 [DOI] [Google Scholar]
  27. Strang G., Introduction to Linear Algebra (Wellesley–Cambridge, 2003). [Google Scholar]
  28. Martin D. R., Friesen A. D., and Matyushov D. V., “Electric field inside a “rossky cavity” in uniformly polarized water,” J. Chem. Phys. 135, 084514 (2011). 10.1063/1.3628679 [DOI] [PubMed] [Google Scholar]
  29. Jackson J. D., Classical Electrodynamics, 3rd ed. (Wiley, 1998). [Google Scholar]
  30. Gunner M. R., Saleh M. A., and Cross E., “Backbone dipoles generate positive potentials in all proteins: Origins and implications of the effect,” Biophys. J. 78, 1126–1144 (2000). 10.1016/S0006-3495(00)76671-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Kornyshev A. A., Rubinshtein A. I., and Vorotyntsev M. A., “Model nonlocal electrostatics: I,” J. Phys. C 11, 3307 (1978). 10.1088/0022-3719/11/15/029 [DOI] [Google Scholar]
  32. Hildebrandt A., Blossey R., Rjasanow S., Kohlbacher O., and Lenhof H.-P., “Novel formulation of nonlocal electrostatics,” Phys. Rev. Lett. 93, 108104 (2004). 10.1103/PhysRevLett.93.108104 [DOI] [PubMed] [Google Scholar]
  33. Basilevsky M. V. and Parsons D. F., “An advanced continuum medium model for treating solvation effects: Nonlocal electrostatics with a cavity,” J. Chem. Phys. 105(9), 3734 (1996). 10.1063/1.472193 [DOI] [Google Scholar]
  34. Jayaram B., Fine R., Sharp K., and Honig B., “Free energy calculations of ion hydration: An analysis of the Born model in terms of microscopic simulations,” J. Phys. Chem. 93, 4320–4327 (1989). 10.1021/j100347a081 [DOI] [Google Scholar]
  35. Sandberg L. and Edholm O., “Nonlinear response effects in continuum models of the hydration of ions,” J. Chem. Phys. 116, 2936–2944 (2002). 10.1063/1.1435566 [DOI] [Google Scholar]
  36. Gong H. and Freed K. F., “Langevin–Debye model for nonlinear electrostatic screening of solvated ions,” Phys. Rev. Lett. 102, 057603 (2009). 10.1103/PhysRevLett.102.057603 [DOI] [PubMed] [Google Scholar]
  37. Mukhopadhyay A., Fenley A. T., Tolokh I. S., and Onufriev A. V., “Charge hydration asymmetry: The basic principle and how to use it to test and improve water models,” J. Phys. Chem. B 116, 9776–9783 (2012). 10.1021/jp305226j [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from The Journal of Chemical Physics are provided here courtesy of American Institute of Physics

RESOURCES