NONLINEAR MECHANICAL BEHAVIOR OF THE HUMAN COMMON, EXTERNAL AND INTERNAL CAROTID ARTERIES IN VIVO

Abstract

Introduction

The mechanical environment and properties of the carotid artery play an important role in the formation and progression of atherosclerosis in the carotid bifurcation. The purpose of this work was to measure and compare the range and variation of circumferential stress and tangent elastic moduli in the human common (CCA), external (ECA) and internal (ICA) carotid arteries over the cardiac cycle in vivo.

Methods

Measurements were performed in the surgically exposed proximal cervical CCA, distal ECA and distal ICA of normotensive patients (n = 16) undergoing carotid endarterectomy. All measurements were completed in vivo over the cardiac cycle in the repaired carotid bifurcation after the atherosclerotic plaque was successfully removed. B-mode Duplex ultrasonography was used for measurement of arterial diameter and wall thickness, and an angiocatheter placed in the CCA was used for concurrent measurement of blood pressure. A semi-automatic segmentation algorithm was used to track changes in arterial diameter and wall thickness in response to blood pressure. These measurements were then used to calculate the variation of circumferential (hoop) stresses, tangent elastic moduli (the slope of the stress-strain curve at specified stresses), and stress-induced stiffness of the arterial wall (stiffening in response to intraluminal blood pressure fluctuation) for each patient.

Results

The diameter and wall thickness of the segments (CCA, ECA and ICA) of the carotid bifurcation were found to decrease and stress-induced stiffness to increase from proximal CCA to distal ECA and ICA. The circumferential stress from end-diastole (minimum pressure) to peak-systole (maximum pressure) varied nonlinearly from 25±7 to 63±23 kPa (CCA), from 22±7 to 57±19 kPa (ECA) and from 28±8 to 67±23 kPa (ICA). Tangent elastic moduli also varied nonlinearly from end-diastole to peak-systole as follows: from 0.40±0.25 to 1.50±2.05 MPa (CCA), from 0.49±0.34 to 1.14±0.52 MPa (ECA) and from 0.68±0.31 to 1.51±0.69 MPa (ICA). The stress-induced stiffness of CCA and ECA increased more than 3-fold and the stiffness of ICA increased more than 2.5-fold at peak-systole compared to end-diastole.

Conclusions

The in vivo mechanical behavior of the three segments of the carotid bifurcation was qualitatively similar, but quantitatively different. All three arteries – CCA, ECA and ICA – exhibited nonlinear variations of circumferential stress and tangent elastic moduli within the normal pressure range. The variability in the properties of the three segments of the carotid bifurcation indicates a need for development of carotid models that match the in vivo properties of the carotid segments. Finally, the observed nonlinear behavior of the artery points to the need for future vascular mechanical studies to evaluate the mechanical factors of the arterial wall over the entire cardiac cycle.

INTRODUCTION

Atherosclerosis of the carotid artery bifurcation is a leading cause of stroke. The carotid artery is a dynamic, living conduit with complex mechanical properties. These properties appear to be affected by most of the conditions that are risks factors for atherosclerosis (including hypertension, hyperlipidemia and diabetes) ^(1-4).

The two main mechanical factors involved in the pathogenesis of atherosclerosis of the carotid bifurcation are the stresses inside and the mechanical properties of the arterial wall. Stress is a local mechanical quantity that describes a force imparted on the arterial wall normalized by the area on which the force acts. Stresses in arteries are produced mostly from the pressure of the blood circulating in them. Excessive stress can damage the arterial wall and promote the development or progression of arterial disease ⁽⁵⁾. The deformation behavior of the artery under stress depends on the mechanical properties of the arterial wall. A simple way to describe mechanical properties in vivo is to calculate the tangent elastic modulus, defined as the slope of the stress-strain curve. The elastic modulus is large when the material is stiff and small when the material is compliant. In nonlinear materials, such as arterial walls, the elastic modulus is not constant, but increases with increasing stress ⁽⁶⁾. We note that this stiffening due to increasing stress is different from the arterial stiffening that results from atherosclerotic disease ^{(3, 4)}. To distinguish between the two, stiffening due to increased stress is referred to as stress-induced stiffening. The nonlinear stress-induced stiffening of arteries has been observed in vitro in cadaveric carotids by many investigators ^(7-11). However, whether the nonlinearity is evident within the normal in vivo stress range is still an open question ^{(12, 13)}.

In vivo carotid studies are rare and have usually been performed on animals ^{(14, 15)} or are limited to the CCA ^{(12, 13, 16-18)}. Here, we present a systematic evaluation of the in vivo mechanical behavior of the human proximal common (CCA), external (ECA) and internal (ICA) carotid arteries over the range of blood pressures seen during the cardiac cycle from a group of normotensive patients undergoing carotid endarterectomy. Thorough knowledge of the actual in vivo mechanical behavior of the carotid artery can further improve our understanding of the carotid bifurcation pathophysiology.

METHODS

Patients

The research protocol was approved by the institutional review board of the Nebraska-Western Iowa Veterans Affairs Medical Center and informed consent was obtained from all patients. The common (CCA), internal (ICA) and external (ECA) carotid artery mechanical properties were evaluated with B-mode duplex ultrasound (Pro Focus 2202, Probe 8809 (linear array transducer), B-K Medical, Herlev, Denmark) in 16 male patients (mean age 68±8) with severe (>80% diameter reduction) carotid bifurcation occlusive disease. The demographics of the subjects recruited for evaluation are presented in Table 1. None of the patients had previous open or endovascular interventions performed on their carotids. Because it affords improved quality of imaging (due to absence of surrounding tissues with direct insonation of the carotid artery) and optimal access to distal segments of the ICA and ECA, we performed our measurements intra-operatively after the carotid bifurcation was surgically dissected and exposed for the performance of carotid endarterectomy. Measurements were performed after completing the endarterectomy, closing the arteriotomy and reestablishing flow.

Table 1.

Demographics for subjects recruited for evaluation of the in vivo mechanical behavior of their common, external and internal carotid arteries

	Subjects
n	16
Age (years)a	68±8
Smoking never/former/currentb	6/2/8
CAD	6 (38 %)
Obesity	3 (19 %)
Dyslipidemia	15 (94 %)
DM	4 (25 %)
HTN	13 (81 %)
Carotid stenosis a	90%±1%

^aValues are means ± SD,

^bnumber of subjects in each category, CAD=Coronary Artery Disease, DM= diabetes mellitus, HTN=hypertension, ABI= Ankle brachial index.

B-mode duplex ultrasound evaluation

All patients were supine with arteries immersed in saline such that the ultrasound probe was not in physical contact with the artery during insonation. The arteries were fully dissected from surrounding tissues in their anterior, medial and lateral aspects, and therefore the effect of surrounding tissues was assumed to be minimal. Natural orientation of the carotid artery was preserved during insonation. We used the duplex to confirm the absence of residual stenosis or intimal flaps in CCA, ECA and ICA prior to performing our measurements. All operations and measurements were performed by the same vascular surgeon, and all patients received carotid endarterectomy using longitudinal arteriotomy and primary closure. Patients had a mean preoperative stenosis of 90% (range 80% to 95% based on measurements obtained from preoperative computerized tomographic angiography).

For each patient, B-mode ultrasound measurements were obtained in three locations: 1) the CCA 40 mm proximal to the level of the bifurcation, 2) the ICA 50 mm distal to the bifurcation and 3) the ECA 30 mm distal to the bifurcation. For the CCA and ICA, the measurements were taken at least 20 mm proximal or distal (respectively) to the end of the endarterecomy and the arteriotomy closure which minimized the potential effects of the operative intervention on our measurements. These locations were chosen based on data describing the distance from the bifurcation where flow reorganizes to become laminar ^{(19, 20)}. In each location, the transducer was positioned perpendicular to the artery to provide a transverse view of the pulsating blood vessel (B-mode). The pulsating vessel was recorded using the video recording function of the ultrasound device, and the data were used for further segmentation and image analysis.

Blood Pressure Measurement

Simultaneously with B-mode ultrasound evaluation, the blood pressure waveform was measured in the CCA. Pressure was measured with a 21-gauge angiocatheter placed in the CCA 50 mm proximal to the level of the bifurcation. Measurements of arterial deformation (obtained using ultrasound) and pressure waveform (obtained with the indwelling angiocatheter) were synchronized. Placing separate angiocatheters in the ICA and ECA introduces additional risk to the patient and therefore was not performed. However, using previously published data from Younis et al. ⁽²¹⁾ and Kaazempur-Mofrad et al. ⁽²²⁾, we estimate that the pressure drop (decrease in pressure from the most proximal CCA to the most distal ICA location) across a carotid bifurcation without stenosis does not exceed 5% of the peak systolic pressure. Therefore, the pressure was assumed to be the same in the CCA, ECA and ICA, and the pressure waveform measured in the proximal CCA was used for all calculations.

Image segmentation

Manual measurement of the arterial diameter is often subjective and therefore may not be consistent and reproducible. To minimize the subjectivity of our measurements, we used a semi-automatic computerized segmentation method to detect the boundary between the adventitia and the surrounding tissues and between the intima and the flow lumen of the artery on the ultrasound images ⁽²³⁾. Original images of 640×480 pixel matrix size (pixel size 46 μm) were obtained by analyzing the video recorded by the Ultrasound device frame by frame. Each frame was rescaled to 1068×800 pixel matrix size (pixel size 28 μm) using sub-pixel interpolation. This interpolation has been shown to detect changes that are smaller than the resolution of the ultrasound transducer ⁽²³⁾. Segmentation was performed under the supervision of a vascular surgeon who reviewed the results produced by the algorithm and further delineated segments of the automatically detected boundary that were partially obscured by residual flow artifacts or periadventitial fat or were not welldefined due to poor contrast. The outer (periadventitial) and inner (luminal) areas bound by the edited contour were then computed and used for calculating the equivalent outer and inner diameters (i.e., the diameters of the circles with areas equivalent to those measured from the area contour), respectively. The wall thickness was then calculated as half of the difference between the outer and inner equivalent diameters. A representative image of the CCA at peak-systole and end-diastole with periadventitial and luminal contours outlined using the described technique is shown in Figure 1.

Figure 1.

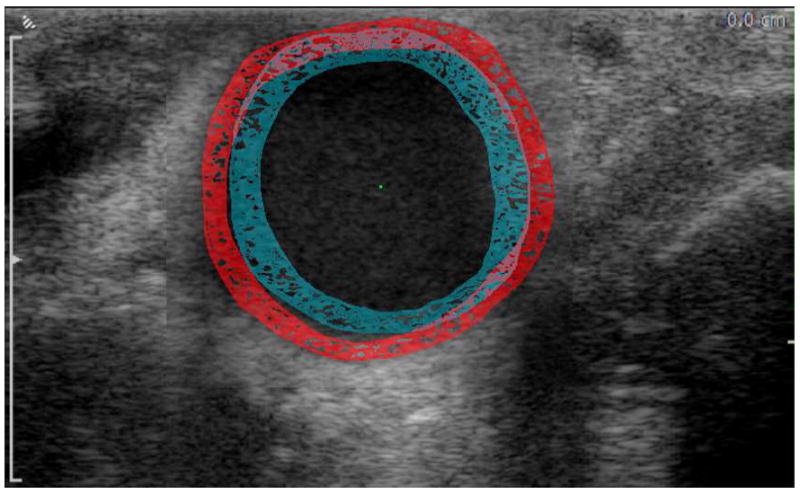
Representative image of the CCA with periadventitial and luminal contours outlined at end-diastole (blue) and peak-systole (red). The figure is a composite of two superimposed images, one obtained at peak-systole and the other at end-diastole. The figure demonstrates the increase in the arterial diameter and decrease in wall thickness as the artery transitions from end-diastole to peak-systole.

Calculation of mechanical properties

When the artery is subjected to blood pressure, three mutually perpendicular principal stresses develop in its wall: radial, longitudinal and circumferential (see Figure 2). Since the diameter of the carotid artery is substantially larger than its wall thickness, radial stress can be considered small compared to other stresses ⁽²⁴⁾. Accurate calculation of longitudinal (axial) stress requires knowledge of the axial force that elongates the artery. However, measurement of this force is not possible in vivo. Circumferential (hoop) stress is the dominant stress that develops in the arterial wall to resist the bursting effect of the blood pressure. This stress can be calculated using the measured blood pressure, vessel diameter, and wall thickness as follows:

$${\sigma }_{\theta }=\frac{\mathit{Pd}}{2h}$$

where P is the blood pressure d, is the inner diameter of the artery and h is the wall thickness.

Figure 2.

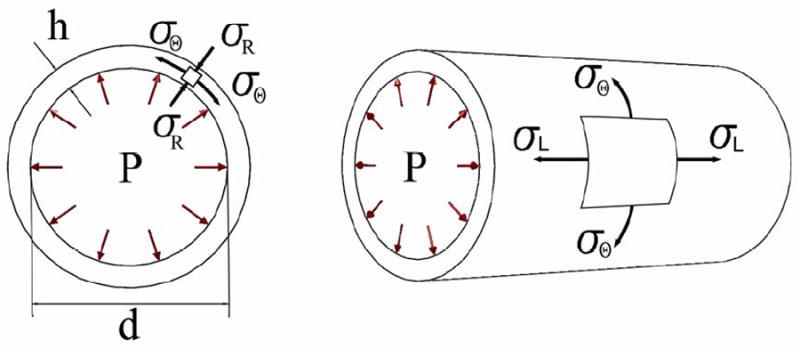
Schematic of the three principal stresses (radial σ_R, longitudinal σ_L and circumferential σ_θ) that arise in the arterial wall due to blood pressure P. Here h is wall thickness and d is internal diameter of the artery.

Apart from stress, characterization of mechanical properties requires evaluation of strain. Circumferential strain can be calculated as:

$${\mathit{\in }}_{\theta }=\frac{\mathit{\delta d}}{d}$$

where δd is the increase in inner diameter during the cardiac cycle.

The tangent elastic modulus can then be calculated as the slope of the stress-strain curve for any given stress. A representative stress-strain curve for the carotid wall is shown in Figure 3. Two tangent moduli E_diastole and E_systole were calculated by measuring the slopes of this curve at end-diastole and peak-systole, respectively.

Figure 3.

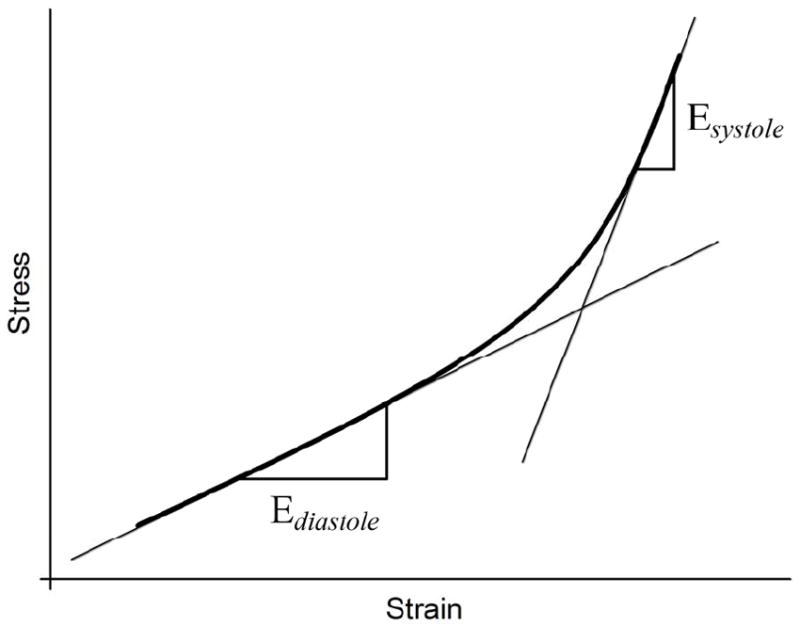
Representative stress-strain curve for the wall of the carotid artery. The tangent elastic moduli E_diastole and E_systole were calculated as the slopes of the curve at end-diastole and peak-systole respectively. Increase in the stress-strain curve slope clearly indicates the stress-induced stiffening of the arterial wall from end-diastole to peak-systole.

RESULTS

Diameter and wall thickness

Patient demographics including age, peak-systolic and end-diastolic pressures, and inner diameter and wall thickness of CCA, ECA and ICA for all 16 patients are presented in Table 2. For brevity, pressure, diameter and thickness data points between end-diastole and peak-systole are omitted from the table, but they were used to calculate the stress-strain curves and tangent elastic moduli.

Table 2.

Demographics of 16 patients recruited in the study. Parameters include age, peak systolic and end diastolic pressures, inner radius and wall thickness presented for CCA, ECA and ICA. Bottom line contains mean values and standard deviation (SD).

No	Age, years	Pressure, mmHg		Inner diameter (mm), peak systole			Wall thickness (mm), peak systole			Inner diameter (mm), end diastole			Wall thickness (mm), end diastole
		Peak systole	End diastole	CCA	ECA	ICA	CCA	ECA	ICA	CCA	ECA	ICA	CCA	ECA	ICA
1	72	148	65	8.98	4.59	5.15	0.65	0.58	0.45	7.56	3.90	4.78	0.89	0.76	0.60
2	75	120	51	6.26	5.54	6.17	1.03	0.98	0.96	5.70	4.80	6.01	1.15	1.00	0.99
3	65	93	53	8.64	5.67	5.48	1.53	1.19	1.34	7.85	5.31	5.24	1.62	1.27	1.39
4	76	114	48	12.45	7.88	9.13	1.31	1.28	1.48	11.52	7.46	8.79	1.59	1.34	1.57
5	74	106	54	13.89	4.36	5.55	1.30	0.46	0.76	13.07	3.65	5.17	1.51	0.66	0.89
6	52	117	54	6.27	4.32	3.53	0.87	0.59	0.63	5.58	3.67	3.26	1.04	0.63	0.66
7	75	122	55	7.79	5.78	5.49	1.24	0.70	0.52	7.65	5.62	5.26	1.30	0.72	0.58
8	59	142	66	7.39	6.35	5.83	0.91	0.70	0.62	7.07	6.10	5.45	0.93	0.72	0.71
9	82	120	60	7.68	4.69	4.44	1.19	0.53	0.38	6.89	4.23	4.27	1.37	0.74	0.40
10	63	120	52	7.89	3.80	5.94	1.32	0.92	0.74	7.15	3.74	5.72	1.46	0.93	0.82
11	57	90	53	8.23	4.78	8.02	0.96	1.02	0.81	7.93	4.72	7.79	1.08	1.03	0.92
12	66	139	67	6.48	3.99	5.78	1.00	0.44	0.66	5.75	3.75	5.57	1.18	0.55	0.73
13	66	95	48	7.34	4.12	6.64	1.02	0.66	0.55	6.18	3.92	6.40	1.23	0.75	0.62
14	70	113	57	9.13	5.40	5.31	1.03	0.79	0.65	8.41	5.21	5.16	1.06	0.86	0.69
15	66	100	59	8.73	5.09	7.43	1.02	0.61	0.98	8.28	4.98	7.19	1.05	0.64	1.01
16	69	133	59	7.04	3.39	4.46	0.80	0.45	0.49	6.86	3.16	4.29	0.82	0.53	0.54
Mean ± SD	68 ±8	117 ±18	56 ±6	8.39 ±2.1	4.98 ±1.1	5.90 ±1.4	1.07 ±0.2	0.74 ±0.3	0.75 ±0.3	7.72 ±2.0	4.64 ±1.1	5.65 ±1.4	1.21 ±0.2	0.82 ±0.2	0.82 ±0.3

Our measurements showed that the inner diameter of the CCA was larger than the diameter of the ICA on average by 42%. The diameter of the ICA was larger than the diameter of the ECA on average by 18%. Both results were statistically significant (p<0.001 and p=0.02, respectively). Comparisons of wall thickness showed that the CCA had on average a 45% thicker wall than the ECA and ICA (p<0.001). The average thicknesses of the ECA and ICA walls were quite similar. No significant correlation was found between the age of the patients and the diameters or wall thicknesses of their arteries (Pearson coefficient < 0.37).

Circumferential stress and tangent elastic moduli

The values of circumferential stress and tangent elastic moduli are summarized in Table 3 and Figure 4. The circumferential stress for CCA, ECA and ICA from end-diastole to peak-systole varied nonlinearly from 25±7 to 63±23 kPa, from 22±7 to 57±19 kPa and from 28±8 to 67±23 kPa, respectively. Circumferential stress on average was higher in the ICA than in the ECA (p=0.08) or CCA, although the result for the CCA did not reach statistical significance (p=0.32).

Table 3.

Variation of circumferential stress over the cardiac cycle and values of tangent elastic moduli for CCA, ECA and ICA of 16 patients. Bottom line contains mean values and standard deviation (SD).

No	Variation of σθ, kPa from diastole to systole			Ediastole, MPa			Esystole, MPa
	CCA	ECA	ICA	CCA	ECA	ICA	CCA	ECA	ICA
1	37-137	22-78	35-113	0.41	0.16	0.78	0.63	1.50	2.38
2	17-49	16-45	21-52	0.19	0.09	0.94	0.88	0.89	1.69
3	17-35	15-29	13-25	0.15	0.19	0.16	0.17	0.25	0.40
4	23-72	18-47	18-47	0.45	0.26	0.42	0.83	1.11	1.43
5	31-75	20-67	21-51	0.67	0.19	0.39	0.69	0.33	0.39
6	19-56	21-57	18-44	0.16	0.16	0.21	0.85	0.59	0.65
7	22-51	29-67	33-86	0.88	0.95	0.91	6.25	2.22	2.00
8	33-77	37-85	34-89	0.47	0.78	0.53	2.68	1.60	1.90
9	20-52	23-71	43-94	0.20	0.30	0.76	0.34	0.52	2.43
10	17-48	14-33	24-64	0.22	1.29	0.95	0.83	1.30	0.96
11	26-52	16-28	30-60	0.61	0.66	0.85	1.06	1.32	0.86
12	22-60	31-84	34-81	0.23	0.66	1.06	0.55	1.17	1.60
13	16-45	17-39	33-76	0.17	0.35	0.79	0.17	1.09	1.89
14	30-67	23-52	29-61	0.31	0.63	0.65	0.83	1.22	2.08
15	31-57	31-55	28-50	0.47	0.71	0.32	0.48	1.67	2.25
16	33-78	24-67	31-81	0.88	0.45	1.14	6.82	1.41	1.19
Mean ± SD	25±7 – 63±23	22±7 – 57±19	28±8 – 67±23	0.40±0.25	0.49±0.34	0.68±0.31	1.50±2.05	1.14±0.52	1.51±0.69

Figure 4.

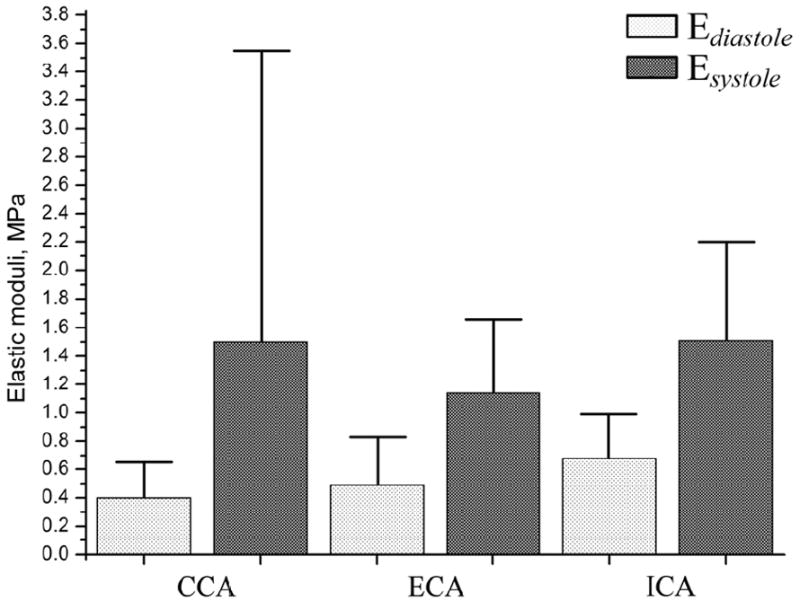
Mean values (vertical bars) and standard deviations (vertical T-lines) of tangent elastic moduli E_diastole and E_systole calculated for two portions of the stress-strain curve (see Figure 2) for CCA, ECA and ICA. The data presented in this figure is a graphical representation of results summarized in Table 2. Light bars represent moduli at end-diastole while darker bars represent moduli at peak-systole.

A comparison of the tangent elastic moduli showed that the ICA was stiffer than the CCA and ECA at both diastole and systole (tangent elastic moduli E_diastole and E_systole of the ICA were higher). This result was statistically significant (p<0.05) for all evaluated properties except $E_{\mathit{systole}}^{\mathit{ICA}}>E_{\mathit{systole}}^{\mathit{CCA}}$. Of interest, the CCA was the most compliant artery during diastole (p=0.21 for ECA, p=0.005 for ICA). However, at peak-systole, its stiffness increased 3.8-fold, more than the increase in the stress-induced stiffness of the ECA or ICA at peak-systole compared to end-diastole. Therefore, the CCA became stiffer than the ECA at peak-systole (p=0.25) and had almost the same stress-induced stiffness as the ICA.

The scatter of tangent elastic moduli was considerable for CCA, ECA and ICA, but it was highest (SD=2.05) for $E_{\mathit{systole}}^{\mathit{CCA}}$ (see Figure 4). The smallest scatter in tangent moduli was observed for the ICA.

Stress-Induced Stiffness

In a linear material, strain varies linearly with stress and the elastic modulus is constant (i.e. does not change with stress or strain). In vitro studies performed on cadaveric carotids have shown that stress-strain relations in the carotid wall are nonlinear and that elastic moduli increase significantly with increasing stress. However, many in vivo studies of the CCA assumed linear behavior under normal blood pressure and calculated a single elastic modulus from the difference between stresses and strains at end-diastole and peak-systole ^{(13, 16, 18)}. In this study, we evaluated this hypothesis by calculating continuously varying tangent elastic moduli over the cardiac cycle. The results demonstrate that all analyzed arteries exhibited significant nonlinearity in the stress-strain relations. The tangent elastic modulus of the arteries varied nonlinearly from end-diastole to peak-systole: 0.4±0.25 MPa to 1.50±2.05 MPa for the CCA, 0.49±0.34 MPa to 1.14±0.52 MPa for the ECA, and 0.68±0.31 MPa to 1.51±0.69 MPa for the ICA. For the CCA, ECA and ICA, the modulus E_systole was higher than the E_diastole (p<0.05) (see Figure 4). This result demonstrates that the artery stiffened under increased stress.

To evaluate how much the artery stiffened during peak-systole compared to end-diastole, we calculated the ratios of tangent elastic moduli, as presented in Figure 5. The mean ratios in Figure 5 were calculated by averaging the individual ratios for each patient rather than calculating the ratios of mean tangent elastic moduli from Figure 4. The average E_systole/E_diastole ratio was similar between the CCA and ECA (3.2±2.3 and 3.2±2.6, respectively) and was smaller for the ICA (2.6±1.5) (p>0.05).

Figure 5.

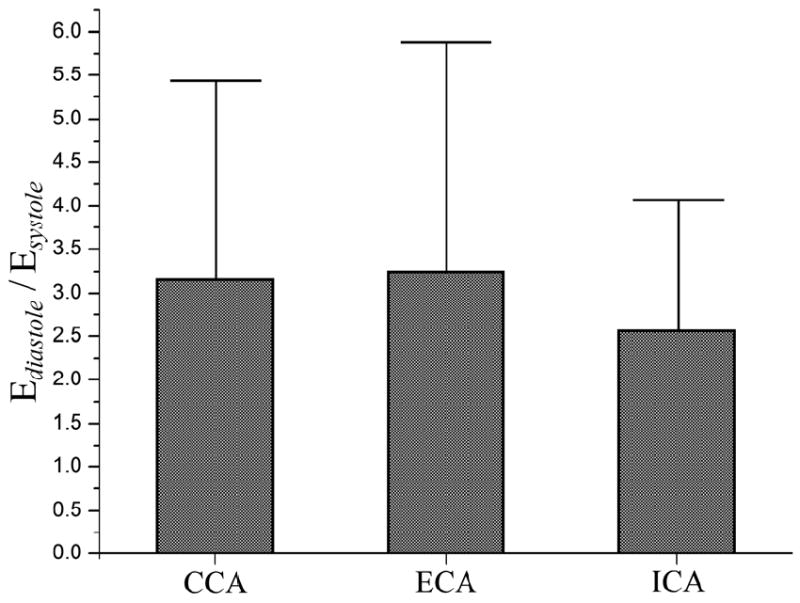
Ratios of tangent elastic moduli E_systole/E_diastole and their standard deviations calculated for CCA, ECA and ICA. Vertical bars represent mean values while vertical T-lines show standard deviations.

No significant correlation was found between the patient’s age and the value of the tangent elastic moduli or E_systole/E_diastole ratio. The highest value of Pearson’s correlation coefficient (0.44) for age-modulus relation was observed for $E_{\mathit{systole}}^{\mathit{ECA}}$.

DISCUSSION

The mechanical properties of the carotid arteries play an important role in the formation and progression of atherosclerotic disease ^(1-4). Excessive deformation and stress in the arterial wall may jeopardize the integrity of the endothelium. This may be followed by platelet deposition, smooth muscle cell proliferation, and slow accumulation of lipoproteins, which may eventually lead to the development or progression of arterial disease ^{(5, 25)}. Using B-mode Duplex ultrasonography and direct measurement of intraluminal blood pressure, we analyzed the in vivo circumferential stresses and tangent elastic moduli of the carotid arteries of 16 normotensive patients.

Our data show that circumferential stress in the normotensive CCA, ECA and ICA from end-diastole to peak-systole varied nonlinearly from 25±7 to 63±23 kPa, from 22±7 to 57±19 kPa and from 28±8 to 67±23 kPa, respectively. This finding is in agreement with in vitro data from cadaveric CCA and ICA samples ⁽⁸⁾. Notably, the average increase (109%) of blood pressure from end-diastole to peak-systole in our patients produced a higher (150%) average increase in circumferential stress. This result suggests that the circumferential stress is quite high in hypertensive patients, which may partially account for the increased incidence of atherosclerosis in this group of patients.

In progressing from proximal CCA to distal ICA, the diameter and wall thickness of the artery decreased and the stress-induced stiffness of the artery increased. These phenomena are known as diameter taper (the arteries become smaller progressing centrally to peripherally) and elastic taper (the arteries become stiffer as we progress from centrally to peripherally) and were previously reported by Maurits et al. ⁽²⁶⁾, Reneman et al. ⁽²⁷⁾, Wang and Parker ⁽²⁸⁾, Wu et al. ⁽¹⁷⁾ and others. Although the diameter and wall thickness of the CCA were larger than those of the ICA, our data demonstrate that the ICA had a larger diameter than the ECA even though the ICA measurements were performed 20 mm more distally than in the ECA. This is probably secondary to the fact that compared to the ECA the ICA has to accommodate much higher flows and does not branch. Our data confirmed the presence of elastic taper as the ICA was the stiffest of all three arteries. However, it is important to note that at peak-systole, the stress-induced stiffness of the CCA was only slightly smaller than that of the ICA.

To our knowledge, this is the first time the nonlinear stress-induced stiffening and tangent elastic moduli have been determined for all three segments of the carotid bifurcation. Compared to end-diastole levels, the CCA and ECA became more than 3-fold stiffer during peak-systole, while the ICA became more than 2.5-fold stiffer. The stress-induced stiffening of arteries serves as a defense mechanism against overstretch. The effect is due to the presence and interplay of collagen and elastin fibers in the arterial wall. When blood pressure is low, stiff collagen fibers wrinkle, and the weaker elastin largely determines the response of the vessel. When blood pressure increases, the artery is stretched and the collagen fibers straighten out, dramatically increasing the overall stress-induced stiffness of the tissue. There are contradicting reports on whether stress-induced stiffening occurs in the normal pressure range in vivo. Our data support the findings of Busse et al. ⁽¹²⁾ and Masson et al. ⁽²⁹⁾ who found that the CCA stiffens in normal pressure ranges, which contradicts the reports of Sugawara et al. ⁽¹³⁾ that pressure varies linearly with the diameter of the CCA. The observed nonlinearity has significant consequences as it demonstrates the need to evaluate the behavior of the artery continuously over the cardiac cycle instead of obtaining one measurement in systole and one in diastole. In addition, the differences in the mechanical properties of the CCA, ECA and ICA and their nonlinear behavior demonstrate that the assumption of homogeneous linear elasticity may not adequately represent the in vivo behavior of the carotid bifurcation. Thus, future mathematical models of the carotid artery should account for these considerations.

We did not find any significant correlations between the age of the patients and the diameter, wall thickness, or tangent elastic moduli of their arteries. Other reports ^{(30, 16)} demonstrated that the arteries get stiffer with age, but those reports evaluated healthy patients in a broad age range (20 to 80 years of age). Patients evaluated in this work were all older than 50 years and had significant comorbidities that may have diminished the effect of age on the mechanical properties of the arteries tested. This is in agreement with the results of Sommer et al. who reported no significant correlation between age and the mechanical properties of cadaveric arteries from a group of patients with atherosclerosis ⁽⁸⁾. We note that atherosclerotic disease has been shown to significantly increase the stiffness of the carotid artery ^{(3, 4)}.

Our data provide a systematic quantification of the nonlinear mechanical properties of the CCA, ICA and ECA in normotensive patients. These detailed in vivo data can be used to design better numerical models that more closely replicate the in vivo hemodynamic conditions of the carotid bifurcation. Such models would help delineate the association between the complex mechanical and flow phenomena present in the carotid bifurcation and the development of disease, such as atherosclerosis and restenosis, and could facilitate in silico development, testing and optimization of vascular and endovascular devices to treat disease in the carotid bifurcation.