Abstract
Statistical experimental designs provided by statistical analysis system (SAS) software were applied to optimize the fermentation medium composition for the production of atrazine-degrading Acinetobacter sp. DNS32 in shake-flask cultures. A “Plackett-Burman Design” was employed to evaluate the effects of different components in the medium. The concentrations of corn flour, soybean flour, and K2HPO4 were found to significantly influence Acinetobacter sp. DNS32 production. The steepest ascent method was employed to determine the optimal regions of these three significant factors. Then, these three factors were optimized using central composite design of “response surface methodology.” The optimized fermentation medium composition was composed as follows (g/L): corn flour 39.49, soybean flour 25.64, CaCO3 3, K2HPO4 3.27, MgSO4·7H2O 0.2, and NaCl 0.2. The predicted and verifiable values in the medium with optimized concentration of components in shake flasks experiments were 7.079 × 108 CFU/mL and 7.194 × 108 CFU/mL, respectively. The validated model can precisely predict the growth of atrazine-degraing bacterium, Acinetobacter sp. DNS32.
1. Introduction
Atrazine is a triazine herbicide used extensively in many parts of the world to control a broad variety of weeds, primarily on corn fields [1]. Atrazine and related triazines are moderately persistent in soil [2], depending largely on soil environmental conditions [3, 4]. So atrazine has been classified by regulatory agencies as one of the major target anthropogenic pollutants requiring immediate attention and effective development of methods for decontamination of contaminated matrices [5–7]. Microbial metabolism has long been regarded as the most important mechanism of atrazine degradation in soil [8, 9]. Microbial bioaugmentation, an addition of sufficient contaminant degrading microorganisms, can be used to achieve more rapid atrazine degradation [10]. Previous studies have reported the identification, characterization of atrazine-degrading microbial strains [11–13], and the effect of cell immobilization for atrazine degradation [14]. Yet, only few studies have looked at fermentation of atrazine-degrading microbial strains. This study, therefore, reports the optimization of fermentation medium for the production of an atrazine-degrading bacterial strain and is the first applied technology to an atrazine pollution remediation study. In order to reduce the fermentation cost, corn and soybean flour, two types of agro-industrial products, were employed as alternative substrates in this study. The other medium components were composed of CaCO3, K2HPO4, MgSO4·7H2O, and NaCl. The atrazine-degrading bacterium, Acinetobacter sp. DNS32, used in the present investigation is isolated from fresh soil. The bacterium used atrazine as sole nitrogen source (the initial concentration of atrazine is 100 mg/L), and its atrazine degradation rate reached 96.86% after 3 d. The bacterial strain in the soil samples had 20 mg/Kg atrazinend the degradation rates of the atrazine in those soil samples were above 99% within 20 d.
Plackett-Burman Design provides a fast and an effective way to screen the important factors among several variables, thereby, saving time and not only maintaining but also convincing information from each parameter [15]. Response surface methodology (RSM) is a collection of mathematical and statistical techniques that are useful for modeling and analyzing problems which involved a response of interest influenced by several variables and the objective is to optimize this response [16, 17]. Plackett-Burman Design and RSM have been successfully used to optimize some bioprocesses using the software of design expert [18–20]. Although the software provided by design expert is good, its module function is less powerful than the statistical software provided statistical analysis system (SAS). Moreover, few studies have employed SAS software. Thus, in this study, experimental designs provided by SAS software were used for the optimization of fermentation medium for atrazine-degrading bacterium, Acinetobacter sp. DNS32.
The aim of this work was to define the optimized composition of fermentation medium for atrazine-degrading bacterium, by experimental design components (i.e., Plackett-Burman Design and RSM) of SAS software.
2. Materials and Methods
2.1. Bacterial Strain
From the corn-planted soil (0–10 cm) under long-term applying atrazine in Heilongjiang Province, one bacterial strain named DNS32 obtained by enrichment culture has been identified according to the morphology and comparison of 16SrDNA gene sequence (Acinetobacter sp.TM1_6). The bacterial isolate was then named Acinetobacter sp. DNS32. The stock culture was maintained on agar slant containing (g/L): glucose 3, K2HPO4 1.6, KH2PO4 0.4, MgSO4·7H2O 0.2, NaCl 0.1, atrazine 0.1, and agar 20, cultured for four days at 30°C, then stored at 4°C and subcultured every month.
2.2. Fermentation Medium and Flask Culture
The components of fermentation medium were: corn flour, soybean flour, CaCO3, K2HPO4, MgSO4·7H2O, and NaCl. The concentrations of components were adjusted according to the experimental design. For the production of the inoculum, one loopful of the bacterial culture was transferred from a slant culture into an Erlenmeyer flask (50 mL) containing 20 mL LB (Luria-Bertani) medium. The pH of the medium was adjusted to 7.0. The flask was incubated in a shaking incubator at 30°C and 130 rpm for 12 h. Subculture was conducted by inoculating 100 μL overnight (~12 h) bacterial culture in a 150 mL Erlenmeyer flask containing 50 mL of the medium each. The fermentation cultures were grown at 30°C on a rotary shaker incubator at 130 rpm for 24 h, and the initial pH was adjusted to 7.0 with 1 mol/L NaOH.
2.3. Experimental Methods and Analysis
2.3.1. Plackett-Burman Design
The importance of 6 components of fermentation culture medium was investigated using a Plackett-Burman Design. Plackett-Burman Design was introduced in this study as a first optimization step to identify the factors that have significant effects on the strain DNS32 production. Hadamard matrix was employed in Plackett-Burman Design. Based on Plackett-Burman factorial design, each variable was examined in two levels: −1 for low level and +1 for high level [21]. This design was used to screen and evaluate the important factor(s) that influence the response of 6 assigned factors and one dummy factor to estimate test error in 8 experimental designs. All experiments were performed in duplicate and the average of the biomass of atrazine-degrading bacterium was taken as the response. The factors included in the screening experiment and their settings are given in Table 1.
Table 1.
Two levels of the factors used in Plackett-Burman Design.
| Factor | Low level (−1) | High level (+1) |
|---|---|---|
| Corn flour concentration (g/L) (X1) | 40.000 | 50.000 |
| Soybean flour concentration (g/L) (X2) | 24.000 | 34.000 |
| CaCO3 concentration (g/L) (X3) | 3.000 | 5.000 |
| K2HPO4 concentration (g/L) (X4) | 2.000 | 4.000 |
| MgSO4·7H2O concentration (g/L) (X5) | 0.200 | 0.400 |
| NaCl concentration (g/L) (X6) |
0.200 |
0.400 |
| Dummy variable (X7) | — | — |
2.3.2. Path of Steepest Ascent
The direction of steepest ascent is the direction in which the response increased most rapidly. The direction of steepest ascent was parallel to the contour line of response curve of (1), and the low level of Plackett-Burman Design was identified as the center point of steepest ascent path. Experiments were performed along the steepest ascent path until the response did not increase anymore. This point would be near to the optimal point and could be used as center point to optimize [22].
2.3.3. Central Composite Design
A central composite design (CCD) was employed to optimize the three most significant factors (corn flour, soybean flour, and K2HPO4) screened by Plackett-Burman Design. The CCD is one of the most commonly used response surface designs for fitting second-order models. A central composite design consists of F factorial points, 2k axial points (±α), and nc center points. The factorial portion is used for fitting all linear and interaction terms. The axial points provide additional levels of the factor for purposes of estimation of the quadratic terms [23]. According to the central composite design, three independent factors, namely, corn flour concentration (X1), soybean flour concentration (X2), and K2HPO4 concentration (X3) were studied at five different levels (coded: −1.682, −1, 0, +1, and +1.682) with six repetitions at the central point and two replicates at axial and factorial points (Table 2).
Table 2.
Coded values for each factor of the central composite design.
| Coded values of the experimental factors | X 1: corn flour concentration (g/L) | X 2: soybean flour concentration (g/L) | X 3: K2HPO4 concentration (g/L) |
|---|---|---|---|
| −1.682 | 23.180 | 7.180 | 1.318 |
| −1 | 30.000 | 14.000 | 2.000 |
| 0 | 40.000 | 24.000 | 3.000 |
| +1 | 50.000 | 34.000 | 4.000 |
| +1.682 | 56.800 | 40.800 | 4.680 |
2.3.4. Statistical Analysis
SAS release 8.01 for Windows (Institute Incorporation, Cary, NC, USA) was employed for the experimental designs and regression analysis of the experimental results.
2.4. Analytical Method
The biomass production of the bacterium was determined by measuring the total biomass using the method of Miles and Misra [24]. Decimal serial dilutions of culture solution were prepared using sterile water. 100 μL were dropped onto 3-4 d agar plates and then incubated at 30°C for 2-3 d. The agar plate composition was as same as in stock slant. The biomass of atrazine-degrading Acinetobacter sp. DNS32 was calculated as log10 colony forming units per mL. Dilutions with less than 10 or more than 130 colonies were discarded [25].
3. Results and Discussion
3.1. Plackett-Burman Design
Plackett-Burman Design was used as a screening method to determine which of the 6 components of the fermentation medium significantly affect the biomass production of the bacterium. The experimental results with the Plackett-Burman Design are shown in Table 3. These are tested simultaneously by shifting factors from a low value (−1) to a high value (+1). The experimental results were interpreted based on the partition of the overall effect of all the factors to the response into individual factor effect. This partition has been made statistically. When the value of the concentration effect, E(Xi), of the tested variable is positive, the conclusion is that the influence of the concerning variable is greater at a high concentration tested, and when negative, this means that the influence of the given variable is greater at a low concentration [26]. The variable with confidence level above 90% is considered a significant factor. Regarding to the effects of the variables, it is apparent from Table 4 that the influence of corn flour concentration, soybean flour concentration, CaCO3 concentration, MgSO4·7H2O concentration, and NaCl concentration is greater on the biomass of atrazine degrading strain DNS32 at a low concentration and that K2HPO4 concentration has a greater effect at a high concentration. The confidence levels of concentrations of CaCO3, MgSO4·7H2O, and NaCl were less than 90% and hence was considered to be insignificant. Thus, low concentrations of these variables were employed in the optimized fermentation culture medium. Only the concentrations of corn flour, soybean flour, and K2HPO4 had confidence levels greater than 90% and were considered to significantly influence the biomass production of the bacterium. The concentrations of corn flour, soybean flour, and K2HPO4 were selected for further optimization to achieve a maximum response.
Table 3.
Experimental design and results of the Plackett-Burman Design.
| Run | X 1 | X 2 | X 3 | X 4 | X 5 | X 6 | X 7 | Biomass (log10 CFU/mL) |
|---|---|---|---|---|---|---|---|---|
| 1 | +1 | +1 | +1 | −1 | +1 | −1 | −1 | 8.561 |
| 2 | −1 | +1 | +1 | +1 | −1 | +1 | −1 | 8.781 |
| 3 | −1 | −1 | +1 | +1 | +1 | −1 | +1 | 8.895 |
| 4 | +1 | −1 | −1 | +1 | +1 | +1 | −1 | 8.722 |
| 5 | −1 | +1 | −1 | −1 | +1 | +1 | +1 | 8.683 |
| 6 | +1 | −1 | +1 | −1 | −1 | +1 | +1 | 8.627 |
| 7 | +1 | +1 | −1 | +1 | −1 | −1 | +1 | 8.690 |
| 8 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | 8.868 |
Table 4.
The effect of variables in the Plackett-Burman Design and associated statistical tests.
| Factor | E (Xi) | t-value | P > |t| |
|---|---|---|---|
| Corn flour concentration (g/L) (X1) | −0.0783 | −16.963 | 0.0375 |
| Soybean flour concentration(g/L) (X2) | −0.0486 | −10.800 | 0.0588 |
| CaCO3 concentration (g/L) (X3) | −0.0122 | −2.634 | 0.231 |
| K2HPO4 concentration (g/L) (X4) | 0.0438 | 9.485 | 0.0669 |
| MgSO4·7H2O concentration (g/L) (X5) | −0.0130 | −2.824 | 0.217 |
| NaCl concentration (g/L) (X6) | −0.0250 | −5.405 | 0.116 |
3.2. The Path of Steepest Ascent
Based on the results of the Plackett-Burman Design, it could be known that concentrations of corn flour (X1), soybean flour (X2), and K2HPO4 (X4) were significant factors. E(X1) and E(X2)were positive, while E(X4) was negative; this means that increasing X1 and X2 while decreasing X4 had positive effect on the biomass of the bacterium. Experimental design of the steepest ascent and corresponding results showed that the biomass of the bacterium had a growing trend before rising to a maximum of the run four and then declined. The other factors were fixed at low level (−1). It suggested that this point was near the region of maximum response. So this point was chosen for further optimization.
3.3. Screened Medium Constituents Optimization with Central Composite Design
Central composite design (CCD) was employed to determine the optimal levels of the three selected factors. The responses of biomass production of the bacterium as a function of the concentrations of corn flour, soybean flour, and K2HPO4 were evaluated. The respective low and high levels with the coded levels for the factors are defined in Table 2. The other factors were fixed at low level (−1). In total, 20 experimental runs with different combinations of three factors were performed and their responses are presented in Figure 1. Based on regression analysis of the experimental results, the following second-order polynomial equation was written:
| (1) |
where Y was the predicted response, X1, X2, and X3 were coded values of corn flour, soybean flour, and K2HPO4 concentrations,respectively.
Figure 1.
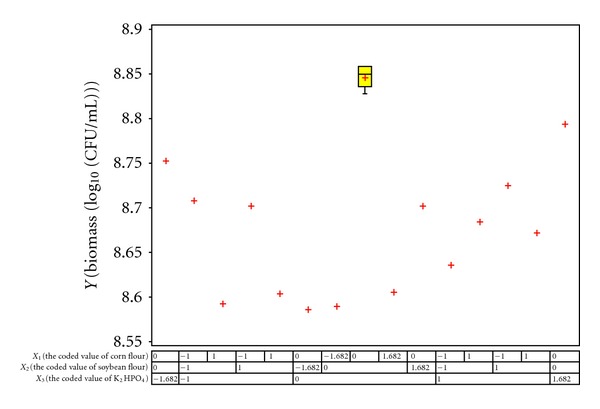
Boxplot of results of the central composite design.
The statistical significance of (1) was evaluated by F-test, and the analysis of variance (ANOVA) for response surface quadratic model is summarized in Table 5. The analysis of variance performed on the model demonstrates that the model is statistically valid (F = 25.598, and P < 0.0001). The regression equation obtained after ANOVA indicated a R2 value of 95.84% which was consistence with the adjusted R2 of 92.1%. Normally, the closer R2 is to 1, the stronger the model and the better it predicts the response [27]. This ensured a satisfactory adjustment of the theoretical responses to the experimental data by this model. The coefficient of variation (CV) indicates the degree of precision with which the treatments were compared [28]. A lower value of CV (0.324) showed a better precision and reliability of the experiments conducted [29]. Both linear and quadratic terms were significant at the 5% level. Consequently, the model equation (1) was selected in this optimization work.
Table 5.
ANOVA for the second-order polynomial model.
| Source | Degree of freedom | Sum of squares | Mean square | F-value | P > F |
|---|---|---|---|---|---|
| Linear | 3 | 0.0106 | — | 4.420 | 0.0318 |
| Quadratic | 3 | 0.167 | — | 69.430 | <0.0001 |
| Cross product | 3 | 0.00706 | — | 2.940 | 0.0854 |
| Total model | 9 | 0.184 | 0.0205 | 25.598 | <0.0001 |
| Total error | 10 | 0.008 | 0.0008 | — | — |
R 2 = 95.8%; Adj. R2 = 92.1%; CV = 0.324.
The significance of the regression coefficients was tested by a t-test. The Student's t-distribution, the corresponding P value, and the parameter estimate are presented in Table 6. The P values are employed to check the significance of each of the coefficients which, in turn, are necessary to understand the pattern of the mutual interactions between the best variables. The smaller the P values, the bigger is the significance of the corresponding coefficient [30]. Table 6 shows that among the independent factors, linear term of X2 (soybean flour concentration) had a significant effect on the biomass production of the bacterium. The positive coefficient of X2 shows a linear effect to increase biomass. The quadratic term of the three variables and the interaction between X1 and X3 also had a significant effect. Notably, X12 and X22 (P < 0.0001), as part of the quadratic term, were considerably higher than other effects demonstrating that these are the most significant factors affecting biomass production of the bacterium.
Table 6.
Effect estimates for the second-order polynomial model.
| Model term | Degree of freedom | Estimate | Standard error | t-value | P > |t| |
|---|---|---|---|---|---|
| Intercept | 1 | 8.846 | 0.0115 | 766.830 | <0.0001a |
| X 1 | 1 | −0.0140 | 0.00765 | −1.831 | 0.0970 |
| X 2 | 1 | 0.0202 | 0.00765 | 2.640 | 0.0247a |
| X 3 | 1 | 0.0131 | 0.00765 | 1.714 | 0.1172 |
| X 1 2 | 1 | −0.0870 | 0.00745 | −11.679 | <0.0001a |
| X 2 2 | 1 | −0.0706 | 0.00745 | −9.470 | <0.0001a |
| X 3 2 | 1 | −0.0250 | 0.00745 | −3.357 | 0.0073a |
| X 1 X 2 | 1 | −0.0107 | 0.0100 | −1.066 | 0.3115 |
| X 1 X 3 | 1 | 0.0262 | 0.0100 | 2.624 | 0.0254a |
| X 2 X 3 | 1 | 0.00893 | 0.0100 | 0.893 | 0.3929 |
aSignificant at 5% level (P < 0.05).
The regression model can be applied to predict future observations on the response corresponding to particular values of the regression factors. Actual values, depicted in Figure 2, are the observed response data for a run arranged by central composite design, and the predicted values assess the models and are generated by using the approximating functions. The value of correlation coefficient of R2 was evaluated as 0.9584. This proves the predicted responses from the second-order polynomial equation are consistent with the observed ones.
Figure 2.
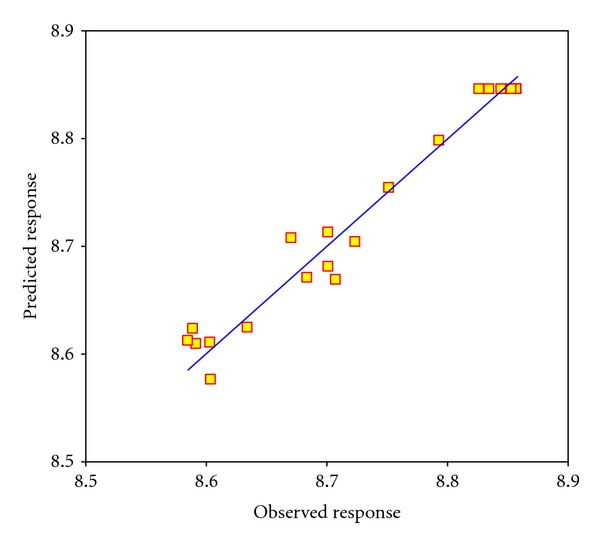
Observed responses predicted responses under the central composite design.
The quadratic polynomial equations to experimental data (1) can be described by the response surface plots that explain the interactions of medium components and the optimum concentration of each component required for the biomass of atrazine degrading strain DNS32 as a function of two factors at a time, maintaining the other factors fixed at level zero. These respective contour plots (Figures 3, 4, and 5) showed a visual interpretation of the interaction between two variables and facilitate the location of optimum experimental conditions. The optimal values of the selected factors in their respective coded values were X1 = −0.0506, X2 = 0.164, and X3 = 0.265. At these values, the actual concentrations of corn flour, soybean flour, and K2HPO4 were 39.494, 25.638, and 3.265 g/L, respectively. The maximum predicted value of the common logarithm of biomass obtained was 8.850 (Biomass of atrazine degrading strain DNS32 is 7.079 × 108 colony forming unit (CFU)/mL).
Figure 3.
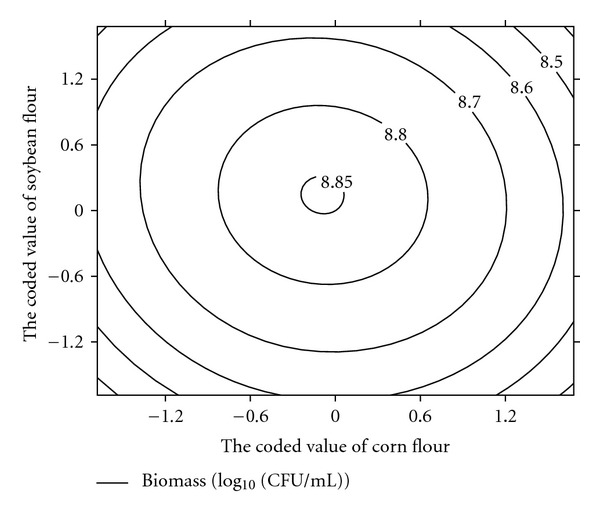
Contour plot for DNS32 strain production as a function of X1 (corn flour concentration) and X2 (soybean concentration) when the coded value of X3 (K2HPO4 flour concentration) was fixed at 0.
Figure 4.
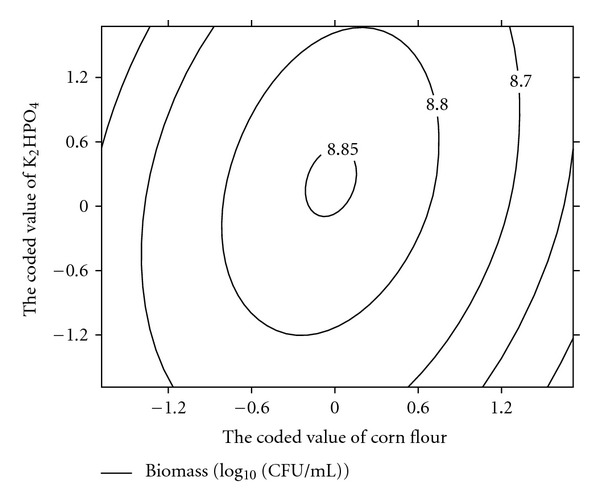
Contour plot for DNS32 strain production as a function of X1 (corn flour concentration) and X3 (K2HPO4 flour concentration) when the coded value of X2 (soybean concentration) was fixed at 0.
Figure 5.
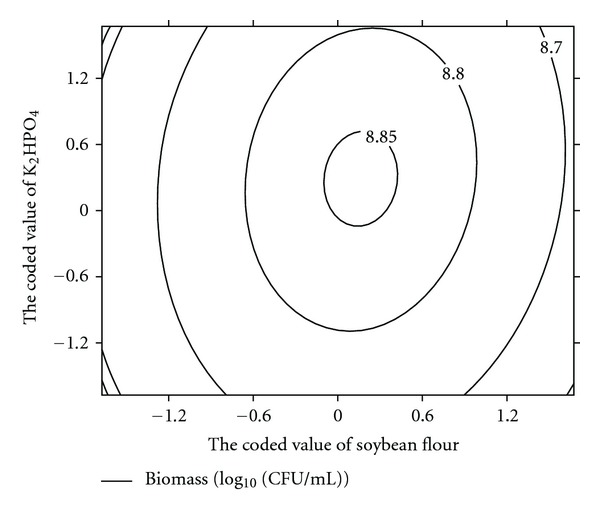
Contour plot for DNS32 strain production as a function of X2 (soybean concentration) and X3 (K2HPO4 flour concentration) when the coded value of X1 (corn flour concentration) was fixed at 0.
To check the model adequacy for predicting the maximum response, triplicate sets of experiments under the optimized medium composition were performed. The mean experimental value of the common logarithm of biomass was 8.857 (Biomass of the bacterium is 7.194 × 108 CFU/mL), this value excellently matches the predicted value. This behavior shows a good predicting pattern of the model to the experimental data, confirming the validity and adequacy of the models.
4. Conclusions
Statistical optimization of fermentation medium components for the production of atrazine-degrading bacterium, Acinetobacter sp. DNS32, had been proved to be a valuable tool for the strain production. These experimental designs can convert the process variable correlations into mathematical model that predicts where the response is likely to be identified. It can be concluded that the optimized medium composition was (g/L): corn flour 39.494, soybean flour 25.638, CaCO3 3, K2HPO4 3.265, MgSO4·7H2O 0.2, and NaCl 0.2. The predicted and verifiable values were 7.079 × 108 and 7.194 × 108 CFU/mL, respectively. The model validation proved a good consistence between the experimental results and predicted response.
Acknowledgments
This research was supported by research Grants of Program for New Century Excellent Talents in University (NCET-10-0145), New Century Excellent Talents in Heilongjiang Provincial University (1155-NCET-006), Science Foundation for Distinguished Young Scholars of Heilongjiang Province (JC201006), National Natural Science Foundation of China (30970525) to Y. Zhang, Chang Jiang Scholar Candidates Program for Provincial Universities in Heilongjiang (CSCP), National Scientific and Technological Supporting Project, China (2011BAD04B02) and a research Grant of (GRF 447610) from Research Grant Council, Hong Kong SAR Government to P. K. Wong.
References
- 1.Solomon KR, Baker DB, Richards RP, et al. Ecological risk assessment of atrazine in North American surface waters. Environmental Toxicology and Chemistry. 1996;15(1):31–76. doi: 10.1002/etc.2050. [DOI] [PubMed] [Google Scholar]
- 2.Pointing SB. Feasibility of bioremediation by white-rot fungi. Applied Microbiology and Biotechnology. 2001;57(1-2):20–33. doi: 10.1007/s002530100745. [DOI] [PubMed] [Google Scholar]
- 3.Topp E. A comparison of three atrazine-degrading bacteria for soil bioremediation. Biology and Fertility of Soils. 2001;33(6):529–534. [Google Scholar]
- 4.Rhine ED, Fuhrmann JJ, Radosevich M. Microbial community responses to atrazine exposure and nutrient availability: linking degradation capacity to community structure. Microbial Ecology. 2003;46(2):145–160. doi: 10.1007/s00248-002-1048-6. [DOI] [PubMed] [Google Scholar]
- 5.Wackett LP, Sadowsky MJ, Martinez B, Shapir N. Biodegradation of atrazine and related s-triazine compounds: from enzymes to field studies. Applied Microbiology and Biotechnology. 2002;58(1):39–45. doi: 10.1007/s00253-001-0862-y. [DOI] [PubMed] [Google Scholar]
- 6.Ghosh PK, Philip L. Environmental significance of atrazine in aqueous system and its removal by biological process: an overview. Global NEST Journal. 2006;8(2):159–178. [Google Scholar]
- 7.Pandey J, Chauhan A, Jain RK. Integrative approaches for assessing the ecological sustainability of in situ bioremediation. FEMS Microbiology Reviews. 2009;33(2):324–375. doi: 10.1111/j.1574-6976.2008.00133.x. [DOI] [PubMed] [Google Scholar]
- 8.Gavrilescu M. Fate of pesticides in the environment and its bioremediation. Engineering in Life Sciences. 2005;5(6):497–526. [Google Scholar]
- 9.Bastos AC, Magan N. Trametes versicolor: potential for atrazine bioremediation in calcareous clay soil, under low water availability conditions. International Biodeterioration & Biodegradation. 2009;63(4):389–394. [Google Scholar]
- 10.Siripattanakul S, Wirojanagud W, McEvoy JM, Casey FXM, Khan E. Atrazine removal in agricultural infiltrate by bioaugmented polyvinyl alcohol immobilized and free Agrobacterium radiobacter J14a: a sand column study. Chemosphere. 2009;74(2):308–313. doi: 10.1016/j.chemosphere.2008.09.005. [DOI] [PubMed] [Google Scholar]
- 11.Rousseaux S, Hartmann A, Soulas G. Isolation and characterisation of new Gram-negative and Gram-positive atrazine degrading bacteria from different French soils. FEMS Microbiology Ecology. 2001;36(2-3):211–222. doi: 10.1111/j.1574-6941.2001.tb00842.x. [DOI] [PubMed] [Google Scholar]
- 12.Han P, Hong Q, He LJ, Yan QX, Li SP. Isolation, identification and characterization of an atrazine-degrading bacteria ADH-2. Agriculture Environment Science. 2009;28(2):406–410. [Google Scholar]
- 13.Yan CF, Lou X, Hong Q, Li SP. Isolation, identification and characterization of an atrazine-degrading strain. Microbiology China. 2011;38(4):493–497. [Google Scholar]
- 14.Siripattanakul S, Wirojanagud W, Khan E, McEvoy J. Effect of cell-to-matrix ratio in polyvinyl alcohol immobilized pure and mixed cultures on atrazine degradation. Water, Air, & Soil Pollution. 2008;8(3-4):257–266. [Google Scholar]
- 15.Abdel-Fattah YR, Saeed HM, Gohar YM, El-Baz MA. Improved production of Pseudomonas aeruginosa uricase by optimization of process parameters through statistical experimental designs. Process Biochemistry. 2005;40(5):1707–1714. [Google Scholar]
- 16.Soni P, Singh M, Kamble AL, Banerjee UC. Response surface optimization of the critical medium components for carbonyl reductase production by Candida viswanathii MTCC 5158. Bioresource Technology. 2007;98(4):829–833. doi: 10.1016/j.biortech.2006.03.008. [DOI] [PubMed] [Google Scholar]
- 17.Montgomery DC. Design and Analysis of Experiments. 7th edition. New York, NY, USA: John Wiley & Sons; 2008. [Google Scholar]
- 18.Mohana S, Shrivastava S, Divecha J, Madamwar D. Response surface methodology for optimization of medium for decolorization of textile dye Direct Black 22 by a novel bacterial consortium. Bioresource Technology. 2008;99(3):562–569. doi: 10.1016/j.biortech.2006.12.033. [DOI] [PubMed] [Google Scholar]
- 19.Ferreira S, Duarte AP, Ribeiro MHL, Queiroz JA, Domingues FC. Response surface optimization of enzymatic hydrolysis of Cistus ladanifer and Cytisus striatus for bioethanol production. Biochemical Engineering Journal. 2009;45(3):192–200. [Google Scholar]
- 20.Zhou JY, Yu XJ, Ding C, et al. Optimization of phenol degradation by Candida tropicalis Z-04 using Plackett-Burman design and response surface methodology. Journal of Environmental Sciences. 2011;23(1):22–30. doi: 10.1016/s1001-0742(10)60369-5. [DOI] [PubMed] [Google Scholar]
- 21.Plackett RL, Burman JP. The design of optimum multifactorial experiments. Biometrika. 1946;33(4):305–325. [Google Scholar]
- 22.Tang XJ, He GQ, Chen QH, Zhang XY, Ali MAM. Medium optimization for the production of thermal stable β-glucanase by Bacillus subtilis ZJF-1A5 using response surface methodology. Bioresource Technology. 2004;93(2):175–181. doi: 10.1016/j.biortech.2003.10.013. [DOI] [PubMed] [Google Scholar]
- 23.Robinson TJ, Wulff SS. Response surface approaches to robust parameter design. In: Khuri AI, editor. Response Surface Methodology and Related Topics. Singapore: World Scientific; 2006. pp. 123–157. [Google Scholar]
- 24.Collins CH, Lyne PM. Microbiological Methods. 5th edition. London, UK: Butterworths; 1984. [Google Scholar]
- 25.Kedia G, Vázquez JA, Pandiella SS. Fermentability of whole oat flour, PeriTec flour and bran by Lactobacillus plantarum. Journal of Food Engineering. 2008;89(2):246–249. [Google Scholar]
- 26.Xu CP, Kim SW, Hwang HJ, Yun JW. Application of statistically based experimental designs for the optimization of exo-polysaccharide production by Cordyceps militaris NG3. Biotechnology and Applied Biochemistry. 2002;36(2):127–131. doi: 10.1042/ba20020032. [DOI] [PubMed] [Google Scholar]
- 27.Mao J, Kwak IS, Sathishkumar M, Sneha K, Yun YS. Preparation of PEI-coated bacterial biosorbent in water solution: optimization of manufacturing conditions using response surface methodology. Bioresource Technology. 2011;102(2):1462–1467. doi: 10.1016/j.biortech.2010.09.088. [DOI] [PubMed] [Google Scholar]
- 28.Box GEP, Hunter WG, Hunter JS. Statistics For Experimenters: An Introduction To Design, Data Analysis and Model Building. New York, NY, USA: John Wiley & Sons; 1978. [Google Scholar]
- 29.Li Y, Cui FJ, Liu ZQ, Xu YY, Zhao H. Improvement of xylanase production by Penicillium oxalicum ZH-30 using response surface methodology. Enzyme and Microbial Technology. 2007;40(5):1381–1388. [Google Scholar]
- 30.Liu JZ, Weng LP, Zhang QL, Xu H, Ji LN. Optimization of glucose oxidase production by Aspergillus niger in a benchtop bioreactor using response surface methodology. World Journal of Microbiology and Biotechnology. 2003;19(3):317–323. [Google Scholar]


