Actinobacillus succinogenes ATCC 55618 Fermentation Medium Optimization for the Production of Succinic Acid by Response Surface Methodology

Abstract

As a potential intermediary feedstock, succinic acid takes an important place in bulk chemical productions. For the first time, a method combining Plackett-Burman design (PBD), steepest ascent method (SA), and Box-Behnken design (BBD) was developed to optimize Actinobacillus succinogenes ATCC 55618 fermentation medium. First, glucose, yeast extract, and MgCO₃ were identified to be key medium components by PBD. Second, preliminary optimization was run by SA method to access the optimal region of the key medium components. Finally, the responses, that is, the production of succinic acid, were optimized simultaneously by using BBD, and the optimal concentration was located to be 84.6 g L⁻¹ of glucose, 14.5 g L⁻¹ of yeast extract, and 64.7 g L⁻¹ of MgCO₃. Verification experiment indicated that the maximal succinic acid production of 52.7 ± 0.8 g L⁻¹ was obtained under the identified optimal conditions. The result agreed with the predicted value well. Compared with that of the basic medium, the production of succinic acid and yield of succinic acid against glucose were enhanced by 67.3% and 111.1%, respectively. The results obtained in this study may be useful for the industrial commercial production of succinic acid.

1. Introduction

Succinic acid is a member of the four-carbon dicarboxylic acid family in tricarboxylic acid cycle (TCA) and has a wide range of applications in the fields of surfactants, green solvents, and pharmaceutical intermediates as an important four-carbon intermediate compound [1]. Succinic acid is classified as the most promising chemical among 12 biobased chemicals by the U.S. Department of Energy [2]. Succinic acid has been conventionally produced from fossil raw materials for more than a century, which can lead to high cost, feedstock exhaustion, and environment pollution [3, 4]. Recent studies suggest that the production of succinic acid by microbe fermentation has the potential to solve the aforementioned problems [5].

As the endproduct of energy metabolism, succinic acid can be produced by many anaerobic microbes, such as Actinobacillus succinogenes, Anaerobiospirillum succiniciproducens, Mannheimia succiniciproducens, and Escherichia coli especially A. succinogenes ATCC 55618, which is a facultative anaerobe isolated from the bovine rumen [6]. It could produce higher concentration succinic acid as a major endproduct than other strains without gene reconstruction and glucose feeding [7]. However, to obtain a high production of succinic acid (i.e., more than 45 g L⁻¹), the fermentation medium compositions were often complicated with the addition of high concentration of glucose and ten kinds of slight vitamins [8–10]. According to the aforementioned reports, about twenty kinds of components were added into the fermentation medium for the succinic acid production, which led to high cost and complex operation. It must be paid attention that the complicated medium is not the assurance of high production of succinic acid [11–13]. So the optimization of fermentation medium of A. succinogenes ATCC 55618 is essential.

Since nine components existed in the fermentation medium (i.e., glucose, yeast extract (YE), corn steep liquor (CSL), KH₂PO₄, K₂HPO₄, NaCl, MgCl₂, CaCl₂, and MgCO₃), a great number of experiments should be simultaneously run, and the possible interactions between these components were also needed to be studied. For fermentation medium optimization, Plackett-Burman design (PBD) was a good choice in rapid screening multifactors to find the most significant independent factors [14]. Moreover, to optimize the concentration of the important factors, statistical methods have been done by using response surface methodology (RSM), in which several factors were simultaneously varied [15]. Compared with the one-factor-at-a-time method, statistical experimental design has the advantages of reducing experiment numbers and improving statistical interaction analysis [16–18]. For the reasons above, we proposed the optimization method including the following steps: (1) using a two-level PBD to identify the key medium components and their experimental levels for further optimization, (2) applying the path of steepest ascent (SA) to move rapidly towards the neighborhood of the optimum response, and (3) employing a Box-Behnken design (BBD) to develop mathematical models to estimate the relationships between the response (i.e., the succinic acid production) and the key components.

2. Materials and Methods

2.1. Maintenance and Preculture of A. succinogenes ATCC 55618

The strain of A. succinogenes ATCC 55618, purchased from American Type Culture Collection (ATCC), was maintained in 20% glycerol at −70°C.

The plate was inoculated with the strain maintained at −70°C and incubated at 37°C for 2 days. Preculture medium consisted of the following components (g L⁻¹): tryptone 17; soya peptone 3; glucose 2.5; NaCl 5; K₂HPO₄ 2.5. The culture pH was adjusted to 7.5. For the first preculture, 50 mL of medium was prepared in a 250-mL anaerobic bottle, and a colony from a plate culture was inoculated, and then incubated for 12 hours at 37°C on a rotary shaker at 120 rpm. For the second preculture, 47.5 mL of medium was prepared in a 250-mL anaerobic bottle, inoculated with 2.5 mL of the first preculture broth, and incubated for 12 hours at 37°C on a rotary shaker at 120 rpm.

2.2. Fermentation Process

Basic fermentation medium with an initial pH of 7.0 was composed of (g L⁻¹): glucose 107; yeast extract (YE) 16; corn steep liquor (CSL) 12; KH₂PO₄ 3; K₂HPO₄ 1.5; NaCl 1; MgCl₂ 0.3; CaCl₂ 0.3; MgCO₃ 40. The fermentation medium was inoculated with 2.5 mL of the second preculture broth in 47.5 mL of medium in a 250-mL anaerobic bottle with CO₂ as the gas phase. The fermentation was incubated at 37°C on a rotary shaker at 180 rpm. The dynamic profile of the succinic acid biosynthesis of A. succinogenes was monitored during the submerged fermentation process. Three flasks were taken each time for sampling. Each data point was expressed by an average with an error bar (i.e., standard error from three independent samples).

2.3. Plackett-Burman Design (PBD)

The purpose of Plackett-Burman design (PBD) was to identify the key medium components for the succinic acid production. Table 1 shows the PBD used in this study [19]. Two dummy variables, whose levels did not change in the design, were introduced to estimate the population standard error. The first order was used to fit data from PBD as follows:

$$\begin{array}{c}Y={\beta }_{\mathrm{0}}+\sum _{}^{}{\beta }_i{x}_i,\end{array}$$ (1)

where Y is the predicted response, β₀ and β_i are constant coefficients, and x_i is the coded independent factors. Analysis for the PBD was carried out as follows.

Table 1.

The Plackett-Burman design experiment design matrix^a and experimental results.

Runs	Variables (g L−1)									OD660	Succinic acid production (g L−1)
	Glucose	YEb	CSLc	K2HPO4	KH2PO4	NaCl	MgCl2	CaCl2	MgCO3
1	80.0	15.0	15.0	1.5	3.0	1.5	0.3	0.6	40.0	7.9 ± 1.6 d	32.5 ± 1.0
2	50.0	15.0	15.0	1.5	3.0	1.0	0.3	0.3	60.0	4.2 ± 0.4	32.2 ± 1.3
3	80.0	10.0	15.0	1.5	1.5	1.0	0.6	0.6	60.0	6.2 ± 0.3	51.9 ± 4.8
4	80.0	15.0	10.0	3.0	1.5	1.0	0.3	0.6	60.0	9.3 ± 0.4	50.2 ± 3.1
5	50.0	10.0	10.0	3.0	3.0	1.5	0.3	0.6	60.0	2.6 ± 0.6	36.2 ± 0.6
6	80.0	10.0	10.0	1.5	3.0	1.5	0.6	0.3	60.0	6.7 ± 0.1	50.4 ± 1.5
7	50.0	10.0	10.0	1.5	1.5	1.0	0.3	0.3	40.0	5.9 ± 0.3	36.0 ± 0.2
8	50.0	15.0	15.0	3.0	1.5	1.5	0.6	0.3	60.0	2.9 ± 0.5	33.2 ± 1.2
9	50.0	10.0	15.0	3.0	3.0	1.0	0.6	0.6	40.0	5.3 ± 0.3	35.4 ± 1.2
10	80.0	15.0	10.0	3.0	3.0	1.0	0.6	0.3	40.0	9.1 ± 0.5	36.3 ± 0.6
11	50.0	15.0	10.0	1.5	1.5	1.5	0.6	0.6	40.0	10.0 ± 0.6	36.5 ± 2.7
12	80.0	10.0	15.0	3.0	1.5	1.5	0.3	0.3	40.0	6.3 ± 0.6	38.3 ± 0.7

^aThe two dummy was not shown in Table 1.

^bYE: yeast extract.

^cCSL: corn steep liquor.

^dStandard error was calculated from three independent samples.

First, the effect of all variables, including dummies, was calculated as follows:

$$\begin{array}{c}{E}_{vi}=\frac{\sum R_{vi(+)}-\sum R_{vi(-)}}{N/\mathrm{2}},\end{array}$$ (2)

where E_vi is the effect of variable i; R_vi(+) and R_vi(−) represent the response parameter (i.e., the succinic acid production) of an assembly in the screening design which contains the high and low levels of variable i, respectively; N is the number of assemblies (in this study, N = 12).

After determining the effect of each variable, the standard deviation (SD) of dummies, which serves as the population standard deviation in the Student's t-test as follows was calculated:

$$\begin{array}{c}\text{SD}=\sqrt{\frac{\sum {\left(E_d\right)}^{\mathrm{2}}}{n}},\end{array}$$ (3)

where E_d is the effect of dummy variables; n is the number of dummy variables (in this study, n = 2).

Finally, a Student's t-test was performed to identify the significant t factors as follows:

$$\begin{array}{c}{t}_{vi}=\frac{E_{vi}}{\text{SD}}.\end{array}$$ (4)

The variable which has no effect will give a t-value of 0. The larger the absolute value of the t-value, the variable is more significant.

2.4. Steepest Ascent (SA)

The method of steepest ascent (SA) design was used to move rapidly towards the neighborhood of the optimum response. Table 2 shows the SA used in this study. The experiments were adopted to determine a suitable direction by increasing or decreasing the concentrations of variables according to the results of PBD [20].

Table 2.

Experiment design and results of the steepest ascent path.

Runs	Glucose (g L−1)	Yeast extract (g L−1)	MgCO3 (g L−1)	OD660	Succinic acid production (g L−1)
1	80	10	60	6.1 ± 0.2a	48.4 ± 1.3
2	85	7	65	3.7 ± 0.7	41.7 ± 2.6
3	90	4	70	0.6 ± 0.0	36.4 ± 2.4
4	95	1	75	0.2 ± 0.0	22.1 ± 5.3
5	100	0	80	0.1 ± 0.0	4.2 ± 1.1

^aStandard error was calculated from three independent samples.

2.5. Box-Behnken Design (BBD)

A 15-run Box-Behnken design (BBD) with three center points was employed in this work, and the maximal values of the productions of succinic acid were shown in Table 3.

Table 3.

The Box-Behnken design of RSM for the optimization of succinic acid production by A. succinogenes ATCC 55618.

Run	Glucose (g L−1)	Yeast extract (g L−1)	MgCO3 (g L−1)	OD660	Succinic acid production (g L−1)
1	70 (−1)a	10 (0)	50 (−1)	6.0 ± 0.7c	38.9 ± 1.3
2	90 (1)	10 (0)	50 (−1)	5.5 ± 0.8	40.3 ± 0.7
3	70 (−1)	10 (0)	70 (1)	0.6 ± 0.1	43.2 ± 5.5
4	90 (1)	10 (0)	70 (1)	5.7 ± 0.4	45.8 ± 0.9
5	70 (−1)	5 (−1)	60 (0)	1.3 ± 0.6	37.0 ± 2.5
6	90 (1)	5 (−1)	60 (0)	1.0 ± 0.8	38.1 ± 4.0
7	70 (−1)	15 (1)	60 (0)	8.0 ± 0.2	45.8 ± 1.3
8	90 (1)	15 (1)	60 (0)	7.8 ± 0.6	50.9 ± 0.7
9	80 (0)	5 (−1)	50 (−1)	0.8 ± 0.6	35.1 ± 1.7
10	80 (0)	5 (−1)	70 (1)	0.5 ± 0.1	34.8 ± 1.1
11	80 (0)	15 (1)	50 (−1)	8.3 ± 0.2	41.5 ± 2.6
12	80 (0)	15 (1)	70 (1)	6.2 ± 0.2	50.7 ± 0.8
13b	80 (0)	10 (0)	60 (0)	6.5 ± 1.0	49.6 ± 1.0
14b	80 (0)	10 (0)	60 (0)	5.8 ± 0.1	50.2 ± 1.5
15b	80 (0)	10 (0)	60 (0)	5.9 ± 0.1	49.0 ± 3.5

^aReal values of independent variables and the corresponding coded level.

^bRuns 13–15 were three replications.

^cFor each trial, the dynamic profile of the succinic acid production was monitored. Multiple flasks were run at the same time, and three flasks were taken at each sampling point. Each data point was expressed by an average with an error bar (i.e., standard error from three independent samples).

To describe the relationships between the succinic acid production and the medium components, a mathematical model was developed by the following second-order polynomial equation to fit data in RSM of BBD:

$$\begin{array}{c}Y={\beta }_{\mathrm{0}}+\sum _{}^{}{\beta }_i{x}_i+\sum _{}^{}{\beta }_{ii}{x}_i^{\mathrm{2}}+\sum _{i=\mathrm{1}}^n{\beta }_{ij}{x}_i{x}_j+\epsilon \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}i\ne j;\hspace{0.17em}\hspace{0.17em}i,j=\mathrm{1,2},\mathrm{3}\dots ,\end{array}$$ (5)

where Y is the predicted response, β₀ is the offset term, β_i is the linear effect, β_ii is the quadratic effect, β_ij is the interaction effect, and ε is an experimental error. And x_i and x_j represent the independent variables (medium components) in the form of coded values as follows:

$$\begin{array}{c}{x}_i=\frac{X_i-X}{\mathrm{\Delta }{X}_i}\hspace{1em}i=\mathrm{1,2},\mathrm{3},\end{array}$$ (6)

where x_i and X_i are the dimensionless and the actual values of independent variable i, X is the actual value of the independent variable i at the central point, and ΔX_i is the step change of X_i corresponding to a unit variation of the dimensionless value.

The model of response was expression in terms of code variables and without the statistically insignificant terms (different models are available in BBD of statistical software package Minitab 15, Minitab Inc., State College, PA 16801-3008, USA).

2.6. Data Analysis

Standardized Pareto charts, representing the estimated effects of parameters and parameter interactions on responses, permitted us to check the statistical significance of the PBD. The Student's t-test permitted to check the statistical significance of the regression coefficients. The analysis of variable (ANOVA) was performed on experimental data to evaluate the statistical significance of the model. The models of each response were expressed in terms of code/uncoded variables and without the statistically insignificant terms. A p value less than 5% indicates that model terms are significant, while less than 1% indicates that model terms are highly significant. A p value is a measure of how much evidence one has against the null hypothesis (the null hypothesis of the test read like this: H0: β₁ = β₂ = ⋯ = β_i = 0; H1: at least one β is not zero) and evidence against null hypothesis is more for smaller p value. A p value of 0.05 or less rejects the null hypothesis at the 5% level, that is, only 5% of the probability the supposed statistical model will fail to predict the response. The model adequacies were checked by the determination coefficients (R²), adjusted R², and predicted R². The determination coefficient (R²) is a measure of how well the regression equation fits the sample data. While R² can be made larger simply by adding more predictor variables to the model, an adjusted R² has been proposed. Adjusted R² is a modification of R² that adjusts for the number of explanatory terms in a model. A predicted R² is used to measure the amount of variation in new data (i.e., other levels among the tested maximal value and minimal value of the factor) explained by the model. It is calculated by systematically removing each observation from the data set, estimating the regression equation, and determining how well the model predicts the removed observation. Predicted R² is used in regression analysis to indicate how well the model predicts responses for new observations, whereas R² indicates how well the model fits the data. Predicted R² can prevent overfitting the model and can be more useful than adjusted R² for comparing models because it is calculated using observations not included in model estimation. Predicted R² larger values of predicted R squared suggest models of greater predictive ability. The predicted R² and the adjusted R² should be within 0.20 of each other. Otherwise there may be a problem with either the data or the model. The “Minitab 15 (Minitab Inc., State College, PA 16801-3008, USA)” software was employed for the regression analysis and the graphical optimization, respectively.

2.7. Sampling and the Determination of Succinic Acid Production

For sampling, three flasks were taken each time, and cell growth was monitored by measuring the optical density at 660 nm (OD₆₆₀). At an OD₆₆₀ of 1.0, A. succinogenes ATCC 55618 has a concentration of 0.626 g dry cell weight (DCW) l⁻¹. For succinic acid determination, 1 mL of methanol and 1 mL of acetonitrile were added to 1 mL of fermentation broth to remove proteins, and the sample was kept at 4°C overnight. After centrifugation at 11,000 rpm for 30 min, the supernatants were diluted and filtrated through a 0.22-μm filter and analyzed by high-performance liquid chromatography (HPLC, Waters) using an Agela Venusil ASB C18 column. The optimized mobile phase was 50 mM KH₂PO₄ water solution, with the pH adjusted to 3.5 by H₃PO₄. The column oven temperature was maintained at 40°C, and the flow rate was 1 mL min⁻¹. The detection wave was fixed at 210 nm.

3. Results and Discussion

3.1. Plackett-Burman Design (PBD)

The methodology of Plackett-Burman design (PBD) is a powerful and useful tool in rapidly searching key factors from a multivariable system. PBD does not determine the exact quantity, but it can provide some important information about each factor by relatively few experiments [19]. As shown in Table 1, PBD for 12 trials with two levels of concentrations was undertaken to evaluate the significances of nine medium components. In order to determine the influence of the most important parameters, a standardized Pareto chart (Figure 1) was employed. Analysis of the measured response variables enabled to obtain standardized Pareto charts and response surface plots. A standardized Pareto chart consists of bars with a length proportional to the absolute value of the estimated effects, divided by the standard error. The bars are displayed in order of the size of the effects, with the largest effects on top. The chart includes a vertical line at the critical t-value for an alpha. Some investigations find that the confidence levels greater than 80% (p < 0.2) are acceptable [21]. In this study, the chart includes a vertical line at the critical t-value for α of 0.20. Effects for which the bars are smaller than the critical t-value are considered as not significant and not affecting the response variables. Effects may be positive or negative.

Figure 1.

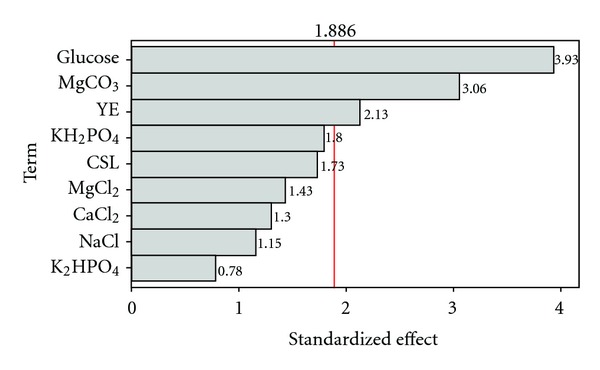
Pareto chart of standardized effects on the succinic acid production. The chart includes a vertical line (i.e., standardized effect = 1.886) at the critical t-value for α of 0.20. The bars are displayed in order of the size of the effects, and the standardized effect of each term was shown on the top of its corresponding bar.

As shown in Figure 1, for the succinic acid production, the variables glucose, yeast extract, and MgCO₃ had a confidence level above 80%. Hence, these were considered to be significant for the succinic acid biosynthesis.

Analyzed by Minitab, a first-order model, was fitted to the results obtained from the twelve experiments as the equation:

$$\begin{array}{c}Y(\text{g}\hspace{0.17em}{\text{L}}^{-\mathrm{1}})=\mathrm{39.09}+\mathrm{4.18}{C}_{\text{glucose}}-\mathrm{2.28}{C}_{\text{YE}}-\mathrm{1.84}{C}_{\text{CSL}}\\ -\mathrm{0.83}{C}_{{\text{K}}_{\mathrm{2}}\text{HP}{\text{O}}_{\mathrm{4}}}-\mathrm{1.93}{C}_{\text{K}{\text{H}}_{\mathrm{2}}\text{P}{\text{O}}_{\mathrm{4}}}-\mathrm{1.24}{C}_{\text{NaCl}}\\ +\mathrm{1.53}{C}_{\text{MgC}{\text{l}}_{\mathrm{2}}}+\mathrm{1.36}{C}_{\text{CaC}{\text{l}}_{\mathrm{2}}}+\mathrm{3.26}{C}_{\text{MgC}{\text{O}}_{\mathrm{3}}}.\end{array}$$ (7)

where Y is the succinic acid production, and C_Glucose, C_YE, C_CSL, C_K2HPO4, C_KH2PO4, C_NaCl, C_MgCl2, C_CaCl2, and C_MgCO3 are the value of glucose, YE, CSL, K₂HPO₄, KH₂PO₄, NaCl, MgCl₂, CaCl₂, and MgCO₃, respectively. The goodness of the regression was checked by the coefficient of determination R² whose value (R² = 95.39%) indicates that only 4.61% of the total variation could not be explained by the model, and it was reasonable to use the regression model to analyze the trend in the response. And then, glucose, yeast extract, and MgCO₃ were selected for further optimization to obtain a maximum response. According to the coefficients of the glucose (4.18), yeast extract (−2.28) and MgCO₃ (3.26), the positive coefficients indicated that the high level of glucose and MgCO₃ concentration in PBD was benefit for the succinic acid production. On the contrary, the negative coefficient indicated that the low level of yeast extract concentration was helpful for the succinic acid accumulation. A maximum succinic acid production of 51.9 g L⁻¹ was obtained with 80.0 g L⁻¹ of glucose, 60.0 g L⁻¹ of MgCO₃, and 10.0 g L⁻¹ of yeast extract. The corresponding productivity and specific productivity were 1.1 g L⁻¹ h⁻¹ and 13.4 g succinic acid g⁻¹ DCW. However, the OD₆₆₀ of 6.2 obtained with this medium was not the highest among the 12 conditions.

According to the metabolic pathway of A. succinogenes, succinic acid was an end-product from the substrate of glucose, which implied that succinic acid formation was decided by the supplement of glucose directly [22]. The yield of succinic acid against glucose was improved by the increase of initial glucose concentration, and it would reach the peak value when the initial glucose concentration was 70.0 g L⁻¹ [23].

The culture pH value is one of the key factors in the production of succinic acid [24]. MgCO₃ was used as a neutralizing agent and added to the fermentation broth to adjust culture pH. Before optimization, the pH value decreased from 7.5 to 5.7 during the fermentation. Compared with the pH value of basic medium, the initial pH increased up to 8.0 and was followed by slow decline after the optimization. So after MgCO₃ was elevated, the extent of system buffering was improved. The final pH value of optimal medium with an initial pH of 7.5 was more close to neutral (about 6.5) during the fermentation, and neutral environment was helpful to accumulate succinic acid. In our previous results, the highest succinic acid production of 48.2 g L⁻¹ was obtained at a culture pH of 7.5 [25]. The pattern of succinic acid production at a culture pH of 7.0 was similar with that obtained at 7.5. When the initial culture pH was adjusted to 6.5 or 8.0, a significant decrease of succinic acid production was observed. So, the effect of medium optimization MgCO₃ may be partly from the influence of the pH.

On the other hand, sufficient CO₂ supplement in the fermentation broth could strongly influence the metabolic flux of carbon and the activities of phosphoenolpyruvate (PEP) carboxykinase, which were the important committed steps for the biosynthesis of succinic acid [24, 26]; therefore, sufficient CO₂ is another key factor influencing succinic acid accumulation. However, in our previous work, there was no significant effect of CO₂ partial pressure on the production of succinic acid when gaseous CO₂ was used as the sole CO₂ donor [27]. As an important CO₂ donor in the A. succinogenes fermentation, MgCO₃ could react with organic acids in fermentation broth and caused an increase in the dissolved concentrations of HCO₃⁻, CO₃²⁻, and CO₂. When gaseous CO₂ was used with MgCO₃, higher amount of MgCO₃ was more effective on promoting the succinic acid synthesis. And the maximum succinic acid production of 61.92 g L⁻¹ was obtained at 159.22 mM dissolved CO₂ concentration, which was supplied by 40 g L⁻¹ MgCO₃ with 100% CO₂ gas. This means that the dissolved CO₂ concentration was another factor affecting succinic acid synthesis. And during the fermentation process, insoluble MgCO₃ caused turbid broth, which made the cells spread uniformly in the broth. This effectively avoids the cell flocculation. All these properties make MgCO₃ to be one of the key factors significantly improved the succinic acid production.

At last, yeast extract was also screened to be a key factor because it affected cell growth directly as the nutrient. It contains many trace substances, such as folic acid, pantothenic acid, biotin, and vitamin B₁, B₂, B₆, and B₁₂. This may be the important reason why many kinds of vitamins could be omitted meanwhile the succinic acid could efficiently be accumulated in this work.

To conclude, the variables of glucose, MgCO₃, and yeast extract had a confidence level above 80% and hence were considered to significantly influence the succinic acid production. The optimal concentrations of these three key components needed to be further studied as follows.

3.2. Steepest Ascent (SA)

Based on the results above, glucose, yeast extract, and MgCO₃ were the three key factors, and the high level of glucose (i.e., 80.0 g L⁻¹) and MgCO₃ (i.e., 60.0 g L⁻¹), while the low level of yeast extract (i.e., 10.0 g L⁻¹) was benefit for the succinic acid production of A. succinogenes ATCC 55618. Thus, the path of SA was moved along the path in which glucose and MgCO₃ increased, while yeast extract decreased (Table 2). The highest succinic acid production of 48.4 ± 1.3 g L⁻¹ and OD₆₆₀ of 6.1 was observed under the point of levels, namely, 80.0 g L⁻¹ of glucose, 10.0 g L⁻¹ of yeast extract, and 60.0 g L⁻¹ of MgCO₃. The corresponding productivity and specific productivity were 1.0 g L⁻¹ h⁻¹ and 12.4 g succinic acid g⁻¹ DCW. This result suggested that the point was near the optimal point and was chosen for further optimization.

As shown in Table 2, the succinic acid production did not further increase with the increase concentrations of glucose and MgCO₃ and the decrease concentration of yeast extract. For glucose, although A. succinogenes could tolerate glucose concentration as high as 150.0 g L⁻¹, the yield of succinic acid would decrease when glucose concentration exceeds 70.0 g L⁻¹ [9, 23]. So when the concentration of glucose increased from 80.0 to 100.0 g L⁻¹, the concentrations of succinic acid could not be further improved. For MgCO₃, the culture pH of fermentation broth was increased with the increase of MgCO₃ concentration (data not shown), which may make the cells more difficult to adapt. Therefore, the succinic acid production was not enhanced. For yeast extract, it was observed that the absence of yeast extract led to almost no succinic acid accumulation, which indicated that this component was the basic nutrient for the cell growth.

To conclude, the highest succinic acid production was obtained under the condition of 80.0 g L⁻¹ of glucose, 10.0 g L⁻¹ of yeast extract, and 60.0 g L⁻¹ of MgCO₃, which suggested that this point was near the optimal point.

3.3. Box-Behnken Design (BBD)

Based on the information above, taking the point (80.0 g L⁻¹ of glucose, 10.0 g L⁻¹ of yeast extract and 60.0 g L⁻¹ of MgCO₃) as the central level of BBD, then the three-factors, three-level BBD was employed (Table 3).

Table 4 shows the analysis of variance (ANOVA) for the BBD. The p values ≤0.05 indicate that the model terms are significant. The Lack of fit (LOF) is the variation of the data around the fitted model. LOF is a model fit test that is used to check how well a model fits the data and help to remove insignificant terms from the model. A p-value of LOF 0.614 indicted that the model fits the response well. The “predicted R²” of 0.9696 was in reasonable agreement with the “adjusted R²” of 0.9911, and it might be also said that the model determination coefficient (R² of 0.9968) was reasonable agreement with the experimental results, indicating that 99.68% of the variability could be revealed by the model.

Table 4.

Analysis of variance (ANOVA) for regression model.

Source	SSa	DF	MS	F	p
Model	481.38	9	53.49	174.13	<0.001
Linear	298.58	3	99.53	324.01	<0.001
Quadratic	155.85	3	51.95	169.12	<0.001
Interactions	26.95	3	8.98	29.24	0.001
Residual	1.54	5	0.31
Lack of fit	0.82	3	0.27	0.75	0.614
Pure error	0.72	2	0.36
Total SS	482.91	14
R 2 = 0.9968, Radj2 = 0.9911, Rpred2 = 0.9696.

^aSS: sum of squares; DF: degrees of freedom; MS: mean square; R²: determination coefficient; adj R²: adjusted R²; pred R²: predicted R².

The polynomial model for the succinic acid production was expressed by (8) (in coded value) and (9) (in uncoded value) (Table 5) consider the following:

$$\begin{array}{c}Y=\mathrm{49.563}+\mathrm{1.274}A+\mathrm{5.495}B+\mathrm{2.346}C+\mathrm{1.008}AB\\ +\mathrm{0.310}AC+\mathrm{2.373}BC-\mathrm{2.562}{A}^{\mathrm{2}}-\mathrm{4.084}{B}^{\mathrm{2}}-\mathrm{4.972}{C}^{\mathrm{2}}\end{array}$$ (8)

$$\begin{array}{c}Y=-\mathrm{285.728}+\mathrm{3.842}{C}_{\text{Glucose}}-\mathrm{0.092}{C}_{\text{YE}}+\mathrm{5.482}{C}_{\text{MgC}{\text{O}}_{\mathrm{3}}}\\ +\mathrm{0.020}{C}_{\text{Glucose}}{C}_{\text{YE}}+\mathrm{0.0031}{C}_{\text{Glucose}}{C}_{\text{MgC}{\text{O}}_{\mathrm{3}}}\\ +\mathrm{0.047}{C}_{\text{YE}}{C}_{\text{MgC}{\text{O}}_{\mathrm{3}}}-\mathrm{0.026}{C_{\text{Glucose}}}^{\mathrm{2}}\\ -\mathrm{0.163}{C_{\text{YE}}}^{\mathrm{2}}-\mathrm{0.050}{C_{\text{MgC}{\text{O}}_{\mathrm{3}}}}^{\mathrm{2}}.\end{array}$$ (9)

Table 5.

Regression coefficients and their significance for response surface model.

Term	Coefficient	Standard error	T (C/S)	p
Intercept	49.563	0.32	154.89	<0.001a
A—Glucose	1.274	0.20	6.50	0.001a
B—Yeast extract	5.495	0.20	28.04	<0.001a
C—MgCO3	2.346	0.20	11.97	<0.001a
AB	1.008	0.29	3.64	0.015b
AC	0.310	0.29	1.10	0.321
BC	2.373	0.29	8.56	<0.001a
A 2	–2.562	0.28	–8.88	<0.001a
B 2	–4.084	0.28	–14.16	<0.001a
C 2	–4.972	0.28	–17.24	<0.001a

^aSignificant at 1% level.

^bSignificant at 5% level.

The model reveals that glucose concentration (A), yeast extract concentration (B), and MgCO₃ concentration (C) had a significant effect (p < 0.0001) on the succinic acid production (Y). Positive coefficient of A, B, and C indicated a linear effect to increase. However, quadratic term A², B², and C² had the negative effect. The graphs (Figure 2) depict the changes in the parameter modeled as the two factors move along those levels, while the other factor held constant at the central point. According to (9), the highest succinic acid production of 52.3 g L⁻¹ was obtained at 14.0 g L⁻¹ of yeast extract and 64.3 g L⁻¹ of MgCO₃, while glucose concentration was held at 80.0 g L⁻¹; the maximal succinic acid production of 50.0 g L⁻¹ could be observed at 82.6 g L⁻¹ of glucose and 62.4 g L⁻¹ of MgCO₃, while holding 10.0 g L⁻¹ of yeast extract; under the conditions of 83.9 g L⁻¹ of glucose, 13.6 g L⁻¹ of yeast extract and 60.0 g L⁻¹ of MgCO₃ (the factor held constant), the succinic acid production could reach its peak value of 51.8 g L⁻¹. According to (8) and (9), it was predicted that a maximum succinic acid production of 53.0 g L⁻¹ was appeared at 84.6 g L⁻¹ of glucose, 14.5 g L⁻¹ of yeast extract, and 64.7 g L⁻¹ of MgCO₃.

Figure 2.

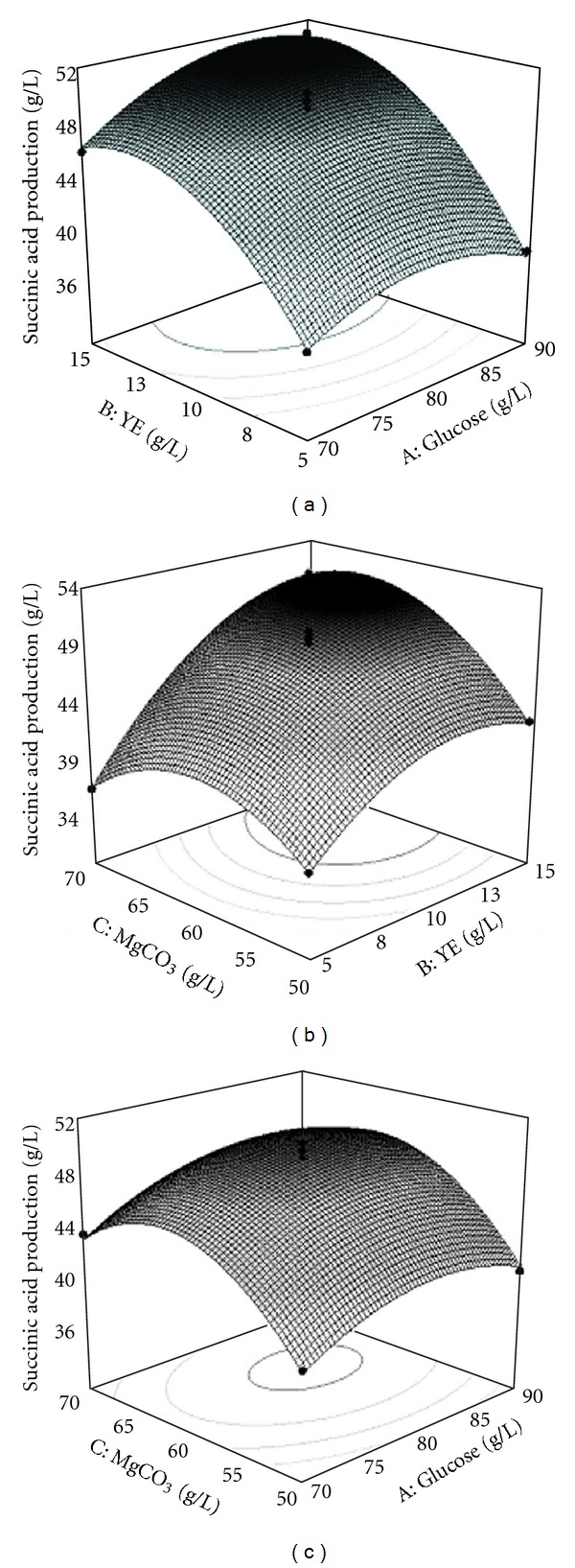
Response surface curve for the succinic acid production by Actinobacillus succinogenes ATCC 55618 showing the combination effects of (a) glucose and yeast extract, (b) yeast extract and MgCO₃, and (c) glucose and MgCO₃. Other factors are constant at zero levels.

In a word, the best level combination of the three key factors (i.e., glucose, yeast extract, and MgCO₃) was predicted by the polynomial model from BBD. Then the reliability of the model and the accuracy of the prediction should be checked by verification experiment.

3.4. Model Verification

The availability of the regression model of the succinic acid production using the calculated optimal medium compositions, namely, 84.6 g L⁻¹ glucose, 14.5 g L⁻¹ yeast extract, and 64.7 g L⁻¹ MgCO₃, was validated with triplicate experiments. The mean maximal value of succinic acid production was 52.7 ± 0.8 g L⁻¹, which agreed with the predicted value (53.0 g L⁻¹) well. As a result, the model was considered to be accurate and reliable for predicting the succinic acid production by A. succinogenes. Theoretically, 1.71 mol succinate can be produced per mol glucose (plus CO₂), based on the available electrons (i.e., 24 electrons in glucose divided by 14 electrons in succinate = 1.71). In this work, compared with that of basic medium (0.45 mol mol⁻¹ glucose), the yield of succinic acid against glucose was enhanced by 111.1% in optimized medium (0.95 mol mol⁻¹ glucose). However, there is a certain gap between the yield and the theoretical value. This may be because there are some factors other than the medium, which affect the yield of succinic acid but are not investigated in this study.

Other authors have reported that the succinic acid production reached 84 g L⁻¹ in the fermentation of Actinobacillus succinogenes NJ113, in which the medium was with similar components to the basic medium in this work, and the corresponding yield of succinic acid was 1.20 mol mol⁻¹ glucose [28]. Since NJ113 is the strain screened by Jiang et al, this strain may have greater ability to synthesize succinic acid.

To conclude, the best level combination of the three key factors (i.e., 84.6 g L⁻¹ glucose, 14.5 g L⁻¹ yeast extract, and 64.7 g L⁻¹ MgCO₃) was obtained by using the statistical experimental design. The succinic acid production reached its peak values of 52.7 ± 0.8 g L⁻¹ under the optimal medium compositions, which agreed with the predicted value (53.0 g L⁻¹) well and was 67.3% higher than that obtained with the basic medium (i.e., 31.5 ± 2.3 g L⁻¹).

4. Conclusion

In this study, a highly efficient optimization method by combining Plackett-Burman design, steepest ascent, and Box-Behnken design was developed. This method was demonstrated to be effective in selecting the significant factors and enhancing succinic acid production in A. succinogenes ATCC 55618 fermentation. Glucose, yeast extract, and MgCO₃ were screened to be key factors for the succinic acid production. A maximal succinic acid production of 52.7 ± 0.8 g L⁻¹ was obtained with 84.6 g L⁻¹ glucose, 14.5 g L⁻¹ yeast extract, and 64.7 g L⁻¹ MgCO₃. This result agreed with the predicted value well and was 67.3% higher than that obtained with the basic medium.