A Library of Cortical Morphology Analysis Tools to Study Development, Aging and Genetics of Cerebral Cortex

Abstract

Sharing of analysis techniques and tools is among the main driving forces of modern neuroscience. We describe a library of tools developed to quantify global and regional differences in cortical anatomy in high resolution structural MR images. This library is distributed as a plug-in application for popular structural analysis software, BrainVisa (BV). It contains tools to measure global and regional gyrification, gray matter thickness and sulcal and gyral white matter spans. We provide a description of each tool and examples for several case studies to demonstrate their use. These examples show how the BV library was used to study cortical folding process during antenatal development and recapitulation of this process during cerebral aging. Further, the BV library was used to perform translation research in humans and non-human primates on the genetics of cerebral gyrification. This library, including source code and self-contained binaries for popular computer platforms, is available from the NIH-Neuroimaging Informatics Tools and Resources Clearinghouse (NITRC) resource (http://www.nitrc.org/projects/brainvisa_ext).

Introduction

Advancements in the magnetic resonance imaging (MRI) RF coil technology, pulse sequences and gradient performance have led to substantial improvements in the quality of structural MRI (sMRI) studies. High-quality, three-dimensional (3D) sMRI studies of cerebral anatomy are being routinely collected at sub-millimeter resolution, even in populations that are prone to head motion, such as children, elderly and non-human primates (Brown et al. 2010; Kochunov et al. 2006). Additionally, several, large high-quality structural datasets, collected in scientifically and clinically important populations such as the Alzheimer’s Disease Neuroimaging Initiative (ADNI), the Human Imaging database (HID), the Open Access Series of Imaging Studies (OASIS), the Bipolar Disorder Neuro-Imaging Database (BiND), the Multisite Imaging Research In the Analysis of Depression (MIRIAD), and the Efficient Longitudinal Upload of Depression in the Elderly (ELUDE), are now publically available. These data were collected to advance the knowledge of normal and abnormal development as well as for disorders such as dementia, schizophrenia, autism, and depression. There is an urgent need for analysis techniques capable of extracting scientifically and biologically meaningful biomarkers from the sMRI studies. This manuscript describes a library of tools, the BV library, which we developed to quantify global and regional gyrification, thickness of cortical GM, and degree of cerebral atrophy.

Structural MRI analysis tools are fundamentally different from the tools developed for analysis of the functional MRI (fMRI) (Smith et al. 2004b). The aim of fMRI analysis tools is to quantify per-subject changes in the neural activity from time-series data. The aim of the sMRI analysis tools is to quantify cerebral morphology from high-resolution three-dimensional (3D) maps of cerebral anatomy. Some sMRI analysis tools, broadly known as the voxel-based morphometry (VBM) techniques, calculate regional volume/densities of cerebral gray matter (GM), white matter (WM) and CSF (Ashburner and Friston 2000; Good et al. 2002; Smith et al. 2002; Studholme et al. 2004). A shortcoming of these techniques is that the spatial registration step. Spatial registration is used to align individual images to a common atlas space. However, even the advanced non-linear spatial normalization techniques are generally insufficient to account for individual variations in the cortical anatomy (Klein et al. 2009). The residual misalignments can confound the results in the regions of the rapidly changing primary folding patterns specifically near major primary sulcal structures as the sylvian fissure (Ashburner and Friston 2000; Mangin et al. 2004a, b). Additionally, the definition of region in VBM methods depends heavily on the accuracy and precision of spatial registration and on the atlas (Klein et al. 2009) rather than individual anatomy. Moreover, the results of the VBM analysis can be difficult to interpret as the findings of lower regional GM volume or density can be produced by a reduced thickness of the cortical mantle, reduced cortical area or increase in the intrasulcal CSF volume (Kochunov et al. 2008; Winkler et al. 2009).

A more intuitive approach, called the Object Based Morphometry (OBM), was developed to classify individual anatomical variability using basic, recurring gyral and sulcal patterns (Mangin et al. 2003). OBM uses a recognition model to parcelate cerebral cortex into a mosaic of surface models for individual gyri and sulci. This supports the analysis of their relationships, as well as their visualization (Mangin et al. 2004a, b). The OBM approach stems from the idea that the cortical folding is driven by genetic, epigenetic and environmental factors and is under various mechanistic and architectural constraints. The intersubject differences in the folding patterns can therefore, be used to probe for population-and-disease related variations in the underlying anatomical organization of the brain (Mangin et al. 2004a, b). Another advantage of OBM versus VBM techniques is that the intersubject analysis can be performed in the native space using sulcal landmarks as the means to carry out the comparisons among subjects. This can be important as some cortical brain structures, such as cortical ribbon, do not scale allometrically when adjusting for brain size (Hutsler et al. 2005) and this can lead to artifactual findings. For instance, greater gender effects in cortication thickness are observed after correcting for individual differences in brain size than before this correction because of gender-specific differences in brain size (Lancaster et al. 2010; Luders et al. 2006a; Sowell et al. 2007).

We aim to provide a comprehensive overview of a library of automated research tools for cortical modeling and analysis and to illustrate examples of their use. This library was developed to support two important areas of morphological analysis: analysis of the intersubject differences in the degree of cortical gyrification and analysis of intersubject differences in the degree of cortical atrophy. The gyrification measuring tools included in this library can help scientists to evaluate global and regional, intersubject differences in cortical gyrification by calculating hemispheric gyrification index and the length and the depth of individual cortical sulci. The atrophy measuring tools can help scientists to study regional differences in cortical atrophy among subjects by measuring the pattern of gray matter thickness along gyral and sulcal surface patches and estimating cortical tissue loss by measuring the width of the inter-sulcal CSF space and the span of intra-gyral WM volume. Such measures may ultimately be used (1) for gauging factors that affect normal aging and development as well as the neurodegenerative disorders associated with maturation and senescence, (2) for assessment of genetic factors that control individual variability in cortical anatomy and predispose one to neurodegenerative disorders and (3) for clinical trials that determine the therapeutic value of anti-aging drugs and their ability to resist degenerative changes.

The style of this manuscript follow that of similar publications that detail libraries of tools including FSL (Smith et al. 2004a) and CARET (Van Essen et al. 2001).The “Methods” section provides detailed description of each of the tools that were previously described in separate publications. The discussion section is a summary of the case studies that demonstrate the use of this library. Examples of these studies include analyses of cortical changes during cerebral development, aging, and analyses of genetic contribution to intersubject variability in cortical anatomy. We believe that manuscripts of this nature address an important need for the scientific community. Such manuscripts provide a succinct overview of research that was carried out over many years and serve as a single reference for a large community of users.

Methods

The BrainVisa (BV) library contains six tools: three for calculation of global and regional degree of gyrification and three for estimation of cortical tissue loss (Table 1 and Fig. 1). This library uses BV OBM pipeline for preprocessing of images and parcellation of the cerebral cortex into cortical (gyral and sulcal) objects. Accurate and robust processing of images by the BV OBM pipeline depends on the quality of the imaging data: a combination of resolution and contrast. For this study we recommend that spatial resolution be optimized for the characteristic sizes of morphological features of cortical structures such as gray matter ribbon, gyri and sulci. An imaging protocol that meets this recommendation acquires six, high-resolution (isotropic 800 μm) volumes using a T1-weighted, 3D TurboFlash sequence (Kochunov et al. 2006). For this sequence imaging parameters were established to produce GM/WM contrast of at least 25% for a 3T MR imager. The acquisition time for each of the six acquisitions is kept at 3 min to help shift intra-scan motion into inter-scan motion and reduce intra-scan motion artifacts (Kochunov et al. 2006). Following scanning, retrospective motion correction is used to compensate for inter-scan motion, forming a single average motion-corrected image. This protocol has been used to collect structural data with over 2,000 human studies and has been modified for use in non-human primates (Kochunov and Duff Davis 2009).

Table 1.

Summary of the tools included in this library

	Input	Output	Purpose (references for examples)
Tools to measure gyrification
Global gyrification index	Pial mesh extracted by BrainVisa OBM Pipeline	Gyrification coefficient	To measure global gyrification coefficient (Kochunov et al. 2010a; Rogers et al. 2010)
Sulcal length	Names of individual sulci and the sulcal graph calculated by BrainVisa OBM Pipeline	Lengths of the top ridge and fundus for individual sulci. Coordinates of the equally spaced control points. Parametric curves stored in a mesh format	To measure regional differences in gyrification among subjects. To study longitudinal changes in regional gyrification. (Kochunov et al. 2010a; Rogers et al. 2010)
Sulcal depth	Names of individual sulci and the sulcal graph calculated by Brain Visa OBM Pipeline	Average sulcal depth. Regional sulcal depth calculated at equidistal intervals along the top ridge and fundus. Coordinates of the equally spaced control points. Parametric curves stored in a mesh format	To measure regional difference in gyrification among subjects. To study longitudinal changes in regional gyrification. (Cykowski et al. 2008; Kochunov et al. 2010a)
Tools to measure cortical atrophy
GM thickness	Pial and GM/WM interface surfaces calculated by BrainVisa OBM Pipeline	Average gray matter thickness per hemisphere and a texture map of regional GM thickness values	To measure regional intersubject differences in cortical thickness during maturation and aging. (Kochunov et al. 2011; Kochunov et al. 2007)
Sulcal span	Pial surface and sulcal graph calculated by BrainVisa OBM Pipeline	Average sulcal span tabulated for individual sulci. Mesh of individual measurements and texture map of regional gyral span across sulcus.	To measure intersubject differences in the dilation of sulcal valleys. (Kochunov et al. 2005; Liu et al. 2011)
Gyral WM span	GM/WM interface surface and gyral graph calculated by Brain Visa OBM Pipeline	Average gyral WM span tabulated for individual gyri. Mesh of individual measurements	To measure intersubject differences in gyral white matter bulk (Kochunov et al. 2009f; Liu et al. 2011)

Fig. 1.

Visual interface for library of Brain Visa tools

BrainVisa (BV) Object-Based Morphology Pipeline

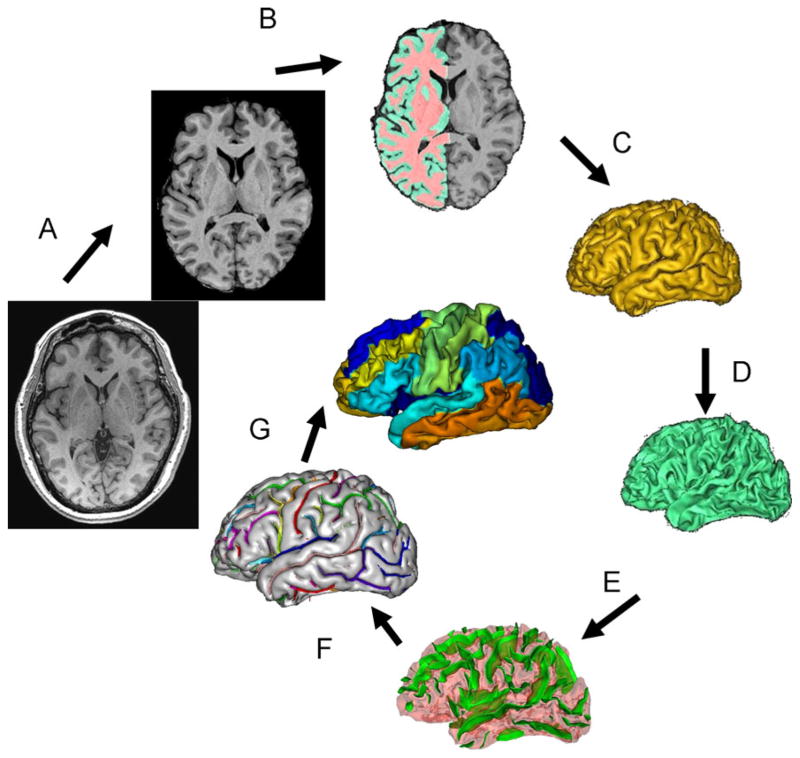
The details of the BV OBM pipeline have been discussed elsewhere (Mangin et al. 2004a, b). The BV OBM pipeline performs automatic recognition of the main cortical sulci and parcellation of the cortical surface into gyral patches from structural MR images. The 2004 pipeline was improved by including sulcal and gyral identification algorithms that provide automated labeling of sulcal and gyral surfaces (Rivière et al. 2002). The BV processing pipeline starts by performing RF inhomogeneity correction to remove low-frequency variations in MRI image intensity (Fig. 1a). This is followed by identification of the brain and cerebellum and removal of non-brain tissues using a technique based on 3-D erosion and template-based 3-D seed growth (Mangin et al. 1996; Mangin et al. 2004a, b) (Fig. 1b). The cortical GM ribbon is then formed using a homotopic erosion technique (Mangin et al. 1995). This is followed by extraction of spherical meshes for the pial and GM/WM interfaces (Fig. 1c, d) A “crevasse detector” is used to reconstruct sulcal structures as the medial surfaces from the two opposing gyral banks that span from the most internal point of sulcal fold to the convex hull of the cortex (Mangin et al. 1995; Mangin et al. 2004a, b) (Fig. 1e).

The sulcal identification program is used to automatically recognize and label individual sulci. This program uses of a collection of 500 artificial neural network-based pattern classifiers. Each classifier is tuned to identify a particular feature of the sulcal patterns (Fig. 1f). These neural networks work collaboratively to perform identification of 56 sulcal structures per hemisphere. The neural networks were trained on a database of twenty six expertly classified images, resulting in a classification accuracy ranging from 95% for primary and secondary furrows to about 70–80% for the more variable secondary and tertiary sulcal structures (Rivière et al. 2002). Manual verification of automated labeling by an expert is used to correct for sulcal misclassifications and takes about 10–20 min per brain for an experienced observer.

Finally, automated parcellation of the cortical regions is done to segment the cortical surface into 14 regions that correspond to primary gyri and lobules (Cachia et al. 2003). This parcellation uses borders identified by the primary and secondary cortical sulci that are present in all subjects (Table 1). Several gyri are combined into “lobules” due to the non-100% penetrance of the secondary sulci defining these gyral areas (Cachia et al. 2003). These lobules include: 1) inferior parietal lobule, composed of supra-marginal and angular gyri; 2) lateral occipital area, spanning the entire surface of the lateral occipital lobe and 3) hippocampal area spanning the cortical surface medial to the fusiform sulcus, including the hippocampus, para-hippocampal gyrus and uncus.

Each BV preprocessing step uses variables that can be modified (and change results), therefore we recommend that any departure from the given processing pipeline be reported in publications so that studies can be replicated.

Global and Regional Measurements of Gyrification

The BV library provides tools to measure subjects’ global and regional gyrification. Global gyrification is quantified using the gyrification index (GI). Regional gyrification is quantified by calculating the length and depth for cortical sulci.

Global Gyrification (Gyrification Index)

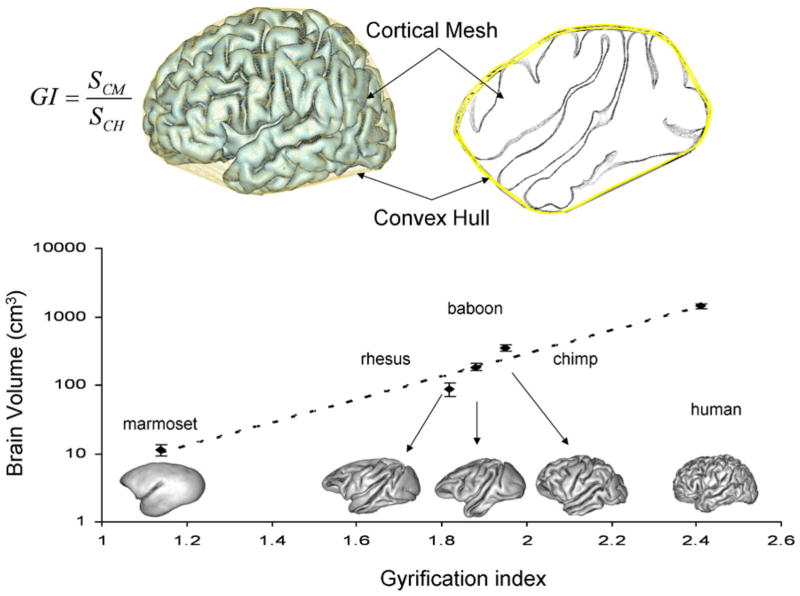
Whole-brain gyrification is quantified by measuring the gyrification index (GI). GI is a measurement invented by Dr. Karl Zilles and detailed in his, now classical, 1988 manuscript (Zilles et al. 1988). Originally, the GI was calculated as the ratio of the perimeter of the total cortical outline to that of the exposed brain surface, trace on 2D histological sections (Zilles et al. 1989; Zilles et al. 1988). We adapted this 2D GI methodology for 3D surfaces by defining the GI as the ratio of the area of the pial cortical mesh (S_CM) to that of its 3D convex hull (S_CH), while excluding the area of the lateral ventricles, Eq 1 (Fig. 2, top). This approach is similar to one implemented in CARET software (Van Essen et al. 2001).

Fig. 2.

BrainVisa object-based morphometry pipeline

$$GI=\frac{S_{CM}}{S_{CH}}$$ (1)

We chose the convex hull (CH) to define the surface area of the exposed brain over other methods, such as curvature-based (Luders et al. 2006b), morphological closing (Cachia et al. 2008) and surface smoothing-based (Toro et al. 2008) approaches, because of its intrinsic mathematical properties (Lancaster et al. 1999). A CH surface is unique for a given cortical mesh. The CH is also the surface of the minimal area that envelops a 3D mesh (Lancaster et al. 1999). The exposed surface obtained with other techniques depends on the interaction between the intrinsic resolution of the imaging data and the methodological parameters such as the size of the structure element used with a morphological closing. The CH of a cortical mesh retains the convex gyral and discard concave sulcal regions (Fig. 2, top) (Lancaster et al. 1999). The discarded concave regions (principally sulci) are replaced with convex equivalents (Fig. 2, top). Convex brain regions are simple to resolve consistently and the convex hull synthesized from the full or partial brain surface can be used for accurate spatial normalization within and between subjects and imaging modalities such as PET and MRI (Lancaster et al. 1999).

The GI measurements performed using this tool have fully replicated the classical finding of a nearly linear relationship between the GI and the logarithm of the brain volume among species of the primate order (Zilles et al. 1989). The brain volume and 3D GI measured using this tool were highly correlated with about 97% of variability in GI being accounted by intraordinal differences in the brain volume (Fig. 2, bottom), which was consistent with previous reports (Luders et al. 2006b; Nopoulos et al. 2000; Pillay and Manger 2007; Zilles et al. 1989; Zilles et al. 1988). The GI tool takes the hemispheric cortical mesh extracted by the standard BV pipeline and calculates the hemispheric GI value in under a minute.

Regional Gyrification (Sulcal Length and Depth)

Intersubject differences in the regional gyrification can be quantified by measuring the length and depth of individual cortical sulci (Amunts et al. 2000; Cheverud et al. 1990; Cykowski et al. 2008; Hulshoff Pol et al. 2006; Le Goualher et al. 2000; Lohmann et al. 2007; Lohmann et al. 1999; Thompson et al. 2002). Earlier research employed analysis techniques, translated directly from postmortem studies, which relied on the observer-dependent, manual tracing and measurements of sulcal landmarks (Amunts et al. 2000; Cheverud et al. 1990; Thompson et al. 1996). Methodological advances led to the development of observer-independent extraction of the spatial course of cortical sulci from high-resolution structural MRI data with two-dimensional (2-D) surfaces representing the median axis of cerebral sulci (Le Goualher et al. 1999; Lohmann et al. 1999; Mangin et al. 1995). We developed methods for automatic calculation of sulcal length and depth that can accommodate for the spatial discontinuity of sulcal ribbons, common observed in human cortical sulci (Ono et al. 1990). Our approach to measurements of regional gyrification is different from these chosen by other software libraries such as CARET (Van Essen et al. 2001) and FreeSurfeer (Fischl and Dale 2000). In the latter two packages, the sulcal depth is represented as a map of linear distance between the vertices of the cortical mesh and the exposed brain area. Our measurement of regional gyrification is based on classical neuroanatomical techniques where sulcal length and depth are calculated as distances along the curvature of the sulcus.

The computation of the sulcal length begins by identifying the exterior boundary (top ridge) and interior boundary (fundus) for a sulcus (Fig. 3, top) (Cykowski et al. 2007). The top ridge is calculaterd as the intersection between the sulcal mesh and the locally convex, exterior cortical surface. The parametric top ridge curve is created by parameterizing these locations using the uniform polynomial B-splines as described elsewhere (Kochunov et al. 2000). We used a freely distributed C++ B-spline library developed by SINTEF (http://www.sintef.org). Next, the algorithm identifies the interior boundary of the sulcal mesh, the fundus (Fig. 3, top). This is done by calculating the intersection between the sulcal mesh and a plane that is perpendicular to the top ridge curve (Fig. 3, top). The intersection point located at the greatest Euclidean distance from the top ridge is taken as one that resides on the fundus. This processing is repeated one hundred times at the uniform spacing along the top ridge curve. Similar to the top ridge curve the parametric fundus curve is created by fitting a B-spline. The sulcal length is calculated as the average length of the top ridge and fundus. Sulcal depth is measured at one hundred locations located at equidistant intervals along the long axis of the sulcus. Each sulcal depth measurement is calculated as the length of a curve, located on the sulcal surface, that connects the top ridge and the fundus. This measurement is made by first subdividing the top ridge and fundus into 100 intervals and then calculating the projection of the line that connects the corresponding points on the top ridge and fundus on to the sulcal mesh. The locations, on the sulcal mesh, identified by this projection are parameterarized and the length of this parametric curve is taken as the local depth measurement (Fig. 3, top).

Fig. 3.

Measurement of gyrification index (GI) using convex hull approach (top). The convex hull of the cortical mesh retains the gyral and discards the sulcal regions. A plot of the logarithm of the cerebral brain volume versus cortical GI shows a nearly linear relationship between brain volume and GI (r²=0.97)

This approach for measuring sulcal length and depth was chosen over other methods, such as parameterization of sulcal surface by solving diffusion equations, using active ribbons or non-uniform rational surface approximation approaches (Coulon et al. 2006; Cykowski et al. 2007; Le Goualher et al. 1999) to accommodate for potential interruptions of the cortical sulci by anastomotic gyrification. In humans, the spatial course of all primary sulci, sole exception is the central sulcus, are commonly (20–80%) interrupted by anastomotic gyri and sulci (Ono et al. 1990). Anastomotic gyrification occurs during postnatal development. It is associated with cerebral myelination and gives the finished look to the mature human cortex (Ono et al. 1990). Methods that parameterize the sulcal surface require contiguity of the sulcal mesh and therefore, are difficult to use outside the central sulcus (Coulon et al. 2006; Cykowski et al. 2007; Le Goualher et al. 1999). The approach that we developed can reconstruct the spatial course of a discontinuous sulcus from multiple mesh segments. The measurements of the top and bottom sulcal length are calculated for the entire sulcus. The measurements of the sulcal depth can optionally be calculated across for the entire sulcus and by discarding measurements performed over the empty, inter-segment space (Fig. 3, bottom).

Measurements of Cortical Gray Matter Thickness

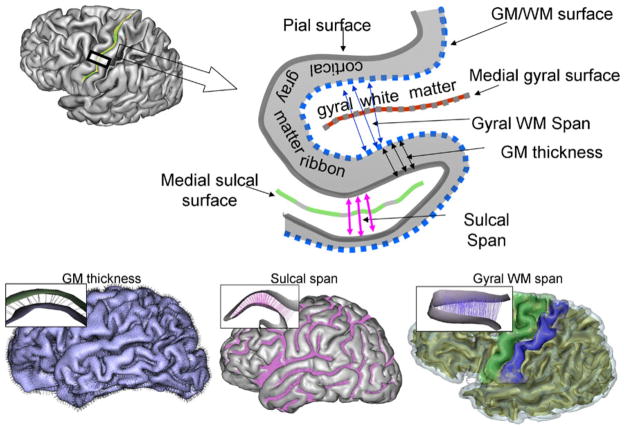
GM thickness (GMT) is commonly defined as the distance from the outer cortical surface to the inner cortical WM-GM boundary (Fig. 4) or a related symmetric measure (Fischl and Dale 2000; Lerch and Evans 2005). GMT is an indirect measure of the complex cortical architecture, with changes due to cortical myelination, synaptic pruning and cell density being the candidate cellular events responsible for its age- and disease-related changes (Huttenlocher and Dabholkar 1997). Computationally, cortical thickness is determined by measuring the distance between two polygonal meshes, one representing the pial cortical surface and the other the white-gray interface. Multiple GMT measurements algorithms have been proposed to deal with the complex topography of the cerebral cortex. Relatively simple and fast techniques that look up the distance between nearest neighbor vertices in the two meshes can produce errors that lead to increased variability (Fischl and Dale 2000; Lerch and Evans 2005). Other methods that iteratively solve the 3D Laplace equation for every point between two meshes, and calculate the streamline distances between two surfaces, are performance-limited as it can take many hours of computations per subject (Fischl and Dale 2000; Lerch and Evans 2005).

Fig. 4.

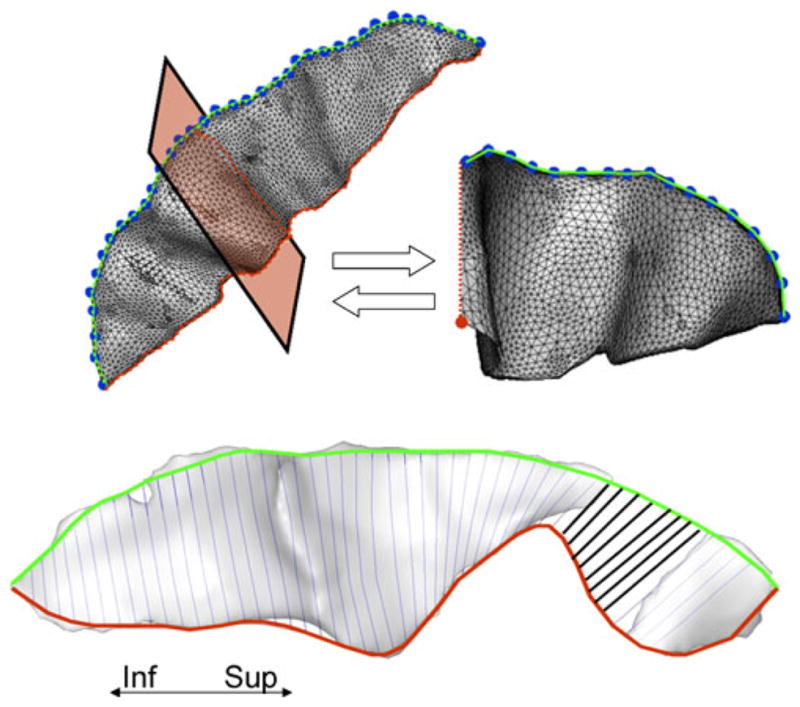
Parameterarization of the sulcal top ridge and fundus is shown in the top panel. Locations of the intersection between sulcal body and exterior convex hull (small green dots) are parameterarized to create the top ridge curve (left). The top ridge curve is re-sampled at equidistant intervals at the original resolution of the image. These locations (large blue points) are used as control points to calculate an intersection between a plane, perpendicular to the curve at this control point (red shaded area of the sulcus), and the sulcal mesh. The bottom ridge location is indentified as the point that belongs to this intersection (red points) and is the furthest from the top (big red dot). These, locations along the sulcal fundus are parameterarized to create the parametric fundus curve (top, right). Measuring the length and depth for an interrupted sulcus (pre-central) is shown in the bottom panel. The pre-central sulcus is commonly interrupted at its superior aspect. The depth measurements across the empty space between segments (bold lines) can be included into the calculation of the average sulcal depth

Our GMT measurement tool implements a “normal-average” algorithm that was judged to be a good compromise between the accuracy and performance (Lerch and Evans 2005). We improved this algorithm by using the surface curvature to cull vertexes whose curvature exceeds a certain threshold. The GMT is measured as the Euclidian distance from an inner mesh vertex to the outer mesh along the direction normal to the inner mesh polygon. The measurement is repeated, inward, along the direction normal the outer mesh and the two distances are averaged (Fig. 3). The consistency of the distance measurements is insured by a verifying that the line that connects the two surfaces does not intersect any other polygons, inner or outer, along the way.

Prior to the GMT measurement, curvature analysis is used to identify vertexes that are likely to produce erroneous GMT measurements. Mean curvature is calculated for each vertex based on local changes in normal vectors along the surface. The curvature values are expressed in degrees or radians with negative values corresponding to concave and positive values correspond to convex deviations from a flat surface. After several trials, we empirically established that the absolute curvature threshold as <±18° (±0.1*π). This threshold corresponds to about four standard deviations from the average curvature. It removes a small fraction of voxels (~2–4%) in regions of high curvature such as gyral crowns and sulcal ridges. This threshold has successfully removed erroneous mesh nodes in images collected with spatial resolution ranging from 1×1×1mm to 0.3×0.3×0.3 mm The entire processing usually takes under 10 min per hemisphere. The whole-brain average GMT measurements calculated with this method were highly correlated (r>0.80) with the whole-brain GMT measurements performed by a more computationally intense GMT measurement method implemented in the FreeSurfer package (Fischl and Dale 2000)

Measurements of Sulcal and Gyral WM Spans

In addition to GMT, the BV library provides two additional measurements, which proved useful to quantity cerebral changes during aging and brain disorders. Aging is associated with regional cerebral atrophy and volume loss observed as an increase in the intra-sulcal CSF spaces and more steeply curved gyri (Magnotta et al. 1999). The magnitude of this loss cannot be explained by changes in the GMT alone and therefore two other measurements—sulcal span and gyral span—were developed to quantify the degree of cerebral atrophy.

Sulcal Span (SS)

SS is defined as the average width of the intra-sulcal CSF space along the normal projections to the medial sulcal mesh (Fig. 3b). SS measurements are performed for individual cortical sulci using the medial sulcal meshes. A medial sulcal mesh transverses the sulcal space in the middle of the sulcal “width” dimension, parallel to the sulcal borders and spans the entire sulcal “depth” dimension. It is obtained by calculating three-dimensional medial axis, also known as skeletonization (Mangin et al. 1996). Sulcal labels and then assigned by automated/manual labeling and covers the entire sulci from the sulcal ridge to the gyral crown (Fig. 1f). Sulcal span is calculated as the Euclidean distance between the two intersection points on the gyral gray matter mesh on either side of the sulcal surface (Fig. 4 top), along directions normal to the medial sulcal surface. SS was calculated as the average of 500–5,000 distance measurements depending on the size of the structure (Fig. 4, bottom). Measurements from points located within 4 mm of an intersection with adjacent sulci were excluded from averaging. Sulcal spans attempts where only one end of the vector intersected the cortical mesh were rejected.

The output of this process is the average width and its standard deviation. Optionally, a regional map of SS values can be saved as a texture mapped on the sulcal mesh. Additionally, this tool can report the average GM thickness measured on the opposing gyral banks. The output is written to a tab delimited text file where each line contains a sulcal name, average span, standard deviation, average cortical thickness (if the GMT map was available) and the number of width measurements used for average and standard deviation.

Gyral Span (GS)

GS is defined as the average width of the intra-gyral WM space with intention to quantify intersubject differences in the gyral WM volume. Axonal WM constitutes the bulk of the gyral tissue and its reduction is responsible for age-related decline in cerebral gyrification with the shape of the cortical gyri becoming more steeply curved (Magnotta et al. 1999). Intuitively, GS is similar to the sulcal span measurement, but it is measured in the gyral WM space.

GS is calculated as the Euclidean distance between two points residing on opposing sides of the gyral white matter mesh in the direction normal to the medial gyral WM surface (Fig. 2). Similar to sulcal mesh, the medial gyral WM mesh is the surface that transverses the gyral WM space, parallel to the gyral GM/WM borders and covers the entire gyral “depth” from crest to base (Fig. 2). GS measurements for individual gyri are made based on the gyral segmentation and labeling step of BrainVisa OBM pipeline (Cachia et al. 2003). It is performed by calculating normal projection from the medial mesh and testing for the intersections with the gyral polygons for the gyral surface. If the intersection points are found for both normal projection the distance between them is taken as a gyral span measurement. The spatial resolution and the number of these measurements per gyrus are based on the number of vertexes for which the normal projection intersects the gyral surface on either end. The medial gyral mesh is sampled with the uniform vertex density that is approximately equal to the spatial resolution of the original imaging. Typically, GS is calculated as the average of 2000 distance measurements depending on the size of the structure. The output of this process is the GS or average width and its standard deviation and saved in the output format that is similar to one used by the SS tool.

Scan-Rescan Variability

Three authors (PK, WR and JL) were imaged three times over a two-week period using an imaging protocol discussed in (Kochunov et al. 2007) using a Siemens Tim-TRIO 3T MRI scanner This protocol included: T1w anatomical MRI data collected at 0.8 mm isotropic resolution, diffusion tensor data (DTI) collected at high-angular (86 direction, b=0 and 700 s/mm2) and spatial (1.7×1.7×3 mm) resolution and resting cerebral blood flow data collected using pseudo-continuous arterial spin labeling (ASL) sequence at the spatial resolution 3.5 mm isotropic resolution. The T1-structural data were processed to measure the following parameters: whole-brain WM/GM volumes, whole-brain average GM thickness, length, depth and sulcal span for the central sulcus and gyral WM span for the precentral gyrus. DTI data were processed to measure whole-brain average FA data using track-based-spatial-statistics approach descried elsewhere (Kochunov et al. 2007). ASL data were processed to measure resting CBF as described elsewhere (Wey et al. 2010). The goal of this analysis was to estimate scan-rescan variability associated with each of the measurements. The results were summarized as the average standard deviation and the highest and lowest standard deviations per-subjects (Table 2). The average scan-rescan variability for the tools included in this library was 1.8% and this was lower than such standard morphological measurements as the cerebral volume of GM and WM tissues (4.3% and 1.9%, respectively). The 3D GI measurements had the lowest variability (1.1%) while measurements of sulcal depth showed the highest variability (2.4%). Overall, the average scan-rescan variability was comparable to this of the DTI-FA measurements and much lower to more physiologically variable measurement of resting-state CBF.

Table 2.

Scan-rescran reproducibility measurement for three subjects imaged three times over two-week period. The data is presented as the average standard deviation expressed as percent of the average value for individual subjects and the highest and lowest standard deviations for individual subjects

	3D GI	GM volume	WM volume	GM thickness	Length*	Depth*	Sulcal Span*	Gyral span**	FA	CBF
Average Standard Deviation	1.12%	4.34%	1.92%	1.72%	1.75%	2.51%	1.71%	2.23%	1.35%	9.50%
Range (lowest-highest)	0.85%–1.35%	4.16%–4.70%	1.44%–2.16%	0.83–2.41%	0.92–2.16%	1.71–2.9%	0.91%–2.3%	1.5%–2.7%	0.8%–1.60%	5.2%–13.1%

Examples with Discussion

The BV library of tools is available as a single integrated software package distributed as a plugin application for popular structural analysis software, BrainVisa. This library can be downloaded as both, the source code and as the natively compiled binary distribution for Linux, MacOS X and Microsoft Windows. It is freely available for academic (noncommercial) use. Below, we summarize several examples demonstrating how this library of tools was used to study cerebral development as primary gyrogenesis, cerebral aging, and the genetics of gyrification.

Cerebral Development: Quantification of Primary Gyrogenesis (PG)

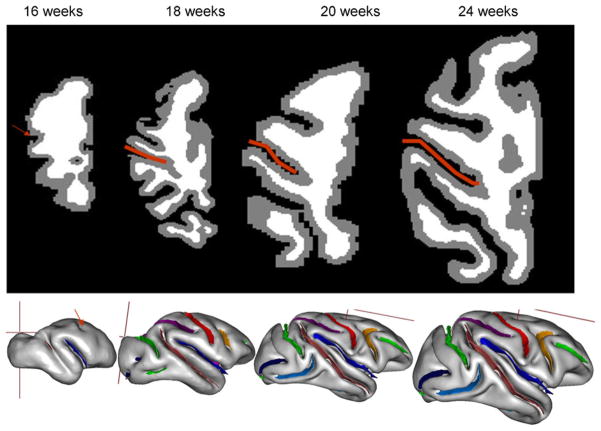
PG is the developmental process that transforms the smooth (lissencephalic) cortex of a developing mammalian brain toward its mature, convolved (gyrencephalic) state by sculpting an intricate pattern of gyri and sulci. Emerging knowledge of the fetal origins of adult diseases now recognizes that many trajectories to health or disease take root because of the developmental alterations in the prenatal stage (Barker 2004). PG consists of a complex series of morphogenetic events influenced by environmental, genetic as well as epigenetic factors. Its mechanisms are poorly understood, preventing a clear understanding of the significance of aberrant cerebral gyrification reported in disorders such as autism and schizophrenia (Bonnici et al. 2007; Gaser et al. 2006). Among the many theories that attempt to explain this process, none has been experimentally validated (Richman et al. 1975; Toro and Burnod 2005; Van Essen 1997; Welker 1990). This is partly because precise morphological measurements of changes during PG are difficult to obtain. In particular, rapid morphological changes lead to difficulties in quantification of the regional trends due to a lack of homologous features from one time point to another (Fig. 5).

Fig. 5.

Regional markers of cerebral atrophy: GM thickness, and sulcal and gyral WM spans (top). A sulcal span (solid line) was defined as a 3D distance between opposing points on the GM mesh along the normal projections to the medial sulcal mesh. A gyral WM span (dotted line) was defined as the 3-D distance between opposing points on the WM mesh along the normal projection to the medial sulcal mesh. These measurements were performed for all vertexes of the corresponding meshes, resulting in averaging of ~2–5000 measurements (bottom)

Earlier research on the morphology of the PG primarily relied on quantification of global descriptors such as brain volume and GI (Grossman et al. 2006; Hu et al. 2009). More recently, Studholme and colleagues applied a deformation field morphometry approach to quantify the regional pattern of growth over time (Habas et al. 2010; Rajagopalan et al. 2010; Studholme et al. 2006). This approach uses a nonlinear alignment to encode a regional spatial transformation between images collected at different times during longitudinal development. Regional volume changes are quantified using the Jacobian determinants. One limitation of this approach is that it requires a homology in the morphological features between two images or the one-to-one transformation cannot be achieved. This is difficult to achieve in a rapidly developing fetal brain where the regional growth rates can be highly non-uniform (Fig. 5 top) (Habas et al. 2010; Rajagopalan et al. 2010; Studholme et al. 2006).

OBM provides a more intuitive solution to the lack of morphological homology during PG (Fig. 5, bottom). The progression of PG is quantified by measuring the rates of growth for individual cortical structures. We used this approach to measure to contribution of regional gyrification toward the changes in the whole-brain GI (Kochunov et al. 2009b). We measured growth of the length and depth for ten primary cortical sulci from longitudinal and cross-sectional antenatal MRI data collected in ten normally developing baboon fetuses from week 17 to week 24 of the 26 week-long pregnancy. We observed that together, the growth in sulcal length and depth sulci explained ~95% of the intersubject differences in the GI. The changes in GI were predominantly driven by the growth in the sulcal length. At the 24th week of the prenatal development, the average sulcal length reached ~80% of its adult value, while the average sulcal depth was only 50% of its adult value. We compared these trend to those reported in ferret (Smart and McSherry 1986) and observed that PG trends in baboons were divergent in several important, possibly due to the species-dependent phenomena. The primary and secondary gyrogenesis are well differentiated in time in baboon but not in ferret. In ferrets, the growth in sulcal length and depth contributed uniformly to changes GI. Additionally, the rate of sulcal elongation in ferret was uniform and proportional to the rate of sulcal deepening. In baboon, the rate of sulcal elongation was uniform across cortex, but the rate of sulcal deepening was regionally variable and was higher in the early maturing, occipital areas of the brain (Kochunov et al. 2009b). These findings suggested that ontogenic processes that constitute PG are diverse and possibly driven by different factors in primates than in non-primates. In summary, the OBM approach provided using the BV tools is analytically robust and provides a quantitative means to monitor rapid changes during primary gyrification (Fig. 6).

Fig. 6.

Axial brain images (top) detail longitudinal development the central sulcus region (red line) during primary gyrification. These images demonstrate the lack of morphological homology among different stages of cerebral development and this limits the usefulness of the voxel-wise approaches. The object based morphology approach (bottom) overcomes this limitation by directly extracting shape descriptors such as the length and depth of cortical sulci

Cerebral Aging: Quantification of Cortical Atrophy

Advances in high-resolution, sMRI paved the way for non-invasive, systematic and regionalized studies of morphology of cerebral aging. To keep track with the technological improvement in the quality of imaging data, sensitive and quantitative measures of cerebral aging process were needed to help study the trajectory of age-related change. The BV tools were developed to help fill this need. Our tools provide measurements that complement more traditional quantitative assessment of cerebral health such as the volumes of hippocampus and temporal lobe (Freedman et al. 1984; Pfefferbaum et al. 1990; Steiner et al. 1985), estimation of cerebral boundary shift (Smith et al. 2002; Studholme et al. 2004; Thompson et al. 2004; Thompson et al. 2001) and voxel-based morphometry techniques (Ashburner and Friston 2000; Good et al. 2002; Winkler et al. 2009). Using the BV tools, our group and others have demonstrated that cerebral aging trends were regionally heterochronic and heterogeneous (Coyle et al. 2006; Kochunov et al. 2005; Kochunov et al. 2009f; Kochunov et al. 2008). The multi-modal cortical regions, responsible for higher cognitive function, showed age-related changes earlier and the rates of age-related decline were higher than these for the unimodal sensory and that motor regions.

During senesces the brain undergoes a recapitulation of the gyrification process observed during development, resulting in age-related de-gyrification (Magnotta et al. 1999). The shape of gyri and sulci starts changing after the 3rd-to-4th decades of life with gyri becoming more sharply curved and sulci becoming more open and shallow (Magnotta et al. 1999; Raz et al. 1997; Raz et al. 1998). We used the sulcal depth, GMT, SS and GS tools to study the regional trends of this age-related de-gyrification process. We observed that the age-related sulcal widening, during the 3rd to 10th decades, occurred at a rate of 0.7 mm/decade (Kochunov et al. 2005). This was partially explained by the reduction in the gyral WM span and decline in cortical GMT (Cruchaga et al. 2009; Im et al. 2008; Janssen et al. 2009; Jouvent et al. 2008; Kochunov et al. 2008; Liu et al. 2010). This age-related decline in gyrification was regionally heterogeneous with multimodal areas showing significantly higher rates of decline than for motor and sensory cortices (Im et al. 2008; Jouvent et al. 2008; Kochunov et al. 2005; Kochunov et al. 2008; Liu et al. 2010). Combined analyses of regional gyrification and measurements of cerebral WM integrity, revealed several novel findings regarding the age-related decline in the cortical glucose metabolism and neurocognitive functions (Kochunov et al. 2009e; Kochunov et al. 2008; Kochunov et al. 2007). We showed that decline in gyral WM volumes, together with an increase in hyper-intense WM lesion volumes significantly correlated with the decline in the cortical glucose metabolism (Kochunov et al. 2009e). We also showed that regionally specific measurements of cerebral gyrification can be useful to help explaining intersubject differences in clinically important measurement of cognition such as the processing speed and executive function (Kochunov et al. 2009a; Kochunov et al. 2009f).

These BV tool measurements of cortical morphology provided an intuitive and precise way to track cortical changes associated with aging. Although sulcal morphology trends do not provide direct insight into the cellular/molecular nature of aging, the mechanisms behind them appear to be intimately tied with the regional reduction in GM and WM tissue volumes and decline in subcortical integrity. These measurements can potentially be used for clinical trials that assess how well neuro-protective and anti-dementia drugs are resisting degenerative changes. A broader use of these morphometric measures should help establish their range of variation in normal aging so that we can better detect deviations that may signal the onset of mild cognitive impairment, Alzheimer’s disease and other ageing related neurodegenerative disorders.

Genetics of Gyrification: Quantification of Genetic Contribution to Intersubject Differences

Neuroimaging and genomics are two rapidly developing fields of modern neuro-biological science with a natural synergy between them (Glahn et al. 2007). Modern genetics uses refined statistical modeling to understand complex trait/environment/gene interactions for quantitative phenotypes, while modern neuroimaging provides quantitative phenotyping with exceptional detail and reproducibility. Combining these fields will help answer central questions regarding our understanding of the neurobiology of human cerebrum (Glahn et al. 2007). A better understanding of the genetic sources and consequences of morphological variation in brain structure should have significant impact on neuroscience, psychology and psychiatry as well as for evolutionary biology. Recently, we applied the BV tools to study the genetic component of cerebral variability and aging (Kochunov et al. 2009d; Kochunov et al. 2010c; Rogers et al. 2007; Rogers et al. 2010; Winkler et al. 2009).

We started by testing two hypotheses regarding the common genetic variance gyrification and brain volume (Kochunov et al. 2009c; Rogers et al. 2010). First, we hypothesized that variations in the whole brain and regional gyrification would be heritable. We tested these predictions in both non-human primates and humans. Genetic analyses showed that the whole brain GI measurements were significantly heritable in both species (Rogers et al. 2010). We also demonstrated evidence for significant genetic contributions to regional gyrification, specifically significant heritability for the length and depth of primary cortical sulci in baboons (Kochunov et al. 2009c). These results indicated that heritability of sulcal length and depth may be regionally modulated by arcuate U-fiber systems. However, additional research incorporating sulcal measurement with white matter tractography are necessary to unravel the complexity of genetic contributions to cortical morphology (Kochunov et al. 2009c). Second, we tested the hypothesis that the genetic factors that influence individual variation in brain volume will also influence gyrification. The genetic correlation coefficients (ρG) between cerebral volume and GI were significant and negative (ρG=−0.73 and −0.77; p<0.05; in humans and baboons, respectively). These results demonstrated that individual variation in global and regional gyrification is under strong genetic control and that there is a common among-species relationship between gyrification and brain volume. This correlation implied that there is an overlapping set of genes that influence both brain volume and gyrification.

We are in the processes of using the BV tools to study the genetics of cerebral aging. Our preliminary findings indicate that measurements of cerebral atrophy such GM thickness (Winkler et al. 2009), SS and GS (unpublished data) are significantly heritable. We showed that the cortical thickness and gyral surface area measurements, two traits commonly used in aging research, were genetically independent traits (Winkler et al. 2009). This suggested that cortical thickness and cortical surface area measurements should be considered separately and preferred over gray matter volume and density measurement for imaging-based genetic studies. We also previously found that the genetic factors that contributed to hypertension also contributed to the atrophy of the cerebral WM (Kochunov et al. 2010b; Kochunov et al. 2009d; Kochunov et al. 2010c) and therefore these factors are the primary candidates for more detailed genetic analysis.

Conclusion

The BV library of tools provide detailed measurements of global and regional gyrification, gray matter thickness and sulcal and gyral white matter spans. We described the individual components in this set of software tools and summarized their use in several research studies from this and other centers. Example studies focused on measurement capabilities during brain development, for assessing the aging brain and to determine the genetic component of intersubject variability in cortical anatomy.