Abstract
Ultra-high dimensional data often display heterogeneity due to either heteroscedastic variance or other forms of non-location-scale covariate effects. To accommodate heterogeneity, we advocate a more general interpretation of sparsity which assumes that only a small number of covariates influence the conditional distribution of the response variable given all candidate covariates; however, the sets of relevant covariates may differ when we consider different segments of the conditional distribution. In this framework, we investigate the methodology and theory of nonconvex penalized quantile regression in ultra-high dimension. The proposed approach has two distinctive features: (1) it enables us to explore the entire conditional distribution of the response variable given the ultra-high dimensional covariates and provides a more realistic picture of the sparsity pattern; (2) it requires substantially weaker conditions compared with alternative methods in the literature; thus, it greatly alleviates the difficulty of model checking in the ultra-high dimension. In theoretic development, it is challenging to deal with both the nonsmooth loss function and the nonconvex penalty function in ultra-high dimensional parameter space. We introduce a novel sufficient optimality condition which relies on a convex differencing representation of the penalized loss function and the subdifferential calculus. Exploring this optimality condition enables us to establish the oracle property for sparse quantile regression in the ultra-high dimension under relaxed conditions. The proposed method greatly enhances existing tools for ultra-high dimensional data analysis. Monte Carlo simulations demonstrate the usefulness of the proposed procedure. The real data example we analyzed demonstrates that the new approach reveals substantially more information compared with alternative methods.
Keywords: Penalized Quantile Regression, SCAD, Sparsity, Ultra-high dimensional data
1 Introduction
High-dimensional data are frequently collected in a large variety of research areas such as genomics, functional magnetic resonance imaging, tomography, economics and finance. Analysis of high-dimensional data poses many challenges for statisticians and calls for new statistical methodologies and theories (Donoho, 2000; Fan and Li, 2006). We consider the ultra-high dimensional regression setting in which the number of covariates p grows at an exponential rate of the sample size n.
When the primary goal is to identify the underlying model structure, a popular approach for analyzing ultra-high dimensional data is to use the regularized regression. For example, Candes and Tao (2007) proposed the Dantzig selector; Candes, Wakin and Boyd (2007) proposed weighted L1-minimization to enhance the sparsity of the Dantzig selector; Huang, Ma and Zhang (2008) considered the adaptive lasso when a zero-consistent initial estimator is available; Kim, Choi and Oh (2008) demonstrated that the SCAD estimator still has the oracle property in ultra-high dimension regression when the random errors follow the normal distribution; Fan and Lv (2011) investigated non-concave penalized likelihood with ultra-high dimensionality; and Zhang (2010) proposed a minimax concave penalty (MCP) for penalized regression.
It is common to observe that real life ultra-high dimensional data display heterogeneity due to either heteroscedastic variance or other forms of non-location-scale covariate effects. This type of heterogeneity is often of scientific importance but tends to be overlooked by existing procedures which mostly focus on the mean of the conditional distribution. Furthermore, despite significant recent developments in ultra-high dimensional regularized regression, the statistical theory of the existing methods generally requires conditions substantially stronger than those usually imposed in the classical p < n framework. These conditions include homoscedastic random errors, Gaussian or near Gaussian distributions, and often hard-to-check conditions on the design matrix, among others. These two main concerns motivate us to study nonconvex penalized quantile regression in ultra-high dimension.
Quantile regression (Koenker and Bassett, 1978) has become a popular alternative to least squares regression for modeling heterogeneous data. We refer to Koenker (2005) for a comprehensive introduction and to He (2009) for a general overview of many interesting recent developments. Welsh (1989), Bai and Wu (1994) and He and Shao (2000) established nice asymptotic theory for high-dimensional M-regression with possibly nonsmooth objective functions. Their results apply to quantile regression (without the sparseness assumption) but require that p = o(n).
In this paper, we extend the methodology and theory of quantile regression to ultra-high dimension. To deal with the ultra-high dimensionality, we regularize quantile regression with a nonconvex penalty function, such as the SCAD penalty and the MCP. The choice of nonconvex penalty is motivated by the well-known fact that directly applying the L1 penalty tends to include inactive variables and to introduce bias. We advocate a more general interpretation of sparsity which assumes that only a small number of covariates influence the conditional distribution of the response variable given all candidate covariates; however, the sets of relevant covariates may be different when we consider different segments of the conditional distribution. By considering different quantiles, this framework enables us to explore the entire conditional distribution of the response variable given the ultra-high dimensional covariates. In particular, it can provide a more realistic picture of the sparsity patterns, which may differ at different quantiles.
Regularized quantile regression with fixed p was recently studied by Li and Zhu (2008), Zou and Yuan (2008), Wu and Liu (2009) and Kai, Li and Zou (2011). Their asymptotic techniques, however, are difficult to extend to the ultra-high dimension. For high dimensional p, Belloni and Chernozhukov (2011) recently derived a nice error bound for quantile regression with the L1-penalty. They also showed that a post-L1-quantile regression procedure can further reduce the bias. However, in general post-L1-quantile regression does not possess the oracle property.
The main technical challenge of our work is to deal with both the nonsmooth loss function and the nonconvex penalty function in ultra-high dimension. Note that to characterize the solution to quantile regression with nonconvex penalty, the Karush-Kuhn-Tucker (KKT) local optimality condition is necessary but generally not sufficient. To establish the asymptotic theory, we novelly apply a sufficient optimality condition for the convex differencing algorithm; which relies on a convex differencing representation of the penalized quantile loss function (Section 2.2). Furthermore, we employ empirical process techniques to derive various error bounds associated with the nonsmooth objective function in high dimension. We prove that with probability approaching one, the oracle estimator, which estimates the zero coefficients as zero and estimates the nonzero coefficients as efficiently as if the true model is known in advance, is a local solution of the nonconvex penalized sparse quantile regression with either the SCAD penalty or the MCP penalty for ultra-high dimensionality.
The theory established in this paper for sparse quantile regression requires much weaker assumptions than those in the literature, which alleviates the difficulty of checking model adequacy in the ultra-high dimension settings. In particular, we do not impose restrictive distributional or moment conditions on the random errors and allow their distributions to depend on the covariates (Condition (C3) in the Appendix). Kim, Choi and Oh (2008) derived the oracle property of the high-dimensional SCAD penalized least squares regression under rather general conditions. They also discovered that for the squared error loss, the upper bound of the dimension of covariates is strongly related to the highest existing moment of the error distribution. The higher the moment exists, the larger p is allowed for the oracle property; and for the normal random errors the covariate vector may be ultra-high dimensional. In fact, most of the theory in the literature for ultra-high dimensional penalized least squares regression requires either the Gaussian or Sub-Gaussian condition.
The rest of the paper is organized as follows. In Section 2, we propose sparse quantile regression with nonconvex penalty, and introduce a local optimality condition for nonsmooth nonconvex optimization. We further study the asymptotic theory for sparse quantile regression with ultra-high dimensional covariates. In Section 3, we conduct a Monte Carlo study and illustrate the proposed methodology by an empirical analysis of an eQTL microarray data set. All technical proofs are given in the online supplementary appendix of this paper.
2 Nonconvex Penalized Quantile Regression
2.1 The Methodology
Let us begin with the notation and statistical setup. Suppose that we have a random sample {Yi, xi1, …, xip}, i = 1, …, n, from the following model:
| (1) |
where β = (β0, β1, …, βp)T is a (p + 1)-dimensional vector of parameters, xi = (xi0, xi1, …, xip)T with xi0 = 1, and the random errors εi satisfy P (εi ≤ 0|xi) = τ for some specified 0 < τ < 1. The case τ = 1/2 corresponds to median regression. The number of covariates p = pn is allowed to increase with the sample size n. It is possible that pn is much larger than n.
The true parameter value β0 = (β00, β01 …, β0pn)T is assumed to be sparse; that is, the majority of its components are exactly zero. Let A = {1 ≤ j ≤ pn : β,0j ≠ 0} be the index set of the nonzero coefficients. Let |A| = qn be the cardinality of the set A, which is allowed to increase with n. In the general framework of sparsity discussed in Section 1, both the set A and the number of nonzero coefficients qn depend on the quantile τ. We omit such dependence in notation for simplicity. Without loss of generality, we assume that the last pn − qn components of β0 are zero; that is, we can write , where 0 denotes a (pn − qn)- dimensional vector of zeros. The oracle estimator is defined as , where β̂1 is the quantile regression estimator obtained when the model is fitted using only relevant covariates (i.e., those with index in A).
Let X = (x1, …, xn)T be the n × (pn + 1) matrix of covariates, where are the rows of X. We also write X = (1, X1, …, Xpn), where 1, X1, …, Xp are the columns of X and 1 represents an n-vector of ones. Define XA to be the submatrix of X that consists of its first qn + 1 columns; similarly denoted by XAc the submatrix of X that consists of its last pn − qn columns. For the rest of this paper, we often omit the subscript n for simplicity. In particular, we let p and q stand for pn and qn, respectively.
We consider the following penalized quantile regression model
| (2) |
where ρτ (u) = u {τ − I(u < 0)} is the quantile loss function (or check function), and pλ(·) is a penalty function with a tuning parameter λ. The tuning parameter λ controls the model complexity and goes to zero at an appropriate rate. The penalty function pλ(t) is assumed to be nondecreasing and concave for t ∈ [0, +∞), with a continuous derivative ṗλ(t) on (0, +∞). It is well known that penalized regression with the convex L1 penalty tends to over-penalize large coefficients and to include spurious variables in the selected model. This may not be of much concern for predicting future observations, but is nonetheless undesirable when the purpose of the data analysis is to gain insights into the relationship between the response variable and the set of covariates.
In this paper, we consider two commonly used nonconvex penalties: the SCAD penalty and the MCP. The SCAD penalty function is defined by
The MCP function has the form
2.2 Difference Convex Program and a Sufficient Local Optimality Condition
Kim, Choi and Oh (2008) investigated the theory of high-dimension SCAD penalized least squares regression by exploring the sufficient condition for local optimality. Their formulation is quite different from those in Fan and Li (2001), Fan and Peng (2004) and Fan and Lv (2009). For the SCAD-penalized least squares problem, the objective function is also nonsmooth and nonconvex. By writing , where and represent the positive part and the negative part of βj respectively, the minimization problem can be equivalently expressed as a constrained smooth optimization problem. Therefore, the second-order sufficient condition (Proposition 3.3.2, Bertsekas, 2008) from constrained smooth optimization theory can be applied. Exploring local optimality condition directly leads to asymptotic theory for SCAD penalized least squares regression under more relaxed conditions.
However, in our case, the loss function itself is also nonsmooth in addition to the non-smoothness of the penalty function. As a result, the above local optimality condition for constrained smooth optimization is not applicable. In this paper, we novelly apply a new local optimality condition which can be applied to a much broader class of nonconvex nonsmoothing optimization problem. More specifically, we consider penalized loss functions belonging to the class
This class of functions are very broad as it covers many other useful loss functions in addition to the quantile loss function, for example the least squares loss function, the Huber loss function for robust estimation and many loss functions used in the classification literature. Numerical algorithms based on the convex differencing representation and their convergence properties have been systematically studied by Tao and An (1997), An and Tao (2005), among others, in the filed of nonsmooth optimization. These algorithms have seen some recent applications in statistical learning, for example Liu, Shen and Doss (2005), Collobert et al. (2006), Kim, Choi and Oh (2008) and Wu and Liu (2009), among others.
Let dom(g) = {x : g(x) < ∞}be the effective domain of g and let ∂g(x0) = {t : g(x) ≥ g(x0) + (x − x0)Tt, ∀ x} be the subdifferential of a convex function g(x) at a point x0. Although subgradient-based KKT condition has been commonly used for characterizing the necessary conditions for nonsmooth optimization; sufficient conditions for characterizing the set of local minima of nonsmooth nonconvex objective functions have not been explored in the statistical literature. The following lemma which was first presented and proved in Tao and An (1997), see also An and Tao (2005), provides a sufficient local optimization condition for the DC program based on the subdifferential calculus.
Lemma 2.1
These exists a neighborhood U around the point x* such that ∂h(x) ∩ ∂g(x*) ≠ ∅, ∀ x ∈ U ∩ dom(g). Then x* is a local minimizer of g(x) − h(x).
2.3 Asymptotic Properties
For notational convenience, we write , where zi = (xi0, xi1, …, xiqn)T and wi = (xi(qn+1), …, xipn)T. We consider the case in which the covariates are from a fixed design. We impose the following regularity conditions to facilitate our technical proofs.
-
(C1)
(Conditions on the design) There exists a positive constant M1 such that for j = 1, … q. Also |xij| ≤ M1 for all 1 ≤ i ≤ n, q + 1 ≤ j ≤ p.
-
(C2)(Conditions on the true underlying model) There exist positive constants M2 < M3 such that
where λmin and λmax denote the smallest eigenvalue and largest eigenvalue, respectively. It is assumed that are in general positions (Section 2.2, Koenker, 2005) and that there is at least one continuous covariate in the true model.
-
(C3)
(Conditions on the random error) The conditional probability density function of εi, denoted by fi(·|zi), is uniformly bounded away from 0 and ∞ in a neighborhood around 0 for all i.
-
(C4)
(Condition on the true model dimension) The true model dimension qn satisfies qn = O(nc1) for some 0 ≤ c1 < 1/2.
-
(C5)
(Condition on the smallest signal) There exist positive constants c2 and M4 such that 2c1 < c2 ≤ 1 and n(1−c2)/2 min1≤j≤qn |β0j| ≥ M4.
Conditions (C1), (C2), (C4) and (C5) are common in the literature on high-dimensional inference, for example, condition (C2) requires that the design matrix corresponding to the true model is well behaved, and condition (C5) requires that the smallest signal should not decay too fast. In particular, they are similar to those in Kim et al. (2008). Condition (C3), on the other hand, is more relaxed than the Gaussian or Subgaussian error condition usually assumed in the literature for ultra-high dimensional regression.
To formulate the problem in the framework of Section 2.2, we first note that the nonconvex penalized quantile objective function Q(β) in (2) can be written as the difference of two convex functions in β:
where and . The form of Hλ(βj) depends on the penalty function. For the SCAD penalty, we have
while for the MCP function, we have
Next, we characterize the subdifferentials of g(β) and h(β), respectively. The subdifferential of g(β) at β is defined as the following collection of vectors:
where vi = 0 if and vi ∈ [τ − 1, τ] otherwise; l0 = 0; for 1 ≤ j ≤ p lj = sgn(βj) if βj ≠ 0 and lj ∈ [−1, 1] otherwise. In this definition, sgn(t) = I(t > 0) − I(t < 0). Furthermore, for both the SCAD penalty and the MCP penalty, h(β) is differentiable everywhere. Thus the subdifferential of h(β) at any point β is a singleton:
For both penalty functions, for j = 0. For 1 ≤ j ≤ p,
for the SCAD penalty; while for the MCP penalty
The application of Lemma 2.1 utilizes the results from the following two lemmas. The set of the subgradient functions for the unpenalized quantile regression is defined as the collection of the vector s(β̂) = (s0(β̂), s1(β̂), …, sp(β̂))T, where
for j = 0, 1, …, p, with vi = 0 if and vi ∈ [τ − 1, τ] otherwise.
Lemmas 2.2 and 2.3 below characterize the properties of the oracle estimator and the subgradient functions corresponding to the active and inactive variables, respectively.
Lemma 2.2
Suppose that conditions (C1)–(C5) hold and that λ = o(n−(1−c2)/2). For the oracle estimator β̂, there exist which satisfies if and if , such that for sj(β̂) with , with probability approaching one, we have
| (3) |
Lemma 2.3
Suppose that conditions (C1)–(C5) hold and that qn−1/2 = o(λ), log p = o(nλ2) and nλ2 → ∞. For the oracle estimator β̂ and the sj(β̂) defined in Lemma 2.2, with probability approaching one, we have
| (4) |
Applying the above results, we will prove that with probability tending to one, for any β in a ball in
 with the center β̂ and radius λ/2, there exists a subgradient ξ = (ξ0, ξ1, …, ξp)T ∈ ∂g(β̂) such that
with the center β̂ and radius λ/2, there exists a subgradient ξ = (ξ0, ξ1, …, ξp)T ∈ ∂g(β̂) such that
| (5) |
Then by Lemma 2.1, we can demonstrate that the oracle estimator β̂ is itself a local minimizer. This is summarized in the following theorem.
Theorem 2.4
Assume that conditions (C1)-(C5) hold. Let
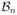 (λ) be the set of local minima of the nonconvex penalized quantile objective function (2) with either the SCAD penalty or the MCP penalty and tuning parameter λ. The oracle estimator
satisfies that
(λ) be the set of local minima of the nonconvex penalized quantile objective function (2) with either the SCAD penalty or the MCP penalty and tuning parameter λ. The oracle estimator
satisfies that
as n → ∞ if λ = o(n−(1−c2)/2), n−1/2q = o(λ) and log(p) = o(nλ2).
Remark
It can be shown that if we take λ = n−1/2+δ for some , then these conditions are satisfied. We can also have p = o(exp(nδ)). Therefore, the oracle property for sparse quantile regression holds in ultra-high dimension without the restrictive distributional or moment conditions on the random errors, which are commonly imposed for nonconvex penalized mean regression. This result greatly complements and enhances those in Fan and Li (2001) for fixed p, Fan and Peng (2004) for large p but p < n, Kim, Choi and Oh (2008) for p > n and Fan and Lv (2009) for p ≫ n.
3 Simulation and Real Data Example
In this section, we investigate the performance of nonconvex penalized high-dimensional quantile regression with the SCAD penalty and the MCP (denoted by Q-SCAD and Q-MCP, respectively). We compare these two procedures with least-squares based high-dimensional procedures, including LASSO, adaptive LASSO, SCAD and MCP penalized least squares regression (denoted by LS-Lasso, LS-ALasso, LS-SCAD and LS-MCP, respectively). We also compare the proposed procedures with LASSO penalized and adaptive-LASSO penalized quantile regression (denoted by Q-Lasso and Q-ALasso, respectively). Our main interest is the performance of various procedures when p > n and the ability of the nonconvex penalized quantile regression to identify signature variables that are overlooked by the least-squares based procedures.
While conducting our numerical experiments, we use the local linear approximation algorithm (LLA, Zou and Li, 2008) to implement the nonconvex penalized quantile regression. More explicitly, while minimizing , we initialize by setting for j = 1, 2, ···, p. For each step t ≥ 1, we update by solving
| (6) |
where denotes the weight and denotes the derivative of pλ(·). Following the literature, when , we take as . With the aid of slack variables , and ζj, the convex optimization problem in (6) can be equivalently rewritten as
| (7) |
Note that (7) is a linear programming problem and can be solved using many existing optimization software packages. We claim convergence of the LLA algorithm when the weights , j = 1, 2, ···, p, stabilize, namely when is sufficiently small. Alternatively, one may obtain the solution by using the algorithm proposed in Li and Zhu (2008) for calculating the solution path of the L1-penalized quantile regression.
3.1 Simulation Study
Predictors X1, X2, ···, Xp are generated in two steps. We first generate (X̃1, X̃2, ···, X̃p)T from the multivariate normal distribution Np(0, Σ) with Σ = (σjk)p×p and σjk = 0.5|j−k|. The next step is to set X1 = φ(X̃1) and Xj = X̃j for j = 2, 3, ···, p. The scalar response is generated according to the heteroscedastic location-scale model
where ε ~ N(0, 1) is independent of the covariates. In this simulation experiment, X1 plays an essential role in the conditional distribution of Y given the covariates; but does not directly influence the center (mean or median) of the conditional distribution.
We consider sample size n = 300 and covariate dimension p = 400 and 600. For quantile regression, we consider three different quantiles τ = 0.3, 0.5 and 0.7. We generate an independent tuning data set of size 10n to select the regularization parameter by minimizing the estimated prediction error (based on either the squared error loss or the check function loss, depending on which loss function is used for estimation) calculated over the tuning data set; similarly as in Mazumder, Friedman and Hastie (2011). In the real data analysis in Section 3.2, we use cross-validation for tuning parameter selection.
For a given method, we denote the resulted estimate by β̂ = (β̂0, β̂1, ···, β̂p)T. Based on simulation of 100 repetitions, we compare the performance of the aforementioned different methods in terms of the following criteria.
Size: the average number of non-zero regression coefficients β̂j ≠ 0 for j = 1, 2, ···, p;
-
P1
the proportion of simulation runs including all true important predictors, namely βj ≠ 0 for any j ≥ 1 satisfying βj ≠ 0. For the LS-based procedures and conditional median regression, this means the percentage of times including X5, X12, X15 and X20; for conditional quantile regression at τ = 0.3 and τ = 0.7, X1 should also be included.
-
P2
the proportion of simulation runs X1 is selected.
-
AE
the absolute estimation error defined by .
Tables 1 and 2 depict the simulation results for p = 400 and p = 600, respectively. In these two tables, the numbers in the parentheses in the columns labeled ‘Size’ and ‘AE’ are the corresponding sample standard deviations based on the 100 simulations. The simulation results confirm satisfactory performance of the nonconvex penalized quantile regression when p > n for selecting and estimating relevant covariates. In this example, the signature variable X1 is often missed by least-squares based methods, but has high probability of being included when several different quantiles are examined together. This demonstrates that by considering several different quantiles, it is likely to gain a more complete picture of the underlying structure of the conditional distribution. From Tables 1 and 2, it can be seen that the penalized quantile median regression improves the corresponding penalized least squares methods in terms of AE due to the heteoscedastic error. Furthermore, it is observed that LASSO-penalized quantile regression tends to select a much larger model; on the other hand, the adaptive-Lasso penalized quantile regression tends to select a sparser model but with substantially higher estimation error for τ = 0.3 and 0.7.
Table 1.
Simulation results (p = 400)
| Method | Size | P1 | P2 | AE |
|---|---|---|---|---|
| LS-Lasso | 25.08 (0.60) | 100% | 6% | 1.37(0.03) |
| Q-Lasso (τ = 0.5) | 24.43 (0.97) | 100% | 6% | 0.95 (0.03) |
| Q-Lasso (τ = 0.3) | 29.83 (0.97) | 99% | 99% | 1.67 (0.05) |
| Q-Lasso (τ = 0.7) | 29.65 (0.90) | 98% | 98% | 1.58 (0.05) |
|
| ||||
| LS-ALasso | 5.02 (0.08) | 100% | 0% | 0.38 (0.02) |
| Q-Alasso (τ = 0.5) | 4.66 (0.09) | 100% | 1% | 0.18 (0.01) |
| Q-Alasso (τ = 0.3) | 6.98 (0.20) | 100% | 92% | 0.63 (0.02) |
| Q-Alasso (τ = 0.7) | 6.43 (0.15) | 100% | 98% | 0.61 (0.02) |
|
| ||||
| LS-SCAD | 5.83 (0.20) | 100% | 0% | 0.37 (0.01) |
| Q-SCAD (τ = 0.5) | 5.86 (0.24) | 100% | 0% | 0.19 (0.01) |
| Q-SCAD (τ = 0.3) | 8.29 (0.34) | 99% | 99% | 0.32 (0.02) |
| Q-SCAD (τ = 0.7) | 7.96 (0.30) | 97% | 97% | 0.30 (0.02) |
|
| ||||
| LS-MCP | 5.43 (0.17) | 100% | 0% | 0.37 (0.01) |
| Q-MCP (τ = 0.5) | 5.33 (0.18) | 100% | 1% | 0.19 (0.01) |
| Q-MCP (τ = 0.3) | 6.76 (0.25) | 99% | 99% | 0.31 (0.02) |
| Q-MCP (τ = 0.7) | 6.66 (0.20) | 97% | 97% | 0.29 (0.02) |
Table 2.
Simulation results (p = 600)
| Method | Size | P1 | P2 | AE |
|---|---|---|---|---|
| LS-Lasso | 24.30 (0.61) | 100% | 7% | 1.40 (0.03) |
| Q-Lasso (τ = 0.5) | 25.76 (0.94) | 100% | 10% | 1.05 (0.03) |
| Q-Lasso (τ = 0.3) | 34.02 (1.27) | 93% | 93% | 1.82 (0.06) |
| Q-Lasso (τ = 0.7) | 32.74 (1.22) | 90% | 90% | 1.78 (0.05) |
|
| ||||
| LS-ALasso | 4.68 (0.08) | 100% | 0% | 0.37(0.02) |
| Q-Alasso (τ = 0.5) | 4.53 (0.09) | 100% | 0% | 0.18 (0.01) |
| Q-Alasso (τ = 0.3) | 6.58 (0.21) | 100% | 86% | 0.67 (0.02) |
| Q-Alasso (τ = 0.7) | 6.19 (0.16) | 100% | 86% | 0.62 (0.01) |
|
| ||||
| LS-SCAD | 6.04 (0.25) | 100% | 0% | 0.38 (0.02) |
| Q-SCAD (τ = 0.5) | 6.14 (0.36) | 100% | 7% | 0.19 (0.01) |
| Q-SCAD (τ = 0.3) | 9.02 (0.45) | 94% | 94% | 0.40 (0.03) |
| Q-SCAD (τ = 0.7) | 9.97 (0.54) | 100% | 100% | 0.38 (0.03) |
|
| ||||
| LS-MCP | 5.56 (0.19) | 100% | 0% | 0.38 (0.02) |
| Q-MCP (τ = 0.5) | 5.33 (0.23) | 100% | 3% | 0.18 (0.01) |
| Q-MCP (τ = 0.3) | 6.98 (0.28) | 94% | 94% | 0.38 (0.03) |
| Q-MCP (τ = 0.7) | 7.56 (0.32) | 98% | 98% | 0.37 (0.03) |
As suggested by one referee, we have also compared the computing time of penalized quantile regression and penalized least squares. As expected, the penalized least squares method needs less computing time, and takes about two-third of computing time of penalized quantile regression. Due to limited space, we do not to present the computing time here. We also did some investigation of the performance of the penalized least squares and penalized median regression when error is Cauchy distribution. As also expected, penalized median regression outperforms the penalized least squares for Cauchy error. We opt not to include the simulation results for Cauchy error to save space.
3.2 An Application
We now illustrate the proposed methods by an empirical analysis of a real data set. The data set came from a study that used expression quantitative trait locus (eQTL) mapping in laboratory rats to investigate gene regulation in the mammalian eye and to identify genetic variation relevant to human eye disease (Scheetz et al., 2006).
This microarray data set has expression values of 31042 probe sets on 120 twelve-week-old male offspring of rats. We carried out the following two preprocessing steps: remove each probe for which the maximum expression among the 120 rats is less than the 25th percentile of the entire expression values; and remove any probe for which the range of the expression among 120 rats is less than 2. After these two preprocessing steps, there are 18958 probes left. As in Huang, Ma, and Zhang (2008) and Kim, Choi, and Oh (2008), we study how expression of gene TRIM32 (a gene identified to be associated with human hereditary diseases of the retina), corresponding to probe 1389163_at, depends on expressions at other probes. As pointed out in Scheetz et al. (2006), “Any genetic element that can be shown to alter the expression of a specific gene or gene family known to be involved in a specific disease is itself an excellent candidate for involvement in the disease, either primarily or as a genetic modifier.” We rank all other probes according to the absolute value of the correlation of their expression and the expression corresponding to 1389163_at and select the top 300 probes. Then we apply several methods on these 300 probes.
First, we analyze the complete data set of 120 rats. The penalized least squares procedures and the penalized quantile regression procedures studied in Section 3.1 were applied. We use five-fold cross validation to select the tuning parameter for each method. In the second column of Table 3, we report the number of nonzero coefficients (# nonzero) selected by each method.
Table 3.
Analysis of microarray data set
| all data | random partition | ||
|---|---|---|---|
|
| |||
| Method | # nonzero | ave # nonzero | prediction error |
| LS-Lasso | 24 | 21.66(1.67) | 1.57(0.03) |
| Q-Lasso (τ = 0.5) | 23 | 18.36(0.83) | 1.51(0.03) |
| Q-Lasso (τ = 0.3) | 23 | 19.34(1.69) | 1.54(0.04) |
| Q-Lasso (τ = 0.7) | 17 | 15.54(0.71) | 1.29(0.02) |
|
| |||
| LS-ALasso | 16 | 15.22(10.72) | 1.65(0.27) |
| Q-ALasso (τ = 0.5) | 13 | 11.28(0.65) | 1.53(0.03) |
| Q-ALasso (τ = 0.3) | 19 | 12.52(1.38) | 1.57(0.03) |
| Q-ALasso (τ = 0.7) | 10 | 9.16(0.48) | 1.32(0.03) |
|
| |||
| LS-SCAD | 10 | 11.32(1.16) | 1.72(0.04) |
| Q-SCAD (τ = 0.5) | 23 | 18.32(0.82) | 1.51(0.03) |
| Q-SCAD (τ = 0.3) | 23 | 17.66(1.52) | 1.56(0.04) |
| Q-SCAD (τ = 0.7) | 19 | 15.72(0.72) | 1.30(0.03) |
|
| |||
| LS-MCP | 5 | 9.08(1.68) | 1.82(0.04) |
| Q-MCP (τ = 0.5) | 23 | 17.64(0.82) | 1.52(0.03) |
| Q-MCP (τ = 0.3) | 15 | 16.36(1.53) | 1.57(0.04) |
| Q-MCP (τ = 0.7) | 16 | 13.92(0.72) | 1.31(0.03) |
There are two interesting findings. First, the sizes of the models selected by penalized least squares methods are different from that of models selected by penalized quantile regression. In particular, both LS-SCAD and LS-MCP, which focus on the mean of the conditional distribution, select sparser models compared to Q-SCAD and Q-MCP. A sensible interpretation is that a probe may display strong association with the target probe only at the upper tail or lower tail of the conditional distribution; it is also likely that a probe may display associations in opposite directions at the two tails. The least-squares based methods are likely to miss such heterogeneous signals. Second, a more detailed story is revealed when we compare the probes selected at different quantiles τ = 0.3, 0.5, 0.7. The probes selected by Q-SCAD(0.3), Q-SCAD(0.5), and Q-SCAD(0.7) are reported in the first column of the left, center and right panels, respectively, of Table 4. Although Q-SCAD selects 23 probes at both τ = 0.5 and τ = 0.3, only 7 of the 23 overlap, and only 2 probes (1382835_at and 1393382_at) are selected at all three quantiles. We observe similar phenomenon with Q-MCP. This further demonstrates the heterogeneity in the data.
Table 4.
Frequency table for the real data
| Q-SCAD(0.3) | Q-SCAD(0.5) | Q-SCAD(0.7) | |||
|---|---|---|---|---|---|
|
| |||||
| Probe | Frequency | Probe | Frequency | Probe | Frequency |
|
| |||||
| 1383996_at | 31 | 1383996_at | 43 | 1379597_at | 38 |
| 1389584_at | 26 | 1382835_at | 40 | 1383901_at | 34 |
| 1393382_at | 24 | 1390401_at | 27 | 1382835_at | 34 |
| 1397865_at | 24 | 1383673_at | 24 | 1383996_at | 34 |
| 1370429_at | 23 | 1393382_at | 24 | 1393543_at | 30 |
| 1382835_at | 23 | 1395342_at | 23 | 1393684_at | 27 |
| 1380033_at | 22 | 1389584_at | 21 | 1379971_at | 23 |
| 1383749_at | 20 | 1393543_at | 20 | 1382263_at | 22 |
| 1378935_at | 18 | 1390569_at | 20 | 1393033_at | 19 |
| 1383604_at | 15 | 1374106_at | 18 | 1385043_at | 18 |
| 1379920_at | 13 | 1383901_at | 18 | 1393382_at | 17 |
| 1383673_at | 12 | 1393684_at | 16 | 1371194_at | 16 |
| 1383522_at | 11 | 1390788_a_at | 16 | 1383110_at | 12 |
| 1384466_at | 10 | 1394399_at | 14 | 1395415_at | 6 |
| 1374126_at | 10 | 1383749_at | 14 | 1383502_at | 6 |
| 1382585_at | 10 | 1395415_at | 13 | 1383254_at | 5 |
| 1394596_at | 10 | 1385043_at | 12 | 1387713_a_at | 5 |
| 1383849_at | 10 | 1374131_at | 10 | 1374953_at | 3 |
| 1380884_at | 7 | 1394596_at | 10 | 1382517_at | 1 |
| 1369353_at | 5 | 1385944_at | 9 | ||
| 1377944_at | 5 | 1378935_at | 9 | ||
| 1370655_a_at | 4 | 1371242_at | 8 | ||
| 1379567_at | 1 | 1379004_at | 8 | ||
We then conduct 50 random partitions. For each partition, we randomly select 80 rats as the training data and the other 40 as the testing data. A five-fold cross-validation is applied to the training data to select the tuning parameters. We report the average number of nonzero regression coefficients (ave # nonzero), where numbers in the parentheses are the corresponding standard errors across 50 partitions, in the third column of Table 3. We evaluate the performance over the test set for each partition. For Q-SCAD and Q-MCP, we evaluate the loss using the check function at the corresponding τ. As the squared loss is not directly comparable with the check loss function, we use the check loss with τ = 0.5 (i.e. L1 loss) for the LS-based methods. The results are reported in the last column of Table 3, where the prediction error is defined as and the numbers in the parentheses are the corresponding standard errors across 50 partitions. We observe similar patterns as when the methods are applied to the whole data set. Furthermore, the penalized quantile regression procedures improves the corresponding penalized least squares in terms of prediction error. The performance of Q-Lasso, Q-ALasso, Q-SCAD and Q-MCP are similar in terms of prediction error, although the Q-Lasso tends to select less sparse models and the Q-ALasso tends to select sparser model, compared with Q-SCAD and Q-MCP.
As with every variable selection method, different repetitions may select different subsets of important predictors. In Table 4, we report in the left column the probes selected using the complete data set and in the right column the frequency these probes appear in the final model of these 50 random partitions for Q-SCAD(0.3), Q-SCAD(0.5), and Q-SCAD(0.7) in the left, middle and right panels, respectively. The probes are ordered such that the frequency is decreasing. From Table 4, we observe that some probes such as 1383996_at and 1382835_at have high frequencies across different τ’s, while some other probes such as 1383901_at do not. This implies that some probes are important across all τ, while some probes might be important only for certain τ.
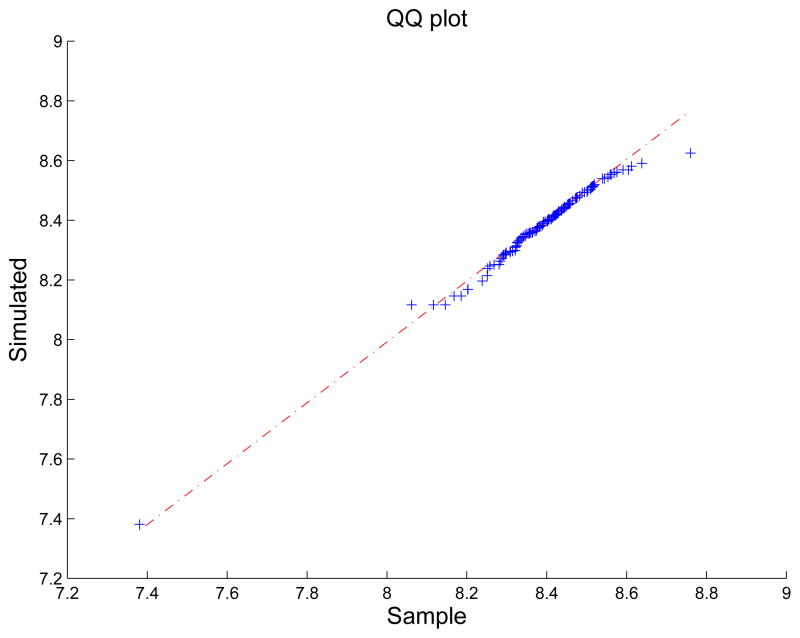
Wei and He (2006) proposed a simulation based graphical method to evaluate the overall lack-of-fit of the quantile regression process. We apply their graphical diagnosis method using the SCAD penalized quantile regression. More explicitly, we first generate a random τ̃ from the uniform (0,1) distribution. We then fit the SCAD-penalized quantile regression model at the quantile τ̃, where the regularization parameter is selected by five-fold cross-validation. Denote the penalized estimator by β̂(τ̃), and we generate a response Y = xTβ̂(τ̃), where x is randomly sampled from the set of observed vector of covariates. We repeat this process 200 times and produce a sample of 200 simulated responses from the postulated linear model. The QQ plot of the simulated sample vs the observed sample is given in Figure 1. The QQ plot is close to 45 degree line and thus indicates a reasonable fit.
Figure 1.
Lack-of-fit diagnosis QQ plot for the real data.
4 Discussions
In this paper, we investigate nonconvex penalized quantile regression for analyzing ultra-high dimensional data under the assumption that at each quantile only a small subset of covariates are active but the active covariates at different quantiles may be different. We establish the theory of the proposed procedures in ultra-high dimension under very relaxed conditions. In particular, the theory suggests that nonconvex penalized quantile regression with ultra-high dimensional covariates has the oracle property even when the random errors have heavy tails. In contrast, the existing theory for ultra-high dimensional nonconvex penalized least squares regression needs Gaussian or Sub-Gaussian condition for the random errors.
The theory was established by novelly applying a sufficient optimality condition based on a convex differencing representation of the penalized loss function. This approach can be applied to a large class of nonsmooth loss functions, for example the loss function corresponding to Huber’s estimator and the many loss functions used for classification. As pointed out by a referee, the current theory only proves that the oracle estimator is a local minimum to the penalized quantile regression. How to identify the oracle estimator from potentially multiple minima is a challenging issue, which remains unsolved for nonconvex penalized least squares regression. This will be a good future research topic. The simulations suggest that the local minimum identified by our algorithm has fine performance.
Alternative methods for analyzing ultra-high dimensional data include two-stage approaches, in which a computationally efficient method screens all candidate covariates (for example Fan and Lv (2008), Wang (2009), Meinshausen and Yu (2009), among others) and reduces the ultra-high dimensionality to moderately high dimensionality in the first stage, and a standard shrinkage or thresholding method is applied to identify important covariates in the second stage.
Acknowledgments
Wang’s research is supported by a NSF grant DMS1007603. Wu’s research is supported by a NSF grant DMS-0905561 and NIH/NCI grant R01 CA-149569. Li’s research is supported by a NSF grant DMS 0348869 and grants from NNSF of China, 11028103 and 10911120395, and NIDA, NIH grants R21 DA024260 and P50 DA10075.
Footnotes
The content is solely the responsibility of the authors and does not necessarily represent the official views of the NCI, the NIDA or the NIH. The authors are indebted to the referees, the associate editor and the Co-editor for their valuable comments, which have significantly improved the paper.
Contributor Information
Lan Wang, Email: wangx346@umn.edu, School of Statistics, University of Minnesota, Minneapolis, MN 55455.
Yichao Wu, Email: wu@stat.ncsu.edu, Department of Statistics, North Carolina State University, Raleigh, NC 27695.
Runze Li, Email: rli@stat.psu.edu, Department of Statistics and the Methodology Center, the Pennsylvania State University, University Park, PA 16802-2111.
References
- 1.An LTH, Tao PD. The DC (Difference of Convex Functions) programming and DCA revisited with DC models of real world nonconvex optimization problems. Annals of Operations Research. 2005;133:23–46. [Google Scholar]
- 2.Bai Z, Wu Y. Limiting behavior of M-estimators of regression coefficients in high dimensional linear models, I. Scale-dependent case. Journal of Multivariate Analysis. 1994;51:211–239. [Google Scholar]
- 3.Belloni A, Chernozhukov V. L1-Penalized quantile regression in high-dimensional sparse models. The Annals of Statistics. 2011;39:82–130. [Google Scholar]
- 4.Bertsekas DP. Nonlinear programming. 3. Athena Scientific; Belmont, Massachusetts: 2008. [Google Scholar]
- 5.Candes EJ, Tao T. The Dantzig selector: Statistical estimation when p is much larger than n. The Annals of Statistics. 2007;35:2313–2351. [Google Scholar]
- 6.Cands EJ, Wakin M, Boyd S. Enhancing sparsity by reweighted L1 minimization. J Fourier Anal Appl. 2007;14:877–905. [Google Scholar]
- 7.Collobert R, Sinz F, Weston J, Bottou L. Large scale transductive SVMs. Journal of Machine Learning Research. 2006;7:1687–1712. [Google Scholar]
- 8.Fan J, Li R. Variable selection via nonconcave penalized likelihood and its oracle properties. Journal of the American Statistical Association. 2001;96:1348–1360. [Google Scholar]
- 9.Fan J, Lv J. Sure independence screening for ultra-high dimensional feature space (with discussion) Journal of Royal Statistical Society, Series B. 2008;70:849–911. doi: 10.1111/j.1467-9868.2008.00674.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Fan J, Lv J. Non-concave penalized likelihood with NP-dimensionality. IEEE Transactions on Information Theory. 2011;57:5467–5484. doi: 10.1109/TIT.2011.2158486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Fan J, Peng H. Nonconcave penalized likelihood with a diverging number of parameters. The Annals of Statistics. 2004;32:928–961. [Google Scholar]
- 12.He X. Technical report. Department of Statistics, University of Illinois; Urbana-Champaign: 2009. Modeling and inference by quantile regression. [Google Scholar]
- 13.He X, Shao QM. On parameters of increasing dimensions. Journal of Multivariate Analysis. 2000;73:120–135. [Google Scholar]
- 14.He X, Zhu LX. A lack-of-fit test for quantile regression. Journal of the American Statistical Association. 2003;98:1013–1022. [Google Scholar]
- 15.Huang J, Ma SG, Zhang CH. Adaptive lasso for sparse high-dimensional regression models. Statistica Sinica. 2008;18:1603–1618. [Google Scholar]
- 16.Kai B, Li R, Zou H. New efficient estimation and variable selection methods for semiparametric varying-coefficient partially linear models. The Annals of Statistics. 2011;39:305–332. doi: 10.1214/10-AOS842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kim Y, Choi H, Oh HS. Smoothly clipped absolute deviation on high dimensions. Journal of the American Statistical Association. 2008;103:1665–1673. [Google Scholar]
- 18.Koenker R. Quantile regression. Cambridge University Press; 2005. [Google Scholar]
- 19.Koenker R, Bassett GW. Regression quantiles. Econometrica. 1978;46:33–50. [Google Scholar]
- 20.Li YJ, Zhu J. L1-norm quantile regression. Journal of Computational and Graphical Statistics. 2008;17:163–185. [Google Scholar]
- 21.Liu YF, Shen X, Doss H. Multicategory psi-learning and support vector machine: computational tools. Journal of Computational and Graphical Statistics. 2005;14:219–236. [Google Scholar]
- 22.Mazumder R, Friedman J, Hastie T. SparseNet: Coordinate descent with nonconvex penalties. Journal of the American Statistical Association. 2011;106:1125–1138. doi: 10.1198/jasa.2011.tm09738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Scheetz TE, Kim KYA, Swiderski RE, Philp AR, Braun TA, Knudtson KL, Dorrance AM, DiBona GF, Huang J, Casavant TL, Sheffield VC, Stone EM. Regulation of gene expression in the mammalian eye and its relevance to eye disease. Proceedings of the National Academy of Sciences. 2006;103:14429–14434. doi: 10.1073/pnas.0602562103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Tao PD, An LTH. Convex analysis approach to D.C. programming: theory, algorithms and applications. Acta Mathematica Vietnamica. 1997;22:289–355. [Google Scholar]
- 25.Wang H. Forward regression for ultra-highdimensional variable screening. Journal of the American Statistical Association. 2009;104:1512–1524. [Google Scholar]
- 26.Wei Y, He X. Conditional Growth Charts (with discussions) Annals of Statistics. 2006;34:2069–2097. 2126–2131. [Google Scholar]
- 27.Welsh AH. On M-Processes and M-Estimation. The Annals of Statististics. 1989;17:337–361. [Google Scholar]
- 28.Wu YC, Liu YF. Variable selection in quantile regression. Statistica Sinica. 2009;19:801–817. [Google Scholar]
- 29.Zhang CH. Nearly unbiased variable selection under minimax concave penalty. The Annals of Statistics. 2010;38:894–942. [Google Scholar]
- 30.Zou H. The adaptive lasso and its oracle properties. Journal of the American Statistical Association. 2006;101:1418–1429. [Google Scholar]
- 31.Zou H, Li R. One-step sparse estimates in nonconcave penalized likelihood models (with discussion) The Annals of Statistics. 2008;36:1509–1533. doi: 10.1214/009053607000000802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Zou H, Yuan M. Composite quantile regression and the oracle model selection theory. The Annals of Statistics. 2008;36:1108–1126. [Google Scholar]