A reaction-diffusion model of CO₂ influx into an oocyte

Abstract

We have developed and implemented a novel mathematical model for simulating transients in surface pH (pH_S) and intracellular pH (pH_i) caused by the influx of carbon dioxide (CO₂) into a Xenopus oocyte. These transients are important tools for studying gas channels. We assume that the oocyte is a sphere surrounded by a thin layer of unstirred fluid, the extracellular unconvected fluid (EUF), which is in turn surrounded by the well-stirred bulk extracellular fluid (BECF) that represents an infinite reservoir for all solutes. Here, we assume that the oocyte plasma membrane is permeable only to CO₂. In both the EUF and intracellular space, solute concentrations can change because of diffusion and reactions. The reactions are the slow equilibration of the CO₂ hydration-dehydration reactions and competing equilibria among carbonic acid (H₂CO₃)/bicarbonate ( ${\text{HCO}}_3^{-}$) and a multitude of ${\text{non}-\text{CO}}_{\text{2}}{/\text{HCO}}_3^{-}$ buffers. Mathematically, the model is described by a coupled system of reaction-diffusion equations that—assuming spherical radial symmetry—we solved using the method of lines with appropriate stiff solvers. In agreement with experimental data (Musa-Aziz et al, PNAS 2009, 106:5406–5411), the model predicts that exposing the cell to extracellular 1.5% CO₂/10 mM ${\text{HCO}}_3^{-}$ (pH 7.50) causes pH_i to fall and pH_S to rise rapidly to a peak and then decay. Moreover, the model provides insights into the competition between diffusion and reaction processes when we change the width of the EUF, membrane permeability to CO₂, native extra-and intracellular carbonic anhydrase-like activities, the ${\text{non}-\text{CO}}_{\text{2}}{/\text{HCO}}_3^{-}$ (intrinsic) intracellular buffering power, or mobility of intrinsic intracellular buffers.

1. Introduction

Extracellular pH (pH_o) and intracellular pH (pH_i) are of broad interest to biologists because pH perturbations can alter a wide range of processes. Thus, maintaining pH_o and pH_i in a normal range is of fundamental importance for correct cellular and tissue function. Cells regulate their pH by transporting acids or bases—particularly the hydrogen ion (H⁺) or the bicarbonate ion ( ${\text{HCO}}_3^{-}$)—across the plasma membrane. In addition, the movements of dissolved gases such as carbon dioxide (CO₂) or ammonia (NH₃) also have major effects on pH_o and pH_i. In fact, fluxes of the above substances generally will have reciprocal effects on pH on opposite sides of the membrane.

The oocyte from the African clawed frog Xenopus laevis is a major experimental model system used extensively in developmental biology, molecular biology, and electrophysiology. Because of their large size (≈1 mm in diameter), these cells can be easily handled and manipulated. For example, they can be injected with RNA from other organisms and then used to study protein expression using biochemical or electrophysiological approaches. In the laboratory of one of the authors, Xenopus laevis oocytes are used to study three categories of proteins that can have a substantial impact on pH: (1) sodium-coupled bicarbonate transporters (NCBTs), which play important roles in pH_i regulation and epithelial acid-base transport (Romero et al., 1997; Choi et al., 2000; Grichtchenko et al., 2001); (2) aquaporins (AQPs) and Rhesus (Rh) proteins, which can serve as conduits (i.e., gas channels) for the diffusion of CO₂ or NH₃ (Nakhoul et al., 1998; Cooper and Boron, 1998; Endeward et al., 2006; Musa-Aziz et al., 2009; Boron, 2010); and (3) carbonic anhydrases (CAs), enzymes that catalyze the interconversion of CO₂ and ${\text{HCO}}_3^{-}$ and play important roles in the transport of CO₂ and ${\text{HCO}}_3^{-}$.

Understanding the transport across the plasma membrane of substances such as H⁺, ${\text{HCO}}_3^{-}$, or CO₂, is not trivial. Cells normally contain and are surrounded by a number of ${\text{non}-\text{CO}}_{\text{2}}{/\text{HCO}}_3^{-}$ buffers. Thus, acid-base transport triggers: (1) a multitude of interconnected extra- and intracellular buffer reactions that explicitly or implicitly involve H⁺ and (2) diffusion events—all of which vary in space and time. The result is changes in solute concentrations, including pH, that vary in space and time throughout the system. These changes are likely to be so complex that it would be impossible to understand them in the absence of an appropriate mathematical model.

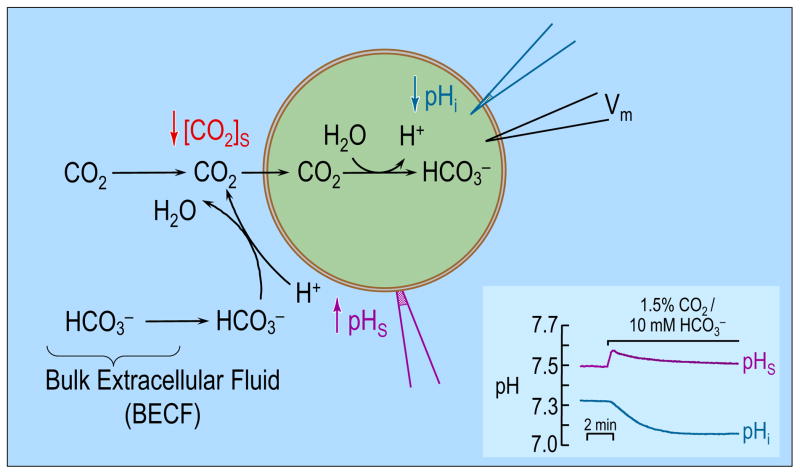
Endeward et al and Musa-Aziz et al exploited a novel technique to assess the CO₂ permeability of a Xenopus oocyte (Endeward et al., 2006; Musa-Aziz et al., 2009). Figure 1 illustrates the approach, in which one measures surface pH (pH_S) by pushing a liquid-membrane pH-sensitive microelectrode against the oocyte surface, thereby dimpling the oocyte membrane slightly. Subsequently applying ${\text{CO}}_{\text{2}}{/\text{HCO}}_3^{-}$ in the bulk extracellular fluid (BECF) causes pH_S to rise to a peak and then decay (Figure 1 inset, upper record). Simultaneous measurements with an intracellular electrode reveal the familiar fall in pH_i (Figure 1 inset, lower record). The events underlying these changes in pH_S and pH_i are summarized by the diagram in the main part of Figure 1. As CO₂ enters the cell, the concentration of CO₂, [CO₂], at the cell surface decreases. The lost CO₂ can be replenished by diffusion from the BECF or by reaction at the cell surface from ${\text{HCO}}_3^{-}$ and H⁺. The observed rise in pH_S reflects the consumption of H⁺ via this reaction. Conversely, in the intracellular space, the influx of CO₂ leads to the generation of H⁺ (and therefore to a decrease in pH_i) via the opposite reaction.

Figure 1.

Model of an oocyte exposed to ${\text{CO}}_2/{\text{HCO}}_3^{-}$. As CO₂ enters the cell, the concentration of CO₂ near the outer surface of the oocyte falls. The lost CO₂ can be replenished by 1) diffusion from the bulk extracellular fluid (BECF) and 2) the reaction(s) ${\text{HCO}}_3^{-}+{\text{H}}^{+}\to {\text{CO}}_2+{\text{H}}_2\text{O}$ at the cell surface. This reaction, which consumes H⁺, causes pH_S to rise. Conversely, the entry of CO₂ into the cell leads to the generation of intracellular H⁺ via the reaction(s) ${\text{CO}}_2+{\text{H}}_2\text{O}\to {\text{HCO}}_3^{-}+{\text{H}}^{+}$, therefore causing a fall in pH_i. (Cell model adapted from ref (Boron, 2010). The inset at the bottom right shows experimental pH_S and pH_i records for a H₂O-injected oocyte exposed to 1.5% CO₂/10mM ${\text{HCO}}_3^{-}$. Data kindly provided by Dr. Musa-Aziz).

The magnitude of the pH_S spike in Figure 1 ought to be an index of CO₂ permeability. Indeed, the expression of AQPs or Rh proteins in oocytes causes the pH_S spike to increase (Endeward et al., 2006; Musa-Aziz et al., 2009)—part of the evidence that these proteins are gas channels. With the appropriate mathematical model, one might be able to extract—from the time course of pH_S in Figure 1—the permeability of the membrane to CO₂. Moreover, one could gain insight into events not directly accessible by experiments (e.g., the time course of intracellular solute concentrations). Finally, an appropriate model would help in the formulation and testing of hypotheses. The requirements of such a model include: (a) a 3-dimensional spherical cell, (b) the transport of CO₂ across the plasma membrane, (c) the reactions of a multitude of extra- and intracellular buffers, (d) diffusion of solutes through the extra- and (d′) intracellular spaces, (e) CA activity at specific loci, and (f) temporal and (f′) spatial variations of solute concentrations.

Several authors have presented mathematical models of acid-base transport that have assisted in the interpretation of data collected in their respective laboratories.

1. In 1976, Boron and De Weer, using a system of two ordinary differential equations, predicted for the first time the time course of pH_i when CO₂ and ${\text{HCO}}_3^{-}$—or NH₃ and ${\text{NH}}_4^{+}$—enter or leave the cell (Boron and De Weer, 1976). Although valuable, this model does not address requirements (a), (c), (d), (d′), (e) or (f′).

2. In 2002, Vaughan-Jones et al recognized the importance of studying the spatio-temporal behavior of pH and developed a two-dimensional mathematical model to study the free diffusion of intracellular H⁺ from a constant source in ventricular myocytes (Vaughan-Jones et al., 2002). The model leads to estimates of the apparent intracellular H⁺ diffusion coefficient. Although it accounts for spatial variability of solutes, it does not address requirements (a), (b), (c), or (e).

3. More recently, this same group has developed reaction-diffusion models to study the relationship between extracellular CAIX and the spatio-temporal coordination of pH_o and pH_i in a multicellular cluster of tumor cells (Swietach et al., 2008; Swietach et al., 2009). This model does not consider a single cell but a spherical cluster of cells and does not address requirements (a), (c), or (d′).

4. Missner et al. developed a one-dimensional reaction-diffusion mathematical model to study the diffusion of CO₂ through planar lipid bilayers at steady state (Missner et al., 2008b). This model is also not suitable for our purposes because it does not address requirements (a), (c) or (f).

5. Gros and coworkers developed a time-dependent mathematical model of six ordinary differential equations to interpret their mass-spectrometric data obtained in a chemically pre-equilibrated system in which they monitored the diffusion of ¹⁸O-labeled ${\text{CO}}_{\text{2}}{/\text{HCO}}_3^{-}$ across the red blood cell (RBC) membrane (Endeward and Gros, 2005). Their approach yielded estimates of the apparent membrane permeabilities to CO₂ and ${\text{HCO}}_3^{-}$. This model does not address requirements (a), (c), (d), (d′), or (f′).

6. More recently, these same authors extended their model to simulate the diffusion of CO₂, ${\text{HCO}}_3^{-}$, and H₂O in one-dimensional space from a stirred bulk solution, through an extracellular unstirred layer, through the cell membrane, and into the RBC (Endeward and Gros, 2009). The model can provide insights into the effect of intra- and extracellular unstirred layers in the estimation of the CO₂ permeability of the RBC membrane. Although this model is a reaction-diffusion model and accounts for spatial variation, it does not address requirements (a) and (c).

It is clear from the above discussion that none of the available models is well suited to the interpretation of the aforementioned oocyte data (Figure 1). In the present paper, we develop a three-dimensional mathematical model under the assumption of spherical symmetry of a cell (e.g., an oocyte) and of its surrounding environment (requirement (a), above), with the goal of simulating the observed changes in pH_S and pH_i caused by the entry of CO₂ (requirement (b)). Each species can react with other solutes in both the intra- and extracellular spaces, including a multitude of buffers (requirement (c)). To our knowledge, ours is the first model capable of handling an indefinite number of buffers. Each species also can move via diffusion through the extra- and intracellular spaces (requirements (d) and (d′)). Finally, the model includes CA-catalysis (requirement (e)) as well as temporal (requirement (f)) and spatial variations (requirement (f′)).

Mathematically, the present model consists of a coupled system of reaction-diffusion equations, describing the diffusion of solutes in the intracellular and extracellular space and through the cell membrane, as well as local chemical interactions between the species. Because we use a spherical model of the cell and assume no directional dependency in the boundary conditions, the symmetry allows us to reduce the model to a radial system. However, the reaction rates may vary as a function of the radius, so the system has non-constant coefficients. We use the method of lines, the spatial discretization being based on finite difference approximation, leading to a stiff system which is solved numerically by appropriate stiff solvers.

We hypothesize that the present model will reproduce the essential features of Figure 1, and serve as the foundation for more advanced models that could provide estimates of parameters such as CO₂ permeability. The model successfully predicts that, when an oocyte is exposed to extracellular CO₂/HCO₃⁻, the influx of CO₂ causes pH_i to fall monotonically and pH_S to rise and then decay. Moreover, the model allows one to extract information on variables (e.g., time and space profiles of solute concentrations) that cannot be measured directly. For example, in typical electrophysiological experiments, one might measure pH_S and pH_i, but not have access to the concentrations of the other solutes involved in the process. The model also provides reasonable predictions when we change the width of the extracellular unconvected layer surrounding the oocyte, the CO₂ membrane permeability, and the extra- and intracellular CA-like activities. The model provides insights into the competition between reaction and diffusion near the outer surface of the cell membrane and makes valuable predictions when we change the intracellular buffering power, or change the ratio of mobile to immobile buffers.

2. Model

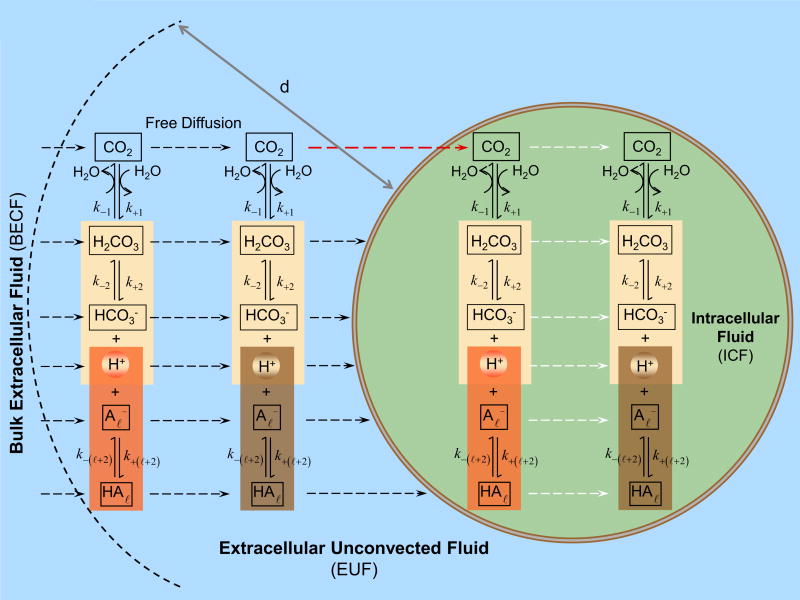
The key components of the model are summarized in the cartoon of Figure 2. The model assumes that the oocyte is surrounded by the extracellular unconvected fluid (EUF) which in turn is surrounded by a volume of bulk extracellular fluid. The EUF is a thin layer adjacent to the surface of the oocyte where no convection occurs, but reactions and diffusion do occur. The bulk extracellular fluid is an infinite reservoir for all solutes where convection (not included in the present model) could occur but not reaction or diffusion. All solutes can diffuse between the BECF and EUF. The plasma membrane may have different permeabilities to different solutes. To avoid the need to specify the thickness of the membrane, in the present implementation, we use a computational model in which we take the limit where the membrane thickness parameter goes to zero, while the permeability is kept constant. Moreover, we assume that the plasma membrane is permeable only to CO₂—a reasonable assumption, given the low permeability of the Xenopus oocyte membrane to H⁺ (Fei et al., 1994; Gunshin et al., 1997; Steel et al., 1997) and ${\text{HCO}}_3^{-}$ (Costa et al., 1989; Toye et al., 2006; Lee et al., 2011). In the EUF and intracellular fluid (ICF), the concentration of solutes can change because of diffusion and reaction processes; each solute has a specific, position-dependent mobility. In both EUF and ICF, the model accounts for the slow equilibration of the CO₂ hydration/dehydration reactions, for competing equilibria among the ${\text{CO}}_{\text{2}}{/\text{HCO}}_3^{-}$ buffer and a multitude of ${\text{non}-\text{CO}}_{\text{2}}{/\text{HCO}}_3^{-}$ buffers. In Figure 2, the ${\text{non}-\text{CO}}_{\text{2}}{/\text{HCO}}_3^{-}$ buffers are indicated by ${\text{HA}}_{\ell }/{\text{A}}_{\ell }^{-}$.

Figure 2.

Key components of the mathematical model. The oocyte is surrounded by the extracellular unconvected fluid (EUF), which in turn is surrounded by the bulk extracellular fluid (BECF). The BECF is an infinite reservoir for all solutes, where convection (not included in the present model) could occur but no reaction or diffusion. All solutes can diffuse between the BECF and EUF. The EUF is a thin layer of thickness d adjacent to the oocyte surface where no convection occurs, but reaction and diffusion do occur. The plasma membrane is permeable only to CO₂. In the intracellular fluid (ICF), both reaction and diffusion occur. In both the EUF and ICF the model accounts for the slow equilibration of the CO₂ hydration/dehydration reactions, competing equilibria among the ${\text{CO}}_2/{\text{HCO}}_3^{-}$ buffers and a multitude of ${\text{non}-\text{CO}}_{\text{2}}{/\text{HCO}}_3^{-}$ buffers (indicated as ${\text{HA}}_{\ell }/{\text{A}}_{\ell }^{-}$).

The objective is to simulate numerically the dynamics of the concentrations of the solutes of interest, and in particular, the pH on both sides of the cell membrane.

Let Ω ⊂ ℝ³ denote the domain occupied by the oocyte and ∂Ω the boundary membrane. The concentration distribution of the CO₂ is denoted by

$$[{\text{CO}}_2]=u_1(t,x),x\in {\mathbb{R}}^3,t\ge 0,$$ (1)

t being the time. Furthermore, the concentration distribution of the H⁺ is denoted by

$$[{\text{H}}^{+}]=v_1(t,x).$$ (2)

The numbering of the concentrations of carbonic acid (H₂CO₃), of the L non-H₂CO₃ weak acids (HA_ℓ, 1 ≤ ℓ ≤ L ), and of their corresponding conjugate weak bases ( ${\text{HCO}}_3^{-}$ and ${\text{A}}_{\ell }^{-}$), respectively, are written as

$$[{\text{H}}_2{\text{CO}}_3]=u_2(t,x),[{\text{HCO}}_3^{-}]=v_2(t,x),$$ (3)

and

$$[{\text{HA}}_{\ell }]=u_{\ell +2}(t,x),[{\text{A}}_{\ell }^{-}]=v_{\ell +2}(t,x),1\le \ell \le L,$$ (4)

respectively. Note that we chose to ignore the dissociation of ${\text{HCO}}_3^{-}$ to form ${\text{CO}}_3^{=}$ plus H⁺ because the pK of this reaction (≈10.3) is much higher than the pH values in the current simulations.

The reactions of carbonic acid formation and the corresponding rate constants are denoted by

$${\text{CO}}_2+{\text{H}}_2\text{O}\underset{k_{-1}}{\overset{k_{+1}}{\rightleftharpoons }}{\text{H}}_2{\text{CO}}_3,$$ (5)

and the reactions of dissociation with the corresponding rate constants are

$${\text{H}}_2{\text{CO}}_3\underset{k_{-2}}{\overset{k_{+2}}{\rightleftharpoons }}{\text{HCO}}_3^{-}+{\text{H}}^{+},$$ (6)

and

$${\text{HA}}_{\ell }\underset{k_{-(\ell +2)}}{\overset{k_{+(\ell +2)}}{\rightleftharpoons }}{\text{A}}_{\ell }^{-}+{\text{H}}^{+},1\le \ell \le L.$$ (7)

Note that the results of recent metadynamic simulations (Stirling and Papai, 2010) are most consistent with a model in which the reactions involving CO₂, H₂CO₃, ${\text{HCO}}_3^{-}$, and H⁺ proceed not as outlined in equations (5) and (6) but in the order ${\text{CO}}_2+{\text{H}}_2\text{O}\rightleftharpoons {\text{HCO}}_3^{-}+{\text{H}}^{+}\rightleftharpoons {\text{H}}_2{\text{CO}}_3$. However, the ordering of these reactions would have no effect on the results of the present paper.

The reaction fluxes Φ_ℓ, indexed according to their respective rate constants k_ℓ, ℓ = ±1, ±2, …, ±(L + 2), are modeled using the law of mass action, that is,

$${\mathrm{\Phi }}_{+1}=k_{+1}[{\text{CO}}_2]=k_{+1}{u}_1,{\mathrm{\Phi }}_{-1}=k_{-1}[{\text{H}}_2{\text{CO}}_3]=k_{-1}{u}_2,$$ (8)

$${\mathrm{\Phi }}_{+2}=k_{+2}[{\text{H}}_2{\text{CO}}_3]=k_{+2}{u}_2,{\mathrm{\Phi }}_{-2}=k_{-2}[{\text{H}}^{+}][{\text{HCO}}_3^{-}]=k_{-2}{v}_1{v}_2,$$ (9)

and

$${\mathrm{\Phi }}_{+(\ell +2)}=k_{+(\ell +2)}[{\text{HA}}_{\ell }]=k_{+(\ell +2)}{u}_{\ell +2},{\mathrm{\Phi }}_{-(\ell +2)}=k_{-(\ell +2)}[{\text{H}}^{+}][{\text{A}}_{\ell }^{-}]=k_{-(\ell +2)}{v}_1{v}_{\ell +2},1\le \ell \le L.$$ (10)

As described below, the rate constants for each reaction (i.e., k_+ℓ and k_−ℓ) respect the equilibrium constant ( K_ℓ) that governs that reaction. Moreover, we can assume that the rate constants depend on location, k_ℓ = k_ℓ(x). This assumption is relevant, for example, when including a non-homogenous distribution of the enzyme carbonic anhydrase which, when present, increases the rate constants k₊₁ and k₋₁.

Consider now a single solute w, whose concentration we denote by c_w = c_w (t, x), that is, c_w = u_j or c_w = v_j for some j. The corresponding reaction-diffusion equation is written as

$$\frac{\partial c_w}{\partial t}=\underset{\begin{array}{c}\text{Diffusion}\\ \text{term}\end{array}}{\underbrace{\nabla ·(D_w\nabla c_w)}}+\underset{\begin{array}{c}\text{Reaction}\\ \text{term}\end{array}}{\underbrace{\sum _{\ell =-L-2,\ell \ne 0}^{L+2}{S}_{w,\ell }{\mathrm{\Phi }}_{\ell }}}.$$ (11)

Here, the first term on the right-hand side of the equation is Fick’s second law of diffusion, where D_w = D_w (x) is the diffusion coefficient of solute w defining its mobility in the medium. The second term describes the chemical reactions among the solutes. The coefficients S_w,ℓ are the stoichiometric coefficients, describing if the ℓth reaction produces the solute w ( S_w,ℓ =1), consumes it ( S_w,ℓ = −1), or does not change its concentration ( S_w,ℓ = 0 ).

The reaction-diffusion equation (11) is assumed to hold inside and outside the boundary membrane ∂Ω. At the membrane, a boundary condition needs to be postulated, reflecting the permeability of the membrane to each one of the solutes. We denote by “ $·{\mid }_{\partial \mathrm{\Omega }}^{\pm }$” the boundary value from inside (−) and outside (+) of the membrane (i.e. in the aqueous phase adjacent to the intracellular and extracellular sides of the plasma membrane), respectively. To find a reasonable boundary condition, assume first that the membrane has a positive thickness h > 0, and assume that the substance moves through the membrane via diffusion. Letting the thickness of the membrane tend to zero while decreasing proportionally the solute mobility at the plasma membrane, the diffusion of solute w through the membrane can be approximated by a transmission boundary condition (see Appendix A). Let D _w,+ and D _w,− denote the diffusion coefficients in the aqueous phases adjacent to the extracellular and intracellular sides of the membrane, respectively. We posit the transmission conditions, which use Fick’s first law to establish the continuity of fluxes across the membrane for solute w. Denoting by $\frac{\partial }{\partial n}$ the outer normal derivative at the boundary, the conservation of flux implies that

$$\underset{\begin{array}{c}\text{Flux}\text{of}\text{solute}w\\ \text{from}\text{EUF}\text{to}\text{membrane}\end{array}}{\underbrace{D_{w,+}\frac{\partial c_w}{\partial n}{\mid }_{\partial \mathrm{\Omega }}^{+}}}=\underset{\begin{array}{c}\text{Flux}\text{of}\text{solute}w\\ \text{from}\text{membrane}\text{to}\text{ICF}\end{array}}{\underbrace{D_{w,-}\frac{\partial c_w}{\partial n}{\mid }_{\partial \mathrm{\Omega }}^{-}}}.$$ (12)

On the other hand, from the analysis in Appendix A, we have

$$\underset{\begin{array}{c}\text{Flux}\text{of}\text{solute}w\\ \text{across}\text{membrane}\end{array}}{\underbrace{D_{w,\pm }\frac{\partial c_w}{\partial n}{\mid }_{\partial \mathrm{\Omega }}^{\pm }}}=\underset{\begin{array}{c}\text{Premeability}\text{of}\\ \text{membrane}\text{to}w\end{array}}{\underbrace{P_{\partial \mathrm{\Omega },w}}}·\underset{\begin{array}{c}\text{Concentration}\text{difference}\\ \text{of}w\text{across}\text{membrane}\end{array}}{\underbrace{\left(c_w{\mid }_{\partial \mathrm{\Omega }}^{+}-c_w{\mid }_{\partial \mathrm{\Omega }}^{-}\right)}},$$ (13)

where P_∂Ω,w is the true membrane permeability to solute w.

The boundary condition at the outer boundary ∂Ω_∞ of the computational domain is a Dirichlet boundary condition,

$$c_w{\mid }_{\partial {\mathrm{\Omega }}_{\infty }}=c_{w,\infty },$$ (14)

where c_w,∞ is the assumed constant concentration in the BECF. The computational domain Ω_∞ comprises the cell and the surrounding EUF while the outer boundary ∂Ω_∞ identifies the BECF.

Finally, we collect the concentrations of all 2L + 4 solutes into a single vector having 2L + 4 components,

$$U=U(t,x)=\left[\begin{array}{l}{u}_1(t,x)\hfill \\ u_2(t,x)\hfill \\ ⋮\hfill \\ u_{L+2}(t,x)\hfill \\ v_1(t,x)\hfill \\ v_2(t,x)\hfill \\ ⋮\hfill \\ v_{L+2}(t,x)\hfill \end{array}\right]\in {\mathbb{R}}^{2L+4}.$$ (15)

The initial-boundary value problem that we consider is the reaction-diffusion equation, the matrix-vector form of equation (11),

$$\frac{\partial }{\partial t}U=\nabla ·(D\nabla U)+S\mathrm{\Phi }(U),$$ (16)

where D = D(x) is a diagonal matrix containing the diffusion coefficients, S is the stoichiometric matrix and Φ = Φ(U) is the reaction flux vector. The components of U satisfy the transmission conditions given by equations (12) and (13) at the cell membrane ∂Ω, the specified initial conditions (i.e., concentrations of all solutes at time zero within the domain of integration), and the boundary conditions. Thus we write

$$U(0,x)=U_0(x),U(t,x){|}_{\partial {\mathrm{\Omega }}_{\infty }}=U_{\infty }(t,x).$$ (17)

where U₀( x) ∈ ℝ^2L+4 is a vector containing the initial concentrations in the computational domain Ω_∞ and U_∞ specifies the boundary conditions at the outer boundary ∂Ω_∞.

Remark: A natural extension of the model would include a convection term in the exterior domain, i.e., a first order term v(x) · ∇ U(x, t), where v is a velocity field modeling the liquid flow. This addition is not included in the present model.

The implementation of this model in a spherical geometry is discussed in the following section.

3. Computational model

In this section, we consider the governing equations in a spherically symmetric case. We apply the method of lines using a spatial semi-discretization by finite difference approximation. Although this technique is rather standard (Iserles, 1996), for the convenience of the reader not familiar with it, we present the method of lines in the geometry considered.

3.1 Spherically symmetric case

Assume from now on that the oocyte can be modeled as a sphere Ω of radius R concentric with the larger sphere Ω_∞ of radius R_∞ defining the computational domain. Furthermore, we assume that the diffusion coefficients and initial values depend on the distance from the origin only, and that the boundary condition is direction independent, i.e., U_∞ (t, x) = U_∞ (t). With these restrictions, the concentration vector is a function of the radial variable r only, U = U (t, r), and the diffusion equation assumes the form

$$\frac{\partial }{\partial t}U(t,r)=\frac{1}{r^2}\frac{\partial }{\partial r}\left(\text{D}(r)r^2\frac{\partial }{\partial r}U(t,r)\right)+\text{S}\mathrm{\Phi }(U(t,r);r),$$ (18)

which is a matrix-vector form of equation (11). The transmission conditions, from equations (12) and (13), are

$$\text{D}(R+)\frac{\partial }{\partial r}U(t,R+)=\text{D}(R-)\frac{\partial }{\partial r}U(t,R-)$$ (19)

and

$$\text{D}(R\pm )\frac{\partial }{\partial r}U(t,R\pm )=\text{P}·(U(t,R+)-U(t,R-)).$$ (20)

Here, P is a diagonal matrix containing the membrane permeability coefficients of each solute in its diagonal. The initial-boundary conditions, analogous to equation (17), are

$$U(0,r)=U_0(r),U(t,R_{\infty })=U_{\infty }(t).$$ (21)

3.2 Semi-discretization

To obtain a numerically feasible form, we use the method of lines and discretize the system in the spatial direction using an appropriate finite difference scheme.

We start by dividing the space interval [0, R_∞] into N subintervals, denoting the grid points as r_j, 0 = r₀ < r₁ < · · ·< r_N = R_∞, and defining the grid functions C_ℓ, 1 ≤ ℓ ≤ 2L + 4,

$$C_{\ell }(t)=\left[\begin{array}{c}{u}_{\ell }(t,r_0)\\ u_{\ell }(t,r_1)\\ ⋮\\ u_{\ell }(t,r_N)\end{array}\right],C_{L+2+\ell }(t)=\left[\begin{array}{c}{v}_{\ell }(t,r_0)\\ v_{\ell }(t,r_1)\\ ⋮\\ v_{\ell }(t,r_N)\end{array}\right],1\le \ell \le L+2.$$ (22)

In Appendix B, we develop for each grid function a finite difference approximation of the diffusion operator, i.e., we write a semi-discretized system,

$$\frac{{dC}_{\ell }}{dt}={\text{L}}_{\ell }{C}_{\ell }+{\stackrel{\sim }{E}}_{\infty }{c}_{\ell ,\infty }+\sum _{{\ell }^{\prime }=-L-2,{\ell }^{\prime }\ne 0}^{L+2}{S}_{\ell ,{\ell }^{\prime }}{\mathrm{\Phi }}_{{\ell }^{\prime }},1\le \ell \le 2L+4,$$ (23)

where L_ℓ ∈ ℝ^{N ×N} is a second order finite-difference matrix that takes into account the sampled values of the diffusion coefficient and transport across the cell membrane, c_ℓ,∞(t) ∈ ℝ is the boundary (scalar) value of the concentration at r = R_∞, and Ẽ_∞ is a constant vector (see Appendix B). Finally, Φ_ℓ′ = Φ_ℓ′ ({C_ℓ}) ∈ ℝ^N is a vector representing the reaction rates of the ℓ′ th reaction at the grid points, and S_{ℓ, ℓ′} is the stoichiometric matrix.

Finally, by stacking all the vectors C_ℓ into a single vector C ∈ ℝ^{N (2L+4)}, and likewise the reaction fluxes, and by organizing the matrices into single block matrices, we can write the system compactly as

$$\frac{d\text{C}}{dt}=\underset{\begin{array}{c}\text{Diffusion}\\ \text{Term}\end{array}}{\underbrace{\text{LC}}}+\underset{\begin{array}{c}\text{Dirichlet}\\ \text{boundary}\text{condition}\end{array}}{\underbrace{{\stackrel{\sim }{\text{E}}}_{\infty }{c}_{\infty }}}+\underset{\begin{array}{c}\text{Reaction}\\ \text{Term}\end{array}}{\underbrace{\text{S}\mathrm{\Phi }}},$$ (24)

where the boundary condition vector is c_∞ (t) ∈ ℝ^2L+4. This is a stiff system of differential equations, whose numerical solution requires a specialized solver.

4. Results and Discussion

4.1 Equilibration of buffers

Before describing the computational experiments in detail in the next section, we address the issue of competing equilibria among buffers (see Figure 2), and how we implement them in the model.

A critical reaction—though not strictly a buffer reaction because it does not involve H⁺—is the CO₂ hydration - dehydration shown in equation (5). In the absence of one of the carbonic anhydrase enzymes, this reaction is extremely slow. We simulate CA-like activity by multiplying the rate constants of reaction (5), k₊₁ and k_−;1, by an acceleration factor A (A_o for extracellular CA-like activity and A_i for intracellular CA-like activity). Note that CA does not change the equilibrium state, only the rate at which it is achieved.

In addition to the above reaction, the model contains 1+L buffer reactions, one for the ${\text{H}}_2{\text{CO}}_3/{\text{HCO}}_3^{-}$ pair plus L reactions for the ${\text{non}-\text{CO}}_{\text{2}}{/\text{HCO}}_3^{-}$ buffers—all of which compete for a common pool of H⁺, and all of which are virtually instantaneous (i.e., limited only by diffusion) (Roughton, 1941; Harned and Owen, 1958). For the ${\text{H}}_2{\text{CO}}_3/{\text{HCO}}_3^{-}$ pair, we denote the equilibrium constant associated with reaction (6) by

$$K_2=\frac{[{\text{H}}^{+}][{{\text{HCO}}_3}^{-}]}{[{\text{H}}_2{\text{CO}}_3]}=\frac{k_{+2}}{k_{-2}}.$$ (25)

To ensure instantaneous equilibrium of reaction (6) we write an approximation

$$k_{+2}=\frac{1}{{\epsilon }_b},k_{-2}=\frac{k_{+2}}{K_2}=\frac{(1/{\epsilon }_b)}{K_2},$$ (26)

and choose the parameter ε_b > 0 (Table 1) so small that, in the time scale of the diffusion and reaction (6), this reaction virtually takes place immediately. This approximation adds to the stiffness of the system (24). However, because the diffusion equation is already stiff, the stiffness depending on the discretization, specialized solvers need to be employed anyway.

Table 1.

Parameter values used in the “standard in-silico experiment”.

		Bulk ECF	Bulk ICF	Reference
Sphere diameter		0.15 cm (d = 100 μm)	0.13 cm
# of subintervals		100	80
Mobility	CO2	1.71× 10−5 cm2/sec	1.71× 10−5 cm2/sec	(Gros and Moll, 1971)
	H2CO3	1.11× 10−5 cm2/sec	1.11× 10−5 cm2/sec	computed* using data from refs. (Vanysek, 2011) and (Swietach et al., 2003)
	HCO3−	1.11× 10−5 cm2/sec	1.11× 10−5 cm2/sec	computed* using data from refs. (Vanysek, 2011) and (Swietach et al., 2003)
	H+	8.69× 10−5 cm2/sec	8.69× 10−5 cm2/sec	computed* using data from refs. (Vanysek, 2011) and (Swietach et al., 2003)
	HA1	1.56× 10−5 cm2/sec	1.56× 10−5 cm2/sec	(Gutknecht and Tosteson, 1973)
	${\text{A}}_1^{-}$	1.56× 10−5 cm2/sec	1.56× 10−5 cm2/sec	calculated** from (Gutknecht and Tosteson, 1973)
Concentration	CO2	0.4720 mM	0 mM
	H2CO3	0.0013 mM	0 mM
	HCO3−	9.9 mM	0 mM
	H+	3.1623× 10−5 mM	6.3096 × 10−5 mM
	HA	2.5 mM	12.0910 mM
	A−	2.5 mM	15.2216 mM
	Total CO2	10.3733 mM	0 mM
pH		7.50	7.20
pKHA		7.50	7.10
H2CO3 acid formation:
Rate constants	k1	0.0302 sec−1	0.0302 sec−1	computed* using data from refs. (Gibbons and Edsall, 1963) and (Zhao et al., 2003)
	k−1	10.9631 sec−1	10.9631 sec−1	computed* using data from refs. (Gibbons and Edsall, 1963) and (Zhao et al., 2003)
Equilibrium constants	K1 (pK1)	0.0028 (2.5599)	0.0028 (2.5599)	calculated as k1/k−1
H2CO3 dissociation:
Rate constants	k2	1 × 1016 sec−1	1 × 1016 sec−1	chosen to achieve equilibrium
	k−2	4.1530 × 1016 mM −1sec−1	4.1530 × 1016 mM−1sec−1	(calculated as k−2= k2/K2)
Equilibrium constants	K2 (pK2)	0.2408 (3.6184) mM	0.2408 (3.6184) mM	calculated
${\text{HA}}_1/{\text{A}}_1^{-}$ reactions:
Rate constants	k3	1 × 1010 sec−1	1 × 1010 sec−1	chosen to achieve equilibrium
	k−3	3.1623 × 1014 mM−1sec−1	1.2589 × 1014 mM−1sec−1	(calculated as k−3= k3/KHA)
Equilibrium constants	KHA (pKHA)	3.1623 × 10−5 (7.5) mM	7.9433 × 10−5 (7.1) mM	assumed
CA-like activity	A-factor	20	20	chosen

^*See supplementary data for how we used the Arrhenius equation to compute this value.

^**See supplementary data for an explanation on how we calculated this value.

When we add a ${\text{non}-\text{CO}}_{\text{2}}{/\text{HCO}}_3^{-}$ buffer pair ${\text{HA}}_{\ell }/{\text{A}}_{\ell }^{-}$, we similarly assume instantaneous equilibrium of the buffering reaction (7) by expressing the corresponding rate constants in terms of the equilibrium constant

$$k_{+(\ell +2)}=\frac{1}{{\epsilon }_{\ell }},k_{-(\ell +2)}=\frac{(1/{\epsilon }_{\ell })}{K_{(\ell +2)}},K_{(\ell +2)}=\frac{[{\text{H}}^{+}][{\text{A}}_{\ell }^{-}]}{[{\text{HA}}_{\ell }]},$$ (27)

with a sufficiently small time constant ε_ℓ > 0 (Table 1).

4.2 Numerical Experiments

All computations are performed in MATLAB. The systems of ODEs arising from the method of lines (24) are solved using the built-in variable-accuracy stiff solver ODE15S. To ensure that the system achieves equilibrium—in time and in space—we not only assigned sufficiently large rate constants as noted above (see Table 1), but also chose a value of 1 × 10⁻¹² for both the relative tolerance (RelTol) and absolute tolerance (AbsTol). The number of discretization points was a compromise between ensuring that the system achieves equilibrium and a reasonable computational time, which was on the order of a couple of minutes in a standard dual-core PC.

4.2.1 The “standard in-silico experiment”

Setting up the model

We start by describing the computational model used in a “standard in-silico experiment”. Consider a control oocyte (i.e., not injected with or expressing a heterologous protein). Before the beginning of the experiment, we assume that the plasma membrane is impermeable to all solutes. We assume that the EUF has thickness d, d being the distance between the plasma membrane and the BECF.

Prior to the beginning of the experiment, the BECF and EUF both contain 1.5% CO₂/9.9 mM ${\text{HCO}}_3^{-}/\text{pH}$ 7.50 plus a single ${\text{non}-\text{CO}}_{\text{2}}{/\text{HCO}}_3^{-}$ buffer ${\text{HA}}_1/{\text{A}}_1^{-}$ with a pK of 7.50 (e.g., HEPES) and a total concentration of 5 mM (i.e., [TA₁]_BECF = [HA₁]_BECF + [A⁻₁]_BECF = 5 mM). Because the membrane is totally impermeable, all solute concentrations throughout the EUF are the same as in the BECF, and all reactions are at equilibrium.

Regarding the intracellular composition before the beginning of the experiment, we assume an initial intracellular pH of 7.20, and that the concentrations of CO₂, H₂CO₃, and ${\text{HCO}}_3^{-}$ are all zero. We also assume that the intracellular fluid contains only a single ${\text{non}-\text{CO}}_{\text{2}}{/\text{HCO}}_3^{-}$ buffer pair, the properties of which we determined as follows. Consistent with experimental data, we assume that exposing an oocyte to 1.5% CO₂ will cause pH_i to fall from 7.20 to 7.00. From the Davenport diagram (Davenport, 1958; Boron, 2009)—a plot of [ ${\text{HCO}}_3^{-}$] vs. pH for CO₂ values, in this case, of 0% and 1.5%—we can conclude that, over the pH_i interval (pH₁, pH₂) = (7.00, 7.20), the mean ${\text{non}-\text{CO}}_{\text{2}}{/\text{HCO}}_3^{-}$ (or “intrinsic”) intracellular buffering power is

$$\overline{\beta }=-\frac{\mathrm{\Delta }{[{\text{HCO}}_3^{-}]}_{\text{i}}}{\mathrm{\Delta }{\text{pH}}_{\text{i}}}=15.6533\text{mM}/\text{pH}.$$ (28)

We arbitrarily assume that the buffer pK is 7.10 (i.e., halfway between the initial and final pH values). To determine the total concentration [TA₁]_i of this single, hypothetical, intracellular buffer, we used an approach similar to one described previously (Boron, 1977). By definition, β̄ over the relevant pH_i range is

$$\overline{\beta }=\frac{{[{\text{TA}}_1]}_{\text{i}}·\text{Z}}{\left({\text{pH}}_2-{\text{pH}}_1\right)},$$ (29)

where [TA₁]_i·Z is the number of moles per liter of H⁺ being buffered in the reaction ${\text{A}}_1^{-}+{\text{H}}^{+}\rightleftharpoons {\text{HA}}_1$. Expressing β̄ in the form

$$\overline{\beta }=\frac{1}{{\text{pH}}_2-{\text{pH}}_1}\underset{{[{\text{TA}}_1]}_{\text{i}}·\text{Z}}{\underbrace{{\int }_{{\text{pH}}_1}^{{\text{pH}}_2}\beta ({\text{pH}}_{\text{i}}){\text{dpH}}_{\text{i}}}},$$ (30)

where the integrand function β(pH )_i is the buffering power of a ${\text{non}-\text{CO}}_{\text{2}}{/\text{HCO}}_3^{-}$ buffer in a “closed system” (i.e., [HA₁]_i + [A₁⁻]_i = constant) (Koppel and Spiro, 1914; Roos and Boron, 1980; Van Slyke, 1922),

$$\beta ({\text{pH}}_{\text{i}})=ln(10){[{\text{TA}}_1]}_{\text{i}}\frac{{10}^{-{\text{pH}}_{\text{i}}}·\text{K}}{{\left({10}^{-{\text{pH}}_{\text{i}}}+\text{K}\right)}^2},$$ (31)

where K = 10^−pK, we can identify [TA ₁]_i·Z with the value of the integral.

Integrating the expression for β(pH_i) yields

$$\overline{\beta }=\frac{{[{\text{TA}}_1]}_{\text{i}}}{{\text{pH}}_2-{\text{pH}}_1}\underset{\text{Z}}{\underbrace{\left(\frac{1}{1+{10}^{{\text{pH}}_1}\text{K}}-\frac{1}{1+{10}^{{\text{pH}}_2}\text{K}}\right)}},$$ (32)

from which it follows that [TA₁]_i ≈ 27.3126 mM. We assume that, before the beginning of the experiment, the pH and the ${\text{non}-\text{CO}}_{\text{2}}{/\text{HCO}}_3^{-}$ buffer components are uniformly distributed throughout the cell and are in equilibrium.

We assume that the BECF, EUF and ICF have the properties of pure water. Wherever possible, we choose parameter values from the literature at 22°C. Otherwise, we compute parameter values from published values at nearby temperatures (see Table 1 and Table 2).

Table 2.

More Parameters^*

Membrane permeability	CO2	34.20 cm/sec	calculated, assuming that the diffusion coefficient in the membrane is the same as an equivalent thickness of water.
	H2CO3	0	assumed
	HCO3−	0	assumed
	H+	0	assumed
	HA1	0	assumed
	${\text{A}}_1^{-}$	0	assumed
Temperature		22°C	(room temperature)
Solubility	CO2	0.0434 mM/mmHg	calculated**

^*In the computer code, we represent zero as 1 × 10⁻²⁰ cm/sec

^**See supplementary data for an explanation on how we calculated this value.

Starting “the standard in-silico experiment”

We begin the experiment—at time zero—by switching the diffusion constant for CO₂ in the membrane (D_M,CO2) from zero to the value that it would have in water (i.e., D_water,CO2 = 1.71× 10⁻⁵ cm² s⁻¹). Thus, we assume that the membrane is a film of water of the same thickness h_M as the membrane. The true membrane permeability P_M,CO2 would be D_M,CO2 divided by h_M, which we assume to be 5 nm. Thus, P_M,CO2 = 34.20 cm/sec.

During the experiment, all solutes are allowed to move freely between the BECF and EUF, while the dynamics in the EUF and ICF are governed by the reaction-diffusion equations. Only CO₂ is allowed to diffuse across the membrane. We also assume that all extracellular and intracellular buffers are mobile, and that the mobilities of solutes are constant over the entire computational domain. We choose an EUF thickness of d = 100 μm, which corresponds to a computational domain of radius R_∞ = 0.15/2 cm (R_∞ = R + d). Further, we assume that CA-like enzymatic activity is uniformly distributed inside the oocyte and on the extracellular surface of the membrane.

In summary, in a “standard in-silico experiment” we implement:

1. A mobile ${\text{non}-\text{CO}}_{\text{2}}{/\text{HCO}}_3^{-}$ buffer in the extracellular space, and a separate mobile ${\text{non}-\text{CO}}_{\text{2}}{/\text{HCO}}_3^{-}$ buffer in the intracellular space.

2. The mobile ${\text{CO}}_2/{\text{HCO}}_3^{-}$ buffer system in both the extracellular and intracellular spaces. A membrane permeable to only CO₂.

3. CA-like activity everywhere inside the oocyte as well as on the extracellular surface of the plasma membrane.

4. An extracellular unconvected fluid with a thickness d = 100 μm.

Table 1 and Table 2 list the parameters used in a “standard in-silico experiment”. When we change a parameter from a value reported in Table 1 and Table 2, we will state this explicitly.

Testing the model: multiple intracellular ${\text{non}-\text{CO}}_{\text{2}}{/\text{HCO}}_3^{-}$ buffers

In the standard experiment, we implement one mobile, ${\text{non}-\text{CO}}_{\text{2}}{/\text{HCO}}_3^{-}$ buffer ${\text{HA}}_1/{\text{A}}_1^{-}$ (see equation (7)) with different total buffer concentrations and pK values in the extra- vs intracellular fluid. To verify that the model can, as intended, handle multiple buffers ${\text{HA}}_{\ell }/{\text{A}}_{\ell }^{-}$, we introduced a second intracellular ${\text{non}-\text{CO}}_{\text{2}}{/\text{HCO}}_3^{-}$ buffer ${\text{HA}}_2/{\text{A}}_2^{-}$. Knowing that the total buffering power of a mixture of buffers is the sum of the individual buffering powers (Boron, 2009), we considered two oocytes, one representing the “standard in-silico experiment” and thus having a single intracellular buffer ([TA₁]_i = 27.3126, pK = 7.1), and an otherwise identical oocyte with two intracellular buffers, each at half the standard concentration ([TA₁]_i = [TA₂]_i = 27.3126/2, pK = 7.1). As expected, the model yielded identical results for the two oocytes (data not shown).

Simulations of “the standard in-silico experiment”

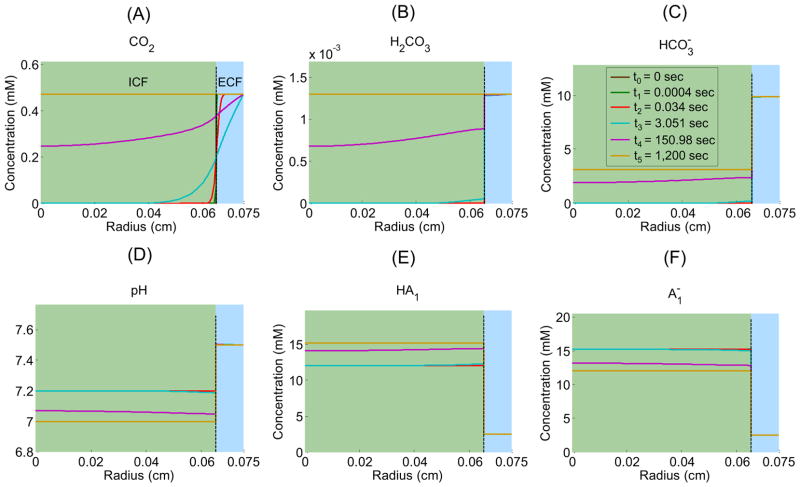
Figure 3 shows the time profiles of each extracellular solute (CO₂, H₂CO₃, ${\text{HCO}}_3^{-}$, H⁺ as pH, HA₁, ${\text{A}}_1^{-}$) in the EUF at five radial distances from the center of the oocyte: 651 μm (i.e., 1 μm away from the outer surface of the membrane), 670 μm, 690μm, 710 μm, and 730 μm as well as in the BECF (i.e., beyond 750 μm). Similarly, Figure 4 shows the time profiles of each intracellular solute at five radial distances from the oocyte center: ≈ 8 μm (i.e., close to the center), ≈ 160 μm, ≈ 320 μm, ≈ 480 μm, and ≈ 640 μm as well as at 650 μm (i.e., the inner surface of the plasma membrane). Figure 5 illustrates how solute concentrations change as a function of the radial distance from the center of the oocyte at six time instances.

Figure 3.

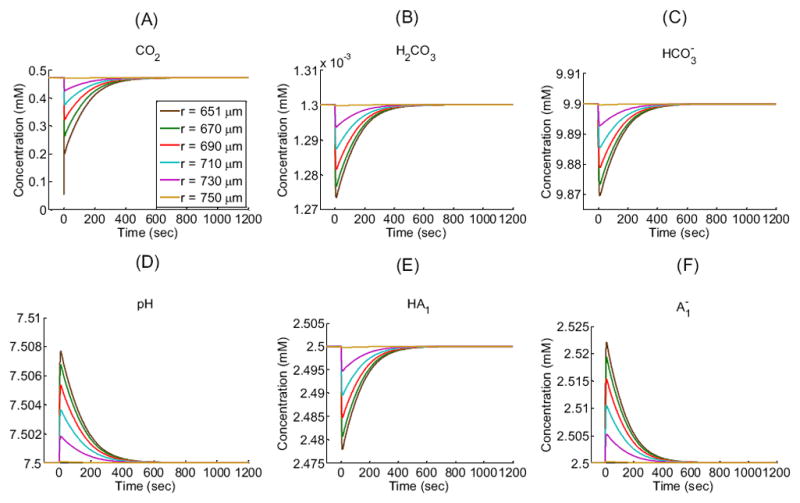
Extracellular concentration-time profiles for solutes (CO₂, H₂CO₃, HCO₃⁻, H⁺ as pH, HA₁, ${\text{A}}_1^{-}$) in a “standard in-silico experiment” at five exterior radial distances (r) from the center of an oocyte of radius R = 650 μm: 651 μm (i.e., 1 μm away from the outer surface of the membrane), 670 μm, 690 μm, 710 μm, and 730 μm in the extracellular unconvected fluid as well as 750 μm at the border with the bulk extracellular fluid. These data are the extracellular counterpart of the data in Figure 4. See Table 1 and Table 2 for parameter values.

Figure 4.

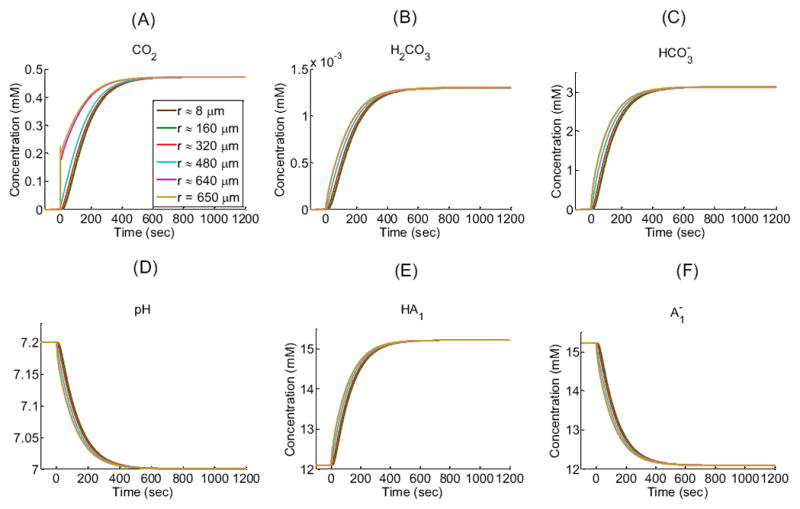
Intracellular concentration-time profiles for solutes (CO₂, H₂CO₃, HCO₃⁻, H⁺ as pH, HA₁, ${\text{A}}_1^{-}$) in a “standard in-silico experiment” for five interior radial distances (r) from the center of an oocyte of radius R = 650 μm: ≈ 8 μm (i.e., close to the center), ≈ 160 μm, ≈ 320 μm, ≈ 480 μm, ≈ 640 μm and at 650 μm (i.e., the cytosolic surface of the plasma membrane). Note that the green curve for r ≈160 μm almost completely overlies the brown curve for r ≈ 8 μm. See Table 1 and Table 2 for parameter values.

Figure 5.

Extra- and intracellular concentration-distance profiles for solutes (CO₂, H₂CO₃, HCO₃⁻, H⁺ as pH, HA₁, ${\text{A}}_1^{-}$) in a “standard in-silico experiment” at six time instances: t₀ = 0 sec, t₁ ≈ 0.0004 sec, t₂ ≈ 0.034 sec, t₃ ≈ 3.051 sec, t₄ ≈ 150.98 sec, and t₅ ≈ 1,200 sec. The dashed black vertical line indicates the oocyte membrane.

The simulation shows that, after the plasma membrane becomes permeable to CO₂ at time t = 0, the CO₂ concentration difference across the membrane (i.e., 0.4720 mM – 0 mM = 0.4720 mM; see Table 1) causes the diffusion of CO₂ into the cell. This influx perturbs the pre-existing equilibria in the regions on opposite sides of the membrane for the ${\text{CO}}_2/{\text{HCO}}_3^{-}$ buffer system and for the ${\text{non}-\text{CO}}_{\text{2}}{/\text{HCO}}_3^{-}$ buffers. Moreover, this perturbation propagates in time away from the membrane in both directions, causing the following events to occur:

1. In the bulk extracellular fluid, the influx of CO₂ from the EUF to the intracellular space produces an initial decrease in [CO₂] (see Figure 3A)—largest and most rapidly in the extracellular fluid closest to the oocyte surface. This decrease in [CO₂] promotes the diffusion of CO₂ from the BECF toward the membrane, thereby in part replenishing the depleted CO₂. The decreases in [CO₂] throughout the EUF also perturb the ${\text{CO}}_2/{\text{HCO}}_3^{-}$ equilibria, causing the reactions ${\text{HCO}}_3^{-}+{\text{H}}^{+}\to {\text{H}}_2{\text{CO}}_3\to {\text{CO}}_2+{\text{H}}_2\text{O}$ to replenish the depleted CO₂, in the process, consuming first H₂CO₃ (Figure 3B) and then ${\text{HCO}}_3^{-}$ (Figure 3C) and H⁺, thereby causing pH_o to rise (Figure 3D). The resulting decrease of [H⁺] throughout the EUF simultaneously perturbs the ${\text{HA}}_1/{\text{A}}_1^{-}$ equilibria, causing the reactions ${\text{HA}}_1\to {\text{H}}^{+}+{\text{A}}_1^{-}$ to replenish the depleted H⁺, consuming [HA₁] (Figure 3E) and producing ${\text{A}}_1^{-}$ (Figure 3F). Notice that the diffusion of CO₂ to the outer surface of the cell membrane and the reaction forming CO₂ from ${\text{HCO}}_3^{-}$ at the outer surface compete to replenish surface CO₂. That is, to the extent that diffusion replenishes CO₂, the contribution of the reaction falls. We quantify this competition by introducing the diffusion/reaction (DRR) ratio. The DRR is calculated in the volume of extracellular fluid that extends out to 1 μm from the plasma membrane, and is defined as the ratio of the rate of CO₂ replenishment (μmoles/sec) by diffusion divided by the rate of CO₂ produced by reaction (5). In the “standard in-silico experiment”, DRR spikes to a value of ≈ 2800 right at t = 0 sec and then rapidly falls to a value of ≈ 35 in approximately 10 sec as the slow reaction catches up. The changes in all solute concentrations become smaller and slower (e.g., the time to maximal change becomes greater) as we move away from the oocyte surface. Moreover, these changes dissipate in time—approaching their respective values in the BECF—as the CO₂ equilibrates across the cell membrane and thus throughout the EUF and ICF (Figure 5A, gold line).

2. In the intracellular fluid, initially no CO₂ is present. As CO₂ enters the cell and diffuses towards its center, the increase in [CO₂] throughout the ICF (Figure 4A) shifts the equilibria of the ${\text{CO}}_2/{\text{HCO}}_3^{-}$ buffer ( ${\text{CO}}_2+{\text{H}}_2\text{O}\to {\text{H}}_2{\text{CO}}_3\to {\text{HCO}}_3^{-}+{\text{H}}^{+}$) towards the right, producing first H₂CO₃ (Figure 4B) and then ${\text{HCO}}_3^{-}$ (Figure 4C) and H⁺, thereby causing pH_i to decrease (Figure 4D). The resulting increase of [H⁺] throughout the intracellular domain simultaneously perturbs the ${\text{HA}}_1/{\text{A}}_1^{-}$ equilibria, causing the reactions ${\text{H}}^{+}+{\text{A}}_1^{-}\to {\text{HA}}_1$ to buffer the newly produced H⁺, consuming ${\text{A}}_1^{-}$ (Figure 4F) and producing [HA₁] (Figure 4E). As we move from the surface towards the center of the oocyte, the changes in solute concentrations begin later and proceed more slowly, reflecting in part the time that the CO₂ takes to diffuse towards the center of the cell. For example, pH requires only 0.12 sec to reach its maximal rate of decline just beneath the membrane, but requires about 46 sec to reach its maximum rate near the cell center. Note that at time t = 0⁺, the [CO₂] at the inner side of the plasma membrane (Figure 4A, gold line) exhibits an overshoot because of the sudden, large influx of CO₂. As the CO₂ equilibrates across the cell membrane, all solute concentrations approach the same respective values throughout the cell. Note that CO₂ and H₂CO₃ are the only solutes whose concentrations—at equilibrium— are the same from the BECF to the cell center (Figure 5A, gold line).

Remark: Our model, simulating a “standard in-silico experiment”, does a reasonably good job predicting the observed shape of the pH profile on the surface of the oocyte (see Figure 3D, r = 651 μm). However, the maximum height of the pH spike at that location is less than 20% as large as the value measured by a surface-pH electrode (Endeward et al., 2006; Musa-Aziz et al., 2009). This difference probably has at least two major causes: (a) The “vitelline membrane” that surrounds the entire oocyte creates an additional unconvected space, in series with the cell membrane. (b) The blunt surface-pH electrode—pushed up against the vitelline membrane—creates yet another unconvected space that, although it represents an extremely small fraction of the surface area of the oocyte, could have a major impact on what the electrode senses. Each of these effects reduces the contribution of diffusion from the BECF and therefore emphasizes the contribution of the reaction ${\text{HCO}}_3^{-}+{\text{H}}^{+}\to {\text{H}}_2{\text{CO}}_3\to {\text{CO}}_2+{\text{H}}_2\text{O}$ in replenishing the depleted CO₂ at the cell surface. The result is an unusually small DRR.

Remark: Our model, simulating a “standard in-silico experiment”, also does a reasonably good job predicting the shape and magnitude of the observed pH_i trajectory (Figure 4D).

4.2.2 Effect of changing d, the width of the EUF

Unstirred layers (ULs) are thin, diffuse layers of fluid, always present near the surface of solid bodies immersed in fluid, where—because of the slow laminar flow of liquid parallel to the surface of the solid—molecules move predominantly via diffusion (Dainty and House, 1966; Korjamo et al., 2009). The presence of unstirred layers on the outer cellular surface as well as within the intracellular space represents a resistance to diffusion that is in series with the resistance of the membrane. As the unstirred layers become thicker, the fractional contribution of the membrane to overall resistance becomes smaller, and may eventually become insignificant (Gutknecht and Tosteson, 1973; Gutknecht et al., 1977; Missner et al., 2008b; Endeward and Gros, 2009; Boron, 2010; Boron et al., 2011).

The width of the unstirred layer (δ) is generally regarded as a steady-state concept. For a particular solute, the thickness of the effective unstirred layer around the membrane is defined as

$$\delta =\frac{D}{P},$$ (33)

where D is the diffusion constant and P is the empirically measured permeability. Note that δ is solute-dependent (Levich, 1962). Finally, the definition of δ does not take into account the effects of chemical reactions—particularly important when working with weak acids and bases—on the size of the UL (Endeward and Gros, 2009). Because (a) our system is dynamic—approaching a steady state (i.e., an equilibrium) only near the end of a simulation, (b) involves multiple solutes, and (c) these solutes react in the “unstirred layer”, it would be virtually impossible to build our model around δ values. Therefore, we chose to focus on the width (d) of the EUF (see Figure 2). Note that EUF has the advantage of being readily applicable to a dynamic system, has the same thickness for all solutes, and is amenable to complex reactions occurring within the layer. Thus, EUF is a generalization of the concept of UL.

The motivation for the studies in this section is two-fold. First, because in real experiments it is difficult to estimate d (Korjamo et al., 2009) or to alter d with precision in order to explore how d influences pH_S and pH_i trajectories, which, in turn, are important tools for studying gas channels. Therefore, we use the model to investigate how changes in d affect the computed profiles of pH_S and pH_i. Second, changing d should give insights into the competition between diffusion and reaction in replenishing the lost CO₂ at the cell surface.

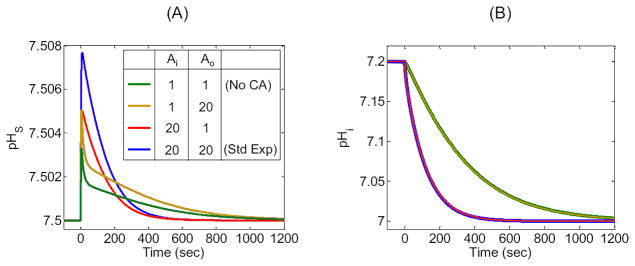
In addition to the standard d = 100 μm, we examine six other cases (Table 3) differing only in the size of the computational domain (i.e., R_∞). Figure 6 displays the results of the simulations for pH_S and pH_i, the two parameters for which experimental data exist.

Table 3.

Values for d and corresponding number of subintervals used in the simulations where we explore the role of the width of the EUF^*

Extracellular Unconvected fluid (EUF)Width d (μm)	Number of Subintervals nout
150	150
100**	100
50	50
25	25
10	10
5	5
1	5

^*The intracellular discretizations are the same as for the “standard in-silico experiment”, 80 subintervals.

^**Standard in-silico experiment.

Figure 6.

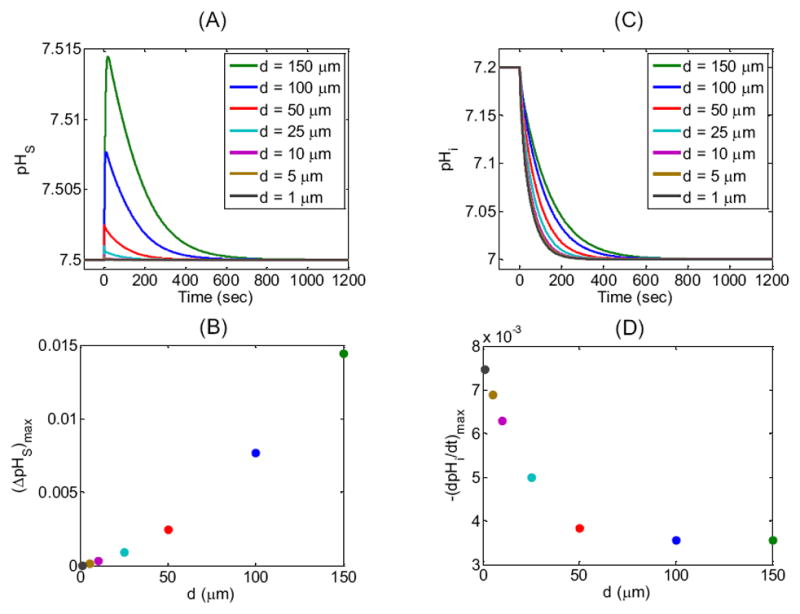
Effect of changing the width d of the extracellular unconvected fluid on the surface (pH_S) and intracellular pH (pH_i) time profiles. (A) pH_S transients for seven simulations corresponding to seven values of d (see legend and Table 3 for parameter values). (B) Maximum height of the pH_S spike—(ΔpH_S)_max—as a function of d for the seven simulations reported in (A). (C) Corresponding pH_i transients at a depth of ≈ 50 μm for the simulations in (A). (D) Maximal rate of pH_i change—(dpH_i/dt)_max—as a function of d for the seven simulations reported in (C).

We define pH_S as the value just outside the cell membrane. ΔpH_S (the difference between the actual and initial values of pH_S) mainly reflects the velocity of H⁺ consumption at the cell surface, which in turn depends on the CO₂ influx as part of a complex cascade of reactions and diffusion events indicated in Figure 2. Figure 6A and B show that, as the thickness of the EUF decreases from 150 μm to 1 μm, the maximum height of the pH_S spike, (ΔpH_S)_max, decreases markedly. The height of the pH_s spike declines because—as d falls, thereby reducing the overall resistance to the diffusion of CO₂—the diffusive flux of CO₂ from the BECF to the external surface of cell membrane becomes increasingly more dominant than the reactions ${\text{HCO}}_3^{-}+{\text{H}}^{+}\to {\text{H}}_2{\text{CO}}_3\to {\text{CO}}_2+{\text{H}}_2\text{O}$ in replenishing CO₂ near the outer surface of the plasma membrane. Thus, DRR rises.

In Figure 6C and D, the intracellular pH corresponds to a depth of 50 μm into the oocyte, which is not unreasonable for the depth of penetration of a microelectrode into an oocyte. The maximal rate of pH_i change, (dpH_i/dt)_max, mainly reflects the velocity of H⁺ production at this intracellular depth, which in turn depends on the CO₂ influx and the complex events outlined in Figure 2. Figure 6C and D show that, as the thickness of the EUF decreases from 150 μm to 1 μm, pH_i declines more rapidly. The magnitude of (dpH_i/dt)_max rises because, as d decreases, the diffusive flux of CO₂ from the BECF increases, causing a rise in [CO₂] on the outer surface of the cell membrane, thereby increasing the CO₂ influx.

4.2.3 Effects of decreasing CO₂ membrane permeability, P_M,CO2

The motivation for the studies in this section is that—in electrophysiology experiments on Xenopus oocytes—both (ΔpH_S)_max (Endeward et al., 2006; Musa-Aziz et al., 2009) and (−dpH_i/dt)_max (Cooper and Boron, 1997; Nakhoul et al., 1998) have provided semi-quantitative indices of the CO₂ permeability of the cell membrane, leading to the initial description of AQP1 as a gas channel. Moreover, pH_S trajectories remain a valuable experimental tool for studying gas channels. Although the present model is not sufficiently sophisticated to permit the extraction of meaningful P_M,CO2 estimates from experimental data, it ought to provide valuable insights into the sensitivity of (ΔpH_S)_max and (−dpH_i/dt)_max to changes in P_M,CO2, and thus the likelihood of eventually being able to extract P_M,CO2 values.

In our “standard in-silico experiment”, we assume that the permeability of the cell membrane corresponds to a film of water (i.e., D_M,CO2 = D_water,CO2 = 1.71× 10⁻⁵ cm²/sec) with the thickness (i.e., h_M = 5 nm) of a typical cell membrane. Thus, in the “standard in-silico experiment” P_M,CO2 is 34.20 cm/sec. In Figure 7, we show the effects of decreasing P_M,CO2 on pH_S and pH_i. The blue curves replicate the “standard in-silico experiment”. Virtually identical curves ensue when we reduce P_M,CO2 by factors of 10¹, 10², and 10³, whereas reducing P_M,CO2 by factors of 10⁴, 2.5·10⁴, 5.0·10⁴, 7.5·10⁴ and 10⁵ has visible and increasingly large effects.

Figure 7.

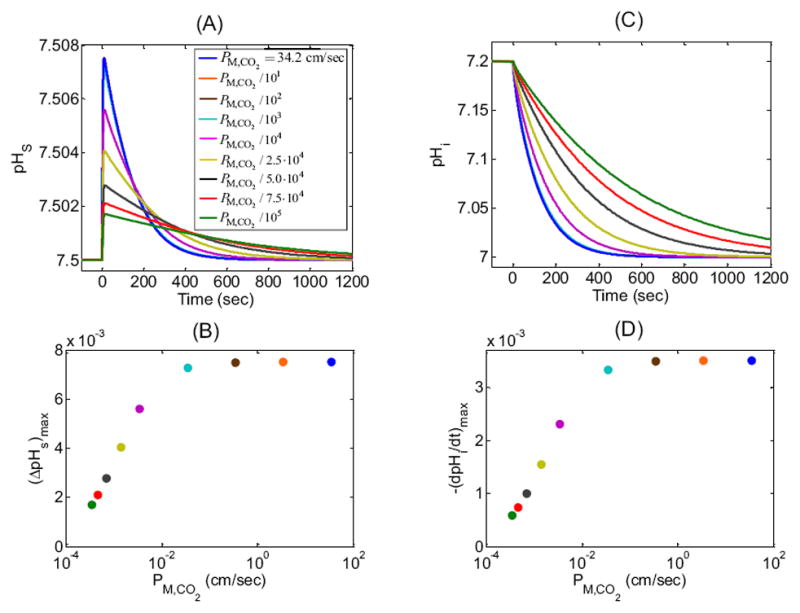
Effect of changing CO₂ membrane permeability (P_M,CO2) on the surface (pH_S) and intracellular pH (pH_i) time profiles. We show results of nine simulations for P_M,CO2 = 34.20 cm/sec (blue, “standard in-silico experiment”, which corresponds to the mobility of CO₂ in H₂O) and for P_M,CO2 reduced by factors of 10¹, 10², 10³, 10⁴, 2.5·10⁴, 5.0·10⁴, 7.5·10⁴ and 10⁵. (A) pH_S transients for the nine simulations. Note that virtually superimposable on the blue curve are the ones for which P_M,CO2 is reduced by factors of 10¹, 10², and 10³. (B) Maximum height of the pH_S spike—(ΔpH_S)_max—as a function of P_M,CO2 for the nine simulations reported in (A). (C) pH_i transients at a depth of ≈ 50 μm for the simulations in (A). Note that virtually superimposable on the blue curve are the ones for which P_M,CO2 is reduced by factors of 10¹, 10², and 10³. (D) Maximal rate of pH_i change—(dpH_i/dt)_max—as a function of P_M,CO2 for the nine simulations reported in (C).

Focusing first on the extracellular cell surface (Figure 7A), we see that, for the P_M,CO2 values examined, the first visible effect on the pH_S trajectory appears when we reduce P_M,CO2 by a factor of 10⁴ (magenta curve): (ΔpH_S)_max is smaller and the decay from the peak to the equilibrium state is slower. Further reductions in P_M,CO2 cause further decreases in both (ΔpH_S)_max and the speed of pH_S equilibration (Figure 7A). Note that the maximal sensitivity of (ΔpH_S)_max to changes in P_M,CO2 occurs near fractional P_M,CO2 decreases of 2.5·10⁴ (Figure 7B).

As is the case for pH_S, the first substantial effects on pH_i trajectories (Figure 7C) occur when we reduce P_M,CO2 by a factor of 10⁴ (magenta curve): (dpH_i/dt)_max is smaller and the decay to the equilibrium state is slower. As P_M,CO2 is decreased further, so do both (dpH_i/dt)_max and the speed of pH_i decline. As for (ΔpH_S)_max, the maximal sensitivity of (−dpH_i/dt)_max to changes in P_M,CO2 occurs near fractional P_M,CO2 decreases of 2.5·10⁴ (Figure 7D).

An explanation for the effects in Figure 7A is that as P_M,CO2 falls, the velocities of both the diffusion and reaction processes also fall, the latter effect reducing the height of the pH_S spike. As the system approaches equilibrium, the total amount of CO₂ that enters the cell is the same, regardless of the speed of CO₂ entry. Thus, decreases in P_M,CO2, which lengthen the time required for a fixed amount of CO₂ to enter the cell, necessarily broaden the descending phase of the pH_S trajectory (Figure 7A) and the entire pH_i (Figure 7C) trajectory. The plots of (ΔpH_S)_max vs P_M,CO2 (Figure 7B) and of (−dpH_i/dt)_max vs P_M,CO2 (Figure 7D) are similar because both (ΔpH_S)_max and (−dpH_i/dt)_max reflect the same fundamental process: the influx of CO₂. The simulations in Figure 7 imply that, for P_M,CO2 values below a certain threshold, one could in principle use either (ΔpH_S)_max or (−dpH_i/dt)_max to estimate P_M,CO2. For this set of simulations, the P_M,CO2 threshold is ≈10⁻² cm/sec, above which the EUF layer becomes rate limiting.

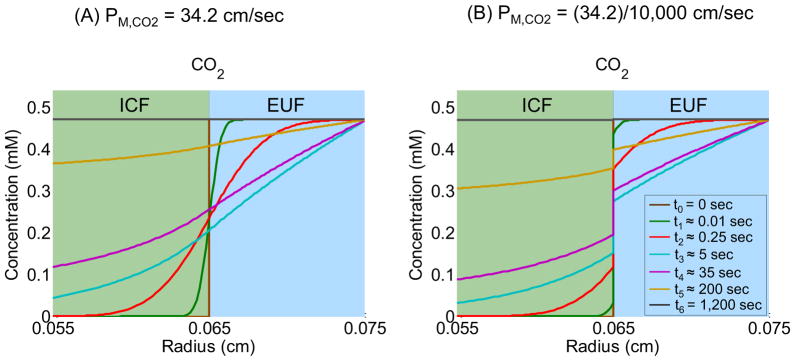
Figure 8 shows how [CO₂] varies with radial distance from the center of the cell at seven time instances, including the initial time t₀ = 0 sec (brown line) and the final time t₆ = 1,200 sec (black line). To the right of the cell membrane (i.e., r > R = 0.065 cm), the figure shows the profiles of [CO₂] in the EUF (d = 100 μm), up to the border with the BECF (i.e., r = R_∞ = 0.075 cm). To the left of the cell membrane (i.e., r < R = 0.065 cm), the figure shows the profiles of [CO₂] inside the oocyte up to a depth of 100 μm. Figure 8A corresponds to the “standard in-silico experiment” (P_M,CO2 = 34.2 cm/sec) and Figure 8B corresponds to the simulation where P_M,CO2 is decreased by a factor of 10⁴. The colors of the curves in Figure 8A correspond to the same time instances as those in Figure 8B (see figure legend). Comparing Figure 8A and Figure 8B, we observe that, at any radial distance, reducing P_M,CO2 increases the time required for [CO₂] to fall or rise to a particular value. Moreover, reducing P_M,CO2 increases, at any given time instance, the discontinuity between the extra- and intracellular [CO₂] trajectories. This discontinuity reflects a smaller CO₂ influx, due to a larger barrier to CO₂ diffusion exerted by the plasma membrane. See Supplementary data for the seven other plots, comparable to those in Figure 8A and Figure 8B, for the P_M,CO2 values introduced in Figure 7.

Figure 8.

Effects of reducing the CO₂ membrane permeability (P_M,CO2) on [CO₂]-distance profiles at seven time instances: t₀ = 0 sec, t₁ ≈ 0.01 sec, t₂ ≈ 0.25 sec, t₃ ≈ 5 sec, t₄ ≈ 35 sec, t₅ ≈ 200 sec and t₆ ≈ 1,200 sec. (A) Simulation corresponding to the “standard in-silico experiment” (P_M,CO2 = 34.2 cm/sec). (B) Simulation corresponding to the experiment in which P_M,CO2 is reduced by a factor of 10⁴.

4.2.4 Effects of changing A_o and A_i, the extra- and intracellular CA-like activities, to mimic native oocytes

The motivation for the studies in this section is that we hypothesized that carbonic-anhydrase activities both at the outer surface of the cell membrane and in the cytosol are important for shaping pH_S and pH_i trajectories. Because the only published oocyte experiments on CO₂ permeability deal with cells having relatively low, native CA activities, our goal is to investigate A_o and A_i values in the native range for the purpose of gaining insight into P_M,CO2.

In our “standard in-silico experiment”, we assume that a CA-like activity amplifies the reaction rates k₁ and k₋₁ by a factor A_i everywhere inside the cell and by a factor A_o outside. The CA-like activity on the outside, however, is limited to the immediate vicinity of the oocyte surface. In our “standard in-silico experiment” we use A_o = A_i = 20. For comparison, A_i in a human erythrocyte is typically 10–25,000 (Geers and Gros, 2000; Endeward et al., 2008). The blue curves in Figure 9A and B replicate the “standard in-silico experiment” for pH_S and pH_i, respectively. The figure also illustrates the results of additional simulations in which we reduced the CA-like activity to A_o = 1, or A_i = 1, or A_o = A_i = 1, that is, no enzymatic activity on the oocyte surface, or throughout the cytoplasm, or both.

Figure 9.

Effects of changing the extracellular CA-like activity (A_o) and intracellular CA-like activity (A_i) on the surface (pH_S) and intracellular pH (pH_i) time profiles. (A) pH_S transients for four simulations corresponding to all combinations of A_o and A_i acceleration factors of 1 or 20. (B) Corresponding pH_i-time profiles at a depth of ≈ 50 μm. Note that, in this panel, the green and gold curves overlap, as do the blue and red curves. The blue curves reproduce the “standard in-silico experiment”.

Focusing first on the extracellular cell surface, we see that with A_o = A_i = 1 (Figure 9A, green curve), pH_S has an unnaturally sharp spike. Raising A_o to 20 while leaving A_i = 1 increases the spike height, making the pH_S spike even sharper (gold curve). On the other hand, raising A_i to 20 while leaving A_o = 1 produces a naturally shaped pH_S trajectory, though (ΔpH_S)_max is still small (red curve). Comparing the blue curve (A_o = A_i = 20) with the red curve (A_o = 1, A_i = 20), we see that implementing modest CA activity on the oocyte surface increases (ΔpH_S)_max and retains a natural trajectory. An explanation for the sharp spikes predicted for the two simulations in which A_i = 1 is that the production of CO₂ on the outer surface of the membrane initially promotes a large CO₂ influx that quickly wanes because of the inability of the cell to dispose of the incoming CO₂. Raising A_i to 20 overcomes this problem.

Turning our attention to pH_i, we see that lowering both A_o and A_i to 1 (Figure 9B, green curve) produces an unnaturally slow fall in pH_i, though to the proper equilibrium level. Raising A_o to 20 while leaving A_i = 1 has virtually no effect, yielding an unnaturally slow pH_i decline (gold curve). Raising A_i to 20 while leaving A_o = 1 produces a reasonably natural pH_i trajectory (red curve), which is nearly indistinguishable from the “standard in-silico experiment” (blue curve). An explanation for these results is that, from the perspective of pH_i and considering only modest levels of CA activity (i.e., A_o = 20 or A_i = 20), the only important factor is the ability of intracellular CA to generate the H⁺ that the intracellular pH microelectrode detects. In the process, the intracellular CA also disposes of incoming CO₂, thereby magnifying the out-to-in CO₂ gradient and also promoting CO₂ influx per se (Musa-Aziz et al., 2005).

4.2.5 Effect of altering intracellular, ${\text{non}-\text{CO}}_{\text{2}}{/\text{HCO}}_3^{-}$, closed-system buffers

The motivation for the studies in this section is that the magnitude of intracellular buffering power ought to have a major influence on the trajectory of pH_i and, by extension, pH_S—both of which are used to assess P_M,CO2 and thus the properties of gas channels. Moreover, before the development of the present model—with its ability to handle multiple buffers—it has been impractical to ask whether reciprocal changes in mobile vs. immobile intracellular buffers (at fixed buffering power) influence pH_S or pH_i trajectories. This question is important because the mobility profile of intracellular buffers is not known with any precision, and because the pH_S and pH_i trajectories are critical for assessing P_M,CO2 in the study of gas channels.

Effect of changing the buffering power

In our “standard in-silico experiment”, we chose the buffering power of the single intracellular, ${\text{non}-\text{CO}}_{\text{2}}{/\text{HCO}}_3^{-}$, closed-system buffer to be β = β_std = 15.6533mM/pH, so that an exposure to 1.5% CO₂ would cause pH to fall from 7.20 to 7.00. In the simulations summarized in Figure 10, we explored β values of 1000β_std (magenta) as an approximation of ∞, 5β_std (cyan), 2β_std (red), β_std (blue), β_std/2 (green), and 0 (black). We achieved these values in the simulation by altering the concentration of total buffer [TA₁]_i = [HA₁]_i + [A₁⁻]_i.

Figure 10.

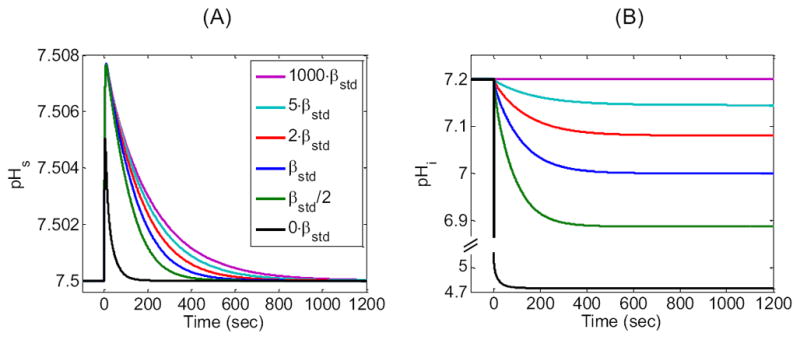
Effect of changing the closed-system intracellular buffering power β on the surface (pH_S) and intracellular pH (pH_i) time profiles. We show the results of six simulations corresponding to β values of 1000·β_std, 5·β_std, 2·β_std, β_std, β_std/2, and 0.·β_std is the buffering power used for the “standard in-silico experiment” (i.e., the β for a single buffer with pK = 7.1 and concentration ≈ 27.3126 mM). The curve for β = 1000·β_std is an approximation of an infinite β. (A) Time course of simulated surface pH. (B) Time course of simulated intracellular pH at a depth of ≈ 50 μm. Note the break in the ordinate, in this panel, which is necessary for showing the large pH_i decrease that would occur with a β of 0.

Figure 10A shows that (ΔpH_S)_max is little affected as we lower β from 1000β_std to β_std/2, but falls off at a β of 0. The rate of pH_S relaxation from the peak pH_S progressively rises as β falls.

Figure 10B shows that, as expected, pH_i does not fall visibly at a β of 1000β_std. At lower values of β, the (−dpH_i/dt)_max progressively increases and the time to reach equilibrium progressively decreases. At the same time, the equilibrium pH progressively falls, reaching, for β = 0, a value of ≈ 4.75 (i.e., the pH that we would achieve if we equilibrated a beaker of pure water with 1.5% CO₂).

The reason that the pH_S relaxation and the pH_i decline are most rapid for β = 0 is that all the H⁺ produced by the intracellular reaction ${\text{CO}}_2+{\text{H}}_2\text{O}\to {\text{HCO}}_3^{-}+{\text{H}}^{+}$ remains free, so that the flux through the reaction is limited by the equal buildup of the two products, ${\text{HCO}}_3^{-}$ and H⁺. In fact, the reaction causes [ ${\text{HCO}}_3^{-}$] and [H⁺] to increase by very little: $\mathrm{\Delta }[{\text{HCO}}_3^{-}]=\mathrm{\Delta }[{\text{H}}^{+}]={10}^{-4.8}\text{M}-{10}^{-7.2}\text{M}\approx 0.016\text{mM}$. In other words, the consumption of CO₂—equivalent to $\mathrm{\Delta }[{\text{HCO}}_3^{-}]$ or Δ[H⁺]—is extremely low (i.e., ≈ 0.016 mM). Thus, free intracellular CO₂ builds up very quickly, and the CO₂ equilibrates rapidly throughout the system. Conversely, at β = ∞, where [H⁺] cannot change from its initial value of 10^−7.2 M, the reaction ${\text{CO}}_2+{\text{H}}_2\text{O}\to {\text{HCO}}_3^{-}+{\text{H}}^{+}$ is limited only by the build-up of ${\text{HCO}}_3^{-}$. Our simulation (and the Henderson-Hasselbalch equation) show that [ ${\text{HCO}}_3^{-}$] rises from 0 before the CO₂ exposure to ≈ 5 mM at equilibrium. In other words, for β = ∞, the consumption of CO₂, equivalent to $\mathrm{\Delta }[{\text{HCO}}_3^{-}]$, is extremely high (i.e., ≈ 5 mM). In fact, the consumption of CO₂ for β = ∞ is 5/0.016 mM ≈ 300-fold greater than the consumption of CO₂ for β = 0. Because ≈ 300-fold more CO₂ must enter the cell, the equilibration requires a much longer time.

Effect of switching to immobile intracellular buffers

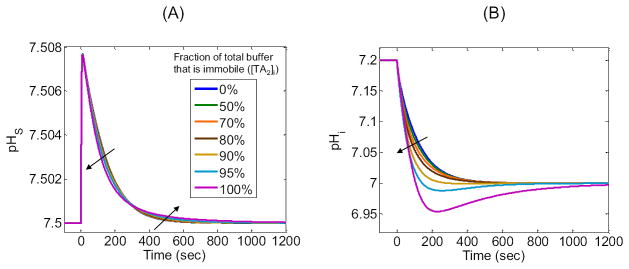
So far, we have implemented a single intracellular, ${\text{non}-\text{CO}}_{\text{2}}{/\text{HCO}}_3^{-}$, closed-system buffer that is mobile. However, real cells have a multitude of ${\text{non}-\text{CO}}_{\text{2}}{/\text{HCO}}_3^{-}$, closed-system buffers that differ in pK, concentration, and mobility. Here we investigate the importance of buffer mobility by splitting our original buffer, ${\text{HA}}_1/{\text{A}}_1^{-}$, with [TA₁]_i equal to a constant (i.e., ≈ 27.3126 mM) that we will now define as [TA]_i, into two buffers ${\text{HA}}_1/{\text{A}}_1^{-}$ and ${\text{HA}}_2/{\text{A}}_2^{-}$. These two buffers have the same pK, and their concentrations sum to [TA]_i (i.e., [TA₁]_i + [TA₂]_i = [TA]_i). We assign ${\text{HA}}_1/{\text{A}}_1^{-}$ the same mobilities as in our “standard in-silico experiment”, and assign ${\text{HA}}_2/{\text{A}}_2^{-}$ mobilities of zero. For the seven simulations summarized in Figure 11, we allow [TA₂]_i to range from 0% of [TA]_i, that is, the “standard in-silico experiment” with all-mobile buffer (blue curves) to 100% of [TA]_i, that is, all-immobile buffer (magenta curves), as summarized in the legends. For example, if 70% of the buffer is immobile, [TA₂]_i = 70%·[TA]_i, then the remaining 30% is mobile, [TA₁]_i = 30%·[TA]_i.

Figure 11.

Mobile versus immobile intracellular buffers. We show the results of simulations in which we split our original intracellular ${\text{non}-\text{CO}}_{\text{2}}{/\text{HCO}}_3^{-}$ buffer HA/A⁻ into two distinct ${\text{non}-\text{CO}}_{\text{2}}{/\text{HCO}}_3^{-}$ intracellular buffers: ${\text{HA}}_1/{\text{A}}_1^{-}$ (assumed mobile) and ${\text{HA}}_2/{\text{A}}_2^{-}$ (assumed immobile). (A) pH_S time profiles for different ratios of immobile to mobile ${\text{non}-\text{CO}}_{\text{2}}{/\text{HCO}}_3^{-}$ buffers, expressed as the fractions (%) of total ${\text{non}-\text{CO}}_{\text{2}}{/\text{HCO}}_3^{-}$ buffer ([TA₂]_i) that are immobile. The blue curve reproduces the “standard in-silico experiment.” (B) Corresponding pH_i time profiles calculated at a depth of ≈ 50 μm. The directions of the arrows in panels A and B show the effects of graded increases in the % of immobile buffer.

Figure 11A shows that, as the percentage of immobile buffer increases from 0% (i.e., “standard in-silico experiment”) to 100%, the pH_S profiles have approximately the same (ΔpH_S)_max, but the initial phase of decay becomes progressively faster as the later phase becomes progressively slower.

Figure 11B shows that, as the percentage of immobile buffer increases from 0% to 100%, (−dpH_i/dt)_max becomes progressively greater, the pH_i values achieved at 200–300 sec become progressively lower (producing a minimum or undershoot at 95% and 100% immobile buffer), and the time to achieve true equilibrium gradually increases.

The reason why 0% immobile buffer corresponds to the smallest (−dpH_i/dt)_max—or the slowest decline in pH_i—is that, as CO₂ enters the cell and leads to the formation of H⁺, which is buffered in the reaction H⁺ + A⁻ → HA, the fully mobile buffer can maximally replenish the consumed A⁻ and dispose via diffusion of the newly formed HA. This counter-diffusion of A⁻ and HA effectively raises the local buffering power, slowing the descent of pH_i. On the other hand, with 100% immobile buffer, the above reaction is limited by the availability of A⁻ and the buildup of HA. Thus, the local buffering power is relatively low, speeding the descent of pH_i. In fact, the local build-up of H⁺ causes pH_i to fall substantially below the equilibrium value reached at infinite time. The slow diffusion of H⁺ away from the membrane, which is the rate-limiting factor for attaining equilibrium, produces the slow increase of pH_i at times greater than ≈ 250 sec.

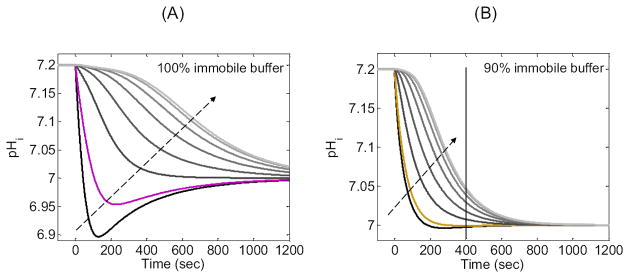
The “pH_i” in Figure 11B is at a depth of ≈ 50 μm below the membrane. Figure 12A is a family of pH_i trajectories from the 100% immobile simulation in Figure 11B, but in Figure 12A we examine a wide range of depths below the membrane. Note that as we move deeper into the cell, the minimum pH value becomes larger and occurs later in time. Eventually, the minimum disappears entirely, and pH falls monotonically, more slowly as we approach the center of the cell. Note also that the delay between the start of the simulation and the time of steepest pH descent increases as we approach the center of the cell.

Figure 12.

Exploring the effects of 100% or 90% immobile ${\text{non}-\text{CO}}_{\text{2}}{/\text{HCO}}_3^{-}$ buffer on the pH_i time profile at eight depths into the cell. (A) Family of pH time profiles based on the simulation in Figure 11B for 100% immobile buffer. The black curve represents a depth of ≈ 10 μm. The magenta curve is the same as in Figure 11B, and represents a depth of ≈ 50 μm. The gray curves, in the direction of the arrow, represent increasing depths beneath the membrane of ≈ 150 μm, ≈ 250 μm, ≈ 350 μm, ≈ 450 μm, ≈ 550 μm and ≈ 650 μm (i.e., near the center of the cell). (B) Family of pH time profiles based on the simulation in Figure 11B for 90% immobile buffer. The gold curve is the same as in Figure 11B, and represents a depth of ≈ 50 μm. The other colors and the arrow have the same meaning as in panel A.

Of particular interest in Figure 12A is the slow pH increase (i.e., “pH recovery” in the physiological literature) at the positions closest to the membrane, and at times after the pH undershoot. This recovery could be mistaken for the “active”, energy-requiring extrusion of acid equivalents that was first described in experiments on squid giant axons, and which provided the first direct evidence for pH_i regulation (Boron and De Weer, 1976; Roos and Boron, 1981). However, the pH_i recoveries in Figure 11B and Figure 12A reflect a purely passive process, the diffusion of H⁺ away from the membrane. Note that in the squid-axon experiments (Boron and De Weer, 1976; Roos and Boron, 1981), the pH electrode was positioned along the axis of the cylindrical axon, analogous to the center of the spherical cell in our simulation in Figure 12A. The pH trajectory at the center of our sphere decreases monotonically, confirming the interpretation in squid-axon study that the pH_i recovery is a reflection of active transport (Boron and De Weer, 1976; Roos and Boron, 1981).

Our last observation begins with the gold curve in Figure 11B. In Figure 11B, all simulations correspond to a depth of ≈ 50 μm. The gold curve represents 90% immobile buffer, the condition in which pH_i appears to reach the equilibrium value of 7.00 most rapidly without an undershoot. However, this apparent rapid equilibration is an illusion. In Figure 12B, the gold curve reproduces the one in Figure 11B. The other curves in Figure 12B (90% immobile buffer) represent the same range of depths presented in Figure 12A (100% immobile buffer). We see in Figure 12B that, even though pH at a depth of ≈ 50 μm appears to be approaching its equilibrium value of 7.00 at a time of ≈ 400 sec (vertical line), pH at greater depths has not yet reached its equilibrium value. The greater the depth, the more distant is pH_i from its equilibrium value at t = 400 sec. Thus, although data obtained at a depth of 50 μm makes it appear as if the system has reached equilibrium within 400 sec, in fact, the system remains far out of equilibrium at this time instance.

4.2.6 Conclusions

We have developed and implemented a three-dimensional reaction-diffusion model for CO₂ influx into a spherical cell with radial symmetry (e.g., a Xenopus oocyte). As hypothesized, this model reproduces the essential features of Figure 1. Namely, the application of CO₂ causes pH_S to rise rapidly to a peak and then decay, and simultaneously causes pH_i to fall monotonically with approximately the same time constant as the decay in pH_S.

The model is flexible because, when we alter parameters as discussed above in Sections 4.2.2 through 4.2.5, the model yields results that either qualitatively match physiological data, or that make intuitive sense to a physiologist:

1. Geometric parameters, including the thickness of the extracellular unconvected fluid. Simulations in which we change d give insight into how altering the width of the EUF impacts both the height of the pH_S spike (Figure 6B) and the maximal rate of intracellular acidification (Figure 6D). The importance of d for the empirically measured membrane permeability to CO₂ is the object of continuing discussion (Boron et al., 2011). Pohl and colleagues argued that the combination of a large d (e.g., 100 μm) and a large true membrane permeability (i.e., the permeability of the lipid phase of a membrane) makes gas channels irrelevant (Missner et al., 2008a; Missner et al., 2008b; Missner and Pohl, 2009). However, the Pohl, Gros, and Boron groups later agreed that, given a sufficiently small P_M,CO2, gas channels could measurably contribute to CO₂ permeability, even with a large d (Boron et al., 2011). Indeed, our simulations show that, even with the relatively large d characteristic of our “standard in-silico experiment” (i.e, 100 μm), both (ΔpH_S)_max and (−dpH_i/dt)_max rise more or less linearly with log(P_M,CO2)—provided P_M,CO2 is below ~10⁻² cm/sec (see Figure 7B and D, respectively). Thus, our model provides an important new physiological insight.

2. Mobilities of solutes in space, including the permeability of the membrane to CO₂. Based on the discussion in (a), as well as the observation that expressing AQPs or Rh proteins in oocytes cause a substantial increase in (ΔpH_S)_max (Endeward et al., 2006; Musa-Aziz et al., 2009), we can conclude that d and P_M,CO2 must be low enough for gas channels to make a significant contribution in oocytes. Moreover, in principle it would be possible to extract, from experimental data, estimates of the CO₂ permeability of gas channels.

3. Activity and localization of carbonic-anhydrase activity. Our simulations lead to the novel conclusion that native Xenopus oocytes must have a small amount of cytosolic CA activity (Figure 9A) in order to account for the general shape of pH_S vs. time in actual recordings from oocytes.

4. Number, concentration, mobility, and pK value of each ${\text{non}-\text{CO}}_{\text{2}}{/\text{HCO}}_3^{-}$ closed-system buffer. A novel insight from our simulations is that at least a small fraction of intracellular buffers must be mobile in order to account for the observed monotonic fall in pH_i that is induced by CO₂ (Figure 11B).

In addition, the model provides interesting new insights into the competition between diffusion and reaction processes near the outer surface of the plasma membrane. First, the DRR changes dynamically during the CO₂ exposure, with diffusion dominating early. Second, (ΔpH_S)_max—a measure of the reaction rate—increases in response to raising d (which reduces the contribution of diffusion, so that the reaction makes a greater contribution by default) or raising A_o (which speeds the reaction).

The model is capable of reproducing qualitatively the shape of the pH_S and pH_i transients in Figure 1. Quantitative agreement with experimental data will require refinements to make the model more realistic. Enhancements might include (a) a vitelline membrane, (b) a surface amplification factor to account for microvilli, (c) a more realistic (i.e., lower) value for D_M,CO2, (d) a reduction of intracellular mobility to reflect the presence of cytoplasm and intracellular vesicles, (e) recognition that an oocyte is not entirely aqueous, as well as the introduction of (f) a discrete surface-pH electrode and (g) convection of the extracellular fluid.

Finally, the model is easily expandable. For example, it would be straightforward to implement additional solutes (e.g., NH₃ and ${\text{NH}}_4^{+}$), allow solutes other than CO₂ to diffuse across the membrane (e.g., NH₃), examine the effects of gas channels (e.g., AQPs and Rh proteins), and to introduce transporter proteins (e.g., a Na/HCO₃ cotransporter) into the plasma membrane.

Highlights.

• Mathematical model of CO₂ influx into a spherical cell

• The model accounts for competing equilibria among multiple buffers

• We simulate the transients in surface and intracellular pH caused by CO₂ influx

Appendix A: Membrane crossing and boundary conditions

We derive the membrane boundary conditions through a limiting process. Consider a substance w with concentration c_w,+ and denote by c_w,+ and c_w,− its concentrations outside and inside the membrane, respectively. Similarly, let D _w,+ and D _w,− denote the diffusion coefficients outside and inside the membrane. To find a reasonable boundary condition, assume first that the membrane has a positive thickness h_M > 0, and assume that the substance traffic through the membrane happens via diffusion. Let D_w,* denote the diffusion coefficient of the membrane, and denote by c_w,* the concentration within the membrane. Without limiting the generality, let us assume that the membrane is locally a spherical surface, the inner and outer boundaries being at r = R and r = R + h_M, respectively. To have the diffusion equation hold in the weak sense, we impose first the boundary condition at the inner membrane boundary, requiring that

$$c_{w,-}(R)=c_{w,\ast }(R),D_{w,-}\frac{\partial c_{w,-}}{\partial r}(R)=D_{w,\ast }\frac{\partial c_{w,\ast }}{\partial r}(R).$$ (A.1)

Similarly, at the outer boundary, we require that

$$c_{w,+}(R+h_M)=c_{w,\ast }(R+h_M),D_{w,+}\frac{\partial c_{w,+}}{\partial r}(R+h_M)=D_{w,\ast }\frac{\partial c_{w,\ast }}{\partial r}(R+h_M).$$ (A.2)

From the Taylor expansion at r = R,

$$c_{w,\ast }(R+h_M)=c_{w,\ast }(R)+h_M\frac{\partial c_{w,\ast }}{\partial r}(R)+\mathcal{O}(h_M^2),$$ (A.3)

and upon substituting (A.1), we have that

$$c_{w,+}(R+h_M)=c_{w,-}(R)+\frac{h_M}{D_{w,\ast }}{D}_{w,-}\frac{\partial c_{w,-}}{\partial r}(R)+\mathcal{O}(h_M^2).$$ (A.4)

By letting the thickness of the membrane go to zero simultaneously with the diffusion constant in such a way that

$$\frac{h_M}{D_{w,\ast }}\to \alpha >0,$$ (A.5)

we arrive at the mixed transmission boundary condition,

$$c_{w,+}(R)-c_{w,-}(R)=\alpha D_{w,-}\frac{\partial c_{w,-}}{\partial r}(R).$$ (A.6)

We observe that the limit (A.5) is not a physiological limit but rather a computational approximation. The idea is that we take the the computational membrane thickness to zero in such a way that the permeability of the membrane is not changed.

Similarly, by using the Taylor expansion at the outer surface and the boundary conditions (A.2), we find through the similar limiting process that

$$c_{w,+}(R)-c_{w,-}(R)=\alpha D_{w,+}\frac{\partial c_{w,+}}{\partial r}(R),$$ (A.7)

which amount to the effective transmission conditions.

Observing that α = 1/P_w, with P_w the true membrane permeability to solute w, we can rewrite equations (A.6) and (A.7) in the forms

$$D_{w,-}\frac{\partial c_{w,-}}{\partial r}(R)=P_w\left(c_{w,+}(R)-c_{w,-}(R)\right)$$ (A.8)

and

$$D_{w,+}\frac{\partial c_{w,+}}{\partial r}(R)=P_w(c_{w,+}(R)-c_{w,-}(R)).$$ (A.9)

Appendix B: Details of the finite difference approximation

In this appendix, we give details concerning the finite difference approximation of the diffusion operator for a single solute w with concentration c_w = c_w (t, r) and diffusion coefficient D_w(r).

Consider first the interior of the cell, r < R. We divide it in n_in spherical shells by the grid points

$$r_j=j\frac{R}{n_{\text{in}}},0\le j\le n_{\text{in}}.$$ (B.1)

Introduce the notation c_w (t, r_j ) = c_w,j (t) and r_j±1/2 = r_j±h/2, where h = R/n_in, and D_w(r_j±1/2) = D_{w, j± 1/2}, 1 ≤ j ≤ n_in − 1. We use the finite difference approximation

$$\frac{1}{r^2}\frac{\partial }{\partial r}\left(D_w{r}^2\frac{\partial c_w}{\partial r}\right)(r_j)\approx \frac{1}{{hr}_j^2}\left(D_{w,j+1/2}{r}_{j+1/2}^2\frac{c_{w,j+1}-c_{w,j}}{h}-D_{w,j-1/2}{r}_{j-1/2}^2\frac{c_{w,j}-c_{w,j-1}}{h}\right),1\le j\le n_{\text{in}}-1.$$ (B.2)

By introducing the notation

$${\xi }_j^{\pm }=D_{w,j\pm 1/2}{\left(\frac{r_{j\pm 1/2}}{r_j}\right)}^2,$$ (B.3)

the formula (B.2) can be written more concisely as

$$\frac{1}{r^2}\frac{\partial }{\partial r}\left(D_w{r}^2\frac{\partial c_w}{\partial r}\right)(r_j)\approx \frac{1}{h^2}\left({\xi }_j^{+}{c}_{w,j+1}-({\xi }_j^{+}+{\xi }_j^{-})c_{w,j}+{\xi }_j^{-}{c}_{w,j-1}\right),1\le j\le n_{\text{in}}-1.$$ (B.4)

For r < r₁, we assume that D_w (r) = D_w,0 is constant. The solution must be smooth and symmetric through the origin, so we can write for r < r₁,

$$\frac{1}{r^2}\frac{\partial }{\partial r}\left(D_w{r}^2\frac{\partial c_w}{\partial r}\right)=D_w\frac{{\partial }^2{c}_w}{\partial r^2}+\frac{2}{r}{D}_w\frac{\partial c_w}{\partial r},$$ (B.5)

where the second term must vanish due to symmetry, and by using symmetric finite differences,

$$\frac{1}{r^2}\frac{\partial }{\partial r}\left(D_w{r}^2\frac{\partial c_w}{\partial r}\right)(0)\approx 2\frac{D_{w,0}}{h^2}(c_{w,1}-c_{w,0}).$$ (B.6)

To find a discretization at the outer boundary of the cell, we use the transmission condition (13)

$$D_w(R-)\frac{\partial c_w}{\partial r}(R-)=P_w(c_w(R+)-c_{w,n_{\text{in}}})$$ (B.7)

and write an approximation

$$\begin{array}{c}\frac{1}{r^2}\frac{\partial }{\partial r}\left(D_w{r}^2\frac{\partial c_w}{\partial r}\right)(r_{n_{\text{in}}})\approx \frac{1}{{hr}_{n_{\text{in}}}^2}\left(r_{n_{\text{in}}+1/2}^2\left(D_w\frac{\partial c_w}{\partial r}\right)(r_{n_{\text{in}}+1/2})-r_{n_{\text{in}}-1/2}^2\left(D_w\frac{\partial c_w}{\partial r}\right)(r_{n_{\text{in}}-1/2})\right)\\ \approx \frac{1}{h}\left(P_w{c}_w(R+)-P_w{c}_{w,n_{in}}\right)-\frac{1}{h^2}{\xi }_{n_{in}}^{-}(c_{w,n_{in}}-c_{w,n_{in}-1}).\end{array}$$ (B.8)

We collect the elements of the grid function c_{w, j} to a vector,

$$C_{w,\text{in}}=\left[\begin{array}{c}{c}_{w,0}\\ c_{w,1}\\ ⋮\\ c_{w,n_{\text{in}}}\end{array}\right]\in {\mathbb{R}}^{n_{\text{in}}+1},$$ (B.9)

and define a vector

$$E_{\text{in}}=\frac{P_w}{h}\left[\begin{array}{c}0\\ 0\\ ⋮\\ 0\\ 1\end{array}\right]\in {\mathbb{R}}^{n_{\text{in}}+1},$$ (B.10)

which will provide coupling of the solutions in the interior domain to the exterior. Furthermore, define

$${\text{L}}_{\text{in}}=\frac{1}{h^2}\left[\begin{array}{rrrrrr}\hfill -2D_{w,0}& \hfill 2D_{w,0}& \hfill & \hfill & \hfill & \hfill \\ \hfill {\xi }_1^{-}& \hfill -({\xi }_1^{-}+{\xi }_1^{+})& \hfill {\xi }_1^{+}& \hfill & \hfill & \hfill \\ \hfill & \hfill {\xi }_2^{-}& \hfill -({\xi }_2^{-}+{\xi }_2^{+})& \hfill {\xi }_2^{+}& \hfill & \hfill \\ \hfill & \hfill & \hfill \ddots & \hfill \ddots & \hfill \ddots & \hfill \\ \hfill & \hfill & \hfill & \hfill {\xi }_{n_{\text{in}}-1}^{-}& \hfill -({\xi }_{n_{\text{in}}-1}^{-}+{\xi }_{n_{\text{in}}-1}^{+})& \hfill {\xi }_{n_{\text{in}}-1}^{+}\\ \hfill & \hfill & \hfill & \hfill & \hfill {\xi }_{n_{\text{in}}}^{-}& \hfill -({\xi }_{n_{\text{in}}}^{-}+{hP}_w)\end{array}\right]\in {\mathbb{R}}^{(n_{\text{in}}+1)\times (n_{\text{in}}+1)}.$$ (B.11)

With these notations, the diffusion equation inside can be approximated as

$$\frac{{d\text{C}}_{w,\text{in}}}{dt}={\text{L}}_{\text{in}}{\text{C}}_{w,\text{in}}+E_{\text{in}}{c}_w(R+).$$ (B.12)

We treat in a similar way the exterior domain, dividing the interval [R, R_∞] in n_out equal intervals. The interior boundary r = R is treated analogously to the exterior boundary of the inner domain. The outer boundary needs to be treated separately. At j = n_out − 1, we approximate

$$\begin{array}{l}\frac{1}{r^2}\frac{\partial }{\partial r}\left(D_w{r}^2\frac{\partial c_w}{\partial r}\right)(r_{n_{\text{out}}-1})\approx \frac{1}{{hr}_{n_{\text{out}}-1}^2}\left(D_{w,n_{\text{out}}-1/2}{r}_{n_{\text{out}}-1/2}^2\frac{c_{w,n_{\text{out}}}-c_{w,n_{\text{out}}-1}}{h}-D_{w,n_{\text{out}}-3/2}{r}_{n_{\text{out}}-3/2}^2\frac{c_{w,n_{\text{out}}-1}-c_{w,n_{\text{out}}-2}}{h}\right)\\ =\frac{1}{{hr}_{n_{\text{out}}-1}^2}\left(D_{w,n_{\text{out}}-1/2}{r}_{n_{\text{out}}-1/2}^2\frac{c_{w,\infty }-c_{w,n_{\text{out}}-1}}{h}-D_{w,n_{\text{out}}-3/2}{r}_{n_{\text{out}}-3/2}^2\frac{c_{w,n_{\text{out}}-1}-c_{w,n_{\text{out}}-2}}{h}\right),\end{array}$$ (B.13)

which, after organizing the terms appropriately in arrays, leads to a matrix equation

$$\frac{{d\text{C}}_{w,\text{out}}}{dt}={\text{L}}_{\text{out}}{\text{C}}_{w,\text{out}}+E_{\text{out}}{c}_w(R-)+E_{\infty }{c}_{w,\infty },$$ (B.14)

where the arrays are given by

$$L_{\text{out}}=\frac{1}{h^2}\left[\begin{array}{rrrrrr}\hfill -({\xi }_1^{+}+{hP}_w)& \hfill {\xi }_1^{+}& \hfill & \hfill & \hfill & \hfill \\ \hfill {\xi }_2^{-}& \hfill -({\xi }_2^{-}+{\xi }_2^{+})& \hfill {\xi }_2^{+}& \hfill & \hfill & \hfill \\ \hfill & \hfill {\xi }_3^{-}& \hfill -({\xi }_3^{-}+{\xi }_3^{+})& \hfill {\xi }_3^{+}& \hfill & \hfill \\ \hfill & \hfill & \hfill \ddots & \hfill \ddots & \hfill \ddots & \hfill \\ \hfill & \hfill & \hfill & \hfill {\xi }_{n_{\text{out}}-1}^{-}& \hfill -({\xi }_{n_{\text{out}}-1}^{-}+{\xi }_{n_{\text{out}}-1}^{+})& \hfill {\xi }_{n_{\text{out}}-1}^{+}\\ \hfill & \hfill & \hfill & \hfill & \hfill {\xi }_{n_{\text{out}}}^{-}& \hfill -({\xi }_{n_{\text{out}}}^{-}+{\xi }_{n_{\text{out}}}^{+})\end{array}\right]\in {\mathbb{R}}^{n_{\text{out}}\times n_{\text{out}}}.$$ (B.15)

Here, the elements ${\xi }_j^{\pm }$ are defined analogously to the interior domain, and

$$E_{\text{out}}=\frac{P_w}{h}\left[\begin{array}{c}1\\ 0\\ ⋮\\ 0\\ 0\end{array}\right]\in {\mathbb{R}}^{n_{\text{out}}},E_{\infty }=\frac{{\xi }_{n_{\text{out}}}^{-}}{h^2}\left[\begin{array}{c}0\\ 0\\ ⋮\\ 0\\ 1\end{array}\right]\in {\mathbb{R}}^{n_{\text{out}}}.$$ (B.16)

Finally, we put the single substance equations together by stacking the vectors as

$${\text{C}}_w=\left[\begin{array}{l}\hfill {\text{C}}_{w,\text{in}}\hfill \\ \hfill {\text{C}}_{w,\text{out}}\hfill \end{array}\right]\in {\mathbb{R}}^{n_{\text{in}}+n_{\text{out}}+1},$$ (B.17)

and, after assembling the matrices,

$$\text{L}=\left[\begin{array}{ccccccccc}& {\text{L}}_{\text{in}}& & & |& E_{\text{in}}& |& 0& \\ --& --& --& --& --& --& --& --& --\\ & 0& |& E_{\text{out}}& |& & & {\text{L}}_{\text{out}}& \end{array}\right]$$ (B.18)

$${\stackrel{\sim }{\text{E}}}_{\infty }=\left[\begin{array}{c}0\\ E_{\infty }\end{array}\right],$$ (B.19)

we arrive at the system

$$\frac{{d\text{C}}_w}{dt}={\text{LC}}_w+{\stackrel{\sim }{\text{E}}}_{\infty }{c}_{w,\infty }.$$ (B.20)