Modulation of Folding Kinetics of Repeat Proteins: Interplay between Intra- and Interdomain Interactions

Abstract

Repeat proteins have unique elongated structures that, unlike globular proteins, are quite modular. Despite their simple one-dimensional structure, repeat proteins exhibit intricate folding behavior with a complexity similar to that of globular proteins. Therefore, repeat proteins allow one to quantify fundamental aspects of the biophysics of protein folding. One important feature of repeat proteins is the interfaces between the repeating units. In particular, the distribution of stabilities within and between the repeats was previously suggested to affect their folding characteristics. In this study, we explore how the interface affects folding kinetics and cooperativity by investigating two families of repeat proteins, namely, the Ankyrin and tetratricopeptide repeat proteins, which differ in the number of interfacial contacts that are formed between their units as well as in their folding behavior. By using simple topology-based models, we show that modulating the energetic strength of the interface relative to that of the repeat itself can drastically change the protein stability, folding rate, and cooperativity. By further dissecting the interfacial contacts into several subsets, we isolated the effects of each of these groups on folding kinetics. Our study highlights the importance of interface connectivity in determining the folding behavior.

Introduction

Understanding the mechanisms that underlie protein folding at the molecular level requires a detailed understanding of how the various interactions, whether short- or long-range and of a native or nonnative nature, contribute to the overall stability and kinetics. It is a challenging task to quantify the nonadditive effects of these interactions, but it is an essential one if we are to predict the effects of point mutations on folding. In many studies, both experimental and computational, investigators have pursued this goal and focused on various small globular domains to decipher folding at the atomistic level (1–5).

Although small globular proteins are attractive because of their small size and the fact that their folding often follows a simple two-state mechanism, repeat proteins may be more suitable for this task. Repeat proteins can be considered as a simple case of multidomain proteins composed of relatively small domains that have a simple topology and interact only with their neighboring domains (on the other hand, repeat proteins can be seen as more complicated because often their domains cannot fold by themselves). Long-range contacts in repeat proteins are rare, and the folding of such proteins is dominated by local interactions. In previous studies, the one-dimensionality of the structure of repeat proteins, which are composed of repetitive units of similar size and structure packed together in a linear chain, enabled the deletion or addition of a particular repeating unit, illustrating their modular nature and their higher tolerance for manipulations relative to globular proteins (6–9). Furthermore, previous works in which repeat proteins were designed to be composed of identical consensus repeats had an additional advantage for dissecting folding energetics because their stability is more homogenously distributed along the proteins (10–14). Despite their simplicity and homogeneity, which has been useful for folding studies, repeat proteins exhibit complex folding behavior similar to that observed in globular proteins, as reflected, for example, by their high stability, cooperative folding, and multiple folding pathways (11,15–23).

The folding kinetics and pathways of repeat proteins have been extensively studied, and it was shown that in natural repeat proteins, where the units are not identical, the local stabilities of the subunits play an important role in dictating them (24–26). To avoid these variations, investigators designed a series of repeat proteins with nearly identical subunits of varying numbers based on consensus sequences (which were determined using evolutionary information) (10,12,14). Using these designed series of proteins, researchers performed in-depth analyses of the folding stability, kinetics, and cooperativity, concentrating on the effects of the number of subunits and their topology (10–14).

Studies of the folding of the two best-studied series, the Ankyrin (ANK) repeat and the tetratricopeptide (TPR) repeat, have revealed interesting trends. In both of these consensus-designed series, the stability of the consensus-designed protein was shown to increase when it was composed of a larger number of subunits (13,27,28). The ANK proteins were observed to fold in a slower manner than their respective TPR analogs, which have a similar number of residues. In addition, whereas the ANK proteins seemed to fold in a highly cooperative manner, even when the protein included a large number of repeating units, the TPR proteins folded sequentially, populating many intermediates with partial numbers of folded repeat subunits (29).

These contrasting behaviors with regard to folding cooperativity were examined in several experimental and computational studies (28,30–32). It was found that the intricate balance between the intrinsic stabilities of the subunits and their stabilization, owing to interface formation with neighboring units, is important for determining the folding cooperativity of the entire protein. Using simple topology-based models, we were previously able to distinguish between these two series, which suggests that the topology of these structures and their internal connectivity are a major factor that influences cooperativity (31). Here, we examine the effects of formation and the relative strength of the interface between the subunits on the cooperativity and kinetics of the proteins. We show that by modulating the relative strength of the interface, one can significantly alter the folding mechanism, the folding rate, and the extent of cooperativity. For the ANK proteins, we further examine the effect of the interface on the folding reaction by elucidating the contribution of different parts of the interface to the folding characteristics.

Materials and Methods

Coarse-grained molecular-dynamics simulations

We used two series of repeat proteins, ANK and TPR, with a growing number of repeat units (2, 3, 4, 6, 8, and 10 units), which are based on designed proteins that have identical repeating units (PDB: 1N0R and 2FO7), to reduce any effects that might be caused by variation among the units. We studied their folding using molecular dynamics (MD) simulated by the Langevin equation. For our simulations, we used a simple native-topology-based model (also termed the Gō model) that assumes a perfectly funneled energy landscape (33). This model has reproduced experimental kinetic rates and pathways, as well as captured other processes involved in folding, such as folding intermediates, protein dimerization, and assembly (19,34–38). More recently, this model was used to study the effects of confinement (39), tethering (40), and modification by natural posttranslational modifications on the folding of the modified protein (41,42).

To make an in-depth study of the thermodynamics and kinetic properties of the studied proteins, we applied a reduced representation of the proteins. In this method, each amino acid is represented by a single bead centered at the Cα atom. Interactions between the residues are arranged so that the lowest energy will be obtained for the native-state structure. Attractive interactions are introduced between native contacts when these pairs are in proximity, whereas the rest of the pairs have repulsive interactions. The contacting residue pairs are determined using the Contacts of Structural Units method (43). In a vanilla model, all interactions are equally scored, with no regard to their original chemical nature. However, to study the relative importance of some of the contacts, such as those in the interfaces, we artificially change the energetic strength by changing the parameter of the corresponding contacts. Details of the energy function appear below:

$$U\left(\Gamma ,{\Gamma }_0\right)=U_{bond}+U_{angles}+U_{dihedral}+U_{contact}+U_{excluded}$$

$$U_{contact}=\sum _{\begin{array}{l}Intra-repeat\\ native-contacts\\ |i-j|>3\end{array}}^M\left\{{\epsilon }_{\mathit{Intra}}\left[5{\left(\frac{r_{0ij}}{r_{ij}}\right)}^{12}-\begin{array}{c}6\end{array}{\left(\frac{r_{0ij}}{r_{ij}}\right)}^{10}\right]\right\}+\sum _{\begin{array}{l}Inter-repeat\\ native-contacts\\ |i-j|>3\end{array}}^N\left\{{\epsilon }_{\mathit{Inter}}\left[5{\left(\frac{r_{0ij}}{r_{ij}}\right)}^{12}-\begin{array}{c}6\end{array}{\left(\frac{r_{0ij}}{r_{ij}}\right)}^{10}\right]\right\}.$$

We manipulate the strength of the intra- and interrepeat contacts by modifying the values of ε_intra and ε_inter, respectively. In the unmodified (wild-type) ANK and TPR proteins with different numbers of repeating units, there is no discrimination between the strengths of the intra- and interrepeat contacts, and both types have identical strength (the strength of all types of contacts is uniform in the original unmodified systems and equals to one). In the modified variants, however, we changed these values in several ways: First, because the ANK proteins have ∼30% more intercontacts than intracontacts, and the situation is nearly opposite in the TPR proteins, we tried to manipulate the original balance of contacts and to imitate the situation in the other series. We therefore increased the strength of the interfaces of the TPR protein series (ε_inter), and decreased it analogously in the ANK protein series. This was carried out in two stages: The first modification adjusted the total strength of the interface (all of the interfacial contacts) to that of the internal repeats, so that the total enthalpy (the multiplication of the number of contacts by their coefficients) would be equal in the interface and the enthalpy inside the repeating units. In other words, we required that the value of the ratio λ = (N × ε_inter)/(M × ε_intra), where (N = the number of intercontacts and M = the number of intracontacts), would be altered to λ = 1. Because the unmodified ANK proteins had a λ-value of ∼1.33, we changed ε_inter^ANK from 1 to 0.78. Similarly, because λ ∼ 0.70 in the unmodified TPR series, we changed ε_inter^TPR to 1.28. Consequently, the second modification further increased (or decreased) the coefficients, so that the total enthalpy in the modified protein series resembled the normal situation in the other series. Thus, we created a TPR-like ANK series by changing ε_inter^ANK to 0.56 (obtaining λ ∼0.70), and an ANK-like TPR series by changing ε_inter^TPR to 1.89 (obtaining a λ-value of ∼1.33). In addition to these manipulations, we modified the ε_intra and ε_inter values, or a subset of these contacts, from 0.5 to 1.5 in selected ANK and TPR systems.

To determine the folding rates of the various systems, we used the mean passage time (MPT) method, in which the folding rate of the protein is correlated with the length of time at which the protein remains unfolded in transition, on average (k_F = ln(1/MPT), and is therefore negative). The more negative it becomes, the slower is the folding reaction. The length and number of simulations for each protein were sufficient to ensure that a large sampling size would be obtained. This measure correlated with experimental folding rates in various studies (31,36,44).

To compute the potential of mean force (PMF, the free energy along a given coordinate; in this case, Q, the number of native contacts) curves of the various systems, we sampled a large array of temperatures around T_F (the folding temperature, at which the stabilities of the folded and unfolded states are equal). We then used the multiple weighted histogram method (WHAM) (45) to compute thermodynamic values such as free energy, enthalpy, and heat capacity.

A simple capillarity theory for the folding of repeat proteins

We constructed a simple model based on the one-dimensional (1D) nature of repeat proteins to determine the dependence of thermodynamic stability on the number of repeats and the intra- and interrepeat stability. Repeat proteins can be modeled so that each repeat unit has enthalpic and entropic contributions that are independent of the other repeats. We assume that the folded state of a repeat protein has a vanishing configurational entropy, and that the unfolded state has a vanishing enthalpic contribution. A protein with a single repeating unit has E_Intra = [−T_F⁽¹⁾S⁽¹⁾], where E_Intra is the enthalpic contribution of a single repeat, S⁽¹⁾ is its entropy in the unfolded state, and T_F⁽¹⁾ is its folding temperature. When considering a protein with n > 1 repeating units, the enthalpic contribution from (n-1) interfaces of E_Inter is added to the contributions from the folding of n repeats. Therefore, we obtain the equation nE_Intra + C(n-1)E_Inter = −T_F⁽ⁿ⁾nS⁽¹⁾. In this equation, we assume extensivity in the entropy, so that S⁽ⁿ⁾ = nS⁽¹⁾. The constant C corrects for different scaling of the enthalpic contribution of the intra- and interrepeat energies. From this, the relationship between folding temperature and the number of repeat units can be easily obtained:

$$\frac{T_{\text{F}}^{\left(\text{n}\right)}}{T_{\text{F}}^{\left(1\right)}}=1+c\frac{n-1}{n}\frac{E_{Inter}}{E_{Intra}}.$$

This simple model can also be used to predict the correlation between the folding barrier, n and λ. To that end, we added a capillarity term, E_cap, to the model, which is the energy cost of forming an additional interface due to surface tension in elongating the 1D protein with n repeating units among the n′ units (which are consecutive) that are folded. The free energy of such a state at an arbitrary temperature T reads F ∼ (n′-1)E_Inter + n′E_Intra – T(n-n′)S⁽¹⁾ + E_cap. At n′ = 0, there is no interface and E_cap vanishes. When n′ increases, this term increases and saturates whenever the folded/unfolded interface has a cross section equal to that of the completely folded protein. The free-energy term can be rewritten as F ∼ n′(T − T_F⁽ⁿ⁾)S⁽¹⁾ − TnS⁽¹⁾ − (1 − n′/n)E_Inter + E_cap. Both E_Inter and E_cap depend on n and n′. E_Inter can be assumed to saturate when n′ = 2. At the folding temperature (T = T_F⁽ⁿ⁾), the maximum free-energy profile follows F^# ∼ E_cap − a(1 − 2/n)E_Inter, which increases as n increases. The constant a corrects for the fraction of the interface that is formed at the transition state.

Results and Discussion

The folding kinetics and cooperativity of repeat proteins are strongly affected by their native-state topology

As previously mentioned, the two best-studied families of repeat proteins, ANK and TPR, exhibit different folding behaviors despite the similarities in their general structural properties (Fig. 1, A and B). Members of the TPR family tend to fold faster and in a sequential manner (16,17), forming many intermediates during their folding reaction. In contrast, their analogs in the ANK family fold more slowly and in a rather cooperative way (7). We note that the slow folding of ANK is partly affected by the presence of proline residues. However, the relative slow rates are observed even in cases where the prolyl-isomerase was added, and therefore its origin corresponds mostly to protein topology. Using a simple coarse-grained model, which results in favorable interactions with contacts in the native state, we were able to reproduce this behavior in ANK and TPR, using the ANK and TPR series of a growing number of identical repeating units (31) (see Fig. 1, C and D).

Figure 1.

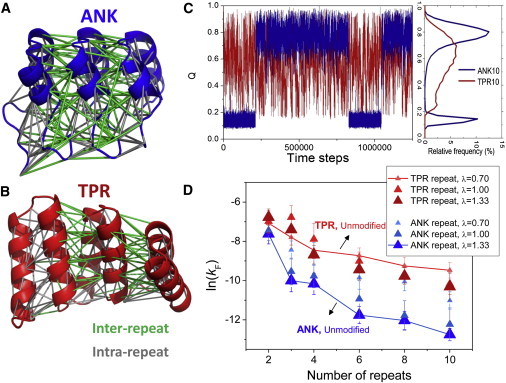
Structure and folding of ANK and TPR proteins. (A and B) The structures of three units of ANK (A, in blue) and TPR (B, in red). In both structures, each inter-and intrarepeat contact is shown in green and gray, respectively. The boundaries of each repeat unit are identical to those used in previous studies (30,31). (C) Folding reactions of ANK10 (blue) and TPR10 (red). Left: The fraction of the total number of native contacts (Q) that are formed during the folding reaction. Right: The relative frequency of Q, illustrating that ANK populates mostly two states, whereas various states of different Qs are significantly populated for TPR. (D) The folding rates (ln(k_F); more-negative values indicate a slower rate) of a series of repeat proteins with modulated strength of interfacial contacts, which is tuned by λ (the ratio between the total strength of the interfacial and internal repeat contacts in the ANK and TPR series) are shown in blue and red, respectively. The value of λ is reflected by the relative size of the triangle and the strength of its color. The number of units of each member in the series (2–10 units) appears on the X axis. The connecting lines serve as a guide to the eye.

In both series, because the protein consists of a larger number of units, its folding rate decreases with the temperature of folding (T_F, the temperature at which the folded and unfolded states are equally stable). This is consistent with experimental results obtained in both the ANK and TPR series (13,27). However, whereas the TPR proteins fold in a sequential manner, forming intermediates with different numbers of folded repeats, the proteins in the ANK series remain largely in a two-state folder, even in proteins with a large number of units. Another prominent difference between the two series is that the longer members of the ANK series fold significantly more slowly than the shorter members in the series (when each is measured at zero stability, at the temperature where the folded and unfolded states have equal stabilities), whereas in the TPR series the differences are not so large (13,27,31).

The delicate balance between the stability of the internal units and their coupling, as manifested in the size and stability of each of their interfaces, is thought to be pivotal in determining the formation of the folding nucleus, the propagation rate, and the overall kinetics and cooperativity. We therefore suspected that the observed differences between the two series may originate in the interface properties of the two families. Although the number of contact pairs within the internal repeats in both families is similar (∼43–48 pairs of residues in contact inside the repeat unit), the number of contacts at the interface is different (∼32 in the TPR family, and ∼60 in the ANK family). It is therefore possible that the higher number of contacts in the ANK family (∼30% more contacts in the interface than in the repeat unit itself) is responsible for the cooperative and slow-folding behavior, whereas the less-dense interface of the TPR (∼30% fewer contacts in the interface than internally in each repeat unit) is related to the faster sequential folding behavior of the TPR series.

Modulation of the interface affects the kinetics and cooperativity of the repeat proteins

We hypothesized that by modifying the relative strength of the interfaces by changing the coefficient of attraction between these residues in our simulation model, we would be able to modify the properties of normal protein, and in particular its folding cooperativity and kinetics. Because all of the contacts in the original systems have equal strength, we can alter a subset of them, and introduce stability variation among the contacts. Therefore, we increased the strength of the interactions at the interfaces of the TPR protein series in an attempt to imitate the situation in the ANK system, where the interface is denser. Analogously, we decreased the strength of the interface of the ANK protein series to imitate the TPR situation with the duller interface. Accordingly, we changed the values of λ (the relative strength of the inter- and intracontacts) of TPR from 0.70 to 1.33, and those of ANK from 1.33 to 0.70. This was carried out in two stages. In the first modification, the total strength of the interface (all of the interfacial contacts) was adjusted to that of the internal repeats so that the enthalpic contribution of the intra- and interrepeat contacts would be equal (namely, λ = 1.0, which is obtained by making M × ε_intra = N × ε_inter, where M and N are the number of intra- and interrepeat contacts, respectively, and ε_intra and ε_inter are the enthalpic contributions gained by forming an individual intra- and interrepeat contact, respectively). This was achieved by reducing the coefficients in the ANK system of each of the interfacial contacts from the original value of 1 to a value of 0.78. In the TPR system, we increased the coefficients of the interface from 1 to 1.28, to achieve equality between the intra- and intercontacts. The second modification further increased (or decreased) the strength of the interrepeat contacts so that the ratio of the enthalpy of the total inter- and intrarepeat contacts in the modified protein series now resembled the normal situation in the other series. Thus, we created a TPR-like ANK series and an ANK-like TPR series in terms of relative interface strength. Our working hypothesis was that the duller and weaker the interface becomes, the less cooperative and faster folding the protein will become.

Our hypothesis was confirmed to a large extent when we examined the kinetics results (Fig. 1 D). With the ANK series, the modified proteins with weakened interfaces fold significantly faster than their original analogs. A striking example is ANK10, whose interface was reduced to ∼56% (λ∼ 0.7; see Materials and Methods), a level similar to that observed for the original TPR10 analog. The folding rate of this interface-reduced ANK10 is equivalent to that of the original ANK3. However, it still folds more slowly than the slowest folder in the original TPR family, demonstrating that there are other determinants at play, such as the connectivity and the stability of the internal units.

With the TPR series, manipulating the interface affected the folding kinetics more modestly, and our ability to slow down the folding reaction and make it more cooperative was less successful. As we increased the strength of the interfacial contacts, the proteins tended to fold more slowly, especially in the longer members of the series; however, the results were not as pronounced as with the ANK series. This may stem from the fact that most of the contacts are relatively short-ranged in the TPR, and therefore attempting to divide them into two groups and prioritizing one of them has modest effects. An alternative explanation is that our manipulations are too strong to reach the desired state, and instead disturb the system so that a stable intermediate form, composed of the group of contacts that have the stronger coefficient, will be formed.

We next examined how the interface manipulations affected the folding cooperativity in the two series. Fig. 2 shows the coupling of unmodified proteins between the folding of individual repeating units in ANK10 and TPR10, and in two manipulated systems with weakened or strengthened interfacial contacts (in the figure, the coupling in folding of each pair of repeats is estimated by the correlation coefficient of finding both repeats in the same states during simulation time). High coupling between most of the repeats is indicative of the degree to which the system folds in an overall two-state manner. In the unmodified ANK10, the systems tend to fold in a highly cooperative manner, which is manifested in the high correlation between the folding behaviors of all the units, except for the outermost ones. As the interface is weakened, however, this cooperativity ceases, and the repeating units become more independent. In the ANK10 system with the weakest interface, the coupling between the units is significantly lower than in the original series and resembles a multistate TPR-like behavior. However, its cooperativity remains higher than in the original TPR10 system (which is in agreement with our observation regarding the kinetics).

Figure 2.

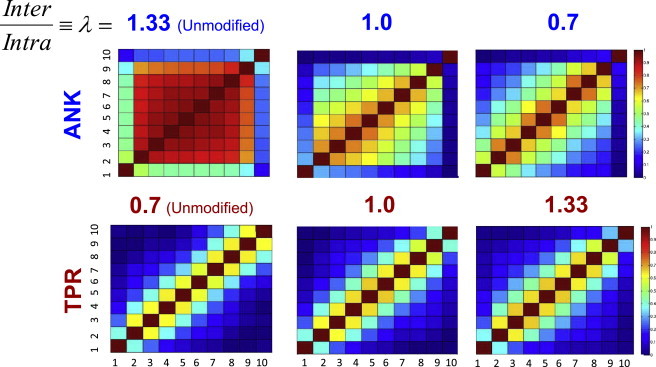
Coupling between the folding of individual repeats. The correlation between the degree of folding of all pairs of repeat units in various ANK (top) and TPR (bottom) systems. The correlation between each pair of repeats was calculated (it indicates the cooperativity in folding of this pair, where strong correlation implies that these two units tend to fold and unfold cooperatively). The ratio λ = (N × ε_inter)/(M × ε_intra) values are shown above the matrices. The matrices of the correlation between the folding of the repeats in unmodified ANK10 and TPR10 are shown on the left. The correlation coefficients between the pairs of repeats are based on the Q value of each repeat throughout the folding reactions of these proteins at T_F.

Strengthening the interface of the TPR10 system results in higher coupling between the units. However, as with the kinetics, the sequential nature of the folding reaction is not drastically modulated, and the coupling is increased between neighboring units but not between units that are not adjacent. This again highlights the role other factors may play in the folding behavior.

To investigate these phenomena in greater molecular detail, we plotted the radius of gyration (R_g) of each system as a function of the number of contacts (Q) that are formed during the folding reaction (Fig. 3). The free-energy landscapes projected along R_g and Q are shown for ANK5 (which folds significantly faster than ANK10 and thus provides better sampling) and TPR10 systems (Fig. 3, A and C). The ANK system clearly displays two-state behavior, i.e., two highly populated regions that correspond to the folded and unfolded states are observed. In contrast to the ANK protein, the TPR protein is characterized by a long, continuous, evenly populated region, which corresponds to the nature of its sequential folding. When the strength of the ANK interface is reduced (Fig. 3 B), the two-state behavior is weakened and consequently the region between the folded and unfolded states becomes more populated, indicating that the system has more modular folding with more intermediates. However, increasing the strength of the interface in the TPR system does not result in a large difference in the population of various folding intermediates (Fig. 3 D).

Figure 3.

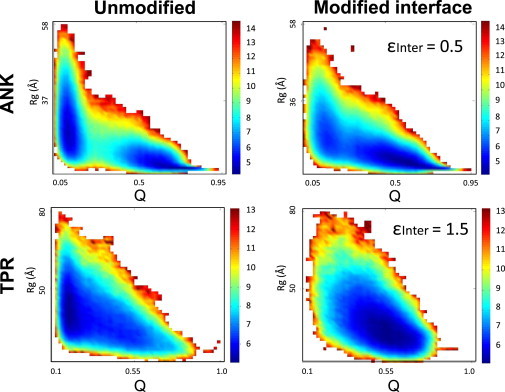
Free-energy landscapes of various ANK and TPR systems projected along R_g and Q. The free energy of the system with a given R_g and a given number of contacts (Q, normalized by the total number of contacts in the native state) is shown; dark-blue regions indicate relatively populated conformations (i.e., low free energy). Top panels: In the ANK system, the appearance of two dark-blue regions, which is indicative of two relatively populated systems (unmodified ANK5, left), indicates that it is becoming a more continuously populated region in the reduced interface system (ANK5 with intercontacts whose strength is reduced by 50% (ε_inter = 0.5; right). Bottom panels: In the TPR system, there is only one continuous dark-blue region, indicative of a population of intermediates (unmodified TPR 10 and TPR with intercontacts with 50% increased strength (ε_inter = 1.5), left and right panels, respectively).

When we manipulated the systems in the opposite direction (i.e., by increasing the strength of the interfaces in the ANK proteins and decreasing the interfaces in the TPR proteins), we observed consistent results (see Fig. S1 in the Supporting Material). Interestingly, the ANK systems with the stronger interface became more cooperative (and their folding rates did not increase), indicating that the ANK systems follow a consistent trend in folding cooperativity and kinetics as a function of interface strength. However, the TPR systems with the weakened interface were not significantly affected by this manipulation, much like the TPR systems in which we increased the interface strength.

A capillarity model for folding of repeat proteins captures the relationship among interface strength, folding stability, and kinetics

To explain the correlation between the number of repeats, the strength of their interfaces, the protein stability, and folding kinetics, we constructed a simple model based on the 1D nature of repeat proteins. The thermodynamic parameters of the model are the inter- and intrarepeat stabilities and the entropy of each repeat in the unfolded state. According to this model, which assumes a vanishing entropy and a vanishing enthalpy in the folded and unfolded states, respectively, the folding temperature of a protein comprising n repeats increases as a consequence of the extra stabilization provided by the interface formed between each neighboring folded repeat. The folding temperature of protein with n repeats, T_F⁽ⁿ⁾, increases with the number of repeats, but reaches a constant value for large n values.

We examined this relationship between the folding temperature and n for the modified and unmodified ANK and TPR proteins by plotting $T_{\text{F}}^{\left(\text{n}\right)}/T_{\text{F}}^{\left(1\right)}$ as a function of (n − 1)/n (see Materials and Methods). We noted that the coarse-grained simulations nicely predict the experimental stability of the series of unmodified TPR proteins with 2–10 repeating units (R = 0.96; Fig. 4 A). Fig. 4 A shows these plots for the different ANK and TPR systems, whose T_F value was estimated from the coarse-grained MD simulations. All of the plots obey linear relationships. The slopes of the linear fits, which correspond to E_Inter/E_Intra (namely, λ), agree very well with the value of λ used in the simulations (when c = 5 in all fits). The success of this simple model in predicting the stability of the various ANK and TPR systems strongly confirms that the stability of repeat proteins is controlled by the number of repeats, n, and the ratio between the energetic strengths of the inter- and intrarepeat, λ.

Figure 4.

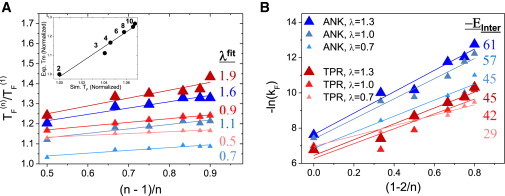
Fitting the simulated stabilities and folding rates of the modified ANK and TPR proteins to a simple capillarity model. (A) Correlation among folding stability, the number of repeat units (n), and the ratio between E_Inter and E_Intra, λ. The folding temperatures (normalized by the T_F of a protein with a single repeat) of each modified and unmodified TPR and ANK repeat (λ = 0.7, 1.0, and 1.3 in various systems) with a different number of repeat units (n) are plotted as a function of (n − 1)/n. All of the systems fit a linear function with correlation coefficients > 0.95. The slope of the linear fits, which corresponds to λ, is in very good agreement with the value of λ used in the simulation (c = 5). The inset shows a comparison between the experimental and simulated folding temperatures of a series of unmodified TPR proteins comprising 2–10 repeat units (correlation coefficient R = 0.96). (B) Correlation among the simulated folding rates, n, and the strength of the interface. The folding rate is plotted as a function of (1 − 2/n). The simulated data of the six series fit linear functions with correlation coefficients > 0.9. The slope of the linear fit, which corresponds to E_Inter, is similar to the value used in the simulations (when a is assigned a value of 10). The values of E_Inter in the simulation model are 58, 45, and 33 for ANK, and 58, 43, and 33 for TPR (where the large numbers refer to the systems with larger λ values). The color scheme is the same as that used in Fig. 1D.

This simple model can also be used to predict the correlation between the folding barrier, n and λ. To that end, we added a capillarity term, E_cap, to the model, which is the energy cost of forming an additional interface due to surface tension in elongating the 1D folded repeat. At the folding temperature, T_F⁽ⁿ⁾, the major energetic barrier in the free-energy profile for folding on a protein with n repeating units follows F^# = E_cap – a(1 − 2/n)E_Inter. To examine the dependence of the folding rate on the number of repeats and the strength of the interface between the repeats, we plotted the simulated folding rates as a function of (1 − 2/n) for the modified ANK and TPR systems. The simulated folding rates depend linearly on (1 − 2/n), as predicted by the simple theoretical model (all correlation coefficients are > 0.9), and they also depend on the strength of the interface. The slopes of the linear fits, which correspond to E_Inter, are indeed larger for systems with tighter interfaces. The value of the slope is similar to the value of E_inter used in the simulations (when a is assigned a value of 10).

Modulation of a specific set of contacts in the ANK system is responsible for altering the folding behavior

A consistent trend is observed in our various analyses regarding the kinetics and cooperativity in the ANK system: When the interface between the ANK units becomes weaker, the protein folds faster and more sequentially (i.e., it becomes TPR-like; see Fig. 1 D and top panels of Fig. 2). Because this simple relationship is important for explaining numerous observations from both experiments and simulations, we analyzed the ANK system in greater detail to pinpoint the contacts or regions of the interface that are responsible for the most significant effects observed during the folding process.

We first analyzed the propensity of each contact to appear in the ANK and TPR systems in the transition-state ensemble, here defined as the ensemble of states in which 25–50% of the contacts are formed (as in most of the studied systems, the occurrence of conformations in this region is rare (see Fig. 3)); other definitions do not significantly alter the results. We noted that unlike the TPR system, where the contacts of the interface are relatively evenly formed, the contacts that are formed with a higher propensity in the ANK system tend to cluster in the interface between the longer loops that connect the units (interloop contacts). Other interfacial contacts, between the helices of two adjacent units (interhelical contacts), tend to form in later stages of the folding reaction (Fig. 4). The cluster of contacts in spatial proximity that are formed earlier in the folding reaction resembles the behavior of various globular proteins that fold through a nucleation process. The fact that many of the TPR contacts are more homogenously formed than the ANK variants is in agreement with the observation that the TPR proteins fold in a sequential manner, populating various intermediates along the way.

We speculated that modulating these two sets of interfacial contacts (the interhelix and interloop subsets of the interface, which include 29 and 31 contacts, respectively) separately would result in very different folding behaviors, and would reveal the regions of the interface that are responsible for the slow, cooperative behavior observed in the ANK proteins. We therefore modified the strength of each of these contact subsets by either increasing or decreasing the ε_inter parameter of these contacts, and studied their folding behavior. Strikingly, when we reduced the strength of the interfacial contacts between the helices (which are only ∼50% of the interfacial contacts), we observed a folding behavior similar to that achieved when we reduced the strength of the contacts in the entire interface. This was observed in the folding rate analysis (see Fig. 6 A), the PMF plots (see Fig. 6 B), and the cooperativity of the modulated system (Fig. S1).

Figure 6.

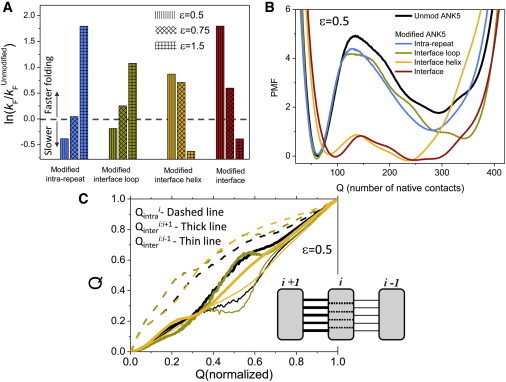
Effects of modulating subregions of the ANK proteins interface. (A) The folding rates of various ANK5 systems with different strengths of a specified group of contacts, normalized by the folding rate of the unmodified ANK5 system. The internal-repeat contacts (intracontacts, in cyan), the interfacial contacts (intercontacts, in green), or a subset of the interfacial contacts (interhelices and interloops, in yellow and in red, respectively) were separately modified by altering their strength to 50%, 75%, and 150% of the original value. Values above the dashed line indicate a relative acceleration. (B) The PMF of various ANK5 systems (i.e., the unmodified ANK5 and the systems with four different sets of contacts whose strength was reduced by 50%). (C) The average number of contacts that are formed at the interface and internally as a function of the total number of contacts formed during simulation time. We plot the average number of contacts at the interface between repeats i and I + 1 (thick line), at the interface formed between repeats i and i − 1 (thin line), and the internal contacts within repeat i (dashed line). We plot these curves for the ANK5 systems in which the interfacial contacts that reside between loops (green) or between helices (orange) were reduced by 50%.

Decreasing the strength of the interfacial contacts between the helices speeds up folding because this modification strengthens the nucleation region (i.e., decreasing the strength of the interfacial contacts between the helices effectively increases the relative strength of the interfacial contacts between the loops, and increases the intrarepeat contacts). A similar argument applies for decreasing the strength of the entire interface, which effectively results in higher stability of the repeating units and thus faster kinetics. The latter effect is due to reducing the cooperativity for folding by prioritizing the formation of the repeating units, which may then fold more sequentially than when the interface between them is tighter. The two systems that have the smallest folding barriers are the systems in which we weakened the strength of either the entire interfacial contacts or just the interhelical contacts (or, alternatively, increased the strength of the intrarepeat contacts alone or with the interfacial contacts between the helices; Fig. 5). Another prominent behavior observed in these systems is the higher population of conformations with an intermediate number of contacts during the folding reaction and the lack of clear, two-state behavior, which was observed in the original, unmodified ANK system (Figs. 3 and 6 B).

Figure 5.

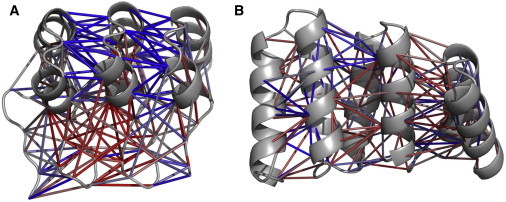
Probability of interfacial contacts occurring in ANK and TPR in the transition-state ensemble of a folding reaction. The probability of each contact occurring in the transition state (as measured by the fraction of frames by which this contact is formed in the transition-state ensemble) for (A) an unmodified ANK system and (B) the TPR system (three central units are shown; red: higher probability, blue: lower probability). In the ANK system, the interfacial contacts between the loops tend to form in a higher fraction than the interfacial contacts between the helices. In the TPR system, the contacts that are formed at the transition-state ensemble are more evenly distributed in the interface.

In contrast, when we reduced the ε_inter value of interfacial contacts between the loops, the system kinetics was not accelerated and the cooperativity remained high (Fig. 6, A and B, and Fig. S2). Weakening the interfacial contacts between the loops does not accelerate folding because these contacts are part of the transition state. Similarly, decreasing the strength of the intrarepeat contacts slows down the folding kinetics because they are part of the folding nucleus as well. Equivalently, increasing the strength of these contacts will result in a significant increase in the folding rate (Fig. 6 A).

We noted that when we manipulated only part of the interface (either the interhelices part or the interloops part), this resulted in a complex perturbation to the system. Reducing the entire interface strength prioritizes the internal repeat contacts, which are relatively short-ranged and spatially clustered, and therefore the effect is relatively straightforward. When we reduce the strength of parts of the interface, we simultaneously indirectly increase the probability of forming contacts with other parts of the interface; however, we also strengthen the internal contacts of the repeating units. Therefore, the latter manipulation results in a complex prioritization process whereby both the short-range internal contacts and some of the longer-range interfacial contacts are prioritized at the expense of the other part of the interface. Therefore, the weakening of the different parts of the interface does simply affect the system in a partial manner in comparison with the weakening of the entire interface. Instead, a more complex behavior is expected to occur, as indeed is observed when the PMF curves (Fig. 6 B) are examined. When we compare the curves of various modified systems with the PMF curve of the unmodified ANK5 system, we can see that the transition state is lowered in some of the systems, resulting in faster folding rates. When we reduce the strength of the contacts of the entire interface (in red), we get a significantly faster kinetics, whereas reduction of the intracontacts strength (in blue) results in a system that folds at a rate similar to that of the original, unmodified ANK5 system. When different subsets of the interfacial contacts are altered, we obtain different results: When we reduce the strength of the interfacial contacts that reside between loops (in orange), we observe a significant acceleration of the folding rate, whereas reducing the strength of the contacts that reside between helices (in cyan) do not lead to significant changes in the kinetics.

To obtain a more microscopic understanding of how manipulating the strength of the inter- and intrarepeat contacts affects the folding mechanism and cooperativity, we follow the fraction of native contacts within a repeat and the interfaces it has with its two neighboring repeats. When the intrarepeat contacts of repeat i are monotonically formed along the folding reaction, we detect a conflict in the formation of the two interfaces it forms with repeat i − 1 and repeat i + 1. This is manifested by attenuated formation of the interface with repeat i + 1 while the interface with repeat i − 1 is formed. This conflict is reminiscent of the topological frustration found in folding some proteins in which there is a preferred ordering of the folding pathway, whereas some alternative pathways that are quite probable may result in slow folding and even need backtracking (46,47). The frustration between the interfaces, which is a consequence of the quasi-1D geometry of the repeat proteins, becomes more severe when the interrepeat contacts between the loops are reduced, which results in a slower folding rate (Fig. 6 C). According to this analysis, the systems that fold faster than the unmodified one (by decreasing the strength of the entire interface or of the interrepeat contacts between the helices) result in smaller frustration in the formation of the two interfaces (and a higher probability for forming the intrarepeat contacts; Fig. 6 C). This lower coupling in forming the two interfaces of a given repeat unit involved is a manifestation of less cooperativity in the folding of repeat proteins.

Conclusions

Investigators have extensively used repeat proteins to study various aspects of protein folding, taking advantage of their simplicity and special attributes. In similarity to the case with multidomain proteins (48,49), the interactions between the domains in repeat units were found to modulate folding and affect misfolding, two factors that affected their evolution (50,51). Here, using coarse-grained MD simulations based on the native-state structure of proteins, we were able to capture some of the unique characteristics of folding in two different series of repeat proteins (the ANK and TPR proteins). The results show that their folding kinetics slows down and their stability increases with the number of repeats. Furthermore, our simulations show that the folding rate and cooperativity of members of the ANK and TPR proteins are very different, as observed in previous experiments. The origin of these differences may lie in the relative stabilities of different regions along the proteins, which was manifested in our simulations by the relative strength of the inter- and intrarepeat regions. By modulating the relative strength of the inter- and intrarepeat interactions, we were able to significantly alter the folding behavior of the ANK proteins and thereby transform them into having a TPR-like behavior in terms of both kinetics and cooperativity. The effect of the relative strength of intra- and intercontacts on the coupling between the folding of neighboring repeating units is reminiscent of the folding determinants of coupled folding-binding processes (52–55).

Our results, which are in line with other theoretical and experimental studies (28,30,32), point to the importance of the relative strength of the interface in the folding behavior of repeat proteins. In general, the more intrinsically unstable are the subunits, and the more they rely on the interaction they form with adjacent units, the more likely it is that the folding reaction will be highly cooperative. The stability of the interface between the ANK repeats was experimentally found to be significantly more stabilizing than that of the repeat itself (15). One way to break this coupling is to increase the heterogeneity of the energy between the repeats (56). Recently, a similar approach was applied for the TPR family, where increasing the stability of the interface between its repeats changed the folding from a multistate mechanism to a two-state one (32). In particular, a simple folding theory based on the capillarity model for propagating the linear protein (57–59) is in very good agreement with the simulation results. This simple model predicts that the folding rate of a protein with n repeating units is controlled by the energetics of the interface, and that its stability is determined by the ratio between the inter- and intrarepeat stabilities.

Our simulations show that these intricate behaviors can be captured by simple models (19,30,31), and point to the importance of the native topology in dictating the folding kinetics and cooperativity of these proteins. In addition, they show that the coupling in the folding of the different repeats, in cases where the interfaces are more stable than the repeats, arises from frustration in forming the interfaces between the two neighboring repeats. Destabilization of the interfaces (or the regions of the interfaces that participate in the transition state for propagation of the folding) diminishes this conflict and accelerates folding via accumulation of intermediates in which only some repeats are folded. We note that these effects on kinetics are still observed when we change the definition of the repeat. Several studies have suggested different definitions of the repeating units (including a repeat unit that is half of the repeat (30) or one and half of the repeat unit (19) that we were using). When we simulated the ANK5 and modulated the strength of newly defined interfaces, we observed a similar acceleration in the kinetics (data not shown). This is because the contacts that affect the folding behavior the most, by participating in the transition state (here called interloop contacts), are part of the newly defined interfaces (or at least a large portion of them; see Fig. S2).

Finally, our molecular analysis of the different regions in the ANK protein’s interface shows how modulation of different subregions can affect the folding reaction very differently. Whereas the interactions that are formed between the loops between adjacent units (interloop contacts) seem to play an important role in forming the transition state, the contacts between the helices (interhelical contacts) seem to appear in later stages of the folding reaction. Therefore, we expect that modulating a subset of regions in the interface of various repeat proteins would result in a diverse array of behaviors, further enriching our understanding of the folding of repeat proteins.