A Biophysical Model of the Mitochondrial ATP-Mg/P_i Carrier

Abstract

Mitochondrial adenine nucleotide (AdN) content is regulated through the Ca²⁺-activated, electroneutral ATP-Mg/P_i carrier (APC). The APC is a protein in the mitochondrial carrier super family that localizes to the inner mitochondrial membrane (IMM). It is known to modulate a number of processes that depend on mitochondrial AdN content, such as gluconeogenesis, protein synthesis, and citrulline synthesis. Despite this critical role, a kinetic model of the underlying mechanism has not been developed and validated. Here, a biophysical model of the APC is developed that is thermodynamically balanced and accurately reproduces a number of reported data sets from isolated rat liver and rat kidney mitochondria. The model is based on an ordered bi-bi mechanism for heteroexchange of ATP and P_i and includes homoexchanges of ATP and P_i to explain both the initial rate and time course data on ATP and P_i transport via the APC. The model invokes seven kinetic parameters regarding the APC mechanism and three parameters related to matrix pH regulation by external P_i. These parameters are estimated based on 19 independent data curves; the estimated parameters are validated using six additional data curves. The model takes into account the effects of pH, Mg²⁺, and Ca²⁺ on ATP and P_i transport via the APC, and supports the conclusion that the pH gradient across the IMM serves as the primary driving force for AdN uptake or efflux. Moreover, computer simulations demonstrate that extramatrix Ca²⁺ modulates the turnover rate of the APC and not the binding affinity of ATP, as previously suggested.

Introduction

The mitochondrial adenine nucleotide (AdN) pool (AdN = ATP +ADP +AMP) is regulated by ATP and P_i transport through the ATP-Mg/P_i carrier (APC) (1) that is localized in the inner mitochondrial membrane (IMM). The APC is a member of the mitochondrial carrier super family SLC25, including the adenine nucleotide translocase (ANT), the dicarboxylate carrier, the 2-oxoglutarate/malate exchanger, and the glutamate/aspartate exchanger (2). Inhibitor titration experiments have detected at least two APC isoforms (3), with molecular cloning techniques identifying an additional isoform (4). This carrier facilitates an electroneutral exchange between MgATP²⁻ and HPO4²⁻ (5), with nonproductive exchanges of the preferred substrates (1,4,6). While under physiological conditions the primary substrates for the APC are ATP (MgATP²⁻) and P_i (HPO4²⁻) (5); ADP (HADP²⁻) can also be transported via the APC in the absence of Mg²⁺ (3).

Transport via the APC is slow compared to oxidative phosphorylation and is believed to regulate energy homeostasis by controlling the mitochondrial AdN pool size (for review, see (1,7)). The maximum ATP transport rate via the APC is only ∼4–5 nmol/min/mg at 30°C (1), whereas for comparison, the maximum P_i transport rate via the inorganic phosphate carrier (PiC) can exceed 3000 nmol/min/mg at the same temperature (8). The carrier requires Ca²⁺ for its operation (3,9,10), as suggested by the primary structure that contains several EF-hand motifs that protrude out into the intermembrane space (2,4). With sufficient Ca²⁺ present, the net ATP uptake or efflux is believed to be primarily controlled by the ATP and pH gradients across the IMM (5).

By regulating the mitochondrial AdN pool, the APC plays an important role in modulating the AdN-dependent metabolic pathways, such as gluconeogenesis, urea synthesis, protein synthesis, and the mitochondrial permeability transition phenomenon (1,4,7,11,12). It is implicated in the mitochondrial ATP uptake experiments seen during Ca²⁺ loading (13), and may be involved with mitochondrial Mg²⁺ regulation (14). Evidence pointing to the need for AdN depletion via the APC before the induction of mitochondrial permeability transition (11), and the role of APC in preventing stress-induced cell death (15), makes the APC an attractive pharmacological target.

Despite its significance, no integrated model of mitochondrial bioenergetics incorporates this transporter to account for mitochondrial AdN pool size regulation (16–18). Here, a biophysically detailed mechanistic model of the APC is developed based on an ordered bi-bi mechanism for heteroexchange of ATP and P_i, which also includes homoexchange of ATP and P_i. The model consists of seven kinetic parameters regarding the APC mechanism and three additional parameters related to matrix pH regulation by external P_i. These parameters are estimated using 19 independent data curves; the estimated parameters are validated using six additional data curves. Model analysis demonstrates that Ca²⁺ does not regulate the carrier activity by modulating the ATP affinity, as previously reported by Nosek et al. (10), but alters the ATP translocation rates as found recently in yeast mitochondria (19).

Methods

Experimental data for model development and validation

The structure of the APC has not yet been solved. However, experimental data on the kinetics of the carrier are available (3,6,10,20). These data include initial rates on influx/efflux of radio-labeled ATP (AdN) and time courses on net AdN content of mitochondria with perturbations in extramatrix (external) [ATP]. Here, the initial rate data of Austin and Aprille (6), Nosek et al. (10), and Hagen et al. (3) are used to develop the kinetic model. The time course data from Austin and Aprille (20) are used to independently validate the kinetic model.

The four data sets used here for parameter estimation and model corroboration all represent measures of AdN uptake/efflux, under a variety of perturbations, in isolated mitochondrial preparations. Austin and Aprille (6) measured the unidirectional influx/efflux rate of tracer labeled ATP in energized isolated liver mitochondria. Specifically, they measured tracer efflux rate while perturbing external [ATP] and [P_i] as well as matrix [ATP]. They also measured the competitive inhibitory effect of external [ATP] and [P_i] over ATP influx rate. Nosek et al. (10) quantified the Ca²⁺-dependent nature of the APC kinetics in liver mitochondria by studying ATP influx as a function of external [Ca²⁺]. Hagen et al. (3) measured unidirectional influx/efflux rate of tracer labeled ATP in energized isolated kidney mitochondria. Specifically, they measured tracer efflux rate while perturbing external [Ca²⁺], matrix [ATP] (in the presence and absence of external [ATP]), external [ATP], and external [P_i] (in the absence of external [ATP]). They also measured tracer influx rate while perturbing external [Ca²⁺], [ATP], and [Mg²⁺]. Their data reveal inhibition of ATP influx rate by external Mg²⁺ above 2 mM. In all experimental protocols measuring unidirectional flux, the incubation medium contained 5 μM carboxyatractyloside (CAT) to avoid rapid mixing of the radioactive pool across the IMM via the ANT. The experimental conditions for the isolated kidney and liver mitochondrial studies on the APC function are outlined in Table 1. The liver and kidney parameters are estimated independently due to known differences in their kinetics (1,3).

Table 1.

Experimental conditions for isolated rat kidney and rat liver mitochondrial experiments

State variables	Rat kidney		Rat liver
	External	Matrix	External	Matrix
[ATP]	1 mM	3.4 mM	1 mM	8.4 mM
[ADP]	0 mM	—	0 mM	1.66 mM
[AMP]	0 mM	—	0 mM	2.5 mM
[Pi]	2 mM	Calculated using Eq. 15	2 mM	Calculated using Eq. 15
[Mg2+]	5 mM (total)	0.5 mM (free)	5 mM (total)	0.5 mM (free)
[Ca2+]	5 μM (free)	250 nM (free)	5 μM (free)	250 nM (free)
[K+]	10 mM (total)	130 mM (free)	10 mM (total)	130 mM (free)
Water volume	—	—	4 mL	0.77 μL/mg protein∗

ΔpH as a function of external [Pi]
[Pi]e→	0 mM	0.5 mM	1 mM	2 mM	4 mM	10 mM
Model†	0.51	0.45	0.39	0.31	0.21	0.12
Data‡	0.81 ± 0.1	0.66 ± 0.03	0.52 ± 0.09	0.43 ± 0.07	0.22 ± 0.11	0.12 ± 0.06

See Hagen et al. (3) and Austin and Aprille (6,20). Note also that external pH was fixed at 7.4 in these experiments.

^∗Final concentration of mitochondria was 1 mg/mL of reaction water volume (20).

^†ΔpH values calculated using Eq. 14 with pH₀ = 0.51, pH_∞ = 0.11, and k_Pi = 0.34 mM⁻¹.

^‡ΔpH values reported in Klingenberg and Rottenberg (24).

Proposed mechanism of ATP/P_i exchange via the APC

Based on the available experimental data, an ordered bi-bi mechanism, with homoexchanges of preferred substrates, is proposed for ATP (MgATP²⁻) and P_i (HPO4²⁻) exchange. The schematic diagram of the mechanism is shown in Fig. 1. The APC is assumed to have one binding site on each side of the IMM. The translocation of the bound substrates (ATP and/or P_i) occurs when both the binding sites are occupied. The carrier facilitates both heteroexchange (ATP for P_i) and homoexchange (ATP for ATP and P_i for P_i).

Figure 1.

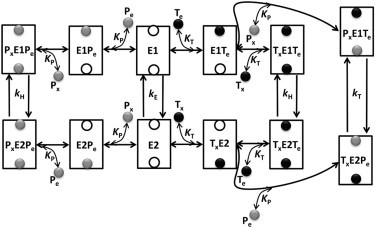
Proposed kinetic mechanism of ATP (MgATP²⁻) and P_i (HPO₄²⁻) exchange via the ATP-Mg/P_i carrier (APC). The mechanism is ordered bi-bi for heteroexchange and random bi-bi for homoexchange of ATP and P_i. It is assumed that the APC has two binding sites: one exposed to the external side and the other to the matrix side. Once both the binding sites are occupied, the APC undergoes conformational change to translocate the bound substrates. E1 is the unbound state of the APC to which either of the external substrates can bind first for homoexchanges, but only external ATP can bind first for heteroexchange. E2 state is analogous to E1 with the exception that matrix substrate can bind first. K_T and K_P represent the binding affinity of the APC for ATP and P_i, respectively; k_E is the rate of futile exchange between the unbound states E1 and E2, k_T is the translocation rate when ATP is exchanged for P_i, and k_H is the translocation rate for homoexchanges. Here, T_x and P_x represent matrix ATP and P_i, whereas T_e and P_e represent external ATP and P_i.

In the proposed mechanism, E1 is the state that first binds to external substrate, whereas E2 is the state that first binds to matrix substrate. For heteroexchange, the E1 (or E2) state is more likely to bind first to external ATP (or matrix ATP). However, when P_i binds first to either E1 or E2, only homoexchange of Pi occurs. This assumption was made because the model did not fit to the available experimental data on ATP/P_i exchange when P_i binds first. Furthermore, with a random bi-bi mechanism, the translocation rate of the substrate-bound conformational states with P_i binding first followed by ATP binding is not necessary to explain the data. For homoexchange, the binding of substrates is assumed to be random. Either of the external substrates can bind first to E1. Similarly, any of the matrix substrate can bind first to E2. Once the first substrate binds to the carrier, the second substrate is able to bind. Thus, there are three different substrate-bound conformations for E1. Similarly, there are three different substrate-bound conformations for E2. The values K_T and K_P represent the binding affinity of the APC for ATP and P_i, respectively; k_E is the rate of futile exchange between the unbound states E1 and E2, k_T is the translocation rate when ATP is exchanged for P_i, and k_H is the translocation rate for homoexchanges. Forward and backward translocation rates are assumed to be equal (21).

APC unidirectional flux expressions

To derive the unidirectional flux expressions via the APC for the ordered bi-bi mechanism with homoexchange (see Fig. 1), we assume that the substrate binding to the carrier is much faster than the translocation rates (22). Consequently, the MgATP²⁻ and HPO₄²⁻ bound forms of E1 and E2 can be expressed as

$$\left[{\text{E}1\text{P}}_{\text{e}}\right]=\left[\text{E}1\right]\frac{{\left[\text{P}\right]}_{\text{e}}}{K_{\text{P}}},\left[{\text{E}1\text{T}}_{\text{e}}\right]=\left[\text{E}1\right]\frac{{\left[\text{T}\right]}_{\text{e}}}{K_{\text{T}}},\left[{\text{T}}_{\text{x}}{\text{E}1\text{T}}_{\text{e}}\right]=\frac{{\left[\text{T}\right]}_{\text{x}}}{K_{\text{T}}}\left[\text{E}1\right]\frac{{\left[\text{T}\right]}_{\text{e}}}{K_{\text{T}}},\left[{\text{P}}_{\text{x}}{\text{E}1\text{P}}_{\text{e}}\right]=\frac{{\left[\text{P}\right]}_{\text{x}}}{K_{\text{P}}}\left[\text{E}1\right]\frac{{\left[\text{P}\right]}_{\text{e}}}{K_{\text{P}}},\left[{\text{P}}_{\text{x}}{\text{E}1\text{T}}_{\text{e}}\right]=\frac{{\left[\text{P}\right]}_{\text{x}}}{K_{\text{P}}}\left[\text{E}1\right]\frac{{\left[\text{T}\right]}_{\text{e}}}{K_{\text{T}}},$$ (1)

$$\left[{\text{P}}_{\text{x}}\text{E}2\right]=\frac{{\left[\text{P}\right]}_{\text{x}}}{K_{\text{P}}}\left[\text{E}2\right],\left[{\text{T}}_{\text{x}}\text{E}2\right]=\frac{{\left[\text{T}\right]}_{\text{x}}}{K_{\text{T}}}\left[\text{E}2\right],\left[{\text{T}}_{\text{x}}{\text{E}2\text{T}}_{\text{e}}\right]=\frac{{\left[\text{T}\right]}_{\text{x}}}{K_{\text{T}}}\left[\text{E}2\right]\frac{{\left[\text{T}\right]}_{\text{e}}}{K_{\text{T}}},\left[{\text{P}}_{\text{x}}{\text{E}2\text{P}}_{\text{e}}\right]=\frac{{\left[\text{P}\right]}_{\text{x}}}{K_{\text{P}}}\left[\text{E}2\right]\frac{{\left[\text{P}\right]}_{\text{e}}}{K_{\text{P}}},\left[{\text{T}}_{\text{x}}{\text{E}2\text{P}}_{\text{e}}\right]=\frac{{\left[\text{T}\right]}_{\text{x}}}{K_{\text{T}}}\left[\text{E}2\right]\frac{{\left[\text{P}\right]}_{\text{e}}}{K_{\text{P}}},$$ (2)

where T denotes MgATP²⁻ and P denotes HPO₄²⁻; the subscripts e and x denote external and matrix spaces. Let [E1]_tot be the total sum of all states involving E1, [E2]_tot be the total sum of all states involving E2, and [E]_tot be the sum of all states (i.e., [E]_tot = [E1]_tot + [E2]_tot). Solving Eqs. 1 and 2 for [E1] and [E2], we have

$$\begin{array}{c}\left[\text{E}1\right]=\frac{{\left[\text{E}1\right]}_{\text{tot}}}{D_1},\\ \left[\text{E}2\right]=\frac{{\left[\text{E}2\right]}_{\text{tot}}}{D_2},\end{array}$$ (3)

where D₁ and D₂ are the binding polynomials for [E1] and [E2] given by

$$D_1=1+\frac{{\left[\text{P}\right]}_{\text{e}}}{K_{\text{P}}}+\frac{{\left[\text{T}\right]}_{\text{e}}}{K_{\text{T}}}+\frac{{\left[\text{P}\right]}_{\text{x}}{\left[\text{T}\right]}_{\text{e}}}{K_{\text{P}}{K}_{\text{T}}}+\frac{{\left[\text{P}\right]}_{\text{x}}{\left[\text{P}\right]}_{\text{e}}}{K_{\text{P}}^2}+\frac{{\left[\text{T}\right]}_{\text{x}}{\left[\text{T}\right]}_{\text{e}}}{K_{\text{T}}^2},$$ (4)

$$D_2=1+\frac{{\left[\text{P}\right]}_{\text{x}}}{K_{\text{P}}}+\frac{{\left[\text{T}\right]}_{\text{x}}}{K_{\text{T}}}+\frac{{\left[\text{T}\right]}_{\text{x}}{\left[\text{P}\right]}_{\text{e}}}{K_{\text{T}}{K}_{\text{P}}}+\frac{{\left[\text{P}\right]}_{\text{x}}{\left[\text{P}\right]}_{\text{e}}}{K_{\text{P}}^2}+\frac{{\left[\text{T}\right]}_{\text{x}}{\left[\text{T}\right]}_{\text{e}}}{K_{\text{T}}^2}.$$ (5)

Assuming steady-state turnover of the carrier, we have

$$-k_{\text{E}}\left[\text{E}1\right]-k_{\text{H}}\left[{\text{T}}_{\text{x}}{\text{E}1\text{T}}_{\text{e}}\right]-k_{\text{H}}\left[{\text{P}}_{\text{x}}{\text{E}1\text{P}}_{\text{e}}\right]-k_{\text{T}}\left[{\text{P}}_{\text{x}}{\text{E}1\text{T}}_{\text{e}}\right]+k_{\text{E}}\left[\text{E}2\right]+k_{\text{H}}\left[{\text{T}}_{\text{x}}{\text{E}2\text{T}}_{\text{e}}\right]+k_{\text{H}}\left[{\text{P}}_{\text{x}}{\text{E}2\text{P}}_{\text{e}}\right]+k_{\text{T}}\left[{\text{T}}_{\text{x}}{\text{E}2\text{P}}_{\text{e}}\right]=0.$$ (6)

Dividing Eq. 6 by k_T reduces the number of adjustable parameters by one and helps in comparing the activity of the APC in rat kidney and rat liver mitochondria (see Table 2). Solving the resulting equation for [E1] and [E2] and normalizing with respect to [E]_tot, we have

$$\frac{\left[\text{E}1\right]}{{\left[\text{E}\right]}_{\text{tot}}}=\frac{D_1\left({\alpha }_2{K}_{\text{P}}^2{K}_{\text{T}}^2+{\alpha }_1{K}_{\text{P}}^2{\left[\text{T}\right]}_{\text{x}}{\left[\text{T}\right]}_{\text{e}}+{\alpha }_1{K}_{\text{T}}^2{\left[\text{P}\right]}_{\text{x}}{\left[\text{P}\right]}_{\text{e}}+K_{\text{P}}{K}_{\text{T}}{\left[\text{T}\right]}_{\text{x}}{\left[\text{P}\right]}_{\text{e}}\right)}{\left(D_1+D_2\right)\left({\alpha }_2{K}_{\text{P}}^2{K}_{\text{T}}^2+{\alpha }_1{K}_{\text{T}}^2{\left[\text{P}\right]}_{\text{x}}{\left[\text{P}\right]}_{\text{e}}+{\alpha }_1{K}_{\text{P}}^2{\left[\text{T}\right]}_{\text{x}}{\left[\text{T}\right]}_{\text{e}}\right)+K_{\text{P}}{K}_{\text{T}}\left({\left[\text{T}\right]}_{\text{x}}{\left[\text{P}\right]}_{\text{e}}{D}_1+{\left[\text{P}\right]}_{\text{x}}{\left[\text{T}\right]}_{\text{e}}{D}_2\right)},$$ (7)

$$\frac{\left[\text{E}2\right]}{{\left[\text{E}\right]}_{\text{tot}}}=\frac{D_2\left({\alpha }_2{K}_{\text{P}}^2{K}_{\text{T}}^2+{\alpha }_1{K}_{\text{P}}^2{\left[\text{T}\right]}_{\text{x}}{\left[\text{T}\right]}_{\text{e}}+{\alpha }_1{K}_{\text{T}}^2{\left[\text{P}\right]}_{\text{x}}{\left[\text{P}\right]}_{\text{e}}+K_{\text{P}}{K}_{\text{T}}{\left[\text{P}\right]}_{\text{x}}{\left[\text{T}\right]}_{\text{e}}\right)}{\left(D_1+D_2\right)\left({\alpha }_2{K}_{\text{P}}^2{K}_{\text{T}}^2+{\alpha }_1{K}_{\text{T}}^2{\left[\text{P}\right]}_{\text{x}}{\left[\text{P}\right]}_{\text{e}}+{\alpha }_1{K}_{\text{P}}^2{\left[\text{T}\right]}_{\text{x}}{\left[\text{T}\right]}_{\text{e}}\right)+K_{\text{P}}{K}_{\text{T}}\left({\left[\text{T}\right]}_{\text{x}}{\left[\text{P}\right]}_{\text{e}}{D}_1+{\left[\text{P}\right]}_{\text{x}}{\left[\text{T}\right]}_{\text{e}}{D}_2\right)},$$ (8)

where α₁ = k_H/k_T and α₂ = k_E/k_T are two independent nondimensional parameters describing substrate translocation. The unidirectional-tracer-labeled ATP influx/efflux rates via the APC are given by

$$\begin{array}{c}{J}_{\text{inf}}=f\left({\text{Ca}}^{2+}\right)\cdot \left(k_{\text{T}}\left[{\text{P}}_{\text{x}}{\text{E}1\text{T}}_{\text{e}}\right]+k_{\text{H}}\left[{\text{T}}_{\text{x}}{\text{E}1\text{T}}_{\text{e}}\right]\right)\\ =f\left({\text{Ca}}^{2+}\right)\cdot V_{\max }\frac{{\left[\text{T}\right]}_{\text{e}}}{K_{\text{T}}}\left(\frac{{\left[\text{P}\right]}_{\text{x}}}{K_{\text{P}}}+{\alpha }_1\frac{{\left[\text{T}\right]}_{\text{x}}}{K_{\text{T}}}\right)\frac{\left[\text{E}1\right]}{{\left[\text{E}\right]}_{\text{tot}}},\end{array}$$ (9)

$$\begin{array}{c}{J}_{\text{eff}}=f\left({\text{Ca}}^{2+}\right)\cdot \left(k_{\text{T}}\left[{\text{T}}_{\text{x}}{\text{E}2\text{P}}_{\text{e}}\right]+k_{\text{H}}\left[{\text{T}}_{\text{x}}{\text{E}2\text{T}}_{\text{e}}\right]\right)\\ =f\left({\text{Ca}}^{2+}\right)\cdot V_{\max }\frac{{\left[\text{T}\right]}_{\text{x}}}{K_{\text{T}}}\left(\frac{{\left[\text{P}\right]}_{\text{e}}}{K_{\text{P}}}+{\alpha }_1\frac{{\left[\text{T}\right]}_{\text{e}}}{K_{\text{T}}}\right)\frac{\left[\text{E}2\right]}{{\left[\text{E}\right]}_{\text{tot}}},\end{array}$$ (10)

where V_max = k_T[E]_tot; [E1]/[E]_tot and [E2]/[E]_tot are as given by Eqs. 7 and 8; f(Ca²⁺) is a multiplying factor associated with a Ca²⁺-dependent essential activation mechanism for the APC operation (see below). Similarly, the unidirectional P_i influx/efflux rates via the APC can be obtained.

Table 2.

Estimated/fixed parameter values for rat kidney and liver mitochondrial APC

Estimated parameters
Parameter	Value (95% CI∗)		Unit
	Kidney	Liver
KT	3.98 ± 0.82	3.22 ± 0.31	mM
KP	6.26 ± 1.27	2.81 ± 0.27	mM
α1	0.28 ± 0.04	0.69 ± 0.10	unitless
α2	0.02 ± 0.01	0.33 ± 0.26	unitless
Vmax	30.66 ± 8.6	24.42 ± 2.75	nmol/min/mg protein
KCa†	1.16 ± 0.08‡	1.75 ± 0.15‡	μM
nH†	1.76 ± 0.10	1.26 ± 0.21	unitless

Fixed parameters (ion dissociation constants)§
Ions	ATP	Value	Pi	Value
H+	HATP3−	6.48	H2PO4−	6.7
K+	KATP3−	1.17	KHPO4−	0.5
Mg2+	MgATP2−	4.19	MgHPO4	1.81
Ca2+	CaATP2−	3.86	CaHPO4	1.6

^∗CI, Confidence Interval.

^†These parameters were optimized only for those data sets in which external [Ca²⁺] is perturbed.

^‡These values are close to the values reported by Aprille (1) for half-maximal activation of the APC.

^§pK values are based on temperature 25°C and ionic strength 0.1 M.

The kinetic model of the APC, described by Eqs. 7–10, is governed by five unknown parameters: K_T, K_P, α₁, α₂, and V_max. The forward and backward rate constants (and the forward and backward translocation rates) are assumed to be equal. The model satisfies microscopic reversibility constraints and is thermodynamically balanced (22). The Ca²⁺-regulation model of the APC (see below) is governed by two additional unknown parameters.

Ca²⁺ regulation of the APC operation

The APC operation is regulated by external [Ca²⁺] (9,10). Here, a simple essential-activation mechanism modulating the turnover rate of the carrier states is found to be sufficient to explain the available experimental data,

$$f\left({\text{Ca}}^{2+}\right)=\frac{{\left[{\text{Ca}}^{2+}\right]}_{\text{e}}^{nH}}{K_{\text{Ca}}^{\text{nH}}+{\left[{\text{Ca}}^{2+}\right]}_{\text{e}}^{nH}},$$ (11)

where K_Ca is the external Ca²⁺ binding constant for the APC and nH is the apparent Hill coefficient. The Ca²⁺ regulatory parameters were estimated based over experiments in which external [Ca²⁺] was varied. The estimated parameter values are listed in Table 2 for isolated rat liver and rat kidney mitochondria.

APC dependence on the ionic concentrations and ΔpH

The substrate ionic species (T = MgATP²⁻ and P = HPO₄²⁻) concentrations governing the APC operation are computed using the equilibrium relationships

$$\left[{\text{MgATP}}^{2-}\right]=\frac{\left[\text{ATP}\right]\left[{\text{Mg}}^{2+}\right]{10}^{{\text{pK}}_{\text{MgATP}}}}{1+\left[{\text{H}}^{+}\right]{10}^{{\text{pK}}_{\text{HATP}}}+\left[{\text{K}}^{+}\right]{10}^{{\text{pK}}_{\text{KATP}}}+\left[{\text{Mg}}^{2+}\right]{10}^{{\text{pK}}_{\text{MgATP}}}+\left[{\text{Ca}}^{2+}\right]{10}^{{\text{pK}}_{\text{CaATP}}}},$$ (12)

$$\left[{\text{HPO}}_4^{2-}\right]=\frac{\left[{\text{P}}_{\text{i}}\right]}{1+\left[{\text{H}}^{+}\right]{10}^{{\text{pK}}_{\text{HPi}}}+\left[{\text{K}}^{+}\right]{10}^{{\text{pK}}_{\text{KPi}}}+\left[{\text{Mg}}^{2+}\right]{10}^{{\text{pK}}_{\text{MgPi}}}+\left[{\text{Ca}}^{2+}\right]{10}^{{\text{pK}}_{\text{CaPi}}}},$$ (13)

where [H⁺], [K⁺], [Mg²⁺], and [Ca²⁺] are the free ion concentrations, and the pK values are as listed in Table 2. It is apparent from Eqs. 12 and 13 that the matrix and external substrate concentrations ([ATP] and [P_i]) as well as free ion concentrations ([H⁺], [K⁺], [Mg²⁺], and [Ca²⁺]) are necessary to evaluate the APC model and identify its parameters. Because the matrix free ion concentrations were not reported for each data set, their values were set at physiologically realistic values, as listed in Table 1. For example, matrix [Mg²⁺] is estimated to be between 0.2 and 0.8 mM (23). A concentration of 0.5 mM is used because it was found that the ATP flux does not vary by >15% for matrix Mg²⁺ between 0.2 and 0.8 mM. Matrix [Ca²⁺] and matrix [K⁺] are set at 250 nM and 140 mM, respectively.

Several studies (24–26) reported a decrease in pH gradient (ΔpH) across the IMM with increasing [P_i] in the incubation medium. To model this decrease in ΔpH as a function of increasing external [P_i], we use the expression

$$\Delta \text{pH}=\Delta {\text{pH}}_0{e}^{-k_{\text{Pi}}{\left[{\text{P}}_{\text{i}}\right]}_{\text{e}}}+\Delta {\text{pH}}_{\mathrm{\infty }}\left(1-e^{-k_{\text{Pi}}{\left[{\text{P}}_{\text{i}}\right]}_{\text{e}}}\right),$$ (14)

where ΔpH₀ and ΔpH_∞ are the pH gradients across the IMM at zero and infinite external [P_i], respectively; k_Pi is the slope of ΔpH decay at zero external [P_i]. The three parameter values governing the ΔpH variation with external [P_i], listed in Table 1, were estimated based on fits to the kinetic data, described below. Given the values in Table 1, ΔpH is >0.3 at external [P_i] equal to 2 mM and is close to the ΔpH range determined by Joyal and Aprille (5) for an incubation medium not containing carboxyatractyloside (CAT), an inhibitor of ANT. With ΔpH estimated from Eq. 14 as a function of external [P_i], the matrix pH was calculated as pH_x = pH_e + ΔpH.

The APC transport rate is slow compared to both the inorganic phosphate carrier (PiC) and the dicarboxylate carrier transport rates (7). Because the PiC transport rate is relatively fast, the matrix [P_i] is effectively controlled by the pH gradient across the IMM (see Joyal and Aprille (5)). Therefore, the matrix $\left[{\text{HPO}}_4^{2-}\right]$ is estimated as

$${\left[{\text{HPO}}_4^{2-}\right]}_{\text{x}}={10}^{2\Delta \text{pH}}{\left[{\text{HPO}}_4^{2-}\right]}_{\text{e}},$$ (15)

which is used in Eqs. 7–10 for computing the APC unidirectional fluxes.

Time course of net AdN content changes

To determine the net uptake or loss of AdN, Austin and Aprille (20) employed an acid-extraction method. During these time-course experiments, no CAT was present in the incubation medium. However, because the mitochondria were energized and the matrix ATP/ADP ratio was much greater than one, the exchange of external ATP for matrix ADP did not occur or was minimal via the ANT over the duration of these experiments (27). The mitochondrial ATP content is modeled by integrating Eqs. 9 and 10 from some t₀ to t:

$${\left[\text{ATP}\right]}_{\text{x}}\left(t\right)=\underset{t_0}{\overset{t}{\int }}\left(J_{\text{inf}}-J_{\text{eff}}\right)dt.$$ (16)

The external ATP content was computed algebraically using the mass conservation relation,

$${\left[\text{ATP}\right]}_{\text{e}}={\left[\text{ATP}\right]}_{\text{tot}}-\gamma \frac{{\left[\text{ATP}\right]}_{\text{x}}}{V_{\text{x}}}.$$ (17)

Here V_x is the matrix water volume determined by Austin and Aprille (20) and γ is the ratio of matrix water volume to external water volume (see Table 2). [ATP]_x is the total matrix ATP content per mg mitochondria. [ATP]_e is the total external ATP content and [ATP]_tot is the total ATP content in the cuvette. External AdN content comprises only external ATP content. Matrix AdN content comprises ATP, ADP, and AMP; however, in the presence of ATP and Mg²⁺, the APC only transports ATP and P_i. Therefore, while predicting the AdN dynamics, the measured ADP and AMP contents were added to the simulated ATP content to calculate the total AdN content.

Parameter estimation and statistical analysis

The APC model parameters δ = (K_T, K_P, α₁, α₂, V_max; K_Ca, nH) characterizing the experimental data (3,6,10) were estimated by simultaneous least-squares fitting,

$$\underset{\delta }{\min }E\left(\delta \right),E\left(\delta \right)=\sum _i^{N_{\text{exp}}}\sum _j^{N_{\text{data}}\left(i\right)}\frac{1}{N_{\text{data}}}{\left(\frac{J_{i,j}^{\text{data}}-J_{i,j}^{\text{model}}\left(\delta \right)}{\max \left(J_{i,j}^{\text{data}}\right)}\right)}^2,$$ (18)

where i represents either unidirectional influx or efflux depending upon the type of tracer experiment. The value N_exp is the total number of experiments to which the model is parameterized and N_data(i) is the number of data points in a particular type of experiment, $J_{i,j}^{\text{data}}$ are the experimental data on unidirectional tracer influx/efflux of ATP, and $J_{i,j}^{\text{model}}$ are the corresponding model simulated outputs given by Eqs. 9 and 10, which depend on the model parameter set δ. The minimization of the mean residual error (objective function) E(δ) for optimal estimation of the APC model parameters δ = (K_T, K_P, α₁, α₂, V_max; k_Ca, nH) is carried out using the FMINCON optimizer in MATLAB (The MathWorks, Natick, MA).

The parameter covariance matrix is used to compute the confidence intervals, which are estimated from the inverse of the Fisher Information Matrix. To avoid inaccurate approximations of the confidence intervals, model outputs comprising the sensitivity matrix were normalized with respect to the best parameter value and experimental standard deviations. When the experimental error is not reported, experimental standard deviation is assumed to be 5% of the experimental observation. The normalized sensitivity matrix is computed as (28)

$$S_{mn}=\frac{\partial J_m}{\partial {\delta }_n}\frac{{\delta }_n^{\ast }}{{\sigma }_m}.$$ (19)

Here, the index is m ∈(1, N), where N is the total number of data points from all experiments, and δ^∗_n is the optimal value of the n^th parameter. A complex-step derivative method (29) is employed to approximate the derivative. The parameter covariance matrix is estimated as

$$V={\left(S^{\text{T}}S\right)}^{-1}.$$ (20)

The 95% confidence interval is estimated based on ${\gamma }_n=1.96\sqrt{V_{nn}},$ where γ_n is the normalized confidence interval for the n^th parameter. The absolute parameter confidence interval for parameter δ_n is given by (1 ± γ_n)${\delta }_n^{\ast }$, and is listed in Table 2 for both the kidney and liver mitochondrial APC.

Results

In this section, we illustrate the model parameterization and corroboration of the mechanism proposed in Fig. 1 for ATP and P_i transport via the APC. The kinetic model is used to fit the independent experimental data sets from Austin and Aprille (6), Nosek et al. (10), and Hagen et al. (3) and predict the time course data from Austin and Aprille (20) under different experimental conditions. The associated model simulations are shown in Figs. 2–6. The estimated model parameter values for isolated rat liver and rat kidney mitochondria are summarized in Table 2. The experimental conditions are the same as listed in Table 1, except for the titrations made to study their effect on unidirectional influx/efflux rate of ATP. Several alternative kinetic mechanisms were unable to explain the experimental data better than the mechanism presented in Fig. 1 (see Discussion).

Figure 2.

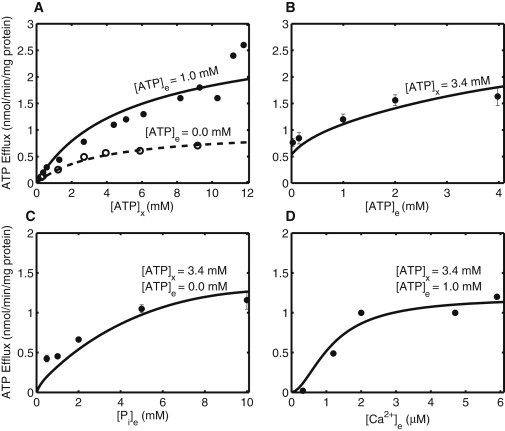
Model simulations of initial tracer (ATP) efflux rates from the experiments of Hagen et al. (3) conducted in isolated rat kidney mitochondria. Experimental conditions are as in Table 1, except for the titration of reagents in panels A–D. (A) ATP efflux rate with increasing matrix [ATP] in presence (solid line; [ATP]_e = 1 mM) and absence (broken line; [ATP]_e = 0 mM) of ATP in the incubation medium. (B) Effect of increasing external [ATP] over ATP efflux rate. (C) Effect of external [P_i] on ATP efflux rate in the absence of [ATP]_e. (D) ATP efflux rate as a function of increasing external [Ca²⁺] in the incubation medium.

Figure 3.

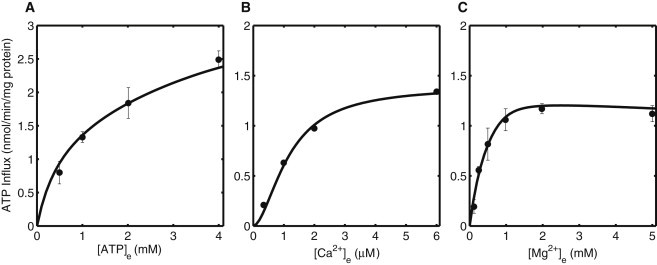
Model simulations of initial tracer (ATP) influx rates from the experiments of Hagen et al. (3). (A) Effect of increasing external [ATP] on ATP influx rate. (B) ATP influx rate as a function of increasing external [Ca²⁺]. (C) ATP influx rate as a function of increasing [Mg²⁺] in the incubation medium.

Figure 4.

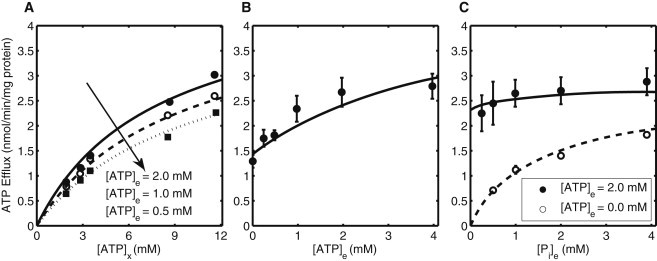
Model simulations of initial tracer (ATP) efflux rates from the experiments of Austin and Aprille (6) conducted in isolated rat liver mitochondria. Experimental conditions are as in Table 1, except for the titration of reagents in panels A–C. (A) ATP efflux rate as a function of matrix [ATP] with [ATP]_e = 2 mM (solid line), [ATP]_e = 1 mM (broken line), and [ATP]_e = 0.5 mM (dotted line). (Arrow) Decrease in external [ATP] (from 2 mM to 0.5 mM). (B) Effect of external [ATP] on ATP efflux rate. (C) ATP efflux rate as a function of external [P_i] with (solid line; [ATP]_e = 2 mM) and without (broken line; [ATP]_e = 0 mM) [ATP] in the incubation medium. Note that [ATP]_e was reported to be 1 mM for plot C, which doesn’t seem to be consistent with the efflux rates at [ATP]_e = 1 mM from plot B; [ATP]_e = 2 mM seems to be more probable, and thus is used for parameter estimation.

Figure 5.

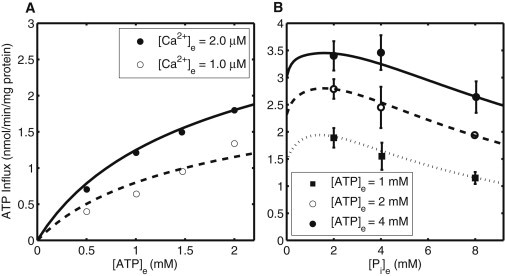
Model simulations of initial tracer (ATP) influx rates from the experiments of Austin and Aprille (6) and Nosek et al. (10). (A) Effect of external [ATP] on ATP influx rate with incubation medium containing 2 μM Ca²⁺ (solid line) and 1 μM Ca²⁺ (broken line). (B) ATP influx rate as a function of external [P_i] with increasing [ATP] in the incubation medium: [ATP]_e = 1 mM (dotted line), [ATP]_e = 2 mM (broken line), and [ATP]_e = 4 mM (solid line).

Figure 6.

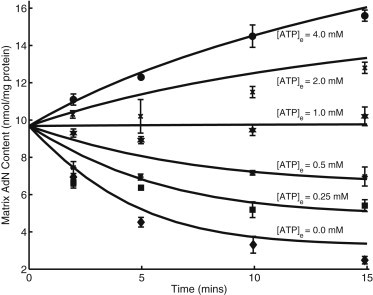
Model simulations of matrix AdN content time course data from the experiments of Austin and Aprille (20). The matrix AdN time course is governed by Eq. 16 and includes the experimentally measured residual matrix AdN content (see text for detail). For simulating the matrix AdN content time course, matrix pH was set at 7.8 based on a ΔpH of 0.4, determined by Joyal and Aprille (5) under the same experimental conditions. In these experiments, isolated rat liver mitochondria were incubated with different external ATP and the net change in matrix AdN content was measured.

The pH gradient across the IMM as a function of external [P_i], determined using Eq. 14, qualitatively reproduces the ΔpH trend reported by Klingenberg and Rottenberg (24) in their P_i titrated experiments (see Table 1); i.e., ΔpH decreases exponentially as external [P_i] increases. However, the ΔpH values determined here and those reported in Klingenberg and Rottenberg (24) cannot be directly compared due to different experimental conditions. The same ΔpH values (listed in Table 1) are used for simulations of both the rat kidney and rat liver mitochondrial experiments.

Unidirectional ATP influx/efflux in rat kidney mitochondria

Figs. 2 and 3 show unidirectional ATP transport data and model simulations for isolated rat kidney mitochondria from Hagen et al. (3). Here, the data pertaining to the CAT-insensitiv isoform of the APC are used. It is apparent from Fig. 2, A and B, that the tracer efflux rate increases with increasing external [ATP]. This phenomenon, known as trans-acceleration, indicates that the tracer efflux is facilitated by a carrier (30). A detailed analysis of the phenomenon can be found in Vinnakota and Beard (31). In Fig. 2, C and D, the ATP efflux rate is plotted as functions of external [P_i] and [Ca²⁺]. In the Ca²⁺ titrated experiments, 5 mM EGTA was added to the incubation medium and a variable amount of CaCl₂ was added to attain desired amount of external [Ca²⁺].

Apart from investigating the effect of different pharmacological conditions over unidirectional tracer efflux, Hagen et al. (3) also measured the unidirectional tracer influx under different experimental perturbations. Fig. 3 A shows ATP influx rate as a function of external [ATP]. Increasing external [ATP] increases the unidirectional ATP uptake rate by the mitochondria. The ATP influx rate does not saturate for the evaluated range of external [ATP] (from 0 mM to 4 mM) that is reflected by the estimated ATP binding affinity for the APC (see Table 2). The effect of increasing external [Ca²⁺] and [Mg²⁺] on the unidirectional tracer influx of ATP is shown in Fig. 3, B and C, respectively. EGTA was used to fix external [Ca²⁺] in the same manner as done for the unidirectional efflux experiments. The ATP uptake rate saturates as external [Ca²⁺] is increased above 2 μM. However, the ATP influx rate decreases slightly when external [Mg²⁺] is increased above 2 mM. This decrease was more prominent when external [Mg²⁺] was increased from 5 mM to 10 mM (found using computer simulations; data not shown). This counterintuitive result can be best explained by the MgHPO₄ complex formation that decreases the HPO₄^2- gradient across the IMM, and thus decreases the driving force for ATP uptake (1,5).

Unidirectional ATP influx/efflux in rat liver mitochondria

Figs. 4 and 5 show model simulations for experiments conducted on isolated rat liver mitochondria by Austin and Aprille (6) and Nosek et al. (10). The method of mitochondrial preparation and incubation medium was identical for Austin and Aprille (6) and Nosek et al. (10). Thus, the experimental conditions are assumed to be the same during parameter estimation (see Table 1). We can observe a decrease in ATP efflux rate when external [ATP] is decreased from 2 mM to 0.5 mM ([ATP]_e = 2 mM (solid line), [ATP]_e = 1 mM (broken line), [ATP]_e = 0.5 mM (dotted line); see Fig. 4 A), or an increase in ATP efflux rate when external [ATP] is increased from 0 mM to 4 mM (see Fig. 4 B). In Fig. 4 C, Austin and Aprille (6) evaluated the effect of increasing external [P_i] on ATP efflux rate in the presence (solid line) and absence (broken line) of external [ATP].

Fig. 5, A and B, shows the effect of experimental perturbations on ATP influx rate via the APC. For measuring ATP influx rate with different external [Ca²⁺], EGTA and CaCl₂ were used to attain desired [Ca²⁺] of 1 μM (solid circle; Fig. 5 A) and 2 μM (open circle; Fig. 5 B) in the external medium. In Fig. 5 B, we report model simulations for the experiments performed by Austin and Aprille (6) to demonstrate competition between ATP and P_i. ATP and P_i both are competitive inhibitors of each other because either external P_i or external ATP can exchange for matrix AdN. The ATP uptake rate is enhanced when external [ATP] is increased from 1 mM to 4 mM. However, this increase is depressed when external [P_i] is increased from 2 mM to 8 mM. This decrease is observed because increasing external [P_i] stimulates P_i homoexchange and reduces the available amount of carrier able to facilitate ATP uptake.

AdN time course in rat liver mitochondria

Austin and Aprille (20) measured net changes in matrix AdN content in isolated rat liver mitochondria with fixed external [P_i] (2 mM) and different concentrations of ATP in the incubation medium (see Fig. 6). The AdN time course was simulated using Eq. 16. A constant ΔpH of 0.4 is used when simulating these time-course experiments based on the range reported by Joyal and Aprille (5) under similar experimental conditions. Experimental conditions and all other parameter values are same as reported in Table 1 and Table 2. It is apparent from Fig. 6 that there is a net uptake of AdN when external [ATP] is above 1 mM, no change in net AdN content when external [ATP] is 1 mM, and a net loss of AdN when external [ATP] is below 1 mM, which conforms with the experimental findings (1,3,5,6,10,20,32). These model simulations independently validate the APC model.

Discussion

This article provides a mechanistic kinetic model of the mitochondrial ATP-Mg/P_i carrier (APC), which is the primary pathway responsible for regulating the matrix adenine nucleotide (AdN) pool size (1,7,20,32). The model is based on an ordered bi-bi mechanism for heteroexchange of ATP and P_i, and also includes homoexchanges of ATP and P_i via the APC (Fig. 1). The model assumes that the binding and dissociation of the substrates ATP (MgATP²⁻) and P_i (HPO4²⁻) is much faster than the turnover rate of the APC (22). The model is thermodynamically balanced and adequately describes the available experimental data sets from Hagen et al. (3), Austin and Aprille (6,20), and Nosek et al. (10) on ATP influx and efflux rates in energized mitochondria isolated from rat liver and rat kidney. The model is validated by an independent, time-course experimental data set on matrix ATP uptake and loss.

The identified kinetic mechanism of the APC is shown in Fig. 1. This model captures the important features of the APC apparent from the available kinetic data: 1), saturating ATP efflux induced by external [P_i], 2), saturating ATP efflux induced by external [ATP], 3), ATP influx inhibition due to competition between external [ATP] and external [P_i], and 4),nonsaturating ATP efflux within physiological range of matrix [ATP]. Different kinetic mechanisms other than the one presented in Fig. 1 (e.g., ordered bi-bi with P_i binding first, random bi-bi, and Ping-Pong, all with and without homoexchanges of ATP and P_i) were also evaluated, but none of them could simultaneously fit all the available data sets. In fact, many mechanisms could not explain the external [P_i]-dependent ATP efflux and influx rates data in Figs. 4 C and 5 B alone. It should be pointed out here that, for a random bi-bi mechanism with homoexchanges of ATP and P_i, the translocation rate of the substrate-bound conformational states with P_i binding first followed by ATP binding is found to be not essential.

The proposed mechanism of the APC incorporates P_i homoexchange because the available experimental data could not be explained without incorporating the P_i homoexchange in the mechanism. Direct measurement of P_i transport through the APC is difficult because the flux through the PiC is much greater in magnitude and no differentiating inhibitors of various P_i transport pathways are available. (Inhibitors of PiC, like NEM and mersalyl, also inhibit the APC (1,5).) We attempted to explain the data, without incorporating the P_i homoexchange, by assuming asymmetry in the substrate translocation rates and binding affinities. The asymmetrical APC model had 10 adjustable parameters (two of them were constrained using microscopic reversibility), compared to five adjustable parameters in the proposed APC model. Thus, the simpler model is better suited to explain the available data.

The estimated correlation matrix reveals that three pairs of parameters are highly correlated for the kidney data set. Specifically, the pair K_Ca and nH, K_T and V_max, and K_P and α₂, have estimated covariance of −0.97, −0.97, and, −0.84, respectively. This means that only one parameter from each pair is independently estimated based on the kidney data set. Thus, for these parameters, the reported confidence limits are meaningful only with the assumption that the value of one of the correlated members is held fixed. For the liver data set, the highest value of the correlation matrix is −0.68, the estimated covariance for K_T and V_max.

It is known that the activity of the APC is higher in liver than in kidney mitochondria (1). However, the expression level of the APC is nearly the same in liver and kidney mitochondria (4). Comparing the V_max values of kidney and liver mitochondrial APC (see Table 2), our analysis predicts that the heteroexchange rates of ATP/P_i are also similar in kidney and liver mitochondria, and suggests differences in other underlying parameters. The model predicts that the higher APC activity observed in liver mitochondria is due to 1), faster ATP homoexchange rate in liver than in kidney mitochondria, and 2), higher binding affinity of APC for P_i, which tend to increase the heteroexchange rate (e.g., compare the values of α₁ and K_P for liver and kidney mitochondrial APC in Table 2).

Although the study of Nosek et al. (10) suggests that a Ca²⁺-dependent binding affinity of ATP for APC may explain the phenomenon shown in Fig. 5 A, the Ca²⁺ dependency is modeled here as a Ca²⁺-dependent increase in the APC turnover rate (see Eqs. 9–11). This model assumption is justified because a Ca²⁺-modulated binding affinity of ATP for APC could explain the isolated rat liver mitochondrial data, but could not simultaneously explain the isolated rat liver and rat kidney mitochondrial data.

Our simulations suggest that at least two Ca²⁺ ions (based on the value of nH; see Table 2) must bind with the APC to modulate the ATP influx/efflux rates. Fiermonte et al. (4) reported that a protein with characteristic features of the APC has three EF-hand Ca²⁺-binding motifs in their N-terminal domains (similar to what we found using our computer simulations). However, the Ca²⁺ dependence of the APC activity could not be detected in their reconstituted system. Therefore, we modeled Ca²⁺ as an essential activator of the APC activity based on the earlier experimental observations of Hagen et al. (3) and Haynes et al. (9). Our model simulations concur with the recent findings of Traba et al. (19) where they reported Ca²⁺ to modulate the V_max of Sal1p (the yeast ortholog) activity rather than the K_m for ATP. Given the uncertainty in the sensitivity of APC to external [Ca²⁺] and the site of Ca²⁺ modulation, additional new studies need to be done to more fully characterize the Ca²⁺ dependence of the APC activity in isolated mitochondria from mammals.