Retention of Conformational Entropy upon Calmodulin Binding to Target Peptides Is Driven by Transient Salt Bridges

Abstract

Calmodulin (CaM) is a highly flexible calcium-binding protein that mediates signal transduction through an ability to differentially bind to highly variable binding sequences in target proteins. To identify how binding affects CaM motions, and its relationship to conformational entropy and target peptide sequence, we have employed fully atomistic, explicit solvent molecular dynamics simulations of unbound CaM and CaM bound to five different target peptides. The calculated CaM conformational binding entropies correlate with experimentally derived conformational entropies with a correlation coefficient R² of 0.95. Selected side-chain interactions with target peptides restrain interhelical loop motions, acting to tune the conformational entropy of the bound complex via widely distributed CaM motions. In the complex with the most conformational entropy retention (CaM in complex with the neuronal nitric oxide synthase binding sequence), Lys-148 at the C-terminus of CaM forms transient salt bridges alternating between Glu side chains in the N-domain, the central linker, and the binding target. Additional analyses of CaM structures, fluctuations, and CaM-target interactions illuminate the interplay between electrostatic, side chain, and backbone properties in the ability of CaM to recognize and discriminate against targets by tuning its conformational entropy, and suggest a need to consider conformational dynamics in optimizing binding affinities.

Introduction

Conformational flexibility within the calcium signaling protein calmodulin (CaM) facilitates high-affinity binding to variable linear sequences in over 300 different target proteins (1,2). A fundamental design feature used to modulate target peptide binding may relate to the unusually large flexibility of CaM, suggesting that entropic factors are an important characteristic of its function that has the potential to fine-tune binding to target proteins, and has important implications with respect to cellular signaling, as the stability of protein-protein interactions are strongly influenced by entropic factors (3,4). Central to this understanding has been the measurement of binding thermodynamics between CaM and protein targets with diverse amino acid sequences using isothermal titration calorimetry with complementary NMR measurements of conformational entropy based on selected methyl side-chain motions by Wand and co-workers (5). Five target peptides with measured conformational entropies represent the CaM-binding sequences from CaM-dependent protein kinase kinase (CaMKK) (6), CaM-dependent protein kinase I (CaMK1) (7), smooth myosin light chain kinase (smMLCK) (S. Weigand, L. Shuvalova, T. J. Lukas, S. Mirzoeva, D. M. Watterson, and W. F. Anderson, unpublished), epithelial nitric oxide synthase (eNOS) (8), and neuronal nitric oxide synthase (nNOS) (K. G. Valentine, H. L. Ng, L. Schneeweis, J. K. Kranz, K. K. Frederick, T. Alber, and A. J. Wand, unpublished). CaM binds to all of these target peptides with similar affinities (−11 to −12 kcal/mol (5)) and desolvation entropies (35 to 41 kcal/mol (5)), but very different CaM conformational binding entropies (ΔS_conf), varying according to CaMK1 < CaMKK < smMLCK < eNOS ≪ nNOS (5).

Critical to high-affinity target binding is the flexibility between the N- and C-domains in CaM, arising as a result of a metastable flexible linker (residues 73–82), which allows the N- and C-domains to wrap around target binding sequences (9). Each lobe in CaM consists of two helix-loop-helix calcium-binding sites connected by unstructured sequences; structured elements include helices A (residues 5–17), B (residues 30–39), C (residues 46–54), D (residues 64–73), E (residues 83–91), F (residues 101–110), G (residues 119–129), and H (residues 137–144) (10). Conformationally sensitive interhelical linkers (loops BC, DE, and FG) have been suggested to further contribute to changes in conformational entropy upon target binding (11); in comparison, calcium binding sequences are conformationally restricted by strong Ca²⁺ interactions.

Specific side-chain interactions between CaM and target peptides modulate binding to target sequences. The 21 Glu residues are critical to establishing a favorable CaM-target binding orientation (12–15), and these acidic side chains form rings around hydrophobic Met side chains (four in each domain). These hydrophobic Met “puddles” are conserved target-binding residues that facilitate the initial recognition of target sequences through their ability to detect hydrophobic anchors on the target peptide (2). Met is of special importance because of the extended linear side chain that promotes conformational flexibility, and mirrors the overall conformational entropy of the complex (16). Additional binding specificity is possible through interactions between the polar side chains within the central linker in CaM (Arg-74, Lys-75, Lys-77, Asp-78, Thr-79, Asp-80, Ser-81, and Glu-82) and target peptides, which are able to differentially form hydrogen bonds and salt bridges to modify target interactions (17). These CaM-target binding interactions have the potential to couple linker fluctuations to binding affinity as a result of the differential positioning of polar target side chains in various target sequences. Furthermore, it has been shown that a small number of linker residues facilitate large-amplitude backbone motions (18), and even single residue linker immobilizations due to target binding exhibit widely distributed correlated motions with other side chains, particularly Arg, Lys, and Met residues (19).

Of particular interest is an understanding of the effects of electrostatic CaM-target interactions on CaM conformational entropy and backbone dynamics, which have been shown by Wintrode and Privalov (20) to contribute only entropically to the overall binding thermodynamics. Furthermore, if the motion of CaM backbone atoms is restrained, the electrostatic interactions between CaM and target peptides do not allow CaM to discriminate between different target sequences (14). We seek to gain a more detailed analysis of the CaM-target interactions and motions causing the observed entropies by using classical molecular dynamics (MD) simulations to compare unbound CaM and the five CaM-target complexes with known high-resolution structures whose conformational entropies have been measured experimentally (5). MD has provided insights into the dynamics of calmodulin and calmodulin-target complexes in terms of both backbone and side-chain fluctuations (10,12,21–26), and the conformational entropy is a property that can be calculated from MD trajectories via the quasiharmonic approximation (3,27), thereby allowing a direct comparison to the experimental measurements (5). To better understand how electrostatic interactions between CaM and target binding sequences affect conformational entropy, we employed a fully dynamic method with a longer simulation time than used previously (10,12,21–26). Because salt screening will alter polar CaM-target side-chain interactions (13), we carried out two different sets of simulations using different ionic strength conditions to provide additional clues into how sequence-specific CaM-target interactions relate to CaM structural and dynamic properties. We demonstrate that several dynamic properties correlate with experimentally derived conformational entropies, and suggest a mechanistic role for selected side chains in target peptides that function to tune the conformational entropy of the bound complex.

Computational Methods

Model building

Starting coordinates were obtained from the Protein Data Bank (www.pdb.org) for Ca²⁺-saturated CaM (1x02.pdb) (17) and CaM bound to five peptide targets, corresponding to the CaM-binding sequences in CaM-dependent protein kinase kinase (CaMKK; 1ckk.pdb) (6), CaM-dependent protein kinase I (CaMK1; 1mxe.pdb) (7), smooth myosin light chain kinase (smMLCK, 1qtx.pdb) (S. Weigand, L. Shuvalova, T. J. Lukas, S. Mirzoeva, D. M. Watterson, and W. F. Anderson, unpublished), epithelial nitric oxide synthase (eNOS; 1niw.pdb) (8), and neuronal nitric oxide synthase (nNOS; 2o60.pdb) (K. G. Valentine, H. L. Ng, L. Schneeweis, J. K. Kranz, K. K. Frederick, T. Alber, and A. J. Wand, unpublished). Three structures had incomplete and missing terminal residues, which were added using the SwissPDB editor (28). Specifically, residues Ala-1, Asp-2, Gln-3, and Lys-148 were added to CaM in the complex with CaMK1; residues Ala-1, Asp-2, and Lys-148 in CaM and the missing C-terminal Gly residue in the binding peptide were added to the complex between CaM and eNOS; and residues Ala-1, Asp-2, and Gln-3 were added to CaM in the complex with nNOS. The NMR structures of unbound CaM and CaM in complex with the target peptide in CaMKK consist of multiple structural models, and we chose the first reported structures. CaM bound to CaMKK, eNOS, and nNOS have the same amino acid sequence as unbound CaM; however, the sequences of CaM bound to CaMK1 and smMLCK, respectively, differed by 3 and 9 amino acids. These were modified using the SwissPDB editor (28) to allow for direct comparison between unbound CaM and the other CaM structures. All of the introduced substitutions were between similar residues, such as Phe → Tyr, Thr → Gln, and Leu → Ile. Each structure was inserted into a cubic box with a minimum distance of 15 Å between the complex and the sides of the box, and then the box was filled with water molecules. Sodium counterions were substituted for water molecules at random positions to achieve neutrality (the low ionic strength set, as in (13)). Another set of solvated proteins was created using potassium counterions to achieve neutrality and additional potassium and chloride ions to model 0.15 M ionic strength (the high ionic strength set, as in (11)). Table S1 in the Supporting Material lists the initial cubic box sizes and the number of solute, water, and ion atoms in each simulation.

Equilibration and molecular dynamics calculations

Simulations were run using the AMBER03 force field (29) and TIP3P water model (30) in conjunction with the double precision version of the GROMACS 4.0 MD program (31,32) for the equilibration, dynamics, and trajectory analyses. Electrostatic interactions were calculated using the particle mesh Ewald method with a cutoff of 12 Å and a grid spacing of 1.2 Å. Lennard-Jones interactions were truncated at 12 Å. Hydrogens were left unconstrained, and an integration time step of 1.0 fs was used. Pressure was kept constant (1.0 atm) using the Parrinello-Rahman barostat (33) and temperature was kept at a constant 300 K using a Nosé-Hoover thermostat (34).

Each solvated protein structure was energy minimized to a tolerance of 500 kJ/mol-nm (default GROMACS units), and these structures were used as a starting point for equilibration. Each structure was slowly equilibrated in 1000-ps stages, in which the coordinates and velocities of each equilibration stage were used to initialize each subsequent stage. In the first equilibration stage, heavy atoms were restrained using harmonic position restraints with a force constant of 1000 kJ/mol-nm² and the temperature was set at 100 K. Next, the temperature was increased in 50 K increments to 300 K, and then restraint forces were reduced to zero in 200 kJ/mol-nm² increments. Following equilibration, each system was subjected to 100 ns of unconstrained dynamics. Coordinates were saved every ps, resulting in 100,000 snapshots per simulation.

Analysis

All of the analyses were performed using GROMACS 4.0 analysis programs (31,32), except the salt-bridge analyses, which were done using VMD 1.8.6 (35). Average properties were calculated from 10 to 100 ns.

CaM Cα backbone root mean-square deviation (RMSD)

The g_rms program was used to calculate the distance of each trajectory structure to the structure at the start of MD as a function of time. RMSD was calculated for Cα atoms of full CaM, the N-domain, the C-domain, and central linker after superimposing the same Cα atoms.

Backbone root mean-square fluctuations (RMSF)

The g_rmsf program was used to calculate the RMSF of CaM Cα atoms.

Backbone radius of gyration

The g_gyrate program was used to calculate the radius of gyration (Rg) of the CaM backbone as a function of time.

Average helicity per CaM residue

The g_helix program was used to calculate the CaM backbone helicity at each residue. The helicity is the fraction of the time in which the φ and ψ angles meet the criteria for a perfect α-helix.

Backbone dihedral order parameters

The g_chi program was used to calculate backbone amide dihedral order parameters $\left({\text{O}}_{\text{NH}}^2\right)$. ${\text{O}}_{\text{NH}}^2$ is a measure of the librational freedom of the N-H vector in the molecular reference frame.

CaM interhelix angles

On the basis of the average helicities of individual residues, we defined a range of eight residues for each helix A-H that are common to all of the CaM-target complexes. The helix vectors were defined by the center of mass of the backbone atoms of the three residues at the beginning and end of the helix (calculated with the g_traj program), and then the angles were calculated using the dot product between pairs of vectors.

Mean closest distance

The g_mdmat program was used to calculate CaM-target contacts based on the mean closest distance between all CaM and target peptide side chains. Distances less than or equal to 4.0 Å were discretized into 0.1 Å levels using the –trunc and –nlevels flags.

Salt bridges

Salt bridges between side chains were analyzed using a nitrogen-oxygen cutoff distance of 3.2 Å. VMD updates the list of salt bridges at every frame, allowing for analysis of both transient and permanent salt bridges.

Covariance analysis (essential dynamics)

The g_covar program was used to superimpose CaM backbone atoms and then calculate and diagonalize the covariance matrix using either CaM backbone atoms, all CaM heavy atoms, or all heavy CaM and peptide atoms. The –mwa flag was used so that the program would do a mass-weighted covariance analysis, as required by the quasiharmonic entropy equation (28).

Quasiharmonic entropy

The g_anaeig program reads the covariance matrix eigenvectors and calculates the conformational entropy using the quasiharmonic approximation (36) when the –entropy flag is used. These values in J/K-mol were multiplied by the simulation temperature of 300 K and converted to kcal/mol. Differences between the entropies in the bound CaM relative to the unbound CaM were used to calculate TΔS_quasi.

Quasiharmonic entropy convergence

Although the absolute entropy calculated from a single simulation will not converge to a single value (37), the entropy at the limit of infinite simulation time, S∞, can be extrapolated by fitting to Eq. 1, in which S∞, A, and n are fitting constants and t is simulation time (38):

$$S\left(t\right)=S_{\mathrm{\infty }}-\frac{A}{t^n}.$$ (1)

We calculated the entropy of CaM backbone atoms from 10 to 100 ns in 2-ns increments and fit them to Eq. 1 to obtain estimates of the absolute entropies at the limit of infinite simulation time to evaluate convergence.

Results and Discussion

CaM compaction and rigidification upon target binding

RMSD plots reflect both local motions within specific regions (Fig. S1) as well as changes in the relative distance and orientation between the opposing domains of CaM, whereas Rg describes only the latter (Fig. S2). In all cases, at least 10 ns are required to achieve equilibration (the so-called relaxation phase (10)). Most notably, the 0–20 ns portion of the CaMKK-CaM, CaMK1-CaM, and smMLCK-CaM RMSD plots show large N-domain fluctuations that are due to motion of the unstructured, N-terminal residues 1–5.

In comparison to unbound CaM, the average Rg is ∼7 Å smaller for CaM bound to any of the targets, consistent with prior observations that the opposing domains of CaM are connected through a flexible linker region that results in compaction and conformational rigidification upon binding (9,39–46). Likewise, the RMSD for full-length, unbound CaM has a large amplitude of ∼6 Å, roughly twice as large as in the bound CaM.

In agreement with experimental measurements (44), for unbound CaM, there is a 2 Å increase in Rg at low ionic strength that is indicative of a more extended structure. Average Rg calculated from MD trajectories are similar for CaM bound to all targets (ranging from 15.8 to 17.1 Å). Rg values calculated from the high-resolution structures have a narrower range (between 16.3 and 16.7 Å), and this difference may be related to the removal of crystal lattice forces (present in the structures measured using x-ray diffraction). Small decreases in Rg for CaM bound to target peptides at low ionic strength (relative to high ionic strength) indicate adoption of more compact structures, suggesting a role for electrostatic interactions in modulating the structure and dynamics of the bound complex.

Larger RMSD fluctuations are apparent for the N-domain in comparison to the C-domain, consistent with other modeling and experimental measurements that indicate a greater inherent plasticity within the N-domain, which has been suggested to be important for target protein recognition (10,22,23,47–49). Conformational fluctuations of the N-domain are particularly apparent for CaM bound to the target peptide complex known to retain the most conformational entropy (nNOS) (5). Specifically, the RMSD of the N-domain of nNOS-CaM from simulations using high ionic strength displays a conformational event at 50 ns; the N-domain RMSD plot calculated from the low ionic strength simulation displays two conformational events at t = 65 ns and t = 90 ns. In both simulations, these events are flexing movements in helix A. The low ionic strength nNOS-CaM simulation shows a conformational change in the central CaM linker near 50 ns, which is a twisting motion. In both simulation sets, the N-domain RMSD of eNOS-CaM show a conformational change near 40 ns, and this motion is flexing of loop BC near Gln-41.

These results suggest that specific backbone elements may be responsible for observed differences in conformational dynamics upon association with different target peptides, specifically the central linker of CaM (Arg-74, Lys-75, Lys-77, Asp-78, Thr-79, Asp-80, Ser-81, and Glu-82) and Gln-41 in the linker between helices B and C. Fig. S3 shows the structure of CaM (1x02.pdb) with these residues indicated.

Variable side-chain contact interactions with different target peptides

Because side-chain interactions with target peptides can be stabilizing (hydrogen bonds and salt bridges) or destabilizing (electrostatic repulsion, such as Lys-Lys), these interactions are likely to be important sequence-dependent mechanisms for tuning the CaM conformational entropy changes upon target binding.

Conserved CaM Met side chains involved in target binding are apparent from the minimum distance analysis (Table S2). eNOS (8) and nNOS (50) have a 1-5-8-14 CaM binding motif, smMLCK has a 1-8-14 motif (50), CaMKK has a 1-16 motif (6), and CaMK1 is 1-5-10 (50). The CaM-target contacts between CaM Met and hydrophobic target side chains calculated using minimum distance analysis are consistent with these motifs, except for eNOS and smMLCK. eNOS Val-12 and smMLCK Val-11 bind tightly to CaM residues Ala-88, Val-91, Phe-92, and Leu-112 in the simulations and initial structures.

Contact interactions between Met side chains and the different target peptides are relatively insensitive to differences in ionic strength, with on average ∼80% of side-chain interactions maintained at low and high ionic strength (Fig. S4). In comparison, there are large ionic strength-dependent differences in the number of polar contacts between CaM and different target peptides, consistent with the notion that electrostatic interactions play a dominant role in modulating entropic factors linked to binding affinities (20). Supporting this concept, there are large variations in the interactions between a number of side chains in conformationally sensitive CaM regions (e.g., Gln-41 in loop BC and central linker residues Lys-75, Lys-77, Asp-78, Thr-79, Asp-80, and Ser-81 (Table S2, Fig. S4). As shown in Table 1, these CaM-target interactions are sensitive to changes in ionic strength. For example, Arg-24 in CaMK1 hydrogen bonds to Gln-41 irrespective of ionic strength. In contrast, although Ser side chains in both smMLCK and nNOS hydrogen bond with Gln-41, this binding interaction is ionic strength dependent. CaMKK and eNOS do not hydrogen bond to Gln-41 in either simulation set. All of the targets interact with at least one of the linker residues, and again the interactions are dependent on ionic strength. For instance, Thr-8 in CaMKK hydrogen bonds to Ser-81 in CaM only at low ionic strength, whereas this interaction is disrupted at high ionic strength (i.e., their spatial proximity > 4 Å). In contrast, hydrogen bonds are only present at high ionic strength between Ser-81 in CaM with side chains in smMLCK (Arg-18) and nNOS (Lys-15 and Lys-19). Table S3 lists CaM and target side chains involved in the interactions described in Table 1 and their corresponding average distances (and standard deviations).

Table 1.

Side-chain interactions between targets and conformationally sensitive CaM residues are target sequence dependent

Target	BC linker	Central Linker
	Q41	R74	K75	K77	D78	T79	D80	S81	E82
nNOS	●		□■				○●	●	○
smMLCK	○	□■	■	○□	●			●
eNOS			○●			○●
CaMK1	○●	○●	○●		○●	○
CaMKK			○●					○

Interactions defined by mean closest distances <4 Å between CaM and target side chains. Circles: stabilizing interactions (hydrogen bonds and salt bridges); Squares: destabilizing interactions (electrostatically repulsive contacts); Open circles and squares: low ionic strength; Solid circles and squares: high ionic strength.

Favorable interactions can bring noncomplementary side chains together. For instance, although smMLCK Arg-16 forms a salt bridge with CaM Asp-78, this interaction brings smMLCK Arg-16 into close proximity to CaM Arg-74, Lys-75, or Lys-77, and a similar result was observed for nNOS Lys-19. These unfavorable (electrostatically repulsive) interactions are significant, because smMLCK-CaM and nNOS-CaM maintain the most quasiharmonic entropy, as described below. Table S4 lists the Coulomb potential energy between electrostatically repulsive CaM and target side chains.

Targeted disruptions in secondary structure upon target peptide binding

Changes in secondary structure for complexes of CaM bound to target peptides relative to unbound calcium-activated CaM are apparent upon consideration of backbone amide order parameters $\left({\text{O}}_{\text{NH}}^2\right)$ and time-averaged helicities (Fig. 1). The metastable central linker between helices D and E is disrupted following target peptide binding, resulting in substantial decreases in helical content and ${\text{O}}_{\text{NH}}^2$. Chelation of calcium ions restricts the conformational dynamics of coordinating ligands, resulting in high order parameters despite low helical content in loops AB, CD, EF, and GH. In contrast, the conformational dynamics of loop regions not involved in calcium binding (loops BC, DE, and FG) are very sensitive to target peptide binding as a result of differences in side-chain interactions between CaM and the different target peptides. For example, loop BC ${\text{O}}_{\text{NH}}^2$ (and other dynamic properties discussed below) differ between the different complexes. Specifically, ${\text{O}}_{\text{NH}}^2$ is >0.8 when the target peptide forms a hydrogen bond to Gln-41; O²_NH is <0.5 when there is no hydrogen bond to Gln-41 (Table 1). As expected, the disorder of the central helix is sequence-specific. There are two intramolecular salt bridges in unbound CaM (Lys-75-Asp-78 and Lys-77-Asp-80), and at least one of these salt bridges is disrupted in all target peptide complexes because of competing ionic strength dependent polar interactions with target peptides. As with Gln-41, linker residue O²_NH values are reflective of the presence or absence of interactions with target side chains, particularly notable for smMLCK-CaM and nNOS-CaM, which have electrostatically repulsive CaM-target side-chain interactions (Table 1). Specifically, Arg-16 in the peptide from smMLCK electrostatically repels Lys-75, resulting in low ${\text{O}}_{\text{NH}}^2$ in the linker region. Likewise, Lys-19 in nNOS repels Lys-75, and the linker has low ${\text{O}}_{\text{NH}}^2$.

Figure 1.

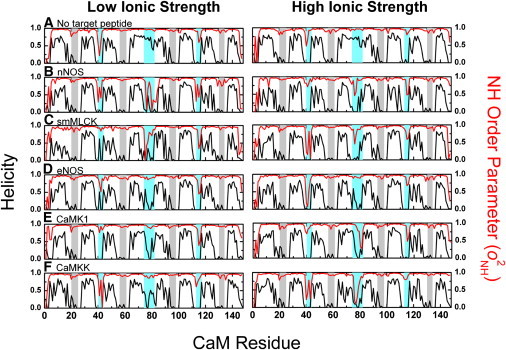
Variable helicity and conformational order in helical linker regions for CaM bound to different target peptides. Time-averaged helical content (black lines, peaks point up) and calculated backbone amide order parameter (${\text{O}}_{\text{NH}}^2$; red lines, peaks point down) for unbound calcium-activated CaM (A) or in association with target peptides (B–F). Calcium binding sites (gray) and conformationally sensitive loops (cyan) are highlighted (see Introduction for residue numbers). Graphs are vertically ordered according to calculated quasiharmonic entropies (Table S6).

Variable backbone conformational dynamics following complex formation

Depending on the target peptide in association with CaM, there are large changes in the magnitude of the RMSF relative to unbound CaM (Fig. 2). In the majority of cases there are reductions in RMSF at all sites in comparison to unbound CaM, in agreement with experimental measurements that show substantially unfavorable changes in conformational entropy upon association with targets that vary between −3.8 kcal/mol (nNOS) and −15.2 kcal/mol (CaMKK) (5). Most notably, in the nNOS-CaM complex under low ionic strength conditions, central linker residues Asp-78, Thr-79, Asp-80, and Ser-81 respectively fluctuate 0.8, 1.7, 1.2, and 0.8 Å more than in unbound CaM, which is indicative of induced local entropy (51). Likewise, in the complex between CaM and smMLCK from the same simulation set, Thr-79 fluctuates 0.2 Å more than in unbound CaM. In comparison the RMSF for all residues in CaM bound to CaMKK, CaMK1, and eNOS are reduced in comparison to unbound CaM. In general, there is more diversity among the RMSF profiles for CaM bound to the different targets in low ionic strength conditions, consistent with the differences between polar CaM-target side-chain interactions observed at low and high ionic strength (Fig. S4).

Figure 2.

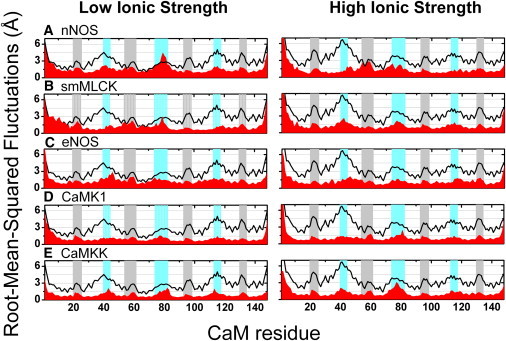
Variable backbone conformational dynamics for peptide target complexes. RMSF for C_α atoms for calcium-activated CaM (black lines) in comparison with indicated complexes between calcium-activated CaM and target peptides (red). Calcium binding sites (gray) and conformationally sensitive loops (cyan) are highlighted. Graphs are vertically ordered according to calculated quasiharmonic entropies (Table S6).

CaM interhelical angles and fluctuations contribute to CaM flexibility

Large amplitude CaM interhelix angle bending is observable on the 100 ns time-scale (Table S5). The angle bending amplitude (one-half the difference between maximum and minimum angles) ranges from 7° to 18°; average angles range between 79° and 100° (the overall average is 90°, corresponding to a perpendicular helix orientation). Fluctuations between helix angle extremes take tens of nanoseconds and vary by target. In general, the CaM-target complexes with the largest TΔS_conf explore a larger range of angles; CaM in complex with CaMKK or CaMK1 explores a smaller range of interhelical angles than smMLCK-CaM or nNOS-CaM, and eNOS-CaM is intermediate. This finding is consistent with the relationship between linker immobilizations and large-amplitude backbone motions previously proposed (20). As shown in Fig. S5, the helix bending amplitudes relative to unbound CaM are ionic strength dependent, and follow the RMSF variation between CaM bound to the different targets (Fig. 2).

CaM quasiharmonic entropy changes upon target binding are consistent with experimental values

Experimental (5) and calculated conformational entropies are tabulated in Table S6. Our value of TΔS_quasi calculated from all heavy CaM atoms in the high ionic strength smMLCK-CaM simulation (−154 kcal/mol) is close to the −70 to −140 kcal/mol range proposed by Wintrode and Privalov (20). A previous calculation of TΔS_quasi for smMLCK-CaM calculated from a 4 ns simulation is significantly lower in magnitude (−32 kcal/mol; see Table 2 in (25)). Prior measurements have suggested that the contributions of side-chain motions play a dominant role in modulating changes in conformational entropy upon target protein binding (5). Consistent with this suggestion, there are uniform increases in the absolute entropy upon inclusion of protein side chains; inclusion of heavy side-chain atoms results in a 2.5-fold increase in absolute quasiharmonic entropy. Irrespective of the inclusion of side-chain fluctuations, there is a correlation between calculated quasiharmonic entropies with the experimentally derived conformational entropy values (5) (the squared correlation coefficient R² = 0.95, Fig. 3). These observations are consistent with prior suggestions that both backbone and side-chain dynamics contribute to CaM conformational entropy (39), and suggest a correspondence between changes in backbone structure with side-chain mobility.

Figure 3.

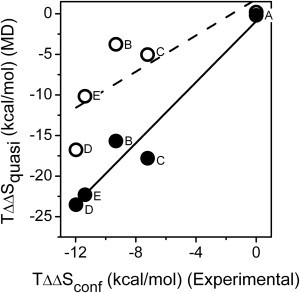
Calculated quasiharmonic conformational entropies from molecular dynamics simulations correlate with experimental conformational entropies. Target-dependent differences in quasiharmonic CaM conformational binding entropy (relative to nNOS-CaM) for backbone atoms (open circles) or all heavy CaM atoms (solid circles) between complexes of calcium-activated CaM bound to different target peptides at high ionic strength (0.15 M KCl). Points are labeled according to peptide targets: (A), neuronal nitric oxide synthase (nNOS; 2o60.pdb); (B), smooth myosin light chain kinase (smMLCK, 1qtx.pdb); (C), epithelial nitric oxide synthase (eNOS; 1niw.pdb); (D), CaM-dependent protein kinase I (CaMK1; 1mxe.pdb); and (E), CaM-dependent protein kinase kinase (CaMKK; 1ckk.pdb). Experimental NMR/isothermal titration calorimetry conformational entropy data were obtained from (5). Lines represent nonlinear least squares fits to the data for backbone atoms (slope = 1.1; R² = 0.67) and all CaM heavy atoms (slope = 1.9; R² = 0.95).

CaM quasiharmonic entropy changes upon target binding are ionic strength dependent

There is also a demonstrated correlation between TΔS_quasi values under low and high ionic strength conditions, irrespective of the inclusion of side-chain atoms (R² = 0.87, Fig. S7). The high ionic strength quasiharmonic entropies are smaller than the low ionic strength values by a factor of 0.17. No permanent ion insertions were observed in either simulation set, which rules out the possibility that ions compete with stabilizing interactions and influence CaM flexibility in that manner. Rather, we attribute the quasiharmonic entropy’s ionic strength dependence to these factors: screening of electrostatic repulsion between CaM domains at physiological ionic strength (13); slower diffusion in a high ionic strength solvent (52); different side-chain interactions under different ionic strength conditions (particularly in smMLCK-CaM and nNOS-CaM (Table 1)); subtle differences in CaM compaction upon binding (Fig. S2); and, in general, the fact that changing experimental conditions to favor one target creates conditions that are less favorable for the others (53).

Quasiharmonic entropy convergence

Comparison of absolute entropies calculated from the 100 ns trajectories with the infinite limit values shows that at least 93% of the absolute quasiharmonic entropy calculated from CaM backbone fluctuations has been captured after 100 ns in all cases except the low ionic strength nNOS-CaM simulation (CaM is the most flexible in this CaM-target simulation), which is 88% of the extrapolated conformational entropy. Fig. S6 and Table S7 show the results of the least-squared fits to Eq. 1.

Transient salt bridges enhance conformational entropy and depend on target sequence and ionic strength conditions

Large amplitude CaM-target interactions such as transient salt bridges have the potential to enhance the range of energetically equivalent conformers of CaM bound to target peptides. Lys-148 at the C-terminus in CaM has large amplitude motions, consistent with the inability to resolve this residue in structures of CaM bound to target peptides from CaMK1 and eNOS. CaMKK Asn-24 forms a permanent hydrogen bond to Lys-148, whereas eNOS Lys-6 interacts unfavorably with Lys-148 (Table S2). The salt bridge analysis indicates that, when CaM is bound to targets, Lys-148 can interact favorably with N-terminal acidic residues (Asp-2, Glu-7, and Glu-11), central linker acidic residues (Asp-78, Asp-80, Glu-82), and acidic side chains on the targets. In this respect, eNOS and nNOS are the only targets with acidic residues (Glu-7 and Glu-12, respectively). However, only the Glu in nNOS is positioned in such a way that it can participate in this three-way transient Lys-148 salt-bridge network (Fig. 4 shows snapshots from the low ionic strength nNOS-CaM simulation depicting the transient salt bridges. Fig. S8 shows the salt bridge distances as a function of simulation time.). Glu-7 in eNOS is two residues away from the Phe-5 hydrophobic anchor, and Glu-12 in nNOS is halfway between its two hydrophobic anchors (Phe-7 and Phe-16). eNOS Glu-7 interacts with Lys-148, although it is extremely rare (<1% of the time). The ability of CaM to exist in multiple conformers through these transient salt bridges is consistent with the unique ability of the nNOS-CaM complex to retain a maximal amount of conformational entropy, and may represent a fundamental design principle that can be used to enhance binding. In terms of the target CaM binding motifs (21), targets with 1-8-14 or 1-5-8-14 motifs (smMLCK, eNOS, and nNOS) allow CaM to maintain more conformational entropy than the other two targets (CaMKK is 1-16, CaMK1 is 1-5-10).

Figure 4.

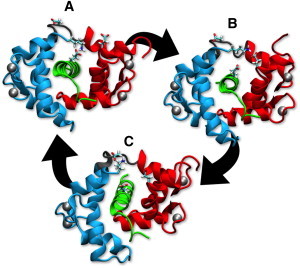
Transient salt bridges enhance conformational entropy. Selected snapshots of nNOS-CaM trajectory (low ionic strength simulation) depicting of CaM Lys-148 transient salt bridges involving Lys-148. Protein residues are shown in ribbons format. Cyan = CaM C-domain (left); Red = CaM N-domain (right); Gray = CaM central linker; Green = nNOS peptide (center). Calcium ions are shown as silver Van der Waals spheres. (A, 13 ns snapshot): salt bridge formed between C-terminal Lys-148 and Glu-12 in target peptide, (B, 29 ns snapshot) salt bridge between Lys-148 and Glu-11 in CaM N-domain, and (C, 39 ns snapshot) salt bridge between Lys-148 and Asp-78 in the CaM central linker.

To investigate the relationship between nNOS-CaM transient salt bridges and linker fluctuations, we evaluated the eigenvectors of the covariance matrix for CaM and nNOS heavy atoms and identified the lowest index eigenvectors containing the transient salt bridge movements. Examination of the nNOS-CaM structures at the eigenvector extremes was used to visualize the relationship between these two movements. Fig. S9 includes the eigenvector projections over the 100 ns trajectories and corresponding structure extremes, and shows that the linker flexing movement and transient salt bridge network are coordinated in the low ionic strength simulation but not in the high ionic strength simulation (because the linker does not fluctuate as much as in the low ionic strength simulation (Fig. S1)).

Conclusions

MD simulations of CaM in complex with target peptides from five different target proteins reasonably reflect experimental observations relating to differences in CaM conformational binding entropy (5), in terms of low (CaMKK and CaMK1), intermediate (smMLCK and eNOS), and high (nNOS) amounts of conformational entropy preservation upon target binding, and provide insight into the underlying mechanisms responsible for the sequence-dependent tuning of conformational entropy upon complex formation. Although the quasiharmonic description of conformational entropy compares favorably to an experimental benchmark, as shown previously (3), the quasiharmonic entropy is sensitive to the trajectory length (21) and does not converge when derived from a single MD simulation (37). Therefore, we cannot claim that the calculated entropy differences are definitive, and instead consider this result to be a useful tool to assess the other structural and dynamic properties underlying mechanistic aspects associated with target binding.

Results from trajectory analysis explain that the conformational binding entropies are driven by backbone fluctuations that are exaggerated at low ionic strength, because of the more extended CaM structure (44). Previous studies have concluded that both CaM backbone and side-chain properties are at the heart of its differential conformational entropy changes upon binding to diverse target sequences (39), and our results support this idea because quasiharmonic entropies correlate with experimental conformational entropies whether or not side-chain heavy atoms are included. Furthermore, our results support the hypothesis that side-chain fluctuations mirror the overall conformational entropy (16), inasmuch as the side chains “ride along” with the backbone, which is restricted or stimulated by side-chain interactions with the targets.

Central to the retention of conformational entropy is the destabilization of the central DE linker upon association with target peptides, which exists as a metastable helix in solution for calcium activated CaM (9,43,44). However, helix disruption is insufficient to maximize entropy, as side-chain interactions with target peptides demonstrate an ability to restrict the central linker’s conformational dynamics. Our results show that, in addition to stabilizing interactions between the target and the central linker, one must also consider the stimulation of motions incurred by unfavorable (electrostatically repulsive) interactions. Binding peptides from smMLCK and nNOS allow CaM to maintain the most quasiharmonic entropy among the set included in this study, and both have basic residues that repel like-charged Lys residues in the CaM flexible linker, causing the central linker to be more disordered. It is also important to consider target hydrogen bonds to Gln-41 in the conformationally sensitive loop BC. The complex with nNOS stands out in terms of maintained flexibility upon target binding, and we partly attribute this to the transient Lys-148 salt bridges alternating between the C-domain, central linker, and the target Glu. Although eNOS also has a Glu residue, it is not positioned properly for this type of interaction. Among the five peptide targets studied, targets with 1-8-14 or 1-5-8-14 motifs (smMLCK, eNOS, and nNOS) allow CaM to maintain more conformational entropy.

Extension of these simulations to consider complexes with more diverse binding affinities will provide additional insight relating to mechanisms of molecular recognition that fine-tune binding, and are expected to provide insights both with respect to the prediction of relative binding affinities between the >300 different target peptides that bind CaM, as well as for protein engineering efforts aimed at developing affinity reagents.