A Deconvolution-Based Method with High Sensitivity and Temporal Resolution for Detection of Spontaneous Synaptic Currents In Vitro and In Vivo

Abstract

Spontaneous postsynaptic currents (PSCs) provide key information about the mechanisms of synaptic transmission and the activity modes of neuronal networks. However, detecting spontaneous PSCs in vitro and in vivo has been challenging, because of the small amplitude, the variable kinetics, and the undefined time of generation of these events. Here, we describe a, to our knowledge, new method for detecting spontaneous synaptic events by deconvolution, using a template that approximates the average time course of spontaneous PSCs. A recorded PSC trace is deconvolved from the template, resulting in a series of delta-like functions. The maxima of these delta-like events are reliably detected, revealing the precise onset times of the spontaneous PSCs. Among all detection methods, the deconvolution-based method has a unique temporal resolution, allowing the detection of individual events in high-frequency bursts. Furthermore, the deconvolution-based method has a high amplitude resolution, because deconvolution can substantially increase the signal/noise ratio. When tested against previously published methods using experimental data, the deconvolution-based method was superior for spontaneous PSCs recorded in vivo. Using the high-resolution deconvolution-based detection algorithm, we show that the frequency of spontaneous excitatory postsynaptic currents in dentate gyrus granule cells is 4.5 times higher in vivo than in vitro.

Introduction

Quantitative analysis of postsynaptic currents (PSCs) in neurons is of critical importance to our understanding of the function of central synapses. In brain slice preparations in vitro, transmitter release not only occurs in a tightly regulated manner following presynaptic spikes, but also spontaneously in the absence of presynaptic action potentials (APs, Katz (1)). Although the functional significance of spontaneous transmitter release is unclear, it provides key information about various mechanistic aspects of transmission, such as quantal size, release probability, and changes in any of these parameters (2,3). Similarly, in neuronal networks in vivo, synaptic activity is not only generated in response to behavioral stimuli (4), but also in an apparently random manner during dynamic network activity (5,6). Analysis of spontaneous synaptic events in vivo may provide important clues regarding the processes underlying rhythmic network activity, such as network oscillations (5,6). For the quantitative analysis of both spontaneous activity in vitro and in vivo, powerful detection algorithms with high temporal resolution are required.

Several methods for the detection of spontaneous PSCs were previously proposed. The simplest detection method uses amplitude threshold algorithms, in which the threshold is either fixed at an absolute level or shifted in parallel to a sliding baseline (7). As these algorithms exclusively use information about the amplitude of synaptic events, their performance is low, especially for events generated in distal dendrites, which are attenuated substantially (7). Alternative detection methods are based on first-derivative algorithms (8). These algorithms have a high temporal resolution, but typically show a high false event rate. False positive (FP) events will be produced by baseline noise, amplified by the derivative method, whereas false negative (FN) events will be produced by slowly rising PSCs escaping detection. Miniature PSCs in central neurons are generated at synapses distributed over the entire dendritic tree (9). Therefore, PSCs will suffer from attenuation and filtering, and only the perisomatically generated subset of events may rise rapidly and become detectable. Thus, the performance of both methods is substantially below that of a by eye/manual analysis of an experienced investigator, in which a priori knowledge about the time course of PSCs allows to distinguish real events from experimental artifacts.

To incorporate information about the kinetics of PSCs, template fit algorithms have been proposed by Jonas et al. (10), Abdul-Ghani et al. (11), and Clements and Bekkers (12). These methods correlate the experimental trace with a previously specified template sample point by sample point, detecting events as the correlation coefficient or the signal/noise ratio (SNR) exceeds a critical value (10–12). These algorithms show a low false event rate, but have a temporal resolution limited by the duration of the template. Thus, whereas these methods work well for events generated at low frequency, superimposed events are difficult to analyze. This limitation is particularly relevant in vivo, where synaptic events are generated in high-frequency bursts (6,13). In such a scenario, for any given event both preceding (contributing to the baseline) and following events (contributing to the decay phase) will markedly degrade the correlation with the template. Another disadvantage of template fit algorithms is that the SNR depends on the template length, and the detection threshold is therefore difficult to specify (10–12).

To overcome these limitations, we developed what we believe to be a new method for detecting miniature and spontaneous PSCs. Unlike other algorithms published to date, the technique is based on deconvolution (14–17). The basic principle is that deconvolution converts a train of PSCs into a series of delta-like functions, the maxima of which can be precisely measured. We used the deconvolution-based detection technique to test the hypothesis that the frequency of excitatory synaptic events is higher under in vivo than in vitro conditions, as often assumed, but never shown by rigorous comparison.

Materials and Methods

A deconvolution-based method for detection of spontaneous synaptic currents

To detect spontaneous PSCs in vitro and in vivo, we implemented a deconvolution-based method. Although deconvolution-based algorithms were previously applied to various scientific problems (calculation of the time course of release (15–17) 1995 - 2005; calculation of the time course of postsynaptic conductances from potentials (18) 2008; measurement of unbinding rates of competitive antagonists (19), 2001), this work describes, to our knowledge, the first application to spontaneous PSC detection. Like the template fit method (10–12), the deconvolution-based method exploits prior information about the time course of individual synaptic events. However, in comparison to other methods, the deconvolution-based method has a markedly higher temporal resolution.

The basic principle of the method of detection of spontaneous PSCs is that we describe the recorded trace as the convolution of time course of transmitter release and quantal conductance. More formally, the recorded signal can be described by the convolution integral

$$\text{h}\left(\text{t}\right)=\underset{0}{\overset{\text{t}}{\int }}\text{f}\left(\text{t}-{\text{t}}^{\prime }\right)\text{g}\left({\text{t}}^{\prime }\right){\text{dt}}^{\prime },$$ (1)

where f(t) is the release function and g(t) is the quantal conductance. For each release event, f(t) is given by the Dirac delta function

$$\text{f}\left(\text{t}\right)=\mathit{\delta }\left(\text{t}-{\text{t}}_0\right)=\{\begin{array}{cc}\mathrm{\infty }& \text{for}\text{t}={\text{t}}_0\\ 0& \text{for}\text{t}\ne {\text{t}}_0\end{array},$$ (2)

where t₀ is the time point of the release event.

Furthermore, the time course of the quantal conductance is represented as a multiexponential function

$$\text{g}\left(\text{t}\right)=\{\begin{array}{cc}\frac{\text{A}}{A^{\prime }}\left[-\text{Exp}\left(-\frac{\text{t}}{{\mathit{\tau }}_1}\right)+\text{Exp}\left(-\frac{\text{t}}{{\mathit{\tau }}_2}\right)\right]& \text{for}\text{t}>0\\ 0& \text{for}\text{t}\le 0\end{array},$$ (3)

where τ₁ is the rise time constant, τ₂ is the decay time constant (τ_2 > τ₁), A is the peak amplitude, and A′ is a normalization factor:

$${\mathit{A}}^{\prime }={\frac{{\tau }_2}{{\tau }_1}}^{\frac{{\tau }_1}{{\tau }_1-{\tau }_2}}.$$

Under these conditions, f(t) can be obtained by deconvolution, provided that g(t) is accurately specified.

In the practical implementation, the method of detection of spontaneous PSCs was composed of four steps (Fig. 1 A). First, a multiexponential template was generated, based on the time course of spontaneous synaptic events. These events are selected manually or automatically by any available detection method, averaged, and fitted with standard analysis software for electrophysiology to reveal the time course of the template. Although a sum of two exponentials was used in this study, other template functions can be arbitrarily used.

Figure 1.

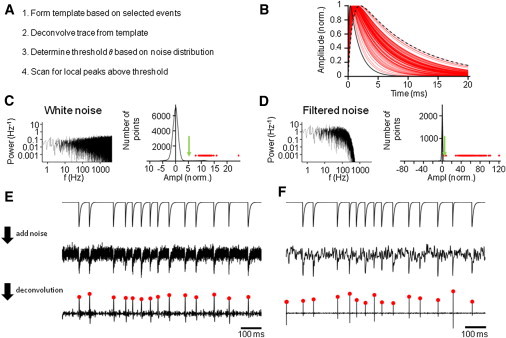
A deconvolution-based algorithm for detection of EPSCs can markedly increase the SNR. (A) Individual steps of the deconvolution procedure. (B) Testing the power of the method using simulated EPSCs with a different time course. EPSCs were simulated by the sum of two exponentials (Eq. 3), with both time constants scaled randomly. Fastest and slowest events are depicted in black (continuous and dashed, respectively), other events in red. (C and D) Characteristics of different forms of noise added to the data (white noise in C, filtered noise of matched variance in D). Left panel shows power spectrum, right panel shows all-point histogram of the deconvolved signal. Green arrows indicate the SNR of the original simulated data. (E and F) Detection of PSCs by deconvolution. Upper traces, idealized EPSC waveforms. Center traces, EPSC waveforms after addition of noise. Bottom traces, corresponding deconvolved signals. Red dots indicate local maxima corresponding to detected events (also included in all-point histograms in C and D).

Second, 1- to 5-min long experimental traces were deconvolved from the template PSCs, using discrete Fourier transformation-based deconvolution algorithms of Mathematica 8.0.1 (ListDeconvolve) and Igor Pro 6.22 (Deconvolution; Scripts S1 and S2 in the Supporting Material). In theory, if amplitude and kinetics of PSCs are uniform and the template accurately fits the experimental PSCs, the resulting deconvolution trace will be a series of delta functions. In reality, both amplitudes and PSC kinetics are variable. Thus, deconvolution will result in a series of delta-like functions with variable amplitude and time course. Before analysis, the deconvolution trace was passed through a low-pass filter as required.

Third, a detection threshold (θ) was defined. Although θ is the only free parameter in the analysis, its value critically determines the number of FP events and FN events. Thus, the selection of θ is a tradeoff between the two types of errors. Increase of θ decreases the FP events, but at the same time increases the FN events. Conversely, decrease of θ increases FP events, but decreases FN events. To appropriately set the value of θ, an all-point histogram of the deconvolved trace was generated. Because of the rapid time course of the delta-like events, the histogram is mainly contributed by baseline noise. To allow a precise estimate of the type 1 error, corresponding to FP events, the entire distribution, or the left portion, was fitted with a Gaussian function with mean near 0 and standard deviation σ. Typically, θ was set to a value 4 to 4.5 times the standard deviation σ of the Gaussian function, corresponding to a proportion of FP sample points of 0.0032–0.00034%. For a sample rate of 10 kHz, this corresponds to a FP event rate of 0.32–0.034 s⁻¹.

Fourth, the deconvolution trace was scanned for local maxima, which are defined as sample points fulfilling the criterion y_i−1 < y_i > y_i+1 or y_i−2 < y_i−1 < y_i > y_i+1> y_i+2 with y_i > θ. These local maxima corresponded to detected PSCs and additionally defined their onset times. All analysis steps were performed using Mathematica or Igor Pro running under Windows. Deconvolution-based detection of miniature and spontaneous PSCs was computationally efficient. For example, automatic analysis of a 60-s recording epoch sampled at 10 kHz took 13 s computation time on a 2.67 GHz Intel i7 PC, compared to 24.5 and 15.5 s for derivative and template fit, respectively.

After event detection in the deconvolved trace, the corresponding PSCs were further analyzed in the originally recorded trace. 20–80% rise time, peak amplitude, and decay time constant were determined as described previously (20). Alternatively, the experimental trace was backfitted with a sum of individual PSC waveforms, the total number and timing of which was constrained by the maxima of the deconvolution trace above threshold.

Simulation of excitatory postsynaptic currents (EPSCs)

EPSCs were simulated in two different ways. First, EPSCs were randomly generated as multiexponential waveforms according to Eq. 3. Interevent interval (IEI) values were randomly chosen according to an exponential distribution (event rate 10 s⁻¹), whereas kinetics of EPSCs were randomized by multiplying rise and decay time constant of the default waveform (τ₁ = 0.4 ms, τ₂ = 5 ms) with a normally distributed random factor (mean one, standard deviation 0.3). Alternatively, EPSCs were simulated using a detailed passive cable model. A previously published cable model was used, based on reconstruction of soma, dendrites, and axon of a biocytin-labeled rat dentate gyrus granule cell (21,22). Spine correction was performed by scaling length and diameter of dendritic segments appropriately. R_m, C_m, and R_i were chosen as 30,000 Ω cm², 0.9 μF cm⁻², and 150 Ω cm; values were similar to those reported for dentate gyrus granule cells in mice (9). Synapses were placed on dendrites with random locations and activated with random onset times. Locations were set based on equally distributed random numbers, whereas onset times were chosen using exponentially distributed IEI values (event rate 10 s⁻¹). The postsynaptic conductance was computed as the sum of two exponential functions, one for rise and one for decay, with a rise time constant of 0.2 ms, a decay time constant of 2.5 ms, and a reversal potential of –5 mV (23). The synaptic peak conductance was 1 nS. Modeling was performed using NEURON 7.1 (24). For all simulations, the fixed time step integration method was used; the time step was set to 10 μs. Voltage-clamp recordings of PSCs were simulated using a SEClamp with a series resistance R_s of 5 MΩ.

To determine the effects of noise, fluctuations with three different spectral characteristics were simulated (25). First, white noise was generated using normally distributed random numbers. Second, filtered noise was generated by passing white noise through a Gaussian filter. Finally, mixed noise with a white noise component and a 1/f component (each with 50% contribution to the total variance) was simulated using a previously described procedure (26). In all cases, the amplitude of the noise was scaled appropriately to give an SNR of 5. Finally, noise was added to the simulated PSCs. Random numbers were obtained with the RandomReal and RandomInteger random number generator procedures of Mathematica.

Recording of EPSCs in vitro

Whole-cell patch-clamp recording of spontaneous and miniature EPSC from dentate gyrus granule cells was performed in hippocampal slices obtained from 19- to 21-day-old Wistar rats of either sex (27–29). Animals were decapitated and transverse slices were cut with a vibratome (VT 1200, Leica). For storage of slices, a solution containing 87 mM NaCl, 25 mM NaHCO₃, 75 mM sucrose, 10 mM D-glucose, 2.5 mM KCl, 1.25 mM NaH₂PO₄, 0.5 mM CaCl₂, and 7 mM MgCl₂ was used. For the experiments, slices were superfused with physiological saline containing 125 mM NaCl, 25 mM NaHCO₃, 2.5 mM KCl, 1.25 mM NaH₂PO₄, 2 mM CaCl₂, 1 mM MgCl_2, and 25 mM D-glucose, equilibrated with 95% O₂/5% CO₂ gas mixture. Patch pipettes were pulled from borosilicate glass tubing (2 mm outer diameter, 1 mm inner diameter, Hilgenberg). When filled with intracellular solution, the pipette resistance was 2–3 MΩ. The internal solution used for in vitro recordings contained: 110 mM KCl, 35 mM Kgluconate, 10 mM EGTA, 2 mM MgCl₂, 2 mM Na₂ATP, and 10 mM HEPES (pH adjusted to 7.3 with KOH). The series resistance ranged from 7 to 10 MΩ. Series resistance was not compensated, but regularly monitored during experiments. Cells with >15% change were discarded. EPSCs were recorded using an Axopatch 200A amplifier (Molecular Devices), low-pass filtered at 5 kHz (Bessel filter), and sampled at 10 kHz using a CED power laboratory interface (Cambridge Electronic Design). The holding potential was set to –80 mV (no correction for junction potentials). Spontaneous EPSCs were recorded in pharmacological isolation in the presence of 10 μM bicuculline methiodide in the bath solution. Miniature EPSCs were measured in the presence of 1 μM tetrodotoxin (TTX) and 10 μM bicuculline methiodide. The recording temperature was 22–24°C or 32–34°C in a subset of experiments (as indicated).

Recording of EPSCs in vivo

Whole-cell patch-clamp recording of EPSCs in vivo from dentate gyrus granule cells was performed in 27- to 29-day-old Wistar rats of either sex (30). Experiments were made in strict accordance with national and European guidelines for animal experiments. Experimental protocols were approved by the Bundesministerium für Wissenschaft und Forschung (BMWF-66.018/0008-II/3b/2010). Animals were anesthetized using a combination of medetomidine (Dormitor; Roche, 300 mg/kg), midazolam (Dormicum, Roche, 8 mg/kg), and fentanyl (Janssen-Cilag, 10 mg/kg), applied intraperitoneally. After anesthetization, animals were fixed in a stereotaxic frame and a craniotomy with a diameter of ∼2 mm was made. Patch pipettes were pulled from borosilicate glass tubing (1 mm outer diameter, 0.5 mm inner diameter; Hilgenberg). Patch pipettes were gently inserted into the brain, targeting the dentate gyrus granule cell layer (anteroposterior –3.5 to –5.0 mm, lateral 2.5 to 3.0 mm, and dorsoventral –2.9 to –3.2 mm from bregma). Positive pressure between 500 and 900 mbar was applied to the pipette interior while traversing the neocortex and the corpus callosum, until ∼200 μm before reaching the target zone. Pressure was then gradually reduced to ∼20 mbar and a patch-clamp recording was obtained ∼2 min later. Patch pipettes used for patch-clamp recording had tip resistances of 5–7 MΩ. The access resistance was 48 ± 2 MΩ (n = 10, range: 37–58 MΩ). Pipettes were tip-filled with a solution containing 120 mM K-methanesulfonate, 20 mM KCl, 10 mM EGTA, 2 mM MgCl₂, 2 mM Na₂ATP, 10 mM HEPES, 5 mM QX-314 (pH adjusted to 7.3 with KOH), and 3 mg/ml biocytin and backfilled with a similar solution in which the K-methanesulfonate was replaced by Cs-methanesulfonate. A reference electrode (Ag/AgCl) was placed on the skull close to the craniotomy (∼1 mm separation distance). EPSCs were recorded with an EPC-10 amplifier using Patchmaster software (version 2.32), low-pass filtered at 10 kHz (Bessel filter) and sampled at 20 kHz. The holding potential was set to –70 mV (no correction for junction potentials). Under our recording conditions, the measured brain temperature was 33–35°C while the body temperature was kept at ∼37°C. Recordings were taken at least 10 min after the whole-cell configuration was obtained, allowing sufficient time for clearance of K⁺ that may have accumulated during the patch-clamp procedure.

Validation of deconvolution-based detection

To test the power of detection, the deconvolution-based method was compared against previously published PSC detection methods, 1995: a first-derivative method (8), 1994, and a template fit algorithm (10–12), 1993 - 1997. For the derivative method, event detection was optimized by pre-processing the traces with a Gaussian low-pass filter at 100 Hz (12). For the template fit algorithm, the duration of the template was varied between 6.25 and 50 ms, because this parameter is a key determinant of sensitivity and specificity (12).

Comparison of the different methods was performed as follows. First, a list of temporal tags was generated by expert scoring of experimental data.

Second, the list of manually generated tags was converted into a binary scoring trace (see Fig. 7 A), with a sampling rate identical to that of the original trace. A temporal window of 2.4 ms (± 1.2 ms) was defined symmetrically around each tag. The score was set to one for all data points within the window and to zero otherwise.

Figure 7.

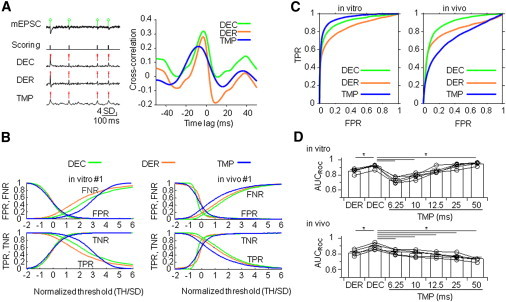
Comparison of different detection methods using experimental data. (A) Example trace of mEPSCs with the corresponding manual scoring trace and the detector traces of the different methods. Left panel from top to bottom: mEPSC trace, expert scoring, deconvolution (DEC), first derivative (DER), and template fit (TMP). Right panel, cross correlation between the expert scoring trace and the detector trace for each method. All detector traces were normalized to 1 SD. The detected events are marked with green circles in the original data and with red crosses in the detector traces. (B) FPR, FNR, TPR, and TNR plotted versus normalized threshold for the different methods and the experiments shown in Figs. 3 and 5. The threshold was normalized by the SD of the corresponding detector trace. (C) Average ROC curve for in vitro (n = 5) and in vivo data sets (n = 5) for different methods. (D) Summary bar graph of the area under the curve for the three different detection methods applied to in vitro (top) and in vivo (bottom) experimental data. P < 0.05 (^∗).

Third, the cross correlation between the scoring trace and a given detection method output (i.e., detector trace) was computed and the time lag of the cross-correlation peak was measured. As different methods produced different time lags, the lag was subtracted before final comparison.

Finally, a threshold was applied to the detector traces and the result was compared sample point by sample point to the scoring trace. For each threshold value, a sample-based confusion matrix containing the number of true positive (TP), true negative (TN), FP, and FN sample points was computed. Furthermore, the true positive rate (TPR = TP/(TP + FN)), the true negative rate (TNR= TN/(FP + TN)), the false positive rate (FPR = FP/(FP + TN)), and the false negative rate (FNR = FN/(TP + FN)) were calculated. Subsequently, TPR was plotted against FPR, leading to the receiver operator characteristics (ROC) curves (31) for each method. The performance of each method was then quantified as the integral (i.e., area) under the corresponding ROC curve (AUC_ROC). A value of 0.5 corresponds to random detection, whereas a value of 1 implies perfect detection. The AUC_ROC is related to the SNR as follows (32):

$$\text{SNR}=2{\text{erf}}^{-1}\left(\left(2{\text{AUC}}_{\text{ROC}}\right)-1\right)=\{\begin{array}{cc}0,& \text{for}{\text{AUC}}_{\text{ROC}}=0.5\\ >0,& \text{for}{\text{AUC}}_{\text{ROC}}>0.5\end{array},$$ (4)

where the erf⁻¹ is the inverse of the Gaussian error function. Eq. 4 implies that the larger the AUC_ROC, the higher the SNR.

Statistical analysis

Values are given as mean ± SE. Error bars in figures also indicate the mean ± SE. Significance of differences was assessed by a two-sided nonparametric Wilcoxon signed-rank test at the significance level (P) indicated.

Results

Methods for detection of spontaneous synaptic events are substantially more powerful if information about the time course of the spontaneous events is incorporated, as exploited by template fit algorithms (10–12). However, a serious limitation of these methods is the low temporal resolution, which is particularly relevant for the analysis of synaptic currents in vivo (6,33). To overcome this limitation, we considered alternative ways of how information about the time course of the synaptic events may be incorporated. We reasoned that deconvolution (14–16) could be used to transform sequences of PSCs into series of delta-like functions, which would be simple to analyze (Fig. 1 A).

Validation of the deconvolution-based detection method using simulated data

We first tested the deconvolution-based detection technique on simulated data (Fig. 1). EPSCs were generated at random time points and with random kinetics, with IEI chosen according to an exponential distribution. Kinetics of miniature PSCs were randomized by multiplying a rise and decay time constant of a multiexponential waveform with a normally distributed random factor (mean one, standard deviation 0.3; Fig. 1 B). In this set of temporally scaled EPSCs, the ratio of maximal/ minimal value of the kinetic shape factor was 4.8. Simulated EPSCs with unitary peak amplitude were then superimposed with white noise or filtered noise (Fig. 1, C and D). The noise had a standard deviation of 0.2, leading to an SNR of 5.

Testing of the deconvolution-based method on these simulated EPSC data revealed a high sensitivity and specificity under the chosen conditions. Remarkably, deconvolution increased the SNR of the delta-like events in the deconvolution trace in comparison to that of the original EPSC trace (Fig. 1, C–F). For EPSCs generated by temporal scaling, the SNR increased from 5 to 11.8 for white noise and 56.0 for filtered noise. Thus, depending on both the shape of the EPSCs and the temporal structure of the noise, deconvolution can substantially increase the SNR. The percentage of TP events was 98% and 99%, the percentage of FP events was 1% and 2%, and the percentage of FN events was 2% and 1%, respectively. Thus, the deconvolution-based detection technique had a high sensitivity and specificity.

To test the detection performance under more realistic conditions, we simulated EPSCs in the presence of mixed noise, containing both a white noise component and a 1/f component (Fig. 2, A–C). As with the simple forms of noise, the deconvolution-based detection method increased the SNR, from 5 to 6.9 under the present conditions (Fig. 2, A and B). The percentage of TP events was 98%, the percentage of FP events was 2%, and the percentage of FN events was 2%. To further test the detection performance under conditions of more realistic PSC time courses, we simulated EPSCs in a detailed cable model of a dentate gyrus granule cell (Fig. 2, D–F). Synapses were activated at random locations and at random time points, normalized to the same peak amplitude, and superimposed with mixed noise to give an SNR of 5. As in the simulation with temporally scaled EPSCs, the deconvolution-based detection method increased the SNR from 5 to 6.8 in the detailed cable model (Fig. 2, D and E). The percentage of TP events was 75%, the percentage of FP events was 9%, and the percentage of FN events was 25%. A major advantage of the deconvolution technique over alternative techniques, such as template fit (10–12), was the high temporal resolution. Pairs of EPSCs generated randomly at short time intervals were reliably detected (Fig. 2 F). Thus, for a wide range of noise spectral characteristics and PSC time courses, the deconvolution-based method detected the underlying events with high reliability and high temporal resolution.

Figure 2.

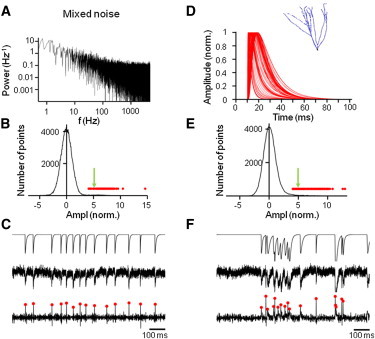
Deconvolution-based detection algorithm for mixed noise and EPSCs generated in detailed cable models. (A) Frequency characteristics of mixed noise (white noise and 1/f component, each with 50% contribution to the total variance). (B) All-point histogram of the deconvolved signal. Green arrows indicate the SNR of the original simulated data. (C) Detection of EPSCs by deconvolution. Upper traces, idealized EPSC waveforms. Center traces, EPSC waveforms after addition of mixed noise. Bottom traces, corresponding deconvolved signals. Red dots indicate local maxima corresponding to detected events (also included in all-point histogram in B). (D–F) Simulations of EPSCs generated in a detailed cable model of a granule cell. Mixed noise was added to the simulated data as in A–C. Inset in D shows the cable model used for simulation (21,22). Individual events are reliably detected even in high-frequency trains (F).

Detection of miniature EPSCs recorded in vitro

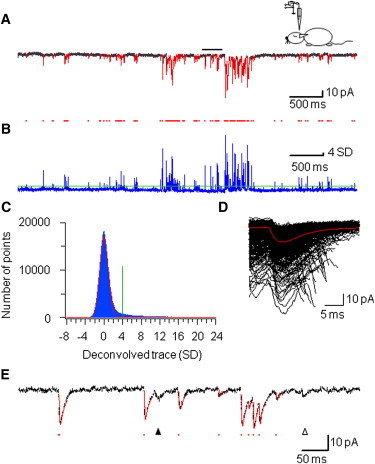
Next, we used the deconvolution-based technique for the detection of miniature EPSCs in vitro (Fig. 3). Whole-cell recordings were made from dentate gyrus granule cells in hippocampal slices in the presence of TTX to block presynaptic action potential generation. Under our experimental conditions, the baseline noise was 2.76 ± 0.07 pA (5 kHz bandwidth; 10 cells). Similar to the simulated data, deconvolution converted a train of miniature EPSCs into a series of delta-like pulses (Fig. 3, A and B). To adequately set the detection threshold, an all-point histogram of the deconvolution trace was constructed and fitted with a Gaussian function (Fig. 3 C). The detection threshold (θ) was then set to four times the standard deviation of the normal distribution. Using these settings, 970 ± 100 events were detected in a 5-min recording period in a sample of 10 hippocampal granule cells.

Figure 3.

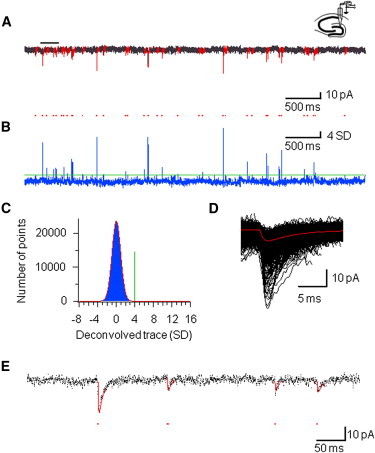
Detection of miniature EPSCs in vitro. (A) Continuous trace of miniature EPSCs in a dentate gyrus granule cell in a slice. Bath solution contained 1 μM TTX. Bar represents the region of the trace shown at expanded timescale in E. (B) Corresponding result of deconvolution, band-pass filtered at 0.1 to 100 Hz (blue trace). Red dots, peaks of the deconvolution function, corresponding to detected events. Green horizontal line: detection threshold. (C) All-point histogram of a 5-min deconvolved trace (blue bars). Data were fitted with a Gaussian function (red trace). The threshold θ was set to four times the standard deviation of the Gaussian (vertical green line). (D) 1252 detected EPSCs during 5 min of continuous recording, horizontally aligned to the peak of the deconvolution function and superimposed. Red trace indicates the average EPSC. (E) Backfitting of the experimental trace. Black dots show sample points, red curves represent the results of fitting. Red dots, peaks of the deconvolution function, corresponding to onset times of detected events.

Next, the kinetic properties of the detected events were quantitatively analyzed (Fig. 4). For the cell depicted in Fig. 3, the mean 20–80% rise time was 1.75 ± 0.02 ms, the mean decay time constant was 4.2 ± 0.06 ms, and the mean peak amplitude was 8.0 ± 0.21 pA (Fig. 4, A–C). In the total sample of 10 recorded granule cells, the mean rise time was 1.81 ± 0.03 ms, the mean decay time constant was 4.1 ± 0.2 ms, and the mean peak amplitude was 7.6 ± 0.3 pA (Fig. 4, D–F; 10 cells). The distributions of peak amplitudes and IEIs showed that EPSCs with small amplitude or bursts of EPSCs generated with short IEI were reliably detected (Fig. 4, A and G).

Figure 4.

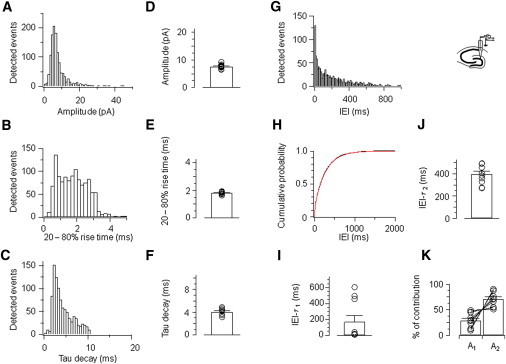
Quantitative analysis of miniature EPSCs in vitro. (A) Peak amplitude of miniature EPSCs. (B) 20–80% rise time. (C) Decay time constant. (D–F) Summary for mean peak amplitude, 20–80% rise time, and decay time constant in 10 cells. (G–H) IEI histogram and cumulative distribution (red trace: double exponential fitting). (I–K) Time constants of the fast (IEI-τ₁; I) and the slow (IEI-τ₂; J) component in the IEI distribution, as well as the amplitude contribution of the two components (K). Histograms (A–C and G–H) are taken from a single representative experiment; same cell as illustrated in Fig. 3.

It is generally assumed that miniature EPSCs are generated by a homogenous Poisson process, leading to a single exponential distribution of IEIs. Interestingly, the adequate description of our experimental IEI distribution in vitro required two exponential components (Fig. 4, G–K). For the cell illustrated in Figs. 3 and 4, A–C, the first time constant in the IEI distribution was 14.0 ± 0.7 ms (12.7% amplitude contribution), whereas the second time constant had a value of 272.0 ± 0.5 ms (87.2%; Fig. 4 H). On average, the first time constant was 167.9 ± 77.7 ms (39.4%), whereas the second time constant had a value of 398.3 ± 28.1 ms (71.7%; 10 cells; Fig. 4, I–K). Thus, the deconvolution-based detection technique revealed a short component of IEIs of miniature EPSCs in vitro, inconsistent with a homogenous Poisson process underlying miniature release. This short IEI component was not detected by the template fit method with 10 or 50 ms template duration (Fig. S1, A–C).

Detection of spontaneous EPSCs recorded in vivo

Next, we wanted to explore whether the deconvolution-based method was able to reliably detect spontaneous EPSCs in vivo, where the recording conditions are less favorable (Fig. 5). Whole-cell patch-clamp recordings were made from dentate gyrus granule cells in anesthetized rats (see Materials and Methods). Under these experimental conditions, the baseline noise was 3.9 ± 0.9 pA (5 kHz bandwidth; 10 cells), slightly higher than in the in vitro recordings. For a similar detection threshold setting (threshold was set to 4.3 times the standard deviation of the normal distribution), 1086 ± 99 events were detected in a 1-min recording period in a sample of 10 granule cells. Despite the slightly larger noise and the higher EPSC frequency, individual events were reliably detected by deconvolution-based techniques (Fig. 5, A and B).

Figure 5.

Detection of spontaneous EPSCs in vivo. (A) Continuous trace of spontaneous EPSCs recorded from a dentate gyrus granule cell in an anesthetized animal. Bar represents the region of the trace shown at expanded timescale in E. (B) Corresponding result of deconvolution, band-pass filtered at 0.1 to 100 Hz (blue trace). Red dots, peaks of the deconvolution function, corresponding to detected events. Green horizontal line: detection threshold. (C) All-point histogram of a 1-min deconvolved trace (blue bars). Data were fitted with a Gaussian function (red trace). The threshold θ was set to 4.3 times the standard deviation of the Gaussian (vertical green line). (D) 1053 detected EPSCs during 1 min of continuous recording, horizontally aligned to the peak of the deconvolution function and superimposed. Red trace indicates the average EPSC. (E) Backfitting of the experimental trace. Black dots show sample points, red curve represents the results of fitting. Red dots, peaks of the deconvolution function, corresponding to onset times of detected events. Arrowheads indicate two events, which were undetected at the specified threshold, but recovered by lowering the threshold to 3.5 and 2.3 SD (open and solid arrowhead, respectively).

Quantitative analysis revealed that the properties of EPSCs in hippocampal granule cells in vivo were similar to those in vitro. For the cell depicted in Fig. 5, the mean 20–80% rise time was 1.8 ± 0.02 ms, the mean decay time constant was 5.6 ± 0.1 ms, and the mean peak amplitude was 9.8 ± 0.2 pA (Fig. 6, A–C). On average, the mean rise time was 2.2 ± 0.07 ms, the mean decay time constant was 5.4 ± 0.3 ms, and the mean peak amplitude was 8.2 ± 0.6 pA (Fig. 6, D–F; 10 cells). As observed under in vitro conditions, the adequate description of our experimental IEI distribution required two exponential components (Fig. 6, G–K). For the cell depicted in Figs. 5 and 6, A–C, the first time constant was 20.2 ± 0.3 ms (75% amplitude contribution) and the second time constant was 163.5 ± 2.8 ms (25%; Fig. 6 H). On average (10 cells), the first time constant was 18.8 ± 2.7 ms (68.4%), whereas the second time constant was 158.2 ± 27.1 ms (31.6%; Fig. 6, I–K). Thus, the deconvolution-based detection technique revealed a short component of the IEI of spontaneous EPSCs in vivo. This short IEI component was severely underestimated by the template fit method with 10 ms template duration and remained entirely undetected with 50 ms template duration (Fig. S1, D–F).

Figure 6.

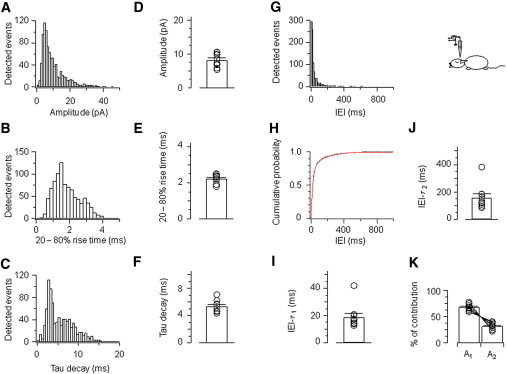
Quantitative analysis of EPSCs in vivo. (A) Peak amplitude of spontaneous EPSCs. (B) 20–80% rise time. (C) Decay time constant. (D–F) Summary for mean peak amplitude, 20–80% rise time, and decay time constant in 10 cells. (G–H) IEI histogram and cumulative distribution (red trace: double exponential fitting). (I–K) Estimation of IEI-τ₁, IEI-τ₂ and their relative amplitude contribution (see Fig. 4). Histograms (A–C and G–H) are taken from a single representative experiment; same cell as illustrated in Fig. 5.

Comparison of different detection methods

Our results suggest that the deconvolution-based detection method is very powerful when applied to simulated data (Figs. 1 and 2). To test whether this conclusion also holds for real experimental data, we compared the deconvolution-based method with other previously published methods using EPSCs recorded under in vitro and in vivo conditions (Fig. 7). First, we compared the results of the different detection methods (deconvolution, derivative, and template fit) with those of expert scoring (see Materials and Methods; Fig. 7 A). Next, we calculated FPR, FNR, TPR, and TNR for a wide range of threshold values. A major complication preventing a direct comparison of the different methods was that FPR, FNR, TPR, and TNR were highly dependent on threshold; FPR and TPR decreased, whereas FNR and TNR increased as a function of threshold (Fig. 7 B). To compare the different methods independently of the exact setting of the detection threshold, we plotted TPR against FPR, leading to a ROC curve with a shape that is independent of threshold (Materials and Methods). Finally, we calculated the AUC_ROC as a measure of detection performance (Fig. 7 D). Comparison of the deconvolution-based method with the derivative-based method revealed that the deconvolution-based method was consistently superior under both in vitro and in vivo conditions. Comparison of the deconvolution-based method with the template fit method revealed a more complex picture. For in vitro data sets, the deconvolution method was statistically superior to the template fit method for template durations of 6.25 and 10 ms, but comparable for 12.5 and 25 ms, and inferior for 50 ms. For in vivo data sets, the deconvolution method was consistently better than the template fit method with all template durations tested. Thus, the deconvolution-based detection method will be the method of choice for the analysis of in vivo data.

Frequency of spontaneous synaptic events in vitro and in vivo

It is generally assumed that the frequency of spontaneous synaptic events is much higher under in vivo conditions than in the in vitro slice preparation, where a substantial proportion of afferent inputs are cut. To test this prediction directly, we compared the average frequency of EPSCs in dentate gyrus granule cells in both in vitro and in vivo conditions, using deconvolution-based detection algorithms with similar settings. Under in vitro conditions, the average miniature EPSC frequency was 0.9 ± 0.1 Hz (10 cells; Figs. 3 and 4). In contrast, under in vivo conditions, the average spontaneous EPSC frequency was more than an order of magnitude higher, 18.2 ± 2.0 Hz (10 cells; Figs. 5 and 6).

The higher EPSC frequency under in vivo conditions could be due to higher temperature, a substantial contribution of presynaptic APs, or higher connectivity. To distinguish between these possibilities, we tried to mimic the in vivo situation by first increasing the temperature from 22 to 32°C and second omitting TTX from the extracellular solution to enable the generation of presynaptic APs (Fig. 8). Raising the temperature increased the frequency of miniature EPSCs 1.88-fold (to 1.7 ± 0.2 Hz; 8 cells). This confirms that miniature release in dentate gyrus granule cells is temperature dependent (34,35). In the absence of TTX, the frequency of spontaneous EPSCs was 3.22-fold higher at 22°C (2.8 ± 0.2 Hz, 10 cells) and 2.35-fold larger at 32°C (4.0 ± 0.9 Hz, 8 cells) than in the presence of TTX. Thus, a major portion of spontaneous EPSCs in granule cells under in vitro conditions are driven by presynaptic APs. However, even at near-physiological temperature and in the absence of TTX, the mean spontaneous EPSC frequency in vitro (4.0 ± 0.9 Hz) was substantially lower than in vivo (18.2 ± 2.0 Hz). On average, the frequency in vivo was 4.5-times higher than that in vitro in the same type of neuron. Although slight differences in experimental conditions cannot be excluded, our results suggest that dentate gyrus granule cells are exposed to a markedly stronger excitatory synaptic activity in the intact network than in the acute slice preparation.

Figure 8.

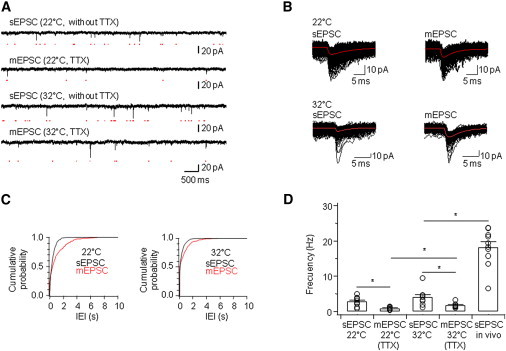
Frequency of EPSCs is higher in vivo than in vitro under comparable conditions. (A) Example traces of spontaneous EPSCs (sEPSC) and miniature EPSCs (mEPSCs) recorded in vitro in hippocampal slices at 22 and 32°C in the absence or presence of TTX to block presynaptic action potential activity. Detected events are indicated with red dots. Traces without and with TTX were obtained from the same cells, respectively. (B) All detected events during 5 min of recording in the experiments illustrated in A. Red trace indicates the average EPSCs. (C) IEI cumulative probability distribution of the sEPSC (black) and mEPSC (red) shown in A and B. (D) Summary bar graph of average EPSCs frequency in different experimental conditions in vitro: mEPSC and sEPSC in slices at 22 and 32°C, in presence (n = 10) or absence (n = 8) of TTX. The average frequency of EPSCs in vivo is shown on the right for comparison (n = 10). P < 0.05 (^∗).

Discussion

Although recording of spontaneous synaptic events is often easier than that of evoked PSCs, the reverse is true for the analysis of these events. In this work, we report a, to our knowledge, new method for detecting spontaneous PSCs based on deconvolution. This method is superior to derivative methods, because it exploits information about both rise and decay phases of synaptic events, whereas derivative methods only take into account information about rise. Furthermore, deconvolution is better than template matching algorithms, because its temporal resolution is not limited (e.g., by template length) and individual superimposed events are correctly assigned. Exploiting the high temporal resolution of the method, we show that in hippocampal granule cells the frequency of EPSCs is ∼4.5-fold higher in vivo than in vitro under comparable conditions.

Advantages of deconvolution-based detection

In comparison to previous methods, the deconvolution-based detection method offers several advantages. First, the deconvolution-based method increases the SNR. The extent of increase depends on the kinetic properties of the PSCs and the characteristics of noise. If the kinetics of PSCs is uniform, the template fits precisely, and the spectral characteristics of PSCs are well separated from that of the baseline noise, the gain in SNR is substantial.

Second, the deconvolution-based detection method has a high temporal resolution, allowing detection of high-frequency bursts of events, as often occurring in vivo. If the kinetics of PSCs is uniform, and the template fits precisely, the temporal resolution of the deconvolution method is unique. In contrast, for template fit methods, the temporal resolution is limited by the total duration of the template used for analysis (10–12).

Third, the target FP event rate can be chosen easily. Both the baseline noise and the derived deconvolution signal are well described by normal distributions. Thus, if the threshold is set in units relative to the standard deviation of the Gaussian function, the threshold value directly translates into a corresponding FP event rate. Although this targeted FP event rate is only an approximation, setting the rate is more reliable than in the other detection methods where the distribution of points of the detector trace differs from a normal distribution.

These theoretical advantages translate into major practical improvements. Comparison of the deconvolution-based method with the derivative-based method revealed that the deconvolution-based method was consistently superior under both in vitro and in vivo conditions. Furthermore, comparison of the deconvolution-based method with the template fit method indicated that the deconvolution-based method was comparable under in vitro conditions, but consistently superior for in vivo data sets (Fig. 7 D).

How is it possible that the deconvolution-based technique can increase the SNR? Intuitively, the deconvolution technique can be seen as a filter with highly specific properties (36). It selectively passes signals with characteristic frequencies corresponding to the rise and decay time course of PSCs, whereas other frequencies are largely blanked. Thus, if the template precisely fits the experimental PSCs, and the spectral characteristics of signal and noise are well separated, the result of deconvolution is a Dirac delta function, leading to an SNR approaching infinity.

Further applications

We used the deconvolution-based detection technique for the analysis of miniature EPSCs in vitro and spontaneous EPSCs in vivo. However, several additional applications are conceivable. For example, the deconvolution-based method will be suitable for the analysis of asynchronous release following a single action potential or trains of APs (17,37). Furthermore, the deconvolution-based method will be useful for the analysis of miniature PSCs in the presence of factors increasing release frequency, such as hyperosmotic solution (38) or α-latrotoxin (39). Finally, the deconvolution-based method could be used for the analysis of postsynaptic conductances underlying rhythmic activity and network oscillations in vivo (5,6,40).

Biological significance

The deconvolution-based detection method allowed us to examine the IEI distribution of EPSCs recorded in dentate gyrus granule cells in vitro and in vivo. In both conditions, the IEI distributions were not monoexponential, but were better described by a fast and a slow exponential component. Thus, spontaneous exocytosis events occur in bursts. This suggests that the generation of miniature and spontaneous EPSCs is not driven by a homogenous Poisson process, but is mechanistically more complex. Bursting may be explained by positive cooperativity between fusion events of individual synaptic vesicles. Alternatively, temporal fluctuations in intracellular Ca²⁺ concentration in presynaptic terminals could be responsible.

The deconvolution-based approach also allowed us to compare the frequency of EPSCs in dentate gyrus granule cells in the in vitro and in vivo preparations. Our results show that the frequency of both miniature EPSCs and spontaneous EPSCs in vitro increases with temperature, with a Q10 of ∼1.4 (see 34,35), and that a major fraction of spontaneous EPSCs in vitro (∼60%) is dependent on presynaptic APs. However, even if the experimental conditions are assimilated, the frequency of spontaneous EPSCs is ∼fivefold lower under in vitro than in vivo conditions. This may be explained by the larger number of intact afferent glutamatergic inputs in the in vivo than the in vitro preparations.

Synaptic noise has substantial effects on information processing in cortical microcircuits. Such a form of noise may trigger APs in fluctuation driven regimes (41,42). Synaptic noise may be of particular relevance for action potential initiation in hippocampal granule cells, which have a highly negative membrane potential in comparison to other cell types. Thus, the high-frequency generation of EPSCs may define time windows of excitability in granule cells, allowing the representation of information by sparse coding in the dentate gyrus.