Deriving dispersional and scaled windowed variance analyses using the correlation function of discrete fractional Gaussian noise

Abstract

Methods for estimating the fractal dimension, D, or the related Hurst coefficient, H, for a one-dimensional fractal series include Hurst’s method of rescaled range analysis, spectral analysis, dispersional analysis, and scaled windowed variance analysis (which is related to detrended fluctuation analysis). Dispersional analysis estimates H by using the variance of the grouped means of discrete fractional Gaussian noise series (DfGn). Scaled windowed variance analysis estimates H using the mean of grouped variances of discrete fractional Brownian motion (DfBm) series. Both dispersional analysis and scaled windowed variance analysis have small bias and variance in their estimates of the Hurst coefficient. This study demonstrates that both methods derive their accuracy from their strict mathematical relationship to the expected value of the correlation function of DfGn. The expected values of the variance of the grouped means for dispersional analysis on DfGn and the mean of the grouped variance for scaled windowed variance analysis on DfBm are calculated. An improved formulation for scaled windowed variance analysis is given. The expected values using these analyses on the wrong kind of series (dispersional analysis on DfBm and scaled windowed variance analysis on DfGn) are also calculated.

1. Introduction

Davies and Harte [1] presented a method (DHM) for generating one-dimensional discrete fractional Gaussian noise (DfGn) series which preserve the desired correlation structure among the elements of the series. DfGn series are completely specified by two parameters, σ², the variance of the series, and H, the Hurst coefficient, which is related to the fractal dimension, D, by H = 2 − D. DHM extended to higher dimensions by [2] gives the expected value of the correlation function, r(τ), between elements with separation τ as r(τ) = (σ²/2)(|τ − 1|^2H − 2|τ|^2H + |τ + 1|^2H) [3–5]. Other generating methods, which were developed earlier, such as spectral synthesis and successive random addition [6], do not preserve the expected value of the correlation function. DHM generated series have been used as a reference standard for DfGn signals in subsequent research. Caccia et al. [7] showed that a method developed by [8], dispersional analysis, was preferable to the classic method of analysis presented by [9], having less bias and variance in the estimate of H for any given series length.

The values of a discrete fractional Brownian motion (DfBm) are the cumulative sums of a DfGn. The Hurst coefficient characterizes the increments, differences between adjacent elements, of a DfBm. Cannon et al. [10] tested three variants of scaled windowed variance methods, one of which is basically the same as the detrended fluctuation analysis of [11] and found the simple, undetrended method to have the least bias and variance in estimates of the Hurst coefficient. The evaluation studies of [7] and [10] suggested that these methods gave better estimates of the Hurst coefficient than did standard Fourier spectral analysis. The Fourier analysis is based on the idea of self-similarity of the power spectral density function, which varies as 1/f^β, where f is the frequency. In general, for DfGn, the relationship between the power-law exponent β and the Hurst coefficient H is β = 2H − 1. Signals with β <0 or H <1/2 are “blue” noises with increasing power at high frequencies and negative correlation between neighboring series elements. Signals with β = 0 or H = 0.5 are “white” noise with uncorrelated elements. Signals with 0 <β <1 or H >0.5 are “red” noises with positive correlation between neighboring elements. For 1 <β <3, β = 2H + 1 in accordance with the generality for continuous systems, that is, that the power slope increases by two when the signal is integrated. However, these power law perspectives are only approximate and hold only for low frequencies [5]. The reality is that continuous systems which exhibit power-law behavior are different from their discretely sampled realizations. The only discretely sampled fractional series which exhibits power law behavior over all sampled frequencies is white noise. The high-frequency behavior of discrete fractional time series deviates markedly from simple power-law behavior.

The messages derived from these ideas are: (1) if an exact fractional series (either a DfGn or dfBm) is an appropriate model for a given time series, then power spectral analysis is inappropriate, and (2) methods specifically suited to exact fractals should be used to estimate the Hurst coefficient. Having found that dispersional analysis is particularly suited for DfGn and scaled windowed variance is likewise suitable for DfBm, we demonstrate that the strength of both is their basic relationship to the correlation structure of exact fractal signals. Thus this is not merely an academic point, but one of practical importance.

2. Deriving dispersional analysis using the correlation function for DfGn

Define the DfGn series X = {X_i, i = 1, …, N}. Let N be exactly divisible by m and E[X] = 0 (series has zero mean) and E[X_jX_k] = (σ²/2)(|k − j − 1|^2H − 2|k − j|^2H + |k − j + 1|^2H) is the expected value of the correlation function for DfGn [6], where σ² = var[X], and H is the Hurst coefficient. We also define the expected value alternatively as r(τ) = (σ²/2)(|τ − 1|^2H − 2|τ|^2H + |τ + 1|^2H) where τ = k − j.

Define the estimated sample variance of the noise series as

$${SD}_1^2=\sum _{i=1}^N{X}_i^2/N,$$ (1a)

where the subscript 1 on SD₁ indicates a window of length m = 1.

Normally, the sum of the squares is normalized by N − 1, but this would be incorrect if the expected value of the series is zero and the estimated mean is not subtracted from each element of the series before it is squared. Explicitly, we have the expected variance of the original series,

$$E[{SD}_1^2]=E\left[\sum _{i=1}^N{X}_i^2/N\right]=\sum _{i=1}^{N}E[X_i{X}_i]/N=N{\sigma }^2/N={\sigma }^2.$$ (1b)

The estimated sample variance over windows of size m is given as

$${SD}_m^2=\sum _{i=1}^{N/m}{\left(\sum _{j=1}^m\frac{X_{m(i-1)+j}}{m}\right)}^2/(N/m).$$ (1c)

This can be rearranged as

$$mN·{SD}_m^2=\sum _{i=1}^{N/m}{\left(\sum _{j=1}^m{X}_{m(i-1)+j}\right)}^2,$$ (1d)

and expanded to yield

$$mN·{SD}_m^2=\sum _{i=1}^{N/m}\left(\sum _{j=1}^m\left(\sum _{k=1}^m{X}_{m(i-1)+j}·X_{m(i-1)+k}\right)\right),$$ (1e)

which separates into a sum of squares term and cross terms:

$$mN·{SD}_m^2=\sum _{i=1}^{N/m}\sum _{j=1}^m{X}_{m(i-1)+j}^2+2\sum _{i=1}^{N/m}\left(\sum _{j=1}^{m-1}\left(\sum _{k=j+1}^m{X}_{m(i-1)+j}·X_{m(i-1)+k}\right)\right).$$ (1f)

The sum of squares terms can be simplified as can the cross terms:

$$mN·{SD}_m^2=\sum _{i=1}^N{X}_i^2+2\sum _{i=1}^{N/m}\left(\sum _{j=1}^{m-1}\left(\sum _{k=1}^{m-j}{X}_{m(i-1)+j}·X_{m(i-1)+j+k}\right)\right).$$ (1g)

Taking the expected value of each side yields

$$E[mN·{SD}_m^2]=N{\sigma }^2+2\sum _{i=1}^{N/m}\left(\sum _{j=1}^{m-1}\left(\sum _{k=1}^{m-j}E[X_{m(i-1)+j}·X_{m(i-1)+j+k}]\right)\right).$$ (1h)

This can be rewritten as

$$\begin{array}{l}mN·E[{SD}_m^2]=N{\sigma }^2+2\sum _{i=1}^{N/m}\left(\sum _{j=1}^{m-1}\left(\sum _{k=1}^{m-j}r(k)\right)\right)\\ =N{\sigma }^2+2\frac{N}{m}\sum _{s=1}^{m-1}(m-s)r(s).\end{array}$$ (1i)

Substituting for r(s) yields

$$mN·E[{SD}_m^2]=N{\sigma }^2+2\frac{N}{m}\sum _{s=1}^{m-1}(m-s)\left(\frac{{\sigma }^2}{2}\right)(\mid s-1{\mid }^{2H}-2\mid s{\mid }^{2H}+\mid s+1{\mid }^{2H}),$$ (1j)

which simplifies to

$$mN·E[{SD}_m^2]=N{\sigma }^2\left(1+\sum _{s=1}^{m-1}\left(\frac{(m-s)}{m}\right)(\mid s-1{\mid }^{2H}-2\mid s{\mid }^{2H}+\mid s+1{\mid }^{2H})\right).$$ (1k)

This in turn becomes by summing and rearranging

$$E[{SD}_m^2]={\sigma }^2{m}^{2H-2}.$$ (1l)

Dividing by the expected value of the variance computed over windows of size n gives

$$\frac{E[{SD}_m^2]}{E[{SD}_n^2]}={\left(\frac{m}{n}\right)}^{2H-2}.$$ (1m)

Usually, the expected values are left off the formula and the square root is taken on both sides to give the dispersional relationship in the form used by [8]

$${SD}_m={SD}_n·{\left(\frac{m}{n}\right)}^{H-1}={SD}_n·{\left(\frac{m}{n}\right)}^{1-D},$$ (1n)

where D is the fractal dimension for the one-dimensional series.

Thus, the dispersional relationship is a statement about the ratio of expected values of variances rather than the ratio of estimated values of standard deviations, as is commonly assumed.

In Eq. (1c), not all the terms of the estimated correlation calculation are present. For example, in the case m=2, the first lag of the calculated correlation function represents the sum of half the terms in the usually estimated correlation function, i.e., X₁X₂ +X₃X₄ +X₅X₆ +··· instead of X₁X₂ +X₂X₃ +X₃X₄ +···. Caccia et al. (1997) showed that using all possible overlapping windows instead of non-overlapping windows improves the calculation of H using dispersional analysis. Rederiving dispersional analysis using all possible overlapping windows shows that the estimated correlation function contains all of the possible cross terms of the m− 1 lags, but with linearly tapering weights for the calculations over the first and last windows.

3. Deriving scaled windowed variance analysis for DfBm using the correlation function for DfGm

The scaled windowed variance methods explored by [10] are variants of detrended fluctuation analysis developed by [11]. Here we relate the basic method without any trend corrections to the expected fractal correlation value. We add an additional definition to those given in the first paragraph of Section 2 for deriving dispersional analysis. Define the motion series B = {B_k, k = 1,…, N where $B_k={\sum }_{i=1}^k{X}_i$}.

Next, we derive the scaled windowed variance relationship expressed in terms of the expected value of the correlation function. Define the estimated averaged variance of the motion series over windows of size m as

$$\overline{{SD}_m^2}=\frac{1}{(N/m)}\sum _{k=1}^{N/m}\left(\sum _{j=1}^m{(B_{m(k-1)+j}-\overline{B_{m(k-1)+1,mk}})}^2/(m-1)\right),$$ (2a)

where the average value of the motion series inside the window from m(k − 1) + 1 to mk is given by

$$\overline{B_{m(k-1)+1,mk}}=\sum _{k=m(k-1)+1}^{mk}{B}_k/m=\sum _{k=m(k-1)+1}^{mk}\left(\sum _{i=1}^k{X}_i/m\right),$$ (2b)

or by compressing the double summation into two single summations, as

$$\overline{B_{m(k-1)+1,mk}}=\sum _{i=1}^{m(k-1)+1}{X}_i+\sum _{i=m(k-1)+2}^{mk}{X}_i·\left(\frac{mk-i+1}{m}\right).$$ (2c)

Substituting the sums of noise terms for the motion terms yields

$$\overline{{SD}_m^2}=\frac{m}{N}·\sum _{k=1}^{N/m}\times \frac{\{{\sum }_{j=1}^m{([{\sum }_{i=1}^{m(k-1)+j}{X}_i]-[{\sum }_{i=1}^{m(k-1)+1}{X}_i+{\sum }_{i=m(k-1)+2}^{mk}{X}_i·(\frac{mk-i+1}{m})])}^2\}}{(m-1)},$$ (2d)

and simplifies to

$$\overline{{SD}_m^2}=\frac{m}{N}·\sum _{k=1}^{N/m}\left(\sum _{j=2}^m\left(\sum _{i=2}^j\frac{(m+1-j)2(i-1)}{(m-1)m(1+{\delta }_{i,j})}·X_{m(k-1)+j}·X_{m(k-1)+i}\right)\right)$$ (2e)

(see Appendix A), where δ_{i, j} = 1 if i = j, and δ_{i, j} = 0 otherwise. We note that the variance in each window (k = 1, k = 2, etc.) is dependent on only the associated noise values for the same window even though the variance is calculated on the cumulative sum of the noise values because of the subtraction of the mean in each window. We now take the expected value of this expression to yield

$$E[\overline{{SD}_m^2}]=\frac{m}{N}·\sum _{k=1}^{N/m}\left(\sum _{j=2}^m\left(\sum _{i=2}^j\frac{(m+1-j)2(i-1)}{(m-1)m(1+{\delta }_{i,j})}·E[X_{m(k-1)+j}·X_{m(k-1)+i}]\right)\right).$$ (2f)

Substituting

$$E[X_{m(k-1)+j}·X_{m(k-1)+i}]=({\sigma }^2/2)(\mid i-j-1{\mid }^{2H}-2\mid i-j{\mid }^{2H}+\mid i-j+1{\mid }^{2H}),$$ (2g)

Eq. (2f) simplifies to

$$E[\overline{{SD}_m^2}]=\left(\frac{{\sigma }^2}{2}\right)\sum _{j=2}^m\times \left(\sum _{i=2}^j\frac{(m+1-j)2(i-1)}{(m-1)m(1+{\delta }_{i,j})}·(\mid i-j-1{\mid }^{2H}-2\mid i-j{\mid }^{2H}+\mid i-j+1{\mid }^{2H})\right).$$ (2h)

This expression can be simplified by writing the elements of the summation as a lower triangular matrix where j indexes the rows and i indexes the columns and then summing each diagonal separately from upper left to lower right. Designating the main diagonal s = 0, and each subsequent off diagonal as s = 1, s = 2,…,s = m − 2, there is a common closed expression for each diagonal, and summing over the common closed expression for each diagonal, we are able to write

$$E[\overline{{SD}_m^2}]=\left(\frac{{\sigma }^2}{2}\right)\sum _{s=0}^{m-2}\times \frac{(2-{\delta }_s)(m-s)(m-1-s)(m+1-s)}{6m(m-1)}(\mid s-1{\mid }^{2H}-2\mid s{\mid }^{2H}+\mid s+1{\mid }^{2H}),$$ (2i)

where δ_s = 1 when s = 0 and δ_s = 0 otherwise.

This reduces to

$$E[\overline{{SD}_m^2}]=\left(\frac{{\sigma }^2}{2}\right)\left(\sum _{s=1}^m\frac{2(m-s)·s^{2H}}{m(m-1)}\right).$$ (2j)

This can be approximated by the integral,

$$\widehat{E}[\overline{{SD}_m^2}]=\frac{{\sigma }^2}{2}{\int }_0^m\frac{2(m-s)s^{2H}}{m(m-1)}ds=\frac{{\sigma }^2}{2}\left(\frac{m^{2H+1}}{(m-1)(H+1)(2H+1)}\right),$$ (2k)

where Ê is used for the approximated expected value. For large m, this simplifies to

$$\widehat{E}[\overline{{SD}_m^2}]=\frac{{\sigma }^2}{2}·\frac{m^{2H}}{(2H+1)(H+1)}.$$ (2l)

The scaled windowed variance relationship for motion series is seen to hold,

$$\widehat{E}[\overline{{SD}_m^2}]/\widehat{E}[\overline{{SD}_n^2}]={\left(\frac{m}{n}\right)}^{2H}.$$ (2m)

Like dispersional analysis, the scaled windowed variance relationship is written usually with the expected value notations (or in this case, the approximate expected value notations) removed, and the square root is taken on both sides and expressed as

$$\overline{{SD}_m}/\overline{{SD}_n}={\left(\frac{m}{n}\right)}^H.$$ (2n)

It should be kept in mind that the scaled windowed variance relationship is a statement about the ratio of approximated expected values of the averaged variances rather than the ratio of estimated values of averaged standard deviations. It would be interesting to explore the possibility of using Eq. (2j) as a model for scaled windowed variance analysis instead of Eq. (2m), especially for short series of length less than 1024 points.

Finally, we determine over what range of m and H the approximate expected value, $\widehat{E}[\overline{{SD}_m^2}]$, in Eq. (2l) represents the formal expected value, $E[\overline{{SD}_m^2}]$, in Eq. (2j). We compute the percent difference between the expected averaged variance (Eq. (2j)) and the approximated expected averaged variance (Eq. (2k)) as a function of the window size, m. The values are plotted in Fig. 1 for H = 0.1 (solid diamonds) and H = 0.9 (open circles) to cover a range of values. For that range of Hurst coefficients, a window size greater than 16 gives approximations to within 3% of the correct expected values. Clearly, the approximate values are quite good when the window size is greater than 16. This supports the conclusion of [10], that in calculating the Hurst coefficient using Eq. (2n), the values from the smallest windows should be excluded.

Fig. 1.

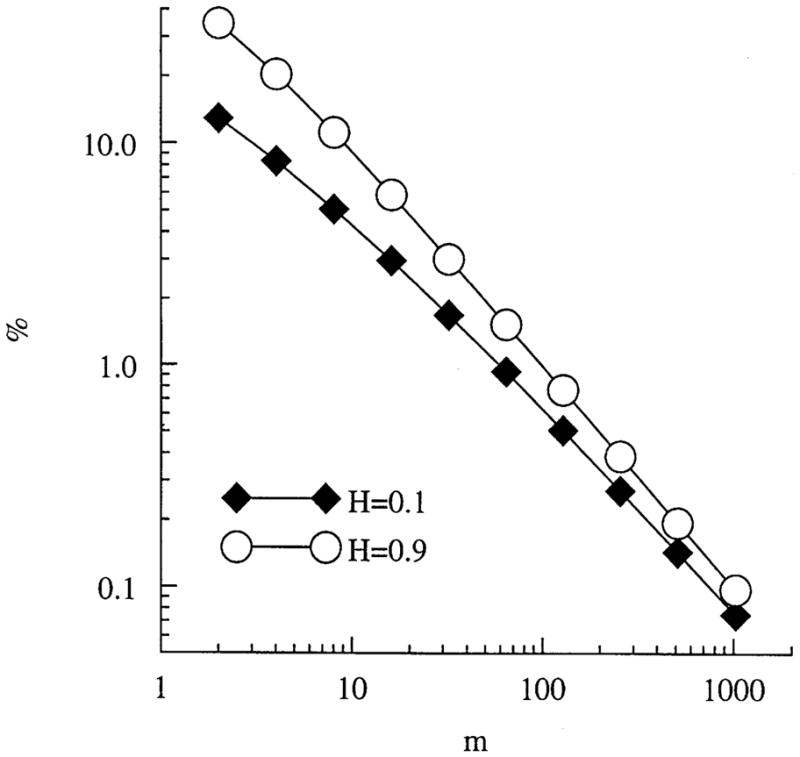
Accuracy of the standard approximate scaled windowed variance relationship for DfBm. The percent difference between the expected value of the averaged variance (Eq. (2j)) and the approximate expected value of the averaged variance (Eq. (2k)), is plotted as a function of window size, m, and H.

4. Results of misapplying dispersional analysis to DfBm

When dispersional analysis is mistakenly applied to DfBm, it yields highly biased estimates for the Hurst coefficient. The estimates of H are all near 1.0 for DfBm of all H’s. To show why this happens we derive the expected value of the sample variance over windows of size m when the series is a DfBm.

We use the same definitions given at the beginning of Sections 2 and 3. The estimated sample variance over windows of size m is now defined as

$${SD}_m^2=\sum _{i=1}^{N/m}{\left(\sum _{j=1}^m\frac{B_{m(i-1)+j}}{m}\right)}^2/(N/m),$$ (3a)

where B_m(i−1)+j, the elements of a motion series, have replaced X_m(i−1)+j, the elements of a noise series, in Eq. (1c).

This can be expanded to

$${SD}_m^2=\frac{m}{N}·\sum _{i=1}^{N/m}\left(\sum _{j=1}^m\left(\sum _{k=1}^m\left(\sum _{i1=1}^{m(i-1)+j}\left(\sum _{i2=1}^{m(i-1)+k}\frac{X_{i1}{X}_{i2}}{m^2}\right)\right)\right)\right).$$ (3b)

Taking the expected value of both sides and substituting E[X_i1X_i2] = r(i1 − i2), we have, without going into the tedious details,

$$E[{SD}_m^2]={\sigma }^2·\left(\frac{1}{N}·\sum _{i=1}^N{i}^{2H}-\frac{1}{m^2}\sum _{i=1}^m(m-i)·i^{2H}\right).$$ (3c)

This can be approximated by substituting integrals for the summations, and yields

$$\begin{array}{l}\widehat{E}{[{SD}_m^2]}_{\text{DfBm}}={\sigma }^2·\left(\frac{1}{N}·{\int }_0^N{x}^{2H}dx-\frac{1}{m^2}{\int }_0^m(m-x)x^{2H}dx\right)\\ ={\sigma }^2·\frac{((2H+2)N^{2H}-m^{2H})}{(2H+2)(2H+1)}.\end{array}$$ (3d)

The dominant term is (2H + 2) · N^2H, which always exceeds m^2H. On a plot of the logarithm of the approximated expected value of the variance versus the logarithm of m, the slope is almost flat. Assuming incorrectly that the signal is a DfGn, using dispersional analysis forces the estimated Hurst coefficient to be near 1 for all H’s. Given the almost total lack of dependence of the expected value of the variance on the window size, even having the correct expression for the expected value of the variance of the grouped means for DfBm does not make it feasible to estimate H using dispersional analysis on DfBm series.

5. Results of misapplying scaled windowed variance analysis to DfGn

Like applying dispersional analysis to DfBm, applying scaled windowed variance analysis to DfGn series gives biased estimates for the Hurst coefficient. The estimates of H are all close to zero no matter the actual value of H. The derivation of the expected value of the averaged variance from scaled windowed variance analysis of a DfGn series follows. The result contrasts with Section 3.

We use the same definitions given at the beginning of Sections 2 and 3. Define the estimated averaged variance of the noise series over windows of size m as

$$\overline{{SD}_m^2}=\frac{1}{(N/m)}\sum _{k=1}^{N/m}\left(\sum _{j=1}^m{\left(X_{m(k-1)+j}-(1/m)\sum _{i=1}^m{X}_{m(k-1)+i}\right)}^2/(m-1)\right),$$ (4a)

where X_m(i−1)+j, the elements of a noise series, have replaced B_m(i−1)+j, the elements of a motion series, in Eq. (2a).

This expands to the following three terms,

$$\overline{{SD}_m^2}=\frac{m}{N(m-1)}\sum _{k=1}^{N/m}\sum _{j=1}^m(X_{m(k-1)+j}·X_{m(k-1)+j})+\frac{m}{N(m-1)}\sum _{k=1}^{N/m}\sum _{j=1}^m-(2/m)·\sum _{i=1}^m(X_{m(k-1)+i}·X_{m(k-1)+j})+\frac{m}{N(m-1)m^2}\sum _{k=1}^{N/m}\sum _{j=1}^m\sum _{i=1}^m\sum _{l=1}^m{X}_{m(k-1)+i}·X_{m(k-1)+l}.$$ (4b)

Taking the expected value of both sides, this reduces to

$$E[\overline{{SD}_m^2}]=\frac{m}{N(m-1)}\left(\left(\frac{N}{m}\right)m{\sigma }^2+\left(\frac{N}{m}\right)·\left(-\frac{2}{m}\right)\sum _{j=1}^m\sum _{i=1}^{m}r(i-j)+\left(\frac{N}{m}\right)\frac{m}{m^2}\sum _{j=1}^m\sum _{i=1}^{m}r(i-j)\right).$$ (4c)

This simplifies to

$$E[\overline{{SD}_m^2}]=\frac{m}{N(m-1)}·\left(\left(\frac{N}{m}\right)m{\sigma }^2+\left(\left(\frac{N}{m}\right)·\left(-\frac{2}{m}\right)+\left(\frac{N}{m}\right)·\left(\frac{1}{m}\right)\right)\sum _{j=1}^m\sum _{i=1}^{m}r(i-j)\right).$$ (4d)

and since

$$\sum _{j=1}^m\sum _{i=1}^{m}r(i-j)={\sigma }^2{m}^{2H}$$ (4e)

finally reduces to

$$E{[\overline{{SD}_m^2}]}_{\text{DfGn}}={\sigma }^2·\left(\frac{m-m^{2H-1}}{m-1}\right).$$ (4f)

The expected value of the averaged variance for a noise series depends weakly on H being <σ² for $H>\frac{1}{2}$ and >σ² for $H<\frac{1}{2}$. For increasing m, it asymptotically approaches the value of σ² very quickly. For white noise, it is exactly the variance. If we wrongly assume the form for the expected value of the averaged variance for DfBm from scaled windowed variance analysis, we would get a zero slope and would estimate H to be zero. Given the weak dependence of Eq. (4f) on H, it does not appear feasible to estimate H using scaled windowed variance on a DfGn even if one uses the correct form of the expected value of the averaged variance.

6. Summary and discussion

We have shown that dispersional analysis and scaled windowed variance analysis can be derived by using the expected value of the correlation function for DfGn. These methods of analysis have been shown by others [10, 7] to do exceptionally well when applied to series generated using the Davies–Harte method which is based on the same correlation function. These methods of analysis are correct for DfGn and DfBm because the “model” analysis is based on the same model as the signal generator, a point which cannot be emphasized too strongly.

Eq. (2j) suggests a new model for scaled windowed variance analysis that makes use of smaller windows and may be suitable and more successful for short series than the approximate result, Eq. (2m), now in general use [11, 10].

The failure of estimating the Hurst coefficient by using dispersional analysis on DfBm and scaled windowed variance analysis on DfGn derives from assuming incorrect relationships between the Hurst coefficients and the estimated variances from those analyses. The correct forms of those relationships are weak functions of the Hurst coefficient, H, and window size, m, and most likely are unsuitable for obtaining estimates of the Hurst coefficient.

Finally, for processes which depend on H but are not DfGn and DfBm, it would be useful to calculate the expected value of the values generated by the models used to estimate their Hurst coefficients.

Appendix A. Proof of simplifying Eqs. (2d)–(2e) in Section 2

Prove

$$\sum _{k=1}^{N/m}\left\{\sum _{j=1}^m{\left(\left[\sum _{i=1}^{m(k-1)+1}{X}_i+\sum _{i=m(k-1)+2}^{mk}{X}_i·\left(\frac{mk-i+1}{m}\right)\right]-\left[\sum _{i=1}^{m(k-1)+j}{X}_i\right]\right)}^2\right\}=\sum _{k=1}^{N/m}\left\{\sum _{j=2}^m\left(\sum _{i=2}^j\frac{(2-{\delta }_{i,j})(m+1-j)(i-1)}{m}·X_{m(k-1)+j}·X_{m(k-1)+i}\right)\right\},$$ (A.1)

where δ_{i, j} = 1 if i = j, and δ_{i, j} = 0 otherwise. The left-hand side of Eq. (A.1) is the right-hand side of Eq. (2d) and the right-hand side of Eq. (A.1) is the left-hand side of Eq. (2e) with (2 − δi, j) replacing 2/(1 + δi, j), the signs inside the squared term reversed for convenience and extraneous coefficients removed, i.e. ((m/N)/(m − 1)). Without loss of generality, let k = 1. Then

$$\sum _{j=1}^m{\left(X_1+\left[\sum _{i=2}^m{X}_i·\left(\frac{m-i+1}{m}\right)\right]-\left[\sum _{i=1}^j{X}_i\right]\right)}^2=\sum _{j=1}^m{\left(\left[\sum _{i=1}^m{X}_i·\left(\frac{m-i+1}{m}\right)\right]-\left[\sum _{i=1}^j{X}_i\right]\right)}^2,$$ (A.2)

which expands to the following four terms:

$$=\sum _{j=1}^m\left(\left[\sum _{i=1}^m{X}_i·\left(\frac{m-i+1}{m}\right)\right]\left[\sum _{s=1}^m{X}_s·\left(\frac{m-s+1}{m}\right)\right]\right),$$ (A.3a)

$$-\sum _{j=1}^m\left(\left[\sum _{i=1}^m{X}_i·\left(\frac{m-i+1}{m}\right)\right]\left[\sum _{s=1}^j{X}_s\right]\right),$$ (A.3b)

$$-\sum _{j=1}^m\left(\left[\sum _{i=1}^j{X}_i\right]\left[\sum _{s=1}^m{X}_s·\left(\frac{m-s+1}{m}\right)\right]\right),$$ (A.3c)

$$+\sum _{j=1}^m\left(\left[\sum _{i=1}^j{X}_i\right]\left[\sum _{s=1}^j{X}_s\right]\right).$$ (A.3d)

Consider the term (A.3a). The outer summation is over j which occurs nowhere else in the term. Hence the outer summation may be replaced by multiplying by m. Substitute j for the index i, and i for the index s to rewrite the terms as

$$\sum _{j=1}^m\sum _{i=1}^m{X}_i{X}_j\left(\frac{m-j+1}{m}\right)(m-i+1)=\sum _{j=1}^m\sum _{i=1}^j{X}_i{X}_j(2-{\delta }_{ij})\left(\frac{m-j+1}{m}\right)(m-i+1).$$ (A.4)

Consider the terms (A.3b) and (A.3c) which are the same after the s and i indices are interchanged, and can be combined to yield

$$-2\sum _{j=1}^m\left(\left[\sum _{i=1}^j{X}_i\right]\left[\sum _{s=1}^m{X}_s·\left(\frac{m-s+1}{m}\right)\right]\right).$$ (A.5a)

The two leftmost summations can be condensed to yield

$$-2\sum _{j=1}^m{X}_j(m-j+1)\left[\sum _{s=1}^m{X}_s·\left(\frac{m-s+1}{m}\right)\right],$$ (A.5b)

and by substitution of indices become

$$-2\sum _{j=1}^m\sum _{i=1}^j{X}_j(m-j+1)(2-{\delta }_{ij})X_i\left(\frac{m-i+1}{m}\right).$$ (A.5c)

Term (A.3d) becomes

$$\sum _{j=1}^m\sum _{i=1}^j{X}_i{X}_j(2-{\delta }_{ij})(m-j+1).$$ (A.6)

Combining terms (A.4), (A.5c), and (A.6) completes the proof.