Analysis of overdispersed count data: application to the Human Papillomavirus Infection in Men (HIM) Study

SUMMARY

The Poisson model can be applied to the count of events occurring within a specific time period. The main feature of the Poisson model is the assumption that the mean and variance of the count data are equal. However, this equal mean-variance relationship rarely occurs in observational data. In most cases, the observed variance is larger than the assumed variance, which is called overdispersion. Further, when the observed data involve excessive zero counts, the problem of overdispersion results in underestimating the variance of the estimated parameter, and thus produces a misleading conclusion. We illustrated the use of four models for overdispersed count data that may be attributed to excessive zeros. These are Poisson, negative binomial, zero-inflated Poisson and zero-inflated negative binomial models. The example data in this article deal with the number of incidents involving human papillomavirus infection. The four models resulted in differing statistical inferences. The Poisson model, which is widely used in epidemiology research, underestimated the standard errors and overstated the significance of some covariates.

INTRODUCTION

Count data occur in many fields, including public health, medicine and epidemiology. A few common examples are the number of deaths, number of cigarettes smoked, and number of disease cases. For such count data the Poisson model is a commonly applied statistical model. A key feature of the Poisson model is that the mean and the variance are equal. However, this equal mean-variance relationship rarely happens with real-life data [1–4]. In most cases, the observed variance is larger than the assumed variance, which is known as overdispersion^†. If the overdispersion is ignored, statistical inference results in an inaccurate conclusion by underestimating the variability of the data [1].

Departures from a Poisson model can occur in a variety of ways; the main reasons are: (1) some covariates may be omitted and/or may not have a uniform effect on all subjects so that population heterogeneity has not been accounted for, and (2) an excess number of zero events occurred compared to the Poisson distribution [6, 7]. For the excessive zeros situation, it could be assumed that a sample is collected from two different sub-populations ; one population always produces zero, or no event, while the other behaves like a Poisson distribution.

This issue of overdispersion with excessive zeros clearly exists in a dataset we recently analysed. The Human Papillomavirus Infection in Men (HIM) Study established a prospective cohort of men in three countries to determine the incidence of genital human papillomavirus (HPV) infections. A HPV incidence rate, along with the exact 95% confidence interval, was estimated based on a Poisson distribution. However, inspection of the data revealed severe over-dispersion, as well as a very large proportion of zero counts for specific HPV-type infections. (For more details about the HIM Study see the papers by Giuliano et al. [8, 9].)

There are two major approaches to adjust for over-dispersion. First, the simplest adjustment approach is to scale the variance of the Poisson distribution by introducing a dispersion parameter and multiplying it to the variance. The other approach is to introduce a new probability distribution to handle the dispersion, such as the negative binomial [10], zero-inflated Poisson (ZIP) [10–12], or zero-inflated negative binomial (ZINB) [10, 13, 14].

A considerable amount of statistical methodology has been developed to deal with overdispersed data arising from excessive zero-count data. Applications for the zero-inflated models can be found in several papers [2, 11, 14–17]. However, using these alternatives to the Poisson model seems to be a relatively new approach among many researchers in applications. This is partly because once a statistical method becomes widely used in published literature, alterations to its usage are slow. This paper attempts to encourage researchers to be clearly aware of the issues surrounding Poisson model usages. In addition, statistical software packages have recently developed a procedure to fit zero-inflated models, and we believe that a follow-up primer is necessary to increase use of the appropriate method.

In this paper, we demonstrate four models for count data: Poisson, negative binomial, ZIP, and ZINB models, all with explanatory factors or confounders. The models were compared in terms of covariate estimates along with their statistical inferences. Akaike’s Information Criterion (AIC) values were used to consider the relative model fitting for the models as a goodness-of-fit statistic. The illustration of the analysis of the example data is mostly conceptual rather than computational. We avoid undue technicalities so that those with a broad range of professional backgrounds will be able to follow the material presented.

METHODS

Four statistical models for count data

Naive Poisson model

The most widely used regression model for count data is the log linear or Poisson model [12]. If we denote µ as the mean of the count data Y, then the variance of the data equals to the mean so that

$$\mu =\mathrm{E}(Y)=\text{Var}(Y),$$

which is a key feature of the Poisson model. We designate this the naive Poisson model hereafter.

Scaled Poisson model

There is a way to account for dispersion with respect to the Poisson model. That is, a dispersion parameter is introduced into the Poisson variance so that the Poisson model is scaled. This method simply gives a correction term for testing the parameter estimates under the Poisson model. Although this approach has been popular, it only produces an appropriate inference if overdispersion is modest [1]. Further, if the data are observed from a population that consists of two subpopulations, this simple correction may not be sufficient to describe the population. The dispersion parameter is estimated by deviance or Pearson’s χ² test statistic divided by its degrees of freedom from the fitted model. If the estimated dispersion is >1, the data may be overdispersed, while a dispersion <1 indicates that the data may be underdispersed, a phenomenon less common in practice. A scaled Poisson model assumes that the variance is

$$\text{Var}(Y)=\varphi \mu .$$

The model is fit in the usual way, and the parameter estimates are not affected by the value of ϕ, but the estimated variance is inflated to adjust for overdispersion.

Negative binomial model

Another popular model for count data is the negative binomial model. The negative binomial model can be derived from the Poisson distribution when the mean parameter is not identical for all members of the population, but itself is distributed with a gamma distribution. This is a way of modelling heterogeneity in a population, and is thus an alternative method to allow for overdispersion in the Poisson model. The relationship between mean and variance for negative binomial distribution has the form

$$\text{Var}(Y)=\mu +k{\mu }^2,$$

where k is the negative binomial dispersion parameter, which can be estimated by maximum likelihood.

Zero-inflated models

Count data that have an incidence of zeros greater than that expected for the underlying probability distribution of counts can be modelled with a zero-inflated distribution. In this case, the population is considered to consist of two types of individuals. The first type involves counts of event in a Poisson or Poisson-like process, which might also contain zeros. The second type always gives a zero count. As a hypothetical example, we consider the processes that could lead to a response variable value of zero, such as the number of STD infections in an individual. At baseline survey, a male subject is likely to be negative for any STDs if he has not had any sexual experiences in the past year as a given specific time period. Another male subject might have a negative on STD even though he has had a single or multiple sexual partners. These two men will have an identical number of STD infections, 0 (the same response), through two different processes. A naive Poisson model would not distinguish between these two processes, but a zero-inflated model allows for and accommodates this complication. When analysing a dataset with an excessive number of outcome zeros, which may have two possible processes that arrive at a zero response, a zero-inflated model needs to be considered.

ZIP model

The ZIP model incorporates excessive zeros by including a proportion of zeros and a proportion from the Poisson distribution, which results in greater variance than the Poisson model. For the ZIP model, the mean and variance are respectively

$$\mu =\mathrm{E}(Y)=\lambda (1-p)\text{ and Var}(Y)=\mu +\left(\frac{p}{1-p}\right){\mu }^2,$$

where p denotes the probability of being an individual having zero count and λ denotes the underlying distribution mean. With exploratory covariates, λ is fitted to a log-linear model (Poisson model) and p can be fitted as a zero probability regression model with a link function, such as logit or probit. The ZIP model allows common explanatory variables to appear in both the Poisson model and the zero-probability regression model.

ZINB model

The ZINB model is based on the negative binomial model, but with a different variance function. As a zero-inflated model like ZIP, the ZINB model generates two separate models and then combines them. First, a logit or probit model is generated for the cases that always produce zeros (zero probability model). Then, a negative binomial model is generated predicting the counts for those subjects who do not always produce zeros. Finally, the two models are combined. The mean and the variance of ZINB are

$$\mu =\mathrm{E}(Y)=\lambda (1-p)\text{ and Var}(Y)=\mu +\left(\frac{p}{1-p}+\frac{k}{1-p}\right){\mu }^2,$$

where p is the zero probability and λ is the underlying distribution mean. In addition, k is the negative binomial dispersion parameter.

RESULTS

The motivating example: description of the HIM Study

HPV, a sexually transmitted infection, causes disease in both men and women, and male-to-female HPV transmission increases the risk of invasive cervical, vaginal, and vulvar cancer in females. In particular, HPV is known to be responsible for nearly 100% of cervical cancers. A prospective HPV cohort study was launched in 2004 to develop a fuller understanding of HPV infection in men. The study was the first international study of the natural history of anogenital HPV infection, enrolling men from the USA, Brazil, and Mexico. A cohort of men, aged 18–70 years, who were examined every 6 months for 4 years, was established. Early analysis results of the study have been reported elsewhere; see Giuliano et al. [8, 9] for a description and report of the study design, the baseline characteristics of the study participants, and HPV prevalence by country and age among cohort members at enrolment.

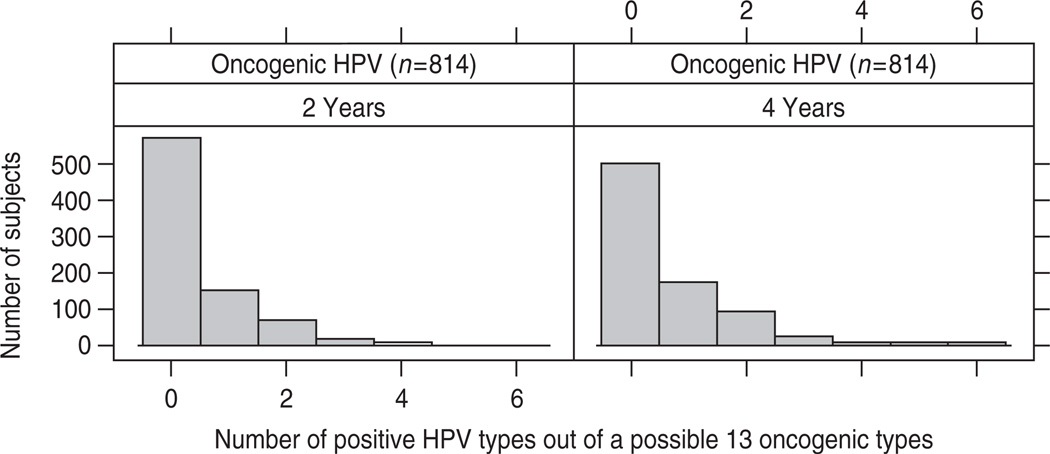
A participant was considered positive for oncogenic HPV if he tested HPV-positive by polymerase chain reaction or by genotyping. The following 13 HPV types were categorized as oncogenic : 16, 18, 31, 33, 35, 39, 45, 51, 52, 56, 58, 59, and 66 (an illustration of the type of data analysed is shown in Fig. 1). Figure 1 illustrates distributions of the total number of infections, out of a possible 13 types, through visit 4 (2 years) and visit 8 (4 years) follow-up periods of the study. For a positive infection, at least one visit must be positive in the given time period. There was a considerable spike of excessive zeros, representing HPV infection-free men. Particularly, in the first 2-year study period the proportion of zero counts (no infection) was very high (70%) and up to 4 years 62% of the cohort had no infection for oncogenic HPV type. The large number of males with zero-value counts is typical for HPV distributions. In this case, the Poisson distribution inappropriately represents the data.

Fig. 1.

Distribution of oncogenic infections for the HIM study through 2 years (four visits) and 4 years (eight visits). HPV, Human papillomavirus.

Analysis of HIM Study data

Oncogenic HPV is defined as the total number of oncogenic types detected in a participant in a given time period. Of the 1159 men at baseline, the 345 who were infected with oncogenic HPV types were excluded from the analysis. The remaining 814 patients who had no oncogenic HPV infection at baseline were available for our analysis of oncogenic HPV. The mean (variance) of the number of oncogenic HPV types was 0·5 (0·7) over 2 years and 0·7 (1·1) over 4 years. The difference between the sample mean and the sample variance implied a deviation from the Poisson model assumption.

HIM Study

In the HIM Study, the scientific question focused on the association between demographic and social behaviour variables with the probability of type-specific HPV infections, as well as the grouped types, such as any HPV types, oncogenic HPV types, and non-oncogenic HPV types. The outcome variable we chose to focus on was the number of oncogenic HPV types infected for eight follow-up visits, and was related to the factors : country (USA=1, Brazil=2, Mexico=3), age (at enrolment in years), number of female partners in the past 6 months (NP), and circumcision status (CS; 1 if circumcised vs. 0 if not circumcised). Smoking (heavy, moderate, mild, nonsmoking) and STD status (yes vs. no) variables were initially tested, but they contributed insignificantly to model, showing that the two variables did not improve the model, and therefore were excluded from the final model. Country and age are design effects for the study, and therefore forced into the multivariable models regardless of significance.

For the Poisson model, a log-linear relationship between the mean (μ) and the covariate factors was specified as

$$\text{log}(\mu )=\text{log}(n)+\text{intercept}+\text{country}+\text{age}+\text{NP}+\text{CS}.$$

The unknown parameters for intercept, country, age, NP and CS were estimated by the genmod procedure in SAS v. 9.2 (SAS institute Inc., USA). The logarithm of n (person’s time in months) was used as an offset (i.e. a regression variable with a constant coefficient of 1 for each subject).

The scaled Poisson model was fitted using the deviance estimate as a dispersion parameter by specifying the scale=deviance option in SAS.

Two zero-inflated models, ZIP and ZINB, were fitted. For the Poisson model and the negative-binomial model components within each of ZIP and ZINB, the intercept and four covariates, country, age, NP and CS, were estimated. The component of the zero-inflated model was specified as

$$\text{log it}(p)=\text{intercept},$$

where p is the probability of being in the zero population. We implemented the models, using the zeromodel statement in the genmod procedure in SAS, in which the ZIP and the ZINB model procedures have been most recently updated.

Table 1 summarizes the results of the Poisson (naive and scaled), negative binomial, ZIP, and ZINB regression models. From the naive Poisson model, there were significant associations between oncogenic HPV infection and age, CS, and NP at a 0·05 significance level. However, the estimated dispersion parameter ϕ in the Poisson model implied overdispersion with 1·36. The scaled Poisson model showed that the parameter estimates did not change, but their standard errors were inflated by the value of the scale parameter. The resulting P values for age and NP were no longer significant, leaving only CS as a significant factor.

Table 1.

Analysis results from four different multivariable models: Naive Poisson model, Scaled Poisson, Negative binomial, Zero-inflated Poisson (ZIP), and Zero-inflated negative binomial (ZINB) models for oncogenic HPV infection

	Naive Poisson			Scaled Poisson		Negative binomial			ZIP			ZINB
	Estimated parameter	s.e.	P value	s.e.	P value	Estimated parameter	s.e.	P value	Estimated parameter	s.e.	P value	Estimated parameter	s.e.	P value
Intercept	−3·584	0·204	0·001	0·238	<0·001	−3·542	0·253	<0·001	−3·163	0·244	<0·001	−3·542	0·215	<0·001
Mexico	0·056	0·166	0·737	0·194	0·774	−0·021	0·209	0·919	−0·043	0·190	0·822	−0·021	0·209	0·919
Brazil	−0·176	0·168	0·948	0·196	0·369	−0·198	0·206	0·335	−0·238	0·191	0·212	−0·198	0·206	0·335
Age	−0·010	0·006	0·047	0·007	0·137	−0·009	0·007	0·194	−0·008	0·006	0·222	−0·009	0·007	0·194
Circumcised	0·334	0·141	0·008	0·165	0·043	0·299	0·176	0·090	0·230	0·168	0·170	0·299	0·176	0·090
NP	0·006	0·003	0·0003	0·003	0·069	0·006	0·004	0·122	0·007	0·006	0·178	0·008	0·004	0·122
Dispersion				1·36		0·79	0·193	<0·001				0·79*	n.a.	n.a.
AIC value		1217		1217		1183			1181			1185
Inflated intercept									−0·739	0·223	0·001	−20·0†	44806†	0·999†

s.e., Standard error ; NP, number of female partners at visit 1; AIC, Akaike’s Information Criterion (smaller is better) ; n.a., not available.

^*The proc genmod (v. 9·2, SAS Institute Inc.) procedure does not estimate the s.e. or the P value for the dispersion parameter in ZINB. They can be estimated using a more complex procedure, such as nlmixed in SAS, which would be difficult for many non-statisticians.

^†The extremely large s.e. for the zero-inflation model’s intercept is clear evidence that this parameter is not well estimated by the SAS procedure.

The negative binomial model indicated that the negative binomial dispersion parameter was significantly large (k=0·79, P<0·001), and the result showed that none of the covariates were significantly associated with oncogenic HPV infection. The AIC value was lower than the naive and scaled Poisson models, indicating the negative binomial is a better model.

The ZIP model showed the same results as the negative binomial model regarding the covariates at a 0·05 significance level. The proportion of zeros predicted by the ZIP model was 0·34 for oncogenic HPV (P<0·001, data not shown), which indicates that the ZIP is preferred to the Poisson model and the AIC was smaller than Poisson and negative binomial models. The ZINB model resulted in the same conclusion as the ZIP model, with the negative binomial dispersion parameter k=0·79. However, AIC was not smaller than the ZIP model. In addition, we found computational difficulties with a zero-inflated model fitting in the ZINB model: the model did not always converge or a model diagnostic indicated that the estimated model was not reliable. This may be due to the sample size, skewed data, and the mixed model fitting. Currently, the proc genmod procedure does not estimate the standard error or the P value for the dispersion parameter, k, in the ZINB. They can be estimated using a more complex procedure, such as nlmixed in SAS, which would be difficult for many non-statisticians. In addition, the extremely large standard error for the zero-inflation model’s intercept is clear evidence that this parameter is not well estimated by the SAS procedure.

DISCUSSION

In this paper, we used several models to deal with count data when the Poisson model assumption is not met because of an excessive incidence of zero counts. In addition to the Poisson model, we applied the negative binomial and zero-inflated models to the data from a HPV study. We compared the results from the models with several explanatory variables and high-lighted how the statistical inferences drawn from the models are different : the naive Poisson model yielded the smallest standard errors and over-stated the significance of some covariates compared to the negative binomial and zero-inflated models. When the Poisson model was scaled with the dispersion parameter, the model seemed slightly closer to the other alternative models, yet still showed a discrepancy.

Prior to considering which statistical model should be used for data analysis, the researcher must examine the distribution of the data. The first step should be the visual inspection of the data to ascertain whether they approximately follow a certain probability distribution. The histogram is a common tool to visually inspect data. Summary statistics can be studied (e.g. the sample mean and variance of the observed data) to try to gauge if the data are overdispersed along with a histogram of the response variable.

The Poisson distribution can be applied in counting the number of rare events. However, the Poisson model should only be used in cases where there is evidence that the distribution is correctly specified. This is the case only if the mean and the variance of the data are assumed to be equal.

As we illustrated with the scaled Poisson model in this paper, the estimate of the dispersion parameter (deviance or Pearson’s χ² statistic divided by the degrees of freedom) is often used to indicate overdispersion or underdispersion for Poisson models, and scaling by dispersion is simply a way to account for overdispersion. Most Poisson computational programs estimate these dispersion parameters so that the validation of the assumed distribution can be checked. However, this dispersion estimate might also indicate other problems such as an incorrectly specified model or outliers in the data. It should be carefully assessed whether this type of model is appropriate for the data.

A way of interpretation for the zero-inflated models for the HIM Study is to consider a population that consists of two groups: one of people who are not at risk of developing a certain disease, and one of people who are at risk and may develop the disease several times. However, it is our experience that the zero-inflated models should also be applied with caution, as small sample size cases and variable selection of covariates in the zero model components have not yet been well studied in the literature.

Although currently there is no solid built-in test from the commercial software to test whether or not the underlying data are Poisson, a score test for the ZIP model over the Poisson model is available in the literature [18]. If the P value for the score test is <0·05, a zero-inflated model may be more appropriate to fit the data. However, we conducted simulation studies for the score test and found a considerably inflated Type I error (detailed simulation results are not shown). Therefore, at this moment we are uncomfortable to use it ourselves or to recommend it to others. Consequently we decided not to present the score test result, even though the test showed our data involves significantly excessive zero counts and it may be a useful test if validated. Currently we are working on this subject.

The SAS code for the four models used in this article is given in the Appendix, using generic dataset and variable names.

APPENDIX. Generic SAS code for the four models used to analyse the example data

*- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -*
SAS Data File Name:=TEMP.sas7badat
Outcome variable:=Y (e.g., # of infection)
Covariates :=X1, X2, X3, X4, X5 (e.g., age, country, education,…)
Offset:=logt [e.g., (log (time)]
     (*<- account for varying length of observation time per subject)
*- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -*;
Title1 ‘Model 1-1. Naive Poisson Model’;
proc genmod data=TEMP;
     model Y=X1 X2 X3 X4 X5/ offset=logt dist=p link=log;
run;
Title1 ‘Model 1-2. Scaled Poisson Model’;
proc genmod data=TEMP;
     model Y=X1 X2 X3 X4 X5 /offset=logt dist=p link=log scale=d;
run;
Title1 ‘Model 2. Negative Binomial Model’;
proc genmod data=TEMP;
     model Y=X1 X2 X3 X4 X5/ offset=logt dist=nb link=log;
run;
Title1 ‘Model 3. Zero Inflated Poisson (ZIP) Model’;
proc genmod data=TEMP;
     model Y=X1 X2 X3 X4 X5 /offset=logt dist=zip link=log;
     zeromodel/link=logit ; output out=temp1 pzero=p;
run;
proc print data=temp1 (obs=1);
Title2 ‘p=zero inflation probability for logistic transform of the linear predictor’;
     var p;
run;
Title1 ‘Model 4. Zero Inflated Negative Binomial (ZINB) Model’;
proc genmod data=TEMP;
class country;
        model Y=X1 X2 X3 X4 X5
      /offset=logt dist=zinb link=log;
      zeromodel /link=logit ;
      output out=temp2 pzero=p;
run;
proc print data=temp2 (obs=1);
Title2 ‘p=inflation probability for zeros logistic transform of the linear predictor’;
     var p;
run;