Population-based input function and image-derived input function for [¹¹C](R)-rolipram PET imaging: methodology, validation and application to the study of major depressive disorder

Abstract

Quantitative PET studies of neuroreceptor tracers typically require that arterial input function be measured. The aim of this study was to explore the use of a population-based input function (PBIF) and an image-derived input function (IDIF) for [¹¹C](R)-rolipram kinetic analysis, with the goal of reducing—and possibly eliminating—the number of arterial blood samples needed to measure parent radioligand concentrations.

Methods

A PBIF was first generated using [¹¹C](R)-rolipram parent time-activity curves from 12 healthy volunteers (Group 1). Both invasive (blood samples) and non-invasive (body weight, body surface area, and lean body mass) scaling methods for PBIF were tested. The scaling method that gave the best estimate of the Logan-V_T values was then used to determine the test-retest variability of PBIF in Group 1 and then prospectively applied to another population of 25 healthy subjects (Group 2), as well as to a population of 28 patients with major depressive disorder (Group 3). Results were also compared to those obtained with an image-derived input function (IDIF) from the internal carotid artery. In some subjects, we measured arteriovenous differences in [¹¹C](R)-rolipram concentration to see whether venous samples could be used instead of arterial samples. Finally, we assessed the ability of IDIF and PBIF to discriminate depressed patients (MDD) and healthy subjects.

Results

Arterial blood-scaled PBIF gave better results than any non-invasive scaling technique. Excellent results were obtained when the blood-scaled PBIF was prospectively applied to the subjects in Group 2 (V_T ratio 1.02 ± 0.05; mean ± SD) and Group 3 (V_T ratio 1.03 ± 0.04). Equally accurate results were obtained for two subpopulations of subjects drawn from Groups 2 and 3 who had very differently shaped (i.e. “flatter” or “steeper”) input functions compared to PBIF (V_T ratio 1.07 ± 0.04 and 0.99 ± 0.04, respectively).

Results obtained via PBIF were equivalent to those obtained via IDIF (V_T ratio 0.99 ± 0.05 and 1.00 ± 0.04 for healthy subjects and MDD patients, respectively). Retest variability of PBIF was equivalent to that obtained with full input function and IDIF (14.5%, 15.2%, and 14.1%, respectively). Due to [¹¹C](R)-rolipram arteriovenous differences, venous samples could not be substituted for arterial samples.

With both IDIF and PBIF, depressed patients had a 20% reduction in [¹¹C](R)-rolipram binding as compared to control (two-way ANOVA: p=0.008 and 0.005, respectively). These results were almost equivalent to those obtained using 23 arterial samples.

Conclusion

Although some arterial samples are still necessary, both PBIF and IDIF are accurate and precise alternatives to full arterial input function for [¹¹C](R)-rolipram PET studies. Both techniques give accurate results with low variability, even for clinically different groups of subjects and those with very differently shaped input functions.

Introduction

One disadvantage of quantitative brain positron emission tomography (PET) studies is that they typically require measurement of radioligand in arterial plasma in order to calculate delivery of radioligand to brain. While the risk of adverse events resulting from arterial cannulation is relatively low (Everett et al., 2009), the potential for discomfort associated with this procedure often discourages subjects from participating in PET studies. Moreover, the handling and analysis of many blood samples can be burdensome for research personnel. To avoid arterial catheterization, population-based input function (PBIF) and image-derived input function (IDIF) are the two most common alternative approaches.

PBIF uses an appropriately scaled standard input function created by normalizing individual input functions from a population of subjects. PBIF has been validated almost exclusively for [¹⁸F]FDG (Takikawa et al., 1993; Vriens et al., 2009; Wakita et al., 2000), but rarely has this approach been applied to neuroreceptor PET radiotracers (Takikawa et al., 1994; Zanotti-Fregonara et al., 2012b). PBIF has two putative limitations. First, it may yield inaccurate results when applied to subjects whose input function manifests a shape that differs markedly from that of the average PBIF. Second, it may not be suitable for longitudinal intra-subject studies, because the shape of the PBIF remains constant. Previous studies have not adequately addressed these issues.

IDIF also has several attributes that may limit its usefulness in neuroreceptor studies. In brain PET studies, the large thoraco-abdominal blood pools are situated outside the imaging field-of-view, so that the IDIF must be obtained from the intracranial blood vessels, in particular the internal carotid arteries (Chen et al., 1998; Su et al., 2005). Given the small diameter of these vessels (about 5 mm), reliable quantification of their intravascular radioactivity is technically challenging and often proves unsuccessful (Zanotti-Fregonara et al., 2011a). In order to overcome such difficulties, we showed that combining the IDIF method with a limited number of arterial blood samples permitted reliable quantification of the binding of [¹¹C](R)-rolipram, a tracer used to image brain cyclic adenosine monophosphate (cAMP) phosphodiesterase-4 (Zanotti-Fregonara et al., 2011c). Our IDIF method was validated using a High Resolution Research Tomograph (HRRT), which affords a spatial resolution of 2.5 mm. Thus, the question remains as to whether this method could be used on standard PET cameras, whose spatial resolution is only about 6 mm. Moreover, we validated our IDIF method only in healthy volunteers; depressed patients, for instance, have significantly lower cortical uptake of [¹¹C](R)-rolipram (Fujita et al., 2012), which leads to a different amount of spill-in artefact for the intravascular radioactivity in the internal carotid artery.

With both PBIF and IDIF, some blood samples are still necessary to scale the estimated curves (Takikawa et al., 1993; Wakita et al., 2000; Zanotti-Fregonara et al., 2009; Zanotti-Fregonara et al., 2011b). To avoid arterial cannulation altogether, the most straightforward option would thus be to use venous blood samples. Scaling with venous samples has been used for [¹⁸F]FDG for both PBIF (Takagi et al., 2004) and IDIF (Chen et al., 1998). However, different radiotracers have distinct kinetics, and arteriovenous equilibrium must be validated independently for each tracer (Greuter et al., 2011). Moreover, using [¹⁸F]FDG, some authors scaled the PBIF without any blood samples, using only individual parameters such as body weight or body surface area (BSA) (Shiozaki et al., 2000; Tsuchida et al., 1999). Although methods that apply non-invasive scaling for non-FDG tracers have not been reported, it is conceivable that full kinetic modeling using such non-invasive scaling also may be achieved without the use of blood samples for other radiotracers.

Finally, in the literature, new IDIF or PBIF methods are often validated only from a methodological perspective. Therefore it is important to test these methods in actual clinical protocols as well.

This study aimed to: 1) evaluate the ability of PBIF to quantify [¹¹C](R)-rolipram binding; 2) replicate our previous findings with IDIF validated on a high resolution camera using a common standard resolution camera; 3) measure the accuracy of PBIF in a test-retest study; 4) to assess whether PBIF derived from healthy subjects can be applied either to depressed patients or to subjects whose input function shape is atypical; 5) determine whether venous blood can be used instead of arterial blood; 6) investigate the possibility of eliminating blood sampling altogether in PBIF by using non-invasive individual parameters for scaling, such as weight, BSA, or lean body mass (LBM); and 7) assess the ability of IDIF and PBIF to detect a difference in the mean [¹¹C](R)-rolipram binding between unmedicated individuals with major depressive disorder (MDD) and healthy controls.

Methods

Radioligand preparation

[¹¹C](R)-rolipram was synthesized as previously described (Fujita et al., 2005) and according to our Investigational New Drug Application #73,149, submitted to the US Food and Drug Administration. A copy of our application is available at: http://pdsp.med.unc.edu/snidd/nidpulldownPC.php. The radioligand was obtained in high radiochemical purity (> 99%).

Subjects

Three subject populations were used for this study. PBIF was obtained using the scans of 12 healthy volunteers from a previous protocol (2 females and 10 males, 28 ± 11 years of age, body weight of 74 ± 12 kg; Group 1) (Zanotti-Fregonara et al., 2011c). This PBIF was then prospectively applied to 53 other consecutive subjects from a different clinical protocol (Fujita et al., 2012) that included 25 healthy subjects (9 females and 16 males, 37 ± 11 years of age, body weight of 83 ± 16 kg; Group 2) and 28 patients with MDD (9 females and 19 males, 36 ± 11 years of age, body weight of 86 ± 23 kg; Group 3). Two of the MDD subjects were excluded because their arterial input function was obtained only for the first 60 minutes. In the MDD sample the severity of depressive symptoms was in the moderate-to-severe range, as assessed using the Montgomery Asberg Depression Rating Scale (MADRS) and the Hamilton Rating Scale for Depression (HRSD) (mean MADRS score = 30 ± 6; mean HRSD score = 20 ± 6 at the time of scanning). See (Fujita et al., 2012) for more details. All subjects provided written informed consent to participate, as approved by the Combined Neuroscience Institutional Review Board of the NIH Intramural Research Program.

PET scans

The images of the first 12 subjects (Group 1) were acquired using an HRRT (Siemens/CPS, Knoxville, TN) for 120 minutes. This PET camera has spatial resolution of 2.5 mm measured as the reconstructed full-width at half maximum. Two [¹¹C](R)-rolipram scans were performed for each subject (test-retest study). The mean injected activity was 421 ± 144 MBq for the test scans and 420 ± 121 MBq for the retest scans. Head motion was corrected by monitoring its position during the scan with the Polaris Vicra Optical Tracking System (NDI, Waterloo, ON, Canada) (Bloomfield et al., 2003). The dynamic scan consisted of 33 frames (6 frames of 30 seconds each, then 3 × 60 s, 2 × 120 s, and 22 × 300 s). Because 90 minutes of brain and plasma data are adequate to measure the V_T of [¹¹C](R)-rolipram with small bias and good identifiability (Zanotti-Fregonara et al., 2011c), only the first 90 minutes of image data were used. All PET images were corrected for attenuation and scatter. PET data were reconstructed on a 256 × 256 matrix with a pixel size of 1.22 × 1.22 × 1.23 mm³ using the Motion-compensation OSEM List-mode Algorithm for Resolution-recovery (MOLAR) (Carson et al., 2004).

Images for all other subjects (Groups 2 and 3) were acquired with an Advance scanner (GE Healthcare, Milwaukee, WI) for 90 minutes, using a time-schedule similar to that of the HRRT studies. An 8-min ⁶⁸Ge transmission scan was obtained before injection of the radiotracer for attenuation correction. The mean injected activity was 726 ± 97 MBq for Group 2 and 703 ± 108 MBq for Group 3. A head holder was used to minimize head movements during the scan.

Magnetic resonance imaging (MRI)

To provide an anatomical reference for analysis of the PET images, magnetic resonance imaging (MRI) was performed for all subjects. For Group 1, a 1.5-T Signa scanner (GE, Milwaukee, WI) was used. Three sets of axial images were acquired parallel to the anterior-commissure-posterior commissure line with Spoiled Gradient Recalled (SPGR) sequence of TR/TE/flip angle = 12.4 ms/5.3 ms/20°, voxel size = 0.94 × 0.94 × 1.2 mm, and matrix = 256 × 256. For Groups 2 and 3 we used either a 3-T Signa scanner (GE, Milwaukee, WI) or an Achieva 3-T MRI scanner (Philips Health Care, Andover, MA). With both scanners, similar T1-weighted structural images were acquired with a voxel size of 0.86 mm × 0.86 mm × 1.2 mm (Signa) or 1 mm × 0.94 mm × 0.94 mm (Achieva). The image acquisition sequences were: time of repetition (TR): 7.3 ms; echo time length (TE): 2.8 ms; and flip angle: 6° for Signa, and TR: 8.1 ms, TE: 3.7 ms, and flip angle: 8° for Achieva.

Measurement of [¹¹C](R)-rolipram in plasma

All blood samples (1 mL each) were drawn from the radial artery at 15-second intervals for the first 150 seconds, followed by 3 mL samples at 3, 4, 6, 8, 10, 15, 20, 30, 40, and 50 minutes, and 4.5 mL at 60, 75, and 90 minutes. The plasma time-activity curve was corrected for the fraction of unchanged radioligand (Fujita et al., 2005; Zoghbi et al., 2006). The plasma free fraction (f_P) of [¹¹C](R)-rolipram was determined by ultrafiltration (Sawada et al., 1990) for each scan. Possible assay-by-assay fluctuation in f_P measurement was corrected based upon f_P of a standard plasma sample assayed with the subject’s sample (Abi-Dargham et al., 1999). In addition to arterial samples, venous samples from the antecubital vein of the contralateral arm were also obtained for 13 healthy volunteers from Group 2. Venous samples were drawn at 6, 20, 60, and 90 minutes, processed and analyzed in the same manner as the arterial samples.

Finally, three subjects (not belonging to Groups 1, 2, or 3 described above) were studied to assess whether venous concentrations of the tracer were similar when veins were heated, and if blood was drawn from a hand vein. Therefore, in addition to arterial sampling from the radial artery, simultaneous venous sampling was performed from the contralateral antecubital and hand veins. For these three subjects, venous blood samples were drawn while the arm and the hand were warmed up using multiple air-activated disposable hand-warmers. Three simultaneous samples (one from the artery and one from each venous line) were drawn at 3, 6, 10, 15, and 20 minutes, and then every 10 minutes until 90 minutes. The determination of the parent radioligand plasma concentration was performed for the samples obtained at 6, 20, 60, and 90 minutes. For the other samples only the whole-blood activity was counted. No brain imaging was performed in these three subjects.

Image analysis

Predefined regions of interest (ROIs) were positioned on the PET images using the following methods. The MR image from each subject was coregistered using SPM5 (Wellcome Department of Imaging Neuroscience; University College London, UK) to the average PET image created by summing all of the dynamic image frames. The MR and PET images were normalized to a standardized spatial array (Montreal Neurological Institute space) based on transformation parameters from the MR images. The predefined ROIs were positioned on the spatially normalized MR images to overlie thalamus (12.6 cm³), caudate (5.6 cm³), putamen (6.5 cm³), cerebellum (51.2 cm³), frontal (27.2 cm³), parietal (26.6 cm³), lateral temporal (25.0 cm³), occipital (31.2 cm³), anterior cingulate (7.5 cm³), and medial temporal (14.3 cm³) cortices.

Generation of the population-based input function

The PBIF was generated by averaging the normalized input functions of the subjects in Group 1, fitted with a linear interpolation of the concentrations before the peak and a tri-exponential function after the peak. To create the PBIF, only the 12 test scans were used. Delays between individual curves were adjusted by shifting the curves until the time to maximum coincided with the mean time to the peak for all the curves. We also created a PBIF using median, instead of mean, values of the individual input functions. However, the two curves were almost indistinguishable visually. Therefore we used the PBIF generated from the mean values.

Choice of the scaling factor for PBIF

To determine the best scaling method, we used a leave-one-out procedure (Meyer et al., 2006); briefly, PBIF was generated for each of the 12 subjects in Group 1 by averaging the measured input functions of the remaining 11 subjects. This procedure was chosen to avoid any bias caused by including in the PBIF the individual input function that needs to be calculated. Different scaling methods were tested. The first was traditional scaling using blood samples. In the present study, we used arterial samples obtained at 10 and 75 minutes after injection. These samples were selected after performing a Pearson’s linear correlation analysis (Takikawa et al., 1993) between the measured plasma activity at a given time and the total area under the curve (AUC). In the case of one sample, the sampling time giving the highest correlation coefficient was assumed to yield the plasma sample that best predicted the AUC. In the case of two samples, the correlation was calculated the same way, except that the average plasma activity of two samples was used instead of a single sample (covering all possible combinations). The mean activity of individual samples obtained at 15 and 75 minutes yielded the highest correlation coefficient (r = 0.9914) (Table 1).

Table 1.

Correlation coefficients for the area-under-the-curve of the plasma time-activity curve (AUC) using the concentrations of [¹¹C](R)-rolipram measured at two time points

		Time of first plasma concentration (min)
		1.5	3	4	6	8	10	15	20	30	40	50	60	75	90
Time of second plasma concentration (min)	1.5	−0.022	0.117	0.097	0.079	0.071	0.065	0.058	0.057	0.060	0.063	0.065	0.065	0.063	0.060
	3		0.677	0.738	0.760	0.768	0.774	0.790	0.807	0.833	0.849	0.856	0.859	0.858	0.853
	4			0.796	0.826	0.843	0.855	0.877	0.894	0.919	0.933	0.942	0.947	0.950	0.950
	6				0.855	0.871	0.881	0.900	0.919	0.947	0.963	0.973	0.978	0.981	0.981
	8					0.883	0.889	0.903	0.921	0.955	0.975	0.985	0.990	0.991	0.990
	10						0.891	0.900	0.917	0.954	0.976	0.987	0.991	0.991	0.988
	15							0.900	0.914	0.949	0.970	0.981	0.985	0.984	0.980
	20								0.924	0.952	0.969	0.977	0.980	0.979	0.976
	30									0.963	0.968	0.970	0.969	0.968	0.965
	40										0.965	0.961	0.957	0.953	0.950
	50											0.953	0.947	0.941	0.937
	60												0.939	0.931	0.925
	75													0.920	0.912
	90														0.903

The values along the diagonal (in italics) use only one sample and represent the correlation coefficients between the activities of individual time points with the AUCs. Values above the diagonal represent the correlation coefficients between the AUC and the mean activities of pairs of individual samples. The value at 1.5 minutes is the peak value. The highest (best) correlation was obtained using blood samples at 10 and 75 min.

To assess whether blood sampling could be eliminated altogether, we also investigated the possibility of scaling PBIF non-invasively, using individual parameters (weight, BSA and LBM) that are assumed to be parallel with the initial distribution volume of the tracer. We tried several different formulas to calculate BSA and LBM (Table 2). Because [¹¹C](R)-rolipram is not a highly lipophilic tracer (logD at pH 7.4 = 2.16), we expected that the non-fat body compartments would better reflect this radiotracer’s volume of distribution. The first BSA formula was calculated by DuBois and DuBois (DuBois and DuBois, 1916). Over the last century, several other formulas have been proposed (Boyd, 1935; Gehan and George, 1970; Haycock et al., 1978; Mosteller, 1987); the most recent ones, based on 3D scanned data and sophisticated computer algorithms, may provide more accurate results (Tikuisis et al., 2001; Yu et al., 2010). Normalization of PBIF with the actual LBM value (Hume, 1966; James, 1976), which should accurately reflect the distribution in non-fatty tissues, has never been reported. Several studies suggest that LBM is a better morphometric measurement than BSA to predict physiologic volumes (Sawyer and Ratain, 2001).

Table 2.

Formulae used to calculate Body Surface Area (BSA) and Lean Body Mass (LBM)

Reference (unit) [year]	BSA formulas
DuBois (m2) [1916]	0.20247 × Height (m) 0.725 ×Weight (kg) 0.425
Boyd (m2) [1935]	0.0003207 × Height (m) 0.3 ×Weight (g) (0.7285 − (0.0188 × LOG Weight (g))
Gehan (m2) [1970]	.0235 × Height (cm) 0.42246 × Weight (kg) 0.51456
Haycock (m2) [1978]	0.024265 × Height (cm) 0.3964 × Weight (kg) 0.5378
Mosteller (m2) [1987]	(Height (cm) × Weight (kg) / 3600)½
Tikuisis (cm2) [2001]	128.1 × Weight (kg) 0.44 × Height (cm) 0.60 (men)
	147.4 × Weight (kg) 0.47 × Height (cm) 0.55(women)
Yu (cm2) [2010]	71.3989 × Height (cm) 0.7437 × Weight (kg) 0.4040
Reference (unit) [year]	LBM formulas
James (kg) [1976]	(1.10 × Weight (kg)) − 128 × Weight (kg)2/(100 × Height (m))2 (men)
	(1.07 × Weight (kg)) − 148 × Weight (kg)2/(100 × Height (m))2 (women)
Hume (kg) [1966]	(0.32810 × Weight (kg)) + (0.33929 × Height (cm)) − 29.5336 (men)
	(0.29569 × Weight (kg)) + (0.41813 × Height (cm)) − 43.2933 (women)

Test-retest study

The PBIF obtained from the test scans of the first 12 subjects of Group 1, scaled with the method that provided the best results, was used to measure the retest accuracy. To avoid possible bias, the PBIF used for each retest study did not include the input function from the test study of the same subject.

Retest variability (expressed as the absolute difference between the two scans divided by the mean of the two scans) and intraclass correlation coefficient (ICC) were calculated for V_T/f_P values obtained with PBIF and compared with the values obtained with full arterial sampling and IDIF from a previous publication using the same subjects (Zanotti-Fregonara et al., 2011c).

Prospective evaluation of PBIF

The scaling method that provided the best results was then prospectively tested on the subjects in Groups 2 and 3. To better assess the robustness of PBIF to variations in the shape of the input function, we selected two subsamples of subjects from each group who had very differently shaped input functions compared to the PBIF. We compared two ways of selecting these subpopulations: based on high and low clearance of the radioligand, or based on the ratio of the concentration of parent radioligand to the concentration of total radioactivity in whole blood. We found that the latter method (i.e., parent to whole blood ratio) provided the most divergent groups. These two subsamples comprised 15 subjects with the highest parent/whole blood ratio -i.e. the 15 “flattest” curves (6 healthy and 9 MDD, 7 females and 8 males, 37 ± 12 years of age, body weight of 94 ± 19 kg); and 15 subjects with the lowest parent/whole blood ratio -i.e. the 15 “steepest” curves (8 healthy and 7 MDD, 6 females and 9 males, 38 ± 10 years of age, body weight of 74 ± 11 kg).

Generation of the image-derived input function

The method used here was originally proposed by Chen et al. for [¹⁸F]FDG (Chen et al., 1998), and validated for [¹¹C](R)-rolipram by our laboratory (Zanotti-Fregonara et al., 2012a; Zanotti-Fregonara et al., 2011c). Briefly, the carotid signal measured from the images is represented as a linear combination of the radioactivity from the blood and spill-in from the surrounding tissue.

$${\mathrm{C}}_{\text{carotid}}(\mathrm{t})=\text{RC}\times {\mathrm{C}}_{\text{wb}}(\mathrm{t})+\text{SP}\times {\mathrm{C}}_{\text{surround}}(\mathrm{t})$$ (1)

where C_carotid is the carotid concentration of radioactivity obtained from the image; C_wb is the actual concentration of radioactivity in arterial whole blood; C_surround is the radioactivity in the surrounding tissues; RC and SP are the recovery and the spill-in coefficients, which were estimated with linear least square fitting of C_carotid, C_wb, and C_surround in equation (1) at the sampling times (t). C_wb was measured at 6, 20, 60, and 90 minutes. In one subject the whole-blood IDIF was obtained using only the first three samples (6, 20 and 60 minutes) because the addition of the fourth sample in this case resulted in a curve whose shape was inconsistent with that of an input function. When the fourth sample was excluded, the IDIF was correctly estimated. A variation of equation (1), where SP = 1-RC, has been described (Cook et al., 1999). In the present study, however, we used the original equation proposed by Chen, because RC + SP were generally not equal to 1. To perform radiometabolite correction, the concentration of [¹¹C](R)-rolipram was also measured at the four blood samples at 6, 20, 60, and 90 minutes and used to derived the concentrations of [¹¹C](R)-rolipram for the entire duration of the scan. This step was performed by fitting a monoexponential function to the parent/whole blood concentration at the four time-points and then by multiplying these values by the whole-blood IDIF.

Calculation of [¹¹C](R)-rolipram binding in brain and statistical analysis

V_T values were obtained using the Logan analysis, which yields results equivalent to compartmental modeling for [¹¹C](R)-rolipram (Zanotti-Fregonara et al., 2011c). We calculated the estimated/reference mean Logan-V_T/f_P (i.e.V_T divided by the individual plasma free fraction) ratio for each subject. The reference Logan-V_T/f_P was obtained with the arterial input function. Group data are expressed as mean ± 1 SD.

Logan-V_T/f_P values obtained within the ten ROIs in the control (Group 2) and MDD patients (Group 3) were compared using repeated measures two-way analysis of variance with regions as the within-subjects (repeating) factor. The analysis was repeated three times, using the Logan-V_T/f_P values obtained with the reference arterial input function, with the IDIF and with the PBIF. The statistical analyses were performed using IBM SPSS Statistics 20 (Armonk, NY).

Results

PBIF

Choice of the scaling factor for PBIF

A comparison of the different scaling methods tested in the 12 subjects from Group 1 showed that using the two blood samples taken at 10 and 75 minutes was superior to any of the non-invasive scaling methods. None of the scaling factors showed any significant bias, suggesting that non-invasive scaling is, on average, accurate. However, all of the non-invasive methods had large standard deviations (Table 3), due to the presence of many outliers. Errors of 20–30% in the estimated V_T/f_P values were not uncommon, with even larger occasional errors. Different BSA and LBM formulas yielded nearly identical results, and all were more accurate than scaling by weight alone, a finding that echoes results obtained previously by Shiozaki et al. for [¹⁸F]FDG (Shiozaki et al., 2000).

Table 3.

The accuracy (ratio) and precision (SD) of various scaling methods to estimate plasma area-under-the-curve (AUC) and distribution volume (V_T) compared to arterial input function

Scaling method	AUC (ratio ± SD)	VT (ratio ± SD)
Two blood samples	0.99 ± 0.11	1.00 ± 0.05
Weight	1.04 ± 0.22	1.01 ± 0.32
Lean Body Mass
James	1.03 ± 0.19	1.00 ± 0.25
Hume	1.03 ± 0.19	1.00 ± 0.26
Body Surface Area
Du Bois	1.03 ± 0.18	1.00 ± 0.27
Boyd	1.03 ± 0.19	1.00 ± 0.28
Gehan	1.03 ± 0.19	1.00 ± 0.28
Haycock	1.03 ± 0.19	1.00 ± 0.28
Mosteller	1.03 ± 0.19	1.00 ± 0.27
Tikuisis	1.03 ± 0.19	1.00 ± 0.27
Yu	1.03 ± 0.18	1.00 ± 0.27

Test-retest results

The inter-subject variability using PBIF among the 12 subjects of Group 1 was 14.5%, which is very similar to the values previously obtained in these same subjects, with full arterial sampling (15.2%) and with IDIF (14.1%) (Zanotti-Fregonara et al., 2011c). ICC values were slightly higher for PBIF (0.66) and IDIF (0.60) than for arterial input (0.47), but these differences were not significant by F-test.

Results of the prospective evaluation of PBIF

For most subjects, the blood-scaled PBIF matched well the shape of the reference input function, except for differences in the height of the peak and in the portion of the curve at the transition between the peak and the tail. Occasional differences in the slope of the tails were observed, but the total AUC was, in general, well-estimated (Table 4). PBIF gave similar mean V_T/f_P estimates in subjects from both Groups 2 and 3: 1.02 ± 0.07 (ICC = 0.953) for healthy subjects (Group 2) and 1.04 ± 0.06 (ICC = 0.987) for MDD patients (Group 3) (Figure 1A). However, the V_T/f_P of three outliers (two healthy subjects and one MDD patient) had an error of 20–25% (Table 5). Analysis of the input functions of these subjects revealed that these errors were caused by outlying values in one of the two blood samples used to scale the PBIF (Fig 1B). To reduce the influence of these outlying blood samples, the analyses were repeated for all 51 subjects using a PBIF scaled with three, instead of two, blood samples, obtained at 10, 40, and 75 minutes. The 40-minute sample was chosen because it had the highest correlation coefficient for a single sample in the Pearson’s correlation analysis (Table 1). After scaling with three blood samples, the results improved for subjects in both Groups: the mean V_T/f_P estimates were 1.02 ± 0.05 (ICC = 0.977) for healthy subjects and 1.03 ± 0.04 (ICC = 0.995) for MDD patients (Tables 4 and 5).

Table 4.

The effect of number of plasma samples and subject population on the accuracy (ratio) and precision (SD) of PBIF and IDIF to estimate area-under-the-curve (AUC) and distribution volume (V_T) compared to arterial input function.

Method	Population	Number of plasma samples	AUC (ratio ± SD)	VT (ratio ± SD)
PBIF	healthy	2	1.02 ± 0.07	1.02 ± 0.07
PBIF	healthy	3	1.02 ± 0.07	1.02 ± 0.05
PBIF	MDD	2	1.02 ± 0.08	1.04 ± 0.06
PBIF	MDD	3	1.04 ± 0.07	1.03 ± 0.04
PBIF	mixed (flat curves)	2	1.08 ± 0.06	1.08 ± 0.05
PBIF	mixed (flat curves)	3	1.10 ± 0.05	1.06 ± 0.04
PBIF	mixed (steep curves)	2	0.97 ± 0.06	0.99 ± 0.06
PBIF	mixed (steep curves)	3	0.96 ± 0.05	0.99 ± 0.04
IDIF	healthy	4	1.02 ± 0.06	0.99 ± 0.05
IDIF	MDD	4	1.00 ± 0.04	1.00 ± 0.04

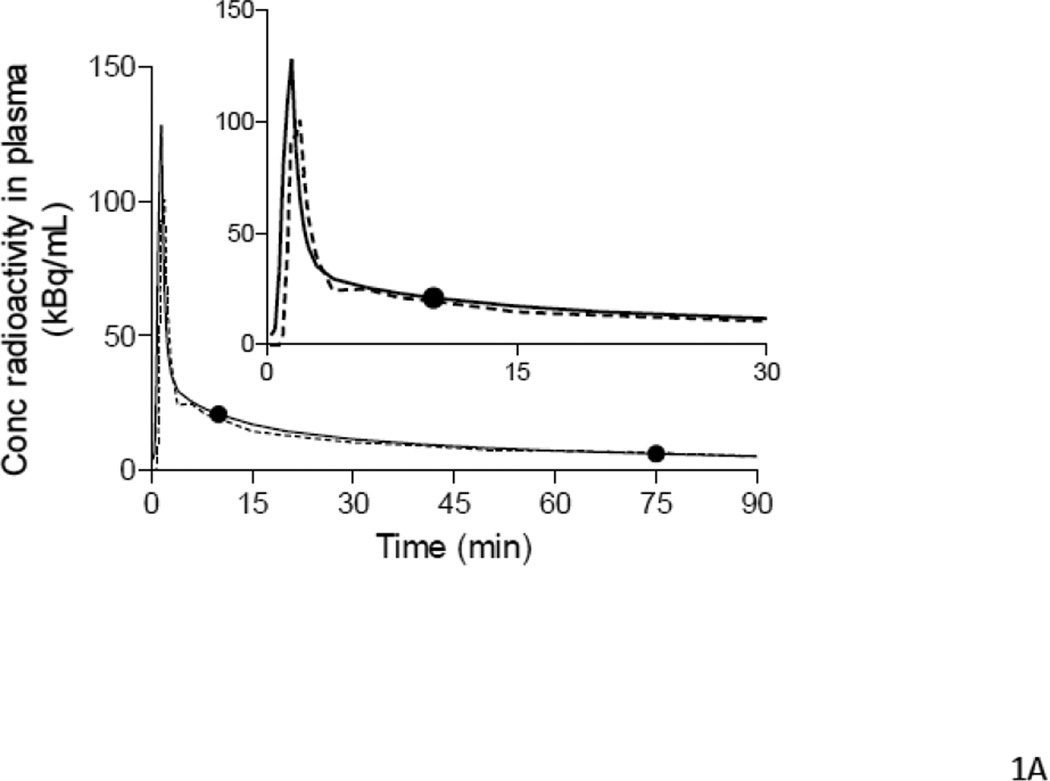
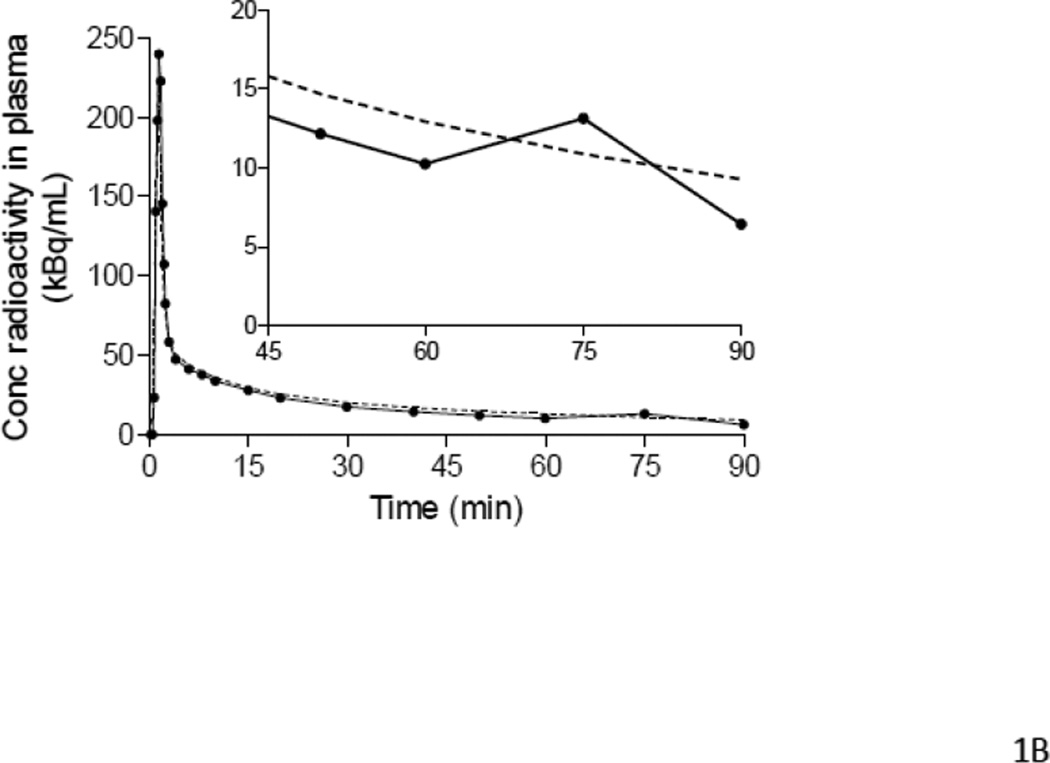
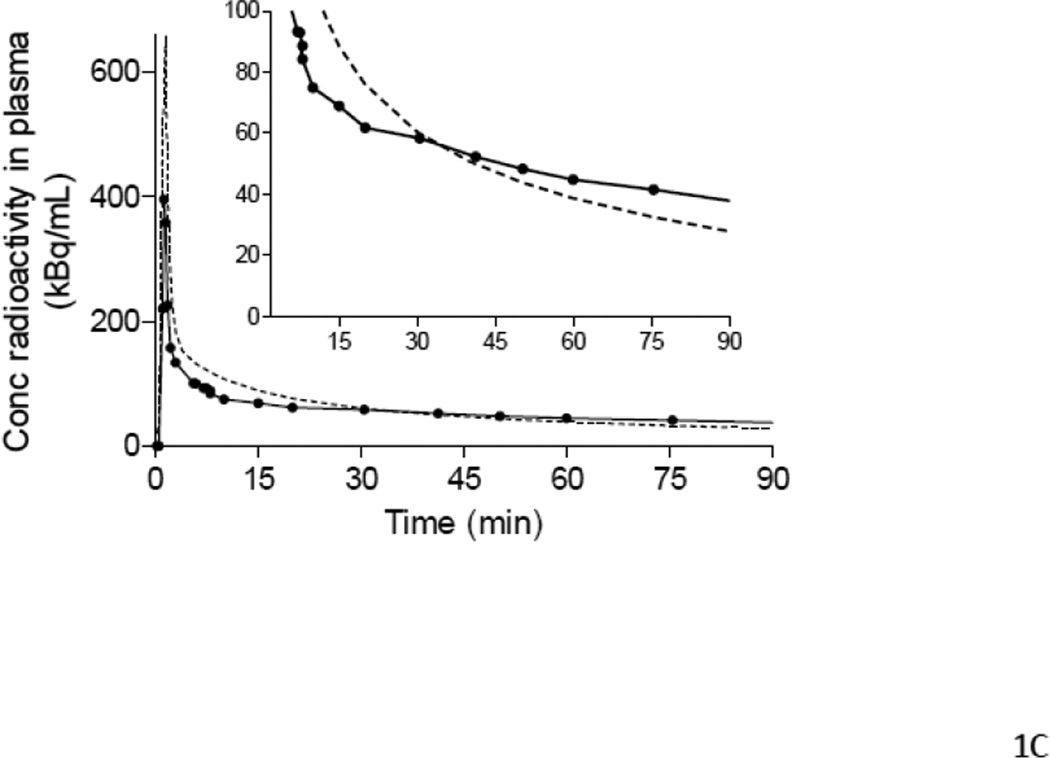
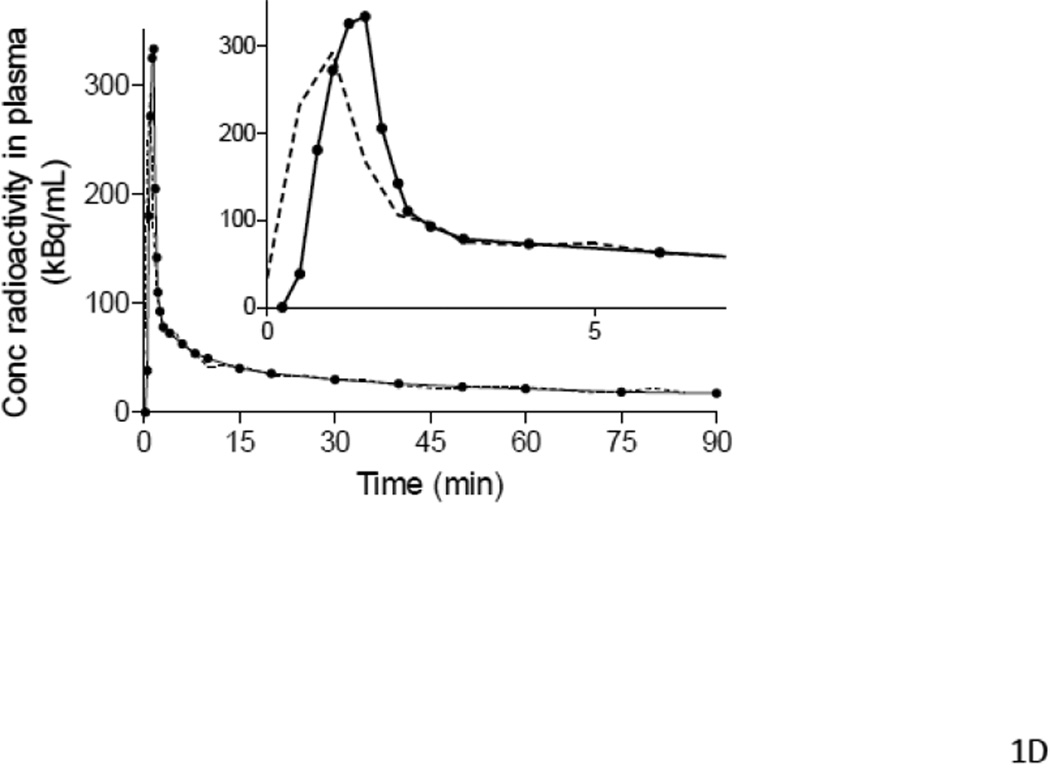
Figure 1.

Examples of input functions estimated with PBIF (A, B, C) and IDIF (D), plotted against the reference arterial input functions. PBIF and IDIF are shown with a dashed line. The arterial input functions are shown with solid line, where (●) represents individual measurements. (A) PBIF of a representative subject. In this example, the curve was positioned to overlie two plasma concentrations of [¹¹C](R)-rolipram measured at 10 and 75 minutes. (B) One of the three outliers with a distribution volume (V_T) estimation error >20%. The arterial input function has an apparent “bump” at 75 minutes, which is highlighted in the insert. This “bump” may have been caused by an error in the measurement of that particular blood sample. Since only two blood samples were used to scale PBIF, the bump in the arterial input function led to an overestimation of the PBIF and an underestimation of V_T (−20.2%). In the other two outliers (Table 5), the curves had a “dip” at 75 minutes. Thus, PBIF was underestimated and V_T was overestimated (+22.0% and +24.0%). When PBIF was scaled with three blood samples (10, 40 and 75 minutes), the errors became +14.2%, −13.7%, and −8.0%, respectively. (C) One of the most “extreme” cases of mismatch between the PBIF and the individual input function. The arterial input function of this subject had a particularly “flat” shape to the tail of the curve. This flatness of the arterial curve and its disparity compared to PBIF are more visible in the insert. In addition, PBIF overestimated the peak. Despite these errors in early and late portions of the input curves, PBIF overestimated total AUC by 10% and V_T by only 7%. (D) Representative curves of IDIF (----) and arterial input function (●) from a single subject. In contrast to PBIF, IDIF always matched the tail of the curve well, but often matched the peak poorly.

Table 5.

Logan-VT error	PBIF (2 samples)	PBIF (3 samples)	IDIF
0–5%	35	40	41
5–10%	10	7	9
10–15%	3	4	1
15–20%	0	0	0
20–25%	3	0	0
Total	51	51	51

Note: All three subjects with an error range of 20–25% with PBIF scaled with two samples displayed a clear error in the plasma sample measurement taken at 75 minutes after injection (see also Figure 1B).

To determine the sensitivity of the PBIF method to individual variations in the shape of the input function, we selected two subpopulations from Groups 2 and 3 with very differently shaped input functions compared to the reference PBIF (Fig. 1C). The parent/whole blood ratio of the PBIF subjects was 0.80 ± 0.33 (n = 12), while the corresponding ratio for the subjects with “flat” curves was 1.19 ± 0.13 (n = 15; p = 0.0002), and the ratio for the subjects with “steep” curves was 0.53 ± 0.12 (n = 15; p = 0.0055). Despite these significant differences based upon in the shape of the input functions, PBIF scaled with two blood samples gave similar results with low variability. The mean V_T/f_P ratios for the 15 subjects with “flat” and “steep” curves were 1.08 ± 0.05 and 0.99 ± 0.06, respectively. When a third sample was added to scale the PBIF, the results converged further (1.06 ± 0.04 and 0.99 ± 0.04, respectively).

Please note that the parent/whole blood ratio can be higher than 1, because the numerator is the concentration of parent radioligand in plasma, whereas the denominator is concentration of total radioactivity in whole blood.

IDIF

Similar to previous results obtained using HRRT (Zanotti-Fregonara et al., 2011c), we found that IDIF was an excellent substitute for the arterial input function using a lower resolution (~6 mm) PET camera (GE Advance). Although errors in the estimation of the peaks were apparent in most subjects, the shape of the image-derived curves closely matched that of the arterial input at later times (Fig 1D). Therefore, the total AUCs (with the image time-points taken at mid-frame) were well estimated (Table 4) because the late part of the curve accounts for the majority (>90%) of the AUC.

To determine whether IDIF performs comparably for depressed subjects as well as healthy subjects, we compared results from 26 patients with MDD (Group 3) and 25 healthy subjects (Group 2). The estimated Logan-V_T/f_P values closely approached the reference values for both populations (Table 4). Only one of 51 subjects had a V_T/f_P error >10% (Table 5).

Arteriovenous differences

To evaluate whether V_T/f_P can be validly estimated without arterial cannulation, we compared the concentration of parent radioligand in plasma sampled from the radial artery versus plasma sampled from the antecubital vein. However, it took the radiotracer a long time (~30–40 minutes) to achieve steady state conditions for the forearm; furthermore, this did not occur in all subjects. In the 13 subjects who had simultaneous sampling from the radial artery and the antecubital vein, the concentrations of whole-blood radioactivity in the vein were lower than in the artery at 6 and 20 minutes (−37 ± 16% and −16 ± 10%, respectively); at 60 and 90 minutes the average concentration was comparable (−4 ± 8% and +2 ± 4%). These data suggest that arteriovenous equilibrium of whole-blood radioactivity should be reached at about 30–40 minutes after injection. Even after apparent steady state, an inter-individual variability remained. Several subjects showed arteriovenous differences in whole blood concentrations between 20 and 35% even at 60 and 90 minutes. The difference in the parent radioligand concentrations between the artery and the vein followed kinetics similar to that of whole blood, although the parent radioligand concentration in the venous blood was slightly higher (6–9%) than those in arterial blood.

Similarly to the previous analysis of 13 subjects, in the three subjects who had sampling from the warmed veins of the forearm and the hand, the venous values differed from the arterial values. For instance, at early time points the arteriovenous differences in parent concentration were >20% and at the final time point (90 minutes) this difference ranged from 1% to 12%. No significant differences were noted between the venous values obtained from the forearm versus those obtained from the hand.

Differences in [¹¹C](R)-rolipram binding between control and MDD subjects

Logan-V_T/f_P obtained with the reference arterial input function showed a widespread and statistically significant decrease of [¹¹C](R)-rolipram binding in the MDD group. The magnitude of the decrease was about 20% and similar across all the brain regions (mean V_T/f_P in controls: 13.5 ± 1.05 mL/g, MDD: 10.9 ± 0.93, two-way ANOVA p=0.005 for group difference in the 10 brain regions). Very similar results were obtained when the Logan-V_T/f_P values were calculated using both IDIF (controls: 13.4 ± 1.05 mL/g, MDD: 10.9 ± 0.93, p=0.008) and PBIF (controls: 13.7 ± 1.07 mL/g, MDD: 11.1 ± 0.95, p=0.005).

Discussion

Our study extended previous methodological results to address several unresolved issues regarding the validity of PBIF and IDIF for estimating [¹¹C](R)-rolipram binding from PET images. First, we found that V_T/f_P values derived using a PBIF are accurate and precise alternative to serial arterial sampling for [¹¹C](R)-rolipram PET studies. Second, a blood-scaled PBIF obtained from a population of healthy volunteers was successfully applied to a population of patients with MDD and performed well, even in the subgroups that manifested differently shaped input functions. Third, PBIF was successfully applied to a test-retest study, with results equivalent to those of full arterial sampling. Fourth, our IDIF method, validated on healthy volunteers using a HRRT, gave excellent results when applied to healthy volunteers and MDD patients acquired using a camera with a lower resolution. Fifth, the arterial plasma samples necessary to scale both PBIF and the IDIF could not be replaced by venous samples. Sixth, noninvasive scaling using weight, BSA, or LBM yielded unreliable results. Finally, using IDIF and PBIF enable us to detect a widespread decrease in the [¹¹C](R)-rolipram binding in MDD subjects, as compared to controls, thus replicating previously published results using distinct and less invasive methodologies (Fujita et al., 2012).

Although the PBIF approach was introduced almost 20 years ago (Takikawa et al., 1993), its application to neuroreceptor PET tracers has been minimal (Takikawa et al., 1994; Zanotti-Fregonara et al., 2012b). Nevertheless, PBIF affords many practical advantages, especially when compared to IDIF. In contrast to IDIF, PBIF does not depend on scanner characteristics, partial volume effects, reconstruction algorithms, or quality of acquisition. In addition, PBIF better estimates the peak than most IDIF methods. Moreover, because PET cameras cannot distinguish the parent compound from its radiometabolites, correcting for radiometabolites is very challenging with the IDIF approach (Zanotti-Fregonara et al., 2011a). In contrast, scaling the PBIF with a few blood samples inherently includes a correction for radiometabolites, because the scaling uses the concentration of only parent radioligand.

PBIF was previously validated using arterial (Takikawa et al., 1994; Takikawa et al., 1993) or venous blood samples (Takagi et al., 2004) as scaling factors. In an effort to avoid blood sampling altogether, several researchers investigated the possibility of scaling the PBIF of [¹⁸F]FDG using non-invasive individual parameters but obtained conflicting results. While some studies demonstrated good results using body weight (Tsuchida et al., 1999) or BSA (Shiozaki et al., 2000), others found scaling with BSA to be unreliable (Wakita et al., 2000). The present study found that, regardless of the physiological parameter or formula used, non-invasive scaling methods proved imprecise, at least partly because they were insensitive to inter-individual differences in tracer metabolism in subjects with similar physical characteristics.

In general, the rationale of non-invasive scaling is that individual parameters such as BSA or LBM are assumed to be parallel with the initial volume of distribution of the tracer. However, depending on the substance, these parameters may be poor indicators of the initial volume of distribution, especially in obese subjects and in the elderly (Cheymol, 1993; Klotz, 2009), where changes in the body composition cannot be properly accounted for by height and weight. Moreover, scaling with BSA or LBM assumes a common clearance from the body among all subjects. Nevertheless renal and hepatic function vary among healthy subjects, and especially so in older subjects and those with particular diseases and therapies. Indeed, BSA and LBM are poorly correlated to organ functions (Morgan and Bray, 1994; Sawyer and Ratain, 2001). The use of blood samples to scale the PBIF implicitly solves at once all the uncertainties related to the estimation of the volume of distribution and the elimination kinetics for any tracer.

It is important to note here that the choice of which blood samples to use for scaling PBIF was not made arbitrarily; instead, the times of the blood samples were rationally selected based on correlations with the AUC of the input function. For example, Seike and colleagues assessed PBIF for quantitative analysis of [¹²³I]iomazenil SPECT studies and concluded that this method produced significant errors that made it unsuitable for clinical practice (Seike et al., 2004). However, the blood sample that Seike and colleagues used to scale PBIF was arbitrarily chosen at 30 minutes after injection, which may not have provided the optimum calibration time; rather, the blood sample(s) that best predict(s) AUC of the input function would yield the best estimate. Moreover, Seike and colleagues used only one blood sample to scale the PBIF, whereas a combination of two samples would be expected to provide more accurate and robust scaling than a single sample, as shown in the present study and several others (Meyer et al., 2006; Takikawa et al., 1994; Takikawa et al., 1993). By averaging two samples at the ends of the tail of the input function, PBIF can compensate for variation in the slope of the curves. In fact, Seike and colleagues noticed a significant improvement in their results when scaling was performed by adding a second late blood sample (Seike et al., 2004).

From our relatively large sample of 51 subjects for prospective validation, we had three subjects with substantial V_T/f_P errors estimated using PBIF. These errors were caused by outlying measurement of one of the two samples used to scale PBIF. No previous PBIF studies reported a similar problem. This may be because our population was larger than that of most other studies, or because at late time points the measurement of ¹¹C can be less accurate than the longer-lived ¹⁸F. Notably, these outliers were not due to intrinsic limitations associated with PBIF technique (e.g. a different curve shape in some subjects), but were due to problems that would be encountered with any technique that estimates the input function using such a limited number of blood samples. Several methods of PBIF (Vriens et al., 2009; Wakita et al., 2000), IDIF (Berradja et al., 2009; Naganawa et al., 2005), simultaneous estimation of the input function (Jouvie et al., 2011; Ogden et al., 2010), and bolus/constant infusion (Kimura et al., 2012) methods that rely on a single blood sample have been proposed. However, if the assay result for that single blood sample is inaccurate, the whole estimated input function will be wrong. Our study suggests that adding one or two more blood samples would increase the robustness of these methods without increasing invasiveness, given that an arterial line is already in place.

One drawback commonly attributed to PBIF is that the average shape obtained from a given population may not apply to other populations with different clinical conditions or physiological characteristics. To date, the few existing studies that evaluated the PBIF approach had not adequately addressed this issue. In such studies, a population of patients was typically halved, and a PBIF obtained from the first half was applied to the second (Takagi et al., 2004; Takikawa et al., 1993; Tsuchida et al., 1999). Moreover, PBIFs were often calculated by mixing data from healthy subjects and patients with various and heterogeneous diseases (Iida et al., 1994; Takagi et al., 2004; Takikawa et al., 1993). Only few studies applied PBIF from healthy subjects to patients (Seike et al., 2004); however, the number of patients was small and the studies did not report whether the shape of the input functions actually differed between the two groups.

In this study, we demonstrated that a PBIF from a population of healthy subjects could be applied to a sample of depressed MDD subjects with excellent results. To further test the robustness of the method, we selected two subsamples (of 15 subjects each) with very different shapes (i.e. one with “flatter” and one with “steeper” curves) of the input function, as compared to the shape of the PBIF. In both cases, the PBIF yielded very reliable results (Table 4). It is important to understand that precise estimation of the shape of the input function is not essential for PBIF. That is, V_T values calculated with the Logan graphical analysis are accurate as long as the AUC is correctly estimated. For this reason, blood samples used to scale the PBIF should be selected based on their correlation with AUC, for example using a Pearson’s correlation test.

Another potential drawback of PBIF is that it may not be a suitable technique for all types of intra-subject longitudinal studies (test-retest studies, studies involving the administration of pharmacological challenge drugs or displacement agents), since the shape of the PBIF would remain constant for a given subject. This is certainly true if a non-invasive scaling (e.g. BSA, LBM) is used. In this case, the retest analysis would have the same low reliability of a simple brain SUV comparison, because the amplitude of the estimated input function would change only as a function of the injected activity. In contrast, scaling with blood samples largely accounts for intra-individual differences in tracer metabolism. Indeed, our study shows that PBIF gives very similar retest variability and ICC values as compared to arterial sampling and IDIF. It should be noted that, using serial sampling, retest variability of V_T values is quite high (about 15%). Possible causes that may contribute to this high variability are: measurement errors, physiological changes in the [¹¹C](R)-rolipram target itself (phosphodiesterase-4) and the relatively low temporal resolution used for arterial sampling and tissue time-activity curves.

The present study also prospectively tested the IDIF method we previously validated on an HRRT using a low-resolution machine. Indeed, it has been shown that the same method applied to the same tracer but with different machines may yield different results (Mourik et al., 2008a; Mourik et al., 2008b). We found that, despite the lower spatial resolution of the PET camera used in the present study, the results were very accurate. This is largely due to the fact that this IDIF method relies on some blood samples to estimate the input function by linear least square analysis. Therefore, it is relatively insensitive to noise and partial volume effects. In addition, when IDIF is applied to neuroreceptor tracers, some blood samples are unavoidable because the radioactivity of the parent must be separated from that of its radiometabolites (Zanotti-Fregonara et al., 2011a). In contrast to our PBIF results, the IDIF portion of our study had no major outliers - i.e., error >20%. The most likely reason is that IDIF used four blood samples, whereas PBIF used two or three. The greater number of samples may also explain the marginally more accurate results obtained with IDIF compared to PBIF (Table 5).

Finally, using both PBIF and IDIF, we were able to demonstrate a widespread decrease in [¹¹C](R)-rolipram binding in depressed patients as compared to healthy subjects, proving that the clinical results obtained with full arterial input function (Fujita et al., 2012) can be obtained using either technique.

In summary, both PBIF and IDIF yielded reliable and comparable results. The PBIF approach holds the technical advantages of reducing the investigator time required for image processing and of being operator independent. Nevertheless, both the PBIF and IDIF approaches require some arterial blood samples. To avoid arterial cannulation, we also assessed whether arterial samples could be substituted with venous samples. However, we found that the kinetics of [¹¹C](R)-rolipram in arterial plasma differ substantially from those in venous plasma for at least 30–40 minutes after injection. Even at the end of the scan, we observed high inter-individual variability, with differences in parent concentrations as high as 20–30% between the artery and the vein. As regards [¹¹C](R)-rolipram in particular, the reasons for such variability are unknown. Nevertheless, differences in arteriovenous concentrations of drugs and molecules are common (Chiou, 1989a, b). Specifically, arterial concentrations are higher than venous concentrations soon after tracer injection due to sampling tissue uptake. When there is no net tissue uptake, a transient equilibrium phase is reached in which no arteriovenous difference exists. In addition, during the terminal phase when arterial concentrations progressively decrease, the drug retained by the sampling tissue begins to diffuse through the capillary wall into the venous blood, resulting in higher venous concentrations (Chiou, 1989a). Thus, venous samples can be substituted for arterial samples only when obtained during the transient equilibrium phase. Notably, the time when this equilibrium is reached differs for each tracer and depends on several factors such as the efficiency of the initial uptake by the sampling tissue, the chemical composition of the drug, the degree of plasma protein binding, and the local blood flow (Chiou, 1989a). With few exceptions (Chen et al., 1998; Hahn et al., 2012; Ito et al., 1995), attempts at using venous samples with radiotracers have proven disappointing due to the lack of a suitable equilibrium (Greuter et al., 2011; Zanotti-Fregonara et al., 2012b). Two approaches that have been proposed for overcoming the arteriovenous differences have been “arterialization” of the venous blood through heating (Phelps et al., 1979) or sampling from a hand vein, where the blood may be more similar to arterial blood than that obtained from the antecubital vein (Ito et al., 1995). Unfortunately, neither of these techniques worked for [¹¹C](R)-rolipram. It should also be noted that sampling from the hand is technically challenging, because hand veins are relatively small and often collapse after repeated blood sampling.

In summary, arterial plasma sampling cannot be avoided for [¹¹C](R)-rolipram studies. However, even if PBIF and IDIF do not translate into a less invasive procedure for the patient, they have several advantages over full arterial sampling. First, a significant reduction in the number of arterial blood samples increases the number of scans that can be performed daily in facilities like ours, where personnel required to analyze the blood samples are capacity-limiting. Second, fewer persons are necessary to acquire the input function, because the early rapid phase is estimated. Third, even if some centers use a continuous on-line sampling machine, manual samples are still needed for radiometabolite correction. However, when Logan-V_T is the parameter of interest, the same manual samples that must be taken for metabolite analysis can be used to estimate IDIF or PBIF, thus effectively replacing the on-line machine. Fourth and last, a reduced number of blood samples minimizes radiation exposure to the personnel. Eberl and colleagues showed a dose reduction of 84% with [¹⁸F]FDG PBIF as compared to full sampling (Eberl et al., 1997).

Conclusion

Although some arterial plasma samples are still necessary, both the PBIF and IDIF approaches provide accurate and precise alternatives to the full arterial input function for [¹¹C](R)-rolipram PET studies, even in a test-retest setting. Both techniques reliably measure V_T/f_P for groups of subjects with different clinical conditions and with very different shapes of the input function.

Highlights.

PBIF and IDIF are equivalent to arterial sampling for [¹¹C](R)-rolipram studies

PBIF obtained from healthy subjects can be used for depressed patients

PBIF can successfully be applied to a test-retest study

IDIF and PBIF showed a decrease in [¹¹C](R)-rolipram binding in depressed subjects